② 中国石化胜利油田分公司勘探开发研究院, 山东东营 257015
② Research Institute of Exploration & Development, Sinopec Shengli Oilfield, Dongying Shandong 257015, China
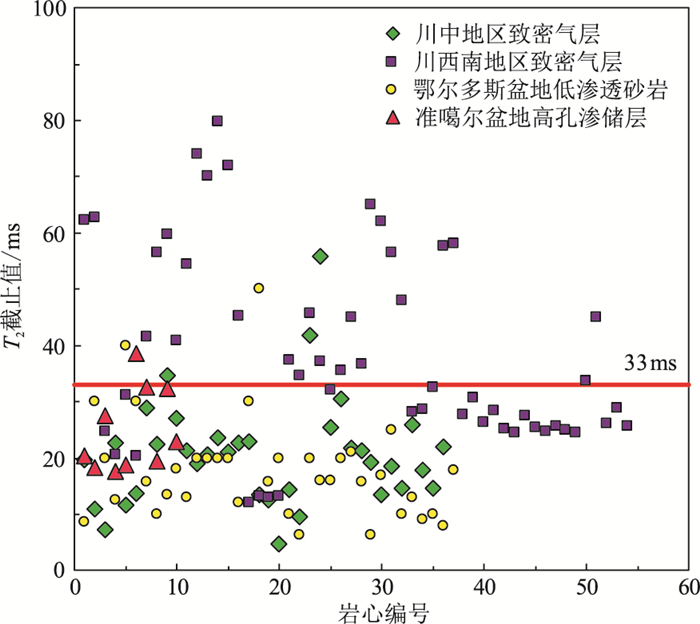
核磁共振测井作为一种能够直接提供储层孔隙大小及其分布信息的测井方法,在复杂油气藏勘探开发中发挥着越来越重要的作用[1-2]。通过对核磁共振T2谱进行处理和解释,能够获取反映储层总孔隙度、有效孔隙度、束缚水饱和度、可动流体饱和度以及渗透率等参数[3-5]。在实际处理、评价中,为了准确计算上述参数,需要首先确定核磁共振T2截止值[6-7]。T2截止值是核磁共振T2谱上束缚流体和可动流体的T2分界值[8-9],利用该值可将岩石的孔隙空间划分为大孔隙和小孔隙两个部分。核磁共振T2谱上弛豫时间小于T2截止值的T2谱包围的区域反映小孔隙束缚流体体积,而弛豫时间大于T2截止值的那部分T2谱包围的区域则反映可动流体所占的体积,并将束缚流体体积与总T2谱所包围区域的比值定义为束缚水饱和度[10]。T2截止值选取方式主要有固定T2截止值和可变T2截止值两种。固定T2截止值是指在某一地区或某一层位,选择固定不变的T2截止值对整个地层的核磁共振T2谱进行解释,进而计算束缚水饱和度和渗透率等[11]。对于固定T2截止值的选取,目前各大油田和测井公司主要借用美国墨西哥湾低渗透砂岩和碳酸盐岩的实验结果,碎屑岩地层取值为33.0ms,碳酸盐岩地层取值为92.0ms[12-14]。然而中国各油田不同类型地层的岩心核磁共振实验和实际资料处理结果表明,碎屑岩地层的T2截止值取33.0ms明显偏高,利用其进行储层解释时,容易将部分大孔隙可动流体误判为束缚流体,低估实际地层的生产潜力[7]。同时,对于非均质性相对较强的低渗透—致密砂岩地层,核磁共振T2截止值并非一个固定值,而是发散的量(图 1),如果始终采用单一固定的T2截止值对储层进行解释,势必得出错误的结果。
|
图 1 中国不同地区、不同类型油气藏岩心实验的核磁共振T2截止值统计[8] |
针对选取单一固定T2截止值进行储层解释时存在的诸多问题,学者们提出采用变化的T2截止值计算束缚水饱和度。吴丰等[15]根据储层岩性差异将地层划分为四种类型,对每一种岩性的地层分别选取不同的T2截止值对储层进行评价。Parra等[16]和刘蝶[17]分别采用流动单元指数和综合物性指数对储层进行分类,每一类储层分别选用各自的T2截止值计算束缚水饱和度。随后针对同一种岩性或同一类型的地层,进一步考虑地层埋深、流体性质等因素对T2截止值的影响,针对不同类型、不同埋深的地层,选取可变的T2截止值。高楚桥等[18]建立了T2截止值与油柱高度之间的相关关系;汪中浩等[19]基于岩心实验结果,建立了T2截止值与综合物性指数之间的统计关系;邵维志等[20]针对不同类型的核磁共振T2谱,分别确定出各自对应的T2截止值。上述方法为复杂储层核磁共振评价提供了新的思路。然而,这些方法都是基于岩心实验基础上的一种经验统计方法,其适用性受到限制,无法大规模推广应用。
为了提高核磁共振测井在复杂储层束缚水饱和度评价中的精度,本次研究对21块砂砾岩岩心核磁共振实验结果进行了分析,根据饱含水状态核磁共振T2谱的形态对其进行分类,提出了采用正态分布函数拟合出离心束缚水(或大孔隙可动水)状态的核磁共振T2谱,在此基础上,建立了一种基于核磁共振T2谱形态特征差异的可变T2截止值计算方法。
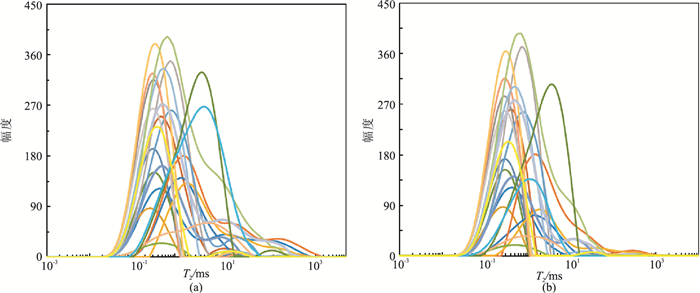
2 岩心核磁共振实验及核磁T2谱形态特征分析 2.1 岩心核磁共振实验选取准噶尔盆地西北缘5口井二叠系佳木河组21块砂砾岩岩心,分别开展饱含水和离心束缚水状态的核磁共振实验,表 1记录了实验结果,相应的饱含水及离心束缚水状态核磁共振T2谱如图 2所示。由常规岩心分析可知,研究目标区域的孔隙度介于1.18%~24.99%,平均孔隙度为12.15%;渗透率介于0.01~57.20mD,平均渗透率为0.14mD,属于典型的致密砂砾岩储层。核磁共振实验得到饱含水状态核磁共振T2谱主要分布范围为0.03~100.00ms,且以短T2弛豫组分为主;离心束缚水状态核磁共振T2谱主要分布在0.03~10.00ms,表明岩石的孔隙结构整体较差。
|
|
表 1 准噶尔盆地西北缘二叠系佳木河组21块砂砾岩岩心核磁共振实验结果 |
|
图 2 21块岩心饱含水状态(a)和离心束缚水状态(b)核磁共振T2谱 |
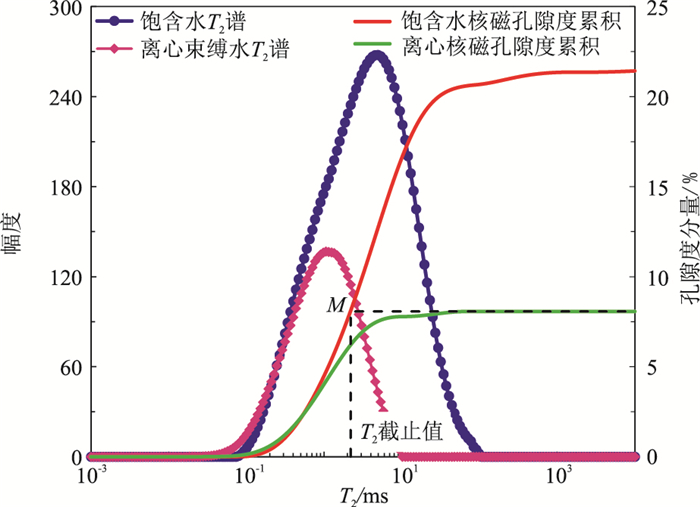
基于岩心核磁共振实验结果,分别确定每一块样品的T2截止值,步骤如下:首先,将同一岩心饱含水和离心束缚水状态的核磁共振T2谱展示于同一张图上;然后,分别将饱含水和离心束缚水状态的核磁共振T2谱的幅度按照T2弛豫时间从小到大的顺序逐次累加,得到两种状态的核磁孔隙度累积曲线;之后,过离心束缚水状态的核磁孔隙度累积曲线做一条平行于T2弛豫时间轴的直线,该直线与饱含水状态的核磁孔隙度累积曲线交于点M;最后,过交点M做一条垂直于T2弛豫时间轴的直线,该直线与T2弛豫时间轴的交点所对应的弛豫时间,即为T2截止值。利用岩心核磁共振实验确定T2截止值的原理和方法如图 3所示。
|
图 3 利用岩心核磁共振实验确定T2截止值原理图 |
按照上述方法,计算了21块砂砾岩岩心的核磁共振T2截止值,并做岩心T2截止值(图 4a)及相应的束缚水饱和度统计图(图 4b)。由图可见,研究区致密砂砾岩储层的核磁共振T2截止值极低,除极个别岩心外,大部分低于3.0ms,且其取值是不固定的发散量值。相应岩石的束缚水饱和度介于55.0%~95.0%,平均束缚水饱和度达到78.35%。此时,如果仍然采用传统的T2截止值计算束缚水饱和度并识别优质储层,势必得出错误的结果。

|
图 4 准噶尔盆地西北缘二叠系佳木河组岩心核磁共振T2截止值(a)和束缚水饱和度(b)统计结果 |
为了研究不同类型岩心核磁共振T2谱的响应规律,基于饱含水状态测量的核磁共振T2谱的峰值个数、主峰位置及所反映的岩石孔隙结构差异,将21块岩心核磁共振T2谱划分为五种类型,分别为单峰小孔型、单峰大孔型、双峰小孔型、双峰大孔型及三峰型。具体定义如下:
单峰小孔型:核磁共振T2谱为单峰,主峰位置相对靠左,且主峰对应的T2弛豫时间小于3.0ms。
单峰大孔型:核磁共振T2谱为单峰,主峰位置相对靠右,且主峰对应的T2弛豫时间大于3.0ms。
双峰小孔型:核磁共振T2谱为双峰,T2谱以短T2弛豫分布为主,且主峰对应的T2弛豫时间小于3.0ms。
双峰大孔型:核磁共振T2谱为双峰,T2谱以长T2弛豫分布为主,且主峰对应的T2弛豫时间大于3.0ms。
三峰型:核磁共振T2谱为三峰。
基于上述分类方法,得到五类岩石典型核磁共振T2谱形态特征图(图 5)。由图可见:①对于所有的岩心样品,离心束缚水状态核磁共振T2谱主峰对应的T2弛豫时间均小于3.0ms,T2谱的形态近似于一个标准的正态分布,且该正态分布收敛于10.0ms。②对于孔隙结构极差、几乎无大孔隙空间的单峰小孔型岩石,饱含水状态的核磁共振T2谱主要分布在0.03~10.00ms,且其形态与离心束缚水状态的T2谱基本重合(图 5a)。③对于孔隙结构相对较好、有一定大孔隙空间的岩石,饱含水状态的核磁共振T2谱主要分布在0.03~100.00ms(图 5b~图 5d);对于孔隙结构最好、大孔隙组分占比最高的岩石,饱含水状态的核磁共振T2谱主要分布在0.03~1000.00ms(图 5e)。④五种类型岩石的饱含水状态核磁共振T2谱的形态近似于一个或多个正态分布的叠加。对于单峰型核磁共振T2谱,其形态近似于一个标准的正态分布;对于双峰型或三峰型核磁共振T2谱,其形态可看成是两个或三个正态分布的叠加。⑤离心束缚水状态核磁共振T2谱与饱含水状态核磁共振T2谱的起始位置基本重合,且对于双峰型或三峰型岩石而言,两种状态核磁共振T2谱的左边第一个峰基本重合。

|
图 5 五种类型岩心核磁共振T2谱形态特征对比 (a)单峰小孔型;(b)单峰大孔型;(c)双峰小孔型;(d)双峰大孔型;(e)三峰型 |
要准确计算岩石的T2截止值,必须测量出饱含水和离心束缚水两种状态的核磁共振T2谱。这两个数据在实验室岩心实验阶段比较容易取得。然而,实际核磁共振测井中,只能获得饱含流体状态的核磁共振T2谱,无法测量得到离心束缚水状态的T2谱。导致无法直接应用图 3所示方法确定T2截止值进而计算出束缚水饱和度和渗透率。为了利用实测核磁共振测井确定连续准确的T2截止值,必须设法得到离心束缚水状态的核磁共振T2谱。
如图 5所示,除单峰大孔型岩石外,其他类型的岩石离心束缚水状态核磁共振T2谱的形态近似于一个标准的正态分布,且其幅度和位置与饱含水状态核磁共振T2谱上左边第一个峰基本重合。因此,本文提出采用正态分布函数,从饱含水状态的核磁共振T2谱中拟合出束缚水状态核磁共振T2谱,并利用拟合的T2谱代替实际岩心实验的束缚水状态T2谱确定T2截止值,将会得到准确的结果。
3.1 正态分布函数| $ f\left( x \right) = {\rm{A}} \times {{\rm{e}}^{ - \frac{{{{\left( {x - \mu } \right)}^2}}}{{2{\sigma ^2}}}}} $ | (1) |
式中:f(x)为拟合的离心状态核磁共振T2谱的幅度;A为饱含水状态核磁共振T2谱上左边第一个峰的幅度值;x为进行正态分布拟合时设定的T2弛豫时间;μ为数学期望值,其数值决定了拟合的正态分布函数的位置,在利用正态分布函数拟合离心束缚水状态核磁共振T2谱时,μ的取值为饱含水状态核磁共振T2谱上左边第一个峰所对应的T2弛豫时间。σ为方差,决定了正态分布曲线的宽度。
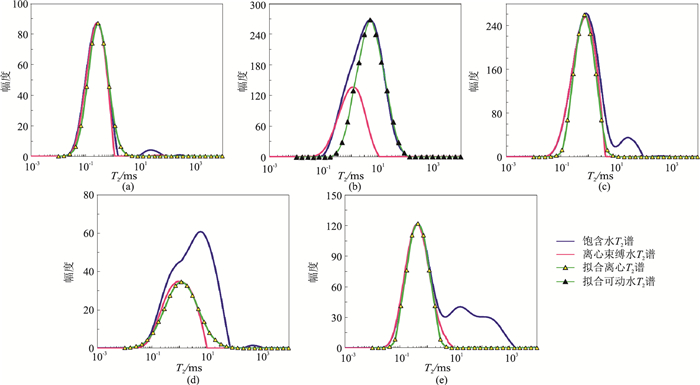
利用图 6所示方法在饱含水状态核磁共振T2谱上自动搜索出正态分布拟合函数中输入参数A、μ和σ的值。结合式(1),即可从饱含水状态的核磁共振T2谱中拟合出离心束缚水状态T2谱(图 7a、图 7c~7e)。

|
图 6 利用饱含水状态核磁共振T2谱确定正态分布函数中的输入参数 |
|
图 7 不同类型岩心基于正态分布函数拟合的离心(可动水)T2谱与岩心核磁共振实验T2谱形态对比 (a)单峰小孔型;(b)单峰大孔型;(c)双峰小孔型;(d)双峰大孔型;(e)三峰型 |
然而对于单峰大孔型岩石,饱含水状态核磁共振T2谱主要反映大孔隙部分可动流体的弛豫性质,离心束缚水状态核磁共振T2谱的主峰位置对应于饱含水状态核磁共振T2谱的左翼(图 7b),由于两者主峰位置差异,导致无法直接采用正态分布函数拟合出离心束缚水状态的核磁共振T2谱。对于这种类型的岩石,可以采用正态分布函数拟合出大孔隙可动流体部分的T2谱,再求得饱含水和拟合可动水部分的核磁共振T2谱之间的差异,即反映岩石束缚流体弛豫性质。
3.2 正态分布拟合效果根据饱含水状态核磁共振T2谱的形态对21块岩心进行分类,在此基础上利用式(1)对其进行拟合处理。对于单峰大孔型岩石,拟合出可动水T2谱;对于其他类型的岩石,直接拟合出离心束缚水状态的核磁共振T2谱。将拟合结果与实验室岩心测量的结果进行对比(图 7),可见,除了单峰大孔型岩石外(图 7b),其他采用正态分布函数拟合的离心束缚水状态核磁共振T2谱与岩心实验的束缚水T2谱基本重合。图 7b中拟合可动水T2谱的右翼与饱含水状态核磁共振T2谱的右翼基本重合,左翼部分则明显存在差异,这部分差异主要反映了小孔隙部分饱含束缚水的核磁共振弛豫性质。
3.3 束缚水饱和度评价从图 7对比结果可以看到,采用正态分布函数能够从饱含水状态核磁共振T2谱中拟合出离心束缚水(或可动水)T2谱,方法可靠。利用拟合的T2谱代替实际岩心实验结果,即可实现在只进行饱含水状态核磁共振实验的情况下,采用图 3所示方法确定岩石的T2截止值,并利用以下公式求取岩石的束缚水饱和度。
对于单峰大孔型岩石,为
| $ {S_{{\rm{wi}}}} = 100 - \frac{{\int_{{T_{{\rm{2min}}}}}^{{T_{{\rm{2max}}}}} {S{'} ({T_2}){\rm{d}}{T_2}} }}{{\int_{{T_{{\rm{2min}}}}}^{{T_{{\rm{2max}}}}} {S({T_2}){\rm{d}}{T_2}} }} \times 100 $ | (2) |
对于其他类型岩石,为
| $ {S_{{\rm{wi}}}} = \frac{{\int_{{T_{{\rm{2min}}}}}^{{T_{{\rm{2max}}}}} {S''({T_2}){\rm{d}}{T_2}} }}{{\int_{{T_{{\rm{2min}}}}}^{{T_{{\rm{2max}}}}} {S({T_2}){\rm{d}}{T_2}} }} \times 100 $ | (3) |
式中:Swi为束缚水饱和度;T2min和T2max分别为最小和最大横向T2弛豫时间;S(T2)为饱含水状态核磁孔隙度分布函数;S′(T2)为采用正态分布函数拟合的大孔隙可动水部分核磁孔隙度分布函数; S′′(T2) 为采用正态分布函数拟合的小孔隙束缚水部分核磁孔隙度分布函数。
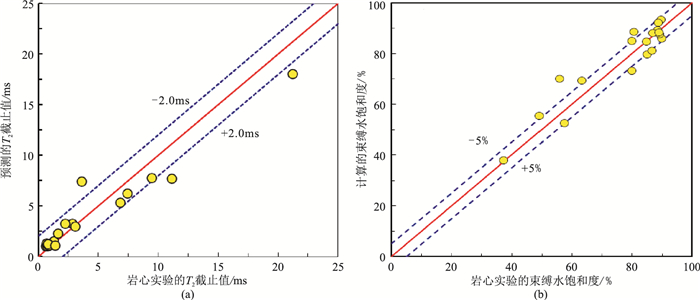
3.4 精度验证按照上述原理方法拟合出束缚水状态核磁共振T2谱和大孔隙可动水部分T2谱,利用式(2)、式(3)计算得到T2截止值和束缚水饱和度,并将计算结果与岩心实验结果进行对比(图 8),以验证本文方法的可靠性。图中红色实线为45°对角线,反映计算结果和岩心实验结果之间的一致性,数据越靠近对角线,表明二者之间的一致性越好。蓝色虚线为统计的计算结果与岩心实验结果之间的误差限。对比结果显示,绝大多数数据点落在45°对角线附近,表明采用本文方法确定的T2截止值及束缚水饱和度与岩心实验结果之间具有很好的一致性。利用基于正态分布函数拟合方法确定的T2截止值与岩心实验的T2截止值之间的绝对误差小于2.0ms。相应的两种束缚水饱和度之间的绝对误差基本控制在±5.0%范围之内。这充分证明基于本文方法能够比较准确地确定致密砂砾岩储层的T2截止值,并能准确计算储层的束缚水饱和度。将该方法推广到实际地层,即可从实际测量的核磁共振测井资料中确定随地层深度变化的可变T2截止值,并进一步计算出可靠的束缚水饱和度。该方法对于提高致密砂砾岩储层的流体性质判别准度具有重要意义。
|
图 8 利用本文方法计算的T2截止值(a)和束缚水饱和度(b)与岩心实验结果的对比 |
除计算储层孔隙度和束缚水饱和度外,核磁共振测井在渗透率评价方面也具有无可比拟的独特优势[23-25]。目前,利用核磁共振测井估算储层渗透率的经典模型包括Timur-Coates模型(简称Timur模型)和SDR(Schlumberger Doll Research Center)模型。其中,Timur模型认为储层渗透率与孔隙度呈正比,与束缚水饱和度呈反比。Timur模型的数学表达式为[26-29]
| $ {\rm{KTIM}} = {\left( {\frac{\phi }{C}} \right)^m} \times {\left( {\frac{{100 - {S_{{\rm{wi}}}}}}{{{S_{{\rm{wi}}}}}}} \right)^n} $ | (4) |
式中:KTIM为利用Timur模型计算的渗透率;ϕ为储层核磁孔隙度;C、m和n为模型中的待定系数,其值通过岩心数据得到。
本次研究利用表 1所示21块岩心核磁共振实验数据,标定Timur模型中C、m和n的值分别为7.25、1.21和1.56,得到相应的渗透率评价模型公式
| $ {\rm{KTIM}} = {\left( {\frac{\phi }{{7.25}}} \right)^{1.21}} \times {\left( {\frac{{100 - {S_{{\rm{wi}}}}}}{{{S_{{\rm{wi}}}}}}} \right)^{1.56}} $ | (5) |
利用可变的T2截止值计算出束缚水饱和度后,即可由式(5)连续求取砂砾岩储层的渗透率。同时,利用上式模型计算渗透率的准确程度,从侧面验证了基于正态分布函数拟合方法计算可变T2截止值的可靠性。
4 应用实例分析利用本文研究建立的方法模型,对准噶尔盆地西北缘沙湾凹陷二叠系佳木河组实际测量的核磁共振测井资料进行了处理。首先,根据实测核磁共振测井T2谱的形态进行分类,在此基础上采用正态分布函数分别拟合出离心束缚水状态核磁共振T2谱或大孔隙可动流体T2谱(针对单峰大孔型地层),以确定随地层深度变化的可变T2截止值,并求取地层的束缚水饱和度和渗透率。将可变T2截止值、束缚水饱和度及渗透率与相应深度的岩心实验结果进行对比,结果如图 9所示。从对比结果可以看出,二者均具有很好的一致性,说明本文方法能够很好地推广到实际地层,从实测核磁共振测井资料中得到可靠的束缚水饱和度和渗透率。根据处理结果,2127.0~2132.5m、2135.0~2156.5m及2163.9~2171.8m三个井段计算的束缚水饱和度低于60.0%,渗透率大于0.5mD,结合研究区储层物性下限[30],综合判断为油气层。判别结果得到了试油资料的证实,2138.0~2142.0m和2164.0~2170.0m井段的联合试油结果日产油221.04t、日产天然气1.054×104m3,为高产油气层。证明了本文方法在计算可变T2截止值、估算束缚水饱和度和渗透率,以及判别复杂储层流体性质等方面的有效性。

|
图 9 基于本文方法确定的可变T2截止值、束缚水饱和度及渗透率与岩心实验结果对比 图中第一道显示自然伽马(GR)、自然电位(SP)和井径(CALI)曲线,用以指示地层的岩性和划分渗透层;第二道显示深度;第三道显示声波时差(AC)、体积密度(DEN)和中子(CNL)曲线,参与计算地层孔隙度;第四道包含了深、中、浅电阻率曲线,分别测量了原状地层(Rt)、过渡带(Ri) 和冲洗带(Rxo)的电阻率,用以指示储层的流体性质;第五道显示气测曲线(TGAS),用以辅助判别储层的流体性质;第六道中TASPEC为采用MRIL-P型仪器测量的核磁共振测井T2谱,红色曲线为采用本文方法计算的随地层深度变化的可变T2截止值,蓝色杆状为4块岩心核磁共振实验的T2截止值;第七道显示利用可变T2截止值计算的束缚水饱和度(SWIRR)和岩心实验获取的束缚水饱和度(CSWI);第八道显示基于Timur模型计算的渗透率(KTIM)与岩心实验的渗透率(CPERM)。 |
(1) 本文提出一种基于核磁共振T2谱形态特征差异的可变T2截止值计算方法。首先对21块实验岩心不同饱和状态的核磁共振T2谱形态进行分析,在此基础上将饱含水状态的核磁共振T2谱划分为五类,针对每种类型采用正态分布函数分别拟合出离心束缚水状态或大孔隙可动水部分(针对单峰大孔型岩石)的T2谱。利用拟合的T2谱代替岩心实验的核磁共振T2谱,可从饱含水状态核磁共振T2谱中确定T2截止值,并进一步计算得到束缚水饱和度和渗透率。
(2) 将本文方法推广到准噶尔盆地西北缘二叠系致密砂砾岩储层,实现了从实测核磁共振测井T2谱中连续确定随地层深度变化的可变T2截止值,进而得到储层的束缚水饱和度和渗透率。计算结果与岩心实验结果之间具有较高的一致性,验证了本文方法的可靠性。结合计算的束缚水饱和度和渗透率参数,可准确判断目标储层的含油气潜力。
| [1] |
谭茂金. 油气藏核磁共振测井理论与应用[M]. 北京: 科学出版社, 2017. TAN Maojin. Theory and Application of NMR Logging in Oil and Gas Reservoirs[M]. Beijing: Science Press, 2017. |
| [2] |
孟祥宁. 致密砂岩储层核磁共振测井评价方法[M]. 北京: 中国石化出版社, 2019. MENG Xiangning. NMR Logging Evaluation Method for Tight Sandstone Reservoir[M]. Beijing: China Petrochemical Press, 2019. |
| [3] |
肖立志, 谢然红, 廖广志. 中国复杂油气藏核磁共振测井理论与方法[M]. 北京: 科学出版社, 2012. XIAO Lizhi, XIE Ranhong, LIAO Guangzhi. Theory and Method of NMR Logging for Complicated Oil and Gas Reservoirs in China[M]. Beijing: Science Press, 2012. |
| [4] |
刘卫, 肖忠祥, 杨思玉, 等. 利用核磁共振(NMR)测井资料评价储层孔隙结构方法的对比研究[J]. 石油地球物理勘探, 2009, 44(6): 773-778. LIU Wei, XIAO Zhongxiang, YANG Siyu, et al. Comparative studies on methods of evaluation of re-servoir pore structure by using NMR (nuclear magne-tic resonance) well logging data[J]. Oil Geophysical Prospecting, 2009, 44(6): 773-778. DOI:10.3321/j.issn:1000-7210.2009.06.022 |
| [5] |
张超. 利用核磁共振T2谱计算致密砂岩储层渗透率新方法[J]. 测井技术, 2018, 42(5): 550-556. ZHANG Chao. A new method for calculating permeability of tight sandstone reservoir by using NMR T2 spectrum[J]. Well Logging Technology, 2018, 42(5): 550-556. |
| [6] |
张伟, 万钧, 吴意明, 等. 基于多元统计的核磁共振测井可变T2截止值预测模型[J]. 核电子学与探测技术, 2020, 40(1): 193-199. ZHANG Wei, WAN Jun, WU Yiming, et al. Prediction of nuclear magnetic resonance (NMR) T2 cutoff based on multivariate statistical method[J]. Nuclear Electronics & Detection Technology, 2020, 40(1): 193-199. DOI:10.3969/j.issn.0258-0934.2020.01.037 |
| [7] |
匡立春, 毛志强, 孙中春, 等. 核磁共振测井技术在准噶尔盆地油气勘探开发中的应用[M]. 北京: 石油工业出版社, 2015. KUANG Lichun, MAO Zhiqiang, Sun Zhongchun, et al. Application of NMR in Junggar Basin Exploration and Development[M]. Beijing: Petroleum Industry Press, 2015. |
| [8] |
Xiao L, Li J R, Mao Z Q, et al. A method to determine nuclear magnetic resonance (NMR) T2 cutoff based on normal distribution simulation in tight sandstone reservoirs[J]. Fuel, 2018, 225(8): 472-482. |
| [9] |
Ge X M, Fan Y R, Zhu X J, et al. Determination of nuclear magnetic resonance T2 cutoff value based on multifractal theory: An application in sandstone with complex pore structure[J]. Geophysics, 2015, 80(1): D11-D21. DOI:10.1190/geo2014-0140.1 |
| [10] |
Cao G, Hou J G, Zou J Y, et al. The reservoir para-meter calculation method using the nuclear magnetic resonance log data[C]. 11th International Conference on Natural Computation (ICNC), 2015, 588-593.
|
| [11] |
Xiao L, Mao Z Q, Jin Y. Calculation of irreducible water saturation (Swirr) from NMR logs in tight gas sands[J]. Applied Magnetic Resonance, 2012, 42(1): 113-125. DOI:10.1007/s00723-011-0273-x |
| [12] |
Straley C, Morriss C E, Kenyon W E, et al. NMR in partially saturated rocks: laboratory insights on free fluid index and comparison with borehole logs[C]. 32nd Annual SPWLA Logging Symposium Transactions, 1991, 1-25.
|
| [13] |
Staley C. Magnetic resonance digital image analysis and permeability of porous media[J]. Applied Physics Letter, 1987, 51(15): 1146-1148. DOI:10.1063/1.98766 |
| [14] |
Morriss C E, Maclnnis J, Freedman R, et al. Field test of an experimental pulsed nuclear magnetism tool[C]. 34th Annual SPWLA Logging Symposium Transactions, 1993, 1-23.
|
| [15] |
吴丰, 司马立强, 杨洪明, 等. 柴西地区复杂岩性核磁共振T2截止值研究[J]. 测井技术, 2014, 38(2): 144-149. WU Feng, SIMA Liqiang, YANG Hongming, et al. Research on NMR T2 cutoff of complex lithology in the west Qaidam Basin[J]. Well Logging Technology, 2014, 38(2): 144-149. |
| [16] |
Parra J O, Hackert C L, Collier H A, et al. NMR and acoustic signatures in vuggy carbonate aquifers[C]. 42nd Annual SPWLA Logging Symposium Transacting, 2001, 1-11.
|
| [17] |
刘蝶. 核磁共振在低渗透砂岩低对比度油层成因分析及评价中的应用[D]. 北京: 中国地质大学(北京), 2020, 1-73. LIU Die. Application of Nuclear Magnetic Resonance in Genesis Analysis and Recognition of Low Permeability and Low Contrast Oil Layers[D]. China University of Geosciences (Beijing), 2020, 1-73. |
| [18] |
高楚桥, 何宗斌, 吴洪深, 等. 核磁共振T2截止值与毛细管压力的关系[J]. 石油地球物理勘探, 2004, 39(1): 117-120. GAO Chuqiao, HE Zongbin, WU Hongshen, et al. Relationship between NMR T_2 cutoff and capillary pressure[J]. Oil Geophysical Prospecting, 2004, 39(1): 117-120. DOI:10.3321/j.issn:1000-7210.2004.01.022 |
| [19] |
汪中浩, 章成广, 肖承文, 等. 低渗透储层T2截止值实验研究及其测井应用[J]. 石油物探, 2004, 43(5): 508-510. WANG Zhonghao, ZHANG Chengguang, XIAO Chengwen, et al. T2 cutoff value in low-permeability reservoirs and its application[J]. Geophysical Prospecting for Petroleum, 2004, 43(5): 508-510. DOI:10.3969/j.issn.1000-1441.2004.05.022 |
| [20] |
邵维志, 丁娱娇, 肖斐, 等. 利用T2谱形态确定T2截止值的方法探索[J]. 测井技术, 2009, 33(5): 430-435. SHAO Weizhi, DING Yujiao, XIAO Fei, et al. On the method of determining T2 cutoff value with the T2 spectrum characteristics[J]. Well Logging Technology, 2009, 33(5): 430-435. DOI:10.3969/j.issn.1004-1338.2009.05.006 |
| [21] |
王谦, 谭茂金, 石玉江, 等. 径向基函数神经网络法致密砂岩储层相对渗透率预测与含水率计算[J]. 石油地球物理勘探, 2020, 55(4): 867-872. WANG Qian, TAN Maojin, SHI Yujiang, et al. Prediction of relative permeability and calculation of water cut of tight sandstone reservoir based on radial basis function neural network[J]. Oil Geophysical Prospecting, 2020, 55(4): 867-872. |
| [22] |
金昌昆, 王延光, 尚新民, 等. 微测井与方位加权插值精细近地表速度建模技术[J]. 石油地球物理勘探, 2020, 55(2): 257-265. JIN Changkun, WANG Yanguang, SHANG Xinmin, et al. Near-surface velocity modeling based on micro-log and azimuth-weighted interpolation[J]. Oil Geophysical Prospecting, 2020, 55(2): 257-265. |
| [23] |
Peng L, Zhang C, Ma H L, et al. Estimating irreducible water saturation and permeability of sandstones from nuclear magnetic resonance measurements by fractal analysis[J]. Marine and Petroleum Geology, 2019, 110(7): 565-574. |
| [24] |
Rezaee R, Saeedi A, Clennell B. Tight gas sands permeability estimation from mercury injection capillary pressure and nuclear magnetic resonance data[J]. Journal of Petroleum Science and Engineering, 2012, 88/89: 92-99. DOI:10.1016/j.petrol.2011.12.014 |
| [25] |
Mao Z Q, Xiao L, Wang Z N, et al. Estimation of permeability by integrating nuclear magnetic resonance (NMR) logs with mercury injection capillary pressure (MICP) data in tight gas sands[J]. Applied Magnetic Resonance, 2013, 44(4): 449-468. DOI:10.1007/s00723-012-0384-z |
| [26] |
Zhang H T, Li G R, Guo H P, et al. Applications of nuclear magnetic resonance (NMR) logging in tight sandstone reservoir pore structure characterization[J]. Arabian Journal of Geosciences, 2020, 13(12): 572. DOI:10.1007/s12517-020-05590-6 |
| [27] |
Wei D F, Liu X P, Hu X X, et al. Estimation of permeability from NMR logs based on formation classification method in tight gas sands[J]. Acta Geophysica, 2015, 63(5): 1316-1338. DOI:10.1515/acgeo-2015-0042 |
| [28] |
Lis-Śledziona A. Petrophysical rock typing and permeability prediction in tight sandstone reservoir[J]. Acta Geophysica, 2019, 67(6): 1895-1911. DOI:10.1007/s11600-019-00348-5 |
| [29] |
Marta H J, Ricardo I F T, Marsha F, et al. Nuclear magnetic resonance characterization of porosity preserving microcrystalline quartz coatings in Fontainebleau sandstones[J]. AAPG Bulletin, 2019, 103(9): 2117-2137. DOI:10.1306/01301918104 |
| [30] |
董雪梅, 胡婷婷, 霍进杰, 等. 统计法在确定卡拉麦里气田物性下限中的应用[J]. 新疆地质, 2011, 29(2): 242-245. DONG Xuemei, HU Tingting, HUO Jinjie, et al. Application of statistics method in determination lower bound of property in Kelameili gas field[J]. Xinjiang Geology, 2011, 29(2): 242-245. DOI:10.3969/j.issn.1000-8845.2011.02.026 |



 胡婷婷, 新疆乌鲁木齐市迎宾北一路27号中国石油新疆油田分公司勘探开发研究院地球物理研究所, 830013。Email:
胡婷婷, 新疆乌鲁木齐市迎宾北一路27号中国石油新疆油田分公司勘探开发研究院地球物理研究所, 830013。Email: 