② 海洋石油勘探国家工程实验室, 北京 100028;
③ 中国石油大学(华东)地球科学与技术学院, 山东青岛 266580
② National Engineering Laboratory for Offshore Oil Exploration, Beijing 100028, China;
③ School of Geosciences, China University of Petroleum(East China), Qingdao, Shandong 266580, China
近年来,潜山构造逐渐成为油气勘探的重要目标之一。潜山构造广泛分布于渤海、南海等地区的多个盆地。以渤海湾盆地潜山为例,继渤中19-6构造获得油气发现之后,其北又发现了渤中13-2亿吨级油气田,因此潜山呈现巨大的油气勘探潜力。
储层识别是潜山油气藏勘探的重点和难点之一[1-2]。渤中H构造潜山发育于盆地中深层,多期构造运动形成多期断裂,同时又受到风化溶蚀作用,潜山风化带内裂缝和孔隙均比较发育,是寻找优质储层的有利相带。裂缝既可以作为油气的储集空间,也可以作为油气运移通道,因此裂缝预测是潜山储层及油气评价的重点工作之一。
渤中H构造潜山裂缝多为近垂直高角度裂缝,且定向排列,基于等效介质理论可抽象为HTI介质。由于裂缝发育,导致HTI等效介质模型的弹性分界面处地震响应呈现方位各向异性。如何实现HTI介质方位各向异性的定量表征,是实现裂缝预测的必要手段。
方位反射系数特征方程是实现裂缝识别的理论基础。Rüger[3]利用Thomsen弱各向异性参数[4]表征、构建了HTI介质下的拟Thomsen参数,并利用纵、横波速度、密度实现了方位变化特征与地震响应之间的定量表达。Vavryuk等[5]同样利用纵、横波速度、密度和各向异性参数建立了任意各向异性介质方位反射系数近似方程。杜炳毅等[6]利用杨氏模量、泊松比与纵、横波速度的定量关系,结合Rüger近似方程表征形式,发展了杨氏模量、泊松比与各向异性梯度表征的方位反射系数近似方程。根据介质分解理论和扰动思想构建方位反射系数近似方程的可行性,Wu等[7]构建了TI介质岩石弹性模量一阶扰动近似公式。根据中远炮检距对传统近似方程精度的影响,单俊臻等[8]推导了HTI介质纵波反射系数一阶扰动近似方程。
基于方位反射系数特征方程,构建方位变化特征的地震属性是实现裂缝预测的主要方法。Mallick等[9]认为地震反射振幅和旅行时具有随方位余弦变化的特征。Grechka等[10]认为各向异性地层动校正速度具有椭圆特性。Downton等[11]利用Rüger近似方程反演得到裂缝密度和走向。王洪求等[12]分析不同地震属性的方位各向异性特征,利用融合属性预测裂缝。孙炜等[13]对方位角道集进行速度分析,保留速度各向异性信息,提高了裂缝预测精度。孙炜等[14]通过对HTI介质的各向异性正演实现了裂缝敏感属性的优选,认为利用优选属性的椭圆拟合结果也可达到裂缝预测的目的。王康宁等[15]对方位反射系数进行傅里叶级数展开,利用展开式中各向异性参数项实现裂缝预测。詹仕凡等[16]利用多尺度方位各向异性分析、研究了OVT域地震道集的裂缝预测方法。林娟等[17]、熊金红等[18]、王景春等[19]将方位各向异性裂缝预测方法应用于实际工区,均取得了较好的效果。
上述裂缝预测方法多采用传统近似方程作为理论基础,但传统近似方程在中角度范围内精度较低,因而无法准确定量描述方位各向异性特征。由于介质上覆界面与下伏界面的方位反射系数AVO特征可能存在差异,因而会增加裂缝预测结果的不确定性[20]。杨氏模量是表征储层岩石脆性、评价储层含气特征的重要参数,且能够很好地表征地层延展性。本文借鉴弹性阻抗对介质层内信息的定量表征[21],利用杨氏模量方位变化特征[22],以HTI介质一阶扰动近似方程作为理论基础,推导了一种基于地震杨氏模量表征的方位弹性阻抗方程。基于该方程,建立概率化地震反演方法,实现方位杨氏模量和各向异性参数的定量表征。最后,基于方位杨氏模量和各向异性参数实现裂缝预测。该方法可有效避免顶、底界面信息指示裂缝走向的模糊性问题。利用该方法开展模型试算,并应用于渤中凹陷H构造潜山勘探中,证实了方法的有效性和适用性。
1 方法原理根据岩石物理分析,杨氏模量与岩石内部结构、矿物组分、孔隙度等有关,其定量表征了岩石的抗形变能力,可用于描述裂缝发育特征。杨氏模量具有随方位变化的特征,因此可以构建基于杨氏模量表征的方位反射系数近似方程,该方程是实现裂缝预测的正演基础。
地震响应和弹性介质参数的定量表征是叠前反演的理论基础。区别于传统HTI介质反射系数线性近似方程,参考各向异性参数高精度线性扰动量表征,基于弱各向异性假设,结合扰动理论和介质分解理论,可得到HTI介质纵波反射系数一阶扰动近似方程[8],即
| $ \begin{aligned} R_{\mathrm{PP}}(\theta, \phi)=& \frac{1}{2}\left(1+\tan ^{2} \theta_{\mathrm{P}}\right) \frac{\Delta V_{\mathrm{P} 0}}{V_{\mathrm{P} 0}}+\frac{1}{2}\left(1-4 k^{2} \sin ^{2} \theta_{\mathrm{P}}\right) \frac{\Delta \rho}{\rho}-\\ & 4 k^{2} \sin ^{2} \theta_{\mathrm{P}} \frac{\Delta V_{\mathrm{S} 0}}{V_{\mathrm{S} 0}}-4 k^{2} \sin ^{2} \theta_{\mathrm{P}} \cos ^{2} \phi \Delta \gamma^{(\mathrm{V})}+\frac{1}{2} \sin ^{2} \theta_{\mathrm{P}} \cos ^{2} \phi\left(1+\sin ^{2} \theta_{\mathrm{P}}\right) \times \\ &\left(1-\sin ^{2} \theta_{\mathrm{P}} \cos ^{2} \phi\right) \Delta \delta^{(\mathrm{V})}+\frac{1}{2} \sin ^{4} \theta_{\mathrm{P}} \cos ^{4} \phi\left(1+\sin ^{2} \theta_{\mathrm{P}}\right) \Delta \varepsilon^{(\mathrm{V})} \end{aligned} $ | (1) |
式中: RPP(θ,ϕ)为纵波的方位反射系数;θP为纵波入射角或反射角;ϕ为方位角;k为垂直入射的横纵波速度比;VP0和ΔVP0、VS0和ΔVS0、ρ和Δρ分别表示弹性分界面两侧垂直入射的纵波速度、横波速度、密度的均值和差值;Δδ(V)、Δε(V)和Δγ(V)分别为弹性分界面两侧Thomsen弱各向异性参数的差值。
纵、横波速度与杨氏模量E、泊松比σ之间存在如下关系
| $ \left\{\begin{array}{l} V_{\mathrm{P} 0}=\sqrt{\frac{E(1-\sigma)}{\rho(1+\sigma)(1-2 \sigma)}} \\ V_{\mathrm{S} 0}=\sqrt{\frac{E}{2 \rho(1+\sigma)}} \\ k=\frac{V_{\mathrm{S} 0}}{V_{\mathrm{P} 0}}=\sqrt{\frac{1-2 \sigma}{2(1-\sigma)}} \end{array}\right. $ | (2) |
将式(2)代入式(1)中,整理可得
| $ \begin{aligned} R_{\mathrm{PP}}(\theta, \phi)=&\left(\frac{1}{4} \sec ^{2} \theta_{\mathrm{P}}-\frac{1-2 \sigma}{1-\sigma} \sin ^{2} \theta_{\mathrm{P}}\right) \frac{\Delta E}{E}+\left(\frac{1}{2}-\frac{1}{4} \sec ^{2} \theta_{\mathrm{P}}\right) \frac{\Delta \rho}{\rho}+\\ &\left\{\frac{1}{4} \sec ^{2} \theta_{\mathrm{P}} \frac{\left(\frac{1-2 \sigma}{1-\sigma}-3\right)\left(\frac{1-2 \sigma}{1-\sigma}-1\right)^{2}}{\frac{1-2 \sigma}{2(1-\sigma)}\left[\frac{2(1-2 \sigma)}{1-\sigma}-3\right]}+\frac{1-2 \sigma}{1-\sigma} \sin ^{2} \theta_{\mathrm{P}} \frac{1-\frac{1-2 \sigma}{1-\sigma}}{3-\frac{2(1-2 \sigma)}{1-\sigma}}\right\} \frac{\Delta \sigma}{\sigma}+\\ & \frac{1}{2} \sin ^{2} \theta_{\mathrm{P}} \cos ^{2} \phi\left(1+\sin ^{2} \theta_{\mathrm{P}}\right)\left(1-\sin ^{2} \theta_{\mathrm{P}} \cos ^{2} \phi\right) \Delta \delta^{(\mathrm{V})}+\\ & \frac{1}{2} \sin ^{4} \theta_{\mathrm{P}} \cos ^{4} \phi\left(1+\sin ^{2} \theta_{\mathrm{P}}\right) \Delta \varepsilon^{(\mathrm{V})}-\frac{2(1-2 \sigma)}{1-\sigma} \sin ^{2} \theta_{\mathrm{P}} \cos ^{2} \phi \Delta \gamma^{(\mathrm{V})} \end{aligned} $ | (3) |
式(3)为基于方位杨氏模量、泊松比、密度以及各向异性参数表征的HTI介质一阶扰动近似方程。与传统利用方位杨氏模量表征的近似方程[23]相比,该方程主要对各向异性参数项的系数进行了修正。若忽略各向异性参数扰动量,则该方程退化为各向同性介质YPD方程[23],即杨氏模量表示的反射系数方程。若式(2)纵横波速度比表征形式中σ为泊松比均值σ0,假设
| $ \begin{aligned} R_{\mathrm{PP}}(\theta, \phi)=&\left(\frac{1}{4} \sec ^{2} \theta_{\mathrm{P}}-2 \kappa \sin ^{2} \theta_{\mathrm{P}}\right) \frac{\Delta E}{E}+\left(\frac{1}{2}-\frac{1}{4} \sec ^{2} \theta_{\mathrm{P}}\right) \frac{\Delta \rho}{\rho}+\\ &\left[\frac{1}{4} \sec ^{2} \theta_{\mathrm{P}} \frac{(2 \kappa-3)(2 \kappa-1)^{2}}{\kappa(4 \kappa-3)}+2 \kappa \sin ^{2} \theta_{\mathrm{P}} \frac{1-2 \kappa}{3-4 \kappa}\right] \frac{\Delta \sigma}{\sigma}+\\ & \frac{1}{2} \sin ^{2} \theta_{\mathrm{P}} \cos ^{2} \phi\left(1+\sin ^{2} \theta_{\mathrm{P}}\right)\left(1-\sin ^{2} \theta_{\mathrm{P}} \cos ^{2} \phi\right) \Delta \delta^{(\mathrm{V})}+\\ & \frac{1}{2} \sin ^{4} \theta_{\mathrm{P}} \cos ^{4} \phi\left(1+\sin ^{2} \theta_{\mathrm{P}}\right) \Delta \varepsilon^{(\mathrm{V})}-4 \kappa \sin ^{2} \theta_{\mathrm{P}} \cos ^{2} \phi \Delta \gamma^{(\mathrm{V})} \end{aligned} $ | (4) |
反射系数近似方程由介质分界面两侧弹性参数表征,描述了介质分界面的地震响应特征。为了证实本文所推导近似方程式(3)的准确性,设计了三层模型,从上至下分别为各向同性介质、HTI介质和各向同性介质。当上覆为各向同性介质、下伏为HTI介质时,本文推导的基于杨氏模量表征的一阶扰动近似方程相比传统近似方程具有更高精度,在中角度至大角度范围内与精确方程差异较小(图 1a)。当上覆为HTI介质、下伏为各向同性介质时,传统近似方程仅在小角度入射情况下具有较高的精度;当入射角增大时,本文所推导的近似方程与精确方程差异远小于传统近似方程(图 1b)。
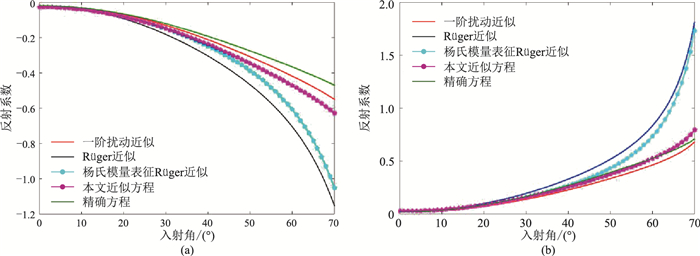
|
图 1 纵波反射系数精度对比 (a)各向同性/HTI界面;(b)HTI/各向同性界面 |
为了定量描述介质内部的参数特征,引入方位弹性阻抗与方位反射系数之间的关系[21],即
| $ \begin{array}{L} R(\theta, \phi)=\frac{\mathrm{EI}_{2}(\theta, \phi)-\mathrm{EI}_{1}(\theta, \phi)}{\mathrm{EI}_{2}(\theta, \phi)+\mathrm{EI}_{1}(\theta, \phi)} \approx \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \frac{1}{2} \Delta \ln \mathrm{EI}(\theta, \phi) \end{array} $ | (5) |
式中EI1(θ,ϕ)、EI2(θ,ϕ)分别表示介质分界面两侧方位弹性阻抗。将式(5)代入式(4)可得
| $ \begin{aligned} \frac{1}{2} \Delta \ln E \mathrm{I}(\theta, \phi)=&\left(\frac{1}{4} \sec ^{2} \theta_{\mathrm{P}}-2 \kappa \sin ^{2} \theta_{\mathrm{P}}\right) \Delta \ln E+\frac{1}{2}\left(1-\frac{1}{2} \sec ^{2} \theta_{\mathrm{P}}\right) \Delta \ln \rho+\\ &\left[\frac{1}{4} \sec ^{2} \theta_{\mathrm{P}} \frac{(2 \kappa-3)(2 \kappa-1)^{2}}{\kappa(4 \kappa-3)}+2 k \sin ^{2} \theta_{\mathrm{P}} \frac{1-2 \kappa}{3-4 \kappa}\right] \Delta \ln \sigma+\\ & \frac{1}{2} \sin ^{2} \theta_{\mathrm{P}} \cos ^{2} \phi\left(1+\sin ^{2} \theta_{\mathrm{P}}\right)\left(1-\sin ^{2} \theta_{\mathrm{P}} \cos ^{2} \phi\right) \Delta \delta^{(\mathrm{V})}+\\ & \frac{1}{2} \sin ^{4} \theta_{\mathrm{P}} \cos ^{4} \phi\left(1+\sin ^{2} \theta_{\mathrm{P}}\right) \Delta \varepsilon^{(\mathrm{V})}-4 \kappa \sin ^{2} \theta_{\mathrm{P}} \cos ^{2} \phi \Delta \gamma^{(\mathrm{V})} \end{aligned} $ | (6) |
对式(6)等号两侧积分,之后将两侧同时转换至指数域。为了限定方位弹性阻抗方程的量纲变化幅度、确保方程的稳定性,需要对指数域方程标准化处理,最终方位弹性阻抗可表征为
| $ \begin{aligned} \mathrm{EI}(\theta, \phi)=& \mathrm{EI}_{0}\left(\frac{E}{E_{0}}\right)^{a(\theta)}\left(\frac{\sigma}{\sigma_{0}}\right)^{b(\theta)}\left(\frac{\rho}{\rho_{0}}\right)^{c(\theta)} \times \\ & \exp \left[d(\theta, \phi) \delta^{(\mathrm{V})}+e(\theta, \phi) \varepsilon^{(\mathrm{V})}+\right.\\ &\left.f(\theta, \phi) \gamma^{(\mathrm{V})}\right] \end{aligned} $ | (7) |
其中
| $ \left\{\begin{array}{l} a(\theta)=\frac{1}{2} \sec ^{2} \theta_{\mathrm{P}}-4 \kappa \sin ^{2} \theta_{\mathrm{P}} \\ b(\theta)=\frac{1}{2} \sec ^{2} \theta_{\mathrm{P}} \frac{(2 \kappa-3)(2 \kappa-1)^{2}}{\kappa(4 \kappa-3)}+ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ 4 \kappa \sin ^{2} \theta_{\mathrm{P}} \frac{1-2 \kappa}{3-4 \kappa} \\ \begin{array}{l} c(\theta)=1-\frac{1}{2} \sec ^{2} \theta_{\mathrm{P}} \\ d(\theta, \phi)=\sin ^{2} \theta_{\mathrm{P}} \cos ^{2} \phi\left(1+\sin ^{2} \theta_{\mathrm{P}}\right) \times \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left(1-\sin ^{2} \theta_{\mathrm{P}} \cos ^{2} \phi\right) \\ e(\theta, \phi)=\sin ^{4} \theta_{\mathrm{P}} \cos ^{4} \phi\left(1+\sin ^{2} \theta_{\mathrm{P}}\right) \\ f(\theta, \phi)=-8 \kappa \sin ^{2} \theta_{\mathrm{P}} \cos ^{2} \phi \\ \mathrm{EI}_{0}=E_{0}^{\frac{1}{4}} \sigma_{0}^{\frac{\left(2 \kappa {-3}\right)\left(2 \kappa-1\right)^{2}}{4 \kappa\left(4 \kappa-3\right)}} \rho_{0}^{\frac{1}{4}} \end{array} \end{array}\right. $ |
式中:EI0、E0、ρ0分别为介质弹性阻抗、杨氏模量、密度的均值;δ(V)、ε(V)、γ(V)为三个各向异性参数。
2 反演方法假设地下介质为线性时不变系统,根据褶积模型可知,地震信号d与地震子波G、反射系数序列m的关系为
| $ \boldsymbol{d}=\boldsymbol{Gm} $ | (8) |
一般来说,地震反演是基于最小二乘关系构建反演目标泛函,以地震记录与合成记录之间的方差衡量反演结果的准确性。概率化理论作为约束弹性阻抗反演的目标函数,具有较好的抗噪性[24-25],因此选取贝叶斯理论构建叠前概率化地震反演框架。假设目的层的m由M个待反演参数构成,m=[m1,m2,…,mM];对目的层进行n次观测,获得观测的地震数据样本为d=[d1,d2,…,dn]。基于贝叶斯理论,m的后验概率密度为
| $ p(\boldsymbol{m} \mid \boldsymbol{d})=\frac{p(\boldsymbol{m}) p(\boldsymbol{d} \mid \boldsymbol{m})}{\int p(\boldsymbol{d} \mid \boldsymbol{m}) \mathrm{d} m} \propto p(\boldsymbol{m}) p(\boldsymbol{d} \mid \boldsymbol{m}) $ | (9) |
式中:p(m)为先验概率密度;p(d|m)为似然函数。如式(9)所示,后验概率密度函数在待反演参数取值空间先验信息的基础上,考虑了观测数据与待反演参数之间的不确定性。结合背景噪声对反演结果的影响,引入背景噪声高斯分布函数,并且假设待反演参数概率特征符合柯西分布,则式(9)可变为
| $ \begin{array}{*{20}{c}} {p(\mathit{\boldsymbol{m}}\mid \mathit{\boldsymbol{d}}) = \frac{1}{{{{\left( {{\rm{ \mathsf{ π} }}{\sigma _{\rm{m}}}} \right)}^M}}}\prod\limits_{i = 1}^M {\left( {\frac{1}{{1 + m_i^2/\sigma _{\rm{m}}^2}}} \right)} \times }\\ {\exp \left[ { - {{(\mathit{\boldsymbol{Gm}} - \mathit{\boldsymbol{d}})}^{\rm{T}}}(\mathit{\boldsymbol{Gm}} - {\bf{d}})/2\sigma _{\rm{n}}^2} \right]} \end{array} $ | (10) |
式中:σn2为观测数据中噪声的方差;σm2为模型参数的方差。为了给反演目标泛函提供背景约束,引入平滑后的低频速度场模型作为背景约束项。假设背景模型参数与待反演参数之间的拟合误差符合高斯分布,则后验概率密度可表征为
| $ \begin{array}{*{20}{c}} {p(\mathit{\boldsymbol{m}}\mid \mathit{\boldsymbol{d}}) = \frac{1}{{{{\left( {{\rm{ \mathsf{ π} }}{\sigma _{\rm{m}}}} \right)}^M}}}\prod\limits_{i = 1}^M {\left( {\frac{1}{{1 + m_i^2/\sigma _{\rm{m}}^2}}} \right)} \times }\\ {\exp \left[ { - {{(\mathit{\boldsymbol{Gm}} - \mathit{\boldsymbol{d}})}^{\rm{T}}}(\mathit{\boldsymbol{Gm}} - \mathit{\boldsymbol{d}})/2\sigma _{\rm{n}}^2} \right] \times }\\ {\exp \left[ { - {{(\mathit{\boldsymbol{Cm}} - \mathit{\boldsymbol{\zeta }})}^T}(\mathit{\boldsymbol{Cm}} - \mathit{\boldsymbol{\zeta }})/2\sigma _{{\rm{m}}\mathit{\boldsymbol{\zeta }}}^2} \right]} \end{array} $ | (11) |
式中:σmζ2为待反演参数与背景模型之间的方差;ζ为背景模型数据;C为积分矩阵。对上述方程进行对数域表征,得到反演目标函数
| $ \begin{aligned} F(\boldsymbol{m})=& F_{\mathrm{G}}(\boldsymbol{m})+F_{\text {Cauchy }}(\boldsymbol{m})+F_{\text {If }}(\boldsymbol{m}) \\ =&(\boldsymbol{G} \boldsymbol{m}-\boldsymbol{d})^{\mathrm{T}}(\boldsymbol{G} \boldsymbol{m}-\boldsymbol{d})+\alpha \sum\limits_{i=1}^{M} \ln \left(1+\frac{m_{i}^{2}}{\sigma_{\mathrm{m}}^{2}}\right)+\\ & \mu(\boldsymbol{C m}-\boldsymbol{\zeta})^{T}(\boldsymbol{C m}-\boldsymbol{\zeta}) \end{aligned} $ | (12) |
式中:FG(m)表示正演结果与地震数据的相似度;FCauchy(m)表示Cauchy约束反演结果的稀疏程度;Flf(m)表示光滑背景约束;α为柯西约束权值;μ为背景模型约束权值。对式(12)求导、计算得到最终反演方程
| $ \left(\boldsymbol{G}^{\mathrm{T}} \boldsymbol{G}+\alpha \boldsymbol{Q}+\mu \boldsymbol{C}^{\mathrm{T}} \boldsymbol{C}\right) \boldsymbol{m}=\boldsymbol{G}^{\mathrm{T}} \boldsymbol{d}+\mu \boldsymbol{C}^{\mathrm{T}} \boldsymbol{\zeta} $ | (13) |
可以利用α和μ两个权值控制反演稳定性和准确性,实现反射系数序列的稳定反演;最终结合背景模型数值和道积分,计算得到方位弹性阻抗反演结果。
以上方法实现了初始模型约束下的稳定的方位弹性阻抗反演。由于在低频模型中考虑了工区的真实背景信息,因此加入低频模型后,既可保证反演结果的合理性,又可增加反演的稳定性。
如式(7)所示,利用方位弹性阻抗反演结果可以计算得到杨氏模量、泊松比、密度和各向异性参数。由于式(7)是非线性的,为了简化求解难度,可将式(7)等号两侧转换至对数域,即
| $ \begin{aligned} \ln \frac{\mathrm{EI}(\theta, \phi)}{\mathrm{EI}_{0}}=& a(\theta) \ln \frac{E}{E_{0}}+b(\theta) \ln \frac{\sigma}{\sigma_{0}}+\\ & c(\theta) \ln \frac{\rho}{\rho_{0}}+d(\theta, \phi) \delta^{(\mathrm{V})}+\\ & e(\theta, \phi) \varepsilon^{(\mathrm{V})}+f(\theta, \phi) \gamma^{(\mathrm{V})} \end{aligned} $ | (14) |
式(14)为对数域的标准化方位弹性阻抗方程,可看作弹性参数线性叠加的结果。由于式(7)包含了6个待求解参数,因此需要6个对数域方位弹性阻抗数据体构建矩阵求解参数,矩阵表征为
| $ \left[\begin{array}{llllll} a_{1} & b_{1} & c_{1} & d_{1} & e_{1} & f_{1} \\ a_{2} & b_{2} & c_{2} & d_{2} & e_{2} & f_{2} \\ a_{3} & b_{3} & c_{3} & d_{3} & e_{3} & f_{3} \\ a_{4} & b_{4} & c_{4} & d_{4} & e_{4} & f_{4} \\ a_{5} & b_{5} & c_{5} & d_{5} & e_{5} & f_{5} \\ a_{6} & b_{6} & c_{6} & d_{6} & e_{6} & f_{6} \end{array}\right]\left[\begin{array}{c} \ln \frac{E}{E_{0}} \\ \ln \frac{\sigma}{\sigma_{0}} \\ \ln \frac{\rho}{\rho_{0}} \\ \delta^{(\mathrm{V})} \\ \varepsilon^{(\mathrm{V})} \\ \gamma^{(\mathrm{V})} \end{array}\right]=\left[\begin{array}{c} \ln \frac{\mathrm{EI}_{1}}{\mathrm{EI}_{0}} \\ \ln \frac{\mathrm{E} \mathrm{I}_{2}}{\mathrm{EI}_{0}} \\ \ln \frac{\mathrm{E} \mathrm{I}_{3}}{\mathrm{EI}_{0}} \\ \ln \frac{\mathrm{EI}_{4}}{\mathrm{EI}_{0}} \\ \ln \frac{\mathrm{EI}_{5}}{\mathrm{EI}_{0}} \\ \ln \frac{\mathrm{EI}_{6}}{\mathrm{EI}_{0}} \end{array}\right] $ | (15) |
如式(15)所示,在叠前地震反演框架下,利用分方位部分角度叠加地震数据、地震子波和背景模型反演所得的方位弹性阻抗数据体作为输入,通过求解系数矩阵的广义逆矩阵,可得到稳定的方位杨氏模量、泊松比、密度和各向异性参数反演结果。与原始方程相比,对数域方程仅变换数据域,因此在简化多参数反演难度的同时不会降低反演的准确性。
由于沿裂缝走向与倾向的方位杨氏模量具有明显的差异性[22],杨氏模量具有方位变化特征,因此方位杨氏模量椭圆拟合能够较好地指示裂缝发育方向。基于YPD方程,利用方位弹性阻抗反演得到每个方位的杨氏模量[22],根据最小二乘原理椭圆拟合思想,可实现基于方位杨氏模量的裂缝特征预测。椭圆一般方程为
| $ A x^{2}+B x y+C y^{2}+D x+E y+F=0 $ | (16) |
式中A、B、C、D、E、F为六个方位的杨氏模量。假设椭圆任意一点坐标为(x,y),椭圆中心点坐标为(x0,y0),p和q分别为椭圆长轴和短轴。椭圆一般方程可转换为标准椭圆方程[26],即可求得
| $ \left\{\begin{array}{l} x_{0}=\frac{B E-2 C D}{4 A C-B^{2}} \\ y_{0}=\frac{B D-2 A E}{4 A C-B^{2}} \\ \theta=\frac{1}{2} \arctan \frac{B}{A-C} \\ p^{2}=2 \frac{A x_{0}^{2}+C y_{0}^{2}+B x_{0} y_{0}-1}{A+C-\sqrt{(A-C)^{2}+B^{2}}} \\ q^{2}=2 \frac{A x_{0}^{2}+C y_{0}^{2}+B x_{0} y_{0}-1}{A+C+\sqrt{(A-C)^{2}+B^{2}}} \end{array}\right. $ | (17) |
以椭圆一般方程为基础,结合最小二乘椭圆拟合原理构建椭圆方程目标函数,进而建立线性方程组求解椭圆长轴、短轴和椭圆率,实现裂缝发育方向预测。假设横纵波速度比为已知定值,则当裂缝为干裂缝或裂缝仅包含无黏滞流体时,各向异性参数与裂缝密度之间有着良好的线性关系[27],因此结合方位杨氏模量最小二乘椭圆拟合结果与各向异性参数,可实现裂缝发育强度和发育方向的预测。
3 模型试算为了验证本文反演方法的可行性,选择实际工区测井数据作为一维模型进行试算。
选取实际工区某井的杨氏模量、泊松比、密度和各向异性参数δ(V)、ε(V)、γ(V)数据,选定入射角分别为10°、20°、30°,方位角分别为15°、105°,利用HTI介质方位反射系数特征精确方程(式(4))分别计算方位反射系数序列,结合雷克子波得到方位合成地震记录。将该方位道集作为输入,利用多次平滑后的方位弹性阻抗作为低频约束(一般不超过10Hz),得到方位弹性阻抗反演结果。基于反演的六个方位弹性阻抗数据体,在对数域求解线性方程组(式(15)),可实现对杨氏模量、泊松比、密度和各向异性参数的反演。
图 2为方位弹性阻抗反演结果。由图可见,反演结果与模型曲线吻合程度较高。由于各向异性参数扰动量具有方位各向异性特征,因而导致反演的不同方位的弹性阻抗具有差异。
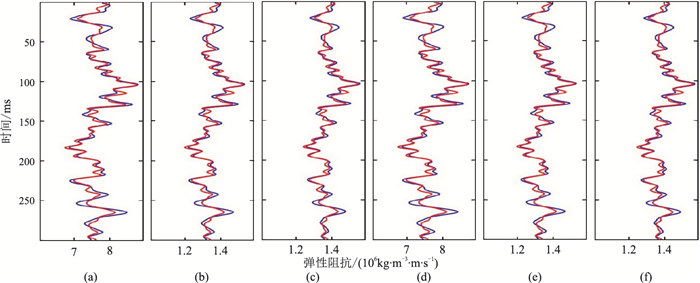
|
图 2 不同入射角、方位角方位弹性阻抗反演结果 (a)10°、15°;(b)20°、15°;(c)30°、15°;(d)10°、105°;(e)20°、105°;(f)30°、105°。红线为模型数据,蓝线为反演结果 |
图 3为杨氏模量、泊松比、密度和各向异性参数的反演结果。由图可见,本文方法反演结果与实际数据整体上吻合较好,误差相对较小,仅在泊松比、密度突变处误差相对较大,证实了本文推导方程的反演结果精度较高,稳定性较好。

|
图 3 反演的弹性参数和各向异性参数 (a)杨氏模量;(b)泊松比;(c)密度;(d)δ(V);(e)ε(V);(f)γ(V)。红线为模型数据,蓝线为反演结果 |
渤中凹陷H构造潜山顶面位于始新统孔店组二段之下,埋藏深度约为2400m,上覆新近系沙河街组、东营组多套快速沉积体。钻井揭示,潜山顶面风化带内孔隙和裂缝较发育,风化带之下为致密的花岗岩潜山。受构造运动和深部CO2溶蚀作用,潜山内幕发育多套裂缝,横向非均质性强,各向异性特征明显。由于潜山内幕地震反射信息较少,因此裂缝识别难度较大。
利用研究区宽方位地震资料,应用方位杨氏模量预测裂缝技术流程如图 4所示。首先,将炮检距域叠前地震道集转化为角度域道集,对角道集进行优选、分析,确定入射角叠加范围和方位角叠加范围;其次,利用偏移速度场构建各向同性的弹性阻抗低频模型,作为每个方位弹性阻抗反演的初始输入,得到方位弹性阻抗体;然后,利用分方位弹性阻抗分别计算对应方位的杨氏模量、泊松比和密度等;最后对方位杨氏模量进行最小二乘椭圆拟合,结合各向异性参数反演结果与椭圆拟合方向,实现裂缝发育密度和发育方向的预测。
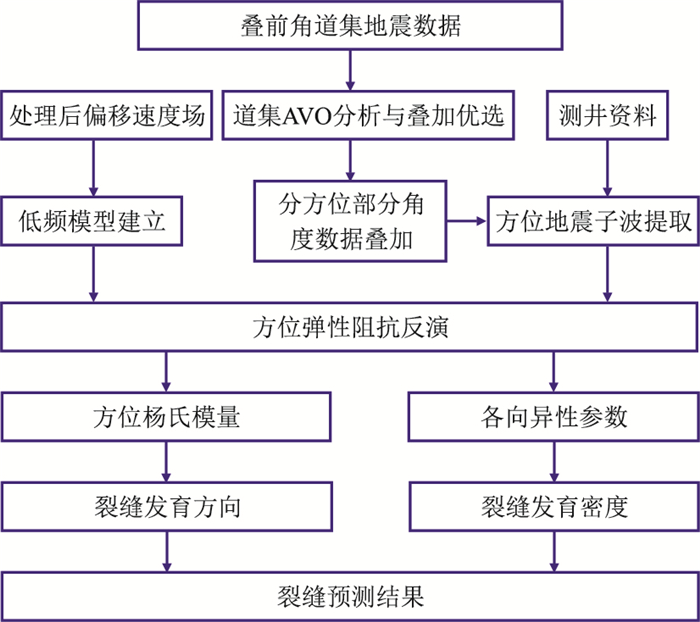
|
图 4 宽方位杨氏模量裂缝预测技术流程 |
利用分方位的部分角度叠加地震数据可反演得到分方位的部分角度弹性阻抗数据体(图 5),基于方位弹性阻抗数据体可提取方位杨氏模量与各向异性参数(图 6)。由图 5、图 6可见,潜山顶面之上地层表现为低弹性阻抗、低杨氏模量特征,潜山表现为高弹性阻抗、高杨氏模量特征。
|
图 5 方位弹性阻抗反演结果 方位角为105°,入射角为20°。粉线为潜山顶界面 |
|
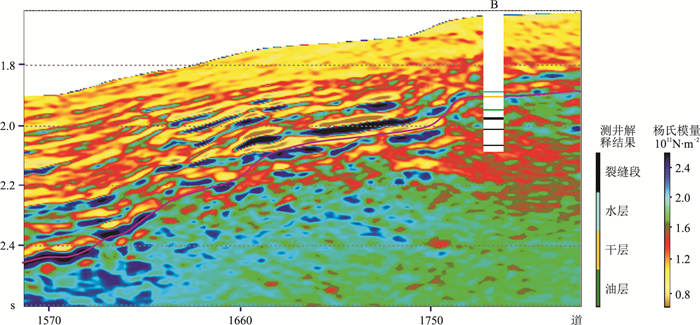
图 6 方位杨氏模量反演结果 方位角为105°,粉线为潜山顶界面 |
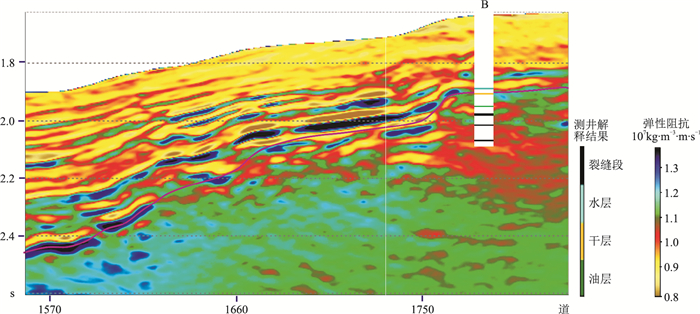
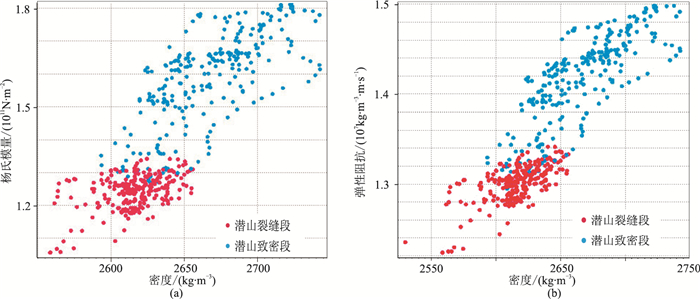
B井揭示潜山发育多个裂缝段,在高杨氏模量、高弹性阻抗潜山背景下表现为相对低值,反演结果与测井解释结果(图 7)一致性较好。
|
图 7 测井岩石物理参数交会分析 (a)杨氏模量—密度;(b)弹性阻抗—密度 |
利用最小二乘椭圆拟合方法对方位杨氏模量进行椭圆拟合,椭圆长轴指示裂缝发育方向;同时,由于各向异性参数与裂缝发育密度存在线性关系,两者结合可预测潜山风化带及内幕裂缝发育方向和裂缝密度。
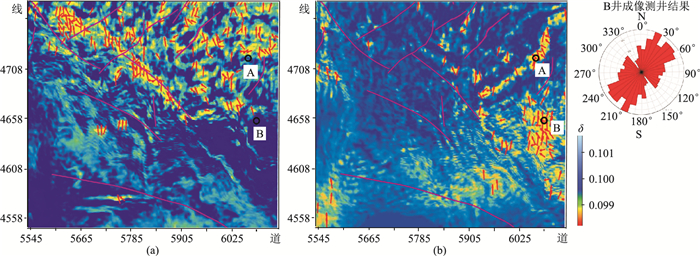
由图 8a可见,预测的裂缝发育方向与断裂一致,多为北东向或北西向;断裂发育处裂缝发育密度大。在潜山顶面风化带A井处裂缝较发育,B井处裂缝发育程度相对较低,这与两口井的测井解释结果一致。
|
图 8 预测的裂缝发育方向和各向异性强度叠合 (a)潜山风化带(潜山顶面之下0~30ms);(b)潜山内幕裂缝带(潜山顶面之下165~195ms)。粉线表示潜山顶面断裂,红箭头表示裂缝发育方向 |
与潜山风化带的裂缝发育特征相比,潜山内幕段整体上各向异性强度较低(图 8b),表明该层段风化剥蚀程度较低。另外,潜山内幕层段东部裂缝相对较发育;潜山顶部部分断裂(图 8北部)未断至潜山内幕层段,因而内幕层段北部裂缝欠发育。B井证实潜山内幕层段裂缝较发育,裂缝倾角主要为50°~70°,裂缝发育方向整体上呈北东向,与本文方法预测结果吻合较好。
5 结束语基于杨氏模量的方位变化特征与岩石力学性质之间的关系,本文以宽方位观测的HTI介质一阶扰动近似方程为基础,推导了基于杨氏模量、泊松比和各向异性参数表征的方位反射系数近似方程,该方程在中角度至大角度时比传统近似方程具有更高的精度。以该方程为地震叠前反演的理论基础,结合贝叶斯理论,形成了方位杨氏模量和各向异性弹性参数反演方法。对于裂缝性储层,杨氏模量具有方位变化特征,利用方位杨氏模量椭圆拟合结果和反演的各向异性参数可实现裂缝发育方向和裂缝密度的表征,避免了顶、底界面AVO特征差异导致的裂缝方向预测不准确的问题,提高了反演的可靠性和稳定性。
本文方法应用于渤中凹陷H构造潜山,预测的裂缝发育特征与断裂发育特征、钻井具有较好的一致性。本文基于方位杨氏模量的裂缝预测方法,可为潜山裂缝型储层评价提供一种较可靠的技术手段。
| [1] |
赵邦六, 王喜双, 董世泰, 等. 渤海湾盆地物探技术需求及发展方向[J]. 石油地球物理勘探, 2014, 49(2): 394-409. ZHAO Bangliu, WANG Xishuang, DONG Shitai, et al. Geophysical prospecting requirement and development direction in Bohai Bay Basin[J]. Oil Geophysical Prospecting, 2014, 49(2): 394-409. |
| [2] |
赵政璋, 杜金虎, 牛嘉玉, 等. 渤海湾盆地"中石油"探区勘探形势与前景分析[J]. 中国石油勘探, 2005, 10(3): 1-7. ZHAO Zhengzhang, DU Jinhu, NIU Jiayu, et al. Exploration situations and prospects in PetroChina Blocks, Bohai Bay Basin[J]. China Petroleum Exploration, 2005, 10(3): 1-7. DOI:10.3969/j.issn.1672-7703.2005.03.001 |
| [3] |
Rüger A. Reflection Coefficients and Azimuthal AVO Analysis in Anisotropic Media[D]. Colorado School of Mines, Colorado, 1996.
|
| [4] |
Thomsen L. Weak elastic anisotropy[J]. Geophysics, 1986, 51(10): 1954-1966. DOI:10.1190/1.1442051 |
| [5] |
Vavryčuk V, Pšenčík I. PP-wave reflection coefficients in weakly anisotropic elastic media[J]. Geophysics, 1998, 63(6): 2129-2141. DOI:10.1190/1.1444506 |
| [6] |
杜炳毅, 杨午阳, 王恩利, 等. 基于杨氏模量、泊松比和各向异性梯度的裂缝介质AVAZ反演方法[J]. 石油物探, 2015, 54(2): 218-225. DU Bingyi, YANG Wuyang, WANG Enli, et al. AVAZ inversion based on Young's modulus, Poisson's ratio and anisotropy gradient in fractured media[J]. Geophysical Prospecting for Petroleum, 2015, 54(2): 218-225. DOI:10.3969/j.issn.1000-1441.2015.02.014 |
| [7] |
Wu G C, Zhao X L, Tang J, et al. First-order perturbation approximation for rock elastic moduli in transversely isotropic media[J]. Science China(Earth Sciences), 2017, 60(9): 1645-1654. DOI:10.1007/s11430-016-9064-8 |
| [8] |
单俊臻, 吴国忱, 龚诚诚. HTI介质方位观测PP波反射系数一阶扰动近似[J]. 石油地球物理勘探, 2019, 54(2): 371-379. SHAN Junzhen, WU Guochen, GONG Chengcheng. First-order perturbation approximation of PP wave reflection coefficient for HTI medium based on azimuthal geometry[J]. Oil Geophysical Prospecting, 2019, 54(2): 371-379. |
| [9] |
Mallick S, Craft K L, Meister L J, et al. Determination of the principal directions of azimuthal anisotropy from P-wave seismic data[J]. Geophysics, 1998, 63(2): 692-706. DOI:10.1190/1.1444369 |
| [10] |
Grechka V, Tsvankin I. NMO-velocity surfaces and Dix-type formulas in anisotropic heterogeneous media[J]. Geophysics, 2002, 67(3): 939-951. DOI:10.1190/1.1484536 |
| [11] |
Downton J, Gray D. AVAZ parameter uncertainty estimation[C]. SEG Technical Program Expanded Abstracts, 2006, 25: 234-238.
|
| [12] |
王洪求, 杨午阳, 谢春辉, 等. 不同地震属性的方位各向异性分析及裂缝预测[J]. 石油地球物理勘探, 2014, 49(5): 925-931. WANG Hongqiu, YANG Wuyang, XIE Chunhui, et al. Azimuthal anisotropy analysis of different seismic attributes and fracture prediction[J]. Oil Geophysical Prospecting, 2014, 49(5): 925-931. |
| [13] |
孙炜, 何治亮, 李玉凤, 等. 改进的方位各向异性裂缝预测方法及其应用[J]. 石油地球物理勘探, 2014, 49(6): 1170-1178. SUN Wei, HE Zhiliang, LI Yufeng, et al. An improved method of fracture prediction based on P-wave aniso-tropy and its application[J]. Oil Geophysical Prospecting, 2014, 49(6): 1170-1178. |
| [14] |
孙炜, 何治亮, 李玉凤, 等. 基于HTI介质各向异性正演的裂缝预测属性优选[J]. 石油物探, 2014, 53(2): 223-231. SUN Wei, HE Zhiliang, LI Yufeng, et al. Seismic attributes optimization for fractures prediction based on the anisotropy forwarding of the HTI media[J]. Geophysical Prospecting for Petroleum, 2014, 53(2): 223-231. DOI:10.3969/j.issn.1000-1441.2014.02.013 |
| [15] |
王康宁, 孙赞东, 侯昕晔. 基于傅里叶级数展开的纵波方位各向异性裂缝预测[J]. 石油物探, 2015, 54(6): 755-761. WANG Kangning, SUN Zandong, HOU Xinye. Fracture prediction by P-wave azimuthal anisotropy based on Fourier series decomposition[J]. Geophysical Prospecting for Petroleum, 2015, 54(6): 755-761. DOI:10.3969/j.issn.1000-1441.2015.06.014 |
| [16] |
詹仕凡, 陈茂山, 李磊, 等. OVT域宽方位叠前地震属性分析方法[J]. 石油地球物理勘探, 2015, 50(5): 956-966. ZHAN Shifan, CHEN Maoshan, LI Lei, et al. OVT-domain wide-azimuth prestack seismic attribute analysis[J]. Oil Geophysical Prospecting, 2015, 50(5): 956-966. |
| [17] |
林娟, 娄兵, 张淑萍, 等. 准噶尔盆地玛湖1井区高密度三维OVT域裂缝预测的应用[J]. 石油地球物理勘探, 2017, 52(增刊2): 146-152. LIN Juan, LOU Bing, ZHANG Shuping, et al. Fracture prediction with the high-density 3D OVT domain in the Well Mahu 1 area, Junggar Basin[J]. Oil Geophysical Prospecting, 2017, 52(S2): 146-152. |
| [18] |
熊金红, 陈岑, 曹占元, 等. 基于叠前地震全方位各向异性预测裂缝发育——以普光气田须家河组为例[J]. 地质力学学报, 2017, 23(2): 280-287. XIONG Jinhong, CHEN Cen, CAO Zhanyuan, et al. Fracture development prediction based on azimuthal anisotropy analysis of pre-stack seismic: take Xujiahe formation of Puguang filed for example[J]. Journal of Geomechanics, 2017, 23(2): 280-287. DOI:10.3969/j.issn.1006-6616.2017.02.011 |
| [19] |
王景春, 窦立荣, 徐建国, 等. "两宽一高"地震资料在花岗岩潜山储层表征中的应用——以乍得邦戈盆地为例[J]. 石油地球物理勘探, 2018, 53(2): 320-329. WANG Jingchun, DOU Lirong, XU Jianguo, et al. Granitic buried-hill reservoir characterization based on broadband, wide-azimuth and high-density seismic data: A case study of Bangor Basin in Chad[J]. Oil Geophysical Prospecting, 2018, 53(2): 320-329. |
| [20] |
李春鹏. 基于方位地震道集的裂缝型储层预测方法研究[D]. 山东青岛: 中国石油大学(华东), 2013. LI Chunpeng. Research on Fractured Reservoir Prediction with Azimuthal Seismic Data[D]. China University of Petroleum, Qingdao, Shandong, 2013. |
| [21] |
Connolly P. Elastic impedance[J]. The Leading Edge, 1999, 18(4): 438-452. DOI:10.1190/1.1438307 |
| [22] |
Sayers C M. The effect of anisotropy on the Young's moduli and Poisson's ratios of shales[J]. Geophysical Prospecting, 2013, 61(2): 416-426. DOI:10.1111/j.1365-2478.2012.01130.x |
| [23] |
宗兆云, 印兴耀, 张峰, 等. 杨氏模量和泊松比反射系数近似方程及叠前地震反演[J]. 地球物理学报, 2012, 55(11): 3786-3794. ZONG Zhaoyun, YIN Xingyao, ZHANG Feng, et al. Reflection coefficient equation and pre-stack seismic inversion with Young's modulus and Poisson ratio[J]. Chinese Journal of Geophysics, 2012, 55(11): 3786-3794. DOI:10.6038/j.issn.0001-5733.2012.11.025 |
| [24] |
印兴耀, 曹丹平, 王保丽, 等. 基于叠前地震反演的流体识别方法研究进展[J]. 石油地球物理勘探, 2014, 49(1): 22-34. YIN Xingyao, CAO Danping, WANG Baoli, et al. Research progress of fluid discrimination with pre-stack seismic inversion[J]. Oil Geophysical Prospecting, 2014, 49(1): 22-34. |
| [25] |
罗辑, 吴国忱, 宗兆云, 等. 基于方位弹性阻抗反演的裂缝型储层流体检测方法[J]. 石油地球物理勘探, 2015, 50(6): 1154-1165. LUO Ji, WU Guochen, ZONG Zhaoyun, et al. Fluid identification in fractured reservoirs based on azimu-thal elastic impedance inversion[J]. Oil Geophysical Prospecting, 2015, 50(6): 1154-1165. |
| [26] |
闫蓓, 王斌, 李媛. 基于最小二乘法的椭圆拟合改进算法[J]. 北京航空航天大学学报, 2008, 34(3): 295-298. YAN Pei, WANG Bin, LI Yuan. Optimal ellipse fitting method based on least-squares principle[J]. Journal of Beijing University of Aeronautics and Astronaut, 2008, 34(3): 295-298. |
| [27] |
Bakulin A, Grechka V, Tsvankin I. Estimation of fracture parameters from reflection seismic data, Part Ⅰ: HTI model due to a single fracture set[J]. Geophy-sics, 2000, 65(6): 1788-1802. |



 王建花, 北京市朝阳区太阳宫南街6号院中海油研究总院有限责任公司, 100028。Email:
王建花, 北京市朝阳区太阳宫南街6号院中海油研究总院有限责任公司, 100028。Email: 