② 中国石油大港油田公司, 天津 300280
② Dagang Oilfield Branch Company, Petrochina, Binhai New District, Tianjin 300280, China
复杂碳酸盐岩储层的非均质性强,储层预测难题长期制约油气藏开发动用。溶蚀孔洞和构造裂缝孔隙的存在使储集空间复杂多样,导致储层预测难度加大。因此,利用现有资料综合预测储集类型是储层评价的关键。针对复杂储层的控制因素,前人利用不同方法进行了相关研究,取得了较好的效果。李建东等[1]基于地震属性,利用多变量协同模拟估算裂缝密度、预测裂缝发育区产能,获得了较好效果。贺川航等[2]基于曲线重构的井震联合地质统计学方法提高预测纵向分辨率,可精细刻画薄层裂缝溶洞储层分布。韩长城等[3]基于波形指示反演准确预测塔河油田奥陶系碳酸盐岩非均质岩溶缝洞,反演精度高于传统反演方法。张远银等[4]通过振幅约束进行低频建模,利用确定性波阻抗反演准确描述了西部典型缝洞型储层。李祺鑫等[5]利用高分辨率波阻抗贝叶斯序贯随机反演提高了层状储层反演纵向分辨率。但上述单一储层预测方法在实际应用中仍存在一定局限性,在特殊地区不能全面反映多因素控储的实际地质情况,因此有必要开展基于多数据融合的综合储层预测。
本文综合前人研究成果,针对千米桥潜山奥陶系碳酸盐岩储层地质特征,提出基于波形指示参数反演和敏感地震属性的多数据融合方法,以准确表征受层状溶蚀孔洞和裂缝控制的复杂缝洞储层,为潜山气藏开发动用奠定基础。
1 研究区概况千米桥潜山碳酸盐岩气藏为大港油田增储上产的关键领域。千米桥潜山位于黄骅坳陷中区,西侧紧邻港北潜山,南、北夹持于歧口凹陷、板桥次凹之间(图 1),是一个深埋在古近系构造层之下的低位序潜山构造。研究区经历早期抬升、中期深埋、晚期稳定沉积的构造发育背景,形成了较好的圈闭,具有板桥次凹和歧口凹陷双源供烃的特征[6]。多年来由于储层预测难度较大,导致后期钻井效果参差不齐,制约开发动用。
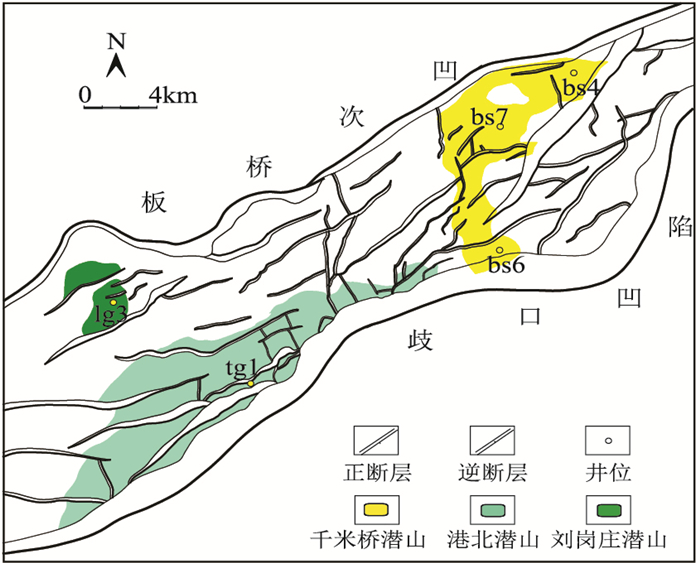
|
图 1 千米桥潜山区域位置 |
千米桥潜山主要目的层为奥陶系峰峰组(Of)和上马家沟组(Oms),发育在距潜山顶面250m以内的潜流带上。潜山上古生界遭受剥蚀,奥陶系长期遭受风化淋滤、侵蚀和溶蚀,形成潜山顺层岩溶储层,后期经历多期构造运动,局部裂缝沟通储层,形成内幕缝洞岩性圈闭[7]。岩溶储集空间主要由孔、洞、缝组成[8],原生孔隙极少,碳酸盐岩储集性能同时受顺层溶蚀孔洞及次生裂缝影响,优势缝洞储层多受层状溶蚀孔洞和裂缝共同控制。储层纵向沟通性较好,横向连通性差,油藏存在渗流屏障,油、气、水关系复杂。
在地震时间剖面上Of及Om优质储层分布于距风化壳顶0~150ms范围(主要研究时窗范围)内。有利储层发育区呈两种地震响应特征:第一种为层状溶蚀孔洞弱反射(图 2a);第二种为裂缝、缝洞杂乱反射(图 2b)。实际钻探发现,层状溶蚀孔洞和裂缝共同控制有利储层分布,仅依靠地震资料预测井间储层分布难度较大。

|
图 2 过q12-18井(a)和q18-18井(b)地震剖面 |
分别分析层状溶蚀孔洞和裂缝对储层的控制程度,在单一控储因素预测的基础上,进而融合多控储因素,以达到优选有利储层的目的。
3.1 溶蚀孔洞型储层预测层状溶蚀孔洞在研究区较发育,钻井证实有利储层均与该因素相关,同时差异剥蚀导致非均质性较强,且地震响应以弱反射为主,可利用井震结合方法追踪。本文利用波形指示反演结合曲线重构技术有效预测层状溶蚀孔洞分布。
3.1.1 基于曲线重构的波形指示反演研究区岩石物理分析证实,碳酸盐岩地层中发育的孔缝洞会造成声波时差增大、密度降低,导致阻抗值偏低。但实际中缝洞体系遭受多次充填和溶蚀作用,储层和非储层波阻抗差异规律复杂,导致原始波阻抗曲线不能完全识别有利储层。通过分析敏感曲线发现,研究区低电阻率值指示有利储层(图 3),因此将电阻率与原始纵波阻抗重构用于反演,可获得较好的储层识别效果[9]。

|
图 3 纵波阻抗—电阻率曲线交会图 |
在保证原始阻抗低频特征的情况下,曲线重构利用电阻率曲线的高频段有效识别同一岩性的有利储层发育区。首先选择Hamming函数对原始纵波阻抗低通滤波,获得曲线低频趋势
| $ g\left( r \right) = \frac{{W\left( r \right)}}{{\sum\limits_{r = - m}^m {W\left( r \right)} }} $ | (1) |
| $ W\left( r \right) = 0.54 + 0.46\frac{{r{\rm{ \mathsf{ π} }}}}{m}\;\;\;\;\;\left| r \right| \le m $ | (2) |
| $ {\rm{im}}{{\rm{p}}_{{\rm{lowpass}}}}\left( i \right) = \sum\limits_{r = - m}^m {g\left( r \right){\rm{imp}}\left( {i + r} \right)} $ | (3) |
式中:g(r)为滤波因子,r为滤波深度;W(r)为Hamming加权函数;[-m,m]为滤波深度区间;implowpass(i)为对应深度i的低通阻抗曲线,imp(i+r)为对应深度i+r的原始纵波阻抗值。
然后将低通阻抗implowpass(r)和电阻率曲线RT线性叠加
| $ {\rm{IMP}} = {\rm{im}}{{\rm{p}}_{{\rm{lowpass}}}}(r) + k{\rm{lgRT}} $ | (4) |
式中:IMP为重构阻抗;k为自定义系数,本研究以有效区分有利储层为标准,选为2000,在实际应用中可调整。
利用井旁道提取的子波制作IMP合成记录(图 4)。可见,原始纵波阻抗和IMP合成记录相似度较高,证明IMP在未改变原始阻抗低频特征的前提下,提高了储层分辨能力。

|
图 4 原始纵波阻抗和IMP合成记录 |
统计分析认为,IMP较原始纵波阻抗能更好地分辨优质储层,阻抗值低于15500g·cm-3·m·s-1指示有利储层(图 5)。因此选择IMP作为反演的基础曲线。

|
图 5 原始纵波阻抗(a)、IMP(b)统计直方图 |
本文选取地震波形指示反演,利用地震波形结构化统计算法,基于波形特征变化表征储层空间结构的变异性。理论上,反演基于贝叶斯判别理论和马尔科夫链—蒙特卡洛抽样算法[3]。首先通过地震波形高效动态聚类,分析待预测点的区域地震波形,优选波形相似度高、空间距离近的井作为有效样本参与该点的反演计算。进一步利用地震解释层位约束建立初始波阻抗模型作为先验信息。随后将初始模型与地震频带阻抗进行匹配滤波,联合似然函数分布和先验分布得到后验概率分布,以地震资料中频阻抗为基础,优化初始模型的高频成分。最终与地震阻抗进行相似性分析,保留相似度高的模拟解,通过多次随机模拟确保随机解的中频成分与地震资料一致,同时保留各样本的确定性结构成分[10-11]。
该方法以地质统计学为基础,在保证反演低频段的稳定性前提下,以地震波形特征约束中高频段,降低反演的随机性,实现相控反演[3],对描述层状储层的横向非均质性具有一定优势。
3.1.2 溶蚀孔洞储层预测效果分析鉴于IMP能够较好地分辨有利储层,因此基于IMP分别开展波形指示反演和稀疏脉冲反演(图 6)。分析反演剖面可知,波形指示反演(图 6b)的纵向预测精度高于稀疏脉冲反演(图 6a),与井吻合度较高,并且符合地震相趋势,能够有效反映层状溶蚀孔洞控制的储层分布。

|
图 6 稀疏脉冲反演(a)与重构阻抗波形指示反演(b)剖面 |
多种资料揭示千米桥潜山裂缝以中高角度缝为主导,局部发育,并受后期断裂控制,既是重要储集空间,也是油气渗滤通道[1]。研究区多数高产井储层位于受裂缝沟通的层状溶蚀孔洞发育区,因此裂缝预测是优选有利储层区的关键。本文利用成像测井解释结论作为约束,优化裂缝敏感地震属性,如蚂蚁体、曲率体,得到了较准确的裂缝预测结果。
3.2.1 地震属性分析利用叠后地震属性预测裂缝,首先通过构造导向滤波强化地震资料的裂缝相关特征[12],再提取相干体、曲率体、蚂蚁体等敏感属性,优选曲率[13]和蚂蚁体[14]属性分别预测区域裂缝和纵向裂缝带。
3.2.2 成像测井约束优化裂缝敏感属性受限于潜山地震资料分辨率的实际情况,地震属性与井符合率较低,因此需要优化地震属性。本文以有限的成像测井资料为约束拟合裂缝孔隙度作为裂缝敏感属性,反映裂缝发育程度,定量分析裂缝发育带。沿井轨迹提取属性体曲线与裂缝孔隙度交会(图 7),可见蚂蚁体(图 7a)、曲率(图 7b)属性值与裂缝孔隙度呈正相关关系。
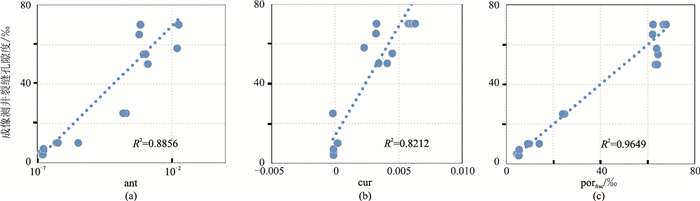
|
图 7 地震属性与裂缝孔隙度交会图 (a)ant—成像测井裂缝孔隙度;(b)cur—成像测井裂缝孔隙度;(c)porfrac—成像测井裂缝孔隙度 |
为保留原始属性体的基本特征,避免过拟合损失真实属性信息,因此基于最小二乘法拟合经验公式参数模型,得到由曲率体、蚂蚁体预测裂缝孔隙度porfrac的经验关系式
| $ {\rm{po}}{{\rm{r}}_{{\rm{frac}}}} = \frac{{2.51}}{{0.04 + {{\rm{e}}^{ - [19.1{{\left( {{\rm{cur}}} \right)}^{0.2}} + 5.4{\rm{lg}}({\rm{ant}}) - 1.3]}}}} $ | (5) |
式中:cur为曲率属性值;ant为蚂蚁体属性值。
通过拟合优化裂缝敏感属性,强化了原属性与裂缝发育程度的正相关关系,预测结果与成像测井符合率较高(图 7c)。
3.2.3 裂缝型储层预测效果分析在井附近通过拟合优化裂缝预测与原始地震属性预测结果。在bs8井轨迹处,成像测井于4177.0m处显示溶蚀缝洞发育(图 8d),曲率体也有较强响应(图 8b);成像测井于4306.5m处发育高角度裂缝(图 8d),蚂蚁体属性也有较强响应(图 8a)。拟合优化结果将曲率体、蚂蚁体属性的优势互补,在保留原始属性主要变化趋势的前提下,预测结果更准确。这种属性优化方法能够刻画裂缝发育带控制的储层,与实际情况更吻合。

|
图 8 裂缝预测效果分析图 (a)蚂蚁体;(b)曲率体;(c)porfrac;(d)成像测井 |
钻探证实,有利储层发育并非受单一因素控制,仅根据单一控储因素预测储层会导致有利储层优选偏差。由于千米桥潜山奥陶系层状溶蚀孔洞整体发育,局部受裂缝沟通,溶蚀孔洞和裂缝同时控制有利储层发育,因此融合两种储层预测结果更符合地质特征。
3.3.1 融合模型优选基于研究区18口井的测井数据,将优质储层进一步区分为Ⅰ类和Ⅱ类,通过井轨迹处反演IMP与porfrac交会分析(图 9)发现:Ⅰ类储层对应porfrac高值区、反演IMP低值区,两类控储因素同时控制储层发育,储层最有利;Ⅱ类储层对应单一控储因素控制储层发育区,储层较有利。在实际预测过程中,通过近似设定阀值划分有利储层的方法并不适用于上述数据,因此需要优选融合方法评价有利储层发育概率,较准确地预测有利储层。
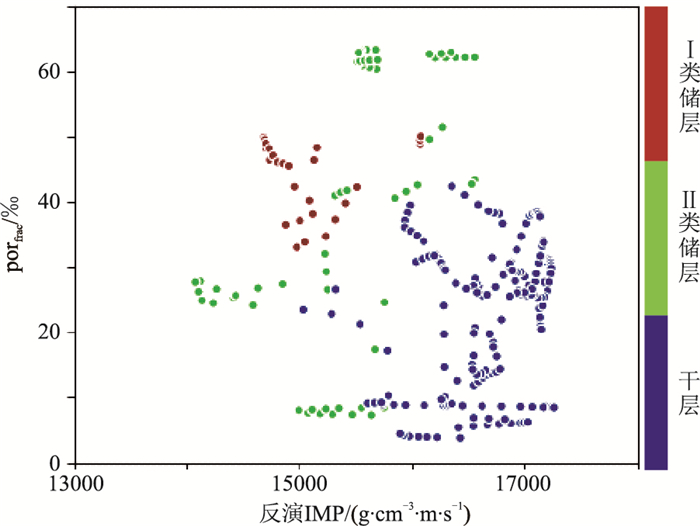
|
图 9 反演IMP—porfrac交会图 |
融合模型优选要求在有限数据点处拟合精度较高,与传统的统计学分类问题不同的是,储层预测分类问题同时要求模型具备较强的泛化能力,因为抽取的分析数据主要为井轨迹数据,这些数据在全部数据体中占比较小,需要避免过拟合现象。基于该认识,选取对异常点数据不敏感、可解释性强的分类方法,如线性模型、支持向量机模型,更适合于解决该问题。
(1) 线性模型
线性模型作为最直观、简洁的融合模型,在数据融合领域得到广泛应用[15-16],该模型基于公式
| $ y = \alpha {\rm{IMP}} - \beta {\rm{po}}{{\rm{r}}_{{\rm{frac}}}} $ | (6) |
进行预测。式中:y为有利储层概率;α、β为系数,由最小二乘法拟合得到。
实际交会分析表明,数据更偏向于非线性分布,因此该模型仅适合作为基准模型。
(2) 支持向量机模型
支持向量机(SVM)是一种基于结构风险最小化理论的机器学习方法,根据有限的数据样本,在训练数据集中构造出最优分类超平面,在合理分开两类数据集的同时使两类的差异最大,具有较强的模型泛化能力,尤其在解决少样本、线性不可分数据分类问题中具有一定优势。该方法广泛用于属性优选及岩性识别[17-18],但在碳酸盐岩储层预测方面应用较少且缺少完整的技术流程。
文中研究了SVM实现过程。首先假设训练样本集为{(xi,yi),i=1,2,…,M},其中xi为样本输入值,yi为样本输出值,每个样本点引入非线性SVM估计函数,将优化问题变为
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathop {\min }\limits_{w, b, {\xi _i}} \frac{1}{2}\parallel \mathit{\boldsymbol{w}}{\parallel ^2} + C\sum\limits_{i = 1}^M {{\xi _i}} \\ {\rm{s}}{\rm{.t}}{\rm{.}}{y_i}\left[ {{\mathit{\boldsymbol{w}}^{\rm{T}}}\phi \left( {{\mathit{\boldsymbol{x}}_i}} \right) + b} \right] \ge 1 - {\xi _i}\;\;\;\;\;i = 1, 2, \cdots , M \end{array} $ | (7) |
式中:w为样本到分类间隔的距离;M为样本个数;ϕ(xi)为xi的映射函数;b为偏置量;ξi≥0i为松弛因子;C为松弛惩罚因子,C值越小,对误分类的惩罚减小,从而将误分类点视为噪声点,导致处于两条边界之间的样本变多(容错率高),对样本的拟合性下降,但得到的模型泛化能力更强,因为实际样本之间往往存在噪声。
然后确定核函数。目前较流行的核函数主要为多项式核函数和高斯核函数,分别为
| $ K(\mathit{\boldsymbol{x, }}{\mathit{\boldsymbol{x}}_i}) = {\left[ {\left( {\mathit{\boldsymbol{x}} \cdot {\mathit{\boldsymbol{x}}_i}} \right) + 1} \right]^q} $ | (8) |
| $ K(\mathit{\boldsymbol{x, }}{\mathit{\boldsymbol{x}}_i}) = {\rm{exp}}\left( { - \frac{{\left| {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_i}} \right|}}{{{\sigma ^2}}}} \right) $ | (9) |
式中:x为输入向量;q为多项式核函数的阶数;σ2为样本方差。
对应的分类决策函数为
| $ f\left( \mathit{\boldsymbol{x}} \right) = {\rm{sign}}\left[ {\sum\limits_{i = 1}^M {{\alpha _i}{y_i}K\left( {\mathit{\boldsymbol{x}}, {\mathit{\boldsymbol{x}}_i}} \right) + b} } \right] $ | (10) |
式中αi为拉格朗日乘子。
最后基于sigmoid函数,将训练的SVM分类器f(x)的概率输出映射到区间[0,100%],距分界面越近的点分类正确的概率越低[19-20]。
3.3.2 模型参数优选分别基于线性模型和SVM融合模型,利用裂缝敏感属性和波形指示反演预测有利储层。
图 10为不同融合模型预测的有利储层概率分布图。由图可见:①线性融合模型基本能够区分有利储层与致密层,但不能较好地区分Ⅰ类、Ⅱ类储层(图 10a)。②SVM模型的数据拟合精度较高,但受参数影响较大,不同模型的泛化能力有一定差异,表现为:高斯核函数SVM模型(图 10b)整体较多项式核函数SVM模型(图 10c、图 10d)泛化能力差,存在较严重的过拟合问题,在井轨迹数据未统计到的值域范围内,预测效果不佳,因此后者的预测效果更好。③在确定合适的核函数后,松弛惩罚因子C取较大值时,模型易受个别数据的影响,在泛化过程中,极值位置易出现与实际不符的情况(图 10c);C取较小值时,多项式核函数SVM预测效果较好(图 10d),选择该模型预测结果作为研究区的有利储层概率分布图板,对全区体数据开展储层预测。
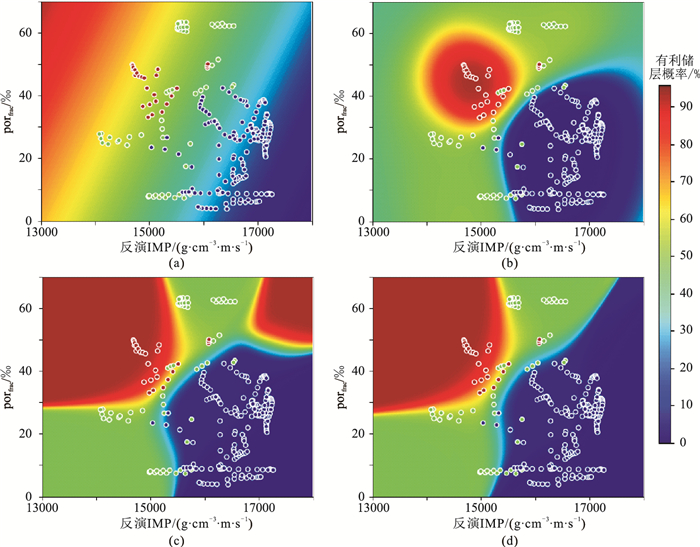
|
图 10 不同融合模型预测的有利储层概率分布图 (a)线性模型;(b)高斯核函数SVM模型;(c)多项式核函数SVM模型(C=1);(d)多项式核函数SVM模型(C=0.01) |
图 11为过bs8井和q12-18井预测剖面。由图可见:①波形指示反演受层状模型限制,对储层纵向沟通性的刻画能力有限(图 11a)。②裂缝敏感属性较好地反映了后期裂缝的空间展布(图 11b)。③数据融合方法能够表征储层的横向、纵向非均质性,预测结果更符合多因素共同控储的地质认识(图 11c、图 11d),其中SVM多数据融合预测效果(图 11d)较线性模型(图 11c)更好,准确地预测了Ⅰ类、Ⅱ类储层发育区,表明潜山表层风化壳储层较内幕储层更有利[21],bs8井和q12-18井分别钻遇2个独立油气藏,与钻井数据吻合度高。
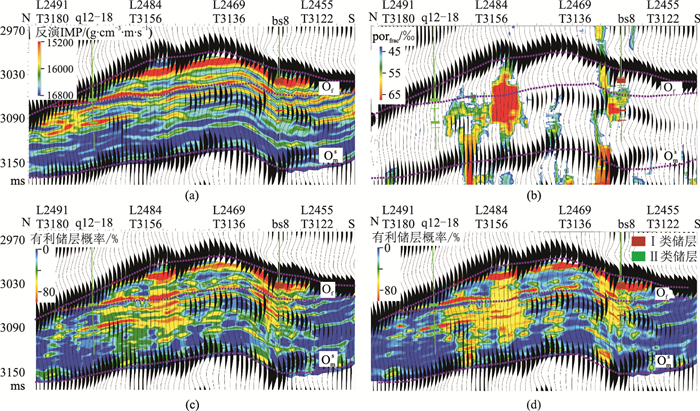
|
图 11 过bs8井和q12-18井预测剖面 (a)波形指示反演IMP;(b)裂缝孔隙度;(c)线性多数据融合;(d)SVM多数据融合 |
井间压力测试证明,bs8井与q12-18井不存在连通关系,验证了预测结果。bs8井储层发育,且纵向连通性好,在较长时间内实现了较高产能。q12-18井位于储层低部位,初期产能高,预测井间高部位储集体有较大开发潜力。
将上述最优SVM多数据融合储层预测方法推广到其他断块,开展全区分析。观察研究区目的层切片发现,有利储层发育区整体沿主要断裂呈带状分布,具有一定规模。研究区共18口井,其中高产井9口(8口位于有利储层发育区)、低产或干井共9口(8口位于非有利储层发育区),即位于预测的有利储层发育区内的钻井均取得较好产能,总体符合率接近89%(图 12)。预测结果能够指导进一步开发井位部署,推动研究区增储上产。
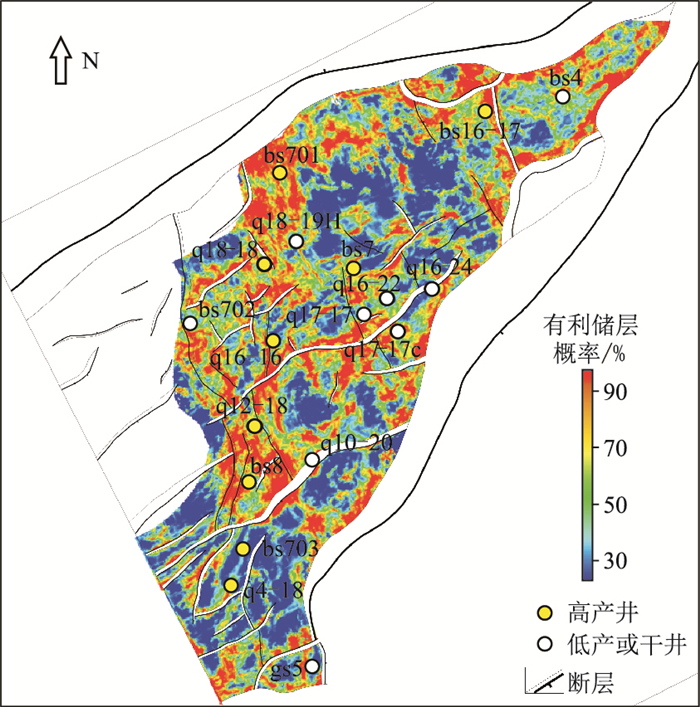
|
图 12 千米桥潜山奥陶系储层预测平面图 |
(1) 多数据融合的前提是原始单数据能够准确、可靠地反映单一控储因素。本文利用波形指示反演预测层状溶蚀孔洞储层发育区,能够有效结合地震波形特征,提高反演稳定性,取得了较好的溶蚀孔洞预测效果;基于测井约束,利用裂缝相关属性预测裂缝控制的储层,最终以拟合的裂缝孔隙度反映裂缝型储层发育区,和实际钻探情况较吻合。
(2) 在千米桥潜山,由于层状溶蚀孔洞和裂缝共同影响有利储层发育,在地质模型的指导下,基于支持向量机的融合方法,将反演结果与裂缝预测结果进行多数据融合,能够在保证层状溶蚀孔洞预测精度的同时,表征裂缝对储层的沟通作用,预测结果符合构造次生裂缝和差异岩溶作用共同控制储层发育的地质特征,井间储层预测真实性得到提高;
(3) 文中提出的针对千米桥潜山的多数据融合储层预测流程,体现了地质模型与地球物理技术结合的思想,最大化利用现有资料,对研究区的勘探、开发具推进作用。另外,融合预测技术对其他地区复杂碳酸盐岩储层预测具有一定的借鉴意义。
| [1] |
李建东, 苏立萍, 赵腊腊, 等. 大港探区千米桥奥陶系潜山裂缝分布预测[J]. 中国石油勘探, 2010, 15(5): 48-53. LI Jiandong, SU Liping, ZHAO Lala, et al. Distribution and prediction of fissures in Qianmiqiao buried hill of Ordovician[J]. China Petroleum Exploration, 2010, 15(5): 48-53. |
| [2] |
贺川航, 刘定锦, 杨东凡, 等. 曲线重构技术在碳酸盐岩薄储层的应用——以四川盆地栖霞组为例[C]. 中国石油学会2019年物探技术研讨会论文集, 2019, 592-595.
|
| [3] |
韩长城, 林承焰, 任丽华, 等. 基于地震波形指示的碳酸盐岩储集体反演方法——以塔河油田中-下奥陶统为例[J]. 石油与天然气地质, 2017, 38(4): 822-830. HAN Changcheng, LIN Chengyan, REN Lihua, et al. Waveform-indication-based seismic inversion of carbonate reservoirs: A case study of the Lower-Middle Ordovician in Tahe oilfield, Tarim Basin[J]. Oil & Gas Geology, 2017, 38(4): 822-830. |
| [4] |
张远银, 孙赞东, 韩剑发, 等. 地震约束建模的强非均质碳酸盐岩储层波阻抗反演[J]. 石油地球物理勘探, 2019, 54(6): 1316-1323. ZHANG Yuanyin, SUN Zandong, HAN Jianfa, et al. Impedance inversion of strongly heterogeneous carbonate reservoir based on amplitude-constrained mo-deling[J]. Oil Geophysical Prospecting, 2019, 54(6): 1316-1323. |
| [5] |
李祺鑫, 罗亚能, 张生, 等. 高分辨率波阻抗贝叶斯序贯随机反演[J]. 石油地球物理勘探, 2020, 55(2): 389-397. LI Qixin, LUO Yaneng, ZHANG Sheng, et al. High-resolution Bayesian sequential stochastic inversion[J]. Oil Geophysical Prospecting, 2020, 55(2): 389-397. |
| [6] |
史长林, 纪友亮, 廖前进, 等. 黄骅坳陷奥陶系碳酸盐岩潜山成藏模式[J]. 油气地质与采收率, 2009, 16(6): 29-31. SHI Changlin, JI Youliang, LIAO Qianjin, et al. Accumulation patterns of Ordovician carbonate buried hill in Huanghua Depression[J]. Petroleum Geology and Recovery Efficiency, 2009, 16(6): 29-31. DOI:10.3969/j.issn.1009-9603.2009.06.007 |
| [7] |
杨池银. 千米桥潜山凝析气藏勘探开发难点与对策分析[J]. 天然气地球科学, 2003, 14(4): 245-249. YANG Chiyin. The exploration and development difficulties and countermeasure analysis for condensate gas reservoir of Qianmiqiao Bureid Hill[J]. Natural Gas Geoscience, 2003, 14(4): 245-249. DOI:10.3969/j.issn.1672-1926.2003.04.003 |
| [8] |
李建英, 卢刚臣, 孔凡东, 等. 千米桥潜山奥陶系储层特征及孔隙演化[J]. 石油与天然气地质, 2001, 22(4): 367-371. LI Jianying, LU Gangchen, KONG Fandong, et al. Reservoir characteristics and pore evolution of Ordovician in Qianmiqiao Buried Hill[J]. Oil & Gas Geo-logy, 2001, 22(4): 367-371. DOI:10.3321/j.issn:0253-9985.2001.04.018 |
| [9] |
张学芳, 董月昌, 慎国强, 等. 曲线重构技术在测井约束反演中的应用[J]. 石油勘探与开发, 2005, 32(3): 70-72. ZHANG Xuefang, DONG Yuechang, SHEN Guoqiang, et al. Application of log rebuilding technique in constrain inversion[J]. Petroleum Exploration and Development, 2005, 32(3): 70-72. DOI:10.3321/j.issn:1000-0747.2005.03.017 |
| [10] |
杨涛, 乐友喜, 吴勇. 波形指示反演在储层预测中的应用[J]. 地球物理学进展, 2018, 33(2): 769-776. YANG Tao, YUE Youxi, WU Yong. Application of the waveform inversion in reservoir prediction[J]. Progress in Geophysics, 2018, 33(2): 769-776. |
| [11] |
陈彦虎, 毕建军, 邱小斌, 等. 地震波形指示反演方法及其应用[J]. 石油勘探与开发, 2020, 47(6): 1149-1158. CHEN Yanhu, BI Jianjun, QIU Xiaobin, et al. A method of seismic meme inversion and its application[J]. Petroleum Exploration and Development, 2020, 47(6): 1149-1158. |
| [12] |
赵凤全, 崔德育, 康婷婷, 等. 构造导向滤波技术在断裂识别中的应用[J]. 石油地球物理勘探, 2018, 53(增刊1): 214-218, 227. ZHAO Fengquan, CUI Deyu, KANG Tingting, et al. Fault identification with structure-oriented filtering[J]. Oil Geophysical Prospecting, 2018, 53(S1): 214-218, 227. |
| [13] |
王文庆, 李玉海, 卢刚臣, 等. 地震地质一体化解释技术在复杂潜山勘探中的应用——以黄骅坳陷乌马营潜山带为例[J]. 石油地球物理勘探, 2018, 53(增刊1): 242-248. WANG Wenqing, LI Yuhai, LU Gangchen, et al. Integrated seismic and geological interpretation for complicated buried hills: An example of Wumaying buried hills, Huanghua Depression[J]. Oil Geophysical Prospecting, 2018, 53(S1): 242-248. |
| [14] |
卢山, 汪勇, 贾颖超, 等. 冀中廊固凹陷杨税务潜山碳酸盐岩有利储层预测[J]. 石油地球物理勘探, 2018, 53(增刊1): 144-150. LU Shan, WANG Yong, JIA Yingchao, et al. Carbo-nate reservoir prediction in Yangshuiwu buried-hills in Langgu Sag, Jizhong[J]. Oil Geophysical Prospecting, 2018, 53(S1): 144-150. |
| [15] |
张林清, 张会星, 姜效典, 等. 弹性参数反演与属性融合技术在"甜点"预测中的应用[J]. 天然气地球科学, 2017, 28(4): 582-589. ZHANG Linqing, ZHANG Huixing, JIANG Xiao-dian, et al. Application of elastic parameters inversion and attribute fusion technology in the "sweet spot" prediction[J]. Natural Gas Geoscience, 2017, 28(4): 582-589. |
| [16] |
冯小英, 杨延辉, 左银卿, 等. 敏感属性与参数反演融合定量预测煤体结构[J]. 石油地球物理勘探, 2019, 54(5): 1115-1122. FENG Xiaoying, YANG Yanhui, ZUO Yinqing, et al. Coal structure quantitative prediction with sensitive-attribute and parameter-inversion fusion[J]. Oil Geophysical Prospecting, 2019, 54(5): 1115-1122. |
| [17] |
张长开, 姜秀娣, 朱振宇, 等. 基于支持向量机的属性优选和储层预测[J]. 石油地球物理勘探, 2012, 47(2): 282-285. ZHANG Changkai, JIANG Xiudi, ZHU Zhenyu, et al. Attributes selection and reservoir prediction based on support vector machine[J]. Oil Geophysical Prospecting, 2012, 47(2): 282-285. |
| [18] |
李雄炎, 周金昱, 李洪奇, 等. 复杂岩性及多相流体智能识别方法[J]. 石油勘探与开发, 2012, 39(2): 243-248. LI Xiongyan, ZHOU Jinyu, LI Hongqi, et al. Computational intelligent methods for predicting complex lithologies and multiphase fluids[J]. Petroleum Exploration and Development, 2012, 39(2): 243-248. |
| [19] |
Platt J. Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods[J]. Advances in Large Margin Classifiers, 1999, 10(3): 61-74. |
| [20] |
Lin H T, Lin C J, Weng R C. A note on Platt's probabilistic outputs for support vector machines[J]. Machine Learning, 2007, 68(3): 267-276. DOI:10.1007/s10994-007-5018-6 |
| [21] |
朱梓强, 卢刚臣, 李玉海, 等. 北大港潜山带翼部成藏特点及勘探前景[J]. 石油地球物理勘探, 2015, 50(1): 150-155. ZHU Ziqiang, LU Gangchen, LI Yuhai, et al. Reservoirs characteristics and exploration prospect in the flank zone of buried hills, northern Dagang[J]. Oil Geophysical Prospecting, 2015, 50(1): 150-155. |



 闫家伟, 天津市滨海新区红旗路中段中国石油集团东方地球物理公司研究院大港分院, 300280。Email:
闫家伟, 天津市滨海新区红旗路中段中国石油集团东方地球物理公司研究院大港分院, 300280。Email: 