② 中国石油冀东油田勘探开发研究院物探所, 河北唐山 063000
② Geophysical Research Institute of Jidong Petroleum Branch, Tangshan, Hebei 063000, China
在陆相断陷盆地中,断层往往控制圈闭的形成,因此准确解释断层具有重要意义。地震剖面中的同相轴错断、扭曲是明显的断层响应,但是当断层断距较小或地震资料信噪比较低时,断层解释的合理性较低,影响圈闭可靠性评价。因此,为提高断层解释精度,人们不断研究有效识别断层的方法[1-3]。
早期人们主要利用各种地震属性体(如相干[4-6]、方差[7-8]、曲率[9-10]等属性)识别断层,虽然可在一定程度上反映断层的空间特征,但对噪声很敏感,对复杂断裂的检测效果不佳。因此有必要对属性体进行断层增强处理,以更精确地识别断层。
随着人们不断研究断层识别方法,出现了许多针对断层增强的处理方法。Barnes[11]利用组合成分滤波器有效去除属性信息中的非断层成分。Donias等[12]沿着断层方向增强断层属性信息,根据断层的平面特征有效增强断层特征。Lavialle等[13]利用基于偏微分方程的非线性滤波技术,在自动提取断层之前去除非断层信息。Machado[14]设计了高斯拉普拉斯算子,沿断层方向增强断层属性的同时抑制非断层信息。Cohen等[15]、Wu等[16]通过扫描所有断层走向和倾角组合平滑断层属性,有效增强断层特征。上述断层增强算法大多首先根据属性体计算断层方向,然后增强断层方向的断层信息,压制非断层方向的其他信息(如残留地层响应、噪声等),可得到理想的计算结果,但计算精度依赖于断层方向的计算精度。
动态时间规整(Dynamic Time Warping,DTW)算法最早由Sakoe等[17]提出并用于语音识别,是一种基于动态规划的模板匹配算法,根据两个信号的相似性局部拉伸或压缩信号,使两个信号最佳匹配。在地震勘探领域,人们将DTW算法用于图像对齐、断层断距计算等方面。Anderson等[18]将DTW算法用于地球物理问题,并称这种算法为“动态波形匹配”。Hale[19]利用DTW算法匹配纵波与转换波地震数据、估计断层断距,取得了较好的效果。Wu等[20]利用DTW算法自动解释断层,在低信噪比地震数据中准确识别了断层。吴天麒等[21]提出了基于互相关的动态时间规整算法(CDTW),可将角道集同相轴拉平且对波形畸变具有良好的鲁棒性。
由于DTW方法能稳定、快速地从两个序列的误差矩阵中求出误差最小路径,因此本文利用DTW方法计算断层图像的最优断层线,并对最优断层线平滑处理,得到的断层图像较原始属性图像的断层特征更清晰、连续。模型和实际资料处理结果表明,所提方法能抑制断层图像的非断层信息,断层增强结果更清晰、连续,具有较好的鲁棒性和适用性。
1 方法原理 1.1 DTW方法原理对于给定的两个离散序列(实际上不一定与时间有关),利用DTW方法能计算它们的相似程度,并且给出一个可最大限度降低两个序列距离的点到点的匹配方案。设f(t)为参考序列,g(t)为待匹配序列,两个序列之间的对齐误差e(i,n)为序列f(i)与g(i+n)之间的欧氏距离(n为序列g(t)相对序列ft的时间滞后),f(t)与g(t)匹配后的累积对齐误差为
| $ e(i, n) \equiv[f(i)-g(i+n)]^{2} $ | (1) |
DTW求解的目标是找到一个时间序列
| $ T(t)=[T(0), T(1), \cdots, T(N-1)] $ | (2) |
使f(t)与g(t)最相似,即
| $ f(i)=g[i+T(i)] $ | (3) |
且满足
| $ T(t)=\underset{l(t)}{\arg \min }\{D[l(t)]\} $ | (4) |
其中l(t)为f(t)与g(t)对齐时(t=0,1,2,…,N-1)对应对齐误差矩阵中从点(0,0)到点(N-1,N-1)的任意一条路径(N为时间序列的长度),且D[l(t)]满足
| $ D[l(t)] \equiv \sum\limits_{i=0}^{N-1} e[i, l(i)] $ | (5) |
并服从约束条件
| $ \left| {T(i) - T(i - 1)} \right|≤1 $ | (6) |
当f(t)与g(t)对齐时,式(6)确保i+T(i)随着采样点的增加不会过快增加或减少。
1.2 最优断层线计算方法断层属性体局部极大值(或极小值)处往往指示断层,断层线的脊线由断层图像中连续属性极值点组成。若将断层属性图像看作DTW的对齐误差矩阵,将DTW求解对齐误差最小值路径相应地变为求解最大值路径,则求取属性图像中的最优断层线变为求取图像中最大值路径问题
| $ \underset{j(i)}{\arg \max }\left\{\sum\limits_{i=1}^{N} C[i, j(i)]\right\} $ | (7) |
式中:j(i)为路径上的纵坐标i(对应垂直方向)对应的横坐标(对应水平方向);C[i,j(i)]为路径上对应的属性值,其约束条件为
| $ |j(i+1)-j(i)| \leqslant \varepsilon \quad 0<\varepsilon \leqslant 1 $ | (8) |
式中ε为计算断层线时的斜率约束,以保证在计算最优路径过程中相邻点之间不会偏离横坐标方向,从而产生过大的横向位移。因此,在计算最优断层线时,为了确保斜率约束的作用,断层必须是近于垂直的。文中以只有一条近垂直断层的断层属性图像(图 1b)为例,说明利用DTW计算最优断层线的方法,具体步骤如下。
|
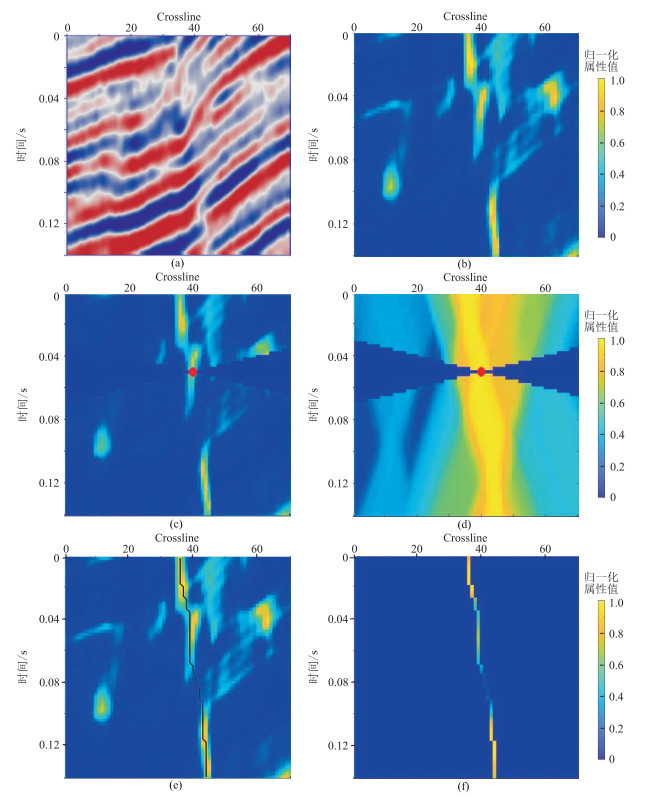
图 1 最优断层线计算结果 (a)原始地震图像;(b)断层属性图像;(c)控制点设置;(d)非线性平滑;(e)计算出的最优断层线;(f)断层增强结果 |
(1) 选取断层上的一个点作为控制点,将断层图像中控制点左、右两侧锥形区域的数据置0(图 1c),确保计算出的最优断层线从控制点通过。
(2) 本文采用Hale[19]提出的三阶段算法(非线性平滑、正向积累和反向追踪)求解断层图像中的最大值路径(最优断层线),求解过程如下。
1) 非线性平滑
| $ f(0, j)=g(0, j) $ | (9) |
| $ \begin{array}{l} f(i, j)=g(i, j)+ \\ \qquad \max \left\{\begin{array}{l} f(i-d, j-1)+\sum\limits_{k=i-d+1}^{i-1} g(k, j-1) \\ f(i-1, j) \\ f(i-d, j+1)+\sum\limits_{k=i-d+1}^{i-1} g(k, j+1) \end{array}\right. \end{array} $ | (10) |
式中:d=[1/ε]为1/ε的取整;i=1,2,3,…,N-1;g(i,j)为输入属性图像;f(i,j)为正向积累(从上至下)计算的图像值,横坐标i对应图像的行方向,纵坐标j对应图像的列方向。
相似地,反向积累(从下至上)计算的图像值为
| $ b(N-1, j)=g(N-1, j) $ | (11) |
| $ \begin{array}{l} b(i, j)=g(i, j)+ \\ \qquad \max \left\{\begin{array}{l} b(i+d, j-1)+\sum\limits_{k=i+1}^{i+d-1} g(k, j-1) \\ b(i+1, j) \\ b(i+d, j+1)+\sum\limits_{k=i+1}^{i+d-1} g(k, j+1) \end{array}\right. \end{array} $ | (12) |
式中i=N-2,N-3,…,0。图像的双边平滑为
| $ s(i, j)=f(i, j)+b(i, j)-g(i, j) $ | (13) |
在正向、反向计算过程中加入低斜率约束平滑,使平滑后的断层图像更平滑、连续,确保计算出的断层线更准确。为了确保计算出的断层线经过控制点,同样在平滑后图像中将控制点左、右锥形区域的数据置0(图 1d)。
2) 正向积累
采用正向积累(式(10))计算平滑后图像的正向积累图像a。
3) 反向追踪
首先找出a中第N-1行中的最大值的点,其位于第l列。然后对a从第N-1行中的最大值的点开始向前依次搜索前一行的最大值,直到找到最大值路径上的所有点(图 1e中的黑线),得到最大值路径,即
| $ j(N-1)=l $ | (14) |
| $ \begin{array}{l} j(i-1)= \\ \qquad \max \limits_{l-1, l, l+1} \left\{\begin{array}{l} a(i-d, l-1)+\sum\limits_{k=i-d+1}^{i-1} s(k, l-1) \\ a(i-1, n) \\ a(i-d, l+1)+\sum\limits_{k=i=d+1}^{i-1} s(k, l+1) \end{array}\right. \end{array} $ | (15) |
式中i=N-1,N-2,…,1。
(3) 计算出最优断层线后,仅保留原始断层图像中最优断层线上的属性值,再沿断层线对断层属性值平滑处理,即可得到最终断层增强结果(图 1f)。若经过控制点的最大值路径记为L(i)=[i,j(i)],i=0,1,2,…,N-1,则该断层线上的新属性值为
| $ C_{\text {new }}[i, j(i)]=\langle C[L(i)]\rangle $ | (16) |
式中:C[L(i)]为断层线的原始属性值;〈·〉表示沿路径的一维高斯平滑。
1.3 断层增强处理流程实际断层属性图像中的断层不能直接用最优断层线计算方法增强处理。本文的断层增强处理方法是将复杂断层分解为局部窗口内的简单断层,然后在局部窗口内计算最优断层线,最后综合局部最优断层线得到最终的复杂断层增强结果。以原始断层图像(图 2a)中的断层为例,说明断层增强的具体实现步骤。
|
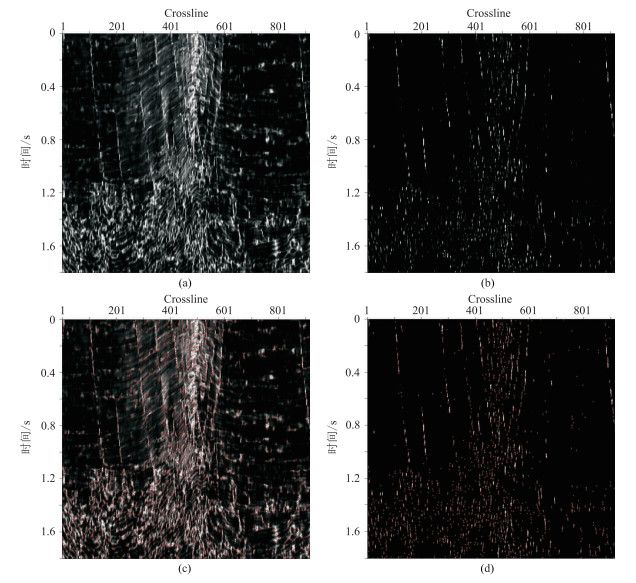
图 2 断层图像滤波及种子点选取效果 (a)原始断层图像;(b)去除非断层信息断层图像;(c)去除非断层信息前选择的种子点;(d)去除非断层信息后选择的种子点 |
为了准确选取分布在断层上的种子点,首先采用组合成分滤波器[9]对断层属性图像滤波处理,去除断层图像中的非断层信息。
组合成分滤波器是一种组合滤波器,相当于构建了一个协方差矩阵
| $ \boldsymbol{E}=\left[\begin{array}{lll} E_{x x} & E_{x y} & E_{x z} \\ E_{y x} & E_{y y} & E_{y z} \\ E_{z x} & E_{z y} & E_{z z} \end{array}\right] $ | (17) |
其中
| $ E_{p q}=\frac{\sum\limits_{i_{1}=1}^{U} \sum\limits_{i_{2}=1}^{V} \alpha_{i_{1}, i_{2}}\left(i_{1}-\bar{p}\right)\left(i_{2}-\bar{q}\right)}{\sum\limits_{i_{1}=1}^{U} \sum\limits_{i_{2}=1}^{V} \alpha_{i_{1}, i_{2}}} $ | (18) |
式中:αi1,i2为断层属性;U、V分别为计算窗口行、列采样点数目;p、q分别为x、y、z三个方向中的任意两个方向;p、q分别为计算窗口行、列的中心点坐标,并有
| $ \bar{p}=\frac{\sum\limits_{i_{1}=1}^{U} \sum\limits_{i_{2}=1}^{V} i_{1} \alpha_{i_{1}, i_{2}}}{\sum\limits_{i_{1}=1}^{U} \sum\limits_{i_{2}=1}^{V} \alpha_{i_{1}, i_{2}}} $ | (19) |
式中p为计算窗口p方向的中心点坐标。同理,也可得出q方向的中心点坐标。
对式(17)进行特征分解得到相应的特征值λ1、λ2、λ3,其中λ1≥λ2≥λ3,对应的特征向量分别为e1、e2、e3。向量e1和e2能确定当前窗口数据的最佳拟合平面(断层平面),e3垂直于最佳拟合平面。根据特征向量分别计算当前点面状构造置信度Λ=(λ2-λ3)/λ1、当前点所在断层主方向及当前点到拟合断层面的欧式距离R。再根据这3个参数设计3个带通滤波器剔除非高角度的拟合平面及Λ较小、R较大的点。由这3个滤波器组成1个组合滤波器可剔除断层图像中的非断层信息(图 2b)。
1.3.2 种子点选取为了获取均匀分布在断层上的种子点(图 2c、图 2d),在去除非断层信息的断层图像中,使用非极大值抑制筛选fast(Features from Accelerated Segment Test)特征点的方法获取种子点。该方法先采用非极大值抑制的方法保留去除非断层信息后断层属性图像脊线上的值,将其他区域的数据置零,得到细化的属性图像。然后从细化的属性中选择种子候选点(保留断层图像属性值中大于某个阈值的所有像素点作为候选点)。再按属性值从大到小的顺序依次选择所有满足条件的候选点作为种子点。在选择种子点时,计算当前候选点和所有候选点之间的欧氏距离,只有候选的种子点与已选择的种子点的最小距离大于预定义的距离阈值r时,当前候选点才被选为种子点。
1.3.3 种子点断层方向计算由于断层不一定是近于垂直的,因此计算前需要估算每个种子点的断层方向(图 3a),这样可以沿着断层方向选取数据进行计算,确保在计算最优路径时局部窗口内断层是近于垂直的(图 3b)。结合先验信息与计算出的断层方向,进一步去掉方向与断层方向不一致的种子点。

|
图 3 断层方向计算及沿断层方向选取数据效果
(a)断层方向扫描;(b)沿断层选取计算数据 沿红框的局部窗口选择数据,断层近于垂直 |
为了更好地估计多方向相交的断层方向,采用方向扫描的方法大致估算每个种子点断层的走向(倾角)。这里定义每个扫描方向的置信度为
| $ Q(\theta)=\sum\limits_{i_{3}=1}^{H} C\left(\theta, P_{i_{3}}\right) $ | (20) |
式中:C(θ,Pi3)为断层属性值,θ为当前扫描的角度,Pi3为当前扫描方向的点;H为倾角扫描数量。从0°~180°每隔一定角度计算当前角度的置信度,Q(θ)最大时对应的θ即为当前种子点所在断层的断层倾角(图 3a中的红线)。由于本文研究的断层为高角度断层且不需要精确估计断层方向,因此扫描间隔(10°)较大,且倾角扫描范围为60°~120°。
1.3.4 种子点最优路径计算对于每个种子点,本文选取一个以种子点为中心的矩形窗口,在这个窗口内计算通过种子点的最优路径。假设断层倾角扫描的方向为u,垂直于断层倾向为v,在选择矩形窗口时,使矩形的长边平行于u。在这样的局部窗口内断层是近于垂直的,此时在每个种子点局部窗口内计算断层线的方法与最优断层线计算方法一致。
1.3.5 断层增强处理由断层增强结果(图 1f)可见,平滑后路径上的属性分布与原始属性分布(图 1b)一致,即原始属性值越大,平滑后路径上的属性值也越大。将所有种子点的计算结果累加,经归一化得到最终的断层增强结果。在完成累加计算后,经过多个路径的点可能是真正位于断层上的点,往往具有较高的属性值计算结果,而经过路径少的点一般指示噪声区域,往往具有较低的属性值计算结果,因此可以设置一个阈值去除非断层上的点。若点(i,j)有m个种子点的最优路径经过,第m个种子点在点(i,j)平滑后的新属性值为Cnew(m),则对所有路径进行平滑处理并累加后,点(i,j)最终的新属性值为
| $ C_{\text {final }}(i, j)=\sum\limits_{i_{4}=1}^{m} C_{\text {new }}\left(i_{4}\right) $ | (21) |
为了验证本文方法的可行性,采用卷积神经网络(CNN)训练地震断层模型的方法[22]制作未加噪(图 4a)、加噪(图 5a)地震模型进行验证,模型中存在平行和相交断层。
|
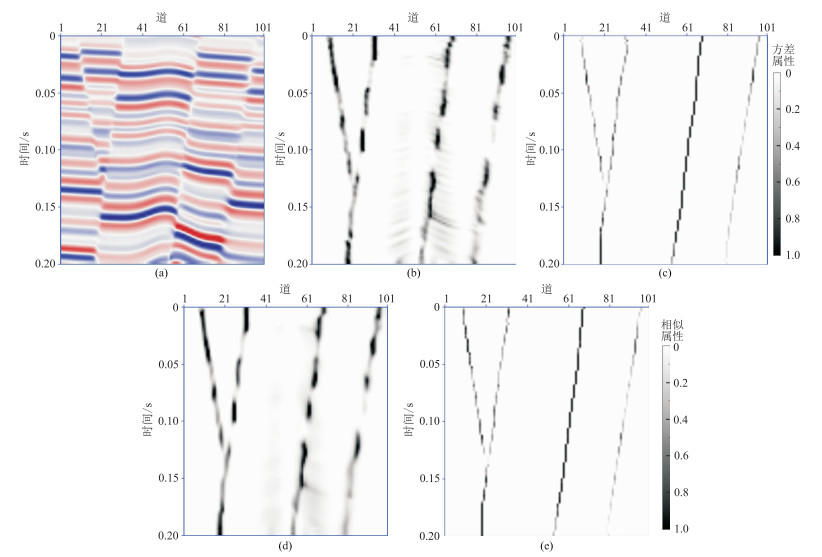
图 4 本文方法对未加噪地震模型的断层增强处理效果
(a)地震正演模型;(b)方差属性;(c)图b增强结果;(d)相似属性;(e)图d增强结果 种子点的预定义欧式距离阈值r=6,倾角扫描间隔Δθ=10°,每个种子点的矩形窗尺度为51×21 |
|
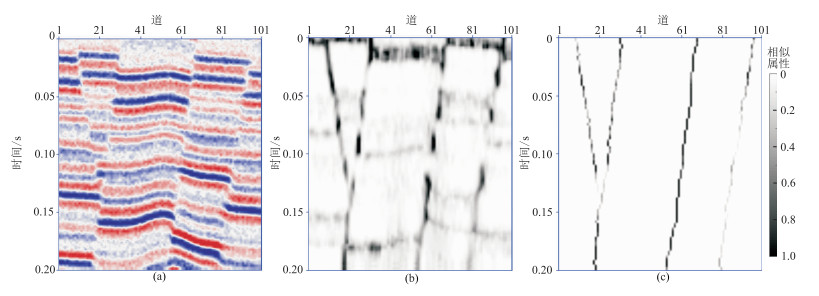
图 5 本文方法对加噪地震模型断层增强处理效果 (a)地震正演模型;(b)相似属性;(c)增强结果 |
由未加噪模型方差属性(图 4b)的增强结果(图 4c)、相似属性(图 4d)的增强结果(图 4e)可见,相交断层的交切关系清楚,在保持断层趋势的同时,断层增强结果更连续、清晰。由加噪模型相似属性(图 5b)的增强结果(图 5c)可见,完全去除了非断层信息,相交断层的交切关系清楚,断层增强结果更连续、清晰。上述结果说明本文方法的抗噪性较好,具有较强的鲁棒性。
此外,对比图 4e和图 5c可见,两者存在细小的局部差异,局部断层线相差1个像素点。这是由于噪声影响相似属性的局部计算结果所致,说明本文算法的增强结果依赖于属性体的断层检测精度,即属性体的断层检测精度越高,增强结果越接近于断层的真实形态。
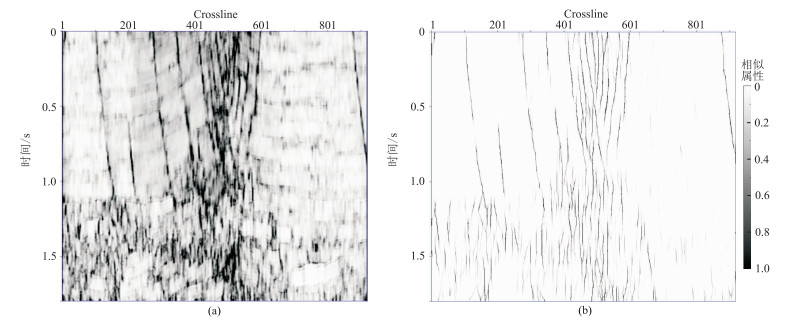
3 实际资料处理为了进一步测试本文算法对实际数据的断层增强效果,选取实际地震资料进行验证。地震数据取自中国东部F油田,该油田处于陆相断陷湖盆,盆地内断裂极其发育,对油气的形成具有控制作用。由于断层间距较小,小断层发育,在相似属性剖面上断层响应互相干扰,噪声导致断层特征不清晰,存在明显的地层残留响应,在纵向上某些断层呈断续的“线段”(图 6a)。经过断层增强处理,基本去除了非断层信息,断层更连续、清晰(图 6b)。
|
图 6 F油田的二维地震剖面A的断层相似属性(a)及其断层增强结果(b) 剖面上部存在一个花状构造,断裂发育,剖面下部断裂多为小断裂 |
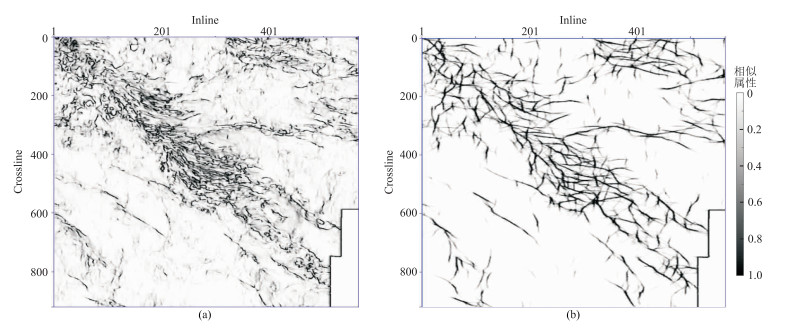
图 7为F油田的断层相似属性水平切片及其断层增强结果。由图可见:①在相似属性水平切片中断层特征不明显,噪声导致部分断层特征不清晰(图 7a);②经过断层增强处理,采用倾角约束得到的最优断层线是沿一定角度缓慢变化的曲线(图 7b),不仅保持了原有断层特征,断层分布、延伸特征更清晰、干脆,明显增强了断层的线性特征,相应地去掉了一些非线性(图 7a中的“圆圈状”信息)局部特征。
|
图 7 F油田的断层相似属性水平切片(a)及其断层增强结果(b) |
基于DTW的断层增强方法不仅适用于简单组合断层的增强处理,而且也适用于复杂组合断层的增强处理。模型试算和实际地震资料处理结果表明,该方法的断层增强效果较好,具有实际应用价值。
(1) 根据DTW方法能稳定、高效地从两个序列的误差矩阵中计算出最小误差路径的特点,将其用于计算断层图像的最优断层线,不受噪声等非断层信息的影响,具有较好的抗噪性和鲁棒性。
(2) 运用非线性平滑、正向积累和反向追踪等方法有效提高了最优断层线的求解精度。
(3) 采用组合成分滤波器[11]对断层属性图像滤波,能较好地去除非断层信息。然后采用非极大值抑制筛选fast特征点的方法选择种子点,能保证种子点均匀分布于断层上,可有效减少种子点数量,提高算法效率。
(4) 基于断层在平面上具有线性特征、在空间上具有平面特征的假设,本文使用DTW方法计算最优断层线。经过算法处理,完全去除了断层属性图像中的非断层信息,使断层更连续、清晰,断层分布、延伸特征更明显,同时去除了地震属性图像中的一些非线性局部特征。本文算法旨在增强地震属性图像中的断层信息,因此去除非断层信息并不影响最终的断层增强结果。
| [1] |
李军, 张军华, 龚明平, 等. 基于魔方矩阵的断层检测方法[J]. 石油地球物理物探, 2018, 53(3): 552-557. LI Jun, ZHANG Junhua, GONG Mingping, et al. Fault detection based on magic matrix[J]. Oil Geophysical Prospecting, 2018, 53(3): 552-557. |
| [2] |
彭达, 肖富森, 冉崎, 等. 基于倾角导向梯度能量熵的断层检测方法[J]. 石油地球物理物探, 2019, 54(1): 191-197. PENG Da, XIAO Fusen, RAN Qi, et al. Fault identification based on dip-oriented gradient energy-entropy coherence estimation[J]. Oil Geophysical Prospecting, 2019, 54(1): 191-197. |
| [3] |
王静, 张军华, 冯德永, 等. 利用不连续性的各向异性扩散滤波方法识别断层[J]. 石油地球物理物探, 2020, 55(6): 1349-1357. WANG Jing, ZHANG Junhua, FENG Deyong, et al. Fault identification based on a discontinuous anisotropic diffusion filter[J]. Oil Geophysical Prospecting, 2020, 55(6): 1349-1357. |
| [4] |
Marfurt K J, Kirlin R L, Farmer S L, et al. 3-D seismic attribute using a semblance-based coherency algorithm[J]. Geophysics, 1998, 63(4): 1150-1165. DOI:10.1190/1.1444415 |
| [5] |
Marfurt K J, Sudhaker V, Gersztenkorn A, et al. Coherency calculations in the presence of structural dip[J]. Geophysics, 1999, 64(1): 104-111. DOI:10.1190/1.1444508 |
| [6] |
蔡涵鹏, 胡光岷, 贺振华, 等. 基于非线性变时窗相干算法的不连续性检测方法[J]. 石油地球物理勘探, 2016, 51(2): 371-375. CAI Hanpeng, HU Guangmin, HE Zhenhua, et al. Subtle discontinuity detection with nonlinear variable-time window coherency algorithm[J]. Oil Geophysical Prospecting, 2016, 51(2): 371-375. |
| [7] |
Van Bemmel P P, Pepper R E F.Seismic signal processing method and apparatus for generating a cube of variance values[P].U.S.Patent 6, 2000, 151, 555.
|
| [8] |
汪杰, 汪锐. 基于方差相干体的断层识别方法[J]. 工程地球物理学报, 2016, 13(1): 46-51. WANG Jie, WANG Rui. Fault identification method based on variance-coherence cubes[J]. Chinese Journal of Engineering Geophysics, 2016, 13(1): 46-51. DOI:10.3969/j.issn.1672-7940.2016.01.008 |
| [9] |
Al-Dossary S, Marfurt K J. 3D volumetric multispectral estimates of reflector curvature and rotation[J]. Geophysics, 2006, 71(5): P41-P51. DOI:10.1190/1.2242449 |
| [10] |
杨国权, 刘延利, 张红文. 曲率属性计算方法研究及效果分析[J]. 地球物理学进展, 2015, 30(5): 2282-2286. YANG Guoquan, LIU Yanli, ZHAGN Hongwen. The calculation method of curvature attributes and its effect analysis[J]. Progress in Geophysics, 2015, 30(5): 2282-2286. |
| [11] |
Barnes A E. A filter to improve seismic discontinuity data for fault interpretation[J]. Geophysics, 2006, 71(3): P1-P4. DOI:10.1190/1.2195988 |
| [12] |
Donias M, David C, Berthoumieu Y, et al. New fault attribute based on robust directional scheme[J]. Geophysics, 2007, 72(4): P39-P46. DOI:10.1190/1.2718605 |
| [13] |
Lavialle O, Pop S, Germain C, et al. Seismic fault preserving diffusion[J]. Journal of Applied Geophysics, 2007, 61(2): 132-141. DOI:10.1016/j.jappgeo.2006.06.002 |
| [14] |
Machado G.Improving Fault Images Using A Directional Laplacian of A Gaussian Operator[D].University of Oklahoma, 2015.
|
| [15] |
Cohen I, Coult N, Vassiliou A A. Detection and extraction of fault surfaces in 3D seismic data[J]. Geophysics, 2006, 71(4): P21-P27. DOI:10.1190/1.2215357 |
| [16] |
Wu X, Zhu Z. Methods to enhance seismic faults and construct fault surfaces[J]. Computers & Geosciences, 2017. DOI:10.1016/j.cageo.2017.06.015 |
| [17] |
Sakoe H, Chiba S. Dynamic programming algorithm optimization for spoken word recognition[J]. IEEE Transactions on Acoustics, Speech, and Signal Proce-ssing, 1978, 26(1): 43-49. DOI:10.1109/TASSP.1978.1163055 |
| [18] |
Anderson K, Gaby J. Dynamic waveform matching[J]. Information Sciences, 1983(83): 90054-3. DOI:10.1016/0020-0255(83)90054-3 |
| [19] |
Hale D. Dynamic warping of seismic images[J]. Geophysics, 2013, 78(2): S105-S115. DOI:10.1190/geo2012-0327.1 |
| [20] |
Wu X, Fomel S. Automatic fault interpretation with optimal surface voting[J]. Geophysics, 2018, 83(5): O67-O82. DOI:10.1190/geo2018-0115.1 |
| [21] |
吴天麒, 王云专, 郭雪豹, 等. 基于互相关改进的DTW在角道集叠加优化中的应用[J]. 地球物理学进展, 2020, 35(5): 1878-1887. WU Tianqi, WANG Yunzhuan, GUO Xuebao, et al. The application of improved dynamic time warping in angle-domain gather stacking[J]. Progress in Geophysics, 2020, 35(5): 1878-1887. |
| [22] |
Wu X, Geng Z, Shi Y, et al. Building realistic structure models to train convolutional neural networks for seismic structural interpretation[J]. Geophysics, 2020, 85(4): WA27-WA39. DOI:10.1190/geo2019-0375.1 |



 董林, 山东省青岛市黄岛区长江西路66号中国石油大学(华东), 266580。Email:
董林, 山东省青岛市黄岛区长江西路66号中国石油大学(华东), 266580。Email: 