2 成都理工大学地球勘探与信息技术教育部重点实验室, 四川成都 610059;
3 电子科技大学资源与环境学院, 四川成都 611731
2 Key Lab of Earth Exploration & Information Techniques of Ministry of Education, Chengdu University of Technology, Chengdu, Sichuan 610059, China;
3 School of Resources and Environment, University of Electronic Science and Technology of China, Chengdu, Sichuan 611731, China
储层裂缝往往在石油与天然气的运移、聚集和成藏等方面发挥着控制作用,但裂缝预测至今仍然属于世界性的研究难点和热点问题。近几十年来,在油气勘探、开发领域,尽管已经形成了野外露头与岩心观察、测井解释[1]、裂缝建模[2]、应力与应变数值模拟[3]、纵波裂缝预测[4](利用相干、曲率、倾角、边缘预测、蚂蚁体追踪、各向异性等)、转换波与横波裂缝预测(利用横波分裂、相对时差、能量比值、最小二乘拟合、Alford旋转)和多波联合裂缝预测等多种裂缝预测方法[5-7],但是针对储层裂缝的三维空间分布预测,受各类方法的适用范畴、数据条件(如转换波或横波地震数据因处理难度大、成本高,而未被普遍采集)、预测精度等多种因素的影响,至今纵波相干体属性仍然是最广泛的裂缝预测手段。
自1995年Bahorich等[8]基于互相关的相干体技术提出三维地震数据相干体(第一代相干,C1)的概念之后,地震相干技术被迅速地应用于油气勘探,计算方法也得到不断发展。C1算法计算量小、易于实现,但不适合低信噪比或存在相干噪声的地震资料。Marfurt等[9]在C1基础上提出了基于多道相似的相干技术(第二代相干,C2),在一定程度上弥补了C1的缺点,但对波形和横向振幅的变化敏感。为了提高横向分辨率,Gersztenkorn等[10]提出了基于本征值结构的第三代相干体技术(C3),具有很高的横向分辨率,但计算量大,而且对倾角不太敏感[4, 11]。梯度结构张量(Gradient Structure Tensor,GST)算法最初主要用于区分图像的平坦、边缘及角点区域,由Randen[12]、Bakker[13]、Faraklioti等[14]最早引入地震勘探,发展了基于GST的相干技术。相比于C3,GST相干技术包含反射界面的倾角和方位角信息,可依据地质体的结构特征直观地提取相干属性,物理特性更明确,因此能更好地描述三维地震数据的结构特征[15],从而更精细地描述地层非连续性变化细节。
近年来,中国的GST相干技术得到进一步发展,在实际应用中取得了不俗的效果。张军华等[15]在GST计算过程中引入高斯函数,提高了相干属性的分辨能力和抗噪性;陈双全等[16]将地震数据瞬时相位作为输入,利用复地震道数据对地震GST的偏导数进行平滑处理,较好地消除了由于噪声而产生的不稳定性;唐成勇[17]通过改进张量平滑函数,采用多尺度径向函数将奇、偶对称敏感的GST生成多个尺度的地震相干属性;陈强等[18]利用GST矩阵特征值计算Chaos及其边缘属性,精细识别和解释了采空区;问雪等[19]研究了基于GST的结构导向平滑方法,有效改善了地震资料品质,为解释断层提供了基础数据;王清振等[20]利用GST检测盐丘,取得了良好的效果;王震等[21]利用GST方法并融合反演孔隙度数据以及蚂蚁属性数据体,进一步表征了断溶体内部溶洞及断裂发育特征,形成了一套刻画断溶体外部轮廓及内部结构的技术;彭达等[22]提出了一种基于倾角导向梯度能量熵的相干分析方法,可以有效地解释三维断层及其边界。从上述研究与应用效果可见,GST相干技术在识别特殊地质构造和断裂特征方面具有明显优势。
GST相干技术能够精细地描述三维地震数据的结构特征,但严重依赖于地震资料品质,尤其对低信噪比的地震资料难以获得理想的计算效果。在提高地震资料信噪比的滤波过程中,在压制剩余噪声的同时会损失部分有效信号,若滤波不当,可能会损失小断距的断层信息,造成大断距的断层出现连续反射现象,对断层解释造成干扰[23]。为此,人们提出了构造导向滤波技术,能在保护地质构造信息的同时压制剩余噪声,在控制噪声和保护有效信号之间保持平衡。Fehmers等[24]最早将构造导向滤波技术应用于构造解释,近年来在业界获得了广泛应用。尹川等[25]结合地层反射倾角信息利用各向异性滤波对复杂构造低品质地震资料滤波处理,提高了信噪比,突出了断层边界特征;黄立良等[26]应用构造导向滤波技术识别隐蔽断层;庄益明等[27]提出并应用构造导向滤波、蚂蚁追踪技术解释煤矿采区断层;赵风全等[28]利用构造导向滤波技术识别断裂,提高了断层识别精度;王静等[29]提出了基于不连续性的三维各向异性扩散滤波方法,在保护断层等不连续边界信息的同时,在连续地层区域增强了同相轴的连续性,为断层解释提供了良好的数据基础。可见,构造导向滤波对于断层的识别和解释十分有利,具有推广应用价值。
GST相干技术和构造导向滤波技术在断层解释方面各具优势,但将二者结合的应用实例并不多见。为此,本文提出基于构造导向滤波与GST相干属性的储层裂缝预测方法。利用构造导向滤波技术提升地震数据的信噪比和突出断裂特征信息,利用GST相干技术描述地震数据的结构特征;再结合沉积、构造、地层微电阻率扫描成像(FMI)测井等综合信息,从地质、地球物理等多角度精细预测裂缝响应特征及走向、发育密度等,形成了基于构造导向滤波与GST相干属性的储层裂缝预测方法。利用该方法对川西龙门山山前复杂构造带的雷口坡组气藏进行基于构造导向滤波的地震数据优化处理和GST属性计算,精细识别了储层的中、小尺度断裂,为气藏的勘探、开发提供了方法支撑。
1 方法原理 1.1 基于构造导向滤波的地震数据优化处理方法构造导向滤波采用各向异性扩散补偿算法,对叠后三维地震数据进行特殊去噪。该法只对平行于反射层方向做平滑,因此首先计算数据体内各样本部位的反射层倾角、倾向和方位角。构造导向滤波不做超出断层或者岩性边界的平滑操作,在有效压制噪声的同时突出地震数据的断裂特征、保持边界信息,获得用于精细解释和预测断裂的基础数据[17]。
各向异性扩散滤波方法最早用于图像处理和分析领域,但由于该方法采用线性算子对含噪图像进行滤波,在削弱噪声的同时也破坏了图像的边缘信息。为了保持图像的结构信息,Weickert等[30]在前人的研究基础上,提出了基于结构张量的各向异性扩散滤波模型(即构造导向滤波)
| $ \frac{{\partial u}}{{\partial t}} = {\rm{div}}\left( {{\mathit{\boldsymbol{D}}}\nabla u} \right) $ | (1) |
式中:u为待处理图像,如地震图像;t为扩散时间;D为扩散张量。Fehmers等[24]将式(1)引入地震勘探,发现经过几次迭代运算,小断层等细小结构特征被抹除。为此,在式(1)中引入一个连续因子ε,改进后的方程为
| $ \frac{{\partial u}}{{\partial t}} = {\rm{div}}\left( {\varepsilon {\mathit{\boldsymbol{D}}}\nabla u} \right) $ | (2) |
式中0 ≤ε≤ 1。在断层附近,ε≈0,在远离断层处,ε≈1。
1.2 基于GST的地震相干属性计算方法基于GST的相干属性计算方法主要包括两个步骤:首先计算三维地震数据每一点的方向导数矢量,在此基础上构建GST;然后计算特征值和特征向量,利用特征值进行组合即可定义GST相干属性。
定义一个三维地震数据体u(x,y,z)的方向导数矢量
| $ {\mathit{\boldsymbol{g}}} = \nabla u\left( {x, y, z} \right) = \left[ \begin{array}{l} \frac{{\partial u\left( {x, y, z} \right)}}{{\partial x}}\\ \frac{{\partial u\left( {x, y, z} \right)}}{{\partial y}}\\ \frac{{\partial u\left( {x, y, z} \right)}}{{\partial z}} \end{array} \right] = \left[ \begin{array}{l} {g_x}\\ {g_y}\\ {g_z} \end{array} \right] $ | (3) |
式中
利用方向导数构建GST
| $ \begin{array}{l} \;\;\;{\mathit{\boldsymbol{T}}} = \left[ \begin{array}{l} {T_{11}}\;\;{T_{12}}\;\;{T_{13}}\\ {T_{21}}\;\;{T_{22}}\;\;{T_{23}}\\ {T_{31}}\;\;{T_{32}}\;\;{T_{33}} \end{array} \right] = \\ {\mathit{\boldsymbol{g}}}{{\mathit{\boldsymbol{g}}}^{\rm{T}}} = \left[ \begin{array}{l} \;g_x^2\;\;{g_x}{g_y}\;\;{g_x}{g_z}\\ {g_y}{g_x}\;\;g_y^2\;\;{g_y}{g_z}\\ {g_z}{g_x}\;\;{g_z}{g_y}\;\;g_z^2 \end{array} \right] \end{array} $ | (4) |
将T用特征值和特征向量表示为
| $ {\mathit{\boldsymbol{T}}}= \left( {{{\mathit{\boldsymbol{v}}}_1}\;\;{{\mathit{\boldsymbol{v}}}_2}\;\;{{\mathit{\boldsymbol{v}}}_3}} \right)\left( \begin{array}{l} {\lambda _1}\;\;0\;\;0\\ 0\;\;{\lambda _2}\;\;0\\ 0\;\;0\;\;{\lambda _3} \end{array} \right){\left( {{{\mathit{\boldsymbol{v}}}_1}\;\;{{\mathit{\boldsymbol{v}}}_2}\;\;{{\mathit{\boldsymbol{v}}}_3}} \right)^{\rm{T}}} $ | (5) |
式中:λ1、λ2、λ3为T的三个非负特征值,且满足λ1≥λ2≥λ3≥ 0;v1、v2、v3分别为λ1、λ2、λ3对应的特征向量。v1、v2、v3构成了一个局部的正交坐标系,v1为局部领域内对比度最大的方向(信号的梯度方向),v2和v3构成一个垂直于v1的局部平面。
通过得到的v1,可定义GST倾角
| $ {\rm{dip = arctan}}\left[ {\frac{{{v_1}\left( z \right)}}{{\sqrt {v_1^2\left( x \right) + v_1^2\left( y \right)} }}} \right] $ | (6) |
和方位角
| $ {\rm{azimuth = arctan}}\left[ {\frac{{{v_1}\left( y \right)}}{{{v_1}\left( x \right)}}} \right] $ | (7) |
式中v1(x)、v1(y)、v1(z)是v1的三个方向分量。
通过得到的λ1即可定义GST相干属性
| $ C = \frac{{{\lambda _1}}}{{{\rm{Tr}}\left( {\mathit{\boldsymbol{T}}} \right)}} $ | (8) |
式中Tr(T)表示T的迹。
2 方法实现思路基于构造导向滤波与GST相干属性的储层裂缝预测流程为(图 1):①利用GST算法计算叠后三维地震数据体反射层的倾角、方位角以及初始GST相干属性。②使用初始GST相干属性估算连续性。若不连续性很强,则算法不对数据平滑;若连续性较弱,则算法沿着倾角、倾向平滑;若不连续性中等,算法将输出与原始样本值混合,这一过程重复进行直至整个数据体达到平滑。窗口出现明显不连续性即可终止迭代,得到构造导向滤波数据体。③在构造导向滤波数据体的基础上再次计算基于GST算法的倾角、方位角属性,利用构造导向滤波数据体和倾角数据即可提取最终的GST相干属性;同时使用传统方法计算相干属性,与最终的GST相干属性进行对比、分析。④将构造导向滤波后的GST相干属性与地震剖面叠加显示,展示最终预测的储层裂缝。
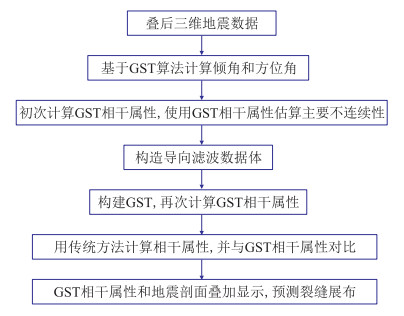
|
图 1 基于构造导向滤波与GST相干属性的储层裂缝预测流程 |
川西龙门山山前构造带夹持于关口断裂与彭县断裂之间,其主体部位发育金马—鸭子河、石羊场两个完整的次级构造[31]。彭州地区雷口坡组分布于龙门山山前构造带中部,主要含气层为雷口坡组四段(雷四段)。雷四段储层主要为碳酸盐岩局限台地—蒸发沉积,发育潟湖、潮坪、台内滩和台缘滩亚相[32]。
雷四段纵向上可划分为上、中、下三个亚段,上亚段白云岩储层横向分布非常广泛,总体具有厚度大、物性优、含气性好的特点,是雷四段气藏的主要聚集段。雷四段上亚段从上至下在岩性、储集空间类型及含气性3个方面上又具有一定的差异性,可进一步划分为上、下两个储层。上储层平均厚度约为35m,岩性以藻砂屑灰岩和微晶白云质灰岩为主,夹杂白云岩;下储层平均厚度为65m,岩性以白云岩类为主[33-34]。雷四段上亚段储层白云岩的孔隙和裂缝较为发育,形成了孔隙—裂缝性储层,主要发育构造裂缝,其次为成岩裂缝[35]。裂缝的非均质性强,影响因素、分布范围、尺度规模、发育密度等特征十分复杂。此外,由于区域构造复杂,雷四段储层埋深大(埋深约为6000m),导致地震资料信噪比低、频带窄、分辨率有限。因此,为了提高储层裂缝预测精度,需要针对性地开展地震数据优化处理。
3.2 地震数据的构造导向滤波优化处理雷四段上亚段地震数据信噪比较低,品质较差,直接使用地震数据不能预测裂缝和解释断层。因此,首先对原始地震数据开展基于以倾角为导向的构造导向滤波优化处理。
图 2为Inline5250测线构造导向滤波前、后地震剖面。由图可见,与原始地震剖面(图 2a)相比,滤波后地震剖面(图 2b)同相轴的断点更清晰、干脆,明显提高了断裂处的横向分辨率(黄色圆圈处)及同相轴的分辨率(黄色箭头处),更易识别弱反射,增强了连续性。整体而言,滤波后地震数据在保证断层清晰的情况下明显提高了信噪比,较大地改善了地震数据品质,突出了断裂特征,利于计算地震属性和描述断层(裂缝)。
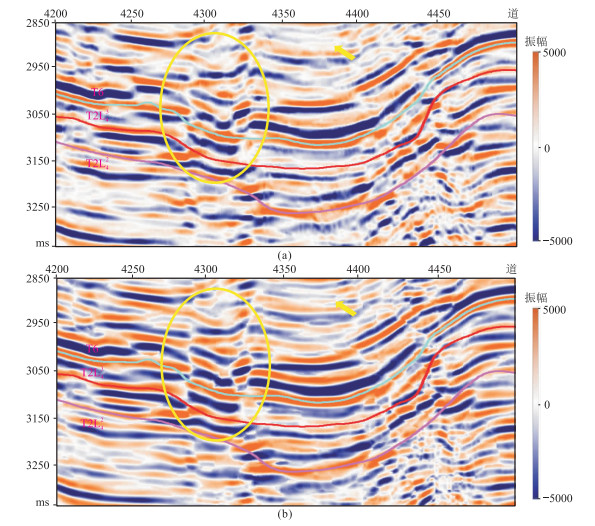
|
图 2 Inline5250测线构造导向滤波前(a)、后(b)地震剖面 T6代表雷四段上亚段顶界面,T2L43代表雷四段中亚段顶界面,T2L42代表雷四段下亚段顶界面,下同 |
在对三维叠后地震数据开展构造导向滤波处理后,首先基于高信噪比、断裂特征突出的地震数据计算了GST相干属性,并与传统相干属性对比、分析;然后将GST相干属性和振幅剖面融合显示,结合FMI测井资料综合预测雷四段上亚段储层裂缝。
利用原始振幅切片的振幅异常识别中、小尺度断层和裂缝较困难,而相干切片可以很好地展示裂缝的形态和分布特征。图 3为不同空间窗口提取的雷四段上亚段上储层C3相干切片和GST相干切片。由图可见:①不同空间窗口的C3相干切片和GST相干切片均能清晰识别大尺度断层(红色箭头处)。②对于中、小尺度断层和裂缝的识别精度以及信噪比,C3相干切片和GST相干切片存在较大区别,如在GST相干切片(图 3b、图 3d绿色箭头和蓝色箭头处)上识别了C3相干切片(图 3a、图 3c)未能识别的中、小尺度断裂。③3道×3道C3相干切片(图 3a)与3道×3道GST相干切片(图 3b)均有效识别了裂缝发育特征(绿色圆圈处),但后者的信噪比更高,更好地刻画了断裂细节,指示该区小断层和裂缝密集发育。④当增大空间分析窗口后,C3相干切片(图 3c)整体分辨率下降,GST相干切片(图 3d)的分辨率和信噪比变化不大。
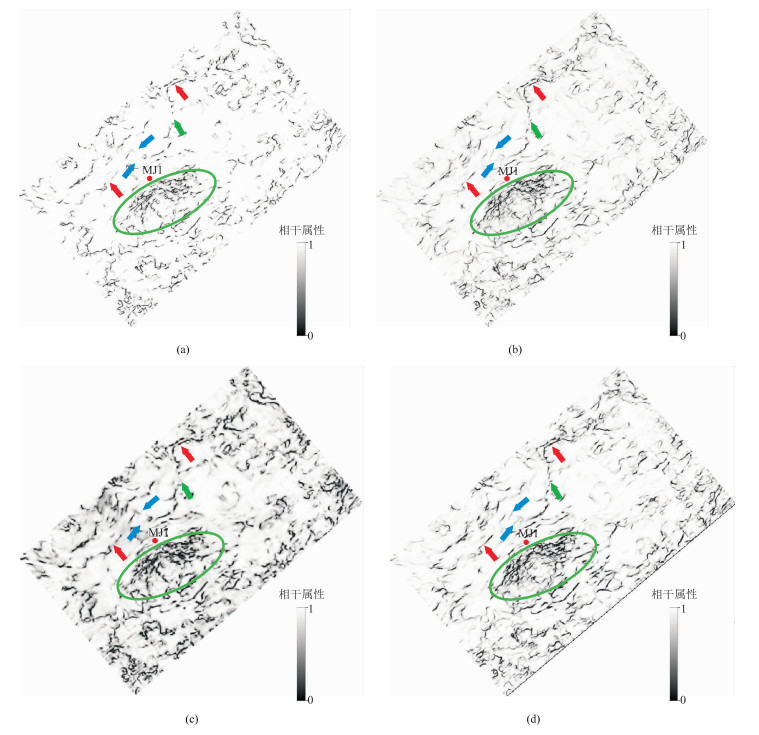
|
图 3 不同空间窗口提取的雷四段上亚段上储层C3相干切片和GST相干切片 (a)3道×3道,C3;(b)3道×3道,GST;(c)7道×7道,C3;(d)7道×7道,GST时窗长度均为30ms |
综上所述,在相同空间分析窗口的情况下,GST相干切片的信噪比和分辨率高于C3相干切片,且3道×3道GST相干切片对储层的中、小尺度断层和裂缝的识别能力更强、刻画更精细、分辨率更高,裂缝预测效果更佳。
为了更好地分析断层和裂缝的展布特征,叠加GST相干属性和地震剖面(图 4)。可见:①断层在地震剖面上往往表现为同相轴明显错断,或引起同相轴局部变化、反射零乱及出现空白带等;裂缝则由于未发生明显位移,地震反射表现为强弱不同的非连续性特征或较小的反射扰动,在地震剖面上难以识别。②断层、裂缝均会引起相应的GST相干属性异常,结合井震资料以及岩心信息发现,当GST相干属性小于0.028(绿色)时主要为裂缝,大于该数值(红色)时则为断层,因此选取0.028作为门槛值。③该区发育大量断层和裂缝,断层和裂缝的展布特征显示:距断层越近,裂缝分布密度越高,且走向与断层接近一致,表明裂缝主要受构造作用控制,属于构造裂缝;距断层较远的裂缝受岩性、沉积环境等影响较大,受构造作用影响较小,属于非构造裂缝。整体而言,裂缝以构造裂缝为主。其中近直立的断层伴生高角度构造缝(蓝色箭头处),近水平断层伴生低角度构造缝(橙色箭头处),低角度构造缝、层间缝与高角度构造缝相互交叉,形成了网状缝。④受倾角影响,低角度缝(裂缝倾角≤30°)、层间缝的地震响应与GST相干属性响应均较差,斜交缝(30°≤裂缝倾角≤60°)、高角度缝(裂缝倾角≥60°)的GST相干属性响应较强。因此,GST相干属性均能清晰地刻画高角度缝的展布特征,斜交缝次之,低角度缝的信息最少。

|
图 4 Inline5357测线GST相干属性和振幅叠加显示 |
图 5为T6层拉平后相干振幅叠加图及储层相干切片。由图可见:T6层拉平后大部分断层和裂缝主要发育在该层以下(图 5a),T6层断裂欠发育,反射连续,地层稳定,形成了良好的盖层;雷四段上亚段上储层(图 5b)和下储层(图 5c)的GST相干属性切片显示断层和裂缝较发育,裂缝在平面上的相对关系更强,裂缝特征更清晰,且以高角度缝为主,对流体的储集、运移起重要作用,说明雷四段上亚段为良好的储集层。

|
图 5 T6层拉平后相干振幅叠加图及储层相干切片 (a)T6层拉平后的地震数据与GST相干属性叠加剖面;(b)雷四段上亚段上储层GST相干切片;(c)雷四段上亚段下储层GST相干切片 |
FMI测井能够提供非常丰富的裂缝信息,可为裂缝预测提供重要判断依据。图 6为雷四段上亚段上储层、下储层FMI测井结果。由图可见,裂缝较发育,裂缝发育带表现为暗色团块,其中上储层主要发育低角度缝和高角度缝(图 6a),下储层主要发育低角度缝和斜交缝,局部发育高角度缝(图 6b)。FMI测井结果证实了GST相干属性的预测结果。

|
图 6 雷四段上亚段上储层(a)、下储层(b)FMI测井结果 |
基于构造导向滤波与GST相干属性的储层裂缝预测方法在川西雷口坡组储层中的应用表明:
(1) 针对三维地震数据开展构造导向滤波处理,在地震数据保真的前提条件下,可以有效地提升地震数据信噪比,增强同相轴的连续性,突出地层的断点、断距、断面等断裂信息。
(2) 基于优化后的地震数据计算的GST相干属性的分辨率、信噪比均较高,对中、小尺度断层和裂缝的刻画能力更强,尤其对于储层埋深大、地震分辨率低、裂缝主控因素多、非均质性强的储层裂缝,GST相干属性的断裂细节刻画效果优于C3相干属性。
(3) 综合沉积、FMI测井、地震等资料,基于构造导向滤波与GST相干属性的储层裂缝预测方法精细预测了川西雷四段上亚段碳酸盐岩储层裂缝。断层和裂缝主要分布在T6层以下,T6层反射连续,地层稳定,形成了良好盖层;雷四段上亚段断层、中小尺度断层和裂缝较发育,以构造缝为主,可作为天然气储集空间和运移通道。
| [1] |
孙炜, 李玉凤, 付建伟, 等. 测井及地震裂缝识别研究进展[J]. 地球物理学进展, 2014, 29(3): 1231-1242. SUN Wei, LI Yufeng, FU Jianwei, et al. Review of fracture identification with well logs and seismic data[J]. Progress in Geophysics, 2014, 29(3): 1231-1242. |
| [2] |
郎晓玲, 郭召杰. 基于DFN离散裂缝网络模型的裂缝性储层建模方法[J]. 北京大学学报(自然科学版), 2013, 49(6): 964-972. LANG Xiaoling, GUO Zhaojie. Fractured reservoir modeling method based on discrete fracture network model[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2013, 49(6): 964-972. |
| [3] |
吴林强, 刘成林, 张涛, 等. "二元法"在构造裂缝定量预测中的应用——以松辽盆地青一段泥页岩为例[J]. 地质力学学报, 2018, 24(5): 16-24. WU Linqiang, LIU Chenglin, ZHANG Tao, et al. The application of two factor method in quantitative prediction of tectonic fractures: a case study of shale in Qing-1 member, Songliao basin[J]. Journal of Geomechanics, 2018, 24(5): 16-24. |
| [4] |
李婷婷, 侯思宇, 马世忠, 等. 断层识别方法综述及研究进展[J]. 地球物理学进展, 2018, 33(4): 1507-1514. LI Tingting, HOU Siyu, MA Shizhong, et al. Overview and research progress of fault identification method[J]. Progress in Geophysics, 2018, 33(4): 1507-1514. |
| [5] |
程冰洁, 徐天吉. 转换波方位各向异性裂缝检测技术研究及应用[J]. 地球物理学进展, 2012, 27(2): 575-581. CHENG Bingjie, XU Tianji. Research and application of fracture detection technique using azimuthal of C-wave[J]. Progress in Geophysics, 2012, 27(2): 575-581. DOI:10.6038/j.issn.1004-2903.2012.02.021 |
| [6] |
唐建明, 程冰洁, 徐天吉. 三维三分量地震勘探[M]. 北京: 地质出版社, 2011. TANG Jianming, CHENG Bingjie, XU Tianji. 3D/3C Seismic Exploration[M]. Beijing: Geological Publishing House, 2011. |
| [7] |
刘敬寿, 丁文龙, 肖子亢, 等. 储层裂缝综合表征与预测研究进展[J]. 地球物理学进展, 2019, 34(6): 2283-2300. LIU Jingshou, DING Wenlong, XIAO Zihang, et al. Advances in comprehensive characterization and prediction of reservoir fractures[J]. Progress in Geophysics, 2019, 34(6): 2283-2300. |
| [8] |
Bahorich M S, Farmer S L. 3-D seismic discontinuity for faults and stratigraphic features[J]. The Leading Edge, 1995, 14(10): 1053-1058. DOI:10.1190/1.1437077 |
| [9] |
Marfurt K J, Kirlin R L, Farmer S H, et al. 3-D seismic attributes using a running window semblance-based algorithm[J]. Geophysics, 1998, 63(4): 1150-1165. DOI:10.1190/1.1444415 |
| [10] |
Gersztenkorn A, Marfurt K J. Eigenstructure-based coherence computations as an aid to 3-D structural and stratigraphic mapping[J]. Geophysics, 1999, 64(5): 1468-1479. DOI:10.1190/1.1444651 |
| [11] |
苑书金. 地震相干体技术的研究综述[J]. 勘探地球物理进展, 2007, 30(1): 7-15. YUAN Shujin. A review of seismic coherence techniques[J]. Progress in Exploration Geophysics, 2007, 30(1): 7-15. |
| [12] |
Randen T.Automatic extraction of fault surfaces from three-dimensional seismic data[C].SEG Technical Program Expanded Abstracts, 2001, 20, SEG-2001-0551.
|
| [13] |
Bakker P.Image Structure Analysis for Seismic Interpretation[D].Technische Universiteit Delft, Netherlands, 2002.
|
| [14] |
Faraklioti M, Petrou M.The use of structure tensors in the analysis of seismic data//Mathematical Me-thods and Modelling in Hydrocarbon Exploration and Production[M].Springer, 2005.
|
| [15] |
张军华, 董猛, 周振晓, 等. 基于GST的相干体方法研究及应用[J]. 天然气工业, 2007, 27(增刊A): 381-383. |
| [16] |
陈双全, 季敏. 地震数据结构张量相干计算方法[J]. 石油物探, 2012, 51(3): 233-238. CHEN Shuangquan, JI Min. Structure tensor coherence computation method of seismic data[J]. Geophysical Prospecting for Petroleum, 2012, 51(3): 233-238. DOI:10.3969/j.issn.1000-1441.2012.03.004 |
| [17] |
唐成勇. 基于局部结构的地震几何属性研究与应用[D]. 四川成都: 西南交通大学, 2012. TANG Chengyong.Research and Application on Local Structure Based Seismic Geometric Attributes[D].Southwest Jiaotong University, Chengdu, Sichuan, 2012. |
| [18] |
陈强, 许玉莹, 曾维望. 基于地震数据结构梯度张量属性的采空区识别方法[J]. 中国煤炭地质, 2013, 25(7): 42-47. CHEN Qiang, XU Yuying, ZENG Weiwang. Goaf identification method based on seismic data gradient structure tensor (GST) attributes[J]. Coal Geology of China, 2013, 25(7): 42-47. DOI:10.3969/j.issn.1674-1803.2013.07.10 |
| [19] |
问雪, 陈雪芳, 陈胜红, 等. 利用结构导向平滑方法解释断层[J]. 石油地球物理勘探, 2017, 52(1): 146-151. WEN Xue, CHEN Xuefang, CHEN Shenghong, et al. Faults interpretation based on structure-oriented smoothing method[J]. Oil Geophysical Prospecting, 2017, 52(1): 146-151. |
| [20] |
王清振, 张金淼, 姜秀娣, 等. 利用梯度结构张量检测盐丘与断层[J]. 石油地球物理勘探, 2018, 53(4): 826-831. WANG Qingzhen, ZHANG Jinmiao, JIANG Xiudi, et al. Salt dome and fault detection based on the gradient-structure tensor[J]. Oil Geophysical Prospecting, 2018, 53(4): 826-831. |
| [21] |
王震, 文欢, 邓光校, 等. 塔河油田碳酸盐岩断溶体刻画技术研究与应用[J]. 石油物探, 2019, 58(1): 149-154. WANG Zhen, WEN Huan, DENG Guangxiao, et al. Fault-karst characterization technology in the Tahe Oilfield, China[J]. Geophysical Prospecting for Petroleum, 2019, 58(1): 149-154. DOI:10.3969/j.issn.1000-1441.2019.01.017 |
| [22] |
彭达, 肖富森, 冉崎, 等. 基于倾角导向梯度能量熵的断层检测方法[J]. 石油地球物理勘探, 2019, 54(1): 191-197. PENG Da, XIAO Fusen, RAN Qi, et al. Fault identification based on dip-oriented gradient-energy-entroy coherence estimation[J]. Oil Geophysical Prospecting, 2019, 54(1): 191-197. |
| [23] |
陈常乐. 地震波场构造导向滤波关键技术及应用[D]. 吉林长春: 吉林大学, 2015. CHEN Changle.Key Technique and Application of Structure Oriented Filter for Seismic Wave Field[D].Jilin University, Changchun, Jilin, 2015. |
| [24] |
Fehmers G C, Hocker C F W. Fast structural interpretation with structure-oriented filtering[J]. Geophysics, 2003, 68(4): 1286-1293. DOI:10.1190/1.1598121 |
| [25] |
尹川, 杜向东, 赵汝敏, 等. 基于倾角控制的构造导向滤波及其应用[J]. 地球物理学进展, 2014, 29(6): 2818-2822. YIN Chuan, DU Xiangdong, ZHAO Rumin, et al. Dip steered structure oriented filter and its application[J]. Progress in Geophysics, 2014, 29(6): 2818-2822. |
| [26] |
黄立良, 韩少博, 刘兴, 等. 应用构造导向滤波技术识别隐蔽断层[J]. 工程地球物理学报, 2014, 11(4): 446-450. HUANG Liliang, HAN Shaobo, LIU Xing, et al. The application of structure-oriented filtering technology to identifying hidden fault[J]. Chinese Journal of Engineering Geophysics, 2014, 11(4): 446-450. |
| [27] |
庄益明, 张兴平, 王琦, 等. 基于构造导向滤波下的蚂蚁追踪技术的应用与实践[J]. 煤炭技术, 2018, 37(9): 150-152. ZHUANG Yiming, ZHANG Xingping, WANG Qi, et al. Application and practice of ant tracking technology based on structure oriented filtering[J]. Coal Technology, 2018, 37(9): 150-152. |
| [28] |
赵凤全, 崔德育, 康婷婷, 等. 构造导向滤波技术在断裂识别中的应用[J]. 石油地球物理勘探, 2018, 53(增刊1): 214-218, 227. ZHAO Fengquan, CUI Deyu, KANG Tingting, et al. Fault identification with structure-oriented filtering[J]. Oil Geophysical Prospecting, 2018, 53(S1): 214-218, 227. |
| [29] |
王静, 张军华, 冯德永, 等. 利用不连续性的各向异性扩散滤波方法识别断层[J]. 石油地球物理勘探, 2020, 55(6): 1349-1357. WANG Jing, ZHANG Junhua, FENG Deyong, et al. Fault identification based on a discontinuous anisotropic diffusion filter[J]. Oil Geophysical Prospecting, 2020, 55(6): 1349-1357. |
| [30] |
Weickert J, Scharr H. A scheme for coherence-enhancing diffusion filtering with optimized rotation invariance[J]. Journal of Visual Communication and Image Representation, 2002, 13(1-2): 103-118. DOI:10.1006/jvci.2001.0495 |
| [31] |
李书兵, 许国明, 宋晓波. 川西龙门山前构造带彭州雷口坡组大型气田的形成条件[J]. 中国石油勘探, 2016, 21(3): 74-82. LI Shubing, XU Guoming, SONG Xiaobo. Forming conditions of Pengzhou large gas field of Leikoupo formation in Longmenshan piedmont tectonic belt, western Sichuan Basin[J]. China Petroleum Exploration, 2016, 21(3): 74-82. DOI:10.3969/j.issn.1672-7703.2016.03.007 |
| [32] |
刘树根, 宋金民, 罗平, 等. 四川盆地深层微生物碳酸盐岩储层特征及其油气勘探前景[J]. 成都理工大学学报(自然科学版), 2016, 43(2): 129-152. LIU Shugen, SONG Jinmin, LUO Ping, et al. Characteristics of microbial carbonate reservoris and its hydrocarbon exploring outlook in the Sichuan Basin, China[J]. Journal of Chengdu University of Techno-logy(Science & Technology Edition), 2016, 43(2): 129-152. DOI:10.3969/j.issn.1671-9727.2016.02.01 |
| [33] |
钟怡江, 陈洪德, 林良彪, 等. 川东北地区中三叠统雷口坡组四段古岩溶作用与储层分布[J]. 岩石学报, 2011, 27(8): 2272-2280. ZHONG Yijiang, CHEN Hongde, LIN Liangbiao, et al. Paleokarstification and reservoir distribution in the Middle Triassic carbonates of the 4th member of the Leikoupo Formation, northeastern Sichuan basin[J]. Acta Petrologica Sinica, 2011, 27(8): 2272-2280. |
| [34] |
徐天吉, 程冰洁, 闫丽丽, 等. 龙门山金马-鸭子河推覆构造带雷四段储层脆性与裂缝预测[J]. 石油地球物理勘探, 2017, 52(3): 562-572. XU Tianji, CHENG Bingjie, YAN Lili, et al. Reservoir brittleness and fracture prediction of Member 4, Leikoupo Formation in Jinma-Yazihe nappe tectonic belt, Longmen Mountain[J]. Oil Geophysical Prospecting, 2017, 52(3): 562-572. |
| [35] |
赵向原, 胡向阳, 肖开华, 等. 川西彭州地区雷口坡组碳酸盐岩储层裂缝特征及主控因素[J]. 石油与天然气地质, 2018, 39(1): 30-39, 152. ZHAO Xiangyuan, HU Xiangyang, XIAO Kaihua, et al. Characteristics and major control factors of natural fractures in carbonate reservoirs of Leikoupo Formation in Pengzhou area, western Sichuan Basin[J]. Oil & Gas Geology, 2018, 39(1): 30-39, 152. |



 程冰洁, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院, 610059。Email:
程冰洁, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院, 610059。Email: 