② 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266071
② Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266071, China
地震反演是获取地下介质弹性参数,揭示地下储层展布规律、物性及含油气性的有效途径[1-4]。随着油田勘探、开发的不断推进,对储层预测的精度要求也越来越高,因此高精度储层反演技术在薄互层识别中的作用越来越重要[5-6]。地震反演分为确定性反演与随机反演两大类,其中确定性反演以正则化方法为基础[7-10],通过弱化反演过程的不适定性,求解一个逼近真实解的最优解或近似解,但是该方法受地震分辨率及带限子波的限制,在识别调谐尺度内薄层时具有一定的局限性。
与传统的确定性反演方法相比,随机反演识别薄层具有一定优势[11]。以地质统计学为基础、以测井资料为条件数据的地震随机反演方法的分辨率高于常规确定性反演[12-15],因此迅速得到广泛应用,但是提高计算效率以及消除随机性一直是难点。基于序贯高斯、模拟退火等地质统计学算法的随机反演利用垂向密集的井点数据求取空间变差函数进行随机建模[16],然而在求取各个方向的变差函数变程时人为因素影响较大,导致反演结果随机性较强[17-19]。王保丽等[20]构建了基于FFT-MA(fast Fourier transform-moving average)谱模拟的快速随机反演方法,采用逐步变形算法快速迭代求解重新构造的目标函数,将复杂的求解问题简单化,有效提高了运算效率。针对随机采样,以蒙特卡洛—马尔科夫链(Monte Carlo Markov chain,MCMC)算法为例,在获取模型参数后验概率密度分布随机样本的基础上,采用统计分析手段获取模型参数的统计特征(如均值、协方差等)[21-23]。Hong等[24]采用多尺度标准遗传算法的MCMC方法不断优化已知模型以获得最优参数,提高了MCMC算法的计算效率以及估值精度;基于Metropolis算法[25],Hastings[26]提出了Metropolis-Hastings(M-H)算法,介绍了蒙特卡洛估计误差的相关理论、应用技术以及误差评估方法;Smith等[27]利用MCMC方法获取模型参数的后验分布,尝试利用MCMC算法逼近贝叶斯统计分析中的积分等运算,可提供大量与未知参数有关的全局信息;张广智等[28-32]提出构建一种自适应的建议分布,能够自适应并不断更新构成的马尔科夫链,有效地加快了马尔科夫链的收敛速度;李坤等[33]在待反演参数服从混合概率先验模型的前提下,提出了基于差分进化MCMC随机模型的相约束叠前地震概率化反演方法,充分模拟了待反演模型的后验概率密度分布(如均值、方差及置信区间)。
针对上述方法存在的随机性强、运算效率低等问题,本文提出了基于地震波形约束的MCMC随机反演方法。充分利用观测地震数据和待反演参数之间的地球物理映射关系,应用相关系数,根据已知的地震波形之间的相似性特征指导井数据进行伪普通克里金插值模拟,建立具有地震波形指示的初始模型;在此基础上,进一步在贝叶斯框架下构建观测地震数据和测井数据协同约束的后验概率密度分布,结合M-H采样算法多次随机模拟具有地震波形指示的初始模型参数,利用后验均值作为模型参数的最优解。该方法有效地提高了反演稳定性和横向连续性,降低了随机性,有效地弱化了地震噪声对反演结果的影响,并且极大地加快了马尔科夫链的收敛速度,有效地提高了该方法的运算效率和估算精度。
1 理论与方法 1.1 初始模型地震振幅的变化间接地反映了地下储层参数的空间变化,由于观测地震数据和储层参数之间存在一定的地球物理映射关系[33],因此可以根据已知观测地震数据指导已知井信息完成地下未知储层参数的插值运算。基于地震波形约束的MCMC随机反演方法借鉴传统的地质统计学建模思想,建立具有地震波形指示的初始模型的基本思想是:在工区所有井数据的基础上,统计所有井的井旁地震道以及井上与井旁地震道对应位置的预测参数曲线,依据统计得到的待预测点处的地震波形与井旁地震道所有样本点处的地震波形之间的相关系数,对所有井进行相关度排序,优选与待预测点关联度高的井样本建立初始模型;利用普通伪克里金插值方法对含有高频成分的井数据进行无偏最优估计,最终反演的地震波形与原始地震特征一致,其中包含确定性较强的宽频(高频成分)弹性参数。
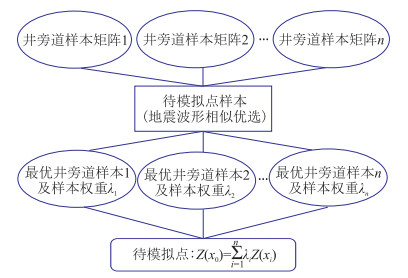
利用相关系数根据地震波形相似性优选井样本(图 1)。根据观测地震数据和待反演参数之间的地球物理映射关系,充分利用地震波形相似性由优选的井样本模拟地下未知模型参数。用普通伪克里金插值公式表示待反演参数的建模过程

|
图 1 地震波形和井参数优选示意图[5] ①为优选样本,②为统计样本 |
| $ Z\left(x_{0}\right)=\sum\limits_{i=1}^{n} \lambda_{i} Z\left(x_{i}\right) $ | (1) |
式中:Z(x0)为待模拟插值参数x0处的值;Z(xi)为由井旁地震数据筛选的已预测井样本点xi处的对应值;λi为Z(xi)在待插值处的权重;n为参与井的个数。本文根据普通克里金的定义,推导了一种新的利用地震波形相似性指导井数据进行无偏最优估计的插值方法,并建立了具有波形指示的初始模型。
在普通克里金定义中,假设对于某区域内任意点p(x,y)的期望c与方差σ2都是相同的,即对于任意一点p(x,y),都有
| $ E[p(x, y)]=E(p)=c $ | (2) |
| $ \varDelta[p(x, y)]=\sigma^{2} $ | (3) |
无偏估计条件为
| $ E\left(\hat{z}_{0}-z_{0}\right)=0 $ | (4) |
普通克里金插值公式为
| $ \hat{z}_{0}=\sum\limits_{i=1}^{n} \lambda_{i} z_{i} $ | (5) |
式中:z0为待预测点处地震数据,
| $ E\left(\sum\limits_{i=1}^{n} \lambda_{i} z_{i}-z_{0}\right)=0 $ | (6) |
化简可得
| $ \sum\limits_{i=1}^{n} \lambda_{i}=1 $ | (7) |
相应地,估计方差为
| $ \begin{aligned} J &=\varDelta\left(\hat{z}_{0}-z_{0}\right) \\ &=\sum\limits_{i=1}^{n} \sum\limits_{j=0}^{n} \lambda_{i} \lambda_{j} \operatorname{Cov}\left(z_{i}, z_{j}\right)-2 \sum\limits_{i=1}^{n} \lambda_{i} \operatorname{Cov}\left(z_{i}, z_{0}\right)+\sigma^{2} \end{aligned} $ | (8) |
令Cij=Cov(zi,zj),则有
| $ J=\sum\limits_{i=1}^{n} \sum\limits_{j=0}^{n} \lambda_{i} \lambda_{j} C_{i j}-2 \sum\limits_{i=1}^{n} \lambda_{i} C_{i 0}+\sigma^{2} $ | (9) |
相关系数为
| $ r_{i j}=\frac{C_{i j}}{\sqrt{\varDelta\left(z_{i}\right)} \sqrt{\varDelta\left(z_{j}\right)}} $ | (10) |
式中rij为地震数据点zi地震波形与地震数据点zj地震波形的相关系数。将式(10)代入式(9),则有
| $ \begin{aligned} J=& \sum\limits_{i=1}^{n} \sum\limits_{j=0}^{n} \lambda_{i} \lambda_{j} r_{i j} \sqrt{\varDelta\left(z_{i}\right)} \sqrt{\varDelta\left(z_{j}\right)}-\\ & 2 \sum\limits_{i=1}^{n} \lambda_{i} r_{i 0} \sqrt{\varDelta\left(z_{i}\right)} \sqrt{\varDelta\left(z_{0}\right)}+\sigma^{2} \\ =& \sum\limits_{i=1}^{n} \sum\limits_{j=0}^{n} \lambda_{i} \lambda_{j} r_{i j} \sigma^{2}-2 \sum\limits_{i=1}^{n} \lambda_{i} r_{i 0} \sigma^{2}+\sigma^{2} \end{aligned} $ | (11) |
我们的目标是寻找使J最小的一组λi,且J是λi的函数。因此将J对λi求偏导数并令其为0,即
| $ \frac{\partial J}{\partial \lambda_{i}}=0 $ | (12) |
求解得到的最佳λi需要满足
| $ W=J+2 \phi\left(\sum\limits_{i=1}^{n} \lambda_{i}-1\right) $ | (13) |
求解最优化问题。式中ϕ为拉格朗日乘数。求解W的最小参数集ϕ及λ1,λ2,…,λn,则能得到在
| $ \begin{array}{l} \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial \left[ {J + 2\phi \left( {\sum\limits_{i = 1}^n {{\lambda _i}} - 1} \right)} \right]}}{{\partial {\lambda _k}}} = 0\quad k = 1,2, \cdots ,n}\\ {\frac{{\partial \left[ {J + 2\phi \left( {\sum\limits_{i = 1}^n {{\lambda _i}} - 1} \right)} \right]}}{{\partial \phi }} = 0} \end{array}\quad \Rightarrow } \right.\\ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial \left[ {\sum\limits_{i = 1}^n {\sum\limits_{j = 0}^n {{\lambda _i}} } {\lambda _j}{r_{ij}}{\sigma ^2} - 2\sum\limits_{i = 1}^n {{\lambda _i}} {r_{i0}}{\sigma ^2} + {\sigma ^2} + 2\phi \left( {\sum\limits_{i = 1}^n {{\lambda _i}} - 1} \right)} \right]}}{{\partial {\lambda _k}}} = 0}\\ {\frac{{\partial \left[ {\sum\limits_{i = 1}^n {\sum\limits_{j = 0}^n {{\lambda _i}} } {\lambda _j}{r_{ij}}{\sigma ^2} - 2\sum\limits_{i = 1}^n {{\lambda _i}} {r_{i0}}{\sigma ^2} + {\sigma ^2} + 2\phi \left( {\sum\limits_{i = 1}^n {{\lambda _i}} - 1} \right)} \right]}}{{\partial \phi }} = 0} \end{array}} \right.\quad \Rightarrow \\ \left\{ {\begin{array}{*{20}{l}} {\sum\limits_{j = 1}^n {{\lambda _j}} \left( {{r_{kj}} + {r_{jk}}} \right){\sigma ^2} - 2{r_{k0}}{\sigma ^2} + 2\phi = 0}\\ {\sum\limits_{i = 1}^n {{\lambda _i}} = 1} \end{array}} \right. \end{array} $ | (14) |
由于rkj=rjk,则式(14)变为
| $ \left\{\begin{array}{l} \sum\limits_{j=1}^{n} \lambda_{j} r_{k j}-r_{k j}+\frac{\phi}{\sigma^{2}}=0 \quad k=1,2, \cdots, n \\ \sum\limits_{i=1}^{n} \lambda_{i}=1 \end{array}\right. $ | (15) |
由式(15)得到了求解权重系数λj的方程组
| $ \left\{\begin{array}{c} r_{11} \lambda_{1}+r_{12} \lambda_{2}+\cdots+r_{1 n} \lambda_{n}+\frac{\phi}{\sigma^{2}}=r_{10} \\ r_{21} \lambda_{1}+r_{22} \lambda_{2}+\cdots+r_{2 n} \lambda_{n}+\frac{\phi}{\sigma^{2}}=r_{20} \\ \vdots \\ r_{n 1} \lambda_{1}+r_{n 2} \lambda_{2}+\cdots+r_{n n} \lambda_{n}+\frac{\phi}{\sigma^{2}}=r_{n 0} \end{array}\right. $ | (16) |
写成矩阵形式
| $ \left(\begin{array}{ccccc} r_{11} & r_{12} & \cdots & r_{1 n} & 1 \\ r_{21} & r_{22} & \cdots & r_{2 n} & 1 \\ & & \vdots & & \\ r_{n 1} & r_{n 2} & \cdots & r_{n n} & 1 \\ 1 & 1 & \cdots & 1 & 0 \end{array}\right)\left(\begin{array}{c} \lambda_{1} \\ \lambda_{2} \\ \vdots \\ \lambda_{n} \\ \frac{\phi}{\sigma^{2}} \end{array}\right)=\left(\begin{array}{c} r_{n 0} \\ r_{n 0} \\ \vdots \\ r_{n 0} \\ 1 \end{array}\right) $ |
对矩阵进行逆运算即可求出已知点处地震数据在待预测点处所占的权重,根据观测地震数据和待反演参数之间的地球物理映射关系,以此矩阵求得的权重λj代替式(1)中的λi,从而完成初始模型的建立(图 2)。
|
图 2 初始模型建立流程 |
从初始模型建立流程(图 2)可知,应用地震波形相似性指导已知井参数信息建立初始模型的过程与常规序贯采样方式不同,在每一个待预测点都经过严格的波形优选进行伪克里金插值,已插值点并不参与下一个未知点的插值过程,每个插值点的模拟都从实际优选样本出发进行无偏最优估计,有效降低了地震噪声的影响和随机误差的累积。
建立具有波形指示的初始模型过程中需要注意地震波形样本选取的时窗和样本井的最高截止频率这两个重要参数的选取。地震波形样本选取的时窗用于对比待预测点地震波形和井旁地震道波形组成点的个数,下文将该参数简称为有效样本数。参与井样本的最高截止频率代表参与井的目标层井数据达到一定相似性时的频率;当参与井目标层的井旁地震道地震波形达到一定的相似度时,通过不断对参与井的目标层纵波阻抗数据进行高频滤波,发现参与井的目标层井数据之间的相关系数随着最高截止频率的降低而增大,当其与井旁地震道的相关系数相同时,频率范围远远大于地震数据的有效频宽[34]。最后,利用普通伪克里金插值方法在地震波形相似性的指导下对含有高频成分的优选井样本数据进行无偏最优估计,并将优选井的纵波阻抗数据作为先验信息,从而建立具有地震波形指示的初始模型,该模型包含了确定性较强(大于地震有效频宽)的宽频纵波阻抗参数。
1.2 M-H算法MCMC算法的主要目的是构成一条平稳分布的马尔科夫链,同时该链是不可约的[21]。M-H算法是构造马尔科夫链的一种常用方法。本文采用M-H算法根据某个建议分布不断迭代后验概率密度函数,使其达到平稳条件。
首先,设q(θ,v)是与目标后验概率密度分布π(θ|D)较接近的某已知分布D,一般称其为建议分布,也称为备选生成密度,q(θ,v)表示参数θ的潜在转移θ→v,满足
| $ \int q(\theta, v) \mathrm{d} v=1 $ | (17) |
(1) 任意选择一个初值θ(t),并令t=0;
(2) 从q[θ(t),v]中生成一个备选值θ*,并从均匀分布U0,1中抽取随机数μ;
(3) 若μ≤α[θ(t),θ*],则θ(t+1)=θ*,否则令θ(t+1)=θ(t),此时接受概率[26](转移核概率)为
| $ \alpha(\theta, v)=\min \left[\frac{\pi(v \mid D) q(v, \theta)}{\pi(\theta \mid D) q(\theta, v)}, 1\right] $ | (18) |
(4) 令t=t+1,并返回到步骤(2),反复迭代直至平稳状态。
很容易证明,以此种方式构建的接受概率α(θ,v)满足细致平衡条件。
1.3 基于地震波形约束的MCMC随机反演方法基于地震波形约束的MCMC随机反演方法,充分利用地震数据之间的相关系数代替测井数据之间的相关系数,构建具有地震波形指示的初始模型。以此为基础,在贝叶斯框架下构建观测地震数据和测井数据协同约束的后验概率密度分布,并将其作为目标函数,结合M-H算法不断扰动模型参数,利用后验均值作为模型参数的最优解,并且取多次有效实现的均值作为期望值输出,有效提高了反演稳定性和横向连续性。
反演问题[35]可以表述为
| $ p(m\mid d) = f(m) + e $ | (19) |
式中:p(m|d)为待反演参数的后验概率密度函数,m为地震波形指示初始模型约束,d为观测数据;f为正演算子;e为观测噪声。在贝叶斯框架下联合似然函数p(d|m)和先验信息p(m)的p(m|d)可写为[36]
| $ p(m\mid d) = p(m) \cdot p(d\mid m) $ | (20) |
利用M-H全局优化算法优选具有波形指示的初始模型,需要建立似然函数,并引入由测井信息提供的先验信息。假设p(m)服从高斯分布[28],其均值为μm,标准差为σm2,则有
| $ p(m) = \frac{1}{{{{\left( {2{\rm{ \mathsf{ π} }}\sigma _m^2} \right)}^{\frac{N}{2}}}}}\exp \left[ { - \sum {\frac{{{{\left( {m - {\mu _m}} \right)}^2}}}{{2\sigma _m^2}}} } \right] $ | (21) |
一般而言,对于似然函数,地震背景噪声满足均值为0、方差为σn2的正态分布[15],在似然函数的基础上加入波形约束信息,可以有效地提高反演的横向连续性和稳定性,则似然函数为
| $ {p(d\mid m) = \frac{1}{{{{\left( {2{\rm{ \mathsf{ π} }}\sigma _n^2} \right)}^{\frac{N}{2}}}}}\exp \left\{ { - \sum {\frac{{{{[d - f(m)]}^2}}}{{2\sigma _n^2}}} } \right\}} $ | (22) |
式中N为采样点的个数。式(20)变为
| $ \begin{array}{l} p(m\mid d) = \lambda \exp \left\{ { - \sum {\frac{{{{[d - f(m)]}^2}}}{{2\sigma _n^2}}} - } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\varepsilon \sum {\frac{{{{\left( {m - {\mu _m}} \right)}^2}}}{{2\sigma _m^2}}} } \right\} \end{array} $ | (23) |
式中:ε为可调因子;λ为常数。
为了得到所估参数的后验概率密度分布p(m|d),利用M-H算法生成马尔科夫链,其建议分布函数取为高斯分布
| $ q\left(m_{k}, m^{*}\right) \sim N\left(0, \sigma_{m}^{2}\right) $ | (24) |
其中q(mk,m*)表示采样点为k时的初始模型的值mk的潜在转移(mk→m*),转移概率[22]为
| $ \alpha\left(m_{k}, m^{*}\right)=\min \left[1, \frac{\pi\left(m^{*}\right) q\left(m^{*}, m_{k}\right)}{\pi\left(m_{k}\right) q\left(m_{k}, m^{*}\right)}\right] $ | (25) |
为了使马尔科夫链最终收敛于未知参数m的后验概率分布,后验概率密度分布即为平稳分布p(m)·p(d|m)。令
| $ J(m)=-\frac{\sum[d-f(m)]^{2}}{2 \sigma_{n}^{2}}-\varepsilon \sum \frac{\left(m-\mu_{m}\right)^{2}}{2 \sigma_{m}^{2}} $ | (26) |
则转移概率[28]为
| $ \alpha\left(m_{k}, m^{*}\right)=\exp \left[\alpha^{\prime}\left(m_{k}, m^{*}\right)\right] $ | (27) |
其中
| $ \begin{aligned} \alpha^{\prime}\left(m_{k}, m^{*}\right) &=\min \left\{0, J\left(m^{*}\right)+\lg \left[q\left(m^{*}, m_{k}\right)\right]\right.\\ &\left.-J\left(m_{k}\right)-\lg \left[q\left(m_{k}, m^{*}\right)\right]\right\} \end{aligned} $ | (28) |
最后,在M-H采样算法下不断扰动模型参数,多次随机模拟具有地震波形指示的初始模型参数,利用后验均值作为模型参数的最优解。
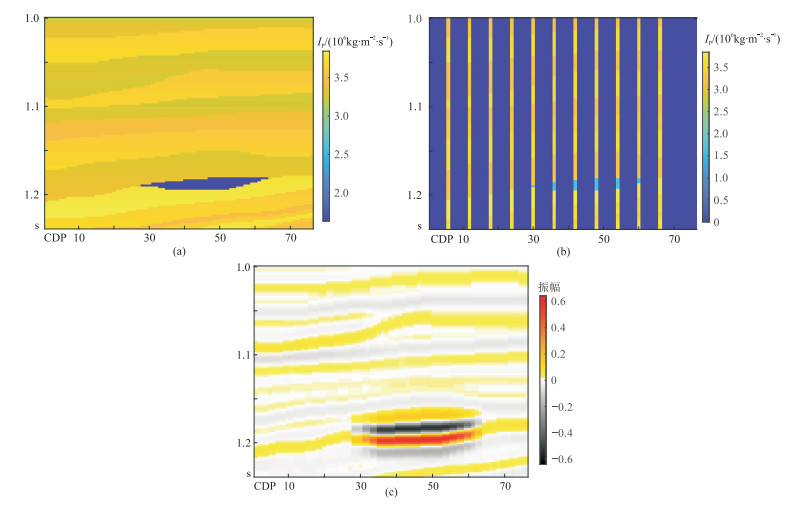
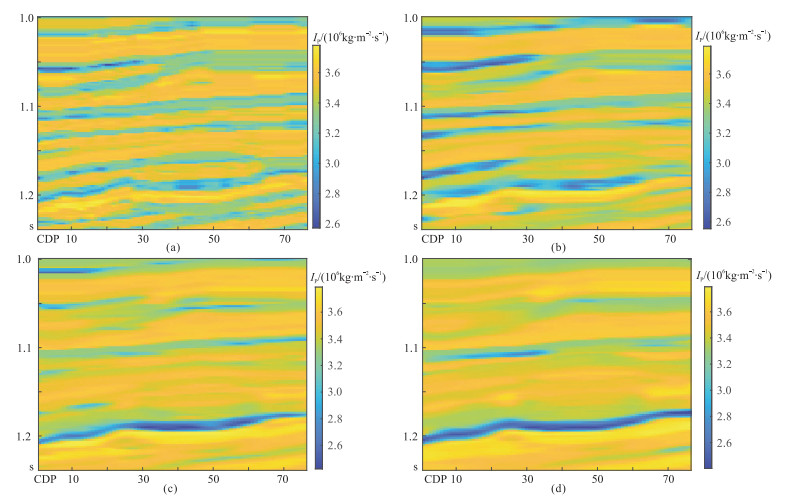
2 二维模型试算为了进一步验证基于地震波形约束的MCMC随机反演效果,抽取部分Marmousi2模型反演试算叠后纵波阻抗IP。模型时窗为1000~1240ms,从部分Marmousi2模型(图 3a)中随机抽取11道纵波阻抗数据作为已知伪井数据(图 3b),利用伪井数据与30Hz的雷克子波合成的地震数据(图 3c)建立初始模型(图 4)。可见:有效样本数越小,初始模型的横向连续性越差,纵向分辨率越高,反之亦然;有效样本数为10时初始模型的纵向分辨率和横向分辨率相对较高(图 4b),间接反映了原始阻抗模型(图 3a)的大致特征,因此取该模型作为模型测试的最终初始模型。
|
图 3 纵波阻抗模型以及原始地震记录 (a)纵波阻抗;(b)纵波阻抗伪井数据;(c)原始地震记录 |
|
图 4 有效样本数分别为5(a)、10(b)、15(c)和20(d)时建立的初始模型 |
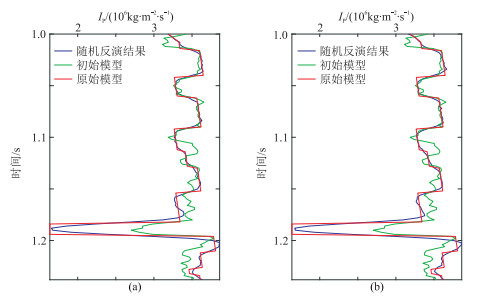
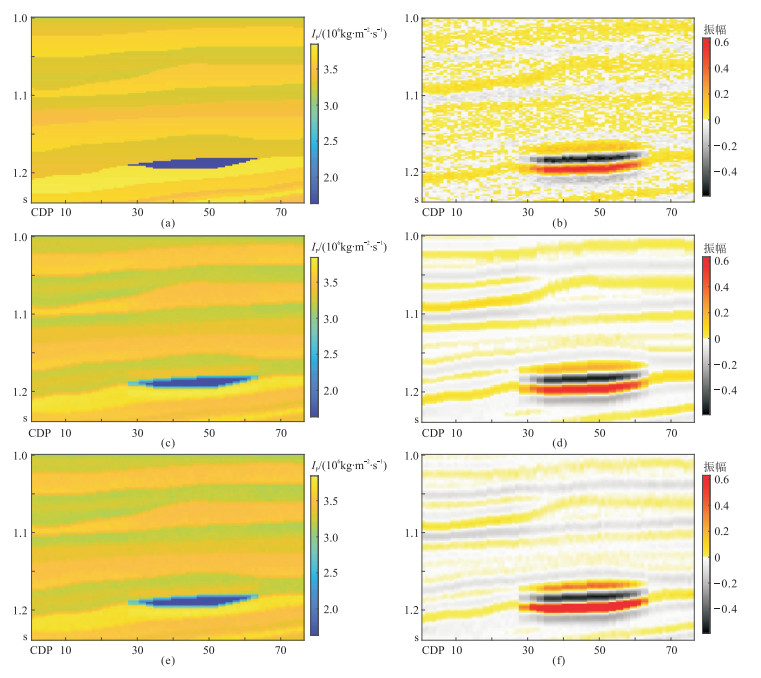
为了更好地测试基于地震波形约束的MCMC随机反演的抗噪性,分别对含噪和无噪地震数据进行二维反演测试。图 5为初始模型第42道数据的基于地震波形约束的MCMC随机反演结果。由图可见,地震噪声对反演结果影响不大。图 6为反演结果及其合成记录。由图可见:无噪数据、含噪数据地震波形约束的MCMC随机反演结果(图 6c、图 6e)与原始模型(图 6a)相近,表明地震波形约束的MCMC随机反演方法具有较好的抗噪性和可行性;无噪数据、含噪数据的地震波形约束的MCMC随机反演结果合成记录(图 6d、图 6f)均与原始地震记录(图 3c)基本一致。
|
图 5 初始模型第42道数据的基于地震波形约束的MCMC随机反演结果 (a)无噪;(b)信噪比为10 |
|
图 6 反演结果及其合成地震记录 (a)原始模型;(b)地震记录(信噪比为10);(c)地震波形约束的MCMC随机反演结果(无噪);(d)图c的合成记录;(e)地震波形约束的MCMC随机反演结果(信噪比为10);(f)图e的合成记录 |
将基于地震波形约束的MCMC随机反演方法应用于中国东部F区实际数据。该区面积约为20km2,区内有11口井,反演时窗为2000~2600ms,采样率为2ms。将经过标准化和精细井震标定的11口井作为样本井,建立具有波形指示的初始模型。任意选取一个过两口井的剖面为研究资料。根据样本井纵波阻抗曲线与对应的井旁地震道分析结果,为了尽可能使井曲线与地震波形具有较好的映射关系,以保证目标层样本井曲线间的相关系数大于目标层井旁地震道间的相关指数,对样本井作低通滤波,选取最高截止频率为130Hz,从而建立地震波形指示的初始模型。基于地震波形约束的MCMC随机反演的目的是提高随机反演方法的确定性和反演结果的分辨率,同时降低反演结果的随机性。
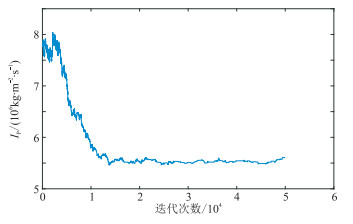
图 7为第57道某点的马尔科夫链,可见经过10000次迭代后纵波阻抗的马尔科夫链基本收敛。鉴于本文利用后验均值作为模型参数的最优解,为了确保反演结果的精度,尽可能降低反演解的随机性,在二维实际资料反演时设置迭代次数为12000,并取后2000次的反演结果均值作为1次随机反演结果输出。
|
图 7 第57道某点的马尔科夫链 |
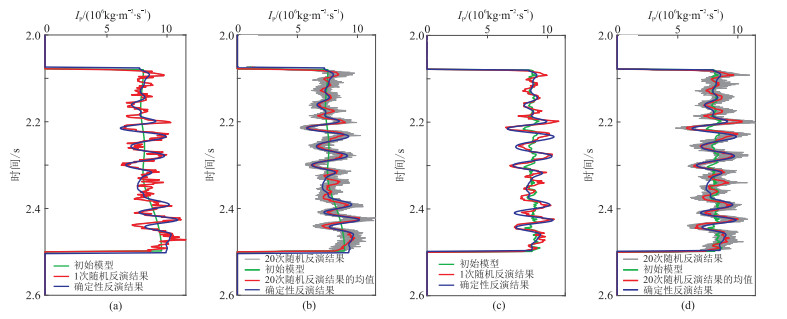
图 8为第57道不同初始模型的反演结果。由图可见:对比不同方法的1次反演结果(图 8a、图 8c)表明,基于地震波形约束的MCMC随机反演结果的稳定性高于确定性反演结果,且后者使用不同的初始模型对反演结果影响不大;对比不同方法的20次反演结果(图 8b、图 8d)表明,不同模型的基于地震波形约束的MCMC随机反演效果好于确定性反演。为了对比基于地震波形约束的MCMC随机反演和确定性反演的效果,在下文前者采用具有地震波形指示的初始模型,后者采用普通低频模型。
|
图 8 第57道不同初始模型的反演结果 (a)常规初始模型1次反演结果;(b)常规初始模型20次反演结果;(c)有效样本数为10的地震波形指示初始模型1次反演结果;(d)有效样本数为10的地震波形指示初始模型20次反演结果 |
图 9为第57道不同样本数的反演结果。由图可见,基于地震波形约束的MCMC随机反演结果的高、低频信息丰富(图 9b、图 9d),有效缓解了确定性反演精度对初始模型的依赖,且反演结果的纵向分辨率较高。

|
图 9 第57道不同样本数的反演结果 (a)有效样本数为10的合成记录与原始地震记录;(b)有效样本数为10的20次反演结果;(c)有效样本数为20的合成记录与原始地震记录;(d)有效样本数为20的20次反演结果 |
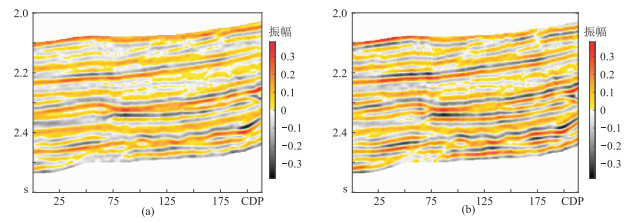
图 10为基于地震波形约束的MCMC随机反演结果及初始模型。由图可见:①有效样本数为10的初始模型(图 10e)效果好于有效样本数为20的初始模型(图 10f),且能反映20次反演结果(图 10b)的基本特征。②有效样本数为10(图 10b)、20(图 10d)的20次反演结果趋势和井曲线趋势大致吻合,且前者的反演精度更高。对比原始地震记录(图 11a)与有效样本数为10的反演结果合成记录(图 11b)可见,两者几乎一致,也证明基于地震波形约束的MCMC随机反演结果的可靠性。

|
图 10 基于地震波形约束的MCMC随机反演结果及初始模型 (a)有效样本数为10的1次反演结果;(b)有效样本数为10的20次反演结果;(c)有效样本数为20的1次反演结果;(d)有效样本数为20的20次反演结果;(e)有效样本数为10的初始模型;(f)有效样本数为20的初始模型将两口验证井的纵波阻抗曲线投射在反演剖面中,为了更好地了解井曲线变化趋势,对井曲线进行了130Hz的低通滤波 |
|
图 11 原始地震记录(a)与有效样本数为10的反演结果合成记录(b) |
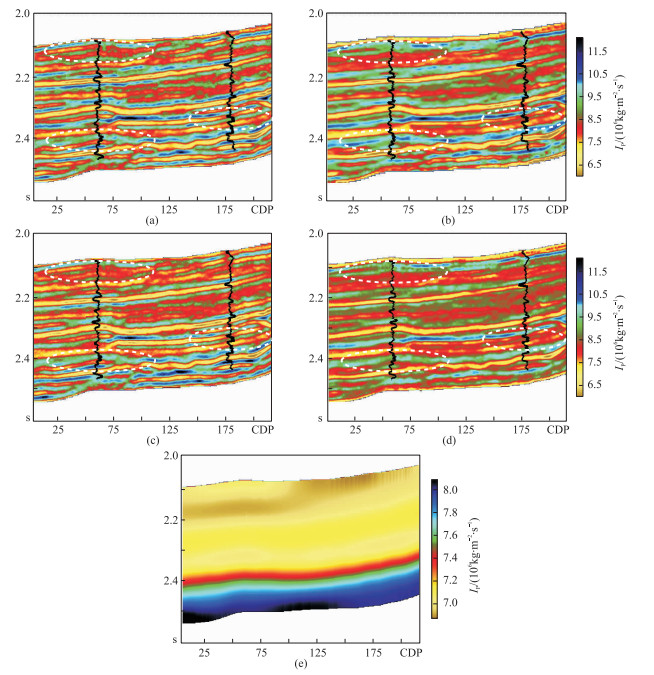
图 12为不同反演结果。由图中的白色虚线标记区域可见:基于地震波形约束的随机反演方法(图 12a)和常规随机反演方法(图 12c)均有效地提高了反演精度,对识别调谐尺度内的薄储层具有一定优势;前者在提高纵向分辨率的同时也提高了横向分辨率,且在引入波形指示初始模型的约束下,反演结果具有丰富的高、低频信息,有效地缓解了常规稀疏脉冲反演(图 12b)精度对初始模型(图 12d、图 12e)的依赖。
|
图 12 不同反演结果 (a)有效样本数为10的基于地震波形约束的MCMC 20次随机反演结果;(b)常规稀疏脉冲反演结果;(c)常规随机反演结果;(d)基于波形指示初始模型的稀疏脉冲反演结果;(e)常规初始模型 |
(1) 本文采用基于地震波形约束的MCMC随机反演方法,利用地震波形的相似性指导测井数据建立具有波形指示的初始模型;此外,在贝叶斯框架下构建了观测地震数据和测井数据协同约束的后验概率密度分布,引入M-H采样算法多次随机模拟初始模型参数,利用后验均值作为模型参数的最优解,有效地提高了反演的稳定性和横向连续性。
(2) 考虑到MCMC随机反演方法的固有性质,其反演精度和马尔科夫链迭代效率受不同建议分布以及不同模型约束条件的影响较大。为了尽可能降低这些不确定因素的影响,提高反演的稳定性,本文在MCMC随机反演方法的基础上加入波形指示的初始模型约束,可以使马尔科夫链快速收敛,间接提高了反演效率,同时也改善了随机反演精度和横向连续性。
(3) 模型试算和实际资料反演效果表明,基于地震波形约束的MCMC随机反演方法具有较好的抗噪性,有效提高了反演精度,对识别调谐尺度内薄储层具有一定优势,在提高纵向分辨率的同时也提高了横向分辨率。
| [1] |
印兴耀, 张世鑫, 张繁昌, 等. 利用基于Russell近似的弹性波阻抗反演进行储层描述和流体识别[J]. 石油地球物理勘探, 2010, 45(3): 373-380. YIN Xingyao, ZHANG Shixin, ZHANG Fanchang, et al. Utilizing Russell approximation-based elastic wave impedance inversion to conduct reservoir description and fluid identification[J]. Oil Geophysical Prospecting, 2010, 45(3): 373-380. |
| [2] |
印兴耀, 曹丹平, 王保丽, 等. 基于叠前地震反演的流体识别方法研究进展[J]. 石油地球物理勘探, 2014, 49(1): 22-34. YIN Xingyao, CAO Danping, WANG Baoli, et al. Research progress of fluid discrimination with pre-stack seismic inversion[J]. Oil Geophysical Prospecting, 2014, 49(1): 22-34. |
| [3] |
印兴耀, 宗兆云, 吴国忱. 岩石物理驱动下地震流体识别研究[J]. 中国科学: 地球科学, 2015, 45(1): 8-21. YIN Xingyao, ZONG Zhaoyun, WU Guochen. Research on seismic fluid identification driven by rock physics[J]. Science China: Earth Sciences, 2015, 45(1): 8-21. |
| [4] |
Li K, Yin X Y, Liu J, et al. An improved stochastic inversion for joint estimation of seismic impedance and lithofacies[J]. Journal of Geophysics and Engineering, 2019, 16(1): 62-76. DOI:10.1093/jge/gxy005 |
| [5] |
高君, 毕建军, 赵海山, 等. 地震波形指示反演薄储层预测技术及其应用[J]. 地球物理学进展, 2017, 32(1): 142-145. GAO Jun, BI Jianjun, ZHAO Haishan, et al. Seismic waveform inversion technology and application of thinner reservoir prediction[J]. Progress in Geophy-sics, 2017, 32(1): 142-145. |
| [6] |
Yin X Y, Li K, Zong Z Y. Resolution enhancement of robust Bayesian pre-stack inversion in the frequency domain[J]. Journal of Geophysics and Engineering, 2016, 13(5): 646-656. DOI:10.1088/1742-2132/13/5/646 |
| [7] |
Li K, Yin X Y, Zong Z Y. Bayesian seismic multi-scale inversion in complex Laplace mixed domains[J]. Petroleum Science, 2017, 14(4): 694-710. DOI:10.1007/s12182-017-0191-0 |
| [8] |
Liu X X, Yin X Y, Li H S. Optimal variable-grid finite-difference modeling for porous media[J]. Journal of Geophysics and Engineering, 2014. DOI:10.1088/1742-2132/11/6/065011 |
| [9] |
王宇, 韩立国, 周家雄, 等. L1-L2范数联合约束稀疏脉冲反演的应用[J]. 地球科学——中国地质大学学报, 2009, 34(5): 835-840. WANG Yu, HAN Liguo, ZHOU Jiaxiong, et al. Application of combined norm constrained sparse spike inverse[J]. Earth Sciences: Journal of China University of Geosciences, 2009, 34(5): 835-840. |
| [10] |
郭朝斌, 杨小波, 陈红岳, 等. 约束稀疏脉冲反演在储层预测中的应用[J]. 石油物探, 2006, 45(4): 397-400. GUO Chaobin, YANG Xiaobo, CHEN Hongyue, et al. Constrained sparse pulse inversion research in north of Haitongji depression[J]. Geophysical Prospecting for Petroleum, 2006, 45(4): 397-400. DOI:10.3969/j.issn.1000-1441.2006.04.011 |
| [11] |
赵晨, 张广智, 张佳佳, 等. 基于Metropolis优化的叠前全局迭代地质统计学反演方法[J]. 地球物理学报, 2020, 63(8): 3116-3130. ZHAO Chen, ZHANG Guangzhi, ZHANG Jiajia, et al. Prestack global iteration geostatistical inversion method based on Metropolis sampling algorithm[J]. Chinese Journal of Geophysics, 2020, 63(8): 3116-3130. |
| [12] |
孙瑞莹. 先验信息构建与地震随机反演方法研究[D]. 山东青岛: 中国石油大学(华东), 2015. SUN Ruiying.Study of the Priori Information Construction and Seismic Stochastic Inversion Method[D].China University of Petroleum (East China), Qingdao, Shandong, 2015. |
| [13] |
杨锴, 艾迪飞, 耿建华. 测井、井间地震与地面地震数据联合约束下的地质统计学随机建模方法研究[J]. 地球物理学报, 2012, 55(8): 2695-2704. YANG Kai, Ai Difei, Geng Jianhua. A new geostatistical inversion and reservoir modeling technique constrained by well-log, crosshole and surface seismic data[J]. Chinese Journal of Geophysics, 2012, 55(8): 2695-2704. |
| [14] |
王小丹, 印兴耀, 金惠, 等. 叠前地震随机反演方法及实际资料应用[J]. 地球物理学进展, 2018, 33(6): 2471-2476. WANG Xiaodan, YIN Xingyao, JIN Hui, et al. Pre-stack seismic stochastic inversion and application on real data[J]. Progress in Geophysics, 2018, 33(6): 2471-2476. |
| [15] |
张繁昌, 肖张波, 印兴耀. 地震数据约束下的贝叶斯随机反演[J]. 石油地球物理勘探, 2014, 49(1): 176-182. ZHANG Fanchang, XIAO Zhangbo, YIN Xingyao. Bayesian stochastic inversion constrained by seismic data[J]. Oil Geophysical Prospecting, 2014, 49(1): 176-182. |
| [16] |
李祺鑫, 罗亚能, 张生, 等. 高分辨率波阻抗贝叶斯序贯随机反演[J]. 石油地球物理勘探, 2020, 55(2): 389-397. LI Qixin, LUO Ya'neng, ZHANG Sheng, et al. High-resolution Bayesian sequential stochastic inversion[J]. Oil Geophysical Prospecting, 2020, 55(2): 389-397. |
| [17] |
李宁. 基于模拟退火的地质统计学反演方法研究[D]. 山东青岛: 中国石油大学(华东), 2013. LI Ning.The Study of Geostatistics Inversion Based on Simulated Annealing Method[D].China University of Petroleum (East China), Qingdao, Shandong, 2013. |
| [18] |
印兴耀, 贺维胜, 黄旭日. 贝叶斯-序贯高斯模拟方法[J]. 石油大学学报(自然科学版), 2005, 29(5): 28-32. YIN Xingyao, HE Weisheng, HUANG Xuri. Bayesian sequential Gaussian simulation method[J]. Journal of the University of Petroleum, China(Edition of Natural Science), 2005, 29(5): 28-32. |
| [19] |
Yin X Y, Sun R Y, Wang B L, et al. Simultaneous inversion of petrophysical parameters based on a geostatistical priori information[J]. Applied Geophysics, 2014, 11(3): 311-320. DOI:10.1007/s11770-014-0445-1 |
| [20] |
王保丽, 印兴耀, 丁龙翔, 等. 基于FFT-MA谱模拟的快速随机反演方法研究[J]. 地球物理学报, 2015, 58(2): 664-673. WANG Baoli, YIN Xingyao, DING Longxiang, et al. Study of fast stochastic inversion based on FFT-MA spectrum simulation[J]. Chinese Journal of Geophy-sics, 2015, 58(2): 664-673. |
| [21] |
潘新朋. 优化MCMC方法在地震反演中的应用研究[D]. 山东青岛: 中国石油大学(华东), 2016. PAN Xinpeng.The Application Study in Seismic Inversion Based on Optimized Markov Chain Monte Carlo Method[D].China University of Petroleum (East China), Qingdao, Shandong, 2016. |
| [22] |
王丹阳. 基于MCMC方法的叠前反演方法研究[D]. 山东青岛: 中国石油大学(华东), 2012. WANG Danyang. Pre-stack Seismic Inversion Based on Markov Chain Monte Carlo Method[D].China University of Petroleum (East China), Qingdao, Shandong, 2012. |
| [23] |
张广智, 王丹阳, 印兴耀. 利用MCMC方法估算地震参数[J]. 石油地球物理勘探, 2011, 46(4): 605-609. ZHANG Guangzhi, WANG Danyang, YIN Xingyao. Seismic parameter estimation using Markov Chain Monte Carlo Method[J]. Oil Geophysical Prospecting, 2011, 46(4): 605-609. |
| [24] |
Hong T C, Sen M K. A new MCMC algorithm for seismic waveform inversion and corresponding uncertainty analysis[J]. Geophysical Journal International, 2009, 177(2): 14-32. |
| [25] |
Metropolis N, Rosenbluth A W, Rosenbluth M N, et al. Equation of state calculations by fast computing machines[J]. The Journal of Chemical Physics, 1953, 21(6): 1087-1092. DOI:10.1063/1.1699114 |
| [26] |
Hastings W K. Monte Carlo sampling methods using Markov chains and their applications[J]. Biometrika, 1970, 57(1): 97-109. DOI:10.1093/biomet/57.1.97 |
| [27] |
Smith A F M, Roberts G O. Bayesian computation via the Gibbs sampler and related Markov Chain Monte Carlo methods[J]. Journal of the Royal Statistical Society, 1993, 55(1): 3-23. |
| [28] |
张广智, 潘新朋, 孙昌路, 等. 纵横波联合叠前自适应MCMC反演方法[J]. 石油地球物理勘探, 2016, 51(5): 938-946. ZHANG Guangzhi, PAN Xinpeng, SUN Changlu, et al. PP- & PS-wave prestack nonlinear inversion based on adaptive MCMC algorithm[J]. Oil Geophysical Prospecting, 2016, 51(5): 938-946. |
| [29] |
张广智, 王丹阳, 印兴耀. 基于MCMC的叠前地震反演方法研究[J]. 地球物理学报, 2011, 54(11): 2926-2932. ZHANG Guangzhi, WANG Danyang, YIN Xingyao. Study on prestack seismic inversion using Markov Chain Monte Carlo[J]. Chinese Journal of Geophy-sics, 2011, 54(11): 2926-2932. DOI:10.3969/j.issn.0001-5733.2011.11.022 |
| [30] |
Pan X P, Zhang G Z, Chen H Z, et al. McMC-based AVAZ direct inversion for fracture weaknesses[J]. Journal of Applied Geophysics, 2017, 138(7): 50-61. |
| [31] |
Pan X P, Zhang G Z, Chen H Z, et al. McMC-based nonlinear EIVAZ inversion driven by rock physics[J]. Journal of Geophysics and Engineering, 2017, 14(2): 368-379. DOI:10.1088/1742-2140/aa5af5 |
| [32] |
Pan X P, Zhang G Z, Zhang J J, et al. Zoeppritz-based AVO inversion using an improved Markov chain Monte Carlo method[J]. Petroleum Science, 2017, 14(1): 75-83. DOI:10.1007/s12182-016-0131-4 |
| [33] |
李坤, 印兴耀, 宗兆云. 岩石物理驱动的相约束叠前地震概率化反演方法[J]. 中国科学: 地球科学, 2020, 50(6): 832-854. LI Kun, YIN Xingyao, ZONG Zhaoyun. Facies-constrained prestack seismic probabilistic inversion dri-ven by rock physics[J]. Science China: Earth Sciences, 2020, 50(6): 832-854. |
| [34] |
章雄, 张本健, 梁虹, 等. 波形指示叠前地震反演方法在致密含油薄砂层预测中的应用[J]. 物探与化探, 2018, 42(3): 545-554. ZHANG Xiong, ZHANG Benjian, LIANG Hong, et al. The application of pre-stack inversion based on seismic waveform indicator to the prediction of compact and thin oil-bearing sand layer[J]. Geophysical and Geochemical Exploration, 2018, 42(3): 545-554. |
| [35] |
李坤, 印兴耀. 混合概率模型驱动的叠前地震反演方法[J]. 石油地球物理勘探, 2020, 55(4): 839-853. LI Kun, YIN Xingyao. Prestack seismic inversion driven by mixture probabilistic models[J]. Oil Geophysical Prospecting, 2020, 55(4): 839-853. |
| [36] |
Holden L. Mixing of MCMC algorithms[J]. Journal of Statistical Computation and Simulation, 2019, 89(12): 2261-2279. DOI:10.1080/00949655.2019.1615064 |



 印兴耀, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
印兴耀, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: 