② 成都理工大学地球勘探与信息技术教育部重点实验室, 四川成都 610059
② Key Lab of Earth Exploration & Information Techniques of Ministry of Education, Chengdu University of Technology, Chengdu, Sichuan 610059, China
图像分析中的边缘检测技术被广泛用于地震数据裂缝检测。目前地震数据边缘检测方法主要有基于图像空间域微分算子(Prewitt算子、Robert算子、Canny算子、Sobel算子、高斯偏导滤波器(LOG)等)的边缘检测法及以变换域小波分析为基础的多尺度边缘检测法[1]。实际勘探经验表明,油气藏中普遍分布孔隙和裂缝,因此可利用地震资料检测边缘特征。Wu等[2-4]、丁燕等[5]利用深度学习算法提取三维地震图像中的断层及其产状信息。
希尔伯特变换广泛应用于检测地震资料不连续边缘信息。党志敏等[6]、熊晓军等[7]利用广义希尔伯特变换检测含噪地震资料的边缘信息。陈学华等[9-10]将高阶伪希尔伯特变换用于地震资料边缘检测。谢静等[11]提出了时间域加窗希尔伯特变换边缘检测方法。基于三维地震资料在深度方向的多尺度特征,李斌等[12]提出了多尺度加窗希尔伯特变换的地震资料体边缘检测方法。在前人的研究[13-17]基础上,Lyu等[18-19]实现了基于二维希尔伯特变换的三维地震资料体边缘检测方法。利用上述方法检测裂缝时,往往没有考虑地震资料不连续信息在方向上的多样化与复杂性。为此,周元茂等[20]联合应用各向异性高斯迭代平滑滤波方法与地震体曲率分析方法,形成了组合型方向体曲率分析方法。
基于希尔伯特变换的边缘检测算法用于实际地震资料时,提取的往往是裂缝综合信息,信息繁杂且会弱化部分有效信息,难以分辨某一特定方向的数据特点,不利于分析裂缝走向。因此,考虑到断层、裂缝等不连续信息的复杂性,为了分析地震资料中各个方向的不连续特征,本文构建了一种任意角度旋转的加窗希尔伯特变换(arbitrarily rotated windowed Hilbert transform,ARWHT)边缘检测算子,将其用于三维地震资料体边缘检测,不仅能提取地震资料在任意方向的不连续特征,还可突出局部异常信息,减少噪声的影响,从而获得更精确的储层裂缝走向及分布信息。
1 方法原理 1.1 ARWHT边缘检测算子为了充分提取、分析三维地震资料中任意方向的不连续信息并突出局部化特征,本文构建了ARWHT边缘检测算子。
若将希尔伯特算子所有点表示为一个几何信息矩阵Q,将其与方向检测模板T相乘﹐就得到旋转变换后的几何信息矩阵Q′,即
| $ {\mathit{\boldsymbol{Q}}}\prime = {\mathit{\boldsymbol{QT}}} $ | (1) |
其中
| $ {\mathit{\boldsymbol{T}}} = \;\left( \begin{array}{l} \;\;\;\;{\rm{cos}}\theta \;{\rm{sin}}\theta \\ \;\; - {\rm{sin}}\theta \;{\rm{cos}}\theta \end{array} \right) $ |
设加窗后的希尔伯特算子序列的样点坐标为P[n,h′(n)],将其逆时针旋转角度θ后,新算子序列的样点坐标为P′[nR,h′R(n)],则有
| $ \left\{ \begin{array}{l} {n_{\rm{R}}} = an + ch\prime \left( n \right)\\ {{h'}_{\rm{R}}}\left( n \right) = bn + dh\prime \left( n \right) \end{array} \right. $ | (2) |
其中
| $ h\prime \left( n \right) = h\left( n \right) \cdot w\left( n \right) $ | (3) |
式中:h(n)为原始希尔伯特变换算子,n为采样点号;w(n)为对算子作局部化处理的窗函数;a、b、c、d为设置的方向检测模板初始形式的组成参数。将式(2)改为矩阵形式
| $ \left[ {{n_{\rm{R}}}\;h{\prime _{\rm{R}}}\left( n \right)} \right] = \left[ {n\;h\prime \left( n \right)} \right]\left( \begin{array}{l} a\;b\\ c\;d \end{array} \right) $ | (4) |
设点P与坐标原点O的连线OP与x轴的夹角为α,则有
| $ \left\{ \begin{array}{l} h\prime \left( n \right) = \overline {OP} \cdot{\rm{sin}}\alpha \\ n = \overline {OP} \cdot{\rm{cos}}\alpha \end{array} \right. $ | (5) |
| $ \left\{ \begin{array}{l} {n_{\rm{R}}} = \overline {OP\prime } {\rm{cos}}\left( {\alpha + \theta } \right) = n{\rm{cos}}\theta - h\prime \left( n \right){\rm{sin}}\theta \\ h{\prime _{\rm{R}}}\left( n \right) = \overline {OP\prime } {\rm{sin}}\left( {\alpha + \theta } \right) = n{\rm{sin}}\theta + h\prime \left( n \right){\rm{cos}}\theta \end{array} \right. $ | (6) |
式中 OP、OP′分别为OP、OP′的长度,则式(4)变为
| $ \left[ {{n_{\rm{R}}}\;h{\prime _{\rm{R}}}\left( n \right)} \right] = \left[ {n\;h\prime \left( n \right)} \right]\left( \begin{array}{l} \;\;{\rm{cos}}\theta \;{\rm{sin}}\theta \\ - {\rm{sin}}\theta \;{\rm{cos}}\theta \end{array} \right) $ | (7) |
为强调地震资料的局部化特征、突出不连续信息,本文选择高斯窗对希尔伯特变换算子进行局部化处理,使检测对象的有效边缘信息更突出、非边缘信息的差异更明显。高斯窗函数的表达式为
| $ w\left( n \right) = \frac{1}{{\sigma \sqrt {2\pi } }}{{\rm{e}}^{ - \frac{{{n^2}}}{{2{\sigma ^2}}}}} $ | (8) |
式中σ为决定窗函数时间宽度的尺度因子,即σ越大,窗函数越宽。图 1为ARWHT算子。
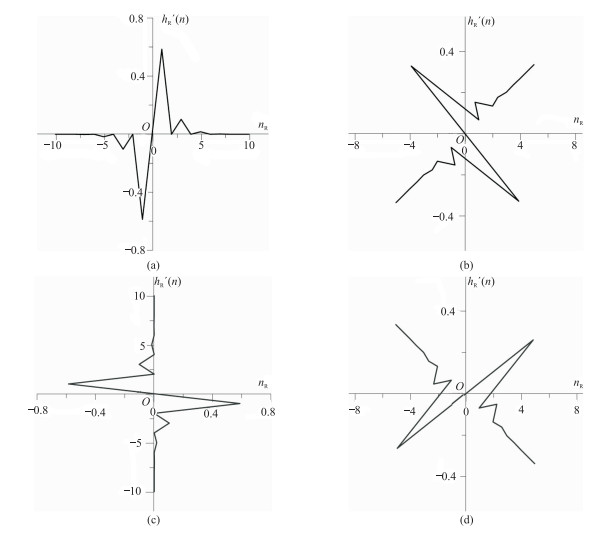
|
图 1 ARWHT算子 (a)不旋转;(b)逆时针旋转45°;(b)逆时针旋转90°;(d)逆时针旋转135° |
将ARWHT算子用于边缘检测,得到一个新的基于ARWHT的边缘提取公式,边缘提取结果为
| $ \begin{array}{l} \tilde x\left( {{n_{\rm{R}}}} \right) = x\left( {{n_R}} \right) * h{\prime _{\rm{R}}}\left( n \right)\\ \;\;\;\;\;\;\;\;\; = \sum\limits_{k = 0}^{N - 1} x \left[ {{n_{\rm{R}}} - \left( {2k - 1} \right)} \right] \cdot h{\prime _{\rm{R}}}\left( {2k - 1} \right) \end{array} $ | (9) |
其中
| $ {n_{\rm{R}}} = n{\rm{cos}}\theta - h\prime \left( n \right){\rm{sin}}\theta $ | (10) |
| $ h{\prime _{\rm{R}}}\left( n \right) = n{\rm{sin}}\theta + h\prime \left( n \right){\rm{cos}}\theta $ | (11) |
式中N为x(nR)的长度。
1.2 基于ARWHT的地震资料体边缘检测算法的实现由式(9)~式(11)计算任意特定方向的边缘提取结果,进而由
| $ D\left( {{m_0}, k, \theta } \right) = \sum\limits_{\lambda = - k}^k {\frac{{\left[ {x\left( {{m_0} + \lambda \cdot\Delta m, {n_\theta }} \right) * {{h'}_\theta }\left( n \right)} \right] + \left| {{{\tilde x}_{\theta , \lambda - \min }}} \right|}}{{{{\tilde x}_{\theta , \lambda - {\rm{max}}}} - {{\tilde x}_{\theta , \lambda - {\rm{min}}}}}}} $ | (12) |
计算基于ARWHT的地震资料体边缘检测结果。式中:D(m0,k,θ)表示算子旋转角度为θ时的地震资料体边缘检测结果,m0为目的层的时间位置,k为三维地震资料在m0上、下的采样点数,则计算的地震资料层段厚度为2k·Δm(Δm为在深度时窗上相邻样点之间的采样间隔);x(m0+λ·Δm,nθ)为沿层地震数据;
对于所有的算子旋转角度θ∈[0°,180°],取每个空间位置的D(m0,k,θ)最大值,由
| $ D'\left( {{m_0}, k} \right) = \mathop {{\rm{max}}}\limits_\theta \left[ {D\left( {{m_0}, k, \theta } \right)} \right] $ | (13) |
得到融合了所有方向的基于ARWHT的三维地震资料体边缘检测结果。
2 模型试算与分析为了验证本文算法的效果,设置一个正八边形模型(图 2a),利用ARWHT算子提取各方向的边缘信息(图 2b、图 2c)。结果表明:逆时针旋转45°的ARWHT算子检测结果(图 2b)着重突出了0°、90°、135°的边缘信息(135°边缘信息绝对值最大),有效过滤了45°的边缘信息;逆时针旋转135°的ARWHT算子检测结果(图 2c)着重突出了0°、45°、90°的边缘信息(45°边缘信息绝对值最大),有效过滤了135°边缘信息。
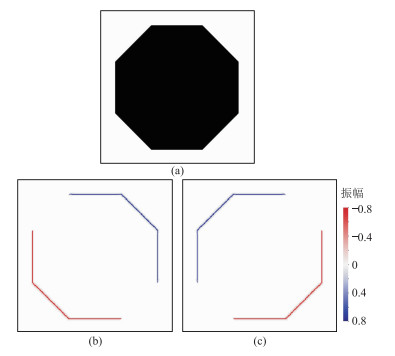
|
图 2 正八边形模型及其ARWHT算子边缘检测结果 (a)正八边形模型;(b)逆时针旋转45°;(c)逆时针旋转135° |
为了验证本文方法提取复杂边缘特征信息的有效性,对经典的Lena图像提取边缘信息(图 3)。结果表明:①原始图像(图 3a)背景中含有较多不同角度的线条,有利于验证算法的有效性。②本文算法弱化了与算子旋转角度一致的边缘信息,同时突显了与其垂直的边缘信息(图 3b、图 3c、图 3e、图 3f),且边缘信息提取效果优于常规希尔伯特变换(图 3d)。如0°算子对帽子的阴影部分表现更好(图 3b红色长方形框处),90°算子提取的帽檐上边缘明显更连续(图 3c黄色箭头处),且唇部线条也更突出。③由45°(图 3e)和135°(图 3f)算子检测结果可见,对于背景中不同方向的边缘信息,不同旋转角度算子侧重提取不同方向的边缘信息(绿色和蓝色箭头处)。④由于眉毛角度的不同,不同旋转角度的算子检测结果对眉毛的表现效果也有差异(红色椭圆框处)。
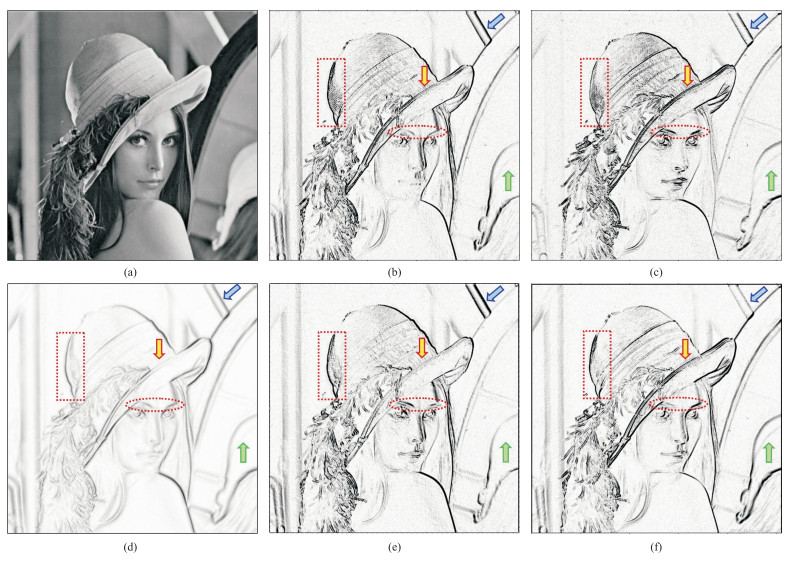
|
图 3 Lena图像及其ARWHT算子边缘检测结果 (a)原始图像;(b)不旋转;(c)逆时针旋转90°;(d)常规方法;(e)逆时针旋转45°;(f)逆时针旋转135° |
为了说明本文方法在实际地震资料处理中的应用效果,以中国KL地区的三维地震资料为例,分别使用旋转0°、45°、90°、135°的算子提取体边缘信息。由KL地区沿目的层振幅切片(图 4)可见,目的层内河道和断层分布极为复杂。

|
图 4 KL地区沿目的层振幅切片 |
基于ARWHT的实际地震资料体边缘检测结果(图 5)表明:①不旋转(图 5a)与逆时针旋转90°(图 5b)算子的方向相互垂直,检测结果差别明显,有利于刻画细小裂缝的方向。表现为:前者着重突出了纵向构造特征,断层及裂隙连续性明显加强,显著减弱了横向构造信息;后者的横向不连续性信息以及构造异常特征明显加强,明显压制了纵向边缘信息,显示出原始地震资料中难以用肉眼分辨的大型横向连续裂缝(红色长方形虚线框处)。另外,还可以看到一条隐蔽的横向河道,在其他提取结果中(图 5a、图 5c、图 5d)难以分辨(蓝色箭头处)。②逆时针旋转45°算子检测结果(图 5c)突显了135°的体边缘信息(黄色箭头处);逆时针旋转135°算子检测结果(图 5d)着重表现了45°的不连续信息(绿色箭头处),还可以追踪到一条走向大致呈45°方向的蜿蜒河道(绿色点状线所示),在其他提取结果(图 5a、图 5b、图 5c)中难以分辨。③综合四个方向的提取结果来看,边缘检测结果的不同区域(黄色方形虚线框和蓝色椭圆虚线框)数据的特征不同,包含的不连续信息方向特征与ARWHT算子提取边缘的规律一致,更好地刻画了地震异常信息的空间分布和走向特征。
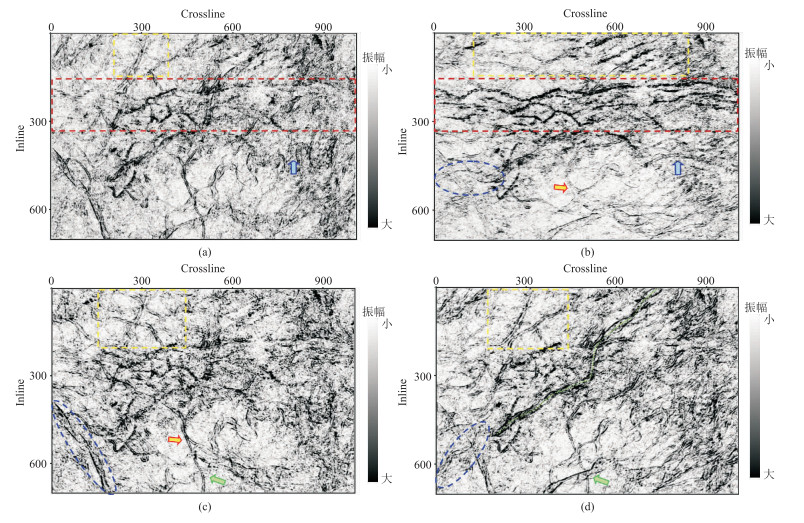
|
图 5 基于ARWHT的实际地震资料体边缘检测结果 (a)不旋转;(b)逆时针旋转90°;(c)逆时针旋转45°;(d)逆时针旋转135° |
在利用本文方法处理实际地震资料时,应考虑数据的具体情况选择算子的旋转角度。对于已知走向信息的大断裂或者某一区域内分布方向大致相同的裂缝系统,应选择与其走向或分布方向垂直的算子旋转角度提取边缘信息,从而加强走向和分布方向的不连续信息特征;对于复杂多变的裂缝系统,其包含各个方向的信息,此时应选择多个旋转角度提取边缘信息进行融合,以显示更丰富的有效信息,利于地震资料精细解释。
为了进一步分析本文方法的应用效果及优势,根据式(13)融合图 5中各方向的边缘信息提取结果(图 6c),并与常规希尔伯特变换边缘检测结果(图 6a)、RMS振幅体切片(图 6b)对比、分析。结果表明:图 6c综合了图 5各结果的优点,包含了各个方向的体边缘特征信息(图中红色虚线框与箭头处);与图 6a和图 6b相比,图 6c的有效信息更全面,不仅清楚地展示了河道和断裂系统的分布特征,还刻画了裂缝不连续地质异常的边界信息,有利于地震资料的精细解释。
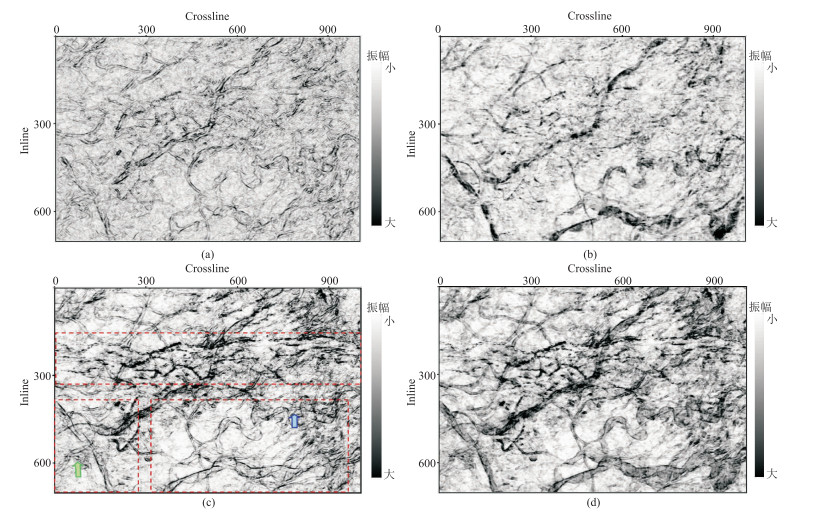
|
图 6 实际地震数据不同方法的边缘检测结果对比 (a)常规方法;(b)RMS振幅体切片;(c)本文方法;(d)RMS+本文方法 |
为了更清晰地展示河道、断层、断裂带等信息,将本文方法的裂缝检测结果(图 6c)与图 6b融合,融合结果(图 6d)不仅展示了多方向的裂缝信息,还刻画了河道走向、裂缝边界信息,展示了丰富的地质信息。
综上所述,本文方法能突显地震资料中任意特定方向的地质异常信息,更全面地展示了地震不连续信息的分布特征,检测结果体现了算法的可行性和优越性。
4 结束语本文在加窗希尔伯特变换理论的基础上,构建了ARWHT边缘检测算子,将其应用于实际地震资料边缘检测,可以得到任意特定方向的不连续异常特征,实现了提取各方向不连续特征的三维地震资料体边缘检测。
地震资料的ARWHT体边缘检测方法在表征储层和地质结构边缘信息时保留了有效的方向特征。因此,可以在实际地震数据中充分挖掘并突显任意特定方向的地质特征。对于具有不同特征的数据,应选择不同旋转角度的算子进行边缘检测。实际地震数据测试表明,ARWHT体边缘检测方法可描述河道、断层、断裂带、构造、储层裂缝分布,强化地震数据在任意特定方向的构造信息,更好地突出地质构造特征,为解释构造、了解不连续地质异常信息及其展布规律、预测储层等提供依据。
| [1] |
陈学华, 贺振华, 文晓涛, 等. 基于广义S变换的裂缝分频边缘检测方法[J]. 吉林大学学报(地球科学版), 2011, 41(5): 1605-1609. CHEN Xuehua, HE Zhenhua, WEN Xiaotao, et al. Fracture multi-frequency edge detection based on ge-neralized S transform[J]. Journal of Jilin University(Earth Science Edition), 2011, 41(5): 1605-1609. |
| [2] |
Wu X M, Liang L M, Shi Y Z, et al. FaultSeg3D: Using synthetic data sets to train an end-to-end convolutional neural network for 3D seismic fault segmentation[J]. Geophysics, 2019, 84(3): IM35-IM45. DOI:10.1190/geo2018-0646.1 |
| [3] |
Wu X M, Liang L M, Shi Y Z, et al. Multitask lear-ning for local seismic image processing: fault detection, structure-oriented smoothing with edge-preserving, and seismic normal estimation by using a single con-volutional neural network[J]. Geophysical Journal International, 2019, 219(3): 2097-2109. DOI:10.1093/gji/ggz418 |
| [4] |
Wu X M, Shi Y Z, Fomel S, et al. FaultNet3D: Predicting fault probabilities, strikes, and dips with a single convolutional neural network[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(11): 9138-9155. DOI:10.1109/TGRS.2019.2925003 |
| [5] |
丁燕, 杜启振, Qamar Yasin, 等. 基于深度学习的裂缝预测在S区潜山碳酸盐岩储层中的应用[J]. 石油物探, 2020, 59(2): 267-275. DING Yan, DU Qizhen, Qamar Yasin, et al. Fracture prediction based on deep learning: Application to a buried hill carbonate reservoir in the S area[J]. Geophysical Prospecting for Petroleum, 2020, 59(2): 267-275. DOI:10.3969/j.issn.1000-1441.2020.02.013 |
| [6] |
党志敏, 贺振华, 黄德济. GHT在含噪信号边缘检测中的应用效果分析[J]. 石油工业计算机应用, 2008, 16(2): 19-21. DANG Zhimin, HE Zhenhua, HUANG Deji. GHT application results analysis in noisy signal edge detection analysis[J]. Oil Industry Computer Applications, 2008, 16(2): 19-21. |
| [7] |
熊晓军, 贺振华, 赵明金. 一种基于GHT的裂缝检测新方法[J]. 石油地球物理勘探, 2009, 44(4): 442-444. XIONG Xiaojun, HE Zhenhua, ZHAO Mingjin. A new GHT-based fractural detection method[J]. Oil Geophysical Prospecting, 2009, 44(4): 442-444. DOI:10.3321/j.issn:1000-7210.2009.04.011 |
| [8] |
Luo Y, Al-Dossary S, Marhoon M, et al. Generalized Hilbert transform and its applications in geophysics[J]. The Leading Edge, 2003, 22(3): 198-202. DOI:10.1190/1.1564522 |
| [9] |
陈学华, 贺振华, 黄德济. 地震资料的高阶伪希尔伯特变换边缘检测[J]. 地球物理学进展, 2008, 23(4): 1106-1110. CHEN Xuehua, HE Zhenhua, HUANG Deji. Seismic data edge detection based on higher-order pseudo Hilbert transform[J]. Progress in Geophysics, 2008, 23(4): 1106-1110. |
| [10] |
陈学华, 贺振华, 黄德济. 高阶伪希尔伯特变换在边缘检测中的应用[J]. 数据采集与处理, 2008, 23(2): 224-227. CHEN Xuehua, HE Zhenhua, HUANG Deji. High-order pseudo Hilbert transform and application in edge detection[J]. Journal of Data Acquisition & Proce-ssing, 2008, 23(2): 224-227. DOI:10.3969/j.issn.1004-9037.2008.02.020 |
| [11] |
谢静, 贺振华, 黄德济. 基于加窗Hilbert变换的高精度边缘检测[J]. 油气地球物理, 2007, 5(1): 27-29. XIE Jing, HE Zhenhua, HUANG Deji. High accuracy edge detection on window-based Hilbert transform[J]. Petroleum Geophysics, 2007, 5(1): 27-29. |
| [12] |
李斌, 陈学华, 贺振华, 等. 基于多尺度加窗希尔伯特变换的地震资料体边缘检测[J]. 石油物探, 2015, 54(3): 345-349. LI Bin, CHEN Xuehua, HE Zhenhua, et al. Seismic data 3D edge detection based on multi-scale windowed Hilbert transform[J]. Geophysical Prospecting for Petroleum, 2015, 54(3): 345-349. DOI:10.3969/j.issn.1000-1441.2015.03.014 |
| [13] |
Read R R, Treitel S. The stabilization of two-dimensional recursive filters via the discrete Hilbert transform[J]. IEEE Transactions on Geoscience Electro-nics, 1973, 7(11): 153-160. |
| [14] |
Kohlmann K. Corner detection in natural images based on the 2-D Hilbert transform[J]. Signal Processing, 1996, 48(3): 225-234. DOI:10.1016/0165-1684(95)00138-7 |
| [15] |
王珂, 肖鹏峰, 冯学智, 等. 基于改进二维离散希尔伯特变换的图像边缘检测方法[J]. 测绘学报, 2012, 41(3): 421-427. WANG Ke, XIAO Pengfeng, FENG Xuezhi, et al. The modified algorithm of image edge features detection based on 2-D discrete Hilbert transform[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 421-427. |
| [16] |
周连敏, 何书梅, 赵郁文, 等. 复合曲流河道内的单河道识别[J]. 石油地球物理勘探, 2019, 54(1): 175-181. ZHOU Lianmin, HE Shumei, ZHAO Yuwen, et al. Single channel identification in a meandering river with compound channels[J]. Oil Geophysical Prospecting, 2019, 54(1): 175-181. |
| [17] |
Liu C, Chen C L, Wang D. Seismic dip estimation based on the two-dimensional Hilbert transform and its application in random noise attenuation[J]. Applied Geophysics, 2015, 12(1): 55-63. DOI:10.1007/s11770-014-0474-4 |
| [18] |
Lyu B N, Chen X H, Li J, et al.An edge detection algorithm of 3D seismic data based on interval two-dimensional Hilbert transform[C].CPS/SEG Beijing 2018 International Geophysical Conference & Exposition, Electronic Papers, 2018.
|
| [19] |
吕丙南, 陈学华, 徐赫, 等. 空间域加窗二维希尔伯特变换在三维地震资料[J]. 石油地球物理勘探, 2020, 55(3): 661-668. LYU Bingnan, CHEN Xuehua, XU He, et al. Application of spatial-windowed 2D Hilbert transform in vo-lumetric edge detection of 3D seismic data[J]. Oil Geophysical Prospecting, 2020, 55(3): 661-668. |
| [20] |
周元茂, 陈学华, 罗鑫, 等. 组合型方位体曲率分析方法[J]. 石油地球物理勘探, 2017, 52(6): 1253-1260. ZHOU Yuanmao, CHEN Xuehua, LUO Xin, et al. An integrated volumetric curvature analysis[J]. Oil Geophysical Prospecting, 2017, 52(6): 1253-1260. |



 陈学华, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院5301室, 610059。Email:
陈学华, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院5301室, 610059。Email: 