② 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266580;
③ 中国地质调查局青岛海洋地质研究所, 山东青岛 266071
② Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266580, China;
③ Qingdao Institute of Marine Geology, China Geology Survey, Qingdao, Shandong 266071, China
天然气水合物又称可燃冰,是在低温高压下,由水的冰晶格架及其吸附的天然气分子组成的一种笼形化合物,广泛分布于大陆边缘海底、深水盆地和永久冻土带中,储量丰富,具备成为21世纪新型能源的潜力[1]。目前在天然气水合物勘探中,地震方法起到了主要作用。如何从地震响应中预测天然气水合物的空间展布特征,是一个需要不断探索的问题。
在地震资料上,天然气水合物通常表现出一些与常规油气储层不同的响应特征,如似海底反射层(BSR)、振幅空白带和极性反转等[2],这些独特的地震反射特征已经被广泛地应用于天然气水合物的识别,是海域天然气水合物存在的重要地球物理标志。但是,这些反射特征与水合物地层的关联程度还存在争议,已发现的水合物与这些响应并不具严格的对应关系[3]。
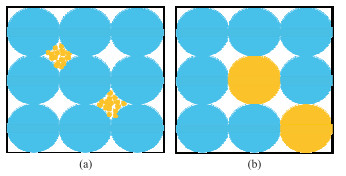
岩石物理模型可用于预测含天然气水合物地层的内部结构和天然气水合物的含量。将沉积层的弹性波速度与密度、孔隙度、各种微观矿物组分及水合物、水和气体的物性参数等联系起来[4],是水合物地层的地震响应分析、高分辨率叠前地震反演及水合物饱和度的定量估算的有效工具[5-6]。因此,众多学者提出了一些水合物岩石物理经验公式和理论模型。Lee等[7]提出基于双相和三相介质时间平均方程和的Wood方程,早期被广泛使用,这类方法简单有效但缺乏实际物理意义,模型参数的选择需要大量的测井资料作为先验信息进行约束。Helgerud等[8]基于等效介质模型将水合物作为基质矿物的一部分构成岩石骨架,临界孔隙度通常取经验值,但实际水合物地层临界孔隙度很难准确确定。Dvokin等[9-10]考虑水合物胶结作用及其对弹性参数的影响,当水合物含量较低时,预测的地层速度会发生急剧增大的现象,计算得到的弹性参数值较实测值高。Zimmerman等[11]使用Kuster-Toksöz模型将水和水合物的混合物作为岩石骨架,黏土作为填充物,该方法适用于低孔隙度的地层。Lee等[12]、Qian等[13]应用Gassmann方程,结合接触理论,计算了水合物储层弹性参数,该方法适用于未固结的海洋沉积物,对于固结沉积物的地层应用效果无法令人满意。刘欣欣等[4]在考虑水合物剪切性质和孔隙微观结构情况下,建立了孔隙填充和颗粒支撑两种模式的水合物模型,在实际资料测试中取到了较好的效果。颗粒支撑模式[14-15]和孔隙填充模式[16-18]是物理意义上的两种极端分布情况,当天然气水合物在固体颗粒边缘沉积作为孔隙空间充填物的一部分时,如图 1a所示,为孔隙填充模式;当水合物饱和度较高时,孔隙填充模式可能变为颗粒支撑模式,增加固体骨架的稳定性,成为固体基质的一部分,如图 1b所示。
|
图 1 水合物微观模式示意图
(a)孔隙填充模式;(b)颗粒支撑模式 白色表示孔隙,黄色表示水合物,蓝色表示固体颗粒 |
孔隙填充和颗粒支撑两种模式的岩石物理模型是对水合物微观赋存情况的极端假设,但实际上水合物同时分布于孔隙和骨架基质中。因此,本文考虑水合物实际的微观分布模式,基于等效介质理论[19-20]和Gassmann固体替换方程[21],将实测纵波速度作为约束,得到更加合理的水合物微观分布情况,构建天然气水合物地层的岩石物理模型。通过测试数据和实际资料验证该模型,效果较好。该方法为后续利用地震数据进行天然气水合物地层物性参数的定量解释提供了技术支持。
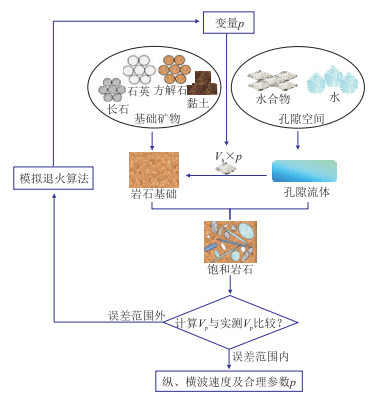
2 方法原理天然气水合物具有类固体特性,因此岩石物理建模时需要考虑水合物的剪切性质及微观分布情况,具体流程如图 2所示。
|
图 2 本文岩石物理建模流程 Vh为水合物体积含量,p为比例参数,VP为纵波速度 |
(1) 基于等效介质理论,固体基质由石英、方解石、黏土等矿物组分均匀混合构成,向基质中加入孔隙结构可构成干燥岩石骨架。假设初始状态水合物作为孔隙填充物的一部分,并构成部分孔隙流体形成饱和沉积物,此时,水合物的体积含量可通过孔隙度和含水饱和度计算得到。
(2) 引入比例参数p(0≤p≤1),对水合物体积含量进行分配,将一部分水合物分配到基质中,成为基质矿物的一部分。部分天然气水合物成为基质矿物后,孔隙度降低,因此认为孔隙度下降的程度即水合物在孔隙中减少的程度。水合物分配到基质中后将影响各基质矿物组分的体积含量,重新计算各个组分的模量,可以求得饱和岩石的体积模量、剪切模量,进而计算得到纵、横波速度。
(3) 受p的影响,各组分的弹性模量处于动态变化中。最后以测井实测的纵波速度约束岩石物理模型的速度,并比较计算值与实测纵波速度的差异;如果这种差异不可接受,则通过迭代更新p,调整天然气水合物微观分布,直到模型计算的纵波速度与实测的误差在允许接受范围内,进而可以计算得到合理的纵波以及横波速度。
在建模过程中,关键步骤包括固体基质、干燥骨架、孔隙流体等效模量及饱和岩石弹性模量的计算。
2.1 固体基质等效模量计算水合物地层涵盖了泥岩、砂岩或砾岩等多种类型,主要由陆源碎屑矿物、黏土矿物和碳酸盐矿物组成[22]。其中,碎屑矿物以石英、白云母、长石等轻矿物为主;黏土矿物主要为伊利石、蒙脱石等;碳酸盐矿物主要为方解石。在计算水合物地层固体基质的等效模量时,如果基质矿物各组分的体积含量和弹性模量已知,那么基质的有效弹性模量必定为Voigt上限和Reuss下限之内[15]。对于各向同性弹性基质,各个固体组分之间几何细节未知时,Hashin-Shtrikman为最窄的上下限[23]。当两种以上矿物组分进行混合时,基质的弹性模量必将位于广义的Hashin-Shtrikman-Walpole界限之内[4],即
| $ \left\{ \begin{array}{l} {K^{{\rm{HS \pm }}}} = {\left( {\sum\limits_{i = 1}^N {\frac{{{f_i}}}{{{K_i} + \frac{{4{\mu ^ \pm }}}{3}}}} } \right)^{ - 1}} - \frac{{4{\mu ^ \pm }}}{3}\\ {\mu ^{{\rm{HS \pm }}}} = {\left( {\sum\limits_{i = 1}^N {\frac{{{f_i}}}{{{\mu _i} + {\zeta ^ \pm }}}} } \right)^{ - 1}} - {\zeta ^ \pm } \end{array} \right. $ | (1) |
其中
| $ {\zeta ^ \pm } = \frac{{{\mu ^ \pm }(9{K^ \pm } + 8{\mu ^ \pm })}}{{6({K^ \pm } + 2{\mu ^ \pm })}} $ |
式中:K±表示各固体组分中最大和最小体积模量;μ±表示各固体组分中最大和最小剪切模量;Ki、μi和fi分别是第i种矿物组分的体积模量、剪切模量、体积含量;N为基质矿物组分所包含的种类。
当天然气水合物的一部分由孔隙中被分配到固体基质中时,孔隙度降低,并改变基质矿物的体积含量。降低后的孔隙度
| $ \left\{ \begin{array}{l} {K_{{\rm{ma}}}} = \frac{{{K^{{\rm{HS + }}}} + {K^{{\rm{HS}} - }}}}{2}\\ {\mu _{{\rm{ma}}}} = \frac{{{\mu ^{{\rm{HS}} + }} + {\mu ^{{\rm{HS}} - }}}}{2} \end{array} \right. $ | (2) |
式中Kma和μma分别为固体基质的体积模量和剪切模量。
2.2 干燥骨架等效模量计算对水合物地层弹性性质的影响因素主要包括孔隙系统的微观结构、矿物组分(影响孔隙纵横比)和孔隙形状等。因此,本文重点考虑孔隙的形状和连通性对水合物地层弹性性质的影响。首先参照前人对孔隙系统的分类,将孔隙分为连通性差的硬币状孔隙和连通性较好的椭球型孔隙[15];然后通过DEM(微分等效介质)模型向固体基质中加入孔隙构成干燥骨架,求取干燥骨架的弹性模量。DEM理论是通过向固体矿物相中逐渐加入包含物相模拟双相混合物,等效体积K*和剪切模量μ*的耦合微分方程组为
| $ \left\{ {\begin{array}{*{20}{l}} {\left( {1 - y} \right)\frac{{\rm{d}}}{{{\rm{d}}y}}\left[ {{K^*}\left( y \right)} \right] = ({K_2} - K){P^{(*2)}}\left( y \right)}\\ {\left( {1 - y} \right)\frac{{\rm{d}}}{{{\rm{d}}y}}\left[ {{\mu ^*}\left( y \right)} \right] = ({\mu _2} - K){Q^{(*2)}}\left( y \right)} \end{array}} \right. $ | (3) |
式中:y为包含物相的含量;K2、μ2分别为包含物相的体积模量、剪切模量,初始条件K*(0)=K1,μ*(0)=μ1,其中K1和μ1为固体基质相的体积模量和剪切模量;P和Q为几何因子,与包含物的形状、体积含量有关;上标“*2”表示包含物相。由于P和Q二者与骨架的体积模量、剪切模量有关,弹性模量与微分方程是耦合的,因此需要将微分等效方程解耦为常微分方程,再进行求解。
2.3 孔隙流体等效模量计算当孔隙充填物为水和(或)游离气等非黏滞性流体时,流体的非黏滞性不会影响沉积物的剪切性质,即孔隙流体的剪切模量为0。但孔隙空间中的等效流体包含天然气水合物时,由于水合物的类固体特性,导致孔隙流体的等效剪切模量不为0。此时,孔隙流体的等效弹性模量可以由体积平均的方法计算,即
| $ \left\{ \begin{array}{l} {K_{\rm{f}}} = {\left( {\frac{{{S_{\rm{w}}}}}{{{K_{\rm{w}}}}} + \frac{{1 - {S_{\rm{w}}}}}{{{K_{\rm{h}}}}}} \right)^{ - 1}}\\ {\mu _{\rm{f}}} = {\left( {\frac{{1 - {S_{\rm{w}}}}}{{{\mu _{\rm{h}}}}}} \right)^{ - 1}} \end{array} \right. $ | (4) |
式中:Kf、μf分别为孔隙流体等效体积模量、剪切模量;Sw为含水饱和度;Kw、Kh分别为水、天然气水合物的体积模量;μh为天然气水合物的剪切模量。
2.4 饱和岩石弹性模量计算对于充填物为具有黏滞性特征的水合物孔隙,刘欣欣等[4]将Brown-Korringa各向异性Gassmann方程进行推广,得到了适用于孔隙空间中包含固体的替换公式,并将该公式进行各向同性假设,得到广义的Gassmann方程,即
| $ \left\{ \begin{array}{l} K_{{\rm{sat}}}^{ - 1} = K_{{\rm{dry}}}^{ - 1} - \frac{{{{\left( {K_{{\rm{dry}}}^{ - 1} - K_{{\rm{gr}}}^{ - 1}} \right)}^2}}}{{\phi \left( {K_{{\rm{if}}}^{ - 1} - K_\phi ^{ - 1}} \right) + \left( {K_{{\rm{dry}}}^{ - 1} - K_{{\rm{gr}}}^{ - 1}} \right)}}\\ \mu _{{\rm{sat}}}^{ - 1} = \mu _{{\rm{dry}}}^{ - 1} - \frac{{{{\left( {\mu _{{\rm{dry}}}^{ - 1} - \mu _{{\rm{gr}}}^{ - 1}} \right)}^2}}}{{\phi \left( {\mu _{{\rm{if}}}^{ - 1} - \mu _\phi ^{ - 1}} \right) + \left( {\mu _{{\rm{dry}}}^{ - 1} - \mu _{{\rm{gr}}}^{ - 1}} \right)}} \end{array} \right. $ | (5) |
式中:Ksat、μsat分别为饱和岩石的体积模量、剪切模量;Kdry、μdry分别为岩石骨架的体积模量、剪切模量;Kgr、μgr分别为基质的体积模量、剪切模量;Kϕ和μϕ是与孔隙有关的体积模量和剪切模量;Kif和μif是与孔隙内部填充物有关的体积模量和剪切模量。
利用广义Gassmann方程可以得到固体(如黏滞性流体)充填于岩石孔隙情况下的饱和岩石的弹性模量。同时,广义Gassmann方程也可以解释孔隙流体在具有不可忽视的剪切模量时,根据等效介质理论计算得到的饱和岩石的剪切模量与干燥骨架的剪切模量差异较大。
当岩石为各向同性时,以上的模量关系为:Kgr=Kϕ;μgr=μϕ。当孔隙填充的是自由流体时,即μif=0。根据等效介质理论,在均匀各向同性弹性介质中,纵、横波速度可由饱和岩石的弹性模量计算得到,即
| $ \left\{ \begin{array}{l} {V_{\rm{P}}} = \sqrt {\frac{{{K_{{\rm{sat}}}} + \frac{{4{\mu _{{\rm{sat}}}}}}{3}}}{{{\rho _{{\rm{sat}}}}}}} \\ {V_{\rm{S}}} = \sqrt {\frac{{{\mu _{{\rm{sat}}}}}}{{{\rho _{{\rm{sat}}}}}}} \end{array} \right. $ | (6) |
式中ρsat为饱和岩石的密度。
3 模型测试为了验证本文所构建模型的合理性,定量分析泥质含量、孔隙度、水合物饱和度对含天然气水合物地层弹性参数的影响。
3.1 泥质含量的影响假设水合物地层的矿物组分为石英、黏土和方解石,水合物存在于孔隙空间中,流体为水,各组分的弹性模量如表 1所示。控制变量参数为泥质含量,且泥质含量变化范围为5%~70%,石英与方解石的比例为4∶1,孔隙度为45%,含水饱和度为40%。
|
|
表 1 各组分弹性参数表 |
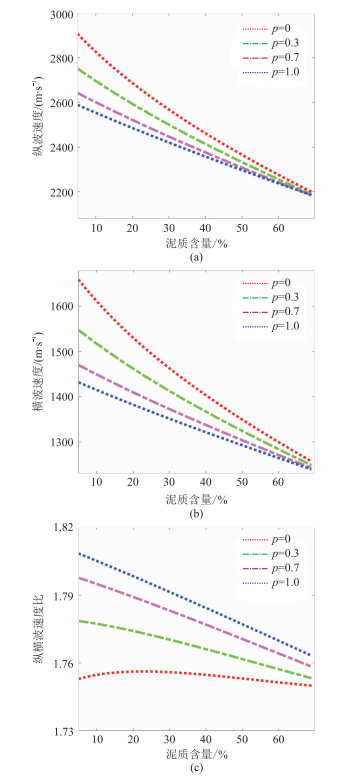
当参数p不断发生变化时,模型计算的纵波速度、横波速度、纵横波速度比的变化如图 3所示。由图可见,随着泥质含量的增加,纵波速度、横波速度减小,纵横波速度比变化范围反映纵、横波速度变化合理。随着p的增加,纵、横波速度呈下降趋势,这是因为p的增加使基质中的水合物含量增加、孔隙度降低,孔隙度降低的部分即是水合物被分配到基质中的体积含量;同时,水合物被分配到基质中,导致基质中原矿物的体积含量降低,因此使矿物基质的弹性模量降低。
|
图 3 不同比例参数情况下纵波速度(a)、横波速度(b)、纵横波速度比(c)随泥质含量的变化 |
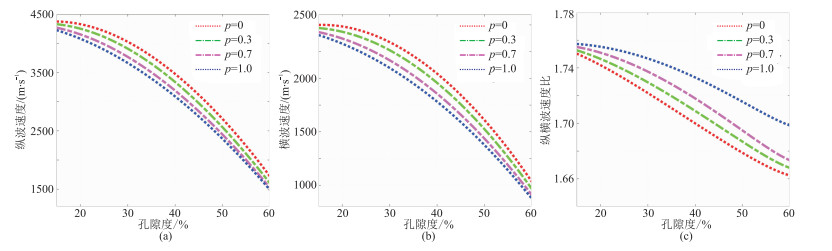
假定沉积物中石英体积含量、方解石体积含量、泥质含量分别占基质矿物的50%、10%、40%,水合物的饱和度为40%,孔隙度的变化范围为15%~60%。纵波速度、横波速度、纵横波速度比随孔隙度的变化如图 4所示。由图可见:孔隙度的增加使纵、横波速度减小;当孔隙度大于50%时,纵、横波速度降低的主控因素为孔隙度,而参数p的影响变小,纵横波速度比变化范围反映纵、横波速度变化合理。
|
图 4 不同比例参数情况下纵波速度(a)、横波速度(b)、纵横波速度比(c)随孔隙度的变化 |
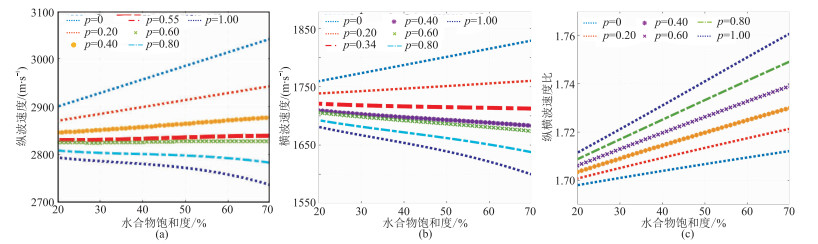
保持沉积物各矿物组分的体积含量不变,孔隙度为45%,水合物饱和度的变化范围为20%~70%。纵波速度、横波速度、纵横波速度比随水合物饱和度的变化如图 5所示。由图可见,当p小于0.55时,纵波速度随着水合物饱和度的增加而增加;当p大于0.55时,纵波速度随着水合物饱和度的增加缓慢降低(图 5a)。这是由于水合物饱和度即使不发生改变,p的变化也会引起孔隙度、基质矿物各组分体积含量发生变化。同理,当p保持不变时,水合物饱和度的增加也会引起孔隙度、基质矿物各组分体积含量发生变化。因此从测试结果看,当p大约在0.55时,纵波速度不随水合物饱和度发生变化。同样,当p大约为0.34时,横波速度不随水合物饱和度发生变化(图 5b)。同时,纵横波速度比变化范围也表明了纵、横波速度变化的合理性。
|
图 5 不同比例参数情况下纵波速度(a)、横波速度(b)、纵横波速度比(c)随水合物饱和度的变化 |
利用某海域SH2井的实测资料验证岩石物理模型。SH2井揭示,水合物位于海底面之下195~220m,厚度约为25m,平均饱和度为25%。沉积物组分以碎屑、黏土、碳酸盐三类矿物为主,其中,碎屑矿物以石英、斜长石、正长石、白云母为主,陆源碎屑矿物含量较高,为40.00%左右;黏土矿物以伊利石、高岭石和蒙脱石为主,平均含量为19.64%;碳酸盐矿物以方解石为主,平均含量为16.46%。
模型所使用的弹性模量及密度参数如表 2所示,水合物压力为5MPa,温度为273K;矿物混合物的具体成分石英、长石、云母、黏土、方解石体积含量分别为28%、12%、26%、20%、14%。
|
|
表 2 SH2井水合物地层的弹性模量和密度参数 |
利用现有测井资料,可计算地层孔隙度和水合物的饱和度。利用密度测井曲线计算孔隙度[24-25],即
| $ \phi = \frac{{{\rho _{\rm{m}}} - {\rho _{\rm{b}}}}}{{{\rho _{\rm{m}}} - {\rho _{\rm{w}}}}} $ | (7) |
式中ρb、ρw和ρm分别为地层、水和骨架密度,水和骨架的密度分别取1.03g/cm3、2.65g/cm3。水合物的饱和度可以应用Archie公式[22, 26]计算,可利用电阻率数据估算水合物饱和度,即
| $ {S_{\rm{h}}} = 1 - {\left( {\frac{{a{R_{\rm{w}}}}}{{{\phi ^m}{R_{\rm{t}}}}}} \right)^{\frac{1}{n}}} $ | (8) |
式中:Rw和Rt分别为水和地层电阻率;a、m和n均为常数,本文取a=1.3,m=n=2.0。
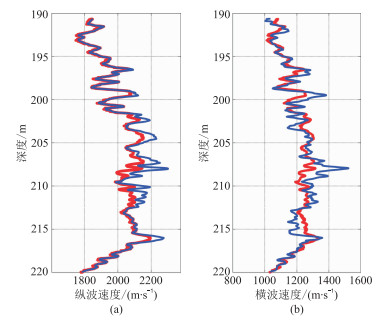
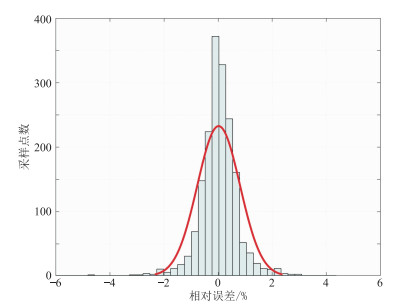
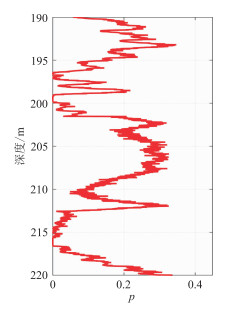
图 6为应用本文模型计算得到的纵、横波速度与实际测井实测速度的对比。结果表明,本文模型计算得到的纵波速度与实测值吻合较好(图 6a);纵波速度误差分布符合正态分布,且在4%以内(图 7);p的变化范围集中在0~0.4(图 8),均值为0.157,说明该地区水合物的微观分布更集中于孔隙中。本文模型计算得到的横波速度与实测横波速度变化趋势大体相同,吻合较好(图 6b),进一步验证了本文构建模型的合理性。
|
图 6 SH2井实测数据与本文模型计算结果对比 (a)纵波速度;(b)横波速度。蓝色、红色曲线分别为实测值、模型计算值 |
|
图 7 SH2井纵波速度相对误差分布 |
|
图 8 SH2井p变化范围 |
本文建立了一种基于等效介质理论的天然气水合物地层岩石物理模型,并分析了矿物组分、孔隙度、水合物饱和度对模型的影响。通过实测纵波速度作为模型计算纵波速度的约束,可以达到不断调整参数p的大小的目的,进而更新水合物在孔隙与基质中的分配比例。模型考虑了水合物的微观赋存状态,使计算得到的纵、横波速度更加合理。将该模型应用于某海域SH2井的实际数据,结果显示,应用效果较好,验证了模型的适用性。
在前人方法的基础上,本文将水合物的微观赋存模式表达成动态形式,并考虑这种变化对孔隙度、含水饱和度、矿物组分的体积含量的影响和孔隙流体的剪切性质,构建了更为合理的岩石物理模型,为天然气水合物地层的速度等物性参数的预测提供了方法支持。
| [1] |
Makogon Y F, Holditch S A, Makogon T Y. Natural gas-hydrates: A potential energy source for 21st century[J]. Journal of Petroleum Science & Engineering, 2007, 56(1): 14-31. |
| [2] |
宋海斌, 吴时国, 江为为. 南海东北部973剖面BSR及其热流特征[J]. 地球物理学报, 2007, 50(5): 1508-1517. SONG Haibing, WU Shiguo, JIANG Weiwei. The characteristics of BSRs and their derived heat flow on 973 in the northeastern South China Sea[J]. Chinese Journal of Geophysics, 2007, 50(5): 1508-1517. DOI:10.3321/j.issn:0001-5733.2007.05.027 |
| [3] |
张如伟, 张宝金, 黄捍东, 等. 天然气水合物沉积层的AVA特征[J]. 石油地球物理勘探, 2011, 46(4): 634-639. ZHANG Ruwei, ZHANG Baojin, HUANG Handong, et al. AVA characters on gas hydrate-bearing sedimentary[J]. Oil Geophysical Prospecting, 2011, 46(4): 634-639. |
| [4] |
刘欣欣, 印兴耀, 栾锡武. 天然气水合物地层岩石物理模型构建[J]. 中国科学: 地球科学, 2018, 48(9): 1248-1266. LIU Xinxin, YIN Xingyao, LUAN Xiwu. Seismic rock physical modeling for gas hydrate-bearing sediments[J]. Science China: Earth Sciences, 2018, 48(9): 1248-1266. |
| [5] |
孟大江, 文鹏飞, 张如伟, 等. 天然气水合物横波速度等效介质模型预测方法[J]. 石油地球物理勘探, 2020, 55(1): 117-125. MENG Dajiang, WEN Pengfei, ZHANG Ruwei, et al. Gas hydrate S-wave velocity prediction method based on effective medium model[J]. Oil Geophysical Prospecting, 2020, 55(1): 117-125. |
| [6] |
薛姣, 顾汉明, 蔡成国, 等. 基于等效介质模型的裂缝参数AVOA反演[J]. 石油地球物理勘探, 2016, 51(6): 1171-1179. XUE Jiao, GU Hanming, CAI Chengguo, et al. Estimation of fracture parameters from P-wave AVOA data based on equivalent media theory[J]. Oil Geophysical Prospecting, 2016, 51(6): 1171-1179. |
| [7] |
Lee M W, Hutchinson D R, Collett T S, et al. Seismic velocities for hydrate-bearing sediments using weighted equation[J]. Journal of Geophysical Research: Solid Earth, 1996, 101(9): 20347-20358. |
| [8] |
Helgerud M B, Dvorkin J, Nur A, et al. Elastic-wave velocity in marine sediments with gas hydrates: Effective medium modeling[J]. Geophysical Research Letters, 1999, 26(13): 2021-2024. DOI:10.1029/1999GL900421 |
| [9] |
Dvorkin J, Nur A.Rock Physics for Characterization of Gas Hydrates[R].US Geological Survey Professional Paper, 1993, 293-298.
|
| [10] |
Dvorkin J, Prasad M, Sakai A, et al. Elasticity of marine sediments: Rock physics modeling[J]. Geophysical Research Letters, 1999, 26(12): 1781-1784. DOI:10.1029/1999GL900332 |
| [11] |
Zimmerman R W, King M S. The effect of the extent of freezing on seismic velocities in unconsolidated permafrost[J]. Geophysics, 1986, 51(6): 1285-1290. DOI:10.1190/1.1442181 |
| [12] |
Lee M W, Collett T S. Pore- and fracture-filling gas hydrate reservoirs in the Gulf of Mexico Gas Hydrate Joint Industry Project Leg Ⅱ Green Canyon 955 H well Science Direct[J]. Marine & Petroleum Geology, 2012, 34(1): 62-71. |
| [13] |
Qian J, Wang X, Collett T S, et al. Gas hydrate accumulation and saturations estimated from effective medium theory in the eastern Pearl River Mouth Basin, South China Sea[J]. Interpretation, 2017, 5(3): 1-39. |
| [14] |
宋海斌, Matsubayashi O, 杨胜雄, 等. 含天然气水合物沉积物的岩石物性模型与似海底反射层的AVA特征[J]. 地球物理学报, 2002, 45(4): 546-556. SONG Haibin, Matsubayashi O, YANG Shengxiong, et al. Physical proerty models of gas hydrate-bearing sediments and AVA character of bottom simulating reflector[J]. Chinese Journal of Geophysics, 2002, 45(4): 546-556. DOI:10.3321/j.issn:0001-5733.2002.04.012 |
| [15] |
印兴耀, 刘欣欣. 储层地震岩石物理建模研究现状与进展[J]. 石油物探, 2016, 55(3): 309-325. YIN Xingyao, LIU Xinxin. Research status and progress of the seismic rock-physics modeling methods[J]. Geophysical Prospecting for Petroleum, 2016, 55(3): 309-325. DOI:10.3969/j.issn.1000-1441.2016.03.001 |
| [16] |
陈玉凤, 梁德青, 吴能友. 南海神狐海域水合物对岩心电阻率的影响[J]. 石油地球物理勘探, 2018, 53(6): 1241-1246. CHEN Yufeng, LIANG Deqing, WU Nengyou. Resistivity characteristics of core samples containing natural gas hydrate in Shenhu Area, the south China Sea[J]. Oil Geophysical Prospecting, 2018, 53(6): 1241-1246. |
| [17] |
Sha Z, Liang J, Zhang G, et al. A seepage gas hydrate system in northern South China Sea: Seismic and well log interpretations[J]. Marine Geology, 2015, 366(1): 69-78. |
| [18] |
Chand S, Minshull T A, Gei D, et al. Elastic velocity models for gas-hydrate-bearing sediments-a comparison[J]. Geophysical Journal of the Royal Astronomical Society, 2010, 159(2): 573-590. |
| [19] |
Lee M W, Collett T S. Gas hydrate saturations estimated from fractured reservoir at Site NGHP-01-10, Krishna-Godavari Basin, India[J]. Journal of Geophysical Research: Solid Earth, 2009, 114(B7): B07102. |
| [20] |
Shankar U, Riedel M. Gas hydrate saturation in the Krishna-Godavari basin from P-wave velocity and electrical resistivity logs[J]. Marine & Petroleum Geology, 2011, 28(10): 1768-1778. |
| [21] |
Sain K, Ghosh R, Ojha M. Rock physics modeling for assessing gas hydrate and free gas: a case study in the Cascadia accretionary prism[J]. Marine Geophysical Researches, 2010, 31(1): 109-119. |
| [22] |
肖昆, 邹长春, 邓居智, 等. 利用声波测井估算裂缝型水合物储层水合物饱和度[J]. 石油地球物理勘探, 2017, 52(5): 1067-1076. XIAO Kun, ZOU Changchun, DENG Juzhi, et al. Gas hydrate saturation estimation in fractured reservoirs with acoustic logging[J]. Oil Geophysical Prospecting, 2017, 52(5): 1067-1076. |
| [23] |
印兴耀, 宗兆云, 吴国忱. 岩石物理驱动下地震流体识别研究[J]. 中国科学: 地球科学, 2015, 45(1): 8-21. YIN Xingyao, ZONG Zaoyun, WU Guochen. Research on seismic fluid identification driven by rock physics[J]. Science China: Earth Sciences, 2015, 45(1): 8-21. |
| [24] |
李坤, 印兴耀. 混合概率模型驱动的叠前地震反演方法[J]. 石油地球物理勘探, 2020, 55(4): 839-853. LI Kun, YIN Xingyao. Prestack seismic inversion driven by mixture probabilistic models[J]. Oil Geophysical Prospecting, 2020, 55(4): 839-853. |
| [25] |
时磊, 王璞, 刘俊州, 等. 致密砂岩储层物性参数预测方法研究[J]. 石油物探, 2020, 59(1): 98-107. SHI Lei, WANG Pu, LIU Junzhou, et al. Physical properties prediction for tight sandstone reservoirs[J]. Geophysical Prospecting for Petroleum, 2020, 59(1): 98-107. DOI:10.3969/j.issn.1000-1441.2020.01.011 |
| [26] |
Wang X, Hutchinson D R, Wu S, et al. Elevated gas hydrate saturation within silt and silty clay sediments in the Shenhu area, South China Sea[J]. Journal of Geo-physical Research Atmospheres, 2011, 116(5): B05102. |



 宗兆云, 山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
宗兆云, 山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: 