② 清华大学周培源应用数学研究中心, 北京 100084;
③ 中国石油勘探开发研究院, 北京 100083
② Zhou Pei-Yuan Center for Applied Mathema-tics, Tsinghua University, Beijing 100084, China;
③ Research Institute of Petroleum Exploration and Development, PetroChina, Beijing 100083, China
常规油气探测中一般视孔隙流体为牛顿流体。但是,在油气勘探和开发过程中普遍存在非牛顿流体流动,这涉及到许多重要的工程,如用加热方法提高重油采收率;用聚合物溶液、油和泡沫溶液的乳状液充当驱替液;用含有悬浮颗粒的化学溶剂充当页岩气压裂液等。当这类流体与固体之间发生相对运动时会产生剪切应力,应力大小跟流体黏性和流体剪切应变率有关。非牛顿流体剪切应力与剪切应变之间一般不满足线性关系,黏性系数是剪切变化率的复杂函数。在化学工程、流变学、石油工程等领域,对非牛顿流体流变学进行了大量的研究。Tan等[1]研究了Maxwell黏性流体在平板之间的流动现象,卢明辉[2]在流体的本构模型中引入了流体抵抗剪切变形的作用,Tong等[3]给出了圆管中非牛顿流体流动的解析解。但是,孔隙介质中非牛顿流体对弹性波场传播的影响机制仍不清楚[4]。
孔隙介质波动力学的研究多采用理想流体或具有黏性的牛顿流体,这使公式推导较为简便。但是,致密油储层地质特征复杂,岩石包含矿物颗粒和固态有机质等物质,流体非均质性强[5],毛细管压力大[6]。这类岩石中主要发育微纳米级孔喉连通体系,孔隙结构复杂[7]、连通性差,孔径范围在纳米、微米量级,且孔隙度一般小于10%、渗透率一般小于0.1mD。研究表明流体在宏观与微观孔隙结构中的流动行为并不一致,当孔隙尺度逐渐变小时流体的连续介质流动特征发生改变[8]。Thomas等[9]发现在微纳米孔中流体呈现接近固体的规则分子排布,其黏性特征已发生改变,表明致密孔隙中流体是介于固体与理想流体之间的复杂状态物质。同时,在微纳米孔隙通道条件下,非牛顿流体表现出“非达西”流动特征,因此常规牛顿流体假设已不适用于致密储层,采用非牛顿本构模型更为合理。
Sochi[10]综述了孔隙介质非牛顿流体的流动,重点叙述含屈服应力的流体、黏弹性流体的性质及流动模型,并讨论了测试流体屈服应力的不同方法。Pearson等[11]建立了复杂非牛顿流体在孔隙介质中流动的数学模型。Dong等[12]研究了重油非牛顿流体在孔隙介质中的流动规律,实验结果表明流体流速与压力梯度呈非线性关系,且部分实验中流体流动具有启动压力梯度。Xiong等[4]通过对三维孔隙网络中的Maxwell流体渗透率建模计算,发现渗透率变化受频率、流体流变学属性和孔隙连通性的影响。Talon等[13]在格子玻尔兹曼框架下,针对含屈服应力非牛顿流体在孔隙介质中的流动问题,推导了广义达西方程以描述流体的流动,并分析各参数的计算方法。Markov[14]研究了饱和Maxwell非牛顿流体孔隙介质瑞利面波沿边界层的传播问题,建立了波动方程并进行频散和衰减分析,指出有可能通过分析波速频散和衰减估计Deborah数。
Teeuw等[15]通过实验手段研究了Bentheim砂岩岩心中高分子溶液的流动特征,实验结果显示,对于较大高分子的溶液,孔隙壁对分子的排斥作用引起了明显的滑移效应,导致孔隙介质中出现较大流动速率;Greaves等[16]进行了Elginshire砂岩的高分子溶液注入实验,发现高分子溶液在孔隙中的黏性大于在实验室容器中,认为这是由溶液与孔隙壁间的相互作用引起的;Cannella等[17]在Berea岩心实验中也发现相同的现象;Hejri等[18]通过实验研究了Ottawa砂岩样本中高分子溶液的流变学行为,发现在溶液流速高于阈值时,非固结砂岩中高分子溶液流动规律不满足线性达西定律,而是满足幂率流模型。
孔隙流体属性是重要的岩石物理参数[19],尽管对孔隙尺度非牛顿流体流动现象的研究较为深入,但基于非牛顿流体—固体骨架耦合作用的孔隙介质波动方程研究却尚未引起足够的重视。传统孔隙介质波场传播模型假设孔隙中填充了经典牛顿流体,然而大量理论和实验研究表明,现有牛顿流体孔隙介质波动方程已不适用于低孔、低渗致密油储层的复杂流动条件。为了更好地利用地震技术发现非常规油藏和提高剩余油采收率,人们试图研究非牛顿流体对多孔介质动力学的影响。一种观点认为孔隙流体的非线性流变性可能是低频范围的主要影响机制[20],这需要对非牛顿流体有更深入的了解。幂律应变—应力关系是一种表征多孔介质(如Bentheim砂岩[15])中聚合物水溶液非线性模型的常见本构关系;同时,Maxwell流体是分析黏弹性特性的另一个常用模型,能够描述特定频率下振荡流速提高现象。Tsiklauri等[21]将波场的共振现象归因于孔隙中非牛顿流体,实验证实了在振荡压力梯度下黏弹性流体的动力响应[22]。现有非牛顿流体模型研究仍处于不断探索阶段,对实际流体流变行为的机理仍不甚了解,需要更灵活的本构关系解释实验现象。
非牛顿流体模型类型众多,主要可分为黏弹性、非时变黏性和时变黏性流体三类。黏弹性非牛顿流体模型主要包括Maxwell和开尔文流体模型,通过弹簧和阻尼的串联、并联实现弹性和黏性的结合。Maxwell流体的流变特性一般采用串联的弹簧阻尼模型,然而该模型通常过于理想化,无法描述真实的非牛顿流体。近年来,分数阶微分模型受到了相当大的关注,在描述物质黏弹性属性方面具有很大优势。分数阶导数模型使用的是非整数阶导数描述应变—应力关系,其优点在于它的非局部结构,适用于对黏弹性流体的记忆特性进行建模。最近的一些研究分析了Maxwell流体的流动[1, 23-24],实验结果证实了聚合物流变学与分数阶导数Maxwell(fractional derivative Maxwell,fdMaxwell)模型一致[25]。目前多孔介质中fdMaxwell流体对弹性波传播影响的研究尚未展开,主要是因为非牛顿流体与固体之间的黏性和弹性耦合机制尚不清楚。
本文从非牛顿流体黏性系数的非线性本构关系出发,基于Biot理论中非泊肃叶流动的框架,考虑振动压力梯度作用下的孔隙微管黏性流体流动,用fdMaxwell模型描述多孔介质中弹性波传播的非牛顿流体效应,通过建立孔隙介质流体动量方程和非牛顿流体本构关系,得到含非牛顿流体的孔隙介质动力学方程组,通过平面波分析方法,得到非牛顿流体效应下波场频散和衰减的计算方法。
1 fdMaxwell流体的黏弹性耗散考虑在多孔介质中存在一个封闭表面∂Ω,内部包含单元体Ω,单元体Ω由饱和Maxwell黏弹性流体的孔隙介质组成,多孔介质骨架是各向同性的、均匀的线性弹性体。单元体内部物质满足连续性法则。其质量连续性方程为
| $ \frac{{\partial {\rho _{\rm{f}}}}}{{\partial t}} + \nabla \cdot \left( {{\rho _{\rm{i}}}{\mathit{\boldsymbol{v}}_{\rm{f}}}} \right) = 0 $ | (1) |
动量守恒方程为
| $ {\rho _{\rm{f}}}\frac{{{\rm{D}}{\mathit{\boldsymbol{v}}_{\rm{f}}}}}{{{\rm{D}}t}} = - \nabla p + \nabla \cdot \mathit{\boldsymbol{\tau }} $ | (2) |
式中:
| $ \mathit{\boldsymbol{\tau }} + {\lambda ^\alpha }{\rm{d}}_t^\alpha \mathit{\boldsymbol{\tau }} = \eta {\lambda ^{\beta - 1}}{\rm{d}}_t^{\beta - 1}\mathit{\boldsymbol{\dot \gamma }} $ | (3) |
式中:η为流体黏性系数;λ=η/μf为弛豫时间,其中μf为流体剪切模量;α和β为分数阶导数的阶次;变形速率张量被定义为
| $ \mathit{\boldsymbol{\dot \gamma }} = \nabla {\mathit{\boldsymbol{v}}_{\rm{f}}} + {\left( {\nabla {\mathit{\boldsymbol{v}}_{\rm{f}}}} \right)^{\rm{T}}} - 2/3 \cdot \nabla \cdot {\mathit{\boldsymbol{v}}_{\rm{f}}}\mathit{\boldsymbol{I}} $ | (4) |
表示应变对时间的一阶导数,其中I表示二阶单位张量。
分数阶导数定义[28]为
| $ {\rm{d}}_t^\alpha f(t) = \frac{{{{\rm{d}}^\alpha }f(t)}}{{{\rm{d}}{t^\alpha }}} = \frac{1}{{\mathit{\Gamma }(m - \alpha )}}\int_0^t {\frac{{{f^{(m)}}(\tau )}}{{{{(t - \tau )}^{\alpha + m - 1}}}}} {\rm{d}}\tau $ | (5) |
式中:m为正整数;m-1≤α≤m;Γ为伽马函数。为了获得流体相的动态方程,对本构方程两边取散度,带入动量守恒方程,可得
| $ \begin{array}{*{20}{c}} {\left( {1 + {\lambda ^\alpha }{\rm{D}}_t^\alpha } \right){\rho _{\rm{f}}}\frac{{{\rm{D}}{\mathit{\boldsymbol{v}}_{\rm{f}}}}}{{{\rm{D}}t}} = - \left( {1 + {\lambda ^\alpha }{\rm{D}}_t^\alpha } \right)\nabla p + }\\ {\eta {\lambda ^{\beta - 1}}{\rm{D}}_t^{\beta - 1}\left[ {{\nabla ^2}{\mathit{\boldsymbol{v}}_{\rm{f}}} + \frac{1}{3}\nabla \left( {\nabla \cdot {\mathit{\boldsymbol{v}}_{\rm{f}}}} \right)} \right]} \end{array} $ | (6) |
上式是流体满足的动力学方程。
对于圆柱形孔隙微管道,流体运动方程存在解析解。在微纳米孔隙介质中,管道半径比孔隙界面的波长要小得多(“长波长近似”假设),因此固壁局部位移可以看作是常数。在低速条件下,孔隙流体的压缩性可以忽略不计,则质量连续性条件可写为
| $ \operatorname{div} \boldsymbol{v}_{\mathrm{f}}=0 $ | (7) |
在微米量级的孔隙管道里流动的黏弹性流体,其雷诺数比失稳临界值要小得多,层流假设依然合理。因此,在柱坐标系(r,θ,z)下,可以假设唯一的非零速度分量是沿z轴(孔隙管道轴向)方向,而且速度只取决于径向坐标,因此有
| $ \left\{\begin{array}{l} \boldsymbol{v}_{\mathrm{f}}=\left(0,0, v_{\mathrm{fz}}\right) \\ \mathrm{D} / \mathrm{D} t=\partial / \partial t \end{array}\right. $ | (8) |
在孔隙介质中,流体速度可以表示为
| $ \boldsymbol{v}_{\mathrm{f}}=\boldsymbol{w}+\dot{\boldsymbol{u}} $ | (9) |
式中:u是固体位移;
| $ \begin{array}{*{20}{c}} {{\rho _{\rm{f}}}\left( {1 + {\lambda ^\alpha }{\rm{d}}_t^\alpha } \right)\mathit{\boldsymbol{\dot w}} = - \left( {1 + {\lambda ^\alpha }{\rm{d}}_t^\alpha } \right)\left( {\nabla p + {\rho _{\rm{i}}}\mathit{\boldsymbol{\ddot u}}} \right) + }\\ {\eta {\lambda ^{\beta - 1}}{\rm{d}}_t^{\beta - 1}\left( {{\nabla ^2}\mathit{\boldsymbol{w}} + {\nabla ^2}\mathit{\boldsymbol{\dot u}}} \right)} \end{array} $ | (10) |
式中ü表示固体位移对时间的二阶导数。在孔隙微管表面上,
| $ \frac{{{\partial ^2}\mathit{\boldsymbol{w}}}}{{\partial {r^2}}} + \frac{1}{r}\frac{{\partial \mathit{\boldsymbol{w}}}}{{\partial r}} + \frac{{{\rm{i}}\omega A}}{\psi } \cdot \mathit{\boldsymbol{w}} = - \frac{A}{\psi }\mathit{\boldsymbol{f}} $ | (11) |
式中:ψ=η/ρf;f=- (
| $ \mathit{\boldsymbol{w}} = - A\left[ {1 - {J_0}\left( {lr} \right)/{J_1}(la)} \right]\mathit{\boldsymbol{f}}/\left( {{l^2}\psi } \right) $ | (12) |
式中:J0为零阶贝塞尔函数;J1为一阶贝塞尔函数;l=
| $ {\left. \mathit{\boldsymbol{\tau }} \right|_{r = a}} = {\left. {\frac{\eta }{A} \cdot \frac{{\partial \mathit{\boldsymbol{w}}}}{{\partial r}}} \right|_{r = a}} = \frac{\eta }{{l\psi }} \cdot \frac{{{J_1}(la)}}{{{J_0}(la)}}\mathit{\boldsymbol{f}} $ | (13) |
将平均速度〈w〉=2/a2∫0arwdr和总应力〈τ〉=2πaτ|r=a结合起来,可得剪切作用力为〈τ〉=8πηF(c)〈w〉,其中黏性耗散函数可表示为
| $ F(c)=-\frac{\mathrm{i} c}{4 \varDelta} \cdot \frac{J_{1}(c \varDelta)}{J_{0}(c \Delta)}\left[1-\frac{2 J_{1}(c \varDelta)}{c \Delta J_{0}(c \varDelta)}\right] $ | (14) |
式中
| $ \varDelta=\sqrt{\mathrm{i}} \cdot \sqrt{\left(D_{\mathrm{e}} c^{2}\right)^{1-\beta}(-\mathrm{i})^{1-\beta}+\left(D_{\mathrm{e}} c^{2}\right)^{\alpha-\beta+1}(-\mathrm{i})^{\alpha-\beta+1}} $ | (15) |
Deborah数定义为De=λ/λψ,表示了黏性效应的弛豫时间和特征时间的比值,刻画了流体—固相系统是否处于耗散状态或弹性状态,其中λψ=a2/ψ。具有较低Deborah数的材料表现为牛顿黏性流体;当Deborah数增加时,弹性行为占主导地位。
2 饱和fdMaxwell流体的孔隙介质波动方程在固体壁面上的流—固耦合剪切作用力为〈τ〉=8πηF(c)〈w〉。在Biot理论中,流—固耦合引起的黏性耗散项是ηϕ2(
| $ \left\{\begin{array}{l} \mu_{\mathrm{S}} \nabla^{2} \boldsymbol{u}+\nabla\left[\left(A+\mu_{\mathrm{S}}\right) \nabla \cdot \boldsymbol{u}+G \nabla \cdot \boldsymbol{U}\right]= \\ \rho_{11} \frac{\partial^{2} \boldsymbol{u}}{\partial t^{2}}+\rho_{12} \frac{\partial^{2} \boldsymbol{U}}{\partial t^{2}}-\frac{\eta \phi^{2} F(c)}{\kappa}(\dot{\boldsymbol{U}}-\dot{\boldsymbol{u}}) \\ \nabla(G \nabla \cdot \boldsymbol{u}+R \nabla \cdot \boldsymbol{U})= \\ \rho_{12} \frac{\partial^{2} \boldsymbol{u}}{\partial t^{2}}+\rho_{22} \frac{\partial^{2} \boldsymbol{U}}{\partial t^{2}}+\frac{\eta \phi^{2} F(c)}{\kappa}(\dot{\boldsymbol{U}}-\dot{\boldsymbol{u}}) \end{array}\right. $ | (16) |
式中:μS是固体相剪切模量;ρ11、ρ12、ρ22分别为Biot理论中固体、流体和流固相互作用密度系数;G和R是Biot理论的弹性系数。将散度和旋度算子应用于波动方程固体和流体位移,令ζ1=
| $ \left\{\begin{array}{l} \left(A+2 \mu_{s}\right) \nabla^{2} \zeta_{1}+G \nabla^{2} \xi_{1}= \\ \rho_{11} \frac{\partial^{2} \zeta_{1}}{\partial t^{2}}+\rho_{12} \frac{\partial^{2} \xi_{1}}{\partial t^{2}}-\frac{\eta \phi^{2} F(c)}{\kappa} \frac{\partial}{\partial t}\left(\xi_{1}-\zeta_{1}\right) \\ G \nabla^{2} \zeta_{1}+R \nabla^{2} \xi_{1}= \\ \rho_{12} \frac{\partial^{2} \zeta_{1}}{\partial t^{2}}+\rho_{22} \frac{\partial^{2} \xi_{1}}{\partial t^{2}}+\frac{\eta \phi^{2} F(c)}{\kappa} \frac{\partial}{\partial t}\left(\xi_{1}-\zeta_{1}\right) \end{array}\right. $ | (17) |
横波波动方程为
| $ \left\{\begin{array}{l} \mu_{\mathrm{S}} \nabla^{2} \boldsymbol{s}=\rho_{11} \frac{\partial^{2}}{\partial t^{2}} \boldsymbol{s}+\rho_{12} \frac{\partial^{2}}{\partial t^{2}} \boldsymbol{S}-\frac{\eta \phi^{2} F(c)}{\kappa} \frac{\partial}{\partial t}(\boldsymbol{S}-\boldsymbol{s}) \\ \rho_{12} \frac{\partial^{2} \boldsymbol{s}}{\partial t^{2}}+\rho_{22} \frac{\partial^{2} \boldsymbol{S}}{\partial t^{2}}+\frac{\eta \phi^{2} F(c)}{\kappa} \frac{\partial}{\partial t}(\boldsymbol{S}-\boldsymbol{s})=0 \end{array}\right. $ | (18) |
根据平面波假设,四种波场可表示为ζ1=C1×exp[i(ωt-k·x)]、ξ1=C2exp[i(ωt-k·x)]、s=T1exp[i(ωt-k·x)]和S=T2exp[i(ωt-k·x)],其中k是波数,C1、C2、T1、T2是波(矢量)常数。则纵波方程变为
| $ \left[\begin{array}{lll} a_{11}\left(\frac{k}{\omega}\right)^{2}+b_{11} & a_{12}\left(\frac{k}{\omega}\right)^{2}+b_{12} \\ a_{21}\left(\frac{k}{\omega}\right)^{2}+b_{21} & a_{22}\left(\frac{k}{\omega}\right)^{2}+b_{22} \end{array}\right]\left[\begin{array}{l} C_{1} \\ C_{2} \end{array}\right]=0 $ | (19) |
式中:a11=A+2μS;b11=-ρ11+iηϕ2F(c)/(κω);a12= a21=G;b12=b21=-ρ12-iηϕ2F(c)/(κω);a22=R;b22=-ρ22-iηϕ2F(c)/(κω)。
将波场表达式代入横波方程,经化简可得
| $ \left[\begin{array}{l} \left(a_{11}^{\mathrm{S}} \frac{k^{2}}{\omega^{2}}+b_{11}^{\mathrm{S}}\right) \boldsymbol{I} \qquad b_{12}^{\mathrm{S}} \boldsymbol{I} \\ b_{21}^{\mathrm{S}} \boldsymbol{I} \qquad \left(a_{22}^{\mathrm{S}} \frac{k^{2}}{\omega^{2}}+b_{22}^{\mathrm{S}}\right) \boldsymbol{I} \end{array}\right]\left[\begin{array}{l} \boldsymbol{T}_{1} \\ \boldsymbol{T}_{2} \end{array}\right]=0 $ | (20) |
式中:a11S=μS;b11S=-ρ11+iηϕ2F(c)/(κω);b12S=-ρ12-iηϕ2F(c)/(κω);b21S=-ρ12-iηϕ2F(c)/(κω);b22S=-ρ22+iηϕ2F(c)/(κω)。
波动方程存在非零解的条件是系数行列式为零,利用平面波分析方法得到速度频散和衰减。因此,可得纵波方程的解
| $ (k / \omega)^{2}=\frac{-B_{\mathrm{P}} \pm \sqrt{B_{\mathrm{P}}^{2}-4 M_{\mathrm{P}} E_{\mathrm{P}}}}{2 M_{\mathrm{P}}} $ | (21) |
式中
| $ M_{\mathrm{P}}=\left(A+2 \mu_{\mathrm{S}}\right) R-G^{2} $ | (22) |
| $ \begin{aligned} B_{\mathrm{P}}=&-\rho_{11} R-\left(A+2 \mu_{\mathrm{S}}\right) \rho_{22}+2 \rho_{12} G+\\ & \frac{\mathrm{i} \eta \phi^{2}}{\kappa \omega} F(c)\left(A+2 \mu_{\mathrm{s}}+2 G+R\right) \end{aligned} $ | (23) |
| $ E_{\mathrm{P}}= \rho_{11} \rho_{22}-\rho_{12}^{2}-\frac{\mathrm{i} \eta \phi^{2}}{\kappa \omega} F(c)\left(\rho_{11}+\rho_{22}+2 \rho_{12}\right) $ | (24) |
求解上面关于k/ω的方程可以得到纵波复速度 VP*=ω/k,进而可得相速度VP=Re(VP*) 和衰减因子QP-1=Im[(VP*)2]/Re[(VP*)2]。
横波的k/ω满足
| $ B_{\mathrm{S}}(k / \omega)^{2}+\varPsi_{\mathrm{S}}=0 $ | (25) |
式中系数为:BS=-ρ22μS+iF(c)μSηϕ2/(κω);ΨS=ρ11ρ22-ρ122μS-iF(c)(ρ11+ρ22+2ρ12)ηϕ2/(κω)。求解上式可得横波复速度VS*=ω/k,则相速度VS=Re(VS*)、衰减因子QS-1=Im[(VS*)2]÷Re[(VS*)2]。
3 数值算例 3.1 流变参数和分数阶导数对流体黏性耗散系数的影响溶液的流动特性和黏弹性取决于临界剪切率,在临界剪切率之上可以观察到剪切稀化(Shear Thinning)和剪切稠化(Shear Thickening)现象。这种非牛顿流体行为受Deborah数的控制,该参数通过可测量参数计算获得,包括流体密度ρf、黏度η、弛豫时间λ和孔隙通道半径a。应用甘油和CPyCL/NaSal(氯化钠和水杨酸钠)溶液定量计算流—固耦合黏性耗散函数F(c)。两种流体的参数[22]为:甘油(牛顿流体)的密度为1250kg/m3,黏性为1 Pa·s;CPyCL/NaSal溶液(非牛顿流体)的密度为1050 kg/m3,黏度为60 Pa·s。
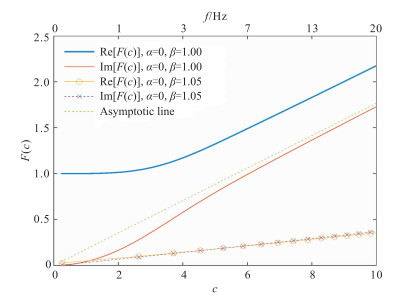
甘油的弛豫时间设定为一个很小的值(10-30s),代表牛顿流体力学行为,其分数阶导数为(0,1.00)和(0,1.05)时的F(c)函数计算结果如图 1所示。从图 1可以看出,当频率接近0时,甘油的黏性耗散修正函数值等于1,表明低频极限下黏性耗散系数退化到Biot理论的低频情况;当频率逐渐增大时,黏性耗散修正函数趋近于线性增长,实部和虚部逐渐平行于一条渐近线(Asymptotic line)。该算例给出的甘油黏性耗散函数随频率变化规律与Biot理论给出的牛顿流体行为完全一致[22],这一结论与Tsiklauri等[30]的研究吻合。计算结果表明,当甘油弛豫时间趋近于零时,牛顿流体可由fdMaxwell模型获得。
|
图 1 甘油(De=0)的F(c)实部和虚部 |
值得指出的是,对于孔隙含有牛顿流体的情况,Biot[29]给出了高频下孔隙介质波动方程的修正方法,在低频情况下牛顿流体黏性耗散修正函数趋近于1,高频情况下黏性耗散系数随频率呈现线性增长,其渐近线为
分数阶导数(与应变延迟有关)对F(c)有显著影响。从图 1可以看出,阶数β增加5%导致F(c)大幅下降,这将显著降低流体与固体之间的黏性作用。因此,分数阶导数的阶数β刻画了应变与应力变化率的关系。
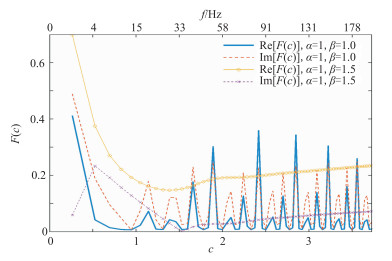
CPyCL/NaSal溶液的弛豫时间设置为1.9s,用于解释其非牛顿流体行为[22],其分数阶导数为(1,1.0)和(1,1.5)的F(c)函数计算结果如图 2所示。
|
图 2 CPyCL/NaSal溶液(De=17.4)的F(c)实部和虚部 |
首先,当α=1和β=1.0时,模型退化为传统的Maxwell模型。CPyCL/NaSal溶液的F(c)在低频率范围内快速衰减,然后呈现多个峰值,这些峰值反映出CPyCL/NaSal溶液具有近似固体的弹性共振现象。采用α=1和β=1.5说明分数阶导数对流固耦合黏性耗散机制的影响。在低频率状态下仍然可以观察到耗散函数的快速衰减,然而并未出现多个峰值。计算结果表明,分数阶导数应变—应力关系控制了非牛顿流体的共振行为,对流体从耗散态到弹性系统的过渡具有重要影响。
3.2 fdMaxwell流体分数阶导数对纵波速度频散和衰减的影响采用平均孔隙度为21%的French Vosgian砂岩[31](表 1)分析纵波速度频散和衰减对黏弹性流体的分数阶导数的依赖关系。
|
|
表 1 French Vosgian砂岩参数 |
盐水的弛豫时间被设定为一个微小的值(10ns)模拟牛顿流体的行为。
图 3为由Biot理论和Maxwell模型(分数阶导数α=1和β=1)计算的砂岩饱含盐水的波速频散和衰减曲线,可见,无论是地震频带还是超声波频带(小于1MHz),非牛顿波动方程的纵波波速度与Biot的理论匹配得很好,微小的差异发生在超高频带,这是因为在波动方程中摩擦损耗被重新定义了。该算例表明,在饱含牛顿流体(盐水)的多孔介质中,Biot理论在弹性波传播方面很有效,在此情况下,黏弹性效应可以忽略不计,两种理论表现一致。

|
图 3 饱含盐水的French Vosgian砂岩的纵波速度频散(a)和衰减(b)曲线 |
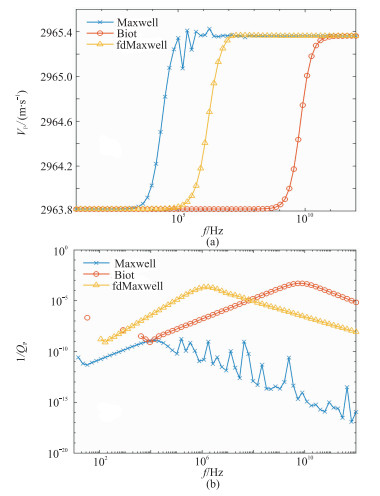
由Biot理论和Maxwell模型(分数阶导数α=1和β=1.0)和fdMaxwell模型(分数阶导数α=1和β=1.5)计算饱含CPyCL/NaSal溶液的French Vosgian砂岩的纵波速度频散和衰减曲线如图 4所示。由图可见,当β从1.0增至1.5时,频散和衰减曲线会变得更加平滑,较大的β值压制了黏弹性共振现象。此外,fdMaxwell模型的速度跃升和衰减峰值会向低频方向移动(出现在大约1MHz),但不像Maxwell模型那样低(大约10kHz);fdMaxwell模型的纵波速度与Biot理论相同,与Maxwell模型有很大不同。fdMaxwell模型的导数阶数表征了Maxwell模型和Biot理论之间的中间流变动态。分数阶导数的值对fdMaxwell流体饱和的多孔介质弹性波速具有明显的影响。
|
图 4 饱含CPyCL/NaSal溶液的French Vosgian砂岩的纵波速度频散(a)和衰减(b)曲线 |
虽然分数阶导数对表征纯弹性和纯黏性之间的黏弹性行为起重要作用,但通过实验确定分数阶导数的阶数仍是一个挑战。许多研究试图从物理上解释分数导数,例如分形流变模型将聚合物链的变形机理与分数阶微分方程联系起来。但是,宏观应力和微结构变形之间的关系只能部分解决真实的聚合物液体,如何提供合理的分数导数参数拟合真实的黏弹性流体仍然十分困难。虽然目前的理想化模型过分简化了分子水平的细节,但含有fdMaxwell流体的多孔介质波速预测模型仍然提供了对非牛顿流体效应机理的深入认识。
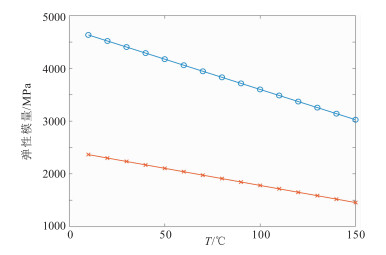
3.3 不同温度下含重油砂岩纵波速度预测利用含非牛顿流体波动方程对不同温度(T)下含重油(API=9.2)砂岩的波速进行了预测。温度变化范围为20~80℃,骨架密度为2630kg/m3,孔隙度为0.326,渗透率为9D[32]。研究表明,在10~150℃范围内,骨架体积模量和剪切模量随温度线性降低[33],如图 5所示。
|
图 5 骨架体积(蓝色)和剪切(红色)模量随温度变化曲线 |
重油黏性、密度、剪切模量随温度变化曲线[32, 34]如图 6所示,随着温度的上升,重油黏性和剪切模量下降,黏性系数下降趋势逐渐变缓。随着温度升高,重油作为黏滞流体的动态渗透率明显升高(图 7),在20~80℃范围内,给出了三个不同频率对应的动态渗透率变化情况,其中25Hz处于地震波频率范围,100kHz和1MHz处于超声波频率范围。从图中可以看出,不同频率的渗透率变化规律基本相同。
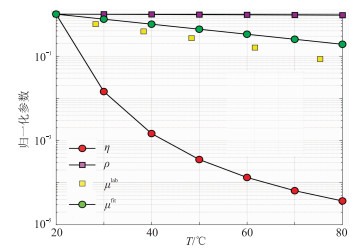
|
图 6 重油基础参数随温度变化 μlab、μfit分别实验室测量和计算的剪切模量 |

|
图 7 动态渗透率随温度、频率变化 |
在1MHz、100kHz和25Hz频率下模拟了纵波速度随温度变化(随温度的升高呈现下降趋势),并与实验数据[32]做了对比(图 8~图 10)。不同频率下,纵波速度随着温度升高逐渐下降,随着频率降低,这种速度下降更剧烈。在实验频率(1MHz)附近,非牛顿流体模型预测速度值更加接近实测数据(图 8)。当频率降到100kHz(图 9)和25Hz(图 10)时,牛顿流体模型和非牛顿流体模型预测速度均低于实验测量值,这是由于速度的频散引起的。计算结果显示,在不同频率下,非牛顿流体波动方程与常规波动方程预测结果均存在明显差异,非牛顿流体本构关系对流固耦合带来新的变化,对孔隙介质波场频散和衰减影响不可忽视。非牛顿流体模型的预测结果在实验频率下与观测数据吻合较好。
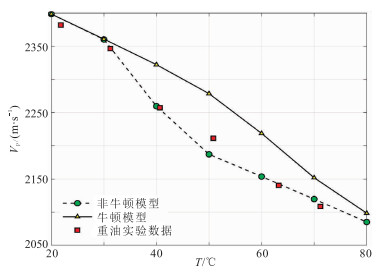
|
图 8 频率为1MHz时速度随温度变化曲线 |
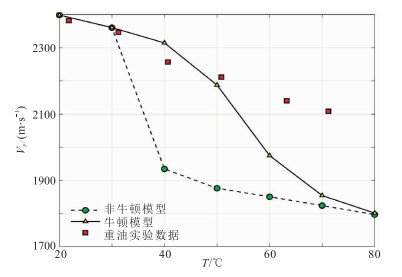
|
图 9 频率为100kHz时速度随温度变化 |
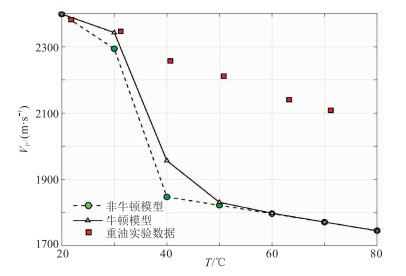
|
图 10 频率为25Hz时速度随温度变化 |
本文提出了基于分数阶Maxwell流体模型的非牛顿流体孔隙介质波动方程方法。根据重新定义的黏性耗散函数,Biot理论被推广到非牛顿流体饱和情况,能够解释更复杂的流—固耦合效应。利用波动方程定量研究流变学参数对多孔弹性介质波场传播的影响,研究表明弹性波速度频散和衰减不仅取决于密度、弹性模量和孔隙度,还取决于孔隙流体流变参数,如Deborah数和分数阶导数的阶数等参数。理论结果与实验数据对比分析表明,在牛顿和非牛顿流体饱和的砂岩中,波速存在显著差异。同时,分数阶导数本构关系控制着从黏性耗散状态到弹性机制的转变,对储层岩石波场传播特征具有重要影响。但是,不同流体如何选取分数阶参数是一个没有完全解决的问题,仍然需要根据实验或者新理论模型进行深入的研究。
| [1] |
Tan W, Pan W, Xu M. A note on unsteady flows of a viscoelastic fluid with the fractional Maxwell model between two parallel plates[J]. International Journal of Non-Linear Mechanics, 2003, 38(5): 645-650. DOI:10.1016/S0020-7462(01)00121-4 |
| [2] |
卢明辉. 双相复杂介质中弹性波传播机理研究[D]. 北京: 清华大学, 2006. LU Minghui. Study on the Propagation Mechanism of Elastic Waves in Complex Two-phase Media[D].Tsinghua University, Beijing, 2006. |
| [3] |
Tong D K, Wang R H. Exact solution of pressure tran-sient model for fluid flow in fractal reservoir including a quadratic gradient term[J]. Energy Sources, 2005, 27(13): 1205-1215. DOI:10.1080/009083190519168 |
| [4] |
Xiong F, Sun W, Ba J, et al. Effects of fluid rheology and pore connectivity on rock permeability based on a network model[J]. Journal of Geophysical Research: Solid Earth, 2020, 125(3): 1-15. |
| [5] |
刘芸菲, 陈学华, 罗鑫, 等. 双相不混溶流体饱和裂缝-孔隙岩石依赖频率的地震响应数值分析[J]. 石油地球物理勘探, 2020, 55(4): 821-830. LIU Yunfei, CHEN Xuehua, LUO Xin, et al. Numerical analysis of frequency-dependent seismic responses from fractured-porous rock saturated with two phase immiscible fluids[J]. Oil Geophysical Prospecting, 2020, 55(4): 821-830. |
| [6] |
汪关妹, 张万福, 张宏伟, 等. 致密砂岩气地震预测关键技术及效果[J]. 石油地球物理勘探, 2020, 55(增刊1): 72-79. WANG Guanmei, ZHANG Wanfu, ZHANG Hongwei, et al. Key technology and effect of prediction of tight sandstone gas based on seismic data[J]. Oil Geo-physical Prospecting, 2020, 55(S1): 72-79. |
| [7] |
李亚龙, 刘先贵, 胡志明, 等. 页岩储层压裂缝网模拟研究进展[J]. 石油地球物理勘探, 2019, 54(2): 480-492. LI Yalong, LIU Xiangui, HU Zhiming, et al. Research progress on fracture network simulation in shale re-servoirs[J]. Oil Geophysical Prospecting, 2019, 54(2): 480-492. |
| [8] |
熊繁升, 甘利灯, 孙卫涛, 等. 裂缝-孔隙介质储层渗透率表征及其影响因素分析[J]. 地球物理学报, 2021, 64(1): 279-288. XIONG Fansheng, GAN Lideng, SUN Weitao, et al. Characterization of reservoir permeability and analysis of influecing factors in fracture pore media[J]. Chinese Journal of Geophysics, 2021, 64(1): 279-288. |
| [9] |
Thomas J A, McGaughey A J H. Water flow in carbon nanotubes: Transition to subcontinuum transport[J]. Physical Review Letters, 2009, 102(18): 1845021-1845024. |
| [10] |
Sochi T. Modelling the flow of yield-stress fluids in porous media[J]. Transport in Porous Media, 2010, 85(2): 489-503. DOI:10.1007/s11242-010-9574-z |
| [11] |
Pearson J R A, Tardy P M J. Models for flow of non-Newtonian and complex fluids through porous media[J]. Journal of Non-Newtonian Fluid Mechanics, 2002, 102(2): 447-473. DOI:10.1016/S0377-0257(01)00191-4 |
| [12] |
Dong X, Liu H, Wang Q, et al. Non-Newtonian flow characterization of heavy crude oil in porous media[J]. Journal of Petroleum Exploration and Production Technology, 2013, 3(1): 43-53. DOI:10.1007/s13202-012-0043-9 |
| [13] |
Talon L, Bauer D. On the determination of a generalized Darcy equation for yield-stress fluid in porous media using a Lattice-Boltzmann TRT scheme[J]. European Physical Journal E, 2013, 36(12): 1-10. |
| [14] |
Markov M G. Rayleigh wave propagation along the boundary of a non-Newtonian fluid-saturated porous medium[J]. Acoustical Physics, 2006, 52(4): 429-434. DOI:10.1134/S1063771006040099 |
| [15] |
Teeuw D, Hesselink F T. Power-law flow and hydrodynamic behaviour of bipolymer solutions in porous media[C].Society of Petroleum Engineers 5th International Symposium on Oilfield and Geothermal Chemistry, 1980, 28-30.
|
| [16] |
Greaves M, Patel K. Flow of polymer solution in po-rous media[J]. Chemical Engineering Research and Design, 1985, 63(3): 199-202. |
| [17] |
Cannella W J, Huh C, Seright R. Prediction of xanthan rheology in porous media[C].The 63rd Annual Technical Conference and Exhibition of the Society of Petroleum Engineers, 1988, 2-5.
|
| [18] |
Hejri S, Willhite G P, Green D W. Development of correlations to predict biopolymer mobility in porous media[J]. SPE Reservoir Engineering, 1991, 6(1): 1-8. |
| [19] |
刘杰, 张懿疆, 王秀玲, 等. 利用反褶积广义S变换提取流体流度属性[J]. 石油地球物理勘探, 2019, 54(3): 617-623. LIU Jie, ZHANG Yijiang, WANG Xiuling, et al. Re-servoir fluid mobility extraction based on the deconvolution generalized S-transform[J]. Oil Gephysical Prospecting, 2019, 54(3): 617-623. |
| [20] |
Iassonov P P, Beresnev I A. A model for enhanced fluid percolation in porous media by application of low-frequency elastic waves[J]. Journal of Geophysical Research: Solid Earth, 2003, 108(B3): 1-9. |
| [21] |
Tsiklauri D, Beresnev I. Properties of elastic waves in a non-Newtonian (Maxwell) fluid-saturated porous medium[J]. Transport in Porous Media, 2003, 53(1): 39-50. DOI:10.1023/A:1023559008269 |
| [22] |
Castrejon-Pita J R, del Rio J A, Castrejon-Pita A A, et al. Experimental observation of dramatic differences in the dynamic response of Newtonian and Maxwellian fluids[J]. Physical Review E, 2003, 68(1): 463011-463015. |
| [23] |
Balankin A S, Elizarraraz B E. Hydrodynamics of fractal continuum flow[J]. Physical Review E, 2012, 85(2): 25302-25307. DOI:10.1103/PhysRevE.85.025302 |
| [24] |
Wang Q, Tong D. The flow analysis of viscoelastic fluid with fractional order derivative in horizontal well[J]. Transport in Porous Media, 2010, 81(2): 295-303. DOI:10.1007/s11242-009-9401-6 |
| [25] |
Hernández-Jiménez A, Hernández-Santiago J, Macias-García A, et al. Relaxation modulus in PMMA and PTFE fitting by fractional Maxwell model[J]. Polymer Testing, 2002, 21(3): 325-331. DOI:10.1016/S0142-9418(01)00092-7 |
| [26] |
Friedrich C. Relaxation and retardation functions of the Maxwell model with fractional derivatives[J]. Rheologica Acta, 1991, 30(1): 151-158. |
| [27] |
Schiessel H, Metzler R, Blumen A, et al. Generalized viscoelastic models: Their fractional equations with solutions[J]. Journal of Physics A, 1995, 28(1): 6567-6584. |
| [28] |
Oldham K B, Spanier J. The Fractional Calculus[M]. New York: Academic Press, 1974.
|
| [29] |
Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid 2:Higher frequency range[J]. Journal of the Acoustical Society of America, 1956, 28(2): 179-191. DOI:10.1121/1.1908241 |
| [30] |
Tsiklauri D, Beresnev I. Enhancement in the dynamic response of a viscoelastic fluid flowing through a longitudinally vibrating tube[J]. Physical Review E, 2001, 63(2): 463041-463044. |
| [31] |
Bacri J C, Salin D. Sound velocity of a sandstone with oil and brine at different concentrations[J]. Geophysical Research Letters, 1986, 13(4): 326-328. DOI:10.1029/GL013i004p00326 |
| [32] |
Han D H, Zhao H Z, Yao Q, et al. Velocity of heavy oil sand[C].SEG Technical Program Expanded Abstracts, 2007, 26: 1619-1623.
|
| [33] |
Zhang J J, Bentley L R. Change of Bulk and Shear Moduli of Dry Sandstone with Effective Pressure and Temperature[R].CREWES Research Report, 1999.
|
| [34] |
Batzle M, Wang Z J. Seismic properties of pore fluids[J]. Geophysics, 1992, 57(11): 1396-1408. DOI:10.1190/1.1443207 |



 孙卫涛, 北京市海淀区清华园1号清华大学航天航空学院, 100084。Email:
孙卫涛, 北京市海淀区清华园1号清华大学航天航空学院, 100084。Email: 