随着石油天然气勘探开发的不断推进,难度在不断增加。研究主体由简单构造油气藏转向复杂构造油气藏、岩性油气藏和裂缝油气藏等。裂缝储层和薄互储层通常情况下表现为各向异性[1],储层中岩石颗粒之间的摩擦作用会导致能量的衰减和速度频散,即表现为黏弹性,而岩石孔隙中的流体和岩石颗粒之间的相互作用则表现为双相性[2]。因此建立更精确的地下介质模型描述地震波在实际介质中的传播特征,成为当前地球物理学者面临的重要难题之一。
近年来,许多学者研究了黏弹性介质地震波场模拟,取得了较好的效果[3-5]。Emmerich等[6]首先提出了基于流变学模型——广义标准线性体(GSLS)模型,Carcione等[7-9]在此基础上发展了广义Zener线性体模型,并应用松弛函数与应变的卷积表示黏弹介质中的应力,建立了线性黏弹性各向异性介质波动方程。蔡瑞乾等[10]基于GSLS模型提出了一种黏声波动方程变机制数有限差分正演方法;毕玉英等[11]提出了二维黏弹介质完全波场计算方法,该方法避免了繁杂的射线追踪,可以获得多种波场的时间-空间正演记录。张中杰等[12]对黏弹性介质中的地震波速度衰减和频散进行了研究;谭未一等[13]研究了黏弹VTI介质中品质因子对qSV和qSH波频率的影响;朱峰等[14]提出了黏声VTI介质高阶傅里叶有限差分波场延拓算子,并将其应用于叠前深度偏移;王小杰等[15]建立了黏弹介质反射系数近似公式,提高了储层预测精度。Ping等[16]利用谱元法建立了黏弹VTI介质波动方程。姚振岸等[17]在黏弹TTI介质中实现了三种微地震基础源的旋转交错网格震源加载方式和照明分析。这些研究从计算域、离散化方法和网格类型等方面对地震波在单相黏弹各向异性介质中的传播规律进行了分析,虽然忽视了介质双相性的影响,但为后续双相黏弹VTI介质的研究奠定了基础。
为了真实地反映地下双相性特征,Biot[18]最先提出双相介质理论并考虑了固相的黏弹性和液相的黏性特征,并建立了双相黏弹介质模型。田迎春[19]利用有限元法对层状黏弹双相介质模型进行了动力响应分析和物性参数反演;王美霞[20]通过引入Birkhoffian系统,提出了一种保辛方法,该方法可以对双相介质和黏弹性介质下的波动方程进行优化处理;韩颜颜[21]利用伪谱法对双相黏弹EDA(Extensive Delatancy Anisotropy)介质进行了数值模拟,并分析了品质因子对纵、横波传播的影响。这些研究有助于更加准确地求解双相波动方程和精确描述地下介质性质,并通过照明分析优化观测系统。如果地下介质结构复杂、观测系统设计不当和存在高速层屏蔽等因素,就会导致复杂地区的地震记录信噪比降低,致使地震成像效果变差。
照明分析技术正是通过对能量较弱区域进行定量分析从而提高目标区地震波能量[22],主要分为基于射线追踪理论的照明方法和基于波动方程的照明方法。基于射线追踪的照明方法最初由Muerdter等[23]提出,但射线理论本身就是高频近似,且在正演模拟中存在射线盲区等缺陷。基于波动方程的照明又可分为单程波照明和双程波照明。Xie等[24]建立了局部平面波分解的单程波地震照明法;陈雪等[25]把单程波方程应用到黏弹VTI介质中,对黏弹VTI介质中qP波的传播及能量分布进行了分析。单程波照明能够解决一些复杂介质的照明问题,但是单程波照明存在波损失、不能解决广角反射等问题[26]。Xie等[27-28]提出了一种基于有限差分方法的双程波方程照明分析方法;皮红梅[29]采用交错网格有限差分方法进行了双程波动方程的照明分析;李金丽等[30]提出了一种黏声各向异性双程波照明技术。这些研究成果说明了双程波照明得到的波场信息比单程波照明更加丰富,不受构造倾角限制,在复杂介质中具有较强的适应性,为观测系统的优化提供全角度范围内的真振幅照明。
本文综合考虑介质的双相性、黏弹性和各向异性,建立双相黏弹性各向异性介质地震波传播方程,精确地描述地下介质的结构和波场传播特征。以VTI介质为例,推导二维黏弹各向异性双相介质的一阶速度-应力方程,并对三个典型模型进行数值模拟,应用该数值模拟对双相黏弹VTI模型进行了照明分析及观测系统优化。
1 方法原理 1.1 黏弹双相VTI介质一阶速度-应力方程实际地球介质表现出非完全弹性、各向异性、多相态的特征。本文根据Carcione等[9]提出的黏弹各向异性介质的应力张量与应变张量的关系,推导出了一种松弛机制下双相黏弹各向异性介质弹性波方程。固相应力-应变关系为
| $ \boldsymbol{\sigma}=\boldsymbol{\psi}(t) * \dot{\boldsymbol{e}}+\boldsymbol{A} \theta $ | (1) |
液相应力-应变关系为
| $ S=\boldsymbol{A}^{\mathrm{T}} \boldsymbol{e}+R \theta $ | (2) |
式中:σ=(σxx,σzz,σxz)T为固相应力;e=(exx,ezz,exz)T为固相应变,
| $ \left\{\begin{array}{l} \tau_{\sigma}=\tau_{\sigma}^{(1)}=\tau_{\sigma}^{(2)}=\frac{1}{\omega}\left(\sqrt{1+\frac{1}{Q_{1}^{2}}}-\frac{1}{Q_{1}^{2}}\right) \\ \tau_{\varepsilon}^{(1)}=\frac{1}{\omega^{2} \tau_{\sigma}} \\ \tau_{\varepsilon}^{(2)}=\frac{1+\omega \tau_{\sigma} Q_{2}}{\omega Q_{2}-\omega^{2} \tau_{\sigma}} \end{array}\right. $ | (3) |
式中:p=1、p=2分别表示胀缩或剪切运动;ω为角频率。
假定固相的速度向量为v=(vx,vz)T,流相的速度向量为V=(Vx,Vz)T,将运动平衡微分方程(附录A)与应力-应变关系相结合,并引入记忆变量消除卷积,可以得到二维双相黏弹各向异性介质的一阶速度-应力方程[31](详细推导见附录A)
| $ \left\{\begin{array}{l} \frac{\partial v_{x}}{\partial t}=-D_{2}\left(\frac{\partial \sigma_{x x}}{\partial x}+\frac{\partial \sigma_{x z}}{\partial z}\right)+D_{3} \frac{\partial S}{\partial x}-\left(D_{2}+D_{3}\right) b_{11}\left(V_{x}-v_{x}\right) \\ \frac{\partial v_{z}}{\partial t}=-D_{2}\left(\frac{\partial \sigma_{x z}}{\partial x}+\frac{\partial \sigma_{z z}}{\partial z}\right)+D_{3} \frac{\partial S}{\partial z}-\left(D_{2}+D_{3}\right) b_{33}\left(V_{z}-v_{z}\right) \\ \frac{\partial V_{x}}{\partial t}=D_{3}\left(\frac{\partial \sigma_{x x}}{\partial x}+\frac{\partial \sigma_{x z}}{\partial z}\right)-D_{1} \frac{\partial S}{\partial x}-\left(D_{1}+D_{3}\right) b_{11}\left(V_{x}-v_{x}\right) \\ \frac{\partial V_{z}}{\partial t}=D_{3}\left(\frac{\partial \sigma_{x z}}{\partial x}+\frac{\partial \sigma_{z z}}{\partial z}\right)-D_{1} \frac{\partial S}{\partial z}-\left(D_{1}+D_{3}\right) b_{33}\left(V_{z}-v_{z}\right) \end{array}\right. $ | (4) |
| $ \left\{\begin{array}{l} \frac{\partial \sigma_{x x}}{\partial t}=\left(\frac{\partial v_{x}}{\partial x} \hat{C}_{11}+\frac{\partial v_{z}}{\partial z} \hat{C}_{13}\right)\left[1+\tau_{\varepsilon}^{(1)}\right]+2 \frac{\partial v_{z}}{\partial z} \hat{C}_{44}\left[\tau_{\varepsilon}^{(1)}-\tau_{\varepsilon}^{(2)}\right]+E_{x x}+A_{1}\left(\frac{\partial V_{x}}{\partial x}+\frac{\partial V_{z}}{\partial z}\right) \\ \frac{\partial \sigma_{z z}}{\partial t}=\left(\frac{\partial v_{x}}{\partial x} \hat{C}_{13}+\frac{\partial v_{z}}{\partial z} \hat{C}_{33}\right)\left[1+\tau_{\varepsilon}^{(1)}\right]+2 \frac{\partial v_{x}}{\partial x} \hat{C}_{44}\left[\tau_{\varepsilon}^{(1)}-\tau_{\varepsilon}^{(2)}\right]+E_{z z}+A_{3}\left(\frac{\partial V_{x}}{\partial x}+\frac{\partial V_{z}}{\partial z}\right) \\ \frac{\partial \sigma_{x z}}{\partial t}=\left(\frac{\partial v_{x}}{\partial z}+\frac{\partial v_{z}}{\partial x}\right) \hat{C}_{44}\left[1+\tau_{\varepsilon}^{(2)}\right]+E_{x z} \\ \frac{\partial S}{\partial t}=A_{1} \frac{\partial v_{x}}{\partial x}+A_{3} \frac{\partial v_{z}}{\partial z}+R\left(\frac{\partial V_{x}}{\partial x}+\frac{\partial V_{z}}{\partial z}\right) \end{array}\right. $ | (5) |
| $ \left\{\begin{array}{l} \frac{\partial E_{x x}}{\partial t}=-\frac{1}{\tau_{\sigma}}\left\{\left(\hat{C}_{11} \frac{\partial v_{x}}{\partial x}+\hat{C}_{13} \frac{\partial v_{z}}{\partial z}\right) \tau_{\varepsilon}^{(1)}+2 \frac{\partial v_{z}}{\partial z} \hat{C}_{44}\left[\tau_{\varepsilon}^{(1)}-\tau_{\varepsilon}^{(2)}\right]+E_{x x}\right\} \\ \frac{\partial E_{z z}}{\partial t}=-\frac{1}{\tau_{\sigma}}\left\{\left(\hat{C}_{13} \frac{\partial v_{x}}{\partial x}+\hat{C}_{33} \frac{\partial v_{z}}{\partial z}\right) \tau_{\varepsilon}^{(1)}+2 \frac{\partial v_{x}}{\partial x} \hat{C}_{44}\left[\tau_{\varepsilon}^{(1)}-\tau_{\varepsilon}^{(2)}\right]+E_{z z}\right\} \\ \frac{\partial E_{x z}}{\partial t}=-\frac{1}{\tau_{\sigma}}\left[\hat{C}_{44} \tau_{\varepsilon}^{(2)}\left(\frac{\partial v_{x}}{\partial z}+\frac{\partial v_{z}}{\partial x}\right)+E_{x z}\right] \end{array}\right. $ | (6) |
式中:
将双相黏弹VTI介质正演模拟引入到双程波照明分析中,分析在双相黏弹VTI介质中地震波传播特征和能量分布。地震照明分析是在已知地质模型和给定观测系统的情况下采用正演模拟方法认识和研究地震波场能量在地下结构中的分布和炮检点对目标体的波场响应,这样有助于对地震观测系统进行优化。地震照明与正演模拟不同,前者是观测系统对地震模型的波场均衡程度,后者是观测系统对地震模型的波场响应。在地下介质中,地震波反射能量弱的区域即可认为是阴影区,通过改善观测系统,使反射能量弱的区域得到加强,从而获得质量更高的地震勘探成果。
在二维双相黏弹VTI介质中,通过董良国等[33]提出的基于目标的照明统计方法,标记照明目标点位置为X0(x0,z0),地表不同位置标记为X(x,z),地表激发点位置标记为Xs(xs,zs)。在地表不同位置激发震源,统计每一炮点在目标点X0(x0,z0)的波场能量,即可得到不同位置震源对该点的源向照明度函数
| $ I\left(\boldsymbol{X}_{\mathrm{s}}\right)=\sum\limits_{\omega} U\left(\boldsymbol{X}_{\mathrm{s}}, \boldsymbol{X}_{0}, \omega\right) $ | (7) |
式中U(Xs,X0,ω)为震源激发传播到目标位置的波场。用此函数得出工区目标照明图,可以方便地找出对目标照明能量影响较大的炮点。
根据互易原理,以目标点X0(x0,z0)为震源,计算地表不同位置处的照明能量,可得到反向照明度函数
| $ I\left(\boldsymbol{X}_{0}\right)=\sum\limits_{\omega} U\left(\boldsymbol{X}_{0}, \boldsymbol{X}, \omega\right) $ | (8) |
式中:U(X0,X,ω)为在目标位置震源激发传播到地表的波场。
反向照明度函数能量强的区域可确定为对目标照明最为有利的激发区域,可用于指导观测系统的炮点加密。
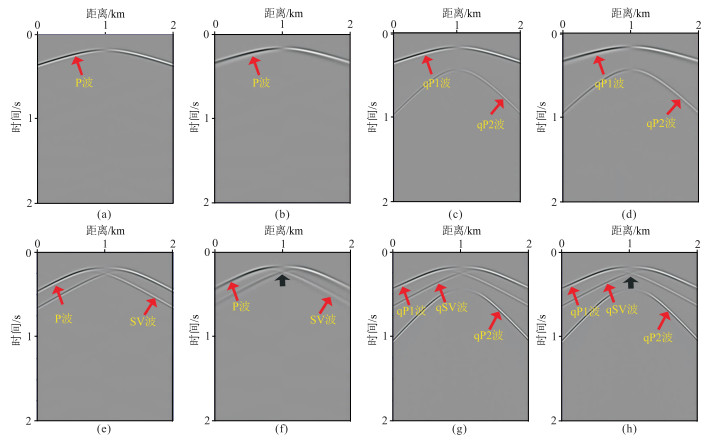
2 模型试算 2.1 均匀速度模型为验证本文提出的双相黏弹VTI介质波动方程可准确地模拟地震波在双相黏弹VTI介质中的传播规律,对均匀速度模型分别进行单相弹性各向同性(模型1)、单相黏弹各向同性(模型2)、双相弹性各向同性(模型3)、双相黏弹各向同性(模型4)、单相弹性VTI(模型5)、单相黏弹VTI(模型6)、双相弹性VTI(模型7)、双相黏弹VTI(模型8)波场模拟。各模型参数如表 1所示(数值模拟中,取A1=A3=A,b11=b33=b)。模型网格数为201×201,网格尺寸为10m×10m,震源主频为20Hz,位于(1010m,500m),激发方式为纵波源,时间采样间隔为1 ms,釆用二维交错网格高阶有限差分模拟,为了更加直观的对比,利用固相的水平分量进行分析(图 1)。
|
|
表 1 均匀模型参数 |
|
图 1 不同介质均匀模型模拟的固相水平分量波场记录 (a)模型1;(b)模型2;(c)模型3;(d)模型4;(e)模型5;(f)模型6;(g)模型7;(h)模型8 |
由图 1a和图 1b可看出,采用的是纵波震源,因此在单相各向同性情况下,弹性介质和黏弹介质中只观测到纵波,而观测不到横波。在图 1c和图 1d中,受介质双相性质的影响,可在双相各向同性弹性介质和黏弹介质中都观测到慢纵波(qP2波)。对比图 1a~图 1d与图 1e~图 1h可以看出,当模型是VTI介质时,在波场记录中可以观测到横波,而且横波出现三分叉现象(如图 1f和图 1h中黑色箭头所示)。而在双相VTI介质中(图 1g和图 1h)还可以观测到慢纵波。
图 2为8个均匀介质模拟的固相水平分量波场快照。对比图 2a、图 2b与图 2c、图 2d可以看出,当模型是单相各向同性时,弹性介质和黏弹介质中只有纵波,没有横波和慢纵波,而当模型是双相各向同性介质时,弹性和黏弹介质同时观测到快纵波和慢纵波。当模型是单相VTI介质时,在图 2e和图 2f中,同时观测到P波和SV波,而没有观测到慢纵波。在各向同性介质中P波的波前面是圆形,而在VTI介质中波前面是椭圆形,表明在各向同性介质中弹性波速度与传播方向无关,而VTI介质中与弹性波速度与传播方向有关。以上均匀速度模型数值模拟结果表明,双相介质比单相介质,各向异性介质比各向同性介质弹性波波前面更加复杂且包含更多波的信息。
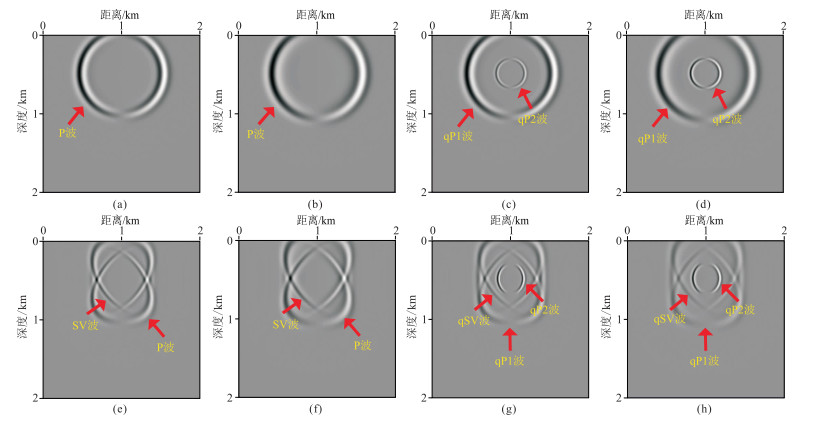
|
图 2 固相水平分量波场快照 (a)模型1;(b)模型2;(c)模型3;(d)模型4;(e)模型5;(f)模型6;(g)模型7;(h)模型8 |
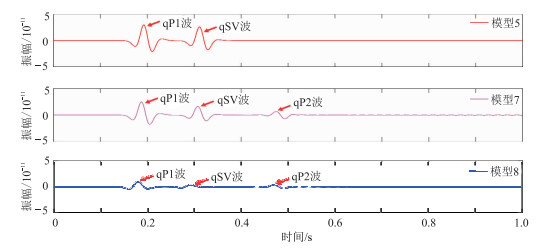
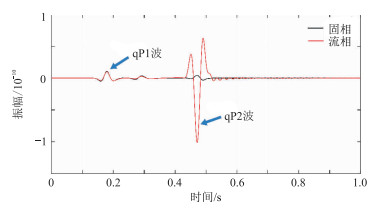
为了进一步验证双相介质中存在慢纵波且黏弹介质中波的能量比弹性介质中的弱,分别抽取单相黏弹、双相弹性、双相黏弹VTI介质波场记录的第80道进行显示,如图 3所示。由图 3可知,三种模型中都能观测到纵波和横波成分,且在双相弹性和黏弹VTI介质中同时存在慢纵波,但在单相黏弹VTI介质中慢纵波位置处的振幅为零,即单相介质中不存在慢纵波;由于介质的黏弹性和双相性,三个模型纵横波振幅有明显差异,振幅由弱到强的顺序为模型8、模型7、模型5,说明双相黏弹介质中地震波衰减现象最严重。图 4为双相黏弹VTI介质第80道固相与流相波形对比,可见,在黏弹VTI双相介质数值模拟中同时存在快纵波、慢纵波和横波。快纵波与横波在固相和流相中相位相同,是同相波;而慢纵波在固相和流相中相位相反,是反相波。
|
图 3 三种VTI介质波场记录第80道波形对比 |
|
图 4 双相黏弹VTI介质第80道固相和流相波形对比 |
为了进一步验证本文提出方法的正确性,采用控制变量法对本文提出方程分别进行各向异性、黏弹性、双相性验证。测试中,炮点位于(500m,450m),检波点位于(0,10m)。首先,将本文提出的方程中的黏弹介质纵横波品质因子设为500,同时将液相介质参数设为零,其他参数不变。正演模拟得到的波形如图 5a中红色实线所示,为了进行对比,采用传统各向异性方程进行有限差分正演模拟得到的波形如图 5a中蓝色虚线所示。两条波形曲线基本一致,表明本文提出的方程能够准确地对VTI介质进行模拟。

|
图 5 本文方法(红色)与其他传统方法(蓝色)模拟结果的波形对比 (a)各向异性正演模拟;(b)黏弹正演模拟;(c)双相正演模拟 |
其次,将本文提出方程中的液相介质参数设为零、各向异性参数C11=C33,并进行正演模拟得到的波形曲线如图 5b中红色实线所示,与传统黏弹介质一阶速度-应力方程正演模拟的结果(图 5b蓝色虚线)对比可知,本文提出的方程可以准确地对黏弹介质进行模拟。
最后,将本文提出方程的品质因子设为500、各向异性参数C11=C33,得到了与传统双相介质正演模拟吻合的结果(图 5c),且可以看到准确的快纵波和慢纵波信息,因此本文提出的方程适用于双相介质。
综上所述,本文提出的黏弹各向异性双相介质方程能够准确模拟地震波在黏弹VTI双相介质的传播特征。
2.2 层状模型为了分析地下波场的反射与透射特征,设计上层为单相弹性各向同性介质、下层为双相黏弹VTI介质的层状模型(表 2)。模型网格数为201×201,网格尺寸为10m×10m,反射界面深度为1010m,震源位于(1010m,700m),时间采样间隔为1 ms,模拟结果如图 6和7所示。
|
|
表 2 水平层状介质参数 |
|
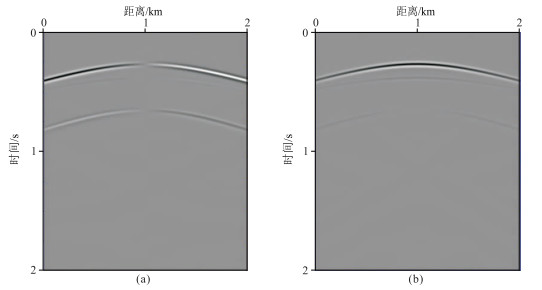
图 6 层状介质固相波场记录 (a)水平分量;(b)垂直分量 |
|
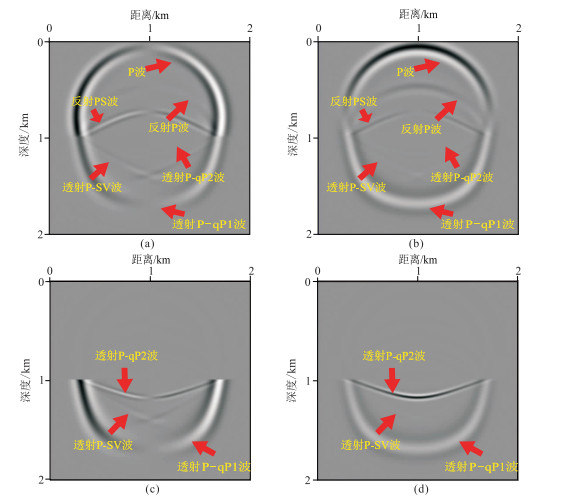
图 7 层状介质250ms时刻波场快照 (a)固相水平分量;(b)固相垂直分量;(c)流相水平分量;(d)流相垂直分量 |
由图 6和图 7可知,当上层为单相弹性各向同性介质时,上层介质中出现直达P波、反射P波和反射PS波,不存在慢纵波。而地震波通过界面后,由于下层介质是双相黏弹VTI介质,因此在固相和流相中能同时观测到透射横波P-SV、透射快纵波P-qP1和透射慢纵波P-qP2,且流相中更易观测到转换慢纵波,由于慢纵波无法穿过上层单相介质,因此波场记录中没有流相成分。除此之外,还可以发现透射横波的波前面不是圆形的,这是由于下层介质是各向异性引起的。由于黏滞性的影响,从图 7可看出,透射P-qP1波流相振幅比固相振幅有所减弱。
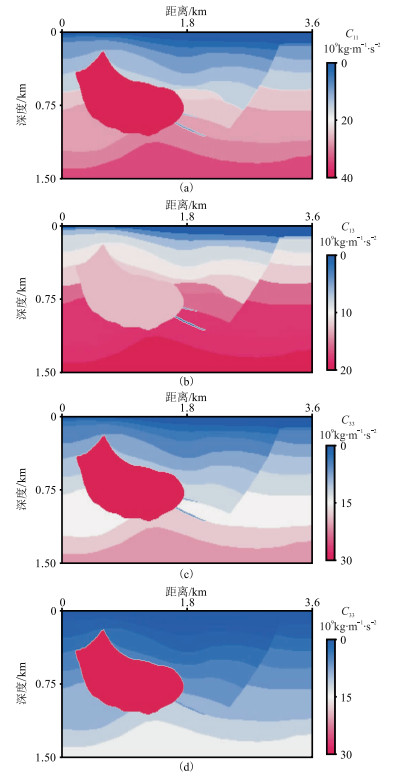
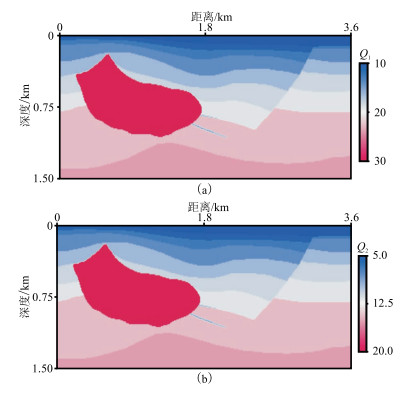
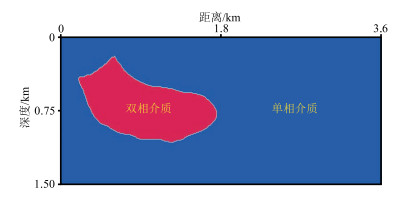
2.3 Hess模型为验证本文双相黏弹VTI介质数值模拟方法对复杂介质的实用性和稳定性,选取Hess模型进行数值模拟,建立了单相弹性VTI介质模型、单相黏弹VTI介质模型和双相黏弹VTI介质模型(图 8~图 10)。弹性系数和纵横波品质因子参数如图 8和图 9所示,单相(蓝色)、双相(红色)介质分布区域如图 10所示。单相介质区域ρ11=2170kg/m3、ρ22=100kg/m3;双相介质参数为:b =5kg·m-3·s-1、A=0.953×109kg·m-1·s-2、R=0.331×109kg·m-1·s-2、ρ12=-83kg/m3、ρ22=191kg/m3、ρ11=2170kg/m3。模型尺寸均为3620m×1500m,网格单元尺寸为10m×10m,时间采样间隔为0.4ms,震源位于(1800m,500m)。
|
图 8 各向异性弹性系数模型 (a)C11;(b)C13;(c)C33;(d)C44 |
|
图 9 品质因子模型 (a)Q1;(b)Q2 |
|
图 10 模型的单相、双相介质分布 |
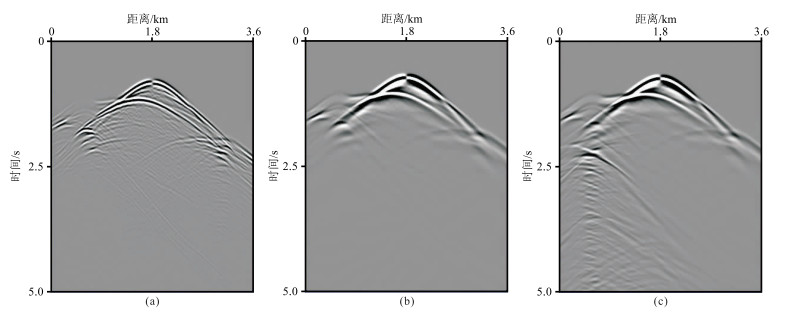
从波场记录(图 11)和波场快照(图 12)可以看出,本文的模拟方法在复杂地质模型中也可以得到较准确的地震记录和波场快照。对比图 11a与图 11b可见,单相黏弹介质中地震波能量明显衰减,分辨率降低,深层反射振幅变弱。对比图 11b与图 11c可见,后者相比前者明显多出了一些波场信息,这正是双相介质异常体产生的影响。从图 12a和图 12b中可以看出,在黏弹性的影响下,固相黏弹VTI介质中的地震波明显衰减(图 12b黄圈所示),有些反射波、透射波能量减弱,且同相轴也变模糊。双相黏弹VTI介质模型波场快照中出现了慢纵波引起的反射波、透射波信息(图 12c红圈所示)。
|
图 11 VTI介质波场记录 (a)单相弹性;(b)单相黏弹;(c)双相黏弹 |

|
图 12 VTI介质800ms时刻波场快照水平分量 (a)单相弹性;(b)单相黏弹;(c)双相黏弹 |
为了使照明结果更加具有实际意义,基于Hess模型分别建立单相弹性各向同性介质模型(图 13)和双相黏弹VTI介质模型(图 8~图 10),然后分析其中的能量分布以说明单相与双相、弹性与黏弹、各向同性与各向异性介质中能量差别。根据能量分布,对已有的观测系统进行优化,增强阴影区的能量。假定优化前的观测系统炮点和接收点均匀分布于地表。在给定的观测系统下,在地表处激发地震波,产生的照明能量分布如图 14所示。

|
图 13 Hess弹性各向同性介质速度模型 |
|
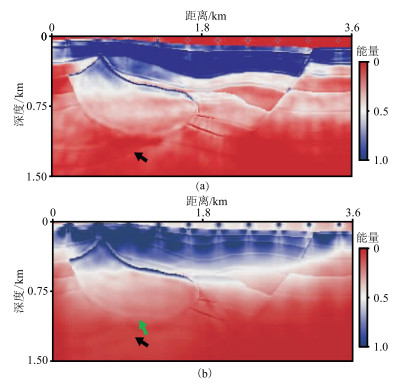
图 14 不同介质Hess模型的源向照明度对比 (a)单相弹性各向同性;(b)双相黏弹VTI |
由图 14可以看出,在双相黏弹VTI介质中能量强度与单相弹性介质相比整体较弱,而且深部能量衰减明显,这是由介质的双相性和黏弹性所致。从黑色箭头所指区域可以看出,在单相弹性各向同性介质中的反射层清晰可见,说明此区域能量较强,而双相黏弹VTI介质却相反。由此可见,双相黏弹VTI介质情况下更加需要照明补偿,且与单相弹性介质相比,达到相同的增强效果所需的施工成本更高,所以为了减少成本,需要针对目标区域进行加密放炮。
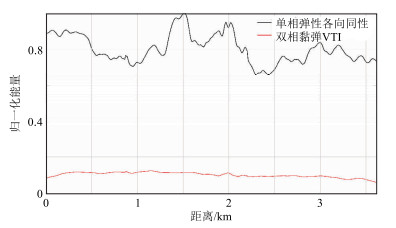
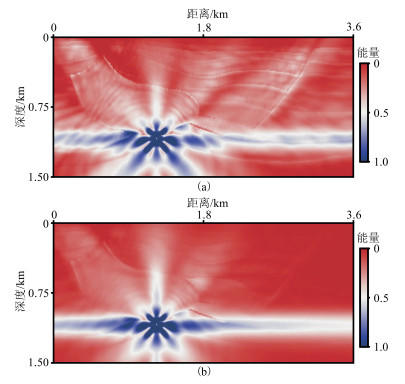
为了进一步比较目标区(图 13中黄圈所示)的能量分布,图 15给出了图 13中黑色实线所示层位的照明度曲线。由曲线可见,由于双相和黏弹共同影响,目标区的能量与单相弹性各向同性介质相比明显要弱,而且双相黏弹VTI介质的曲线幅度整体较低,这说明黏弹VTI介质对地震波的衰减作用更强。因此为了将阴影区的能量变强,将震源布置在阴影区,按照双程波算子计算波场能量,进行反向照明,然后提取地表能量,结果如图 16所示。
|
图 15 不同介质目标区照明度曲线对比 |
|
图 16 不同介质反向照明度对比 (a)单相弹性各向同性;(b)双相黏弹VTI |
由图 16可以看出,在目标区放炮时,单相弹性各向同性介质比双相黏弹VTI介质的能量强,而且地震波穿透能力也强,这是因为在单相弹性介质中地震波的衰减较弱。提取地表处的能量(图 17)可以明显地看出,介质双相性和黏弹性使得地震波发生严重衰减,因此在双相黏弹VTI介质中,地表处的能量整体比单相弹性各向同性介质弱,且两条曲线形状也有一定差别,即在地表处能量的横向分布有差异,这是由于VTI介质中地震波传播速度随方向的变化引起了能量分布的不均匀。由双相黏弹VTI介质在地表处的能量分布可以看出,在1000~1570m区域的能量较强,因此提高阴影区照明度的有利加密炮点区间为1000~1570m。对双相黏弹VTI介质进行加密放炮。加密前总炮数为10,炮间距为360m,均匀分布在地表上。加密后总炮数为16,加密区炮间距为100m。

|
图 17 不同介质地表处照明度曲线对比 |
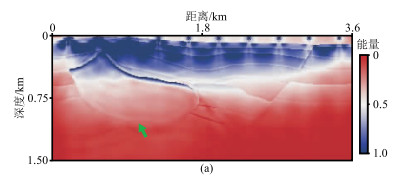
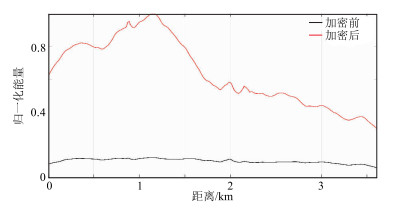
对比加密放炮前后源向照明度(图 18与图 14b)可知,加密放炮后,目标处反射比加密前明显了很多(绿色箭头所示),说明加密放炮后目标区的能量变强。从图 19可以看出,目标区的能量得到了明显的增强,说明加密放炮对目标区域起到了能量加强的作用。因此分区加密放炮的地震观测系统优化可实现低成本、高效的地震采集。
|
图 18 双相黏弹VTI介质加密放炮后源向照明度 |
|
图 19 目标区加密炮前(黑色)、后(红色)目标层的源向照明度曲线对比 |
本文利用有限差分交错网格对双相黏弹VTI介质一阶速度-应力方程进行离散化,并对均匀模型、层状模型和Hess模型进行了波场数值模拟。由正演模拟结果可以看出,本文提出的方法所得到的波场特征体现了介质的双相性、黏弹性和各向异性。与单相弹性各向同性介质相比,在双相黏弹VTI介质中出现了慢纵波,且通过进一步深入分析可知,在固相分量和流相分量中慢纵波是反相波,而快纵波和转换横波同相波。从照明分析可以看出,地震波在单相弹性各向同性介质和双相黏弹VTI介质中的传播特征不同,介质的双相性和黏弹性导致地震波能量吸收衰减严重,介质的各向异性导致地震波能量分布不均匀。因此,在实际采集中需要考虑介质的属性才能针对目标区进行合理的观测系统设计。
附录A 二维双相黏弹各向异性介质的一阶速度-应力方程的推导首先取介质的任意单位正方形,则单位面积的动能可表示为
| $ \begin{aligned} T=& \frac{1}{2} \rho_{11}\left[\left(\frac{\partial u_{x}}{\partial t}\right)^{2}+\left(\frac{\partial u_{z}}{\partial t}\right)^{2}\right]+\\ & \rho_{12}\left(\frac{\partial u_{x}}{\partial t} \frac{\partial U_{x}}{\partial t}+\frac{\partial u_{z}}{\partial t} \frac{\partial U_{z}}{\partial t}\right)+\\ & \frac{1}{2} \rho_{22}\left[\left(\frac{\partial U_{x}}{\partial t}\right)^{2}+\left(\frac{\partial U_{z}}{\partial t}\right)^{2}\right] \end{aligned} $ | (A-1) |
耗散函数定义为
| $ \boldsymbol{G}=\frac{\boldsymbol{b}}{2}\left[\left(\frac{\partial u_{x}}{\partial x}-\frac{\partial U_{x}}{\partial x}\right)^{2}+\left(\frac{\partial u_{z}}{\partial z}-\frac{\partial U_{z}}{\partial z}\right)^{2}\right] $ | (A-2) |
| $ \boldsymbol{b}=\left(\begin{array}{cc} b_{11} & 0 \\ 0 & b_{33} \end{array}\right) $ | (A-3) |
如只考虑x方向,设qx表示沿x方向作用在单位体积元固体上的总应力,Qx表示沿x方向作用在单位体积元流体上的总应力,则
| $ \begin{aligned} q_{x} &=\frac{\partial}{\partial t}\left(\frac{\partial T}{\partial u_{x}}\right)+\frac{\partial G_{11}}{\partial u_{x}} \\ &=\frac{\partial^{2}}{\partial t^{2}}\left(\rho_{11} u_{x}+\rho_{12} U_{x}\right)+b_{11} \frac{\partial}{\partial t}\left(u_{x}-U_{x}\right) \end{aligned} $ | (A-4) |
| $ \begin{aligned} Q_{x} &=\frac{\partial}{\partial t}\left(\frac{\partial T}{\partial U_{x}}\right)+\frac{\partial G_{11}}{\partial U_{x}} \\ &=\frac{\partial^{2}}{\partial t^{2}}\left(\rho_{12} u_{x}+\rho_{22} U_{x}\right)-b_{11} \frac{\partial}{\partial t}\left(u_{x}-U_{x}\right) \end{aligned} $ | (A-5) |
qx和Qx也可以用下面的应力关系表示
| $ \left\{\begin{array}{l} q_{x}=\frac{\partial \sigma_{x x}}{\partial x}+\frac{\partial \sigma_{x z}}{\partial z} \\ Q_{x}=\frac{\partial S}{\partial x} \end{array}\right. $ | (A-6) |
由式(A-1)~式(A-6)可以得到x和z方向的运动平衡方程,分别为
| $ \left\{\begin{array}{l} \frac{\partial_{x x}}{\partial x}+\frac{\partial \sigma_{x x}}{\partial z}=\frac{\partial^{2}}{\partial t^{2}}\left(\rho_{11} u_{x}+\rho_{12} U_{x}\right)+b_{11} \frac{\partial}{\partial t}\left(u_{x}-U_{x}\right) \\ \frac{\partial S}{\partial x}=\frac{\partial^{2}}{\partial t^{2}}\left(\rho_{12} u_{x}+\rho_{22} U_{x}\right)-b_{11} \frac{\partial}{\partial t}\left(u_{x}-U_{x}\right) \end{array}\right. $ | (A-7) |
| $ \left\{\begin{array}{l} \frac{\partial \sigma_{x z}}{\partial x}+\frac{\partial \sigma_{z z}}{\partial z}=\frac{\partial^{2}}{\partial t^{2}}\left(\rho_{11} u_{z}+\rho_{12} U_{z}\right)+b_{33} \frac{\partial}{\partial t}\left(u_{z}-U_{z}\right) \\ \frac{\partial S}{\partial z}=\frac{\partial^{2}}{\partial t^{2}}\left(\rho_{12} u_{z}+\rho_{22} U_{z}\right)-b_{33} \frac{\partial}{\partial t}\left(u_{z}-U_{z}\right) \end{array}\right. $ | (A-8) |
将式(A-7)和式(A-8)的位移分量对时间求二阶偏导,再简化为速度对时间求的一阶偏导;其次,将时间一阶偏导简化为速度分量本身;最后,将式(A-7)和式(A-8)的固相空间导数减去流相空间导数,整理即可得到固相和流相速度分量。
对式(1)两边同时对时间求导,有
| $ \dot{\boldsymbol{\sigma}}=\dot{\boldsymbol{\psi}}(t) * \dot{\boldsymbol{e}}+\dot{\boldsymbol{A}} \dot{\theta} $ | (A-9) |
当模型为1个标准线性固体模型时,式(A-9)中的松弛系数可表示为
| $ \boldsymbol{\psi}(t)=\hat{\boldsymbol{C}}\left[1+\frac{{\tau}_{\mathfrak{\varepsilon}}^{(p)}}{\tau_{\sigma}} \exp \left(-\frac{t}{\tau_{\sigma}}\right)\right] H(t) \quad p=1,2 $ | (A-10) |
式中:H(t)为阶跃函数;
| $ \boldsymbol{C}=\left[\begin{array}{ccc} C_{11} & C_{13} & 0 \\ C_{13} & C_{33} & 0 \\ 0 & 0 & C_{44} \end{array}\right] $ | (A-11) |
通过该弹性刚度矩阵把
| $ {\hat C_{11}} = {C_{11}}{{\mathop{\rm Re}\nolimits} ^2}\left( {\sqrt {\frac{1}{{1 + \frac{{{\rm{i}}{\omega _0}{\tau _\sigma }}}{{1 + {\rm{i}}{\omega _0}{\tau _\sigma }}}\tau _\varepsilon ^{(1)}}}} } \right) $ | (A-12a) |
| $ \left\{ {\begin{array}{*{20}{l}} {{{\hat C}_{33}} = {C_{33}}{{{\mathop{\rm Re}\nolimits} }^2}\left( {\sqrt {\left. {\frac{1}{{1 + \frac{{{\rm{i}}{\omega _0}{\tau _\sigma }}}{{1 + {\rm{i}}{\omega _0}\tau _\sigma ^{(1)}}}}}} \right)} } \right.}\\ {{{\hat C}_{44}} = {C_{44}}{{{\mathop{\rm Re}\nolimits} }^2}\left( {\sqrt {\frac{1}{{1 + \frac{{{\rm{i}}{\omega _0}{\tau _\sigma }}}{{1 + {\rm{i}}{\omega _0}{\tau _\sigma }}}\tau _\varepsilon ^{(2)}}}} } \right)}\\ {{{\hat C}_{13}} = {{\hat C}_{33}}\sqrt {\left( {1 - \frac{{{{\hat C}_{44}}}}{{{{\hat C}_{33}}}}} \right)\left( {1 - \frac{{{{\hat C}_{44}}}}{{{{\hat C}_{33}}}} + 2\delta } \right)} - {{\hat C}_{44}}} \end{array}} \right. $ | (A-12b) |
式中:Re2(·)表示取实部的平方;
| $ \delta=\frac{\left(C_{13}+C_{44}\right)^{2}-\left(C_{33}-C_{44}\right)^{2}}{2 C_{33}\left(C_{33}-C_{44}\right)} $ | (A-13) |
将式(A-10)代入式(A-9)可得到
| $ \begin{aligned} \dot{\boldsymbol{\sigma}} &=\dot{\boldsymbol{\psi}}(t) * \dot{\boldsymbol{e}}+\boldsymbol{A} \dot{\theta} \\ &=\dot{\boldsymbol{\varPhi}} \dot{\boldsymbol{e}}-\frac{1}{\tau_{\sigma}}(\boldsymbol{\varPhi}-\hat{\boldsymbol{C}}) \mathrm{e}^{-t / \tau_{\sigma}} H(t) * \dot{\boldsymbol{e}}+\boldsymbol{A} \dot{\theta} \end{aligned} $ | (A-14) |
式中
| $ \boldsymbol{\varPhi}=\left[\begin{array}{ccc} \hat{C}_{11}\left[1+\tau_{\varepsilon}^{(1)}\right] & \left(\hat{C}_{13}+2 \hat{C}_{44}\right)\left[1+\tau_{\varepsilon}^{(1)}\right]-2 \hat{C}_{44}\left[1+\tau_{\varepsilon}^{(2)}\right] & 0 \\ \left(\hat{C}_{13}+2 \hat{C}_{44}\right)\left[1+\tau_{\varepsilon}^{(1)}\right]-2 \hat{C}_{44}\left[1+\tau_{\varepsilon}^{(2)}\right] & \hat{C}_{33}\left[1+\tau_{\varepsilon}^{(1)}\right] & 0 \\ 0 & 0 & 2 \hat{C}_{44}\left[1+\tau_{\varepsilon}^{(2)}\right] \end{array}\right] $ | (A-15) |
引入记忆变量E=(Exx,Ezz,Exz)T,有
| $ \boldsymbol{E}=-\frac{1}{\tau_{\sigma}}(\boldsymbol{\varPhi}-\hat{\boldsymbol{C}}) \mathrm{e}^{-t / \tau_{\sigma}} H(t) * \dot{\boldsymbol{e}} $ | (A-16) |
将式(A-16)代入式(A-14),可得到
| $ \dot{\boldsymbol{\sigma}}=\boldsymbol{\varPhi} \dot{\boldsymbol{e}}+\boldsymbol{E}+{\boldsymbol{A}} \dot{{\theta}} $ | (A-17) |
对式(2)求时间一阶偏导并结合式(A-17),可以得到固相和流相的应力分量(式(5)),然后再对记忆变量式(A-16)求时间偏导就可得到式(6),最终推导出双相黏弹VTI一阶速度-应力方程(式(4)~式(6))。
| [1] |
季玉新. 用地震资料检测裂缝性油气藏的方法[J]. 勘探地球物理进展, 2002, 25(5): 28-35. JI Yuxin. Detection of fractured reservoirs with seismic data[J]. Progress in Exploration Geophysics, 2002, 25(5): 28-35. |
| [2] |
牛滨华, 孙春岩. 黏弹性介质与地震波传播: 半无限空间各向同性[M]. 北京: 地质出版社, 2007.
|
| [3] |
杜启振, 王延光, 付水华. 方位各向异性粘弹性介质波场数值模拟[J]. 地球物理学进展, 2006, 21(2): 502-504. DU Qizhen, WANG Yanguang, FU Shuihua. Wavefield forward modeling with the pseudo-spectral method in viscoelastic and azimuthally anisotropic media[J]. Progress in Geophysics, 2006, 21(2): 502-504. DOI:10.3969/j.issn.1004-2903.2006.02.025 |
| [4] |
张智, 刘财, 邵志刚, 等. 伪谱法在常Q粘弹介质地震波场模拟中的应用效果[J]. 地球物理学进展, 2005, 20(4): 945-949. ZHANG Zhi, LIU Cai, SHAO Zhigang, et al. The application of pseudo-spectral forward modeling of seismic wave field in constant Q viscoelastic medium[J]. Progress in Geophysics, 2005, 20(4): 945-949. DOI:10.3969/j.issn.1004-2903.2005.04.010 |
| [5] |
曲英铭, 魏哲枫, 刘畅, 等. 面向高陡构造的黏声棱柱波逆时偏移[J]. 石油地球物理勘探, 2020, 55(4): 793-803. QU Yingming, WEI Zhefeng, LIU Chang, et al. Viscoacoustic reverse time migration of prismatic wave for steeply dipped structures[J]. Oil Geophysical Prospecting, 2020, 55(4): 793-803. |
| [6] |
Emmerich H, Korn M. Incorporation of attenuation into time-domain computations of seismic wave fields[J]. Geophysics, 1987, 52(9): 1252-1264. DOI:10.1190/1.1442386 |
| [7] |
Carcione J M, Dan K, Ronnie K. Viscoacoustic wave propagation simulation in the earth[J]. Geophysics, 1988, 53(6): 769-777. DOI:10.1190/1.1442512 |
| [8] |
Carcione J M. Wave propagation in anisotropic linear viscoelastic media: theory and simulated wavefields[J]. Geophysical Journal Internationa, 1990, 101(3): 739-750. DOI:10.1111/j.1365-246X.1990.tb05580.x |
| [9] |
Carcione J M, Behle A. Two-dimensional and three-dimensional forward modeling in isotropic-viscoelastic media[J]. SEG Technical Program Expanded Abstracts, 1989, 8: 1050-1053. |
| [10] |
蔡瑞乾, 孙成禹, 伍敦仕, 等. 黏声波动方程变机制数有限差分正演[J]. 石油地球物理勘探, 2019, 54(3): 529-538. CAI Ruiqian, SUN Chengyu, WU Dunshi, et al. Finite-difference numerical modeling with variable mechanisms for viscoacoustic wave equation[J]. Oil Geophysical Prospecting, 2019, 54(3): 529-538. |
| [11] |
毕玉英, 杨宝俊. 二维粘弹介质中完全波场正演模拟[J]. 石油地球物理勘探, 1995, 30(3): 351-362. BI Yuying, YANG Baojun. Forward modeling of full wave field in 2-D viscoelastic medium[J]. Oil Geophysical Prospecting, 1995, 30(3): 351-362. |
| [12] |
张中杰, 滕吉文, 贺振华. EDA介质中地震波速度、衰减与品质因子方位异性研究[J]. 中国科学E辑: 技术科学, 1999, 29(6): 3-5. ZHANG Zhongjie, TENG Jiwen, HE Zhenhua. Study on the azimuth anisotropy of seismic wave velocity, attenuation and quality factor in EDA medium[J]. Science in China(Series E), 1999, 29(6): 3-5. |
| [13] |
谭未一, 赵兵, 张中杰. 粘弹性VTI介质地震波模拟特征分析[J]. 地球物理学进展, 2007, 22(4): 1305-1311. TAN Weiyi, ZHAO Bing, ZHANG Zhongjie. The analysis of the wave field characteristics in viscoelastic VTI medium[J]. Progress in Geophysics, 2007, 22(4): 1305-1311. DOI:10.3969/j.issn.1004-2903.2007.04.041 |
| [14] |
朱峰, 黄建平, 李振春. 黏声VTI介质傅里叶有限差分叠前深度偏移[J]. 石油地球物理勘探, 2017, 52(5): 956-966. ZHU Feng, HUANG Jianping, LI Zhenchun. FFD prestack depth migration for visco-acoustic VTI me-dium[J]. Oil Geophysical Prospecting, 2017, 52(5): 956-966. |
| [15] |
王小杰, 栾锡武, 王延光, 等. 黏弹性介质叠前地震反演方法[J]. 石油地球物理勘探, 2016, 51(3): 544-555. WANG Xiaojie, LUAN Xiwu, WANG Yanguang, et al. Prestack seismic inversion of viscoelastic medium[J]. Oil Geophysical Prospecting, 2016, 51(3): 544-555. |
| [16] |
Ping P, Xu Y X, Zhang Y, et al. Seismic wave mode-ling in viscoelastic VTI media using spectral element method[J]. Earthquake Science, 2014, 27(5): 553-565. DOI:10.1007/s11589-014-0094-8 |
| [17] |
姚振岸, 孙成禹, 谢俊法, 等. 黏弹TTI介质旋转交错网格微地震波场模拟[J]. 石油地球物理勘探, 2017, 52(2): 253-263. YAO Zhen'an, SUN Chengyu, XIE Junfa, et al. Micro-seismic forward modeling in visco-elastic TTI media based on rotated staggered grid finite-difference method[J]. Oil Geophysical Prospecting, 2017, 52(2): 253-263. |
| [18] |
Biot A M. Generalized theory of acoustic propagation in porous dissipative media[J]. Journal of the Acoustical Society of America, 1962, 34(9A): 1254-1264. DOI:10.1121/1.1918315 |
| [19] |
田迎春. 层状黏弹性双相介质的动力响应与物性参数反演研究[D]. 北京: 北京交通大学, 2007.
|
| [20] |
王美霞. 双相及黏弹性介质中波传播方程的保辛算法及其波场模拟[D]. 北京: 清华大学, 2012.
|
| [21] |
韩颜颜. 双相粘弹EDA介质地震波场数值模拟与特征分析[D]. 吉林长春: 吉林大学, 2011.
|
| [22] |
陈生昌, 马在田, 吴如山. 波动方程双程地下方向照明分析[J]. 同济大学学报(自然科学版), 2007, 35(5): 681-684. CHEN Shengchang, MA Zaitian, WU Rushan. Two-way subsurface directional illumination analysis by wave equation[J]. Journal of Tongji University(Natural Science Edition), 2007, 35(5): 681-684. DOI:10.3321/j.issn:0253-374X.2007.05.022 |
| [23] |
Muerdter D, Ratcliff D. Understanding subsalt illumination through ray-trace modeling, Part 1:Simple 2-D salt models[J]. The Leading Edge, 2001, 20(6): 578-594. DOI:10.1190/1.1438998 |
| [24] |
Xie X B, Wu R S. Extracting angle domain information from migrated wavefield[C].SEG Technical Program Expanded Abstracts, 2002, 21: 1360-1363.
|
| [25] |
陈雪, 韩立国, 杨贺龙, 等. 粘弹VTI介质单程波正演模拟与照明分析[J]. 石油物探, 2015, 54(6): 643-651. CHEN Xue, HAN Liguo, YANG Helong, et al. One-way wave equation forward modeling and illumination analysis in viscoelastic VTI media[J]. Geophysical Prospecting for Petroleum, 2015, 54(6): 643-651. DOI:10.3969/j.issn.1000-1441.2015.06.002 |
| [26] |
裴正林. 波动方程地震定向照明分析[J]. 石油地球物理勘探, 2008, 43(6): 645-651. PEI Zhenglin. Analysis on wave equation seismic directional illumination[J]. Oil Geophysical Prospecting, 2008, 43(6): 645-651. DOI:10.3321/j.issn:1000-7210.2008.06.006 |
| [27] |
Xie X, Yang H. A full-wave equation based seismic illumination analysis method[C].Extended Abstracts of 70th EAGE Conference & Exhibition, 2008, 284-288.
|
| [28] |
Yang H, Xie X B, Luo M, et al. Target oriented full-wave equation based illumination analysis[C].SEG Technical Program Expanded Abstracts, 2008, 27: 2216-2220.
|
| [29] |
皮红梅. 双程波动方程数值模拟和照明分析方法研究[D]. 吉林长春: 吉林大学, 2009.
|
| [30] |
李金丽, 刘建勋, 姜春香, 等. 黏声VTI介质正演模拟与照明分析[J]. 石油地球物理勘探, 2017, 52(5): 906-914. LI Jinli, LIU Jianxun, JIANG Chunxiang, et al. Forward modeling and illumination analysis in visco-acoustic VTI media[J]. Oil Geophysical Prospecting, 2017, 52(5): 906-914. |
| [31] |
Robertsson J O A, Blanch J O. Viscoelastic finite-diffe-rence modeling[J]. Geophysics, 1994, 59(9): 1444-1456. DOI:10.1190/1.1443701 |
| [32] |
Berryman J G. Confirmation of Biot's theory[J]. Applied Physics Letters, 1980, 37(4): 382-384. DOI:10.1063/1.91951 |
| [33] |
董良国, 吴晓丰, 唐海忠, 等. 逆掩推覆构造的地震波照明与观测系统优化[J]. 石油物探, 2006, 45(1): 40-47. DONG Liangguo, WU Xiaofeng, TANG Haizhong, et al. Seismic wave illumination for overthrust nappe structures and seismic survey design[J]. Geophysical Prospecting for Petroleum, 2006, 45(1): 40-47. |
| [34] |
王德利, 雍运动, 韩立国, 等. 三维粘弹介质地震波场有限差分并行模拟[J]. 西北地震学报, 2017, 52(1): 30-34. WANG Deli, YONG Yundong, HAN Liguo, et al. Parallel simulation of finite difference for seismic wavefield modeling in 3-D viscoelastic media[J]. Northwestern Seismological Journal, 2017, 52(5): 906-914. |



 曲英铭, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
曲英铭, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: 