② 青岛国家海洋科学与技术实验室, 山东青岛 266100;
③ 中国海洋大学海底科学与探测技术教育部重点实验室, 山东青岛 266100
② Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266100, China;
③ Key Lab of Submarine Geosciences and Prospecting Techniques, MOE, Ocean University of China, Qingdao, Shandong 266100, China
地震波正演模拟技术是研究地震波传播规律的有效手段,并在地震勘探的采集、处理以及反演等各个环节中都有着广泛的应用。地震波正演模拟必须引入人工边界界定计算区域,而人工边界的处理不当,往往会产生虚假反射污染中心波场,从而降低波场模拟的精度,因而人工边界的处理一直是波动方程数值计算的重要研究内容。
当前的人工边界处理方法主要有三类。第一类是衰减边界方法[1-3]。该类方法是在靠近边界处引入一个衰减区,在衰减区内地震波传播遵循阻尼波动方程,能量按指数衰减。由于该类方法存在阻尼因子难以确定、计算量大和内存消耗较大等问题,因此应用较少。第二类是完全匹配层(PML)方法。该类方法由Berenger[4]在电磁波数值模拟中首先提出,通过在中心波场计算区域外加上一系列的吸收层、层内引入衰减因子以达到消除边界反射的目的。王守东[5]、Hastings等[6]、Collino等[7]将PML法成功应用于声波和弹性波正演模拟。随后,Komatitsch等[8-9]、熊章强等[10]实现了非分裂PML法;罗玉钦等[11]、杨茜娜等[12]发展了复频移及多轴复频移PML法;陈可洋[13]和Wang等[14]提出了基于余弦型和基于高斯型衰减函数的PML方法。PML法现已在地震波数值模拟中获得广泛应用,然而为达到更好的吸收效果,PML法往往需要设计几十甚至上百个匹配层,意味着巨大的计算量和内存消耗,严重限制了该方法在大规模波场模拟中的应用。第三类为基于单程波近似的吸收边界条件。该类方法由Enguist等[15-16]首先提出;Higdon[17-19]提出了一种与其等价的渐进吸收边界条件,可以设计吸收任意角度的入射波,显著提升了吸收精度和适应性。然而由于单程波的高阶近似会导致边界条件方程中出现高阶的混合时间、空间偏导数项,给数值求解带来困难,因此常规方法多采用二阶边界条件,但对大角度入射波的吸收效果较差,其整体吸收效果也难以满足高精度数值模拟的要求。为进一步提升基于单程波近似的吸收边界条件的效果,宋鹏等[20-21]发展了优化系数的四阶吸收边界条件算法。Baffet等[22]、Hagstrom等[23]以及Potter等[24]也通过引入辅助变量实现了高阶吸收边界条件,但这些算法同样存在计算过程复杂且计算效率低等问题。
为提升常规基于单程波近似的吸收边界条件的效果,在不提高阶数的前提下,Liu等[25]提出了一种混合吸收边界条件。该方法在中心波场与边界之间增加一个过渡区域,通过线性加权使过渡区域内双程波波场与单程波波场平滑过渡,最终实现了人工边界的高效吸收。随后,Liu等[26-27]、任志明等[28]以及Liu等[29]实现了三维声波及弹性波正演模拟中的混合吸收边界,Ren等[30]将混合吸收边界推广到频率域数值模拟中,取得了较好的吸收效果。刘学义等[31]将混合吸收边界用于各向异性介质,Wang等[32]、薛浩等[33]分别将混合吸收边界应用于逆时偏移和最小二乘逆时偏移。
当前混合吸收边界已在地震波场正反演延拓中得到广泛应用,然而,该方法的加权系数仍以线性和指数型[34]为主,未能兼顾内边界和外边界的综合吸收效果,在吸收效率上并没有达到最优;此外,当前大规模的波场模拟往往借助于GPU并行提高计算效率,但混合吸收边界差分格式的GPU加速效率远远低于中心波场,严重影响了整个波场模拟的计算效率。本文提出一种基于高斯型加权系数的混合吸收边界条件方法,其更能兼顾内、外吸收边界的吸收效果,具有更高效的整体边界吸收效率;同时本文还推导了一种更适用于GPU加速的一阶Higdon混合吸收边界条件差分格式,可显著提升边界计算的GPU并行效率。
1 基于高斯型加权系数的混合吸收边界条件 1.1 弹性波数值模拟中混合吸收边界原理二维空间中的一阶速度—应力弹性波方程[35]可以表示为
| $ \left\{ {\begin{array}{*{20}{l}} {\rho \frac{{\partial {v_x}}}{{\partial t}} = \frac{{\partial {\sigma _{xx}}}}{{\partial x}} + \frac{{\partial {\sigma _{xz}}}}{{\partial z}}}\\ {\rho \frac{{\partial {v_z}}}{{\partial t}} = \frac{{\partial {\sigma _{{\rm{zx}}}}}}{{\partial z}} + \frac{{\partial {\sigma _{xx}}}}{{\partial x}}}\\ {\frac{{\partial {\sigma _{xx}}}}{{\partial t}} = (\lambda + 2\mu )\frac{{\partial {v_x}}}{{\partial x}} + \lambda \frac{{\partial {v_z}}}{{\partial z}}}\\ {\frac{{\partial {\sigma _{{\rm{zr }}}}}}{{\partial t}} = \lambda \frac{{\partial {v_x}}}{{\partial x}} + (\lambda + 2\mu )\frac{{\partial {v_z}}}{{\partial z}}}\\ {\frac{{{\partial _{{\sigma _{xz}}}}}}{{\partial t}} = \mu \left( {\frac{{\partial {v_z}}}{{\partial x}} + \frac{{\partial {v_x}}}{{\partial z}}} \right)} \end{array}} \right. $ | (1) |
式中:vx、vz分别为水平方向和垂直方向波场速度分量;σxx、σzz、σxz为三个应力分量;ρ为密度,λ和μ为拉梅系数,与纵波速度VP和横波速度VS关系为
| $ {{V_{\rm{P}}} = \sqrt {(\lambda + 2\mu )/\rho } } $ | (2) |
| $ {{V_{\rm{S}}} = \sqrt {\mu /\rho } } $ | (3) |
| $ {U_{i, j}^{k + 1/2} = U_{i, j}^{k - 1/2} + \frac{1}{{{\rho _{i, j}}}}\frac{{\Delta t}}{{\Delta x}}\sum\limits_{m = 1}^N {{a_m}} \left( {P_{i + m - 1/2, j}^k - P_{i - m + 1/2, j}^k} \right) +\\\;\;\;\;\;\; \frac{1}{{{\rho _{i, j}}}}\frac{{\Delta t}}{{\Delta z}}\sum\limits_{m = 1}^N {{a_m}} \left( {R_{i, j + m - 1/2}^k - R_{i, j - m + 1/2}^k} \right)} $ | (4) |
| $ \begin{array}{l} W_{i + 1/2, j + 1/2}^{k + 1/2} = W_{i + 1/2, j + 1/2}^{k - 1/2} + \frac{1}{{{\rho _{i + 1/2, j + 1/2}}}}\frac{{\Delta t}}{{\Delta x}}\sum\limits_{m = 1}^N {{a_m}} \left( {R_{i + m, j + 1/2}^k - R_{i - m + 1, j + 1/2}^k} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{1}{{{\rho _{i + 1/2, j + 1/2}}}}\frac{{\Delta t}}{{\Delta z}}\sum\limits_{m = 1}^N {{a_m}} \left( {Q_{i + 1/2, j + m}^k - Q_{i + 1/2, j - m + 1}^k} \right) \end{array} $ | (5) |
| $ \begin{array}{l} P_{i + 1/2, j}^{k + 1} = P_{i + 1/2, j}^k + \left( {{\lambda _{i, j}} + 2{\mu _{i, j}}} \right)\frac{{\Delta t}}{{\Delta x}}\sum\limits_{m = 1}^N {{a_m}} \left( {U_{i + m, j}^{k + 1/2} - U_{i - m + 1.j}^{k + 1/2}} \right) + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{\lambda _{i, j}}\frac{{\Delta t}}{{\Delta z}}\sum\limits_{m = 1}^N {{a_m}} \left( {W_{i + 1/2, j + m - 1/2}^{k + 1/2} - W_{i + 1/2, j - m + 1/2}^{k + 1/2}} \right) \end{array} $ | (6) |
| $ \begin{array}{l} Q_{i + 1/2, j}^{k + 1} = Q_{i + 1/2, j}^k + {\lambda _{i, j}}\frac{{\Delta t}}{{\Delta x}}\sum\limits_{m = 1}^N {{a_m}} \left( {U_{i + m, j}^{k + 1/2} - U_{i - m + 1, j}^{k + 1/2}} \right) + \left( {{\lambda _{i, j}} + 2{\mu _{i, j}}} \right) \times \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\Delta t}}{{\Delta z}}\sum\limits_{m = 1}^N {{a_m}} \left( {W_{i + 1/2, j + m - 1/2}^{k + 1/2} - W_{i + 1/2, j - m + 1/2}^{k + 1/2}} \right) \end{array} $ | (7) |
| $ \begin{array}{l} R_{i, j + 1/2}^{k + 1} = R_{i, j + 1/2}^k + {\mu _{i, j + 1/2}}\frac{{\Delta t}}{{\Delta x}}\sum\limits_{m = 1}^N {{a_m}} \left( {W_{i + m - 1/2, j + 1/2}^{k + 1/2} - W_{i - m + 1/2, j + 1/2}^{k + 1/2}} \right) + \\ {\mu _{i, j + 1/2}}\frac{{\Delta t}}{{\Delta z}}\sum\limits_{m = 1}^N {{a_m}} \left( {U_{i, j + m}^{k + 1/2} - U_{i, j - m + 1}^{k + 1/2}} \right) \end{array} $ | (8) |
式中:U和W分别表示速度分量vx、vz的离散形式;P、Q和R分别表示应力分量σxx、σzz、σxz的离散形式;Δt、Δx、Δz分别为离散的时间步长、空间水平和垂直网格间隔;i、j、k为空间和时间离散序号;2N为差分阶次;am(1≤m≤N)为差分系数,可通过求解下式方程获取[38]
| $ \left[ {\begin{array}{*{20}{c}} {{1^1}}&{{3^1}}& \cdots &{{{(2N - 1)}^1}}\\ {{1^3}}&{{3^3}}& \cdots &{{{(2N - 1)}^3}}\\ {}&{}& \vdots &{}\\ {{1^{2N - 1}}}&{{3^{2N - 1}}}& \cdots &{{{(2N - 1)}^{2N - 1}}} \end{array}} \right] \cdot \left[ {\begin{array}{*{20}{c}} {{a_1}}\\ {{a_2}}\\ \vdots \\ {{a_N}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1\\ 0\\ \vdots \\ 0 \end{array}} \right] $ | (9) |
应用混合吸收边界方法进行数值模拟时,整个计算区域被划分为中心波场区域Ⅰ、边界过渡区域Ⅱ以及边界区Ⅲ三部分(图 1),其波场计算流程如下:

|
图 1 二维混合吸收边界条件示意图 |
(1) 首先,基于双程波方程计算区域Ⅰ+区域Ⅱ的波场各分量的双程波场值ut=(vxt、vzt、σxxt、σzzt、σxzt)T;
(2) 对于区域Ⅱ和区域Ⅲ,依据单程波方程分别计算速度分量和应力分量的单程波场值u。=(vx。、vz。、σxx。、σzz。、σxz。)T;
(3) 对于M层区域Ⅱ,对双程波场值和单程波场值进行加权求和得到混合波场
| $ {\mathit{\boldsymbol{u}}_l} = \left( {1 - {w_l}} \right){\mathit{\boldsymbol{u}}^{\rm{t}}} + {w_l}\mathit{\boldsymbol{u}}^\circ \;\;\;\;\;\;\;l = 1,2, \cdots ,M $ | (10) |
式中wl为加权系数。
而对于区域Ⅱ和区域Ⅲ的单程波场计算,由于二阶Higdon吸收边界条件稳定性较差,通常采用改进的一阶Higdon吸收边界条件[28],其左边界方程为
| $ \left( {\beta \frac{\partial }{{\partial t}} - {V_{\rm{P}}}\frac{\partial }{{\partial x}}} \right)\mathit{\boldsymbol{u}} = 0 $ | (11) |
式中β=(VP+VS)/(2VS)。定义作用于u上的二维空间和时间平移算子Ex1、Et1以及恒等映射算子I为
| $ \left\{ {\begin{array}{*{20}{l}} {E_x^1\mathit{\boldsymbol{u}}_{i, j}^k = \mathit{\boldsymbol{u}}_{i + 1, j}^k}\\ {E_t^1\mathit{\boldsymbol{u}}_{i, j}^k = \mathit{\boldsymbol{u}}_{i, j}^{k + 1}}\\ {I\mathit{\boldsymbol{u}}_{i, j}^k = \mathit{\boldsymbol{u}}_{i, j}^k} \end{array}} \right. $ | (12) |
则可将一阶Higdon左边界算子表示为[19]
| $ {D^{1{\rm{st}}}}\left( {E_x^1, E_t^{ - 1}} \right) = I + {q_x}E_x^1 + {q_t}E_t^{ - 1} + {q_{xt}}E_x^1E_t^{ - 1} $ | (13) |
其差分格式为
| $ \mathit{\boldsymbol{u}}_{i, j}^{k + 1} = - {q_x}\mathit{\boldsymbol{u}}_{i + 1, j}^{k + 1} - {q_t}\mathit{\boldsymbol{u}}_{i, j}^k - {q_{xt}}\mathit{\boldsymbol{u}}_{i + 1, j}^k $ | (14) |
式中与空间位置和网格剖分相关的常量为[19]
| $ {{q_x} = \frac{{b\left( {\beta + {V_{\rm{P}}}\frac{{\Delta t}}{{\Delta x}}} \right) - {V_{\rm{P}}}\frac{{\Delta t}}{{\Delta x}}}}{{(1 - b)\left( {\beta + {V_{\rm{P}}}\frac{{\Delta t}}{{\Delta x}}} \right)}}} $ | (15) |
| $ {{q_t} = \frac{{b\left( {\beta + {V_{\rm{P}}}\frac{{\Delta t}}{{\Delta x}}} \right) - \beta }}{{\left( {\beta + {V_{\rm{P}}}\frac{{\Delta t}}{{\Delta x}}} \right)(1 - b)}}} $ | (16) |
| $ {{q_{xt}} = \frac{b}{{b - 1}}} $ | (17) |
其中b为常数,通常取值为0.5。
混合边界的角点区域需做特殊处理,以左上角速度水平分量为例,其角点差分格式为
| $ \begin{array}{l} U_{0, 0}^{k + 1/2} = - 0.5{q_x}\left( {U_{1, 0}^{k + 1/2} + U_{0, 1}^{k + 1/2}} \right) - {q_t}U_{0, 0}^{k - 1/2} - \\ \;\;\;\;\;\;\;\;\;\;\;\;0.5{q_n}\left( {U_{1, 0}^{k - 1/2} + U_{0, 1}^{k - 1/2}} \right) \end{array} $ | (18) |
混合边界通过引入过渡区实现波场混叠压制边界反射,过渡区与中心波场相邻的边界可称为内边界,过渡区的最外层边界可称为外边界,混合边界的残余反射通常来自于内边界和外边界反射。内、外边界的残余反射能量可通过混合加权系数的选取进行调整,常用的线性加权系数和指数型加权系数[34]分别为
| $ w_l^{\rm{L}} - \frac{{1 + (l - 1)}}{M} $ | (19) |
| $ w_l^{\rm{E}} = 1 - {\left( {\frac{{M - l + 1}}{M}} \right)^{(1.0 + 0.15M)}} $ | (20) |
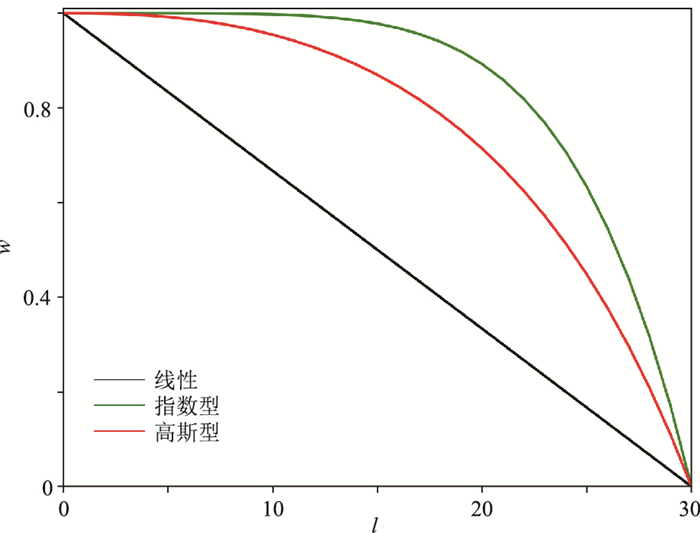
线性加权系数(图 2黑线所示)在内、外边界处梯度变化相同,而由于内边界更靠近内部波场,因此应用线性加权系数的混合边界其通常会产生较强的内边界反射;指数型加权系数(图 2绿线所示)在内边界处变化更加缓慢,使内边界与中心波场区域得到更好的耦合,因此其内边界残余反射得到有效压制,但另一方面,由于其在内边界处的变化过于缓慢导致外边界处的变化过于剧烈,从而易产生较强的外边界反射。因此一个更为理想的混合边界条件必须全面考虑地震波在内、外边界处的综合边界反射压制效果。
|
图 2 线性、指数型、高斯型加权系数变化曲线 |
鉴于以上分析,本文提出了一种高斯型混合加权系数
| $ w_l^{\rm{G}} = 2 - \exp \left[ {\ln 2{{\left( {\frac{{M - l + 1}}{M}} \right)}^a}} \right] $ | (21) |
式中α为高斯型权系数的阶数,控制内、外边界处的变化率。大量的实验证明,当α=2.5时,高斯型混合边界既能保持稳定性,又可达到良好的边界吸收效果。
高斯型加权系数(图 2红线)在内边界处梯度变化虽然比指数型加权系数稍显剧烈,但其较线性加权系数已更为平缓;而外边界处,高斯型加权系数又比指数型加权系数更平缓,较线性加权系数稍剧烈,因此理论上其应有更优的内、外边界残余反射综合压制效果。
当然,采用混合吸收边界时,整个边界的吸收效果还与过渡区层数有关,Liu等[27]证明了当过渡区厚度较小时,混合边界易不稳定,并且考虑到为追求更高精度的波场模拟效果,当前数值模拟时通常大多采用20层以上的混合吸收边界。因此本文将以20层和30层为例讨论高斯型混合加权系数的吸收效果。
1.3 常速模型数值模拟实验为验证本文提出的高斯型混合吸收边界条件的吸收效果,本文设计3200m×3200m、VP=4000m/s、VS=2000m/s、ρ= 2100kg/m3的均匀介质模型。纵、横向空间网格间距均为8m,时间步长为1ms,差分格式精度为空间10阶。震源位于模型中心,采用主频为25Hz的Ricker子波加载于速度垂直分量上,记录长度为2s。
应用20层混合吸收边界得到1s时刻的vx、vz分量波前快照如图 3所示,波前快照的水平和垂直切片(位置见图 3红色虚线)如图 4所示。应用30层混合吸收边界得到1s时刻的vx、vz分量波前快照如图 5所示,波前快照的水平和垂直切片(位置见图 5红色虚线)如图 6所示。

|
图 3 20层混合吸收边界不同加权系数的1s时刻vx分量(a)、vz分量(b)波场模拟快照对比 左:线性;中:指数型;右:高斯型 |
|
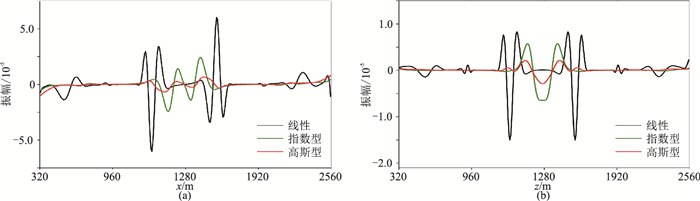
图 4 20层混合吸收边界不同加权系数的1s时刻vx分量(a)、vz分量(b)波场模拟切片对比 |

|
图 5 30层混合吸收边界不同加权系数的1s时刻vx分量(a)、vz分量(b)波场模拟快照对比 左:线性;中:指数型;右:高斯型 |

|
图 6 30层混合吸收边界不同加权系数的1s时刻vx分量(a)、vz分量(b)波场模拟切片对比 |
由图 3~图 6可见,无论是20层还是30层吸收边界,对于vx、vz分量,线性加权系数其波前快照中仍存在较强的内边界残余反射(图 3左、图 5左箭头所示),指数型加权系数其波前快照中则存在着明显的外边界残余反射(图 3中、图 5中箭头所示),而高斯型加权系数的波前快照中无明显边界残余反射波。
2 适用于GPU加速的一阶Higdon混合吸收边界条件差分格式当前大规模的波场模拟往往借助于GPU并行提高计算效率。但应用于大规模波场模拟的混合边界差分格式的GPU加速比远远低于中心波场计算的GPU加速比,严重影响了整个波场模拟的计算效率。本文推导了一种新的混合边界差分计算格式,可显著提高边界计算的GPU加速比。
2.1 适用于GPU并行的混合吸收边界差分格式由式(14)可知,基于常规混合吸收边界差分格式进行GPU并行时,由于每层边界上k+1时刻的波场值计算都要用到该层内侧点k+1时刻的波场值,所以应用GPU计算边界时无法同时启动大量的线程实现边界各点值的同时计算,无法实现高效的GPU并行。为了解决常规边界差分格式中需要由内向外依次计算、无法实现GPU高效并行的问题,本文推导了一种新的边界条件差分格式,具体推导过程如下(以左边界和左上角点为例)。
为避免边界区域计算时,差分格式的右侧不出现k+1时刻项,将时间偏导数和水平方向空间偏导数分别表示为
| $ {\frac{\partial }{{\partial t}} = \frac{{I - E_t^{ - 1}}}{{\Delta t}}} $ | (22) |
| $ {\frac{\partial }{{\partial x}} = \frac{{E_t^{ - 1}\left( {E_x^1 - I} \right)}}{{\Delta x}}} $ | (23) |
则可将一阶Higdon边界算子表示为
| $ \begin{array}{l} {D^{{\rm{new}}}}\left( {E_x^1, E_t^{ - 1}} \right) = \beta \frac{{1 - E_t^{ - 1}}}{{\Delta t}} - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{V_{\rm{P}}}\frac{{E_t^{ - 1}\left( {E_x^1 - I} \right)}}{{\Delta x}} \end{array} $ | (24) |
当Dnew(Ex1,Et-1)u=0时,可实现左边界区域对波场u的吸收,其差分格式为
| $ \mathit{\boldsymbol{u}}_{i, j}^{k + 1} = \mathit{\boldsymbol{u}}_{i + 1, j}^k + \frac{{\Delta t{V_{\rm{P}}}}}{{\beta \Delta x}}\left( {\mathit{\boldsymbol{u}}_{i + 1, j}^k - \mathit{\boldsymbol{u}}_{i, j}^k} \right) $ | (25) |
对于左上角点,可通过上边界和左边界的加权平均得到
| $ \mathit{\boldsymbol{u}}_{0, 0}^{k + 1} = 0.5\left( {\mathit{\boldsymbol{u}}_{1, 0}^k + \mathit{\boldsymbol{u}}_{0, 1}^k} \right) + 0.5\left[ {\frac{{\Delta t{V_{\rm{P}}}}}{{\beta \Delta x}}\left( {\mathit{\boldsymbol{u}}_{1, 0}^k - \mathit{\boldsymbol{u}}_{0, 0}^k} \right) + } \right.\left. {\frac{{\Delta t{V_{\rm{P}}}}}{{\beta \Delta z}}\left( {\mathit{\boldsymbol{u}}_{0, 1}^k - \mathit{\boldsymbol{u}}_{0, 0}^k} \right)} \right] $ | (26) |
对比式(14)与式(25)可知,当计算k+1时刻波场值时,本文推导的差分格式只需用到已计算出的k时刻波场值,因此同一时间切片内所有网格点可同时计算,能实现GPU的高效并行加速。
在常规混合吸收边界算法中,由于第l层边界计算与第l+1层边界计算存在计算先后顺序关系,过渡区Ⅱ中的混合波场计算需要由最内侧开始逐层向外进行,因此同一时间层内,前者需多次启动边界计算核函数(与边界层数相当),且每次核函数只能计算本吸收层内的网格点数,严重降低了GPU的加速效率。基于本文差分格式的混合吸收边界算法,只需一次启动和计算边界计算核函数,可实现所有吸收层内的所有网格点的同时计算,更适合于大规模波场模拟的GPU高效并行计算。
2.2 常速模型数值实验应用上述均匀模型和模拟参数,验证本文推导的混合吸收边界差分格式的正确性。20、30层常规差分格式与本文差分格式vx、vz分量波前快照如图 7、图 8所示。

|
图 7 不同边界差分格式的20层混合吸收边界数值模拟的0.6(左)、1.0(中)和1.4s(右)时刻波前快照对比 (a)常规差分格式vx分量;(b)常规差分格式vz分量;(c)本文差分格式vx分量;(d)本文差分格式vz分量 |

|
图 8 不同边界差分格式30层混合吸收边界数值模拟的0.6(左)、1.0(中)和1.4s(右)时刻波前快照对比 (a)常规差分格式vx分量;(b)常规差分格式vz分量;(c)本文差分格式vx分量;(d)本文差分格式vz分量 |
由图 7、图 8可以看出,在边界层数相同的条件下,两种差分格式的混合吸收边界均能有效压制边界反射。
为评估两种差分格式的计算效率,本文基于RTX-2080Ti-11GB的GPU应用上述均匀模型进行测试,结果如表 1所示。
|
|
表 1 两种边界差分格式正演模拟计算效率对比 |
由表 1可见,若采用20层边界,本文边界差分格式计算效率为常规差分格式3.25倍;若采用30层边界,本文边界差分格式计算效率为常规差分格式4.34倍,因此本文差分格式更适于大规模波场模拟的GPU高效并行计算。
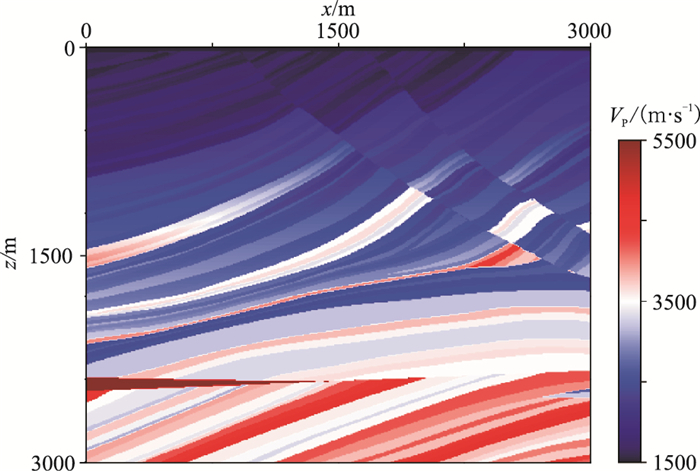
3 复杂模型实验本文截取了Marmousi模型的一部分(图 9)进行正演模拟测试。该模型尺寸为3000m×3000m,纵横波速比为1.73,常密度为2100kg/m3。数值模拟中,横向和纵向网格间隔分别为5m和4m,时间步长为0.4ms。震源采用加载于vz分量上、主频为25Hz的Ricker子波,位于(1500m,4m)处。
|
图 9 部分Marmousi纵波速度模型 |
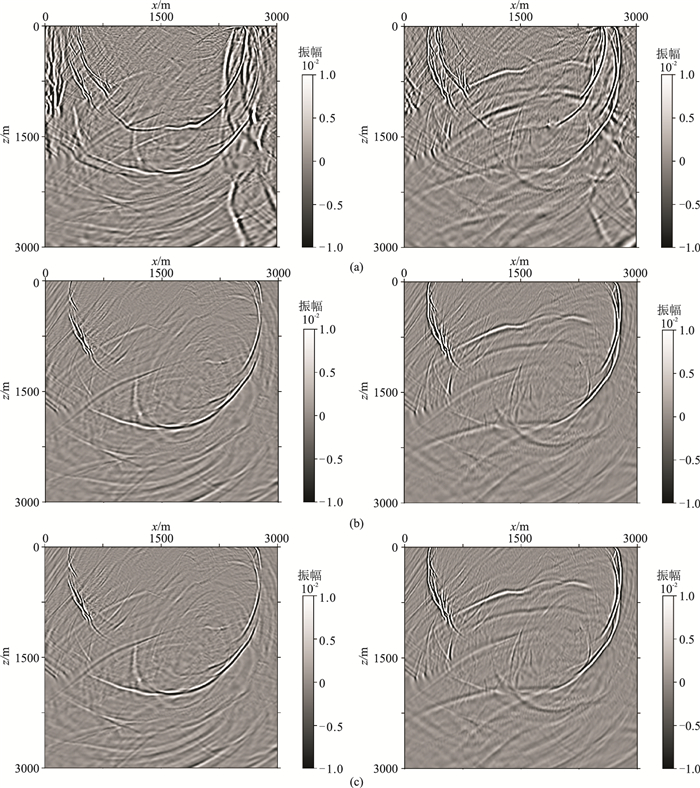
未加吸收边界、常规差分格式的高斯型混合吸收边界(30层)和本文差分格式的高斯型混合吸收边界(30层)模拟的1.4s时vx、vz分量的波前快照如图 10所示。由图可见,未加吸收边界的波场中有明显的强边界反射,而无论采用常规边界差分格式还是本文差分格式的30层混合吸收边界,均可有效吸收边界反射,表明基于高斯型混合加权吸收边界能够适应于复杂构造模型的边界处理。
|
图 10 Marmousi模型不同边界模拟的1.5s时刻的vx分量(左)、vz分量(右)波场快照 (a)不加边界;(b)常规差分格式的高斯型混合吸收边界;(c)本文差分格式的高斯型混合吸收边界 |
基于单卡GPU(型号:RTX-2080Ti-11GB),常规差分格式的高斯型混合吸收边界的部分Mar-mousi模型计算时间为16.6335s,本文差分格式计算时间为5.3510s,可见本文差分格式的计算效率是常规格式的3倍以上,说明本文的边界差分格式更适合大规模数值模拟的GPU高效并行。
4 结论本文在系统分析线性混合边界和指数型混合边界残余反射形成机制的基础上,提出了一种能兼顾内外边界吸收效果的高斯型混合吸收边界条件。在此基础上,推导了更适用于GPU加速的一阶Higdon混合吸收边界条件差分格式及相应的角点计算差分格式。模型实验结果表明,高斯型混合吸收边界能更有效地压制内边界和外边界反射,比线性和指数型混合吸收边界具有更高的吸收效率,适用于复杂构造模型的边界处理;本文推导的边界及其角点的边界差分格式,GPU并行的计算效率更高,更适用于大规模弹性波场数值模拟。
将本文提出的混合吸收边界算法推广至三维弹性波数值模拟及逆时偏移和全波形反演,是今后的研究方向。
十分感谢中国海洋大学地球探测软件技术研发团队提供了资金和软、硬件支持,以及团队成员提供了建设性意见。
| [1] |
Israeli M, Orszag, S A. Approximation of radiation boundary conditions[J]. Journal of Computational Physics, 1981, 41(1): 115-135. DOI:10.1016/0021-9991(81)90082-6 |
| [2] |
Cerjan C, Kosloff R, Reshef M. A nonreflecting boundary condition for discrete acoustic and elastic wave equations[J]. Geophysics, 1985, 50(4): 705-708. DOI:10.1190/1.1441945 |
| [3] |
Kosloff R, Kosloff D. Absorbing boundaries for wave propagation problems[J]. Journal of Computational Physics, 1986, 63(2): 363-376. DOI:10.1016/0021-9991(86)90199-3 |
| [4] |
Berenger J P. A perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Computational Physics, 1994, 114(2): 185-200. DOI:10.1006/jcph.1994.1159 |
| [5] |
王守东. 声波方程完全匹配层吸收边界[J]. 石油地球物理勘探, 2003, 38(1): 31-34. WANG Shoudong. Absorbing boundary condition for acoustic wave equation by perfectly matched layer[J]. Oil Geophysical Prospecting, 2003, 38(1): 31-34. DOI:10.3321/j.issn:1000-7210.2003.01.007 |
| [6] |
Hastings F D, Schneider J B, Broschat S L. Application of the perfectly matched layer (PML) absorbing boundary condition to elastic wave propagation[J]. The Journal of the Acoustical Society of America, 1996, 100(5): 3061-3069. DOI:10.1121/1.417118 |
| [7] |
Collino F, Tsogka C. Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media[J]. Geophysics, 2001, 66(1): 294-307. DOI:10.1190/1.1444908 |
| [8] |
Komatitsch D, Martin R. An unsplit convolutional perfectly matched layer improved at grazing incidence for the seismic wave equation[J]. Geophysics, 2007, 72(5): SM155-SM167. DOI:10.1190/1.2757586 |
| [9] |
Martin R, Komatitsch D. An unsplit convolutional perfectly matched layer technique improved at grazing incidence for the viscoelastic wave equation[J]. Geophysical Journal International, 2009, 179(1): 334-344. |
| [10] |
熊章强, 毛承英. 声波数值模拟中改进的非分裂式PML边界条件[J]. 石油地球物理勘探, 2011, 46(1): 35-39. XIONG Zhangqiang, MAO Chengying. Improved unsplit PML boundary conditions in acoustic wave numerical simulation[J]. Oil Geophysical Prospecting, 2011, 46(1): 35-39. |
| [11] |
罗玉钦, 刘财. 多轴复频移近似完全匹配层弹性波模拟[J]. 石油地球物理勘探, 2019, 54(5): 1024-1033. LUO Yuqin, LIU Cai. Multi-axial complex-frequency shifting nearly perfectly matched layer for seismic forward modeling in elastic media[J]. Oil Geophysical Prospecting, 2019, 54(5): 1024-1033. |
| [12] |
杨茜娜, 张伟. 复频移完全匹配层在复杂速度模型中的应用[J]. 石油地球物理勘探, 2020, 55(6): 1271-1281. YANG Xina, ZHANG Wei. Application of CFS-PML in complex velocity models[J]. Oil Geophysical Prospecting, 2020, 55(6): 1271-1281. |
| [13] |
陈可洋. 完全匹配层吸收边界条件研究[J]. 石油物探, 2010, 49(5): 472-477. CHEN Keyang. Study on perfectly matched layer absorbing boundary condition[J]. Geophysical Prospecting for Petroleum, 2010, 49(5): 472-477. DOI:10.3969/j.issn.1000-1441.2010.05.006 |
| [14] |
Wang H X, Wang H X. A study of damping factors in perfectly matched layers for the numerical simulation of seismic waves[J]. Applied Geophysics, 2013, 10(1): 63-77. DOI:10.1007/s11770-013-0361-9 |
| [15] |
Enquist B, Madja A. Absorbing boundary conditions for the numerical simulation of waves[J]. Applied Mathematical Sciences, 1977, 74(5): 1765-1766. |
| [16] |
Clayton R, Engquist B. Absorbing boundary conditions for acoustic and elastic wave equations[J]. Bulletin of the Seismological Society of America, 1977, 67(6): 1529-1540. |
| [17] |
Higdon R L. Absorbing boundary conditions for diffe-rence approximations to the multidimensional wave equation[J]. Mathematics of Computation, 1986, 47(176): 437-459. |
| [18] |
Higdon R L. Numerical absorbing boundary conditions for the wave equation[J]. Mathematics of Computation, 1987, 49(179): 65-90. DOI:10.1090/S0025-5718-1987-0890254-1 |
| [19] |
Higdon R L. Absorbing boundary conditions for elastic waves[J]. Geophysics, 1991, 56(2): 231-241. DOI:10.1190/1.1443035 |
| [20] |
宋鹏, 王修田. 优化系数的四阶吸收边界条件[J]. 中国海洋大学学报(自然科学版), 2008, 38(2): 251-258. SONG Peng, WANG Xiutian. The fourth-order absorbing boundary conditions with optimal parameters[J]. Periodical of Ocean University of China(Natural Science Edition), 2008, 38(2): 251-258. |
| [21] |
Song P, Liu Z L, Zhang X B, et al. The fourth-order absorbing boundary condition with optimized coefficients for the simulation of the acoustic equation[J]. Journal of Geophysics and Engineering, 2015, 12(6): 996-1007. DOI:10.1088/1742-2132/12/6/996 |
| [22] |
Baffet D, Hagstrom T, Givoli D. Double absorbing boundary formulations for acoustics and elastodyna-mics[J]. Society for Industrial and Applied Mathema-tics, 2014, 36(3): A1277-A1312. |
| [23] |
Hagstrom T, Givoli D, Rabinovich D, et al. The dou-ble absorbing boundary method[J]. Journal of Computational Physics, 2014, 259: 220-241. DOI:10.1016/j.jcp.2013.11.025 |
| [24] |
Potter T, Shragge J, Lumley D. Performance and stability of the double absorbing boundary method for acoustic-wave propagation[J]. Geophysics, 2019, 84(2): T59-T72. DOI:10.1190/geo2018-0161.1 |
| [25] |
Liu Y, Sen M K. A hybrid scheme for absorbing edge reflections in numerical modeling of wave propagation[J]. Geophysics, 2010, 75(2): A1-A6. DOI:10.1190/1.3295447 |
| [26] |
Liu Y, Sen M K. 3D acoustic-wave modeling with time-space domain dispersion-relation-based finite-difference schemes and hybrid absorbing boundary conditions[J]. Exploration Geophysics, 2011, 42(3): 176-189. DOI:10.1071/EG11007 |
| [27] |
Liu Y, Sen M K. A hybrid absorbing boundary condition for elastic staggered-grid modeling[J]. Geophysical Prospecting, 2012, 60(6): 1114-1132. DOI:10.1111/j.1365-2478.2011.01051.x |
| [28] |
任志明, 刘洋. 一阶弹性波方程数值模拟中的混合吸收边界条件[J]. 地球物理学报, 2014, 57(2): 595-606. REN Zhiming, LIU Yang. Numerical modeling of the first-order elastic equations with the hybrid absorbing boundary condition[J]. Chinese Journal of Geophy-sics, 2014, 57(2): 595-606. |
| [29] |
Liu X, Liu Y, Ren Z M, et al. Hybrid absorbing boundary condition for three-dimensional elastic wave modeling[J]. Applied Geophysics, 2017, 14(2): 270-278. DOI:10.1007/s11770-017-0623-z |
| [30] |
Ren Z M, Liu Y. A hybrid absorbing boundary condition for frequency-domain finite-difference modelling[J]. Journal of Geophysics and Engineering, 2013, 10(5): 054003. DOI:10.1088/1742-2132/10/5/054003 |
| [31] |
刘学义, 何兵寿. VTI介质中弹性波方程正演的一阶混合吸收边界[J]. 中国煤炭地质, 2015, 27(3): 59-63. LIU Xueyi, HE Bingshou. First-order hybrid absor-bing boundary condition in VTI media elastic wave equation for modeling[J]. Coal Geology of China, 2015, 27(3): 59-63. DOI:10.3969/j.issn.1674-1803.2015.03.16 |
| [32] |
Wang E J, Liu Y. The hybrid absorbing boundary condition for one-step extrapolation and its application in wavefield decomposition-based reverse time migration[J]. Journal of Geophysics and Engineering, 2017, 14(5): 1177-1188. DOI:10.1088/1742-2140/aa7308 |
| [33] |
薛浩, 刘洋, 杨宗青. 基于优化时空域频散关系的声波方程有限差分最小二乘逆时偏移[J]. 石油地球物理勘探, 2018, 53(4): 745-753. XUE Hao, LIU Yang, YANG Zongqing. Least-square reverse time migration of finite-difference acoustic wave equation based on an optimal time-space dispersion relation[J]. Oil Geophysical Prospecting, 2018, 53(4): 745-753. |
| [34] |
Liu Y, Sen M K. An improved hybrid absorbing boundary condition for wave equation modeling[J]. Journal of Geophysics and Engineering, 2018, 15(6): 2602-2613. DOI:10.1088/1742-2140/aadd31 |
| [35] |
Levander A R. Fourth-order finite difference P-SV seismograms[J]. Geophysics, 1988, 53(11): 1425-1436. DOI:10.1190/1.1442422 |
| [36] |
董良国, 马在田, 曹景忠. 一阶弹性波方程交错网格高阶差分解法稳定性研究[J]. 地球物理学报, 2000, 43(6): 856-864. DONG Liangguo, MA Zaitian, CAO Jingzhong. A study on stability of the staggered-grid high-order difference method of first-order elastic wave equation[J]. Chinese Journal of Geophysics, 2000, 43(6): 856-864. DOI:10.3321/j.issn:0001-5733.2000.06.015 |
| [37] |
董良国, 马在田, 曹景忠, 等. 一阶弹性波方程交错网格高阶差分解法[J]. 地球物理学报, 2000, 43(3): 411-419. DONG Liangguo, MA Zaitian, CAO Jingzhong, et al. A staggered-grid high-order difference method of one-order elastic wave equation[J]. Chinese Journal of Geophysics, 2000, 43(3): 411-419. DOI:10.3321/j.issn:0001-5733.2000.03.015 |
| [38] |
杨庆节, 刘财, 耿美霞, 等. 交错网格任意阶导数有限差分格式及差分系数推导[J]. 吉林大学学报(地球科学版), 2014, 44(1): 375-385. YANG Qingjie, LIU Cai, GENG Meixia, et al. Staggered grid finite difference scheme and coefficients deduction of any number of derivatives[J]. Journal of Jilin University(Earth Science Edition), 2014, 44(1): 375-385. |



 宋鹏, 山东省青岛市崂山区松岭路238号中国海洋大学海洋地球科学学院, 266100。Email:
宋鹏, 山东省青岛市崂山区松岭路238号中国海洋大学海洋地球科学学院, 266100。Email: 