中国油气勘探与开发的持续进行,使得在复杂地震地质条件下寻找油气藏已成为目前及今后陆上勘探的必然趋势。随着地震勘探难度日益增大,地表条件越来越复杂,既有可用炸药震源的山地、沙漠区,又有村庄、城镇、工业园、江河、水库等“禁炮区”,因此野外采集常采用多种类型震源(如炸药震源、可控震源、气枪震源等)混合施工。可控震源具有安全环保、使用高效、方便操控等优势,它的应用和发展不仅符合国家安全需要,更是环保要求;既能降低采集施工成本,还能在保证资料品质基础上大幅度提高现场施工效率,缩短项目周期。
在复杂障碍区应用混合震源采集面临诸多挑战。受激发方式、激发井深、接收仪器、地表地质条件等客观因素影响,采集所得地震资料在子波、振幅能量、相位、频率、信噪比、时差等方面均存在较大差异[1]。例如,炸药震源子波是最小相位,能量较强,频率较高;可控震源子波为零相位,能量、频率可以人为控制;重锤震源子波为最小相位,能量较低,地表因素影响较严重[2]。这些差异使不同震源采集的资料在处理时无法同相叠加,严重降低了资料的信噪比和分辨率。如果采用常规处理流程,地震资料在两种震源拼接处会存在较大差异,地震剖面存在波组特征较差、信噪比和分辨率较低等问题[3-7];混合震源地震剖面存在较大时差(图 1),两者不闭合给后续地震资料精细处理、解释带来很大影响,如分层不清晰、不同(混合)震源之间时差被误认为是假断裂、波阻抗反演的精度难以保证、地震属性参数提取困难等。

|
图 1 可控震源与炸药震源混合区叠加剖面 |
目前,实际数据处理中解决混合震源不一致性问题的主要方法有时移扫描法、反褶积参数调整法和匹配滤波法等。匹配滤波方法通常用于陆上不同震源数据的匹配,或浅海与陆地过渡区域地震数据匹配。唐恩德等[8]认为在处理混合震源地震资料时,要优化模型道及对单炮记录子波进行最小相位化处理以消除子波差异,再通过谱均衡等地表一致性技术处理振幅差异;庄东海等[9]强调,针对混合震源资料,要做好相对振幅保持、提高信噪比和资料一致性等处理,而其中的关键是互均衡处理;娄兵等[10]将子波整形及匹配滤波两种方法应用于不同震源的拼接处理,提高了地震资料信噪比和分辨率;王西文等[11]将基于小波变换的地震子波处理技术应用于均衡连片工区数据在频率、能量、信噪比等方面差异,为地震解释和反演提供高信噪比地震资料;宋玉龙[12]在滩浅海地区利用匹配滤波技术解决由观测系统、激发、接收等因素导致的海陆资料之间差异,利用叠前多点综合串联匹配滤波处理技术解决炸药与可控震源波组特征、频率、相位及能量不一致情况,较好地解决了资料衔接时不匹配问题;高少武等[13-14]采用匹配滤波技术处理炸药震源与可控震源数据的衔接,使这两种震源资料的振幅和相位趋于一致。
但在同一工区因复杂障碍区施工困难而采用混合震源时,两种混合震源资料的重复段叠加剖面由于炮检距范围、频率、叠加速度、静校正等多种因素的影响,信噪比存在较大差异,难以准确求取匹配算子;另外,目前常规匹配滤波处理方法只是计算一个滤波因子,而不考虑地震资料信噪比。
因此,本文在充分考虑信号和噪声的基础上,开展了混合震源高精度匹配处理技术研究,通过综合应用叠前平均振幅谱匹配、混合震源相位匹配、剩余时差校正等处理技术,消除了混合震源间存在的振幅、相位、频率差异及时差不一致等问题,同时兼顾地震子波的变化。将该方法应用于四川盆地大川中北斜坡射洪—盐亭三维复杂障碍区的地震资料处理,提高了不同震源资料匹配处理的成像品质和地震资料信噪比,消除了假断裂和假构造等现象,可为精细地震解释和反演提供高保真、高信噪比的地震资料。
2 研究区概况研究区处于四川盆地川中古隆起平缓构造区仪陇构造群,以山地—丘陵地貌为主。区内河流较发育,包括涪江、梓江及其支流,涪江江面宽为300~1000m,梓江江面宽为80~500m;涉及中小型水库12座,这些水库多为当地一级饮水水源,禁止布设水下检波器;区内主要障碍包括:中华涪江湿地走廊自然保护区、射洪和盐亭县城及城镇、水系、天然气管线和水渠等地面地下设施、风景区等。工区内复合障碍面积大、范围广,严重影响观测系统设计和物理点的均匀布设,因此采用可控震源与炸药震源混合激发施工。

|
图 2 研究区障碍分布示意图 |
常规振幅匹配处理方法只计算一个滤波因子,而很少顾及地震资料信噪比,而地震数据一般包含信号和噪声两部分,在设计两种混合震源地震数据匹配算子时,理想的条件是进行信号之间的匹配,而不是噪声,噪声会影响所求取的匹配算子的稳定性[15-16]。假设有x(t)和y(t)两道地震数据,分别由信号sx(t)、sy(t)和噪ny(t)、ny(t)声组成
| $ x\left( t \right) = {s_x}\left( t \right) + {n_y}(t) $ | (1) |
| $ y\left( t \right) = {s_y}\left( t \right) + {n_y}(t) $ | (2) |
其傅里叶变换为
| $ X\left( f \right) = {S_x}\left( f \right) + {N_x}(f) $ | (3) |
| $ Y\left( f \right) = {S_y}\left( f \right) + {N_y}(f) $ | (4) |
x(t)的自相关谱可写为
| $ X\bar X = {S_x}{\bar S_x} + {N_x}{\bar S_x} + {S_x}{\bar N_x} + {N_x}{\bar N_x} $ | (5) |
式中带上划线为共轭复数。
同理可得x(t)与y(t)的互相关谱表达式
| $ X\bar Y = {S_x}{\bar S_y} + {N_x}{\bar S_y} + {S_x}{\bar N_y} + {N_x}{\bar N_y} $ | (6) |
若是两组地震道数据,那么一组x(t)的平均自相关谱用数学期望可表示为
| $ \begin{array}{l} E\left[ {X\bar X} \right] = E[{S_X}{{\bar S}_X}\left] { + E} \right[{N_X}\left. {{{\bar S}_X}} \right] + \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;E[{S_X}{{\bar N}_X}\left] { + E} \right[{N_X}{{\bar N}_X}] \end{array} $ | (7) |
在平均意义下,信号与噪声是不相关的,则有
| $ E\left[ {X\bar X} \right] = E[{S_X}{\bar S_X}\left] { + E} \right[{N_X}{\bar N_X}] $ | (8) |
同理可得
| $ E\left[ {Y\bar Y} \right] = E[{S_Y}{{\bar S}_Y}\left] { + E} \right[{N_Y}{{\bar N}_Y}] $ | (9) |
| $ E\left[ {X\bar Y} \right] = E[{S_X}{\bar S_Y}\left] { + E} \right[{N_X}{\bar N_Y}] $ | (10) |
进一步假设两种数据的噪声也是不相关的,那么平均互相关谱可变为
| $ E\left[ {\bar X\bar Y} \right] = E[{S_X}{\bar S_Y}] $ | (11) |
从该式可看出,平均互相关谱的相位等于两组地震道数据的信号谱的相位差。
定义x(t)的噪声与信号比值为
| $ {\mu _x}\left( f \right) = \frac{{E\left\{ {{{\left| {{N_x}\left( f \right)} \right|}^2}} \right\}}}{{E\left\{ {{{\left| {{S_x}\left( f \right)} \right|}^2}} \right\}}} $ | (12) |
| $ {\mu _y}\left( f \right) = \frac{{E\left\{ {{{\left| {{N_y}\left( f \right)} \right|}^2}} \right\}}}{{E\left\{ {{{\left| {{S_y}\left( f \right)} \right|}^2}} \right\}}} $ | (13) |
进而可得
| $ \left( {1 + {\mu _x}} \right)\left( {1 + {\mu _y}} \right) = \frac{{E\left\{ {{{\left| {X\left( f \right)} \right|}^2}} \right\}E\left\{ {{{\left| {Y\left( f \right)} \right|}^2}} \right\}}}{{{{\left| {E\left[ {X\left( f \right)\bar Y\left( f \right)} \right]} \right|}^2}}} $ | (14) |
假设两种数据的噪声与信号比值相同,则有
| $ {\mu _x} = {\mu _y} = \frac{{\sqrt {E\left\{ {{{\left| {X\left( f \right)} \right|}^2}} \right\}E\left\{ {{{\left| {Y\left( f \right)} \right|}^2}} \right\}} }}{{\left| {E\left[ {X\left( f \right)\bar Y\left( f \right)} \right]} \right|}} - 1 $ | (15) |
定义两组地震道的谱相关为
| $ {\gamma ^2}\left( f \right) = \frac{{{{\left| {E\left[ {X\bar Y} \right]} \right|}^2}}}{{E\left[ {X\bar X} \right]E\left[ {X\bar Y} \right]}} $ | (16) |
可得
| $ \mu = \frac{1}{\gamma } - 1或\gamma = \frac{1}{{1 + \mu }} $ | (17) |
若γ已知,那么可得到x(t)的信号谱为
| $ E\left[ {X\bar X} \right] = E[{S_X}{\bar S_X}\left] { + E} \right[{N_X}{\bar N_X}] = \frac{1}{\gamma }E\left\{ {{{\left| {{S_X}\left( f \right)} \right|}^2}} \right\} $ | (18) |
显然有
| $ E\left\{ {{{\left| {{S_X}\left( f \right)} \right|}^2}} \right\} = \gamma E[X\bar X] $ | (19) |
同样可得到噪声谱
| $ E\left\{ {{{\left| {{N_X}\left( f \right)} \right|}^2}} \right\} = \left( {1 - \gamma } \right)E[X\bar X] $ | (20) |
为促使y(t)向x(t)匹配,定义匹配算子为
| $ M\left( f \right) = \frac{{E\left\{ {{{\left| {{S_X}\left( f \right)} \right|}^2}} \right\}}}{{E\left\{ {{{\left| {{S_Y}\left( f \right)} \right|}^2}} \right\}}} \times \frac{1}{{1 + \mu }} $ | (21) |
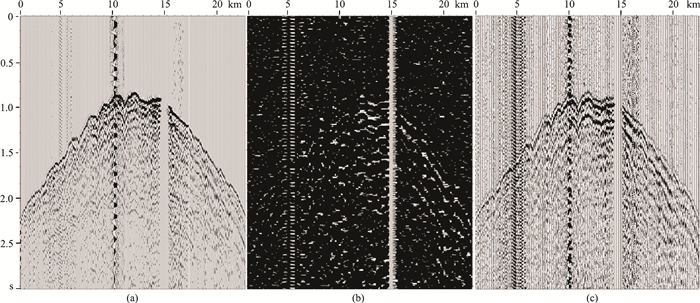
匹配算子包含两项:前一项是整形滤波器;后一项是为了压制噪声,在噪声较大的地震资料上也能得到稳定的匹配算子。显然,该式是匹配算子的振幅谱计算公式,取得的实际效果如图 3所示。
|
图 3 同一位置炸药震源与可控震源对比 (a)炸药震源单炮;(b)可控震源振幅匹配前单炮;(c)可控震源振幅匹配后单炮 |
当炸药震源和可控震源两种混合震源联合处理时,由于两种激发方式获得的地震资料相位不统一,影响叠加剖面成像效果,降低了地震资料信噪比和分辨率[17-18]。最小平方脉冲反褶积、预测反褶积方法假设子波为最小相位,而可控震源子波更接近零相位,因此在地震处理前,需将可控震源子波最小相位化,具体步骤如下:
(1) 通过可控震源扫描频率、扫描长度、坡度及扫描类型等参数,得到可控震源扫描信号;
(2) 对可控震源扫描信号进行自相关计算,得到可控震源的零相位子波;
(3) 利用可控震源零相位子波,提取可控震源的最小相位化转换算子;
(4) 将转换算子在叠前应用于可控震源单炮,即完成相位匹配;再将零相位可控震源子波地震数据转化为最小相位震源子波地震数据。
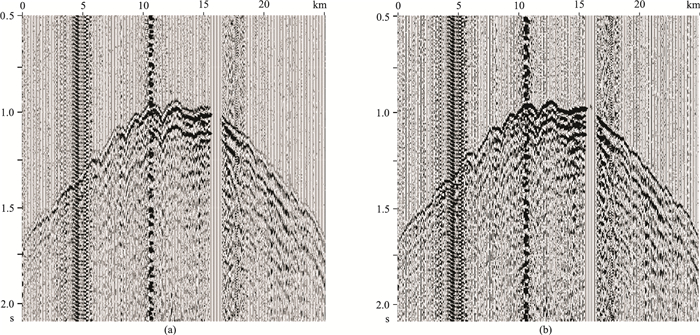
图 4为可控震源子波最小相位化前、后单炮对比。可见通过可控震源最小相位化处理,一方面较好地解决了与炸药震源子波不一致问题,即相位匹配后两种震源都为最小相位子波,形成同相叠加,叠加剖面连续性变好,能量加强;另一方面,最小相位化处理后可控震源单炮初至更光滑,更利于初至拾取,为后续近地表速度模型反演和静校正计算奠定基础。
|
图 4 可控震源最小相位化前(a)、后(b)的单炮对比 |
由于可控震源与井炮震源在激发深度、激发岩性、激发机制、子波形态、工作参数上存在较大差异,使两者激发的子波在振幅、相位、频率、时差上存在较大差异,通过平均振幅谱匹配和混合震源相位匹配两项处理技术,较好地消除了混合震源在振幅、频率、相位上的差异。但由于可控震源是在地面激发,而炸药震源一般选择在地下高速层顶界以下激发,可控震源扫描信号下传过程中,受近地表低降速带和吸收衰减的影响[19],与炸药震源之间仍存在剩余时差的影响,若剩余时差过大,会影响速度分析和同相叠加的精度,直接影响地震资料同相叠加的效果[2]。
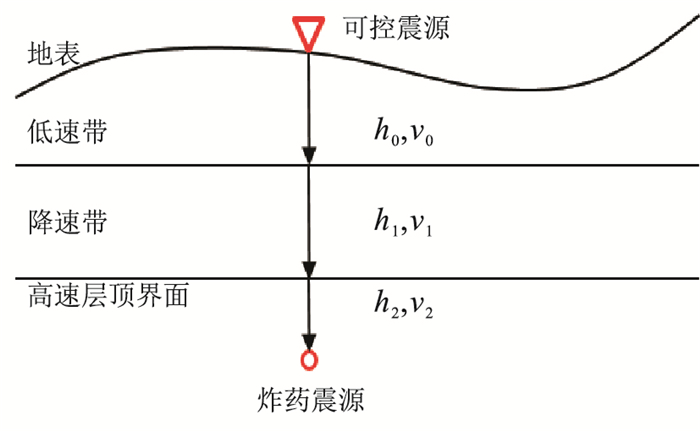
叠前剩余时差校正主要是为了解决叠前平均振幅谱匹配处理和混合震源相位匹配处理后,不同震源在地震剖面拼接处仍存在较大时差的一种方法,具体做法是先对工区炸药震源井深、近地表速度、厚度等信息进行调查[20],如图 5所示,在此基础上对剩余时差进行量化分析。
|
图 5 近地表的地质结构示意图 |
可控震源和炸药震源不考虑炮检距的影响,以垂直入射为例进行时差分析,可得到剩余时差为
| $ \Delta T = \frac{{{h_0}}}{{{v_0}}} + \frac{{{h_1}}}{{{v_1}}} + \frac{{{h_2}}}{{{v_2}}} $ | (22) |
式中:h0、v0分别为低速带厚度和速度;h1、v1对应降速带厚度和速度;h2为炸药震源距高速层顶界距离;v2为高速层速度。
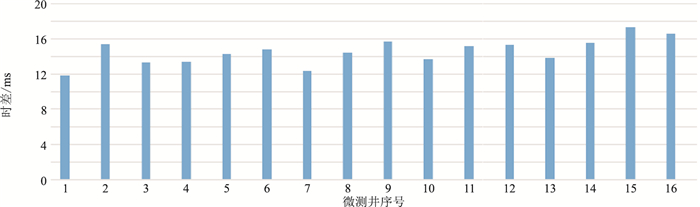
在研究区内选取混合震源附近16口微测井进行分析,根据微测井调查和炸药震源井深信息,按式(22)可求得剩余时差约为14ms(图 6)。
|
图 6 可控震源和炸药震源时差统计直方图 |
除了受近地表因素影响,剩余时差还受炮检距影响。因此,为提高剩余时差分析精度,在以上剩余时差分析的基础上,再对炸药震源和可控震源数据分别进行叠加,在剖面上选取两种混合震源的拼接处,分别求取可控震源和炸药震源各自的叠加道数据xi(t)和yi(t)(道号i=1,2,…,N,其中N为叠加段的道数)。
因为重叠部分是地下同一区域地层的相同反射信息,在地震剖面上具有相同的构造形态,两种地震记录应该具有良好的相关性。而互相关函数是在时间域比较两个信号相似程度的一种方法,互相关结果可定量描述两个信号的时间延迟,通过互相关分析,能定量求取可控震源和炸药震源的剩余时差(图 7)约为18ms。通过叠后剩余时差统计,将该时差校正到可控震源的所有叠前数据上,较好地解决了两种震源系统时差。

|
图 7 炸药震源和可控震源互相关曲线 |
从剩余时差校正前、后的水平叠加对比剖面(图 8)可看出,经过剩余时差校正处理,混合震源重叠区域叠加剖面信噪比和分辨率都得到显著提升,侏罗系大安寨标志层位不连续、混合震源时差误认为的假断裂现象分别得到改善和厘清,有利于后续精细构造解释和圈闭准确落实。

|
图 8 剩余时差校正前(a)、后(b)的水平叠加剖面对比 |
川中古隆起北斜坡是海、陆相主要有利勘探领域和目标区带的叠合区,具有多层系立体勘探优势。本次实际数据取自大川中射洪—盐亭三维工区,满覆盖面积为2052.1km2,跨越四川省遂宁、绵阳、德阳及南充四市,共涉及105个乡镇(图 2)。该区属低丘陵山地地貌,整体地形较平缓,相对高程较小,但局部高程变化较大,海拔高度一般在350~720m,地势低洼处多为涪江及梓江河沿岸,北部地势相对较高。
在现场观测系统方面,由于受到射洪县城及工业园区、盐亭县城、涪江及中华涪江湿地走廊自然保护区等的影响,另外梓江河穿越工区西南部,升钟水渠、武引水渠,天然气管线等贯穿工区,采用炸药震源和可控震源混合震源进行施工,而混合震源采集在复杂障碍区接收到的地震资料在子波、振幅能量、相位、频率、信噪比、时差等方面均存在较大差异,若不进行精细匹配处理,必将影响地震层位精细解释和断裂刻画。
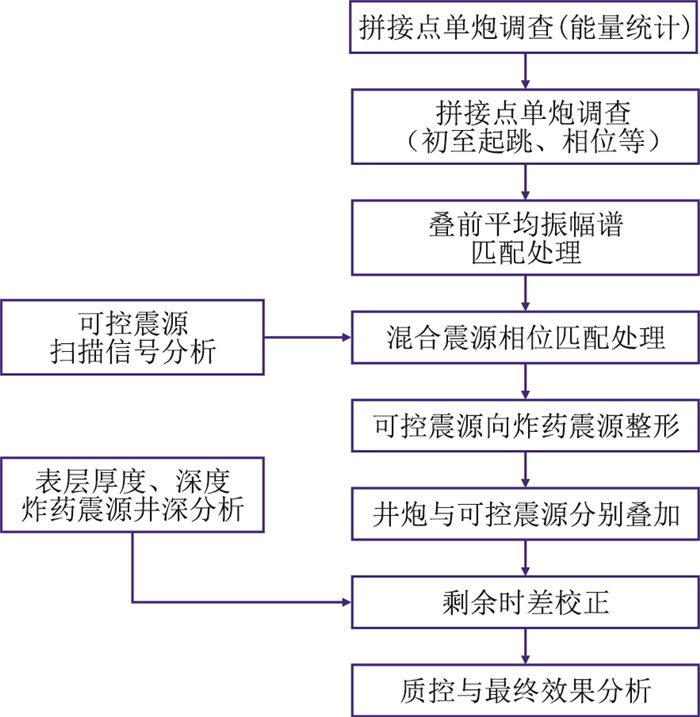
在充分考虑信号和噪声的基础上,开展混合震源高精度匹配处理,具体流程如图 9所示。在该复杂障碍区地震资料处理中,综合应用叠前平均振幅谱匹配、混合震源相位匹配、叠前剩余时差校正等处理技术,消除了混合震源间存在的振幅、相位、频率、时差等不一致现象,提高了混合震源资料的成像品质和剖面信噪比,为精细层位解释、断裂解释、叠前反演和储层预测提供了高保真地震资料。
|
图 9 混合震源高精度匹配处理流程 |
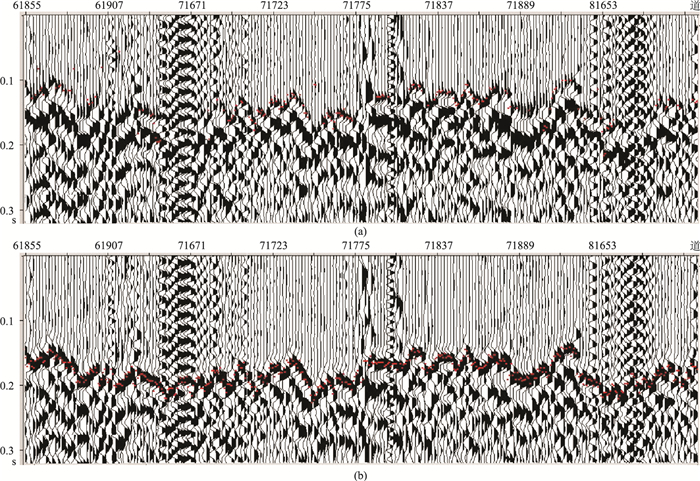
图 10为可控震源单炮最小相位化处理前、后初至拾取对比图,可见最小相位化处理后更利于准确拾取初至、近地表速度模型反演及层析静校正计算。
|
图 10 可控震源单炮最小相位化前(a)、后(b)初至拾取对比 |
图 11为混合震源高精度匹配处理前、后水平叠加对比剖面,可见匹配前可控震源振幅能量明显强于炸药震源资料,且两种混合震源存在系统时差,在浅层侏罗系大安寨(J1dn)标志层存在明显错断;通过高精度匹配处理后,振幅能量趋于一致,标志层错断得到明显消除,信噪比显著提升。

|
图 11 混合震源高精度匹配处理前(a)、后(b)水平叠加剖面对比 |
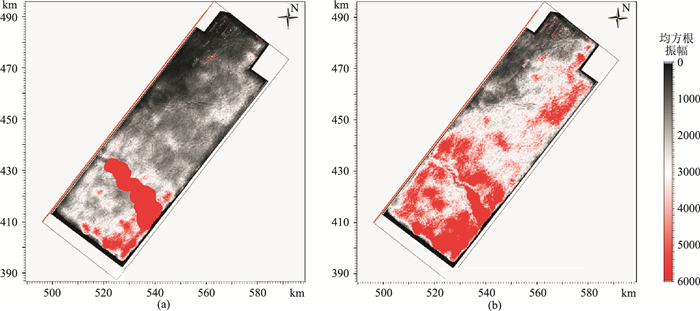
图 12为混合震源高精度匹配处理前、后沿侏罗系大安寨地层的均方根振幅属性平面图。可见在进行高精度匹配处理后,可控震源与炸药震源振幅能量关系一致性更好,为后续叠前保真处理奠定了资料基础。图 13为混合震源高精度匹配处理前、后等时切片(1.4s)属性平面图,经过高精度匹配处理,信噪比得到明显提升,假的构造形态得到了甄别,为精细构造解释和储层预测提供了高保真数据。
|
图 12 混合震源高精度匹配处理前(a)、后(b)沿层均方根振幅属性平面图 |

|
图 13 混合震源高精度匹配处理前(a)、后(b)等时切片(1.4s)属性平面图 |
本文讨论的混合震源高精度匹配处理方法,通过综合应用叠前平均振幅谱匹配、混合震源相位匹配及叠前剩余时差校正等处理技术,方便、快捷地实现了混合震源数据的一致性处理,较好地解决了不同震源激发(接收)造成的振幅、频率、相位、时差等不一致问题。该套技术具有较好的应用前景,不但适用于陆上和海上混合震源采集资料,还可用于不同时间、不同采集因素施工获得的多块地震资料的连片处理,能显著提高资料信噪比,浅、中、深层地震反射都能较好地拼接,实现了不同资料的同相叠加,并便于连续追踪,为后续精细构造解释及储层预测提供了高保真成果数据。
| [1] |
高少武, 赵波, 贺振华. 可控震源与炸药震源地震数据匹配[C]. 中国地球物理年会, 北京, 2008.
|
| [2] |
赵明秋, 牛建国. 连接不同震源数据的匹配滤波技术[J]. 石油地球物理勘探, 2007, 42(增刊1): 136-139. ZHAO Mingqiu, NIU Jianguo. A matched filtering technique linking different sources data[J]. Oil Geophysical Prospecting, 2007, 42(S1): 136-139. |
| [3] |
段云卿. 匹配滤波与子波整形[J]. 石油地球物理勘探, 2006, 41(2): 156-159. DUAN Yunqing. Matched filtering and wavelet shaping[J]. Oil Geophysical Prospecting, 2006, 41(2): 156-159. DOI:10.3321/j.issn:1000-7210.2006.02.008 |
| [4] |
Brotz R, Marschall R, Knecht M. Signal adjustment of vibrseisand impulsive source data[J]. Geophysical Prospecting, 1987, 35(7): 739-766. DOI:10.1111/j.1365-2478.1987.tb02256.x |
| [5] |
Berhout A J. Least-squares inverse filtering and wavelet deconvolution[J]. Geophysics, 1977, 42(7): 1369-1383. DOI:10.1190/1.1440798 |
| [6] |
Wiener N. Extrapolation, Interpolation and Smoo-thing of Stationary Time Series: With Engineering Applications[M]. Cambridge: Technology Press of The Massachusetts Institute of Technology, 1947.
|
| [7] |
高少武, 赵波, 高轩, 等. OBC水陆检数据匹配技术[J]. 石油地球物理勘探, 2015, 50(1): 29-32. GAO Shaowu, ZHAO Bo, GAO Xuan, et al. A me-thod for OBC dual-sensor data matching[J]. Oil Geophysical Prospecting, 2015, 50(1): 29-32. |
| [8] |
唐恩德, 宋锡熊, 陈志刚. 多种震源联合激发地震数据的处理方法[J]. 石油地球物理勘探, 1997, 32(增刊1): 148-156. TANG Ende, SONG Xixiong, CHEN Zhigang. Processing method of seismic data jointly excited by multiple sources[J]. Oil Geophysical Prospecting, 1997, 32(S1): 148-156. |
| [9] |
庄东海, 肖春燕, 许云, 等. 四维地震资料处理及其关键[J]. 地球物理学进展, 1999, 14(2): 33-43. ZHUANG Donghai, XIAO Chunyan, XU Yun, et al. 4D seismic data processing and its key[J]. Progress in Geophysics, 1999, 14(2): 33-43. |
| [10] |
娄兵, 郑鸿明, 蒋立. 地震测线的拼接技术[J]. 新疆石油地质, 2001, 22(3): 208-210. LOU Bing, ZHENG Hongming, JIANG Li. Splicing technology of seismic survey lines[J]. Xinjiang Petroleum Geology, 2001, 22(3): 208-210. DOI:10.3969/j.issn.1001-3873.2001.03.010 |
| [11] |
王西文, 周立宏. 三维地震资料拼接中的地震子波处理[J]. 石油物探, 2002, 41(4): 448-451. WANG Xiwen, ZHOU Lihong. Wavelet transform used in the concatenation of 3-D seismic data sets[J]. Geophysical Prospecting for Petroleum, 2002, 41(4): 448-451. DOI:10.3969/j.issn.1000-1441.2002.04.014 |
| [12] |
宋玉龙. 滩浅海地区地震勘探存在问题及其解决方法[J]. 石油物探, 2005, 44(4): 343-347. SONG Yulong. Problems of seismic survey in neritic area and resolved methods[J]. Geophysical Prospecting for Petroleum, 2005, 44(4): 343-347. DOI:10.3969/j.issn.1000-1441.2005.04.009 |
| [13] |
高少武, 钱忠平, 马玉宁, 等. OBC水陆检数据合并处理技术[J]. 石油地球物理勘探, 2018, 53(4): 703-709. GAO Shaowu, QIAN Zhongping, MA Yuning, et al. OBC dual-sensor data combination processing[J]. Oil Geophysical Prospecting, 2018, 53(4): 703-709. |
| [14] |
高少武, 魏庚雨, 赵波, 等. 可控震源地震数据子波最小相位化方法[J]. 石油地球物理勘探, 2009, 44(6): 685-689. GAO Shaowu, WEI Gengyu, ZHAO Bo, et al. Wavelet minimum-phasing method for vibroseis seismic data[J]. Oil Geophysical Prospecting, 2009, 44(6): 685-689. DOI:10.3321/j.issn:1000-7210.2009.06.008 |
| [15] |
马光凯, 周铮铮, 耿伟峰, 等. 海洋拖缆数据检波器移动时差校正[J]. 石油地球物理勘探, 2020, 55(2): 266-271. MA Guangkai, ZHOU Zhengzheng, GENG Weifeng, et al. Hydrophone moving-related moveout correction for marine streamer data[J]. Oil Geophysical Prospecting, 2020, 55(2): 266-271. |
| [16] |
渥·伊尔马兹著; 刘怀山, 等. 地震数据处理[M]. 北京: 石油工业出版社, 2006.
|
| [17] |
邬达理, 姜游, 陈竹梅. 串联匹配滤波法在混合震源资料处理中的应用[J]. 石油物探, 2006, 45(6): 611-614. WU Dali, JIANG You, CHEN Zhumei. Application of cascade matched filtering in mixed source data processing[J]. Geophysical Prospecting for Petroleum, 2006, 45(6): 611-614. DOI:10.3969/j.issn.1000-1441.2006.06.011 |
| [18] |
肖虎, 唐东磊, 杨国平, 等. 可控震源动态扫描技术及应用[J]. 石油地球物理勘探, 2019, 54(3): 493-499. XIAO Hu, TANG Donglei, YANG Guoping, et al. Vibroseis dynamic sweep[J]. Oil Geophysical Prospecting, 2019, 54(3): 493-499. |
| [19] |
苏勤, 曾华会, 田彦灿, 等. 表层Q值确定性求取与空变补偿方法[J]. 石油地球物理勘探, 2019, 54(5): 988-996. SU Qin, ZENG Huahui, TIAN Yancan, et al. Near-surface Q value estimation and quantitative amplitude compensation[J]. Oil Geophysical Prospecting, 2019, 54(5): 988-996. |
| [20] |
金昌昆, 王延光, 尚新民, 等. 微测井与方位加权插值精细近地表速度建模技术[J]. 石油地球物理勘探, 2020, 55(2): 257-265. JIN Changkun, WANG Yanguang, SHANG Xinmin, et al. Near-surface velocity modeling based on micro-log and azimuth-weighted interpolation[J]. Oil Geophysical Prospecting, 2020, 55(2): 257-265. |



 曾华会, 甘肃省兰州市城关区雁儿湾路535号中国石油勘探开发研究院西北分院, 730030。Email:
曾华会, 甘肃省兰州市城关区雁儿湾路535号中国石油勘探开发研究院西北分院, 730030。Email: 