② 中国石油新疆油田分公司勘探开发研究院, 新疆克拉玛依 834000
② Research Institute of Exploration and Development, PetroChina Xinjiang Oilfield Company, Karamay, Xinjiang 834000, China
现今油气勘探方向已逐步由构造油气藏转向岩性、非常规等油气藏,而这类油气储层多表现为纵向薄、横向变化快的特征,这就要求现场采集到较宽频、高频地震记录,且后期处理采用反Q滤波、反褶积等一系列高频补偿技术。然而,地震信号的高频成分往往含较多噪声,显著降低地震资料的横向连续性和信噪比,严重影响数据的分析和处理效果。去除噪声、获取高信噪比地震记录一直是地震勘探要解决的首要问题[1-2],目前地震数据处理中主要利用有效信号与噪声的频率或视速度差异压制噪声[3-4],常见方法有中值滤波[5-6]、奇异值分解[7-8]、f-x域预测滤波和小波变换等[9-11]。
卡尔曼滤波于1960年由美国控制论专家Kalman[12]首次提出,是一种最优化自回归数据处理算法,即以最小均方差为估计准则,采用状态转移反映系统变化的内在规律,以“预估—测量—校正”的顺序递推,从被污染系统中估计出系统本来面目。卡尔曼滤波算法原理表明其在有效信号恢复方面具有很大优势,已在目标跟踪、自动控制、导航、气象、空间物理、电力系统、医学、通信等领域得到广泛应用[13-20]。在地震勘探领域,Crump[21]最先将其应用于反褶积处理以得到反射系数序列。随后,很多学者在此基础上也将卡尔曼滤波用于地震资料反褶积处理,都取得很好效果。
董敏煜等[22]在Crump[21]和Mendel[23]研究成果的基础上,进一步提出了基于卡尔曼滤波估计时变子波的自适应反褶积方法,显著地提高了地震资料的分辨率、信噪比和同相轴连续性。邓小英等[24]提出一种新的基于卡尔曼滤波的地震记录同相轴跟踪方法。霍国栋等[25-26]通过在贝叶斯约束反演中建立卡尔曼滤波模式,实现纵向和横向同时约束AVO反演,大大提高了反演结果的信噪比和横向连续性。郑笑雪等[27]通过卡尔曼滤波实现反演的横向约束,进而提高反演结果的信噪比和横向连续性,同时表明卡尔曼滤波在提高地震资料信噪比和同相轴连续性方面确有明显优势。
针对地震资料中存在的信噪比低和横向连续性差的问题,本文基于卡尔曼滤波原理建立迭代循环组合滤波模式,将横向(地震道)与纵向(时间)迭代循环滤波次数设定为4∶1,实现地震资料高效滤波,该方法在滤波效果和效率上都优于一般平滑滤波、单一横向或纵向迭代循环滤波。通过Marmousi2理论模型[28]和实际资料测试,处理结果验证了该方法的可靠性和实用性。
1 方法原理 1.1 横向卡尔曼地震滤波卡尔曼滤波分为预测和校正两个步骤,预测是基于上一时刻状态估计当前时刻状态,而校正则是综合当前时刻的估计状态与观测状态,估计出最优状态[24]。本文依据卡尔曼滤波原理[12]建立卡尔曼地震道滤波模式。
目标地质体通常具有的横向相似性导致相邻地震道的高相似性,那么据相邻地震道可估计本道最优状态。首先建立地震道之间的状态转换方程
| $ \mathit{\boldsymbol{X}}_k^{\rm{s}} = {\mathit{\boldsymbol{A}}_k}\left( {{\mathit{\boldsymbol{X}}_{k - 1}} + {\mathit{\boldsymbol{X}}_{k + 1}}} \right) + {\mathit{\boldsymbol{W}}_k} $ | (1) |
式中:Xks为第k道的状态;Xk-1、Xk+1分别是地震剖面中第k-1和第k+1道;Ak为状态变换矩阵,即联系第k道与第k-1和第k+1道的中间量,这里Ak取为单位矩阵以刻画参数的横向连续性;Wk为状态转换误差。
再建立地震道的测量方程
| $ \mathit{\boldsymbol{X}}_k^{\rm{m}} = {\mathit{\boldsymbol{X}}_k} + {\mathit{\boldsymbol{V}}_k} $ | (2) |
式中:Xk、Xkm分别表示地震剖面的第k道及其测量值;Vk为测量误差,对于沉积岩层而言,相邻地震道间具有相似性,可认为Wk与Vk近似相等。
根据上述状态方程可优化地震道数据Xk,对应的Xk道的标准差Pk的更新公式为
| $ {\mathit{\boldsymbol{P}}_k} = {\rm{ }}{\mathit{\boldsymbol{A}}_k}{\mathit{\boldsymbol{P}}_{k - 1}}\mathit{\boldsymbol{A}}_k^{\rm{T}}k + {\mathit{\boldsymbol{R}}_k} $ | (3) |
式中:Pk、Pk-1分别是第k和第k-1道地震道的标准差;Rk为Pk更新过程中的误差标准差。
有了地震道状态的预测结果和地震道的测量值,就可对Xk进行最优化估算
| $ \mathit{\boldsymbol{X}}_k^{{\rm{op}}} = \mathit{\boldsymbol{X}}_k^{\rm{s}} + {\mathit{\boldsymbol{g}}_k}(\mathit{\boldsymbol{X}}_k^{\rm{m}} - \mathit{\boldsymbol{X}}_k^{\rm{s}}) $ | (4) |
式中:Xkop为优化后的地震道;gk为(横向)卡尔曼增益,可由下式求取
| $ {\mathit{\boldsymbol{g}}_k} = \frac{{{\mathit{\boldsymbol{P}}_k}\mathit{\boldsymbol{A}}_k^{\rm{T}}}}{{{\mathit{\boldsymbol{A}}_k}{\mathit{\boldsymbol{P}}_k}\mathit{\boldsymbol{A}}_k^{\rm{T}} + {\mathit{\boldsymbol{Q}}_k}}} $ | (5) |
式中Qk为系统过程的标准差。
到此,实施了对Xk的最优估计。为了进一步对Xk+1进行最优估计,需得到更新后的Pk
| $ {\mathit{\boldsymbol{P}}_k} = {\mathit{\boldsymbol{P}}_k}(1 - {\mathit{\boldsymbol{g}}_k}) $ | (6) |
基于卡尔曼滤波原理建立的以上滤波模式,在确定P0、Rk和Qk后就可对地震资料进行横向滤波。这里,P0取开始滤波的第1道的标准差,而针对沉积岩层,相邻地震道之间的差异可近似看成平稳的随机高斯白噪声,故Pk、Qk可分别由下式求取
| $ {\mathit{\boldsymbol{R}}_k} = {\rm{std}}(\mathit{\boldsymbol{X}}_k^{\rm{m}} - \mathit{\boldsymbol{X}}_k^{\rm{s}}) $ | (7) |
| $ {\mathit{\boldsymbol{Q}}_k} = {\mathit{\boldsymbol{A}}_k}\left[ {{\rm{std}}\left( {{\mathit{\boldsymbol{X}}_k} - {\mathit{\boldsymbol{X}}_{k - 1}}} \right) + {\rm{std}}\left( {{\mathit{\boldsymbol{X}}_{k + 1}} - {\mathit{\boldsymbol{X}}_k}} \right)} \right] $ | (8) |
式中std(·)表示取标准差。
1.2 纵向卡尔曼地震滤波类似于上述横向滤波。依据卡尔曼滤波模式,首先建立地震道相邻时刻之间的状态转换方程
| $ \mathit{\boldsymbol{X}}_t^{\rm{s}} = {\mathit{\boldsymbol{A}}_t}\left( {{\mathit{\boldsymbol{X}}_{t - 1}} + {\mathit{\boldsymbol{X}}_{t + 1}}} \right) + {\mathit{\boldsymbol{W}}_t} $ | (9) |
式中:Xt-1、Xt+1分别是地震剖面中t-1和t+1时刻地震数据;Xts为第t时刻的状态;At-1为状态变换矩阵,即联系t时刻与t-1和t+1时刻的中间量,这里At取为单位矩阵以约束纵向同相轴真实时间位置;Wt为状态转换误差。
再建立地震数据t时刻的测量方程
| $ \mathit{\boldsymbol{X}}_t^{\rm{m}} = {\mathit{\boldsymbol{X}}_t} + {\mathit{\boldsymbol{V}}_t} $ | (10) |
式中:Xtm、Xt分别表示t时刻地震数据的测量值和真实值;Vt为测量误差,对于沉积岩层而言,相邻时刻数据之间具有相似性,可认为Wt与Vt近似相等。
有了状态方程,就可优化t时刻的地震数据Xt,那么对应Xt的标准差Pt的更新公式为
| $ {\mathit{\boldsymbol{P}}_t} = {\rm{ }}{\mathit{\boldsymbol{A}}_t}{\mathit{\boldsymbol{P}}_{t - 1}}\mathit{\boldsymbol{A}}_t^{\rm{T}} + {\mathit{\boldsymbol{R}}_t} $ | (11) |
式中:Pt、Pt-1分别是t和t-1时刻地震数据的标准差;Rt为Pt更新过程中的误差标准差。
基于t时刻地震数据的预测结果和对应的测量值,就可对Xt进行最优化估算
| $ \mathit{\boldsymbol{X}}_t^{{\rm{op}}} = \mathit{\boldsymbol{X}}_t^{\rm{s}} + {\mathit{\boldsymbol{g}}_t}(\mathit{\boldsymbol{X}}_t^{\rm{m}} - \mathit{\boldsymbol{X}}_t^{\rm{s}}) $ | (12) |
式中:Xtop为优化后的t时刻地震数据;gt为(纵向)卡尔曼增益,其计算式如下
| $ {\mathit{\boldsymbol{g}}_t} = \frac{{{\mathit{\boldsymbol{P}}_t}\mathit{\boldsymbol{A}}_t^{\rm{T}}}}{{{\mathit{\boldsymbol{A}}_t}{\mathit{\boldsymbol{P}}_t}\mathit{\boldsymbol{A}}_t^{\rm{T}} + {\mathit{\boldsymbol{Q}}_t}}} $ | (13) |
式中Qt为系统过程的标准差。
到此,完成了对t时刻的Xt的最优估计。为了对Xt+1进行最优估计,需得到更新的Pt
| $ {\mathit{\boldsymbol{P}}_t} = {\mathit{\boldsymbol{P}}_t}(1 - {\mathit{\boldsymbol{g}}_t}) $ | (14) |
基于卡尔曼滤波原理建立的以上滤波模式,在确定P0、Rt和Qt后就可对地震资料进行纵向滤波。此处P0取滤波开始时刻的标准差,而针对沉积岩层,地震相邻时刻之间的差异可近似看成平稳的随机高斯白噪声,因此Rt、Qt分别由下式求取
| $ {\mathit{\boldsymbol{R}}_t} = {\rm{std}}(\mathit{\boldsymbol{X}}_t^{\rm{m}} - \mathit{\boldsymbol{X}}_t^{\rm{s}}) $ | (15) |
| $ {\mathit{\boldsymbol{Q}}_t} = {\mathit{\boldsymbol{A}}_t}[{\rm{std}}({\mathit{\boldsymbol{X}}_t} - {\mathit{\boldsymbol{X}}_{t - 1}}) + {\rm{std}}({\mathit{\boldsymbol{X}}_{t + 1}} - {\mathit{\boldsymbol{X}}_t})] $ | (16) |
倘若只考虑横向滤波,不仅会一定程度拉平地震同相轴,而且会在增加道与道之间相似程度的同时降低地震的横向分辨率,导致地质体横向边界不清晰。为此,本文在对地震剖面进行横向卡尔曼滤波后再做纵向卡尔曼滤波以约束地震同相轴的纵向真实位置。具体方法为:实施一次上述横向滤波模式称为一次迭代循环滤波;更新地震剖面,针对更新剖面进行下次迭代循环滤波,继续对地震剖面横向进行4N(N为整数)次迭代循环滤波;再从时间(纵向)上也进行N次迭代循环滤波;如此以横纵向迭代循环滤波次数比为4∶1进行M轮(次)大循环滤波,这样就可实现地震资料的横纵向滤波。显然,总滤波次数为5MN次。
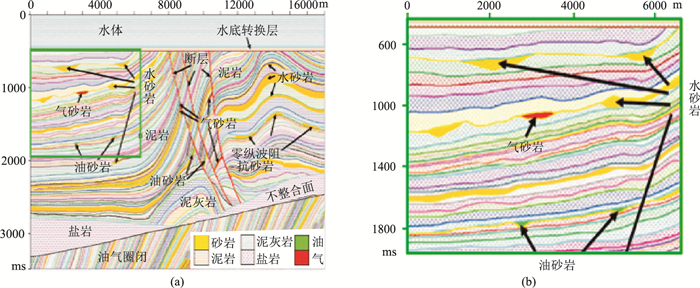
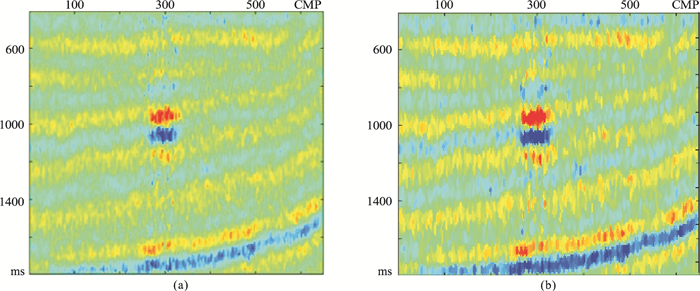
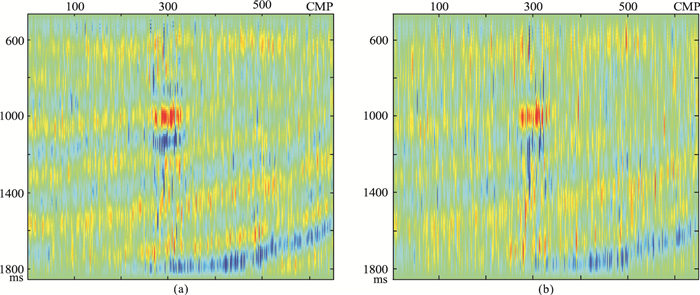
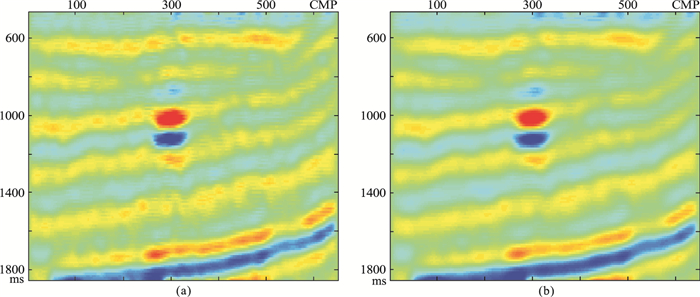
2 方法测试 2.1 模型测试为测试本文所提滤波方法的有效性和可靠性,从Marmousi2模型(图 1a)中选用含有油、气和水的砂岩部分模型(图 1b)。将由Zoeppritz方程计算的反射系数与主频为35Hz的雷克子波进行褶积,得到图 2a所示合成记录剖面,可见剖面上气藏和油藏的反射特征和横向边界较清楚;再对该数据加入信噪比是1∶2的高斯随机噪声(图 2b),可见加噪后剖面上油藏反射特征几乎被噪声淹没。图 3a和图 3b分别为二维中值滤波1次和100次后结果,其噪声得到一定压制,但整体信噪比依然较低,且滤波次数增加对改善噪声压制效果并不明显。图 4a和图 4b分别是单一横向卡尔曼滤波100次和200次后结果,剖面同相轴、油藏和气藏得到一定的恢复,噪声被压制,但出现较多水平层状反射。图 5a和图 5b分别为单一纵向卡尔曼滤波25次和50次剖面显示,可见纵向滤波去噪效果不佳,横向连续性改善甚微,且滤波超过50次后同相轴出现失真。图 6a和图 6b分别为本文方法滤波50次和100次结果,可见该方法较好地恢复了有效信号并合理压制了噪声,同相轴反射特征也得到较好恢复;同时,本文方法滤波效果和效率都优于单一横向或纵向滤波方法。
|
图 1 Marmousi2模型(a)及选取的(绿框)测试部分(b)[1] |

|
图 2 原始合成(a)及加入1∶2高斯随机噪声(b)剖面 |
|
图 3 二维中值滤波1次(a)和100次(b)后剖面对比 |

|
图 4 单一横向卡尔曼滤波100次(a)和200次(b)后剖面对比 |
|
图 5 单一纵向卡尔曼滤波25次(a)和50次(b)后剖面对比 |
|
图 6 横纵向同时滤波50次(a)和100次(b)后剖面对比 |
选用新疆吉木萨尔芦凹陷实际地震资料(图 7)测试本文方法的实用性。针对该区二叠系芦草沟组页岩油储层岩性复杂、纵向薄且目的层小断裂发育导致水平井钻遇率低的问题,重新采集了高密度高次覆盖宽方位地震三维资料。

|
图 7 实际原始地震剖面(a)及本文方法滤波后剖面(b) |
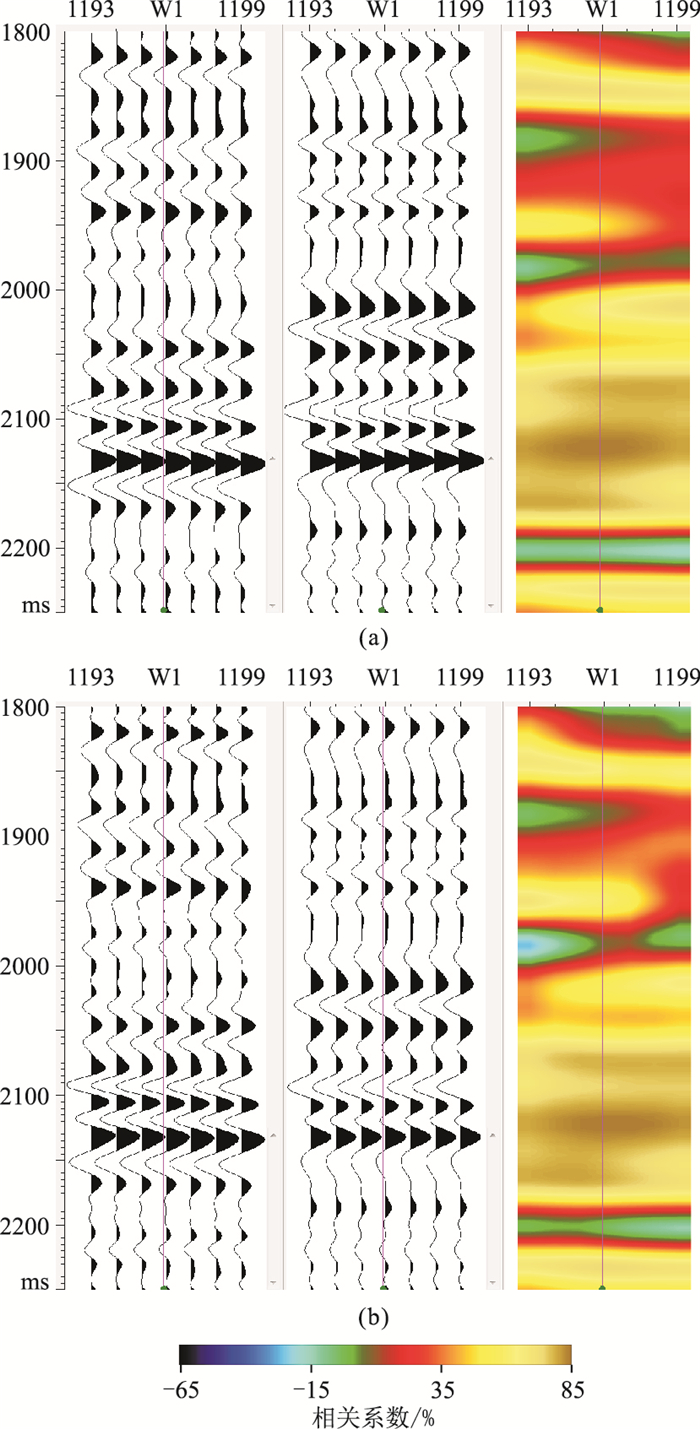
图 7a为OVT域叠前时间偏移成果数据。可见整体断裂特征清楚,合成记录与地震记录对应性较好,整体相关系数为70.5%(图 8a)。但为提高资料的薄层识别能力,保留较多高频信息,高频段的噪声却影响目的层小断裂识别,由于目的层断距大多小于10m,断层的剖面地震相特征主要以同相轴弯曲、挠曲为主,因此曲率属性在识别小断裂方面具有优势。图 9a中目的层断层多以延伸短的正断层为主,但由于噪声干扰,断裂之间组合特征,尤其是靠资料边界的断层特征不清楚(图中红色圆圈内)。通过本文滤波方法后,资料信噪比及横向连续性得到明显改善,剖面上断层特征清晰(图 7b),滤波后地震记录与原始记录在纵、横向上振幅强弱关系以及波组关系都保持较好的一致性,且合成记录与原地震记录对应性仍然较好,整体相关系数保持在大约71.6%(图 8b)。
|
图 8 实际原始地震剖面(a)及本文方法滤波后剖面(b) 左:W1井旁道;中:井数据合成道;右左图与中图的相关 |
|
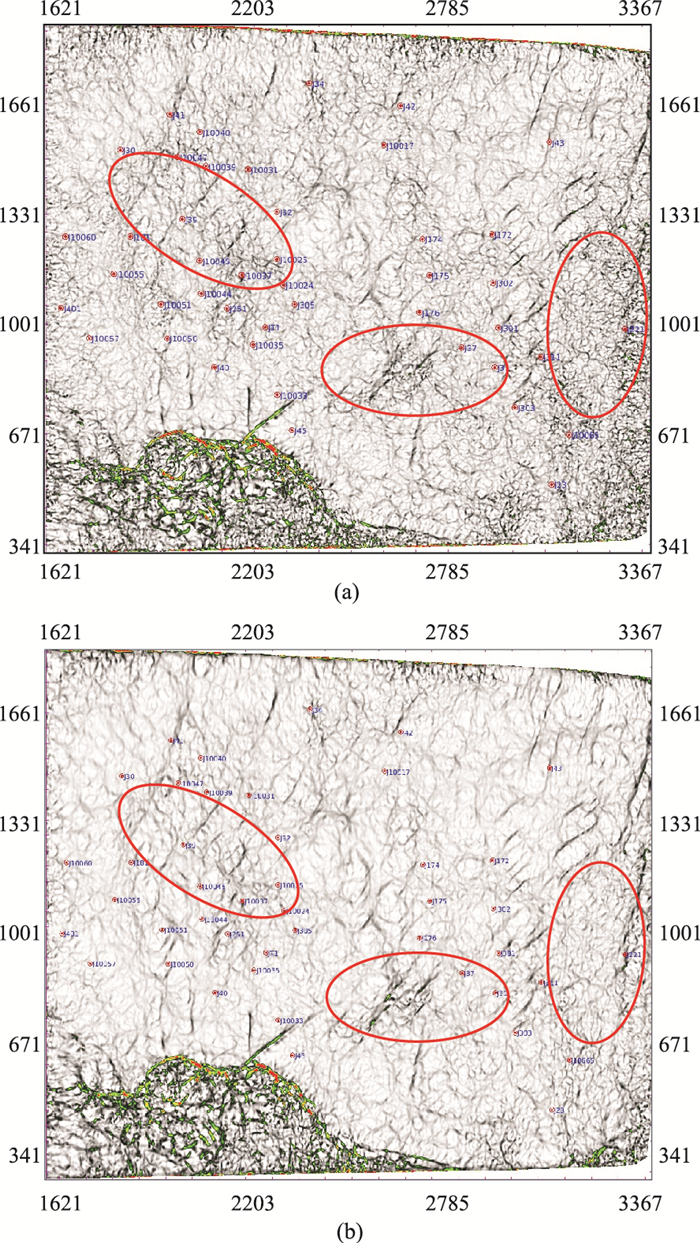
图 9 本文方法滤波前、后目的层曲率属性平面图 |
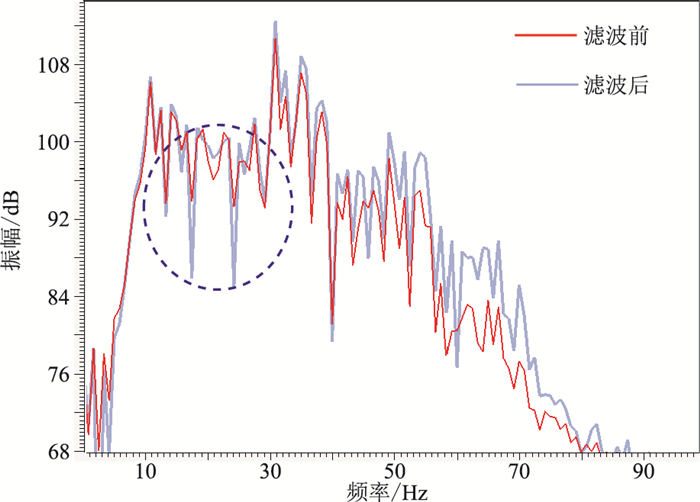
在滤波地震资料上提取目的层的曲率属性,发现小断层及其组合的特征清楚,小断裂主要呈南北向条带状分布,走向以北东—南西向为主,同时在滤波后平面上可较清楚地展示一些与其正交的延续相对较长的断裂,原始资料部分未识别出的断层,在滤波后属性平面上可清晰展示且去除了绝大部分的干扰信息(图 9b);同时从滤波后地震频谱看,该方法与传统的频率滤波方法不同,只是消除高频段的噪声成分,保护了高频有效信号(图 10),还对10~30Hz频带缺失的部分频率成分起到一定改善作用(图 10蓝圈)。这样就为工区目的层微构造精细解释及后续水平井位部署和压裂方案设计提供了有利的保障。
|
图 10 本文方法滤波前(a)、后(b)频谱对比图 |
地震资料经过高频补偿处理后往往会表现出信噪比降低和横向连续性变差等特点,本文鉴于卡尔曼滤波在恢复有效信号方面的优势,提出基于卡尔曼滤波原理对地震资料横纵向同时滤波的方法,目的是提高地震资料信噪比和横向连续性。通过方法研究并针对模型和实际资料测试,取得以下认识:
(1) 对地震资料做横向卡尔曼滤波,所取得的信噪比和连续性的改善远优于单一纵向滤波;
(2) 经过测试发现,基于卡尔曼滤波原理的地震资料横、纵向以迭代循环滤波次数4∶1的形式进行横纵向组合滤波,在改善地震资料的信噪比和连续性的效果和效率两方面都优于单一横向或纵向及二维中值滤波;
(3) 实际资料测试表明,本文方法能显著提高地震资料信噪比及同相轴的连续性,且不会造成高频成分缺失,可有效确保构造解释精度。
| [1] |
梁顺军, 梁霄, 陈江力, 等. 山地复杂构造倒转背斜地震剖面反射特征及油气成藏分析[J]. 中国石油勘探, 2019, 24(3): 377-390. LIANG Shunjun, LIANG Xiao, CHEN Jiangli, et al. Seismic reflection features and analysis of hydrocarbon accumulation of reversed anticlines in complicated mountainous areas[J]. China Petroleum Exploration, 2019, 24(3): 377-390. DOI:10.3969/j.issn.1672-7703.2019.03.011 |
| [2] |
张军华, 吕宁, 田连玉, 等. 地震资料去噪方法综合评述[J]. 石油地球物理勘探, 2005, 40(1): 121-127. ZHANG Junhua, LYU Ning, TIAN Lianyu. Comprehensive review on denoising methods of seismic data[J]. Oil Geophysical Prospecting, 2005, 40(1): 121-127. |
| [3] |
徐彦凯, 曹思远, 潘晓, 等. 随机噪声的局部正交压制方法[J]. 石油地球物理勘探, 2019, 54(2): 280-287. XU Yankai, CAO Siyuan, PAN Xiao, et al. A local orthogonalization for seismic random noise suppression[J]. Oil Geophysical Prospecting, 2019, 54(2): 280-287. |
| [4] |
薛林, 程浩, 巩恩普, 等. Shearlet域自适应阈值地震数据随机噪声压制[J]. 石油地球物理勘探, 2020, 55(2): 282-291. XUE Lin, CHENG Hao, GONG Enpu, et al. Random noise suppression using adaptive threshold in Shearlet domain[J]. Oil Geophysical Prospecting, 2020, 55(2): 282-291. |
| [5] |
董烈乾, 汪长辉, 李长芬, 等. 利用自适应中值滤波方法压制混叠噪声[J]. 地球物理学进展, 2018, 33(4): 1475-1479. DONG Lieqian, WANG Changhui, LI Changfen, et al. Blending noise removal utilizing an adaptive me-dian filter[J]. Progress in Geophysics, 2018, 33(4): 1475-1479. |
| [6] |
孙哲, 王建锋, 王静, 等. 基于时空变中值滤波的随机噪声压制方法[J]. 石油地球物理勘探, 2016, 51(6): 1094-1102. SUN Zhe, WANG Jianfeng, WANG Jing, et al. Random noise elimination based on the time-space variant median filtering[J]. Oil Geophysical Prospecting, 2016, 51(6): 1094-1102. |
| [7] |
张岩, 任伟建, 唐国维. 应用结构聚类字典学习压制地震数据随机噪声[J]. 石油地球物理勘探, 2018, 53(6): 1119-1127. ZHANG Yan, REN Weijian, TANG Guowei. Random noise suppression on seismic data based on structured-clustering dictionary learning[J]. Oil Geophysical Prospecting, 2018, 53(6): 1119-1127. |
| [8] |
赵德斌, 黄真萍, 王春梅. F-X域奇异值分解预测滤波法随机噪声衰减[J]. 石油物探, 1998, 37(3): 29-33. ZHAO Debin, HUANG Zhenping, WANG Chunmei. Random noise attenuation using predictive filtering in F-X domain by singular value decomposition[J]. Geo-physical Prospecting for Petroleum, 1998, 37(3): 29-33. |
| [9] |
康冶, 于承业, 贾卧, 等. f-x域去噪方法研究[J]. 石油地球物理勘探, 2003, 38(2): 136-138. KANG Ye, YU Chengye, JIA Wo, et al. A study on noise-suppression method in f-x domain[J]. Oil Geophysical Prospecting, 2003, 38(2): 136-138. DOI:10.3321/j.issn:1000-7210.2003.02.007 |
| [10] |
高静怀, 毛剑, 满蔚仕, 等. 叠前地震资料噪声衰减的小波域方法研究[J]. 地球物理学报, 2006, 49(4): 1155-1163. GAO Jinghuai, MAO Jian, MAN Weishi, et al. On the denoising method of prestack seismic data in wavelet domain[J]. Chinese Journal of Geophysics, 2006, 49(4): 1155-1163. DOI:10.3321/j.issn:0001-5733.2006.04.030 |
| [11] |
Ouadfeul S A, Aliouane L. Random seismic noise attenuation data using the discrete and the continuous wavelet transforms[J]. Arabian Journal of Geosciences, 2014, 7(7): 2531-2537. DOI:10.1007/s12517-013-1005-3 |
| [12] |
Kalman R. A new approach to linear: filtering and predicted problems[J]. Journal of Basic Engineering, 1960, 82(2): 61-63. |
| [13] |
Thorp J. Optimal tracking of maneuvering targets[J]. IEEE Transactions on Aerospace & Electronic Systems, 1973, AES-9(4): 512-519. |
| [14] |
Reid R E, Tugcu A K, Mears B C. The use of wave filter design in Kalman filter state estimation of the automatic steering problem of a tanker in a seaway[J]. IEEE Transactions on Automatic, 1984, 29(7): 577-584. DOI:10.1109/TAC.1984.1103591 |
| [15] |
Jo G N, Choi H S. Velocity-aided underwater navigation system using receding horizon Kalman filter[J]. IEEE Journal of Oceanic Engineering, 2006, 31(1): 565-573. |
| [16] |
Shi X K, Wen J, Liu J W, et al. Application and improvement of an adaptive ensemble Kalman filter for soil moisture data assimilation[J]. Science China: Earth Sciences, 2010, 53(11): 1700-1708. DOI:10.1007/s11430-010-4107-8 |
| [17] |
乐新安, 万卫星, 刘立波, 等. 基于Gauss-Markov卡尔曼滤波的电离层数值同化现报预报系统的构建——以中国及周边地区为例的观测系统模拟试验[J]. 地球物理学报, 2010, 53(4): 787-795. LE Xin'an, WAN Weixing, LIU Libo, et al. Development of an ionospheric numerical assimilation now cast and forecast system based on Gauss-Markov Kalman filter: an observation system simulation experiment taking example for China and its surrounding area[J]. Chinese Journal of Geophysics, 2010, 53(4): 787-795. DOI:10.3969/j.issn.0001-5733.2010.04.003 |
| [18] |
Vullings R, Vries B D, Bergmans J W M. An adaptive Kalman filter for ECG signal enhancement[J]. IEEE Transactions on Bio-medical Engineering, 2010, 58(4): 1094-1103. |
| [19] |
Valverde G, Terzija V. Unscented Kalman filter for power system dynamic state estimation[J]. IET Ge-neration Transmission & Distribution, 2011, 5(1): 29-37. |
| [20] |
胡志辉, 冯久超. 基于UKF的多用户混沌通信[J]. 物理学报, 2011, 60(7): 83-88. HU Zhihui, FENG Jiuchao. Chaotic communications with multiuser based on unscented Kalman filter[J]. Acta Physica Sinica, 2011, 60(7): 83-88. |
| [21] |
Crump N D. A Kalman filter approach to deconvolution of seismic signals[J]. Geophysics, 1974, 39(1): 1-13. DOI:10.1190/1.1440408 |
| [22] |
董敏煜, 王振华. 地震资料自适应时变卡尔曼反褶积[J]. 地球物理学报, 1991, 34(2): 248-258. DONG Minyu, WANG Zhenhua. Adaptive time-variable deconvolution for seismic data using Kalman predictor model[J]. Chinese Journal of Geophysics, 1991, 34(2): 248-258. DOI:10.3321/j.issn:0001-5733.1991.02.014 |
| [23] |
Mendel J M. White-noise estimators for seismic data processing in oil exploration[J]. IEEE Transactions on Automatic Control, 1977, 22(5): 694-706. DOI:10.1109/TAC.1977.1101597 |
| [24] |
邓小英, 胡健, 李月, 等. 一种新的基于卡尔曼滤波的地震记录同相轴跟踪方法及性能分析[J]. 地球物理学报, 2014, 57(1): 270-279. DENG Xiaoying, HU Jian, LI Yue, et al. A new tracking approach of the seismic record event based on Kalman filtering and its performance analysis[J]. Chinese Journal of Geophysics, 2014, 57(1): 270-279. |
| [25] |
霍国栋, 杜启振, 王秀玲, 等. 纵向和横向同时约束AVO反演[J]. 地球物理学报, 2017, 60(1): 271-282. HUO Guodong, DU Qizhen, WANG Xiuling, et al. AVO inversion constrained simultaneously in vertical and lateral directions[J]. Chinese Journal of Geophysics, 2017, 60(1): 271-282. |
| [26] |
Chen G, Wang X J, Wu B C, et al. Computation of dry-rock VP/VS ratio, fluid property factor, and density estimation from amplitude-variation-with-offset inversion fluid property factor and AVO inversion[J]. Geophysics, 2018, 83(6): R669-R679. DOI:10.1190/geo2017-0621.1 |
| [27] |
郑笑雪, 杜启振, 孟宪军, 等. 横向约束分步叠前弹性参数反演[J]. 石油地球物理勘探, 2017, 52(4): 760-769. ZHENG Xiaoxue, DU Qizhen, MENG Xianjun, et al. Lateral constraint two-step prestack elastic parameter inversion[J]. Oil Geophysical Prospecting, 2017, 52(4): 760-769. |
| [28] |
Martin G S, Wiley R, Martfurt K J. Marmousi2:an elastic upgrade for Marmousi[J]. The Leading Edge, 2006, 25(2): 156-166. DOI:10.1190/1.2172306 |



 陈刚, 新疆克拉玛依市迎宾街道36号新疆油田勘探开发研究院油藏评价研究所, 834000。Email:
陈刚, 新疆克拉玛依市迎宾街道36号新疆油田勘探开发研究院油藏评价研究所, 834000。Email: 