可控震源是由扫描信号(变频的时间信号)控制振子系统输出能量,但扫描信号与输出力信号之间存在差异,此差异来自一个复杂的系统响应。首先是扫描信号转换成驱动信号控制伺服阀,调节液压系统流量输出实现对输出力的控制[1],但伺服阀和液压系统的响应往往存在非线性[2-3],这就造成信号失真。另外,地面的响应与振子系统还存在耦合问题。这些因素造成的综合畸变很难用一个简单的函数描述,而畸变造成的结果首先是输出能量与预期有差异,同时还产生了大量的谐波噪声[4-6],即会将一部分振动能量变成谐波噪声,进而影响了输出信号的信噪比[7-8]。以往是在处理环节解决此类问题[7-8],而现今将这一个过程提前到激发阶段,以保证输出信号的精度。
目前激发阶段主要有两类解决方案:一类是通过硬件改造提高响应精度,从而减少畸变;另一类是通过改变扫描信号减少谐波干扰的产生。现有的激发阶段去谐波技术中,硬件方面主要通过对重锤信号与平板信号非线性二次拟合求取改正量,进而实时控制伺服阀进行改正,提高响应精度,从而减小畸变[4-5, 9-10],此方式存在改造复杂、地面响应与振子系统之间畸变降低不明显的缺陷。而软件方面是通过利用平板信号与重锤信号的差异拟合实现扫描信号的校正[5];该方法简单快捷,主要表达的是振子系统的畸变情况,对地表变化的适应能力较差。
本文基于对扫描信号激发后所得力信号进行离散余弦变换(DCT)的谐波反演结果分析,精确获得谐波干扰信息,并实现扫描信号校正。即预设目标就是使输出的力信号逼近设计扫描信号,从而使震源输出的地震信号形态处于最佳,用力信号作为求差函数要比通过平板信号与重锤信号的差异拟合含有更丰富、更全面的地面与平板耦合信息;而用于校正的差异函数由力信号和预设扫描信号DCT谐波分量得到,因此算法反映谐波变化更完整、直接;初步应用就取得良好效果。
1 实现原理事实上,可控震源激发地震信号时,扫描信号本身即是期望输出信号,但由于振子系统的响应误差以及与地面耦合问题,常规扫描输出得到的信号与扫描信号往往存在较大差异,该差异在时间域表现为某一时刻输出信号的幅度变化,在时频域表现为谐波噪声。一般硬件校正方法是在时间域由当前时刻差异直接实时校正下一时刻输出,但这种自适应改正大多会引起更大的谐波干扰(图 1)。本文通过对扫描信号激发获得的力信号进行DCT,在谐波域进行谐波反演分析,获得精确谐波干扰信息,并加以校正,显然比时间域直接进行校正更稳健。时间域求差异时一些偶发性变化会显著影响改正函数,使改正后扫描信号难以稳定地压制谐波干扰。对比分析可知时间域随机波动在DCT域影响较小,且较稳定,故本文采用在该域进行校正。
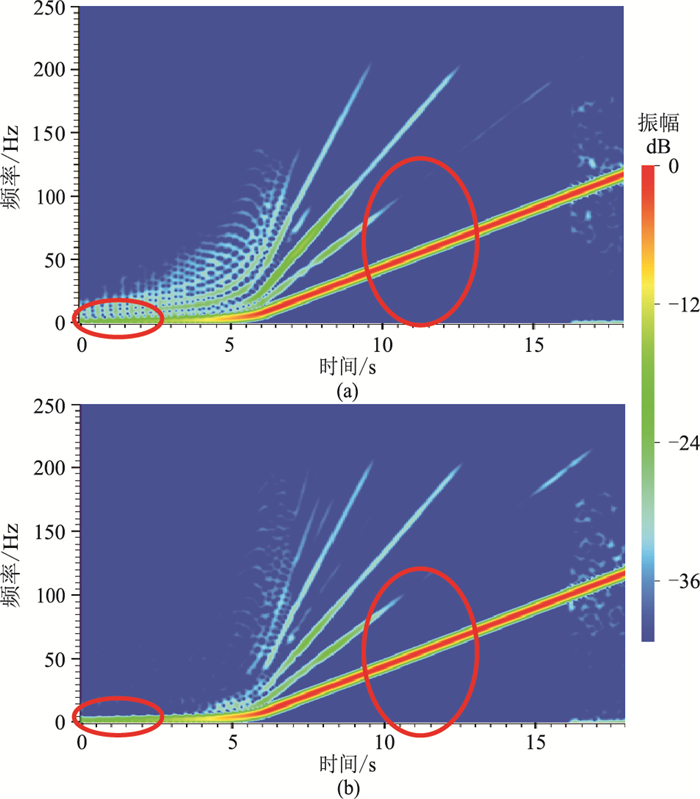
|
图 1 正常(a)和校正后(b)扫描获得的力信号时频谱 |
首先用预设扫描信号控制指定震源在地表进行扫描,获得相应的力信号。
分别对扫描信号与力信号做DCT
| $ {\rm{dct}}\left( u \right) = C\left( u \right)\sqrt {\frac{2}{N}} \mathop \sum \limits_{x = 0}^{N - 1} s\left( x \right){\rm{cos}}\frac{{\left( {2x + 1} \right)u{\rm{ \mathit{ π} }}}}{{2N}} $ | (1) |
| $ C\left( u \right) = \left\{ \begin{array}{l} \frac{1}{{\sqrt 2 }}\;\;\;\;\;\;\;\;\;\;\;\;\;u = 0\\ 1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;u \ne 0 \end{array} \right. $ | (2) |
式中:u为谐波分量;s(x)为需进行谐波分析的信号,做谐波分析时为扫描信号,同理力信号的谐波谱的输入为力信号;N表示扫描次数。
设扫描信号的谐波谱为Sdct,对应的力信号的谐波谱为Fdct。用预设扫描信号谐波谱Sdct减去力信号Fdct的谐波谱,得到剩余谐波谱
| $ {\Delta _{{\rm{dct}}}}\left( u \right) = {S_{{\rm{dct}}}} - {F_{{\rm{dct}}}} $ | (3) |
对剩余谐波谱Δdct(u)做反离散余弦变换(IDCT),得到剩余谐波的时频信号
| $ f\left( t \right) = \mathop \sum \limits_{u = 0}^{N - 1} C\left( u \right){\Delta _{{\rm{dct}}}}\left( u \right){\rm{cos}}\frac{{\left( {2t + 1} \right){\rm{ \mathit{ π} }}}}{{2N}}u $ | (4) |
| $ C\left( u \right) = \left\{ \begin{array}{l} \sqrt {\frac{1}{N}} \;\;\;\;\;\;\;\;\;u = 0\\ \sqrt {\frac{2}{N}} \;\;\;\;\;\;\;\;\;u \ne 0 \end{array} \right. $ | (5) |
然后将剩余谐波的时频信号f(t)对预设扫描信号Sorig(t)进行校正,得到新扫描信号Snew(t);用该新扫描信号替代原设计信号进行扫描,获得校正后的扫描结果
| $ {S_{{\rm{new}}}}(t) = {S_{{\rm{orig}}}}(t) + f(t) $ | (6) |
此过程可用同一震源的多震次力信号进行统计或迭代,优选压制谐波噪声与输出能量达到期望校正量,循环结束,输出新扫描信号。
2 校正扫描信号实现及调整 2.1 校正扫描信号实现按照以上原理,首先从测试或采集地震数据提取相关震源的扫描信号和力信号(图 2)。

|
图 2 扫描信号(红色)和力信号(蓝色)波形示意图 |
分别对扫描信号和力信号进行DCT,获得各自的DCT谱(图 3)。从图 3a与图 3b的对比可知,谐波谱有较大差异,扫描信号的谐波谱集中在基波区间内,而力信号则出现很多基波外的谐波分量,这些谐波分量即是不在扫描范围内的谐波干扰。图 4显示了两者的实际差异,可见除了扫描范围之外的谐波干扰,还存在扫描范围内的谐波干扰,这些谐波在校正过程中都应被消除。由于模拟选择的扫描信号是最大位移(MD)设计的扫描信号,即低频段(1.5~6.0Hz)是非线性扫描,6.0Hz以上是线性扫描,所以从剩余DCT谱中看到连接点处的谐波干扰最大。
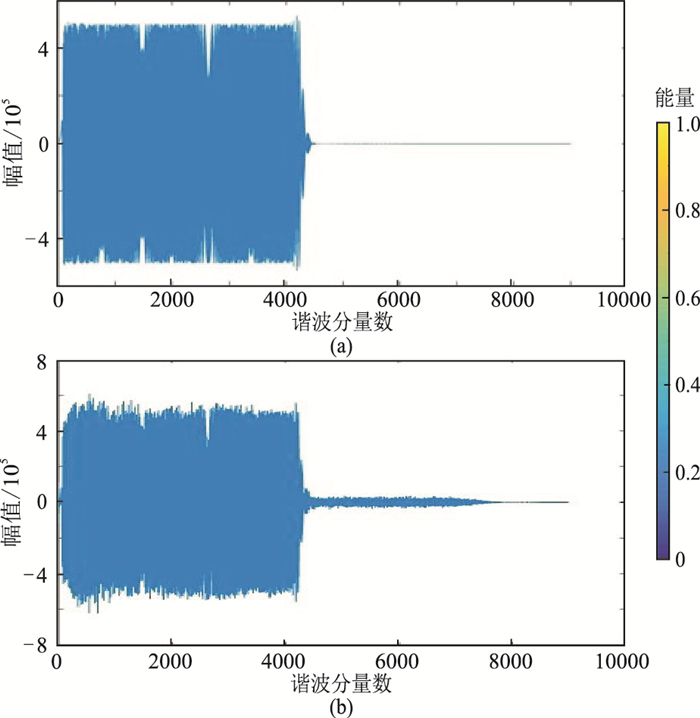
|
图 3 扫描信号(a)与力信号(b)的DCT谱 |
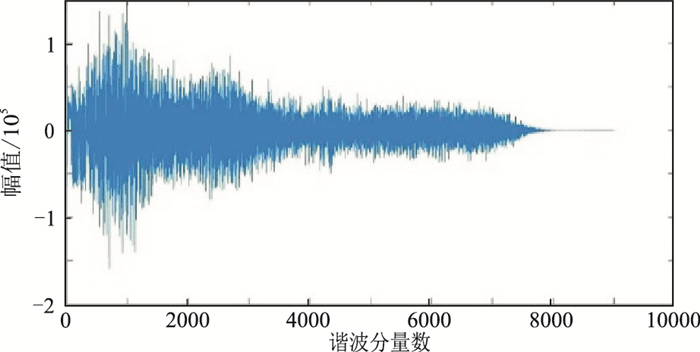
|
图 4 剩余DCT分量 |
将剩余DCT分量变换到时间域,即得到每一时刻时间校正量(图 5a),用该校正量对原设计扫描信号进行校正,获得一个新的扫描信号(图 5b)。
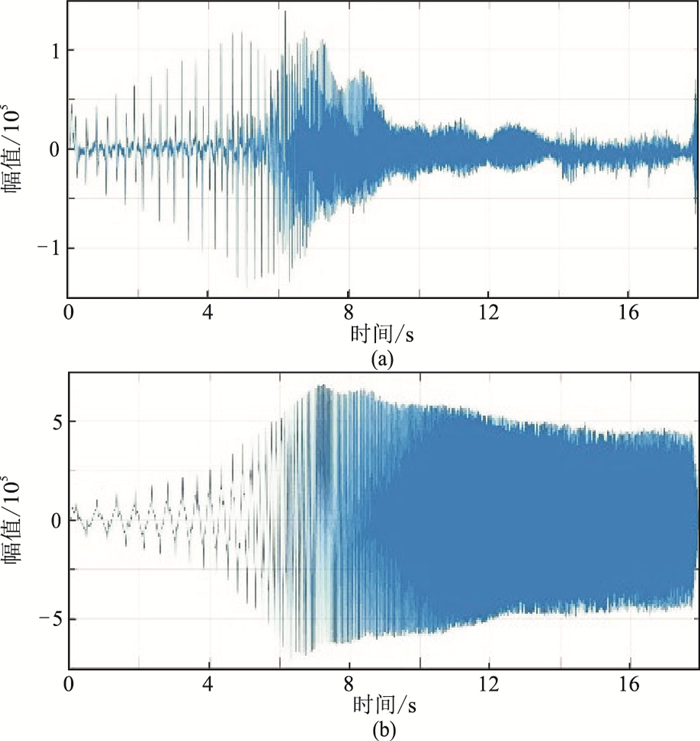
|
图 5 振幅校正量(a)与校正后扫描信号(b) |
对照扫描信号,振幅校正量的时间分布同样可以看到扫描频段连接处的校正量最大。
2.2 校正扫描信号验证在获取指定震源的校正量后,室内验证过程通过将求取的校正量施加到同属于该震源的其他炮点的力信号上,观测该震源的系统畸变以及地表耦合是否一致,若一致表明方法有效。
图 6a和图 7a显示参与计算校正扫描信号激发点力信号的校正效果(放大了低频部分),可直观地看到对本炮的校正是完美的,力信号的振幅波动得到全面改正。
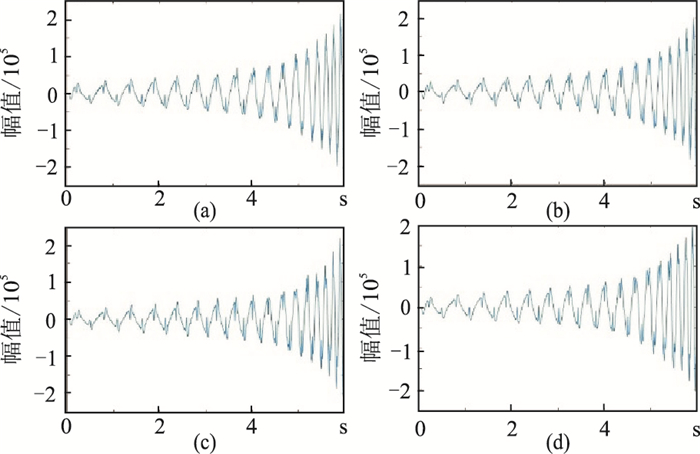
|
图 6 分析用力信号(a)和验证用力信号(b、c、d) |

|
图 7 施加校正量后的分析用(a)和验证用(b、c、d)力信号 |
为了进一步验证此校正结果是否可持续使用,即是否只需做一次扫描信号改正设计就可以用于整个工区,遂将该校正量施加到该震源的所有资料中,并观察其是否有效。图 6、图 7其余三个信号的结果对比显示,其他炮在施加了同样的改正量,力信号也得到极大地改善。其原因是震源振子系统的畸变是基本稳定的,而对于同一种地表而言,耦合畸变也相差不大。而在实施过程中,力信号是被实时监控的,若由于地表变化使校正扫描信号不能满足,现场就实时重新计算一个适用于新地表的校正扫描信号。这里要提醒的是不同震源系统的畸变存在较大差异,不能用一台震源的校正扫描信号代替所有震源的扫描信号。
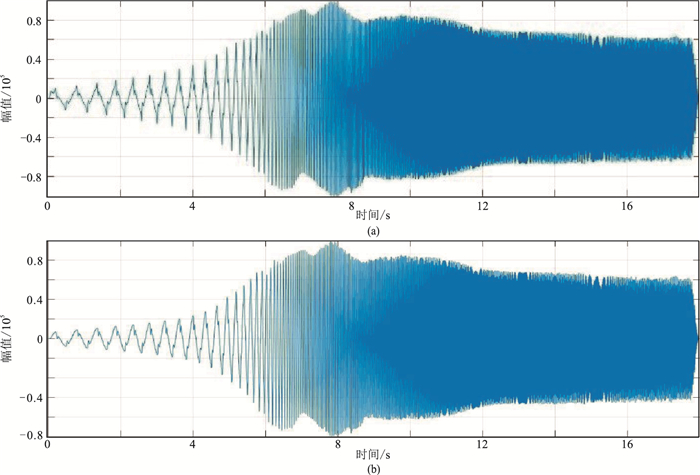
2.3 校正扫描信号调整观测对比原设计扫描信号与校正后扫描信号,发现有许多校正后扫描信号的幅值超出设计扫描信号(图 8),这就意味着震源出力的加大。由于MD设计充分考虑了震源系统低频输出特性极限,那么进一步加大出力输出就会引起超限现象;同时由于低频段扫描信号是逐点设计的非线性扫描,不能用统一的归一化约束力信号的输出。此情形有两套解决方案:一种是在预设扫描参数时,考虑校正的超限问题(如预设最大超限为5%),则可在设计时降低(5%)出力来规划扫描信号;另一种方案是通过限幅函数来调整。限幅函数主要采用以下两种。
|
图 8 常规(红色)与校正后(黄色)扫描信号叠合显示图 |
第一种是通过与预设扫描信号的比对来实现(图 9)。设校正后扫描输出值为Snew(t),设计扫描信号值Sorig(t),那么限制如下
| $ \left\{ \begin{array}{l} {S_{{\rm{new}}}}\left( t \right) = {S_{{\rm{orig}}}}\left( t \right)\;\;\;\;\;{S_{{\rm{new}}}}\left( t \right) > {S_{{\rm{orig}}}}\left( t \right)\\ {S_{{\rm{new}}}}\left( t \right) = {S_{{\rm{new}}}}\left( t \right)\;\;\;\;\;{S_{{\rm{new}}}}\left( t \right) \le {S_{{\rm{orig}}}}\left( t \right) \end{array} \right. $ | (7) |
|
图 9 正常校正(a)及振幅限制后(b)扫描信号 |
第二种是最大差异限幅。设Maxdiff为校正扫描信号与预设扫描信号的最大差异,那么有
| $ {\rm{Maxdiff}}\left( \tau \right) = \max \left\{ {{\rm{abs}}\left[ {{S_{{\rm{orig}}}}\left( t \right) - {S_{{\rm{new}}}}\left( t \right)} \right]} \right\} $ | (8) |
| $ {S_{{\rm{new}}}}\left( t \right) = \frac{{{\rm{Maxdiff}}\left( \tau \right)}}{{{\rm{abs}}\left[ {{S_{{\rm{orig}}}}\left( \tau \right)} \right]}} * {S_{{\rm{new}}}}\left( t \right) $ | (9) |
式中:max代表计算最大值;abs代表求取绝对值;τ代表差异最大的幅值对应的时间。
3 应用效果可控震源通常作业时,若是单台震源进行激发,就会记录力信号,这时利用以往资料就可实现扫描信号校正;若是多台震源激发,力信号是不被要求记录的,因此有必要在现场开工前完成一项测试,即对力信号进行记录以便于进行扫描信号校正。
图 10是在中东地区M项目应用该技术得到的数据分析结果[2],现场仅将技术应用与低频扫描部分校正。从预设扫描信号产生的力信号时频谱(图 10a)上,可见低频部分存在较强谐波干扰,1.5~3.0Hz的谐波干扰甚至超过基波能量;而经校正扫描信号扫描获得的力信号时频谱(图 10b)则显示,谐波能量得到了很好压制,超低频段的响应正常。
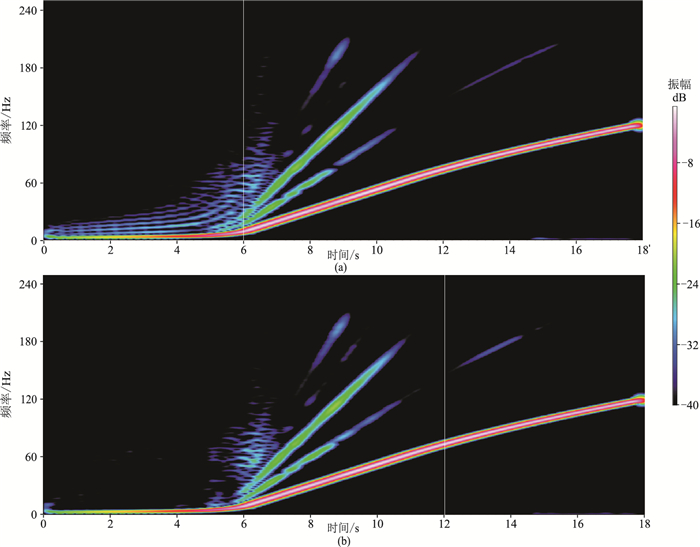
|
图 10 预设扫描(a)与校正扫描(b)获得的力信号时频谱对比 |
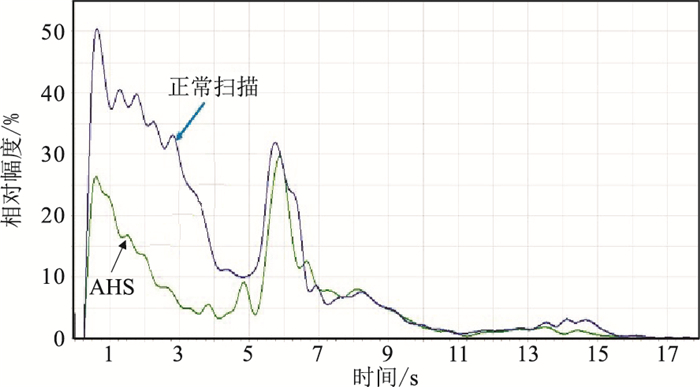
进一步考察震源测试中重要指标谐波畸变有何变化。图 11显示校正扫描前、后的谐波畸变,可见应用校正扫描信号后低频部分的谐波畸变降低了近一倍,极大地改善了震源的输出信号的精度,这也是该方法可降低谐波干扰的根由。
|
图 11 校正前(蓝色)、后(绿色)谐波畸变对比 |
本文AHS方法通过对预设扫描信号产生的力信号进行DCT,精确地提取谐波干扰并加以校正,校正后的扫描可极大地压制谐波干扰的产生,从而改进可控震源的输出子波[11-12],为高精度地震勘探提供优良的地震信号[13-14]。
用DCT实现扫描信号校正的优点在于:时间域中的信号变化不能直接反映谐波干扰的能量变化,即有些时间域瞬时差异的大小不一定对应谐波干扰的差异大小;而将信号变换到谐波域,就可直观地辨别并获取哪些是干扰的谐波成分,将该谐波成分做一次反变换就获得了时间域中代表谐波干扰的差异。因此,也体现了本方法的直接和精确。
这里要说明的是,震源是液压与机械的混动系统,各台震源的对于扫描信号的响应很难保持一致,即谐波干扰产生的时间、能量是会总体上保持在一定水平下变动的,因此每台震源的校正函数是不同的,这要求每台震源都要设定各自专用的校正函数。而且,由于本方法是采用力信号谐波反演分析实现校正的,因此包含了地表因素影响,若地表类型发生变化,则每台震源需重新做扫描信号[11]。
| [1] |
Boucard D and Ollivrin G. Developments in vibrator control[J]. Geophysical Prospecting, 2010, 58(1): 33-40. DOI:10.1111/j.1365-2478.2009.00848.x |
| [2] |
Lebedev A V and Beresnev I A. Nonlinear distortion of signals radiated by vibroseis sources[J]. Geophy-sics, 2004, 69(4): 968-977. |
| [3] |
Lebedev A V, Beresnev I A and Vermeer P L. Model parameters of the nonlinear stiffness of the vibrator-ground contact determined by inversion of vibrator accelerometer data[J]. Geophysics, 2006, 71(3): H25-H32. DOI:10.1190/1.2196870 |
| [4] |
Tellier N and Ollivrin G. Low-frequency vibroseis: current achievements and the road ahead?[J]. First Break, 2019, 37(1): 49-54. DOI:10.3997/1365-2397.n0011 |
| [5] |
Castor K, Bianchi T, Winter O, et al. Noise reduction in vibroseis source[C]. SEG Technical Program Expanded Abstracts, 2014, 33: 16-20.
|
| [6] |
Wei Z and Phillips T F. Enhancing the low-frequency amplitude of ground force from a seismic vibrator through reduction of harmonic distortion[J]. Geophysics, 2013, 78(4): P9-P17. DOI:10.1190/geo2012-0500.1 |
| [7] |
Ras P, Daly M and Baeten G. Harmonic distortion in slip sweep records[C]. SEG Technical Program Expanded Abstracts, 1999, 18: 609-612.
|
| [8] |
Rozemond H J. Slip-sweep acquisition[C]. SEG Technical Program Expanded Abstracts, 1996, 15: 64-67.
|
| [9] |
张慕刚, 骆飞, 魏国伟, 等. 阿联酋超大型地震勘探项目采集技术规划与集成[J]. 天然气勘探与开发, 2019, 42(2): 66-75. ZHANG Mugang, LUO Fei, WEI Guowei, et al. Planning and integration of acquisition technologies for ultra-large seismic exploration project, the United Arab Emirates[J]. Natural Gas Exploration and Development, 2019, 42(2): 66-75. |
| [10] |
张慕刚, 骆飞, 汪长辉, 等. "两宽一高"地震采集技术工业化应用的进展[J]. 天然气工业, 2017, 37(11): 1-8. ZHANG Mugang, LUO Fei, Wang Changhui, et al. Industrialization progress of Wide-azimuth, Broadband, and High-density (WBH) seismic acquisition technique[J]. Natural Gas Industry, 2017, 37(11): 1-8. |
| [11] |
Luo Fei, Liang Xiaofeng, Chen Guodong, et al. Design of broadband sweep signal using the statistical near field wavelet[C]. CPS/SEG Beijing International Geo-physical Conference, 2014, 175-178.
|
| [12] |
许璐, 吴笑荷, 张明振, 等. 基于局部频率约束的动态匹配追踪强反射识别与分离方法[J]. 石油地球物理勘探, 2019, 54(3): 587-593. XU Lu, WU Xiaohe, ZHANG Mingzhen, et al. Strong reflection identification and separation on local-frequency-constrained dynamic matching pursuit[J]. Oil Geophysical Prospecting, 2019, 54(3): 587-593. |
| [13] |
李培明, 宋家文, 柳兴刚, 等. 海上高效混叠采集参数优化设计[J]. 石油地球物理勘探, 2020, 55(4): 707-715. LI Peiming, SONG Jiawen, LIU Xinggang, et al. Optimization of parameter design for high-productivity marine blending acquisition[J]. Oil Geophysical Prospecting, 2020, 55(4): 707-715. |
| [14] |
肖虎, 唐东磊, 杨国平, 等. 可控震源动态扫描技术及应用[J]. 石油地球物理勘探, 2019, 54(3): 493-499. XIAO Hu, TANG Donglei, YANG Guoping, et al. Vibroseis dynamic sweep[J]. Oil Geophysical Prospecting, 2019, 54(3): 493-499. |



 骆飞, 河北省涿州市范阳中路307号中国石油集团东方地球物理公司国际勘探事业部国际项目支持中心, 072751。Email:
骆飞, 河北省涿州市范阳中路307号中国石油集团东方地球物理公司国际勘探事业部国际项目支持中心, 072751。Email: 