② 中国石油化工股份有限公司胜利油田分公司勘探开发研究院, 山东东营 257015
② Exploration and Development Research Institute, Sinopec Shengli Oilfied Company, Dongying Shangdong, 257105, China
断层检测是地震资料解释的一项重要工作[1-2]。人工手动拾取断层不仅耗时、耗力,而且具有较强的主观性[3-4]。为了提高效率,研究人员提出了多种断层自动检测方法。Gersztenkorn等[5]提出的C3相干体技术能极大地提高断层解释精度。张瑞等[6]使用分频蚂蚁追踪技术能够识别深部小断层,识别结果较为清晰、准确。孙振宇等[7]提出了一种基于支持向量机(SVM)的断层自动识别方法,能够有效识别地震数据中的小断层。李军等[8]提出了基于魔方矩阵的断层边缘检测方法,利用断层倾角和倾向等信息可以检测地震数据中断层的分布和发育方向。随着地震勘探技术的不断发展,采集的地震数据量越来越大,传统的断层检测方法在效率和精度方面存在明显的不足。如何从海量的地震资料中高效、准确地挖掘更多的断层信息,是当前地震资料解释面临的一项巨大挑战[9-11]。
近年来,随着计算机运算能力的提升,机器学习方法得到了越来越多的应用。深度学习是机器学习的一个热点领域,具有强大的特征提取能力和高效的特征表达能力,被广泛应用于图像分类、目标检测等,并取得了很好的效果[12-14]。深度学习也广泛应用于油气勘探,如横波速度预测[15]、测井曲线重构[16]、盐丘检测[17]和地震资料构造解释[18]等。
基于深度学习的断层检测方法通常采用像素分类或语义分割深度学习网络。Xiong等[19]应用卷积神经网络自动检测三维地震数据中的断层,识别的断层具有较好的连续性。Guo等[20]提出了基于卷积神经网络的断层检测方法,充分学习、利用解释人员的断层拾取经验,自动检测断层,精度较高。Li等[21]提出了编码器—解码器卷积神经网络断层检测方法,即采用一个较小的训练集训练网络,然后逐像素地预测地震数据中的断层。Wu等[22]基于U-Net卷积神经网络,使用人工合成地震数据对搭建的网络模型进行训练,可快速预测实际地震数据中的断层位置。张政等[23]将深度残差网络与迁移学习相结合,增强了网络的断层识别泛化能力。常德宽等[24]提出基于卷积深度神经网络的地震数据断层识别方法,克服深层网络梯度弥散的不足,提高了网络的训练效率。
实际地震数据中往往存在着不同尺度断层,为了提高断层解释效率、改善断层检测效果,本文提出了一种基于深度学习的多分辨率U-Net网络(MultiResU-Net)断层检测方法。首先引入多分辨率模块增强网络模型的多尺度断层检测能力,使用残差路径代替普通跳跃连接,缩小用于拼接的特征图之间的语义差别;然后使用人工合成的地震数据和断层标签数据训练网络模型,在合成数据测试集和二维实际地震数据中断层检测效果均较好;最后将网络模型扩展为三维并与迁移学习结合后,在三维实际地震数据测试中也取得了很好的效果。
1 多分辨率U-Net网络 1.1 U-Net网络U-Net网络由Ronneberger等[25]在2015年提出,最初用于生物医学图像分割任务,如细胞分割、肿瘤检测等。U-Net网络是一种编码器—解码器结构的网络,因网络结构类似于字母"U"而得名。
U-Net网络主要由两大部分构成:①下采样部分,即特征提取部分,每一层由两个3×3卷积序列和一个最大池化层组成;②上采样部分,即特征恢复部分,每一层由两个3×3卷积序列和一个反卷积操作组成,可以将下采样得到的高级语义特征恢复至上一层的尺度。
U-Net网络与全卷积网络(Fully Convolutional Networks,FCN)[26]虽然结构相似,但却采用了完全不同的特征融合方式。U-Net网络每进行一次上采样后,将恢复的特征图与对应特征提取部分得到的相同尺度的特征图在通道(Channel)维度上进行拼接,从而形成更厚的特征层,使同一大小的特征图拥有更多的特征表示,并且不会因占用过多显存而导致网络训练速度下降过多;而FCN仅仅是特征图的简单相加,并不能形成更厚的特征层。
1.2 多分辨率U-Net网络普通U-Net网络中,下采样部分和上采样部分的每一层中的两个3×3卷积序列运算效果等价于一个5×5卷积层运算[27]。多分辨率U-Net网络(图 1)引入多分辨率模块改进普通U-Net网络,将一个3×3卷积层和一个7×7卷积层与上述的5×5卷积层并行,以此增强网络的多尺度断层检测能力[28]。为了进一步减少网络的内存需求,将多分辨率模块中的7×7卷积层替换为具有等价效果的三个3×3卷积序列,此外还在模块中添加了一个1×1的卷积层,使网络能够获取更多的空间信息。
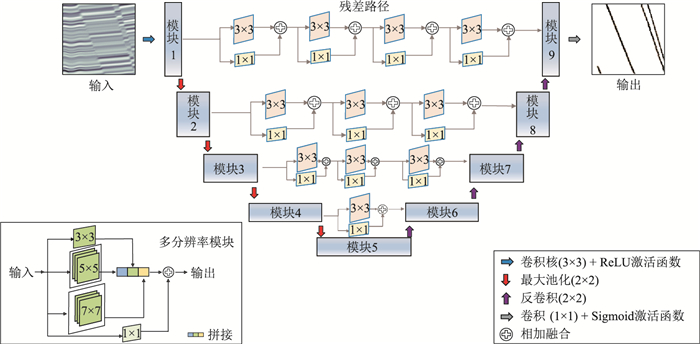
|
图 1 多分辨率U-Net网络结构 |
普通U-Net网络直接将下采样部分得到的特征图与上采样部分得到的相同尺度的特征图通过跳跃连接拼接起来。下采样部分的特征图为浅层、级别较低的特征,而上采样部分的特征图具有更深层、级别更高的特征,因此这两组特征之间存在一定的语义差别,直接拼接可能会对网络训练和预测结果产生不利影响。本文使用残差路径代替普通跳跃连接,残差路径中的非线性操作有望缩小语义差别,使网络模型更容易学习到所需的特征信息。由于下采样部分与上采样部分特征之间的语义差别会随着网络的加深而减小,因而可减少深层残差路径中使用的残差块的数量。本文网络模型从浅层到深层的四条残差路径分别设置4、3、2、1个残差块。
图 1为多分辨率U-Net网络模型结构,将普通U-Net网络中的两个3×3卷积序列替换为多分辨率模块,并通过调整模块中卷积层的卷积核数目防止网络模型的总参数量过多。网络模型分别进行四次下采样和四次上采样,将得到的相同尺度的特征图通过残差路径连接起来,最后输出结果。
2 数据准备与网络训练 2.1 数据集建立深度学习神经网络是一种数据驱动的优化方法,训练数据集的制作是一项重要工作。断层数据集的制作有两种方法可供选择:①人工合成地震数据及其相应的断层标签,以此作为训练和测试数据集分别对网络模型进行训练和测试;②使用实际地震数据和人工拾取的断层标签作为训练集训练网络模型,再将训练完备的网络模型应用于其他实际地震数据进行断层检测。第一种方法解决了训练数据集制作时间长的问题,可以快速制作大量的训练数据,适用于实验研究;第二种方法需要人工标注实际地震数据中的断层位置、制作断层标签数据,或者利用其他传统方法进行断层标注,再从中挑选出较好的断层检测结果作为断层标签数据。人工合成地震数据及其相应断层标签数据的过程如图 2所示。
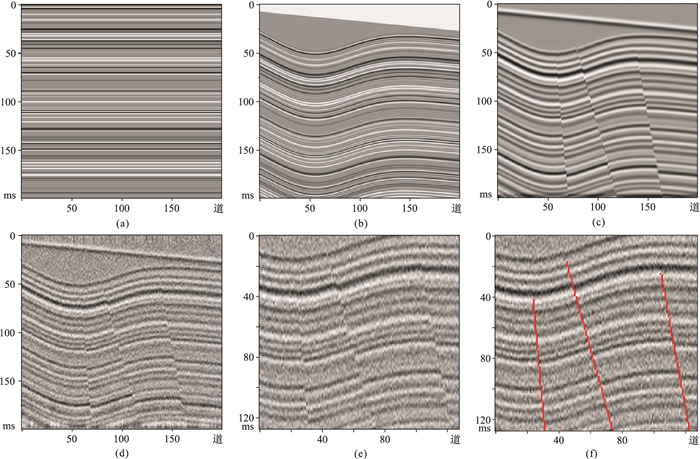
|
图 2 人工合成数据的生成 (a)水平反射系数序列;(b)进行弯曲变形;(c)将数据与雷克子波进行褶积并添加断层;(d)添加噪声;(e)提取的含断层地震数据;(f)提取的断层标签数据 |
首先,创建一个大小为200×200的水平反射系数序列(图 2a),其地质意义为水平沉积地层;其次,在这个水平反射层上应用弯曲变形(图 2b),这个过程相当于水平沉积地层经过地质作用后产生褶皱;再其次,使用雷克子波与模型进行褶积,在模型中添加断层的同时生成相应的断层标签(图 2c),在这一步骤中,还可以使用目标区提取的子波与模型数据的反射系数褶积以进一步减小人工合成数据与实际地震数据之间的差异;然后,添加一定强度的噪声使合成地震数据更具真实性(图 2d);最后,分别从合成地震数据和标签数据中心提取大小为128×128的数据,便可得到含有断层的人工合成地震数据(图 2e)及其相应的断层标签数据(图 2f)。基于此,可以人工合成足量的训练数据和测试数据。
2.2 网络训练本文基于Keras框架搭建网络模型,模型中除了最后一层的激活函数选用Sigmoid外,其他各层均使用ReLU(Rectified Linear Units)激活函数,两者的表达式分别为
| $ {\rm{Sigmoid}}\left( x \right) = \frac{1}{{1 + {{\rm{e}}^{ - x}}}} $ | (1) |
| $ {\rm{ReLU}}(x) = \left\{ \begin{array}{l} x\;\;\;\;x > 0\\ 0\;\;\;\;x \le 0 \end{array} \right. $ | (2) |
ReLU是目前使用最为广泛的一种激活函数,其优点是没有复杂的指数运算,神经网络在训练过程中能以较快的速度收敛,并且在一定程度上避免梯度爆炸和梯度消失问题。最后一层的激活函数选用Sigmoid函数,是因为本文的断层检测任务本质上是一个二分类任务(断层/非断层),Sigmoid函数是二分类神经网络的输出层常用激活函数。
本文使用了5500个大小为128×128的合成地震数据及其对应的断层标签训练并测试网络模型,将其中4455个数据作为训练数据、495个数据作为验证数据、550个数据作为测试数据。训练数据集、验证数据集与测试集不相交。
在正式训练网络之前,首先为网络模型选用不同优化算法(RMSprop、Adam、Adagrad和SGD等函数)进行了30轮(Epoch)的预训练测试,以便选择最合适的优化函数,测试准确度(Accuracy)曲线如图 3所示。由图可见,使用Adagrad和SGD优化函数时,网络训练的收敛速度相对较慢,准确度最终分别收敛至0.94和0.95左右;使用RMSprop和Adam优化函数时收敛相对较快,准确度能达到0.97左右,其中Adam优化函数效果最优。对Adam优化函数的不同学习率(Learning Rate)进行测试,结果如图 4所示。由图可见,当学习率为0.0001时网络训练准确度不仅前期上升较快,且后期能达到最高值。
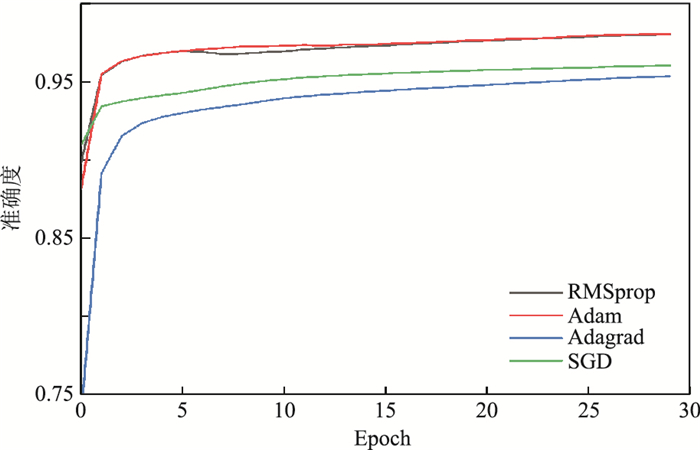
|
图 3 不同优化函数的测试准确度曲线 |
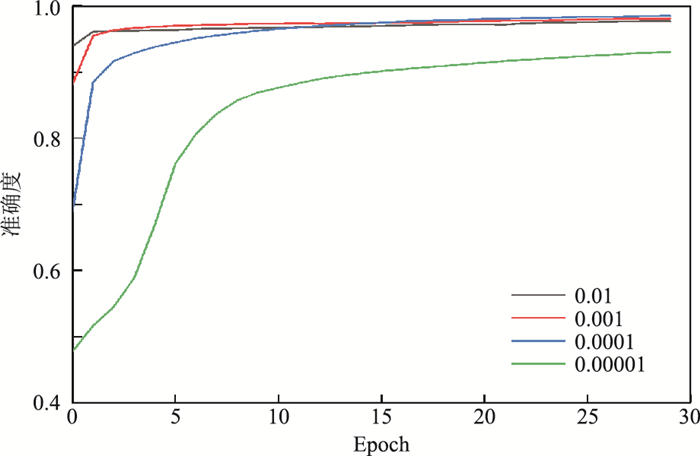
|
图 4 Adam优化函数的不同学习率测试结果 |
在正式训练过程中,使用Adam优化函数对网络模型在反向传播过程中的权重进行优化,学习率设为0.0001;使用二进制交叉熵(Binary Cross-Entropy)损失函数衡量网络的断层预测结果与真实断层标签数据之间的差异。网络训练50轮,将训练得到的准确度曲线(图 5)和损失(Loss)曲线(图 6)分别与普通U-Net网络的准确度曲线和损失曲线对比。
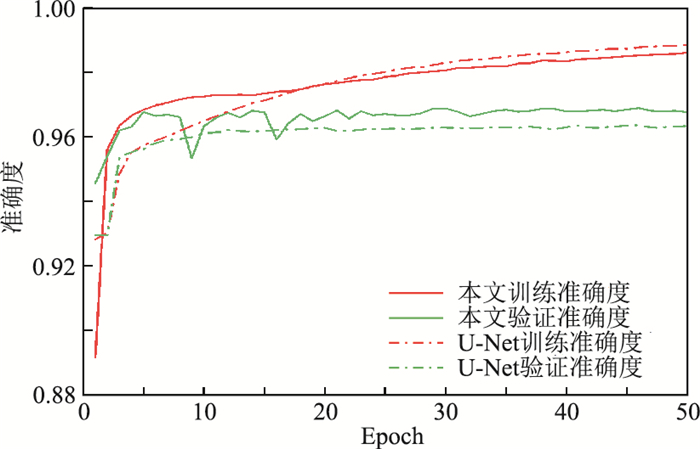
|
图 5 网络准确度曲线 |
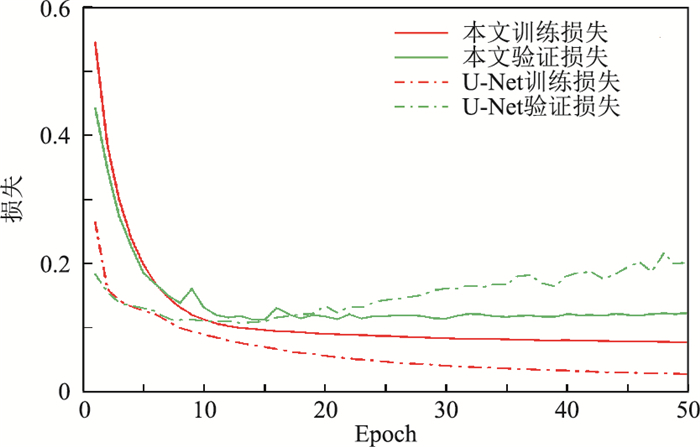
|
图 6 网络损失曲线 |
由图 5和图 6可以看出,多分辨率U-Net网络模型(本文模型)在训练过程中收敛较好,训练准确度曲线(图 5中的红色实线)和验证准确度曲线(图 5中的绿色实线)整体趋势为:在前7轮训练中快速上升,然后趋于稳定,可分别达到98%和97%左右。训练损失曲线(图 6中的红色实线)在前10轮训练中快速下降,训练20轮后便降到0.1以下并在训练50轮后收敛到0.077,验证损失曲线(图 6中的绿色实线)也以较快的速度收敛趋至0.13左右。因此,可初步判断网络模型在训练过程中得到了有效训练,未出现不良训练现象。普通U-Net网络的训练准确度虽然达到了98%以上,可是它的验证准确度却只能趋近于96%左右;其训练损失虽然降到了5%以下,但是验证损失曲线在训练15轮后却开始逐渐上升,这是典型的过拟合现象。如果在实际网络模型训练过程中遇到这一问题,必须提前结束训练或者增加训练样本数量。
2.3 中间层可视化分析为了直观形象地展示数据在网络模型中的变化,分析网络模型各个模块的中间运行状态,对测试数据(图 7)在模块1、3、5、7、9中的部分特征图(图 8) 以及最终断层预测结果(图 9)进行了可视化输出。
|
图 7 输入的测试数据 |

|
图 8 网络中间层的部分特征图 (a)模块1;(b)模块3;(c)模块5;(d)模块7;(e)模块9 |
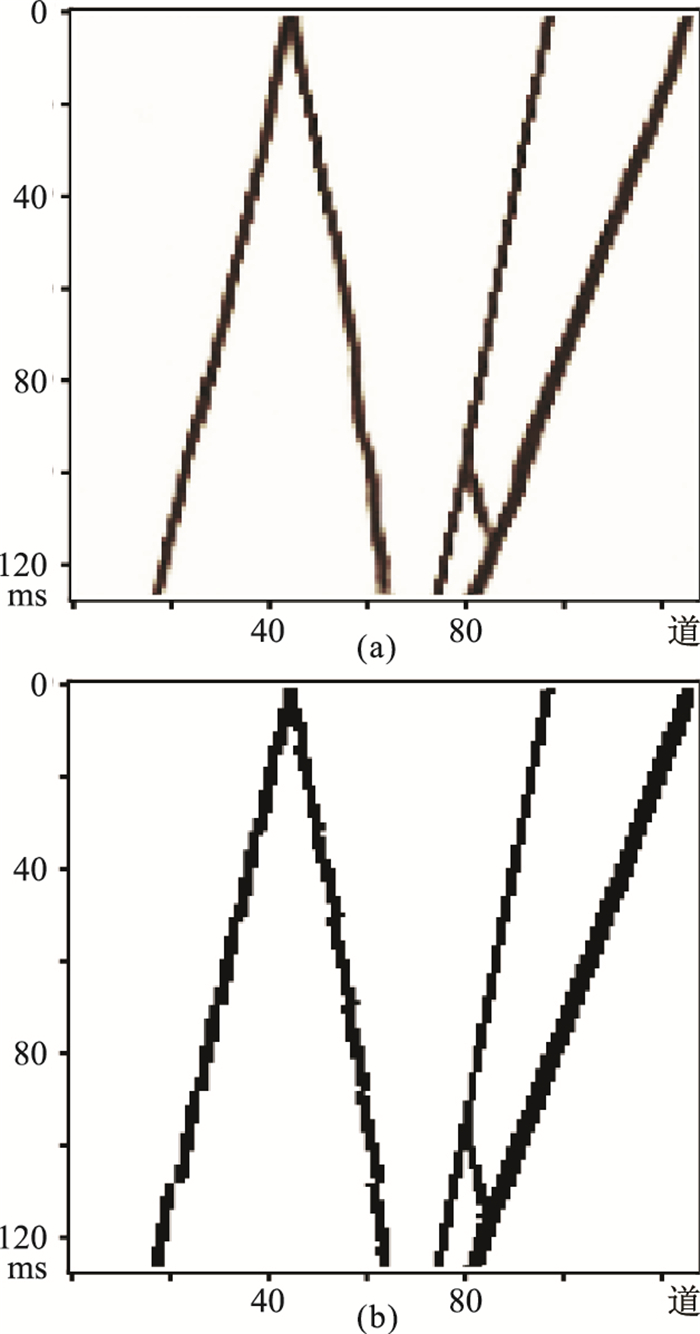
|
图 9 测试数据的断层预测结果(a)与真实断层标签(b)对比 |
其中,模块1、3、5是下采样特征提取模块,模块7、9为上采样特征恢复模块。从图 8a~图 8c中可以直观地看出,模块1、3、5有效地提取出了测试数据中的断层特征,随着网络的加深,提取到的断层特征越来越抽象。模块7(图 8d)和模块9(图 8e)逐步将断层特征信息恢复出来,最终输出断层预测结果(图 9a)。对比图 9a与图 9b可知,网络模型具备了从地震数据中提取断层信息的能力。
图 10展示了普通U-Net网络中的跳跃连接(第1层与第9层、第2层与第8层)特征融合恢复结果和本文使用的残差路径跳跃连接(模块7与模块9、模块2与模块8)特征融合恢复结果。由图可见,相比于普通跳跃连接,残差路径跳跃连接(多分辨率U-Net网络)特征融合的恢复结果具有更加完整的断层特征信息。因此,残差路径中的非线性操作有望缩小下采样部分与上采样部分得到的特征图之间的语义差别,改善预测效果。

|
图 10 普通跳跃连接(U-Net)与残差路径跳跃连接(多分辨率U-Net网络)特征融合恢复结果对比 (a)U-Net第2与第8层特征融合;(b)多分辨率模块2与模块8特征融合;(c)U-Net第1与第9层特征融合;(d)多分辨率模块1与模块9特征融合 |
为了检验网络模型的训练效果,使用与训练数据尺寸相同的550个人工合成地震数据对网络进行测试,并与普通U-Net网络的测试结果进行对比。测试结果如图 11所示。对比图 11中的红色箭头处可知,本文的网络模型训练完备后,比普通U-Net网络的断层检测结果更加完整。
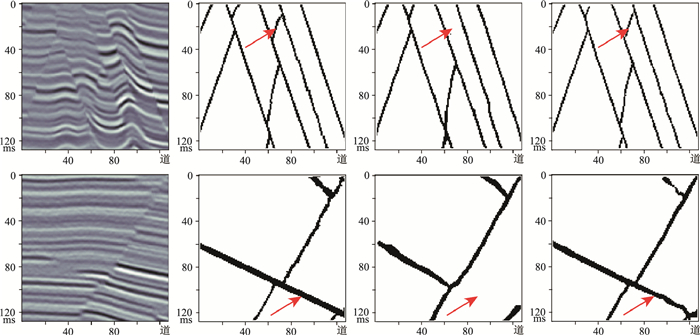
|
图 11 合成地震数据测试结果对比 从上到下分别是两个测试数据,从左到右依次为地震数据、真实断层位置、普通U-Net预测结果和本文方法预测结果 |
为了进一步检验和量化评估网络模型的断层检测能力,引入了Jacard指数和Dice系数两个经典的相似度评价指标量化评估断层预测结果,即
| $ J\left( {\mathit{\boldsymbol{A}}, \mathit{\boldsymbol{B}}} \right) = \frac{{\left| {\mathit{\boldsymbol{A}} \cap \mathit{\boldsymbol{B}}} \right|}}{{\left| {\mathit{\boldsymbol{A}} \cup \mathit{\boldsymbol{B}}} \right|}} $ | (3) |
| $ D\left( {\mathit{\boldsymbol{A}}, \mathit{\boldsymbol{B}}{\rm{ }}} \right) = \frac{{2\left| {\mathit{\boldsymbol{A}} \cap \mathit{\boldsymbol{B}}} \right|}}{{\left| \mathit{\boldsymbol{A}} \right| + \left| \mathit{\boldsymbol{B}} \right|}} $ | (4) |
式中:J(A,B)和D(A,B)分别为计算得到的Jacard指数和Dice系数;|A|为测试数据的真实断层数据集合;|B|为预测结果中的断层数据集合;|A ∩ B|代表预测结果中预测正确的断层数据集合;|A ∪ B|是真实断层数据与预测断层数据的并集。
此外,本文还提出了一种断层预测错误率量化指标作为辅助评价指标,称为EFP(Error of Fault Prediction),定义为
| $ {\rm{EFP}}\left( {\mathit{\boldsymbol{A}}, \mathit{\boldsymbol{B}}} \right) = \frac{{\left| \mathit{\boldsymbol{B}} \right| - \left| {\mathit{\boldsymbol{A}}{} \cap \mathit{\boldsymbol{B}}} \right|}}{\left| \mathit{\boldsymbol{B}} \right|} $ | (5) |
上述三个评价指标如图 12所示。
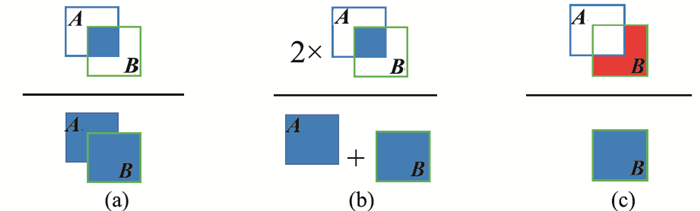
|
图 12 评价指标示意图 (a) Jacard指数;(b) Dice系数;(c) EFP系数。|A|为真实断层数据集合,|B|为预测断层数据集合,两者重叠位置为预测正确的断层数据集合,|B|中红色部分为预测错误的断层数据集合 |
对550个样本数据进行测试后,根据每个样本数据及其测试结果可分别计算得出三个评价指标数值。分别求出所有测试数据的三个指标数值的平均值制成如图 13所示的统计直方图。由图可见,普通U-Net网络和本文方法测试结果的Jacard指数平均值分别为0.588和0.615;Dice系数的平均值分别为0.730和0.751。这表明本文方法检测出的断层与真实断层位置相似度更高,具有更高的准确度。另外,本文方法预测结果的EFP系数平均值为0.137,相比于普通U-Net网络降低了0.094,说明本文方法的预测结果中的错误断层点更少。
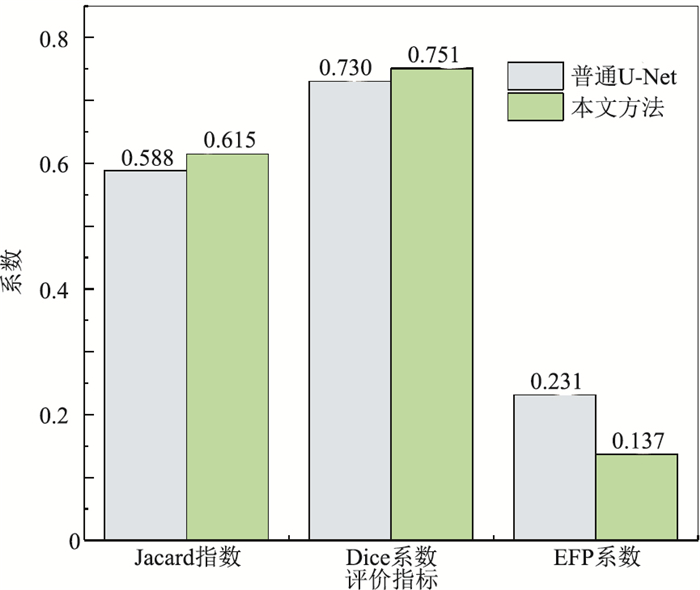
|
图 13 测试结果的Jacard指数、Dice系数和EFP系数对比图 |
为了检验网络模型在实际数据中断层的检测效果,选取了一个大小为570×170的二维实际地震数据对训练完备网络模型进行测试。在预测任意大小(如m×n)的实际地震数据时,数据大小与网络模型的输入不一致,可以使用一个128×128的滑动窗口对地震数据进行滑动预测。具体操作为:首先在实际数据的四周进行填充操作(填充大小为128),得到(m+256)×(n+256)的数据;然后使用一个大小为128×128的滑动窗口以一定步幅预测数据的不同部分;最后将每个数据点的预测值的总和除以该数据点处重叠窗口的数目,得到最终输出数据结果。该方法的优点是:当滑动窗口在填充后的数据上滑动时,数据中的每个数据点都被滑动窗口框定,并且被预测的次数相同。
二维实际地震数据断层预测结果如图 14所示,可以看出,实际数据剖面中的主要断层均被准确预测出来,断层显示清晰。
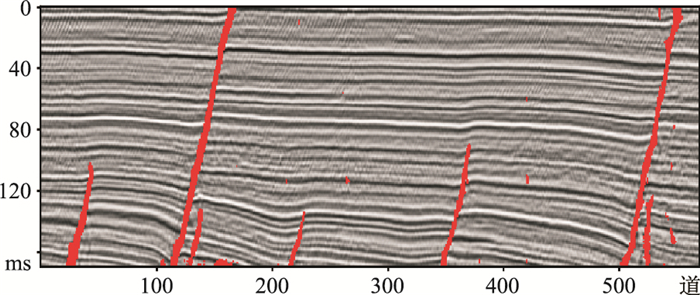
|
图 14 二维实际地震数据断层检测结果 红线表示预测断层 |
为了测试本文方法的应用前景,将二维的多分辨率U-Net网络模型扩展为三维,使用1600个网格大小为64×64×64的三维人工合成地震数据对网络模型进行训练。如果在计算机硬件允许的条件下,可以使用网格更大的训练数据训练网络模型,这样可以在增加网络模型的感受野的同时,减少预测实际数据滑动窗口的滑动次数,从而进一步改善断层检测结果。
三维网络模型训练完备后,通过迁移学习方法,继续利用实际地震数据及其断层标签数据对网络模型进行再训练,可以进一步提高对目标区实际地震数据中的断层检测准确度。
本文用于迁移学习的三维实际地震数据训练样本制作方法及主要过程如下:首先利用现有的断层检测方法对实际数据中的断层进行检测;然后从中人为挑选出较好的断层检测结果作为三维实际地震数据的断层标签数据。
网络模型经过迁移学习再训练之后,选取某一工区(工区1)内的大小为130×260×128的三维实际地震数据(图 15a)进行断层检测。由图可见,相比于相干体属性(图 15b),本文方法(图 15c)能够较清晰地预测三维地震数据中的主要断层。对比图 15c与图 15d可以看出,网络经过迁移学习之后,预测的断层更加清晰、连续性更好。
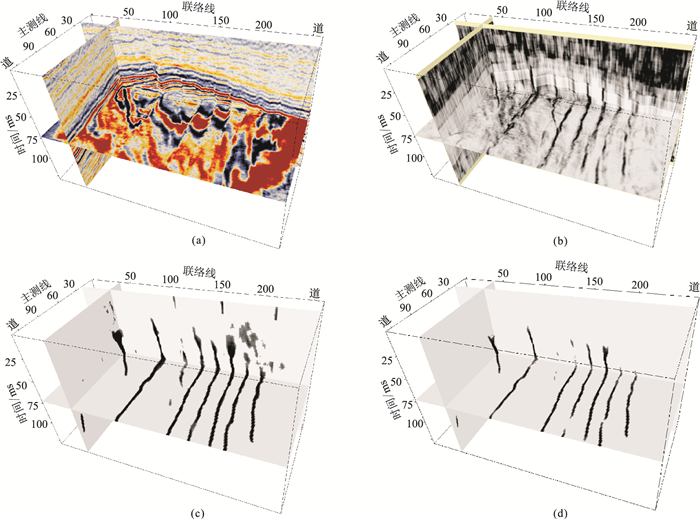
|
图 15 工区1三维实际数据断层检测结果对比 (a)实际数据;(b)相干体属性断层检测结果;(c)三维多分辨率U-Net网络断层检测结果;(d)迁移学习前断层检测结果 |
与迁移学习结合的优点是:可以在一定程度上缩小因训练数据与实际测试数据的差异而引起的不利影响,在实际应用时能够节省训练时间,使训练完备的网络模型不需要重复性训练,仅使用少量目标区的人工拾取的断层标签数据对其进行参数调优就能得到更好的断层检测性能。这非常适合应用于实际生产工作,可以节省人力和时间。
为了进一步检验三维网络模型对实际地震数据中小尺度断层的检测能力,选取了另一工区(工区2)内大小为225×795×150的三维实际地震数据(图 16a),该数据体内含有丰富的小尺度断层。对比相干体属性断层检测结果(图 16b),本文方法能够更加清晰、准确地预测出多数小尺度断层(图 16c)。
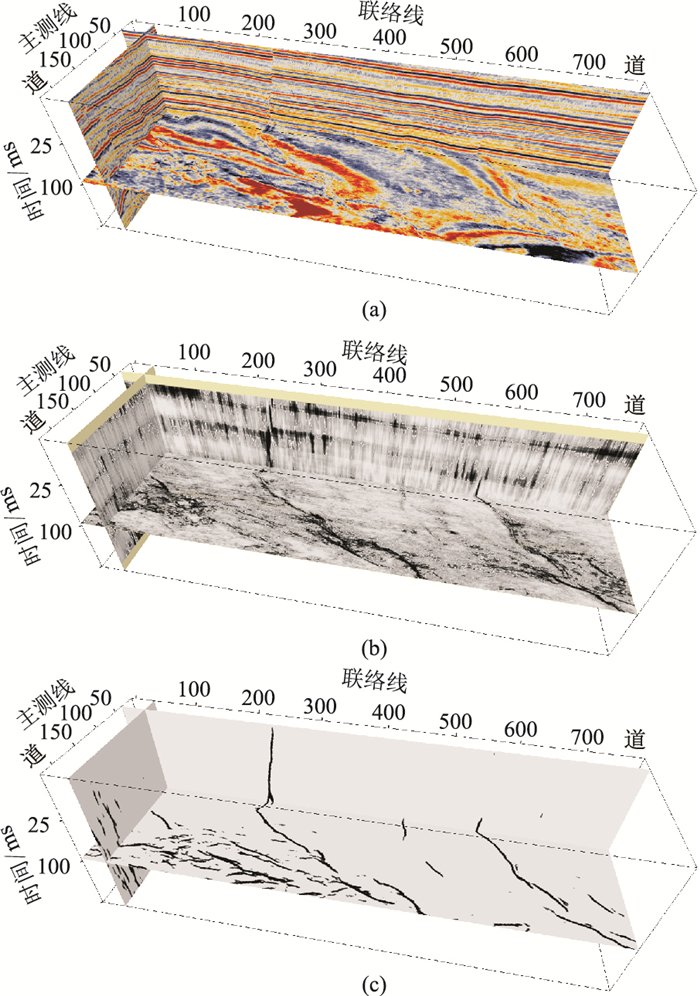
|
图 16 工区2三维实际数据断层检测结果对比 (a)实际数据;(b)相干体属性断层检测结果;(c)三维多分辨率U-Net网络断层检测结果 |
本文提出了一种基于深度学习的多分辨率U-Net网络地震数据断层检测方法,即引入多分辨率模块增强网络模型的多尺度断层检测能力,使用残差路径代替普通跳跃连接缩小用于拼接的特征图之间的语义差别。通过网络中间层可视化分析直观地展示了网络模型对地震数据的特征提取、表达过程。主要结论如下。
(1) 合成地震数据测试集的测试结果和量化评估指标表明,本文提出的多分辨率U-Net网络比普通U-Net网络预测断层具有更高的准确度和更少的错误点,能够准确地预测二维实际地震剖面中主要的断层,并且断层清晰、连续性较好。
(2) 通过三维实际地震数据测试结果可知,三维多分辨率U-Net网络与迁移学习结合之后具有较强的实用性,本文方法比相干体属性检测的断层更加清晰、连续性更好。本文方法有望应用于实际生产工作中,实现高效、自动化断层检测,节省地震资料解释工作所需的人力和时间。
| [1] |
白青林, 杨少春, 路智勇, 等. 复杂断块区低级序断层的井-震联合识别[J]. 石油地球物理勘探, 2019, 54(5): 1131-1140. BAI Qinglin, YANG Shaochun, LU Zhiyong, et al. Low-grade fault identification in complex fault-block zones based on well and seismic data[J]. Oil Geophy-sical Prospecting, 2019, 54(5): 1131-1140. |
| [2] |
吕丙南, 陈学华, 徐赫, 等. 空间域加窗二维希尔伯特变换在三维地震资料体边缘检测中的应用[J]. 石油地球物理勘探, 2020, 55(3): 661-668. LYU Bingnan, CHEN Xuehua, XU He, et al. Application of spatial-windowed 2D Hilbert transform in vo-lumetric edge detection of 3D seismic data[J]. Oil Geophysical Prospecting, 2020, 55(3): 661-668. |
| [3] |
吕文正, 陈骁, 关旭, 等. 特色构造解释及储层预测技术在川西北双鱼石地区的应用[J]. 石油地球物理勘探, 2018, 53(增刊1): 228-233. LYU Wenzheng, CHEN Xiao, GUAN Xu, et al. Cha-racteristic structural interpretation and reservoir prediction in Shuangyushi Area, Northwest Sichuan[J]. Oil Geophysical Prospecting, 2018, 53(S1): 228-233. |
| [4] |
路远, 朱仕军, 朱鹏宇, 等. 利用信噪比差异体改进断层自动识别方法[J]. 地球物理学进展, 2014, 29(1): 155-158. LU Yuan, ZHU Shijun, ZHU Pengyu, et al. Improved fault automatic identification using signal-to-noise ratio cubes[J]. Progress in Geophysics, 2014, 29(1): 155-158. |
| [5] |
Gersztenkorn A, Marfurt K J. Eigenstructure-based coherence computations as an aid to 3-D structural and stratigraphic mapping[J]. Geophysics, 1999, 64(5): 1468-1479. DOI:10.1190/1.1444651 |
| [6] |
张瑞, 文晓涛, 李世凯, 等. 分频蚂蚁追踪在识别深层小断层中的应用[J]. 地球物理学进展, 2017, 32(1): 350-356. ZHANG Rui, WEN Xiaotao, LI Shikai, et al. Application of frequency division ant-tracking in identifying deep minor fault[J]. Progress in Geophysics, 2017, 32(1): 350-356. |
| [7] |
孙振宇, 彭苏萍, 邹冠贵. 基于SVM算法的地震小断层自动识别[J]. 煤炭学报, 2017, 42(11): 2945-2952. SUN Zhenyu, PENG Suping, ZOU Guangui. Automatic identification of small faults based on SVM and seismic data[J]. Journal of China Coal Society, 2017, 42(11): 2945-2952. |
| [8] |
李军, 张军华, 龚明平, 等. 基于魔方矩阵的断层检测方法[J]. 石油地球物理勘探, 2018, 53(3): 552-557. LI Jun, ZHANG Junhua, GONG Mingping, et al. Fault detection based on magic matrix[J]. Oil Geophysical Prospecting, 2018, 53(3): 552-557. |
| [9] |
Badrinarayanan V, Kendall A, Cipolla R. SegNet: a deep convolutional encoder-decoder architecture for image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(12): 2481-2495. DOI:10.1109/TPAMI.2016.2644615 |
| [10] |
蔡涵鹏, 胡浩炀, 吴庆平, 等. 基于叠前地震纹理特征的半监督地震相分析[J]. 石油地球物理勘探, 2020, 55(3): 504-509. CAI Hanpeng, HU Haoyang, WU Qingping, et al. Semi-supervised seismic facies analysis based on pre-stack seismic texture[J]. Oil Geophysical Prospecting, 2020, 55(3): 504-509. |
| [11] |
Waldeland A U, Jensen A C, Gelius L J, et al. Convolutional neural networks for automated seismic interpretation[J]. The Leading Edge, 2018, 37(7): 529-537. DOI:10.1190/tle37070529.1 |
| [12] |
Zhou R, Cai Y, Yu F, et al. Seismic fault detection with iterative deep learning[C]. SEG Technical Program Expanded Abstracts, 2019, 38: 2503-2507.
|
| [13] |
Wu X, Shi Y, Fomel S, et al. FaultNet3D: predicting fault probabilities, strikes, and dips with a single convolutional neural network[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(11): 9138-9155. DOI:10.1109/TGRS.2019.2925003 |
| [14] |
Wu X, Hale D. 3D seismic image processing for faults[J]. Geophysics, 2016, 81(2): IM1-IM11. DOI:10.1190/geo2015-0380.1 |
| [15] |
孙宇航, 刘洋. 利用GRU神经网络预测横波速度[J]. 石油地球物理勘探, 2020, 55(3): 484-492, 503. SUN Yuhang, LIU Yang. Prediction of S-wave velocity based on GRU neural network[J]. Oil Geophysical Prospecting, 2020, 55(3): 484-492, 503. |
| [16] |
王俊, 曹俊兴, 尤加春. 基于GRU神经网络的测井曲线重构[J]. 石油地球物理勘探, 2020, 55(3): 510-520. WANG Jun, CAO Junxing, YOU Jiachun. Reconstruction of logging traces based on GRU neural network[J]. Oil Geophysical Prospecting, 2020, 55(3): 510-520. |
| [17] |
张玉玺, 刘洋, 张浩然, 等. 基于深度学习的多属性盐丘自动识别方法[J]. 石油地球物理勘探, 2020, 55(3): 475-483. ZHANG Yuxi, LIU Yang, ZHANG Haoran, et al. Multi-attribute automatic interpretation of salt domes based on deep learning[J]. Oil Geophysical Prospecting, 2020, 55(3): 475-483. |
| [18] |
Wang Z, Di H, Shafiq M. Successful leveraging of i-mage processing and machine learning in seismic structural interpretation: A review[J]. The Leading Edge, 2018, 37(6): 451-461. DOI:10.1190/tle37060451.1 |
| [19] |
Xiong W, Ji X, Ma Y, et al. Seismic fault detection with convolutional neural network[J]. Geophysics, 2018, 83(5): O97-O103. DOI:10.1190/geo2017-0666.1 |
| [20] |
Guo B, Liu L, Luo Y. Automatic seismic fault detection with convolutional neural network[C]. SEG Technical Program Expanded Abstracts. 2018, 37: 1786-1789.
|
| [21] |
Li S, Yang C, Sun H, et al. Seismic fault detection using an encoder-decoder convolutional neural network with a small training set[J]. Journal of Geophysics and Engineering, 2019, 16(1): 175-189. DOI:10.1093/jge/gxy015 |
| [22] |
Wu X, Liang L, Shi Y, et al. FaultSeg3D: Using synthetic data sets to train an end-to-end convolutional neural network for 3D seismic fault segmentation[J]. Geophysics, 2019, 84(3): IM35-IM45. DOI:10.1190/geo2018-0646.1 |
| [23] |
张政, 严哲, 顾汉明. 基于残差网络与迁移学习的断层自动识别[J]. 石油地球物理勘探, 2020, 55(5): 950-956. ZHANG Zheng, YAN Zhe, GU Hanming. Automatic fault recognition with residual network and transfer learning[J]. Oil Geophysical Prospecting, 2020, 55(5): 950-956. |
| [24] |
常德宽, 雍学善, 王一惠, 等. 基于深度卷积神经网络的地震数据断层识别方法[J]. 石油地球物理勘探, 2021, 56(1): 1-8. CHANG Dekuan, YONG Xueshan, WANG Yihui, et al. Seismic fault interpretation based on deep convolutional neural networks[J]. Oil Geophysical Prospecting, 2021, 56(1): 1-8. |
| [25] |
Ronneberger O, Fischer P, Brox T. U-Net: convolutional networks for biomedical image segmentation[C]. Medical Image Computing and Computer-Assisted Intervention-MICCAI 2015, Springer, 2015, 234-241.
|
| [26] |
Shelhamer E, Long J, Darrell T. Fully convolutional networks for semantic segmentation[J]. IEEE Tran-sactions on Pattern Analysis and Machine Intelligence, 2017, 39(4): 640-651. DOI:10.1109/TPAMI.2016.2572683 |
| [27] |
Szegedy C, Vanhoucke V, Ioffe S, et al. Rethinking the inception architecture for computer vision[C]. IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2016, 2818-2826.
|
| [28] |
Ibtehaz N, Rahman M S. MultiResU-net: Rethinking the U-Net architecture for multimodal biomedical image segmentation[J]. Neural Networks, 2020, 121: 74-87. DOI:10.1016/j.neunet.2019.08.025 |



 唐杰, 山东省青岛市开发区长江西路66号中国石油大学(华东)地球科学与技术学院(工科楼C610), 266580。Email:
唐杰, 山东省青岛市开发区长江西路66号中国石油大学(华东)地球科学与技术学院(工科楼C610), 266580。Email: 