② 中国石油大学(北京) CNPC物探重点实验室, 北京 102249;
③ 中国石油大学(北京)克拉玛依校区石油学院, 新疆克拉玛依 834000;
④ 东方地球物理公司研究院, 河北涿州 072751
② China University of Petroleum(Beijing), Karamay Campus, Karamay, Xinjiang 834000, China;
③ CNPC Key Laboratory of Geophysical Prospecting, China University of Petroleum(Beijing), Beijing 102249, China;
④ Geophysical Research Institute, BGP Inc., CNPC, Zhuozhou, Hebei 072751, China
静校正是地震资料处理的重要环节之一,而初至拾取是计算地表静校正量的一个重要步骤,特别是在地表条件较为复杂的地区,低速风化层速度变化较为剧烈,准确、自动拾取初至成为解决此类地区静校正问题的关键所在。然而,目前大多数的初至拾取方法只能实现部分自动化,需要花费大量时间进行人工质量控制。随着高密度地震采集技术的应用,地震数据量变得十分巨大,导致初至拾取过程中耗费的人工成本急剧增加。基于深度学习的初至自动拾取方法成本低、效率高,可以满足当今地震高密度采集的数据量需求。传统的初至自动拾取方法,如基于能量的方法[1-2]或基于相关性的方法[3-4],普遍要求数据信噪比高、波形一致。在地形变化剧烈或强噪声干扰的情况下,初至拾取精度会降低。
深度神经网络适合于解决模式匹配分类问题,它由神经网络演化而来,结构更加复杂,性能可以随训练数据的增加而提高[5]。
深度学习算法可以挖掘数据的特征。深度学习模型由多个层次组成,以学习具有多个抽象层次的数据表示。这是一种层次渐进的特征学习,先从较低层次的特征中学习,从而定义更高层次的特征[6]。在此意义上,初至拾取问题可以定义为模式识别问题,目的是区分背景噪声与地震有效数据。因此,深层神经网络可以从地震数据中学习特征而无需人工干预,将地震数据分为噪声和有效数据两类。
近几年来,出现了多种应用机器学习进行初至拾取的方法,如神经网络[7-8]、支持向量机[9]、模糊聚类[10]、混合卷积神经网络(Convolutional Neural Network,CNN)[11-12]、全卷积网络(Fully Convolutional Network,FCN)[13-14]、半监督全卷积网络(SS-FCN)[15]、U-Net变体[16-17]和伴有迁移学习的卷积神经网络[18-19]等。在这些方法中,FCN可以逐像素分类、处理不同大小的数据,因此被广泛使用。
FCN起源于CNN,CNN最早由LeCun等[20]提出,但当时计算能力制约了其更为广泛的应用。近十年来,由于图像分类技术的重大突破,卷积神经网络得到了广泛的应用,相继开发了AlexNet[21]、VGG16[22]和GoogleNet[23]等架构。CNN能够逐步减少输入数据占用的空间,并有效增加特征映射的数量,但是在预测分辨率方面存在不足。该问题的一种解决方法是使用语义分割进行像素级分类,并从低清晰度表示中恢复高分辨率输出。目前,语义分割方法一般使用FCN架构。FCN通过下采样和上采样两部分恢复高分辨率输出,通常可以通过转置卷积[24-25]或空洞卷积[26-27]实现。U-Net作为FCN的一种变体,具有多功能性、可处理不同大小的数据且分割性能明显提高[28]等特点。然而,U-Net在实现初至拾取时有一定的局限性,尤其是在数据的信噪比较低时,拾取结果的精度会低于之前的验证精度。因此,网络结构需要进一步优化以减少误差。此外,对图像后续处理也能有效改善拾取结果[29]。由于近年来U-Net应用效果较好,它的结构得到了更为广泛的拓展,例如UNet++[30]和Attention U-Net(aU-Net)[31]能较好地解决复杂分割问题。
针对以上问题,本文提出了四个关键技术点:
(1) 将U-Net网络模型与简单变体网络模型aU-Net、复杂变体网络模型UNet++的效果进行比较,从不同角度分析分割问题;
(2) 通过试验确定网络超参数,包括对损失函数、优化器和激活函数等进行试验;
(3) 制定振幅均衡处理流程,可以提高样本信噪比,均衡训练样本,提高训练稳定性、样本识别率和预测值鲁棒性;
(4) 在拾取初至之前,对分割的边缘添加视速度约束以增加图像分割细节。
最后,使用该方法对一套陆地地震数据集进行初至自动拾取,获得了较好的结果。
1 方法原理 1.1 U-Net模型U-Net模型由两部分组成,第一部分为编码器(下采样),第二部分为解码器(上采样)。编码器是一种传统的CNN,它通过增加特征映射的数量、减少空间采样信息提取高层次至低层次的特征。解码器的作用是恢复数据在编码过程中的特定位置,逐渐降低分辨率。同时,用残差连接(Residual Connections)将高分辨率的局部特征与低分辨率的全局特征相结合,增加更具语义意义的输出。
在用于初至拾取的U-Net结构中,其工作原理是:在输入的空间位置中检测信号具体的特征,这些特征与地震有效数据和背景噪声的特征有关;对检测到的特征逐像素进行二值分类,得到区分有效信号与噪声的分割图像,通过训练U-Net学习有效信号和噪声特征并进行分类;将有效信号与噪声区域之间的分割边缘定义为初至时间。在初至拾取中,由于初至在单炮记录上一般是近似对称出现的,所以边界检测问题比传统的分割问题更简单。
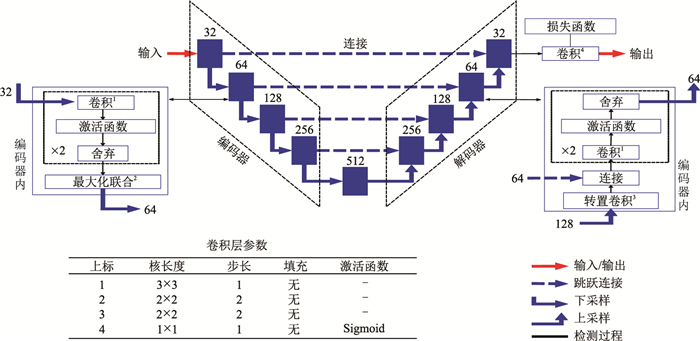
图 1所示为U-Net结构,每个编码器层包括两个无偏差的级联卷积层以提高分类精度,每个卷积层的值为
| $ \mathit{\boldsymbol{Z}}_{i,j,k}^l = \mathit{\boldsymbol{W}}_k^{l\;\;{\rm{T}}}\mathit{\boldsymbol{X}}_{i,j}^l + \mathit{\boldsymbol{b}}_k^l $ | (1) |
|
图 1 U-Net结构 |
式中:Zi, j, kl是第l层、第k维特征图(i, j)处的值;Wkl是第l层、第k维特征映射的权重向量;bkl是第l层、第k维特征图的偏差项;Xi, jl是以第l层(i, j)点为中心的输入面片。卷积核尺寸为3×3,步长为1,无零值填充。
尽管U-Net已经取得了一定的效果,但在分割精度方面仍然存在一些限制。因此,需要使用额外的方法提高分割精度,本文比较了三种不同复杂度的U-Net结构,从不同角度分析该问题。
1.2 UNet++模型UNet++[30]与U-Net有三个不同之处:一是前者的残差连接具有卷积层,可以用来解决编码器特征与解码器语义之间的语义差别;二是前者的残差密集连接可以改进梯度流(Gradient Flow);三是与单一损失层相比,前者的深度监督(Deep Supervision)实现了模型剪枝(Model Pruning),可以更有效地提高性能。
U-Net残差连接直接将高分辨率的特征映射从编码器传送到解码器,通常这个过程会使特征映射产生一定的非相似性。虽然残差连接有助于恢复网络输出的空间分辨率,但是结合来自编码器与解码器的语义上不相等的特征映射可能会降低分割性能。当解码器与编码器网络的特征映射在语义上相似时,分隔精度会得到提高。为了实现这一点,U-Net++引入了一个深度监督的编码器和解码器,其中编码器与解码器通过一系列嵌套和密集的残差连接结合在一起(图 2)。残差连接减少了编码器与解码器特征映射之间的语义差别,并在高分辨率特征映射上捕捉到细节。叠加特征映射的计算公式为
| $ {\mathit{\boldsymbol{X}}_{i, j}} = \left\{ \begin{array}{l} H({\mathit{\boldsymbol{X}}_{i - 1, j}}){\rm{ }}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;j = 0\\ H\left\{ {\left[ {{\mathit{\boldsymbol{X}}_{i, k}}} \right]_{k = 0}^{j - 1}, u({\mathit{\boldsymbol{X}}_{i + 1, j - 1}})} \right\}{\rm{ }}\;\;\;\;j > 0 \end{array} \right. $ | (2) |

|
图 2 UNet++结构 |
式中:Xi, j是节点的输出,i是沿编码器的下采样层,j是沿着残差连接的密集块的卷积层序号;H(·)是紧跟激活函数的卷积运算;u(·)是上采样层;[]是连接层。
1.3 Wide U-Net模型Wide U-Net(wU-Net)[30]的卷积核由U-Net的32×64×128×256×512变为37×70×140×280×560,通过采用更多的超参数提高网络性能。wU-Net和UNet++模型具有相似数量的超参数(表 1),能够客观地度量网络性能。
|
|
表 1 U-Net变体的超参数 |
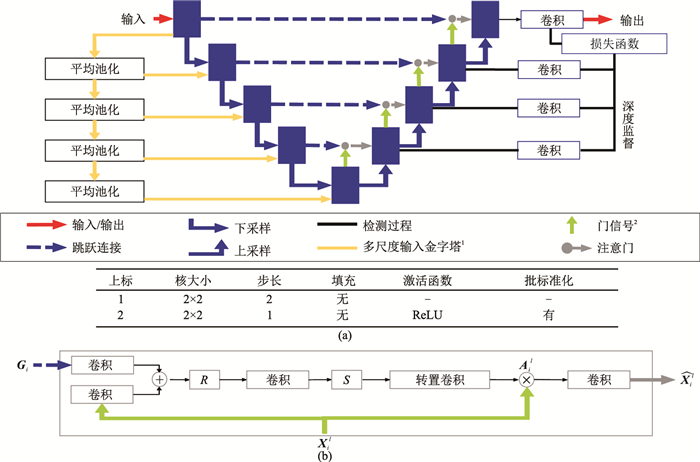
虽然U-Net具有表达能力强、推理速度快、滤波器共享等特点,但是当目标的形状和大小有很大变化时,它需要依赖多级串联的CNN。此外,传统方法会导致计算资源和模型参数的过度冗余使用。为了解决这一问题,发展了Attention U-Net模型,即aU-Net[31]模型(图 3a),引入了注意门(Attention Gates,AGs)(图 3b)。
|
图 3 aU-Net变体 (a)aU-Net结构;(b)注意门R、S分别为ReLU、Sigmiod激活函数 |
AGs可以在没有额外监督的情况下专注于目标结构进行自动学习。在训练过程中,这些门突出对分类任务有用的显著特征。此外,它不会显著增加计算量,也不像多模型框架那样需要大量的模型参数(表 1)。AGs通过抑制不相关区域的特征,提高了模型对稠密标签预测的敏感性和准确性,同时保持了较高的预测精度。
AGs可以通过以下公式表达,即
| $ \mathit{\boldsymbol{Q}}_{\rm{att}}^l = {\mathit{\boldsymbol{\Psi }}^\rm{T}}R(\mathit{\boldsymbol{W}}_\mathit{\boldsymbol{X}}^{\rm{T}}\mathit{\boldsymbol{X}}_i^l + \mathit{\boldsymbol{W}}_\mathit{\boldsymbol{G}}^{\rm{T}}{\mathit{\boldsymbol{G}}_i} + {\mathit{\boldsymbol{b}}_\mathit{\boldsymbol{G}}}) + {\mathit{\boldsymbol{b}}_\psi } $ | (3) |
| $ \mathit{\boldsymbol{A}}_i^l = S\left[ {\mathit{\boldsymbol{Q}}_{{\rm{att}}}^l(\mathit{\boldsymbol{X}}_i^l, {\mathit{\boldsymbol{G}}_i};{\mathit{\boldsymbol{\Theta }}_{{\rm{att}}}})} \right] $ | (4) |
式中:Qattl是第l层处的线性注意系数;Ail是第l层、第i像素处Qattl的注意系数;Xil是第l层、第i像素的输入;Gi是第i像素处的门信号(Gating Signal);AGs通过一组参数Θatt表征,包括线性变换WX、WG、Ψ和偏置项bψ、bG;R是激活函数ReLU;S是激活函数Sigmoid。
1.5 超参数优化通过比较U-Net与基于U-Net的三种不同变体模型的性能,发现U-Net优于复杂化的U-Net变体。下面对U-Net的每个超参数进行详尽测试以得到最优化的结果。测试的参数包括学习率(Learning Rate)、激活功能(Activation Function)、损失函数(Loss Function)、优化器(Optimizer)、舍弃比率(Dropout Rate)和权重初始化(Weight Initialization)等(表 2)。
|
|
表 2 测试的超参数 |
重点分析激活函数和损失函数。首先,传统的U-Net激活函数是ReLU[32],它存在梯度消失问题。为了避免这种情况,研究人员尝试了ELU[31],并取得了一些效果。本文中除了以上两个函数之外,还比较了另外两个激活函数,一个是带泄露修正线性单元(Leaky ReLU,LReLU)[33],这是对传统ReLU的简单改进,可避免梯度消失问题;另一个是SELU[34],这是一个更复杂的解决方案,可以与ELU相媲美。它们的表达式分别为
| $ {R_{1, k}} = \left\{ {\begin{array}{*{20}{l}} {{Z_k}}&{{Z_k} > 0}\\ {{\lambda _1}{Z_k}}&{{Z_k} \le 0} \end{array}} \right. $ | (5) |
和
| $ {R_{s, k}} = {\lambda _s}\left\{ {\begin{array}{*{20}{l}} {{Z_k}}&{{Z_k} > 0}\\ {{a_s}\left( {{{\rm{e}}^{{Z_k}}} - 1} \right)}&{{Z_k} \le 0} \end{array}} \right. $ | (6) |
式中:Rl, k是第k特征图处LReLU的输入;Rs, k是第k特征图处SELU的输入;Zk是第k维特征图处的值;在默认情况下λl为0.001、λs约为1.0507、as约为1.6733,λs和as为固定值,使输入均值为0、标准差为1。
LReLU是经典的ReLU的变体,它在计算导数时设置一个小的梯度,使梯度值不再停留在零上,因而避免了梯度消失问题;由于没有指数运算,因而计算速度比ELU快;缺点是不能避免梯度爆炸问题,因为as值是不可学习的,它是预先定义的,取微分时变成线性函数,而ELU是非线性的。
另一方面,SELU允许网络通过内部规范化特性实现更快收敛,输出自动归一化至零平均值和单位方差。此外,该网络权重初始化需要正态(高斯)分布。它的另外一个优点是不存在梯度消失问题,可通过映射两个连续层之间的均值(μ)和方差(υ)计算as和λs,并找到同时满足两个层的不动点(μ,υ)=(0,1)的解。
在常规的炮点道集中,样本数量大于初至波样本和噪声样本,因此目前初至拾取面临的主要问题之一是样本不平衡(Data Imbalance)。为了克服这一问题,本文测试了四种类型的损失函数:第一种是基于概率分布的二元交叉熵损失函数(Binary Cross Entropy,BCE);第二种是基于区域的损失函数,包括Dice、Tversky和Focal Tversky等;第三种是基于边界的损失函数,例如Huber;第四种是基于合并的损失函数,例如将交叉熵与Dice合并为一个损失函数(二元交叉熵代价函数+Dice)。二元交叉熵代价函数+Dice[30]为
| $ {{\cal L}_{{\rm{bd}}}}(\mathit{\boldsymbol{Y}}, \mathit{\boldsymbol{Z}}) = \frac{1}{N}\mathop \sum \limits_{i = 1}^N \left( {1 - \frac{1}{2}{Y_i}\lg {Z_i} - \frac{{2{Z_i}{Y_i}}}{{{Z_i} + {Y_i}}}} \right) $ | (7) |
式中:Y是真实值;Z是预测结果;N是批大小(Batch Size)。
Dice系数(Dice Coefficient)[35]为预测值与实际值之间相似度的评价指标,局限性在于假阳性(False Positives,FP)与假阴性(False Negatives,FN)的权重相等,即精度高但召回率低。初至拾取是一个高度不平衡的问题,因此要求FN的权重高于FP以提高召回率。
Tversky指数[36]是平衡FP与FN的Dice系数的一个推广,通过最小化,Tversky指数可变成损失函数,即
| $ {{\cal L}_{{\rm{t}}}}(\mathit{\boldsymbol{Y}}, \mathit{\boldsymbol{Z}}) = \frac{1}{N}\mathop \sum \limits_{i = 1}^N \left( {1 - \frac{{{Z_i}{Y_i} + \varepsilon }}{{{Z_i}{Y_i} + \alpha Z_i^2 + \beta Y_i^2 + \varepsilon }}} \right) $ | (8) |
式中:β是假阴性的权重;ε是防止被零除的数值稳定因子。通过调整超参数α和β,可以控制假阳性与假阴性之间的权衡。较大的β值会提高模型的收敛性。当α=β=0.5时,Tversky函数简化为Dice函数。
Focal Tversky函数[37]向前更进一步,引入了一个与标签频率成反比的权重,即
| $ {{\cal L}_{{\rm{ft}}}}(\mathit{\boldsymbol{Y}}, \mathit{\boldsymbol{Z}}) = \frac{1}{N}\mathop \sum \limits_{i = 1}^N {\left( {1 - \frac{{{Z_i}{Y_i} + \varepsilon }}{{{Z_i}{Y_i} + \alpha Z_i^2 + \beta Y_i^2 + \varepsilon }}} \right)^{\frac{1}{\gamma }}} $ | (9) |
式中γ是焦点参数因子,可以控制容易分类的"数据"部分与难以分类的"噪声"部分。该指数对分类良好的样本的误差进行加权,防止了大量分类错误的样本对梯度的影响,进而缓解了类别不平衡。另外,当γ=1时,Focal Tversky函数简化为Tversky函数。
Huber函数[38]是由可调参数δ确定的平均绝对误差(Mean Absolute Error,MAE)与均方误差(Mean Squared Error,MSE)之间的平衡,即
| $ \begin{array}{l} {{\cal L}_{\rm{h}}}(\mathit{\boldsymbol{Y}}, \mathit{\boldsymbol{Z}}) = \\ \left\{ {\begin{array}{*{20}{l}} {\frac{1}{{2N}}\sum\limits_{i = 1}^N {{{\left| {{Y_i} - {Z_i}} \right|}^2}} }&{\left| {{Y_i} - {Z_i}} \right| \le \delta }\\ {\frac{1}{{2N}}\sum\limits_{i = 1}^N \delta \left( {2\left| {{Y_i} - {Z_i}} \right| - \delta } \right)}&{\left| {{Y_i} - {Z_i}} \right| > \delta } \end{array}} \right. \end{array} $ | (10) |
该损失函数用于变化较大的数据或有很少异常值的数据。当δ趋近0时,Huber函数接近MAE;当δ趋近∞时,Huber函数接近MSE。对于较大的异常值,建议使用较小的δ值,因为MSE会影响损失值。但是,当异常值很少时,建议使用较大的δ值,因为MSE会比MAE作用更大。
1.6 数据调节球面扩散引起信号能量的变化、噪声等从而导致地震数据中信号能量的不均衡,进而直接影响网络训练的性能(图 4a)。本文使用基于四分位距法(Inter Quartile Range,IQR)[39]的最小—最大标准化法和百分位限幅以提高振幅,利用传统的2σ-3σ限幅以处理异常值。应用全局百分比归一化方法,数据在该图中位于标准差2σ范围内的百分比为95.45%,而位于3σ范围内的百分比为99.73%。

|
图 4 不同方法对地震数据振幅处理效果对比 (a)原始地震;(b)AGC;(c)RMS;(d)本文方法 |
数据集的差异性可以通过范围和标准差衡量,但是它们对异常值十分敏感。基于上下四分位数测量离散度,且在测量数据离散度时更能规避异常值的影响。通过IQR可以获知第一个和第三个四分位数的间距,可显示数据分布中间50%范围的值。
虽然传统的自动增益控制(Automatic Gain Control,AGC)是一种较有效的方法,但它会加强初至之前的噪声,这对网络正确识别和分类样本而言是一个问题(图 4b),AGC使网络更加难以区分噪声与有效数据。同时,低频噪声可能会出现在初至波的前面,这可能导致分类错误。初至波应当尽可能清晰,以便网络能从数据像素中识别出噪声。
均方根(RMS)振幅归一化方法能够在一定程度上解决这个问题,但也存在一些不足(图 4c):①在较远的地震道中,噪声在整个地震道中都被增强,且在面波周围区域的特征归一化后能量较低;②3000ms以下深层的地震数据能量并没有完全增强。
因此,为了在样本之间获得适当的平衡能量,本文将RMS归一化法与最小—最大标准化法和IQR限幅相结合以截断极值,并加上T平方补偿解决球面发散问题(图 4d)。此方法的优势在于均衡了整炮数据,从而网络在训练过程中可以更容易地正确识别和分类样本。
在神经网络中,Basheer等[40]建议在0.1~0.9内进行归一化以避免饱和,这非常适合网络内部的激活函数,并且不会导致学习率降低。此外,使用该范围(0.1~0.9)进行分类任务时会得出错误的后验概率估值,采用最小—最大标准化将其分布范围限制在0~1内,计算公式为
| $ {\rm{min}}\;{\rm{max}}({x_i}) = \frac{{{x_i} - {\rm{min}}\left( x \right)}}{{{\rm{max}}(x) - {\rm{min}}\left( x \right)}} $ | (11) |
式中:x表示总样本;xi为待标准化的样本;min(x)为采样点中的最小值;max(x)为采样点中的最大值。该方法的主要优点是对原始数据中的信息干扰小,尤其是在非高斯分布或标准差很小的时候。
均值和方差很容易受到异常值的影响。缩尾处理(Winsorization)或限幅(Clipping)可以有效地解决这个问题并能增强统计数据的准确性。振幅范围越大,显示的细节越少。因此,振幅直方图上的四分位数、峰度和偏度有助于分析数据分布,并可适当地剪裁数据,从而避免可能影响归一化的尖脉冲。
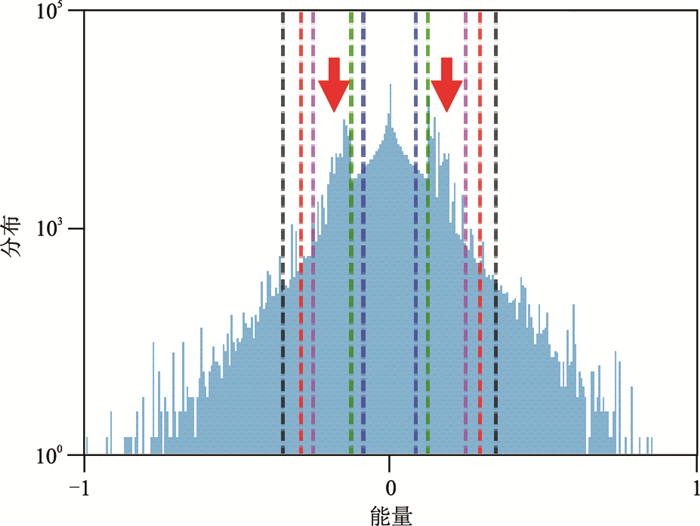
通常,在显示地震剖面时,振幅限制是通过振幅范围的2σ(95.45%)、3σ(99.73%)或99%的对称以避免出现明显的尖峰,如图 5所示。然而,数据通常是非对称的,并且适合于计算用于限幅的各个四分位数,这在选择限幅边界时可以提供直接控制。
|
图 5 IQR与σ的对比图
σ为绿线,2σ为紫线,IQR为蓝线,99% 四分位数为红线,1.5×IQR为黑线 |
四分位距是一个统计度量,其中"中值50"位于数据之中,如图 5所示,其计算公式为
| $ {\rm{IQR}} = {Q_3} - {Q_1} $ | (12) |
式中:Q3是75%以上数据的四分位数;Q1是25%以下数据的四分位数。限幅的原理是:给异常值分配较低的权重或修改权值使其接近集合中的其他值,最小化异常值的影响。在这种情况下,IQR修改Q1与Q3间隔之外的数据点值,不会修改Q1与Q3之间的数据点值。
综上所述,本文设计振幅均衡处理流程如图 6所示。
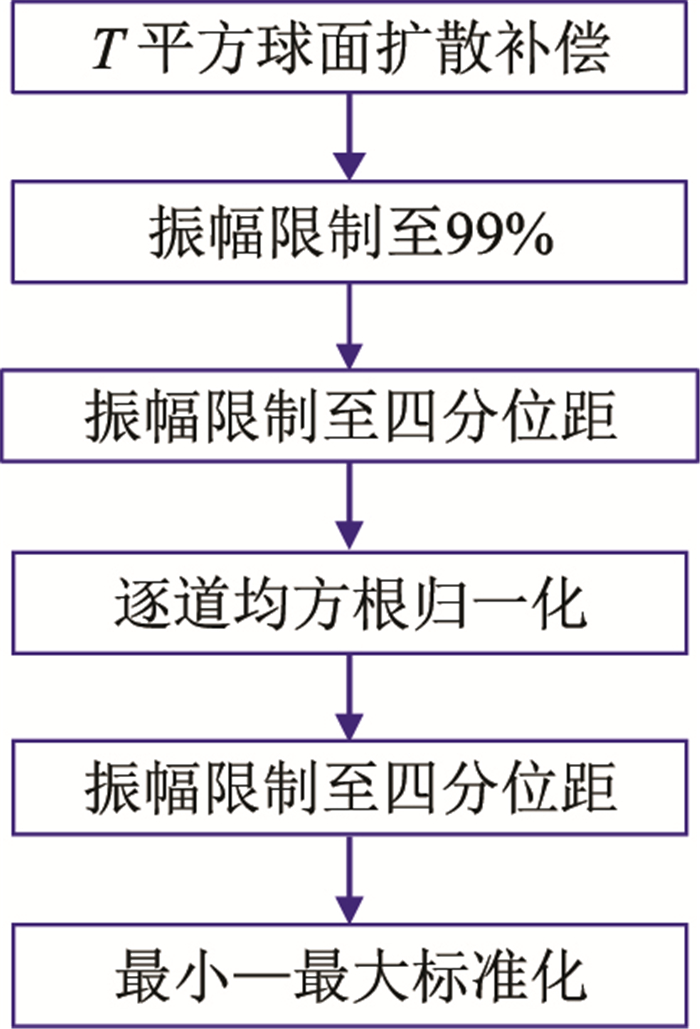
|
图 6 振幅均衡处理流程 |
结合地球物理参数的约束,能间接地提高分割图像的精度,使网络预测更稳定。首先,为了降低不确定性,将高程静校正应用于炮检道集。尽管这些静校正量并不完全准确,但它们减少了地震道之间的变化;然后,为了减少错误分类像素的影响,在初至附近增加视速度约束。错误分类像素与初至波上下的低信噪比相关,可以定义两个视速度约束解决这个问题,一个是初至之上的高速约束解决噪声误分类;另一个是初至之下的低速约束解决有效信号误分类。这些错误分类像素通常出现在远离分割边缘的地方。网络可以处理很宽的边界,且在近地表速度剧烈变化的区域也能获得很高的精度。
图 7为视速度约束的初至拾取流程图,它可以提高分割精度和初至的检测精度。这种地球物理参数约束可通过纠正像素分类错误,解决分割异常问题以获得更高的分辨率。根据区域内不太可能出现的速度值调整上、下限。本文中,速度约束边界值分别为1650m/s和2100m/s。利用如下公式进行速度约束
| $ {\mathit{\boldsymbol{\tilde Z}}_{ij}} = \left\{ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{A}}&{\frac{{\Delta x}}{{\Delta t}} \ge {v_{\rm{u}}}}\\ {{\mathit{\boldsymbol{Z}}_{ij}}}&{{v_{\rm{u}}} > \frac{{\Delta x}}{{\Delta t}} > {v_{\rm{d}}}}\\ \mathit{\boldsymbol{B}}&{\frac{{\Delta x}}{{\Delta t}} \le {v_{\rm{d}}}} \end{array}} \right. $ | (13) |
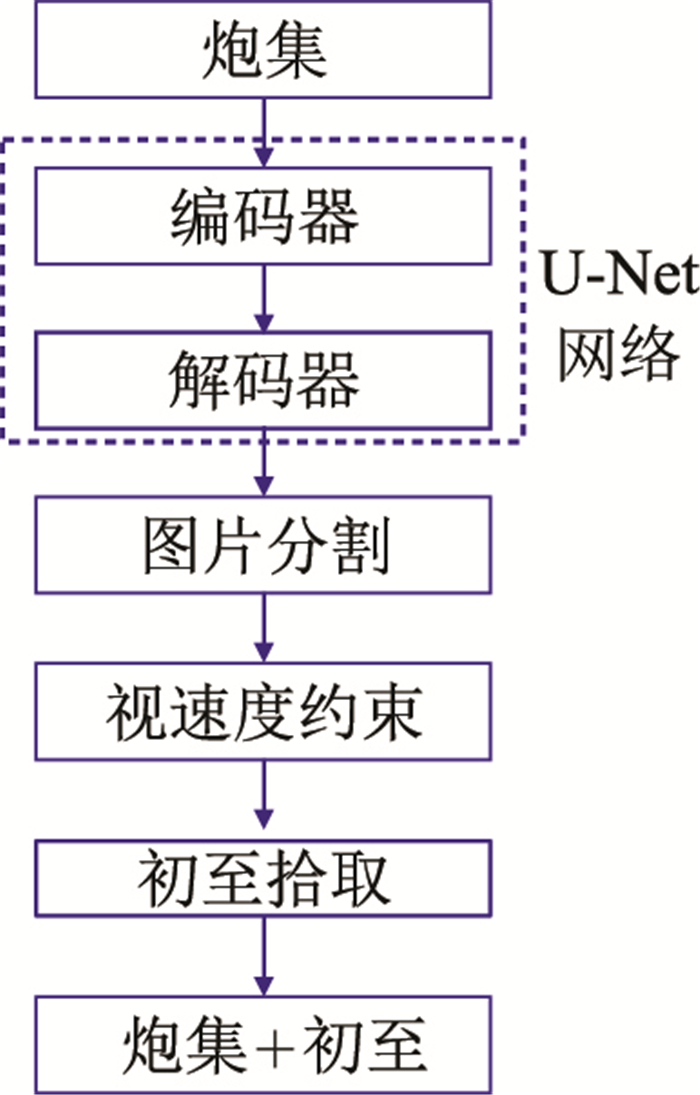
|
图 7 视速度约束的初至拾取流程图 |
式中:
本文采用Dice系数和Jaccard指数两个经典的相似度评价指标评估预测结果。
Dice系数[35]表达式为
| $ D\left( {\mathit{\boldsymbol{Y}}, \mathit{\boldsymbol{Z}}} \right) = \frac{1}{{{N_{\rm{p}}}}}\mathop \sum \limits_{i = 1}^{{N_{\rm{p}}}} \frac{{2{Z_i}{Y_i}}}{{Z_i^2 + Y_i^2}} $ | (14) |
式中Np是样本中的像素总数。
Jaccard指数[41]表达式为
| $ J\left( {\mathit{\boldsymbol{Y}}, \mathit{\boldsymbol{Z}}} \right) = \frac{1}{{{N_{\rm{p}}}}}\mathop \sum \limits_{i = 1}^{{N_{\rm{p}}}} \frac{{{Z_i}{Y_i}}}{{Z_i^2 + Y_i^2 - {Z_i}{Y_i}}} $ | (15) |
本文所用数据为陆上二维地震资料,包含1000个炮集。道间距为25 m,最大炮检距为6 km,每个炮集包含480道,采样间隔为2 ms。振幅随炮检距的增加而衰减是初至拾取面临的主要挑战,但数据调节后,图 4d中显示的振幅更均衡。此外,初至拾取仅限于近、中炮检距(3 km左右)的范围内,远炮检距将用于评估无训练样本区域的预测效果。
2.2 振幅调整振幅调整用于减少数据分类中出现的问题,并平衡相同类别数据间的能量。图 4显示了原始资料、AGC处理后、RMS处理后和振幅调整后的记录。由图可见,与原始资料、AGC处理后、RMS处理后资料相比,经振幅调整后的炮集能量更均衡。图 8显示了振幅调整中每个步骤之后的能量直方图,可见能量得到均衡,振幅异常得到明显衰减(图 8f)。
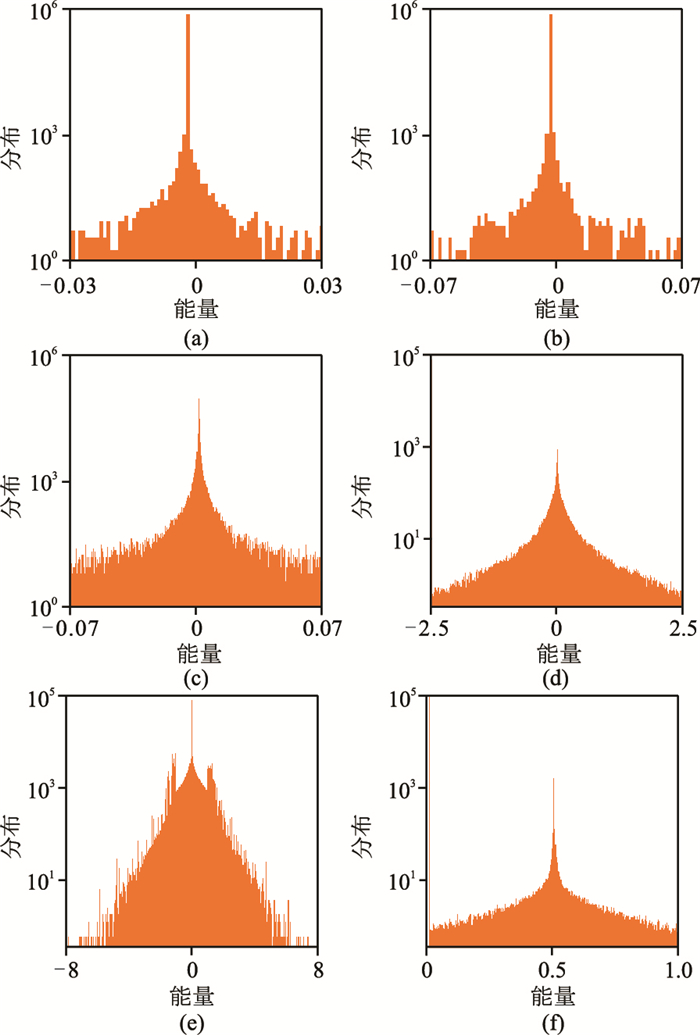
|
图 8 振幅处理过程中的能量直方图 (a)原始地震;(b)T平方球面发散修正;(c)振幅限制至99%;(d)振幅限制至IQR;(e)逐道均方根归一化;(f)最小—最大标准化 |
将采样尺寸设置为64×64像素,这相当于128ms的时间窗长和1600m的炮检距范围,保留噪声样本以增强网络泛化性,而不是像Lu等[42]那样删除它们。
训练标签是利用人工拾取的初至通过二进制编码(例如白色和黑色)填充像素而创建的。标签是手动选取创建的,第一个分隔符上方的像素等于1,下方的像素等于0。然后,在样品提取之后,根据如下公式将样品与标签配对
| $ {S_{ij}} = \left\{ \begin{array}{l} 噪声\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\sum {S_{ij}}}}{{{N_{\rm{p}}}}} = 100\% \\ 初至\;\;\;\;\;\;\;\;\;\;\;\;\;\;20\% \le \frac{{\sum {S_{ij}}}}{{{N_{\rm{p}}}}} \le 80\% \\ 有效数据\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{\sum {S_{ij}}}}{{{N_{\rm{p}}}}} = 0 \end{array} \right. $ | (16) |
式中:S是样本;下标ij表示像素位置。全白(100%)像素填充的样本被标记为噪声,被20%到80%白色像素充填的样本被标记为初至波;无白色像素(0%)的样本被标记为有效数据。从理论上讲,初至波呈高斯分布。在这种情况下,高斯分布的极值容易导致错误分类。因此,为了确保初至波能够被识别,本文将像素数分布限制在20%~80%以保持稳定性。分布在0~20%和80%~100%数据被丢弃。如果像素比例太低(小于10%),则可能会将其错误分类为有效数据;如果比例过高(超过90%),则可能会误判为噪声。
2.4 网络训练在训练数据较少的情况下,可以通过数据增广增加训练数据量[43]。本文通过水平翻转炮集以增加所提取样本的数量,这类似于采集中从两个方向放炮。这种方式既保留了观测系统信息,又将样本数增加了一倍。数据集被随机地分为两个部分,其中80%用于5倍交叉验证(CV),20%用于测试。在训练阶段,5倍交叉验证数据集(80%)分成五个部分,其中四个部分用于训练,一个用于验证。然后,计算平均的训练和验证误差。最后,在对模型进行微调之后,使用测试数据集比较三个U-Net变体的结果。经过100次迭代后实现了收敛。在一个内存(RAM)为4 GB的NVIDIA Quadro K4200中训练时间为26h。最终的训练准确率为99.83%,验证准确率为99.79%。
2.5 超参数检验本文仅测试、评估不同U-Net超参数(学习率、激活函数、损失函数、优化器、舍弃比率权重初始化等)大小以及不同U-Net超参数组合对初至拾取的影响。
学习率决定了神经网络在反向传播过程中每次更新权值的步长,它影响了收敛的速度(图 9)。由图可见,学习率越大,预测值异常越大(图 9a),这是因为解决方案局限于局部最小值;设法减小左侧的预测值异常(图 9b)时,右侧的预测值异常仍然明显;学习率越小,预测精度越高(图 9c),可见左侧和右侧预测值异常均明显减小。
激活函数增加了模型的非线性。将函数ReLU与三种函数(LReLU,ELU,SELU)进行比较(图 10)以选择合适的激活函数。与其他三个函数相比,ReLU具有更广范围的异常值(图 10a);LReLU的异常值较高(图 10b);ELU缩小了异常值范围(图 10c);SELU效果最佳,不仅减少了异常值,且提高了初至预测精度(图 10d)。
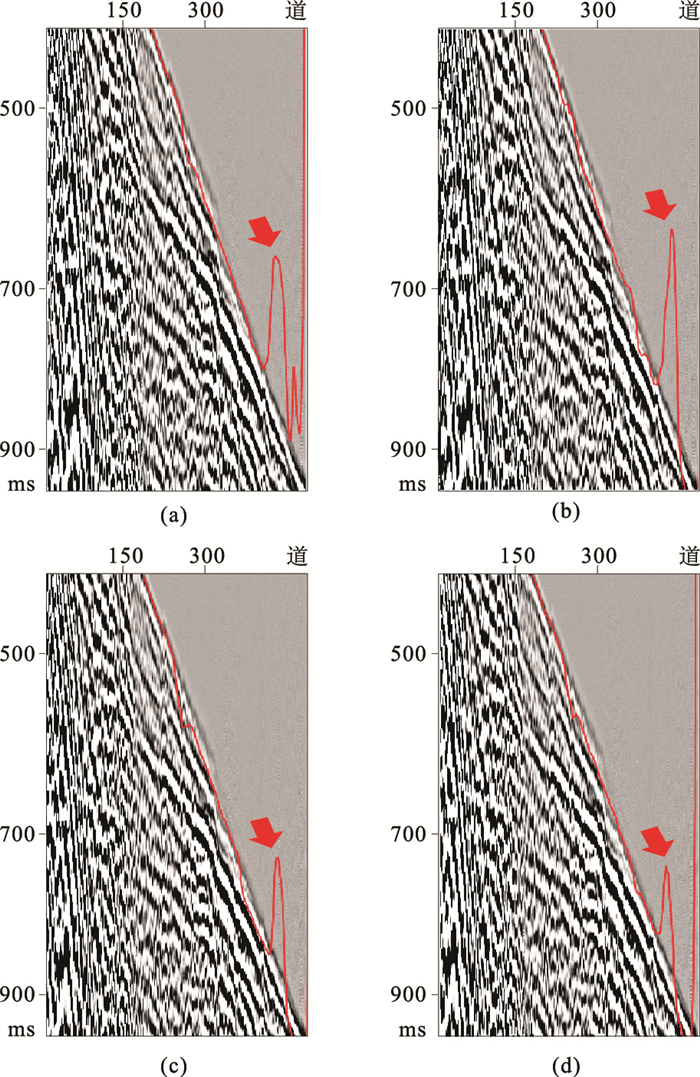
|
图 10 不同激活函数对初至拾取的影响 (a)ReLU; (b)LReLU; (c)ELU; (d)SELU |
损失函数用于衡量学习过程中预测值与实际值之间的差异或偏差(图 11)。由图可见,BCE、Dice和Tversky的函数组合对初至预测的结果相对较好,但有一些较大的异常值(图 11a)。损失函数的组合并非总能产生良好的效果,因为参数差异可能会导致意想不到的破坏作用。Dice和BCE函数组合使异常值减小,连续性降低(图 11b)。BCE尽管使初至预测异常值减小,但其连续性也受到影响(图 11c)。Huber在以少量降低初至波连续性为代价的情况下,提供了减小异常值的最佳方案(图 11d)。

|
图 11 不同损失函数对初至拾取的影响 (a)BCE+Dice+Tversky; (b)BCE+Dice; (c)BCE; (d)Huber |
在超参数优化器类型中,随机梯度下降(SGD)以其脱离局部最小值的速度和能力而闻名[44]。Adadelta根据历史梯度衡量学习率,学习率随着训练过程自动逐渐减小[45]。自适应矩估计(Adam)使用随机梯度下降估计历史梯度的一阶和二阶矩[46]。Adamax是一种基于无穷范数的Adam变体,参数更新的计算要比Adam更简单[46]。RMSprop通过调整更新参数时的步长以加快梯度下降。
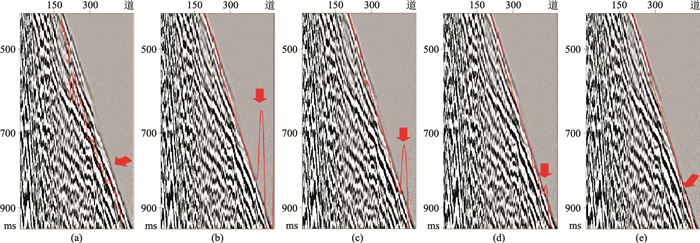
五种优化器对初至拾起的效果如图 12所示。SGD初至拾起的效果不好(图 12a),这可能与内在跳跃相关。与其他方法迭代次数相同时,SGD初至自动拾取效果均不好。相对于SGD而言,RMS-prop初至拾起的效果改善明显,只是预测值异常高(图 12b)。Adadelta对预测值异常减小一半(图 12c)。Adam几乎消除了预测值异常,但初至波出现了轻微的不连续(图 12d)。Adamax不仅消除预测值异常,而且保证了初至拾取的连续性(图 12e)。
|
图 12 不同优化器对初至拾取的影响 (a)SGD;(b)RMSprop;(c)Adadelta;(d)Adam;(e)Adamax |
随机舍弃一些神经元,可以缓解网络过拟合,提高网络的通用性。图 13中展示了舍弃比率对初至拾取的影响。当舍弃比率为0.05时(图 13d),效果最佳;舍弃比率为0.1和0.2时效果较好(图 13b和图 13c);当舍弃比率为0时,预测值异常大(图 13a),如果误差过大,则需要较长的训练时间才能收敛到解而得到满意的拾取效果。

|
图 13 不同舍弃比率对初至拾取的影响 (a)0;(b)0.20;(c)0.10;(d)0.05 |
在训练之前,初始化权重决定了网络的初始状态,可以避免梯度消失或爆炸问题的出现。为此,LeCun等[47]利用高斯分布函数得到初始化权重,再乘以输入数据的平方根。Glorot等[48]和He等[49]改进了LeCun初始化方式。Glorot等[48]初始化更适用于具有Sigmoid的网络层;He等[49]初始化更适用于具有ReLU的网络层。由图 14可见,LeCun正态分布权重初始化对初至拾取的预测值异常在左右两侧均很大(图 14a);He正态分布权重初始化对初至拾取的预测值异常在左侧几乎完全消除,而右侧的异常也减小(图 14b);Glorot正态分布权重初始化对初至拾取的预测值异常在左侧已得到完全校正,而右侧也减小(图 14c)。

|
图 14 不同权重初始化对初至拾取的影响 (a)LeCun正态;(b)He正态;(c)Glorot正态 |
对比不同网络架构初至拾取的结果(图 15)。不建议体系结构之间共享相同的超参数,本文实验选定损失函数Focal Tversky的参数为γ=2、α=0.3、β=0.7、ε=1;Huber损失函数的参数为δ=0.9,目的是将每个网络优化到最佳状态,每个架构的最佳超参数如表 3所示。此外,为了提高实验结果精度,aU-Net模型包含了一种深度监督和金字塔式训练的变体。
|
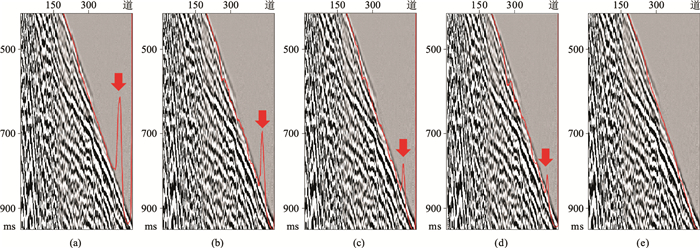
图 15 不同网络架构初至拾取的结果对比 (a)UNet++; (b)aU-Net; (c)aU-Net+DP; (d)wU-Net; (e)U-Net |
|
|
表 3 每个架构的最佳超参数 |
UNet++模型通过一系列嵌套和残差密集连接,形成最复杂的网络架构,拾取的初至连续性好,但没能降低预测值异常(图 15a);aU-Net架构初至预测值异常有所减小,但初至不连续(图 15b),这很可能是由于结构简单及参数的减少导致偏差的增大;伴有深度监督的aU-Net架构,网络架构复杂性增加,可以降低预测值异常(图 15c);wU-Net架构初至拾起中,尽管预测值异常减小,但拾取的连续性受到了很大的影响(图 15d);U-Net架构拾起初至消除了预测值异常且保存了连续性,效果好(图 15e)。
综上所述,在某些情况下,在复杂模型与简单模型之间寻找平衡,不实施新架构而集中更多精力优化超参数时,也有可能获得令人满意的结果。
与传统的BCE相比,U-Net的优势在于损失函数Huber更关注边界。与传统的ReLU和Adamax优化器相比,损失函数SELU可对网络进行归一化并提高准确性,这是对传统的Adam优化器的改进。
3 应用效果 3.1 性能评价计算速度约束前、后分割图像的准确度、查全率、Dice系数和Jaccard指数(表 4,值越大意味着性能越好),结果表明,本文方法提高了初至波预测的精度。
|
|
表 4 速度约束前、后的得分比较 |
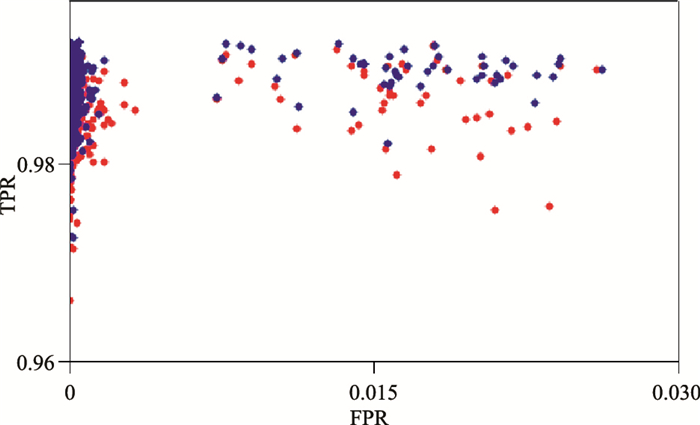
应用接受者操作特性(Receiver Operating Characteristic,ROC)[50]曲线评估最终预测结果。图 16显示了速度约束前、后每道分割结果的ROC曲线。由图可见,平均真正例率(True Positive Rate,TPR)或查全率从0.9854提高到0.9866;而假正例率(False Positive Rate,FPR)仍保持在0.0014。TPR是噪声样本的正确分类,而FPR是数据样本的正确分类。速度约束后的结果更接近理想情况,即FPR=0、TPR=1。这说明速度约束可以改善分类效果。具体来说,在低信噪比的区域(例如远炮检距区域)中,像素无法准确区分有效数据与噪声数据,噪声数据降低了所预测初至波时间的精度,而视速度约束可以修改这些像素,从而提高拾取精度。
|
图 16 速度约束前(红点)后(蓝点)每道分割结果 |
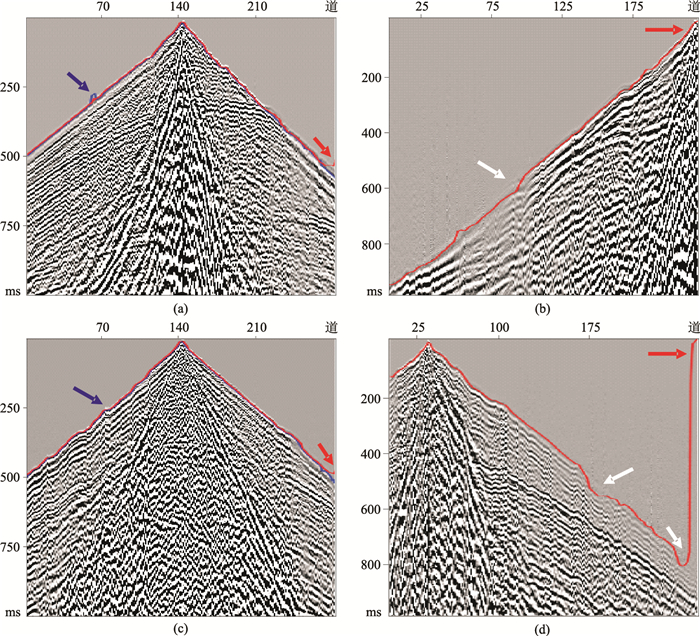
图 17显示了本文方法所预测的初至波。结果表明,自动拾取的初至在近炮检距连续性好,中炮检距也准确,且在低能区(白色箭头)的预测值异常点很少。图 17a中蓝色箭头指示了比原始初至拾取结果精度更高的网络区域;图 17b显示了拾取的初至与地面起伏存在良好的对应关系(蓝色箭头所示);由图 17c可见,在先前标记信息丢失的中炮距检区域初至拾取效果较好,这表明在没有初至波信息的情况下网络能够预测初至;图 17d表明,在能量较弱的区域预测精度会降低(白色箭头所示),并且在末端地震道中拾取结果欠稳定(红色箭头所指),并出现在所有采样点中。这个普遍存在的问题可能是由于计算误差引起的,而不是网络预测中所固有的。
对比并定量分析预测结果与人工拾取的结果,如图 18所示。由图可见,某一单炮负炮检距情况下绝对平均误差为2.5088ms (图 18b);另一单炮正负炮检距情况下绝对平均误差为4.0812ms(图 18d),大于4个样点值。同时,也可以看到在信噪比低的区域预测误差增大。

|
图 18 训练数据的人工拾取初至和本文方法预测结果差异 (a)负炮检距;(b)负炮检距的误差;(c)正负炮检距;(d)正负炮检距的误差 |
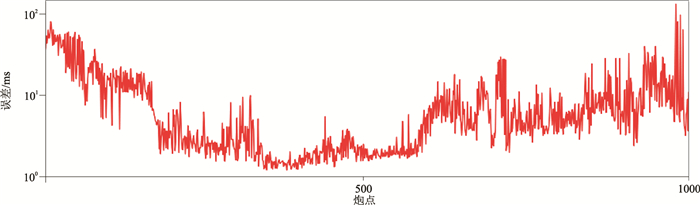
图 19显示的是参与训练的多炮人工拾取初至与本文方法预测结果的对比,平均误差为8.8993 ms,小于5个样点值。
|
图 19 参与训练的多炮人工拾取初至和本文方法预测结果差异 |
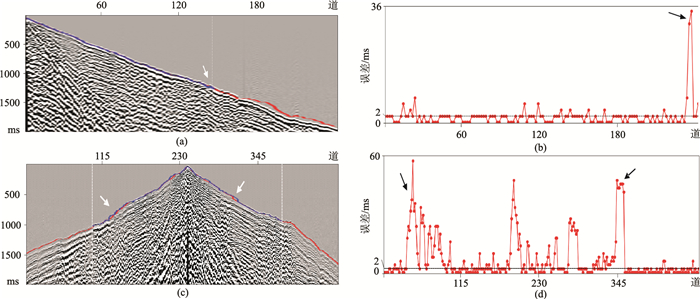
之前所有的训练样本都来自Xline方向,因此选取了一条与训练样本垂直的测线试验。图 20显示在正炮检距和正负炮检距本文方法自动拾取初至的预测值与人工拾取的结果吻合都很好。正炮检距下预测结果和人工拾取一致,绝对平均误差为1.9855ms (图 20b);在正负炮检距在没有人工拾取的情况下,本文方法仍然能够预测出初至结果,绝对平均误差为6.8889ms (图 20d)。
|
图 20 对未参与训练的数据进行初至预测 (a)正炮检距;(b)正炮检距的误差;(c)正负炮检距;(d)正负炮检距的误差 |
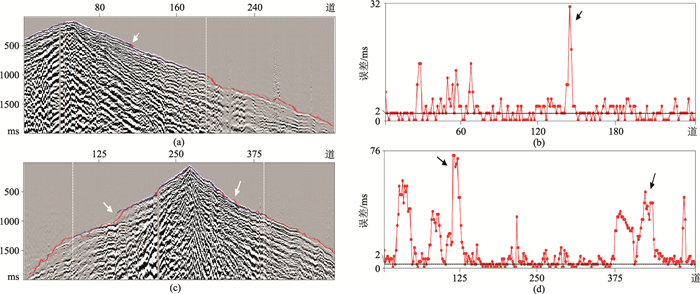
应用本文方法对另一个工区的数据进行试验,未重新训练,而是直接利用以前的训练结果。由于远地震道的初至信噪比很低,自动拾取误差大。单炮记录1预测结果与人工拾取吻合度很高,绝对平均误差为2.9785ms (图 21b);单炮记录2绝对平均误差为13.1448ms (图 21d)。尽管信噪比不高,但是训练网络仍能取得令人满意的预测结果。
|
图 21 对未参与训练的另一工区的数据进行初至预测 (a)单炮记录1;(b)单炮记录1的拾取误差;(c)单炮记录2;(d)单炮记录2的拾取误差 |
本文研究了基于U-Net网络和视速度约束的地震波初至自动拾取方法,并进行了参数试验和实际资料初至拾取试验,取得的主要结论为:
(1) 基于速度约束的方法提高了分割图像中边界识别精度,这些边界指示了初至波的时间;
(2) 最小—最大归一化和四分位距限幅通过平衡样本能量对网络训练性能有积极影响,提高了分类精度;
(3) 该方法在低信噪地震资料中进行应用,预测值异常较小。
| [1] |
刘百红, 李建华, 郑四连, 等. 基于局部相似属性的初至自动拾取[J]. 石油地球物理勘探, 2018, 53(3): 449-453. LIU Baihong, LI Jianhua, ZHENG Silian, et al. Automatic first break picking based on local similarity attribute[J]. Oil Geophysical Prospecting, 2018, 53(3): 449-453. |
| [2] |
宋建国, 李赋真, 徐维秀, 等. 改进的神经网络级联相关算法及其在初至拾取中的应用[J]. 石油地球物理勘探, 2018, 53(1): 8-16. SONG Jianguo, LI Fuzhen, XU Weixiu, et al. An improved neural-network cascade-correlation algorithm and its application in seismic first break picking[J]. Oil Geophysical Prospecting, 2018, 53(1): 8-16. |
| [3] |
刘腾蛟, 高阳, 储仿东, 等. 最小二乘曲线拟合的微地震初至优化拾取方法及应用[J]. 石油地球物理勘探, 2018, 53(增刊2): 124-129. LIU Tengjiao, GAO Yang, CHU Fangdong, et al. Microseismic first arrival picking based on least square curve fitting[J]. Oil Geophysical Prospecting, 2018, 53(S2): 124-129. |
| [4] |
胡瑞卿, 王彦春, 尹志恒, 等. 结合CEEMDAN和主成分分析的低信噪比微地震初至信号检测[J]. 石油地球物理勘探, 2019, 54(1): 45-53. HU Ruiqing, WANG Yanchun, YIN Zhiheng, et al. A first arrival detection method in low SNR microseismic signals based on CEEMDAN-PCA[J]. Oil Geophysical Prospecting, 2019, 54(1): 45-53. |
| [5] |
Goodfellow I, Bengio Y, Courville A C. Deep learning[J]. Nature, 2015, 521(7553): 436-444. DOI:10.1038/nature14539 |
| [6] |
Bengio Y. Deep learning of representations for unsupervised and transfer learning[C]. ICML Unsupervised and Transfer Learning, 2012.
|
| [7] |
庄东海, 肖春燕, 颜永宁. 利用人工神经网络自动拾取地震记录初至[J]. 石油地球物理勘探, 1994, 29(5): 659-664. ZHUANG Donghai, XIAO Chunyan, YAN Yongning. Seismic first arrivel pickup using artificial neural network[J]. Oil Geophysical Prospecting, 1994, 29(5): 659-664. |
| [8] |
曹晓莉, 刘斌, 王淑荣, 等. 综合动量法和可变学习速度的BP神经网络地震初至拾取[J]. 石油地球物理勘探, 2020, 55(1): 71-79. CAO Xiaoli, LIU Bin, WANG Shurong, et al. Seismic first-break picking based on BP neural network integrated with momentum method and adaptive learning rate method[J]. Oil Geophysical Prospecting, 2020, 55(1): 71-79. |
| [9] |
蒋一然, 宁杰远. 基于支持向量机的地震体波震相自动识别及到时自动拾取[J]. 地球物理学报, 2019, 62(1): 361-373. JIANG Yiran, NING Jieyuan. Automatic detection of seismic body-wave phases and determination of their arrival times based on support vector machine[J]. Chinese Journal of Geophysics, 2019, 62(1): 361-373. |
| [10] |
谭家炜, 李静, 李飞达, 等. 基于超虚干涉法约束的模糊C均值聚类地震初至自动提取[J]. 石油地球物理勘探, 2020, 55(5): 979-990. TAN Jiawei, LI Jing, LI Feida, et al. Automatic pick-up of seismic P-wave first arrivals via fuzzy C-means method constrained by super-virtual interferometry[J]. Oil Geophysical Prospecting, 2020, 55(5): 979-990. |
| [11] |
王维波, 徐西龙, 盛立, 等. 卷积神经网络微地震事件检测[J]. 石油地球物理勘探, 2020, 55(5): 939-949. WANG Weibo, XU Xilong, SHENG Li, et al. Detection of microseismic events based on convolutional neural network[J]. Oil Geophysical Prospecting, 2020, 55(5): 939-949. |
| [12] |
Hollander Y, Merouane A, Yilmaz O. Using a deep convolutional neural network to enhance the accuracy of first-break picking[C]. SEG Technical Program Expanded Abstracts, 2018, 37: 4628-4632.
|
| [13] |
Yuan S, Liu J, Wang S, et al. Seismic waveform classification and first break picking using convolution neural networks[J]. IEEE Geoscience & Remote Sensing Letters, 2018, 15(2): 272-276. |
| [14] |
Duan X, Zhang J, Liu Z, et al. Integrating seismic first-break picking methods with a machine learning approach[C]. SEG Technical Program Expanded Abstracts, 2018, 37: 2186-2190.
|
| [15] |
Tsai K C, Hu W, Wu X, et al. First-break automatic picking with deep semisupervised learning neural network[C]. SEG Technical Program Expanded Abstracts, 2018, 37: 2181-2185.
|
| [16] |
李薇薇, 龚仁彬, 周相广, 等. 基于深度学习UNet++网络的初至波拾取方法[J]. 地球物理学进展, 2021, 36(1): 187-194. LI Weiwei, GONG Renbin, ZHOU Xiangguang, et al. UNet++: a deep-neural-network-based seismic arrival time picking method[J]. Progress in Geophysics, 2021, 36(1): 187-194. |
| [17] |
赵明, 陈石, 房立华, 等. 基于U形卷积神经网络的震相识别与到时拾取方法研究[J]. 地球物理学报, 2019, 62(8): 3034-3042. ZHAO Ming, CHEN Shi, FANG Lihua, et al. Earthquake phase arrival auto-picking based on U-shaped convolutional neural network[J]. Chinese Journal of Geophysics, 2019, 62(8): 3034-3042. |
| [18] |
陈德武, 杨午阳, 魏新建, 等. 基于混合网络U-SegNet的地震初至自动拾取[J]. 石油地球物理勘探, 2020, 55(6): 1188-1201. CHEN Dewu, YANG Wuyang, WEI Xinjian, et al. Automatic picking of seismic first arrivals based on hybrid network U-SegNet[J]. Oil Geophysical Prospecting, 2020, 55(6): 1188-1201. |
| [19] |
Xie T, Yue Z, Jiao X, et al. First-break automatic pi-cking with fully convolutional networks and transfer learning[C]. SEG Technical Program Expanded Abstracts, 2019, 38: 4972-4976.
|
| [20] |
LeCun Y, Boser B, Denker J S, et al. Backpropagation applied to handwritten zip code recognition[J]. Neural Computation, 1989, 1(4): 541-551. DOI:10.1162/neco.1989.1.4.541 |
| [21] |
Krizhevsky A, Sutskever I, Hinton G E. ImageNet classification with deep convolutional neural networks: Advance in neural information processing systems[C]. NIPS, 2012, 1097-1105.
|
| [22] |
Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition[C]. International Conference on Learning Representations, 2015.
|
| [23] |
Szegedy C, Liu W, Jia Y, et al. Going deeper with convolutions[C]. IEEE Conference on Computer Vision and Pattern Recognition, 2015: 1-9.
|
| [24] |
Long J, Shelhamer E, Darrell T. Fully convolutional networks for semantic segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 39(4): 640-651. |
| [25] |
Noh H, Hong S, Han B. Learning deconvolution network for semantic segmentation[C]. IEEE International Conference on Computer Vision, 2015, 1520-1528.
|
| [26] |
Chen L C, Papandreou G, Kokkinos I, et al. DeepLab: semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected CRFs[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018, 40(4): 834-848. DOI:10.1109/TPAMI.2017.2699184 |
| [27] |
Yu F, Koltun V. Multi-scale context aggregation by dila-ted convolutions[C]. International Conference on Lear-ning Representations, 2015.
|
| [28] |
Ronneberger O, Fischer P, Brox T. U-Net: Convolutional networks for biomedical image segmentation[C]. International Conference on Medical Image Computing and Computer-Assisted Intervention, 2015.
|
| [29] |
Hu L, Zheng X, Duan Y. U-Net convolutional networks for first arrival picking[C]. SEG Technical Program Expanded Abstracts, 2018, 37: 15-18.
|
| [30] |
Zhou Z, Siddiquee M M, Tajbakhsh N, et al. UNet++: Redesigning skip connections to exploit multisdcal features in image segmentation[J]. IEEE Transactions on Medical Imaging, 2020, 39: 1856-1867. DOI:10.1109/TMI.2019.2959609 |
| [31] |
Abraham N, Khan N M. a novel Focal Tversky loss function with improved attention U-Net for lesion segmentation[C]. IEEE 16th International Sympo-sium on Biomedical Imaging, 2019, 683-687.
|
| [32] |
Ma Y, Cao S, Rector J W, et al. Automatic first arrival picking for borehole seismic data using a pixel-level network[C]. SEG Technical Program Expanded Abstracts, 2019, 38: 2463-2467.
|
| [33] |
Maas A, Hannun L, Awni Y, et al. Rectifier nonlinearities improve neural network acoustic models[C]. International Conference on Machine Learning, 2013, 28.
|
| [34] |
Klambauer G, Unterthiner T, Mayr A, et al. Self-normalizing neural networks[C]. NIPS, 2017.
|
| [35] |
Sudre C H, Li W, Vercauteren T, et al. Generalised Dice overlap as a deep learning loss function for highly unba-lanced segmentations[C]. Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support, 2017, 240-248.
|
| [36] |
Tversky A. Features of similarity[J]. Psychological Review, 1977, 84(4): 327-352. DOI:10.1037/0033-295X.84.4.327 |
| [37] |
Hashemi S R, Seyed S M S, Erdogmus D, et al. Asymmetric loss functions and deep densely-connected networks for highly-imbalanced medical image segmentation: Application to multiple sclerosis lesion detection[J]. IEEE Access, 2019, 7(1): 1721-1735. |
| [38] |
Huber P J. Robust regression: Asymptotics, conjectures and Monte Carlo[J]. Annals of Statistics, 1973, 1(5): 799-821. |
| [39] |
Upton G, Cook I. Understanding Statistics[M]. Oxford University Press, 1996.
|
| [40] |
Basheer I A, Hajmeer M N. Artificial neural networks: fundamentals, computing, design, and application[J]. Journal of Microbiological Methods, 2000, 43(1): 3-31. DOI:10.1016/S0167-7012(00)00201-3 |
| [41] |
Berman M, Triki A R, Blaschko M B. The Lovasz-softmax loss: A tractable surrogate for the optimization of the intersection-over-union measure in neural networks[C]. IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2018, 4413-4421.
|
| [42] |
Lu K, Feng S. Auto-windowed super-virtual interfe-rometry via machine learning: A strategy of first-arrival traveltime automatic picking for noisy seismic data[C]. SEG Technical Program Expanded Abstracts, 2018, 37: 10-14.
|
| [43] |
Dosovitskiy A, Fischer P, Springenberg J T, et al. Discriminative unsupervised feature learning with exemplar convolutional neural networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(9): 1734-1747. DOI:10.1109/TPAMI.2015.2496141 |
| [44] |
Robbins H, Monro S A. Stochastic approximation method[J]. The Annals of Mathematical Statistics, 1951, 22(3): 400-407. DOI:10.1214/aoms/1177729586 |
| [45] |
Zeiler M D. ADADELTA: An adaptive learning rate method[J]. ArXiv Preprint ArXiv: 1212.5701, 2012. |
| [46] |
Kingma D, Ba J. Adam: A method for stochastic optimization[C]. 3rd International Conference on Learning Representations, 2015.
|
| [47] |
LeCun Y, Bottou L, Orr G, et al. Efficient BackProp//Neural Networks: Tricks of the Trade[M]. Springer, 1998.
|
| [48] |
Glorot X, Bengio Y. Understanding the difficulty of trai-ning deep feedforward neural networks[C]. Thirteenth International Conference on Artificial Intelligence and Statistics, JMLR Workshop and Conference Proceedings, 2010, 249-256.
|
| [49] |
He K, Zhang X, Ren S, et al. Delving deep into rectifiers: surpassing human-level performance on image Net classification[C]. IEEE International Conference on Computer Vision(ICCV), 2015, 1026-1034.
|
| [50] |
Zou K H, O'Malley A J, Mauri L. Receiver-operating characteristic analysis for evaluating diagnostic tests and predictive models[J]. Circulation, 2007, 115(5): 654-657. DOI:10.1161/CIRCULATIONAHA.105.594929 |



 刘洋, 新疆维吾尔自治区克拉玛依市安定路355号中国石油大学(北京)克拉玛依校区石油学院, 834000。Email:
刘洋, 新疆维吾尔自治区克拉玛依市安定路355号中国石油大学(北京)克拉玛依校区石油学院, 834000。Email: