② 陆军工程大学石家庄校区, 河北石家庄 050003;
③ 北京市遥感信息研究所, 北京 100192
② Army Engineering University(Shijiazhuang), Shijiazhuang, Hebei 050003, China;
③ Beijing Institute of Remote Sensoring Information, Beijing 100192, China
磁测数据反演主要应用于军事侦察(未爆弹、潜艇和水雷等)、水文、能源及工程地质勘探等领域[1-4]。磁性目标体的三维反演是利用观测面上磁测数据,对其空间形状、位置、磁化强度及磁化方向等参数进行求解的过程,为下一步地质解释提供可靠的数据支持。
磁性体反演主要包括物性反演和形态反演两方面[5]。物性反演的主要思路是将观测面对应的地下区域离散化为规则的长方体网格,通过反演获得这些网格的磁性参数,并最终获得目标体的磁性参数空间分布[6-8]。物性反演过程中,由于目标函数固有的欠定性特征,计算结果存在多解性;同时,由于需要进行多次模型正演计算,核函数矩阵会大大增加计算时间,影响计算效率。形态反演的主要思路是利用一定的计算准则、基于观测数据对地下多面体进行拟合,利用多面体的形态对待测模型的三维分布进行求解[9]。Uieda等[10]利用L2范数定义数据泛函约束函数对待测目标进行形态反演;曹书锦等[11]基于L1范数利用种子反演方法,提高了重力梯度张量反演精度;Uieda等[12]利用重力梯度张量,对不同待测目标的“种子”分配不同密度值,实现特定目标的反演,有效排除了非目标场源的干扰。常规的形态反演方法能够克服物性反演方法在迭代过程中对核函数矩阵进行多次计算以及计算结果存在多解性的问题,但前提是需要获得待测目标的先验信息。然而,实际应用中常利用经验数据对模型的磁性参数和几何参数进行赋值,导致计算结果的精度下降。
针对形态反演方法中存在的问题,本文提出了基于多参数约束的磁性目标三维形态反演方法:首先计算磁性目标的平面位置、深度、磁化方向及磁化强度;然后,联合垂直磁场数据Bz和磁张量数据,对磁性目标进行三维反演,在反演过程中,对磁性目标待反演空间进行划分,建立待增长区域,并计算最优增长模块,实现磁性目标的三维重建。
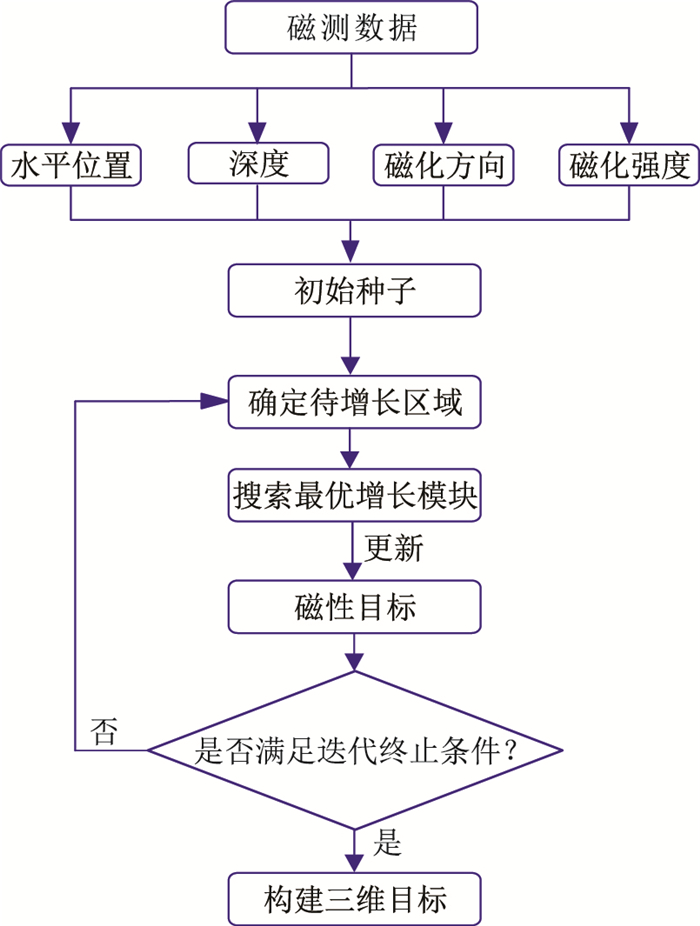
1 方法原理本文计算过程如图 1所示。首先,根据观测面的磁测数据,分别对磁性目标的水平位置、深度、磁化方向和磁化强度进行估计,确定初始种子的磁性参数和几何参数;然后,利用形态反演迭代计算方法,通过确定待增长区域中的最优增长模块,实现模型反演;最终,将满足终止条件的计算结果输出,即最终反演结果。
|
图 1 本文算法流程图 |
假设观测面为平面,d为观测面上的实际观测数据,b为预测模型在观测面上的正演数据。若数据包含较大误差,L2范数比L1范数更敏感[11, 13],因此,利用L1范数能够获得更加稳定的反演结果。基于L1范数定义的数据泛函约束函数为
| $ \phi=\frac{\sum\limits_{i=1}^{N}\left|d_{i}-b_{i}\right|}{\sum\limits_{i=1}^{N}\left|d_{i}\right|} $ | (1) |
式中:i代表观测点序号;N代表观测面上总观测点数;di、bi分别为d、b的元素。磁梯度张量矩阵可表示为
| $ \boldsymbol{B}=\left[\begin{array}{c} \frac{\partial}{\partial x} \\ \frac{\partial}{\partial y} \\ \frac{\partial}{\partial z} \end{array}\right]\left[\begin{array}{lll} B_{x} & B_{y} & B_{z} \end{array}\right]=\left[\begin{array}{lll} B_{x x} & B_{x y} & B_{x z} \\ B_{y x} & B_{y y} & B_{y z} \\ B_{z x} & B_{z y} & B_{z z} \end{array}\right] $ | (2) |
式中:Bx、By和Bz分别为磁场的x、y和z分量;Bαβ(α,β=x,y,z)代表磁梯度张量B的分量。
假设反演过程中需同时对H类数据进行计算,则总数据约束函数Ψ(M)可以表示为
| $ \varPsi(M)=\sum\limits_{l=1}^{H} \phi_{l}(M) $ | (3) |
式中:M为反演模型的磁化强度;ϕl为第l类数据类型的约束函数。例如,当利用磁梯度张分量Bxz、Byz、Bzz进行反演时,H=3,ϕ1(M)=ϕxz(M),ϕ2(M)=ϕyz(M),ϕ3(M)=ϕzz(M),可利用式(1)分别对其进行计算。
形态反演过程中,包含如下约束条件[14-15]:①模型的解是连续的(内部没有空洞);②各网格的磁化强度只能为M或者0;③模型增长过程中,需要设置初始位置,且新增长模块与当前模块至少有一个平面是共面的。根据上述约束条件,形态反演目标函数Γ(M)可以表示为
| $ \varGamma(M)=\varPsi(M)+\rho \theta(M) $ | (4) |
式中:θ(M)为模型在空间上定义的正则化约束函数;ρ为正则化参数,用于调节Ψ(M)与θ(M)两个函数之间的平衡。对正则化参数ρ的选择,本文采用自适应正则化方法
| $ \rho^{(n+1)}=q \rho^{(n)} $ | (5) |
式中:n表示迭代次数;q=0.95。本文设定初始值ρ(0)=0.1。θ(M)可以表示为
| $ \theta(M)=\frac{1}{w+f+g} \sum\limits_{j=1}^{P} \frac{M_{j}}{M_{j}+\varepsilon} L_{j} $ | (6) |
式中:w、f、g分别为当前模型在x、y、z三个方向上的长度;P为当前模型包含的长方体的个数;Mj为第j个长方体的磁化强度;ε为一个很小的正数,用于避免Mj为0时计算的不稳定,本文定义ε=1×10-5;Lj为待增长长方体的中心点与当前模型的第j个长方体的中心点之间的距离。θ(M)在计算过程中加入了模型的位置属性,通过长方体单元间的距离对反演模型施加约束,避免反演结果沿某一方向无限增长,可提高反演结果的准确性[16]。
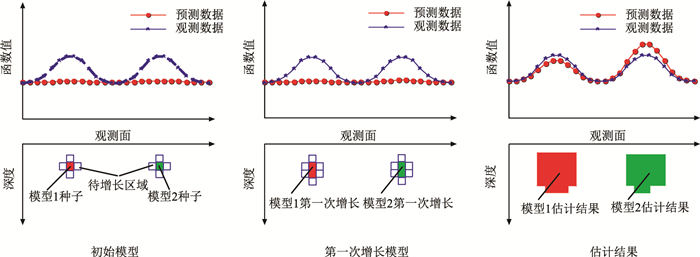
形态反演的具体计算过程如图 2所示。首先,在待测区域内设置初始模型作为种子,即分别对初始模型的位置、磁化方向以及磁化强度进行赋值;然后,利用式(4)计算待增长区域内所有网格的目标函数值,将待增长区域内贡献最大的网格作为增长网格(即确保Ψ(M)变小的前提下Γ(M)最小),并设置增长模型的磁化强度与初始模型一致;最后,反复迭代,直到目标函数Γ(M)达到阈值或者达到最大迭代次数,终止迭代,获得最终反演结果。
|
图 2 形态反演模型增长示意图 |
在形态反演过程中,获得磁性目标的准确初始磁性参数和几何参数,对计算结果有较大的影响。传统的形态反演方法基于先验信息对初始磁性参数和几何参数进行赋值,这会导致对先验信息的依赖性较强,对于部分先验信息未知的目标,计算结果精度低。为了提高方法的适应性,本文采用下述方案分别对磁性目标的水平位置、深度、磁化方向以及磁化强度进行估计。
1.2.1 平面位置估计归一化磁源强度(NSS)是基于磁偶极子磁梯度张量矩阵计算得到的,在剩余磁化条件下,能够对磁性目标的水平位置进行有效计算。NSS的最大值点即对应磁偶极子的实际位置。对于多边形磁性体而言(如水平薄板),当测量面距离多边形较近时(即构造指数为小于3的正整数,模型不能等效为磁偶极子),NSS极大值点即对应磁性目标的边界(存在多个极大值点)[17]。因此,需对观测面磁测数据向上延拓,当延拓面距离模型实际位置足够大时,模型可以等效为磁偶极子。此时,NSS的极大值唯一,且与磁性目标的中心位置一致。对于多个磁性目标而言,需要根据NSS的分布特征划分计算区域,使每个计算区域内仅包含一个磁性目标,然后再利用上述方法分别进行延拓,并最终获得所有磁性目标的中心位置。
定义观测面上(x,y,z)处观测的张量不变量A1=λ1λ2+λ1λ3+λ2λ3和A2=λ1λ2λ3(λ1≥λ2≥λ3),这里特征值λt(t=1,2,3)满足特征方程λt3+A1λt-A2=0。A1、A2以及NSS表达式分别为[18-19]
| $ \left\{\begin{aligned} A_{1}=& B_{x x} B_{y y}+B_{y y} B_{z z}+B_{x x} B_{z x}-\\ & B_{x y}^{2}-B_{y z}^{2}-B_{x z}^{2} \\ A_{2}=& B_{x x}\left(B_{y y} B_{z z}-B_{y z}^{2}\right)+B_{x y}\left(B_{y z} B_{x z}-\right.\\ &\left.B_{x y} B_{z z}\right)+B_{x z}\left(B_{x y} B_{y z}-B_{x z} B_{y y}\right) \\ \mathrm{NSS}&= \sqrt{-\lambda_{2}^{2}-\lambda_{1} \lambda_{3}} \end{aligned}\right. $ | (7) |
因此,本文基于NSS数据的特性,将观测面上各计算区域内的NSS极大值点作为磁性目标的水平中心位置。当计算区域内包含多个极值时,利用向上延拓理论,将观测数据向上延拓[20],直到计算区域内仅包含一个极大值点。
1.2.2 深度估计谢汝宽等[21]提出了最小反演拟合差的深度估计方法,利用空间域单层等效源估计磁性目标的深度。本文在此基础上,提出了频率域单层等效源深度估计方法,可进一步节省计算时间。
假设观测面为水平面,将观测面以下空间划分为不同深度、相同厚度的水平长方体层,且长方体层尺寸相同。假设某一长方体层的顶面深度为z1,底面深度为z2,观测面的高度设置为z0,此长方体层的磁异常分量Bz与磁化强度M在频率域的关系为[22]
| $ \mathrm{F}\left(B_{z}\right)=\left[\frac{\mu_{0}}{2} \gamma_{m} \mathrm{e}^{k z_{0}}\left(\mathrm{e}^{-k z_{1}}-\mathrm{e}^{-k z_{2}}\right)\right] \times \mathrm{F}(M) $ | (8) |
式中:F代表二维傅里叶变换;μ0=4π×10-7H/m为真空中的磁化率;
以第c层为例,假设其顶面深度为zc,其磁化强度反演结果Mc可表示为[23]
| $ \mathrm{F}\left(M_{c}\right)=\frac{2}{\mu_{0} \gamma_{m}} \times \frac{h\left(k_{x}, k_{y}, z_{c}\right)}{\int_{z=z_{0}}^{\infty} h\left(k_{x}, k_{y}, z\right) \times \mathrm{e}^{-k x} \mathrm{~d} z} \times \mathrm{F}\left(B_{z}\right) $ | (9) |
式中h(kx,ky,zc)=(zce-kzc)s,正整数s∈[1, 10],取值越大成像结果的分辨率越高,本文设定s=10。
基于最小反演拟合差的频率域单层等效源深度估计方法的计算过程[21]描述如下:在观测平面下设置某一厚度的长方体等效源层,该长方体层的厚度为z2-z1;将等效源层向下移动一定的距离,分别利用式(8)和式(9)计算不同等效源层在观测平面的正演数据与实际数据的反演拟合差;在不断向下移动过程中,选择拟合差最小时对应的长方体层深度作为模型的中心深度。对于多目标体,将观测面上的磁测数据划分为多个仅包含一个目标的计算区域,分别对不同计算区域内的待测模型利用本文深度计算方法进行计算,实现对不同深度(特殊情形下也可能是同一深度)的多个磁性目标体的深度逐一进行估计。
1.2.3 磁化方向估计在磁化方向未知的情况下,对磁性目标的磁倾角和磁偏角等间隔选取一系列的数据点,组成磁化方向暂定值。对这一系列磁化方向下的化极异常值与归一化磁源强度进行试错,得到不同的互相关系数,当互相关系数取得最大值时,即表明对应的磁化方向为最佳估计值。
定义实测区域内磁异常的化极结果ΔTrtp与归一化磁源强度NSS的互相关系数为
| $ Q=\frac{\sum\limits_{u=1}^{N_{x}} \sum\limits_{v=1}^{N_{y}}\left[\Delta T_{\mathrm{rtp}}(u, v)-\overline{\Delta T_{\mathrm{rtp}}}\right] \times[\mathrm{NSS}(u, v)-\overline{\mathrm{NSS}}]}{\sqrt{\sum\limits_{u=1}^{N_{x}} \sum\limits_{v=1}^{N_{y}}\left[\Delta T_{\mathrm{rtp}}(u, v)-\overline{\Delta T_{\mathrm{rtp}}}\right]^{2} \times[\mathrm{NSS}(u, v)-\overline{\mathrm{NSS}}]^{2}}} $ | (10) |
式中:Nx、Ny分别为x、y轴方向的网格数; ΔTrtp和
在传统磁性目标形态反演方法中,初始磁化强度根据先验信息确定,为了更准确地获得磁性目标的磁化强度,本文提出下述磁化强度估计方法。
(1) 估计磁性目标初始种子的位置及磁化方向信息,给定初始磁化强度,并对磁性目标进行反演。
(2) 根据步骤(1)的反演结果,结合磁性目标的位置信息及磁化方向信息,将磁化强度按照一定的间隔,取一系列值,并按照从小到大的顺序进行正演计算。
(3) 定义均方根误差
| $ \mathrm{RMSE}=\sqrt{\frac{1}{N_{x} N_{y} }\sum\limits_{u=1}^{N_{x}} \sum\limits_{v=1}^{N_{y}}[b(u, v)-d(u, v)]^{2}} $ |
计算不同磁化强度条件下正演数据与观测数据的RMSE,并将RMSE最小值对应的磁化强度作为当前模型的磁化强度;
(4) 重复步骤(1)~步骤(3),并将初始磁化强度定义为上一次计算得到的最优磁化强度值,直到RMSE小于预设的精度或者达到预设的迭代次数。
1.3 形态反演迭代终止准则在形态反演过程中,增长模型为目标函数Γ(M)最小时对应的长方体模型。定义
| $ \eta(M)=\frac{\left|\varPhi_{\text {new }}(M)-\varPhi_{\text {old }}(M)\right|}{\left|\varPhi_{\text {old }}(M)\right|} $ | (11) |
式中Φold(M)、Φnew(M)分别为未加入和已加入最优增长模型的数据约束函数。通过计算η(M)判断是否终止迭代,当η(M)小于预设的计算精度时则停止计算,这个值一般设定为1×10-4~1×10-6。
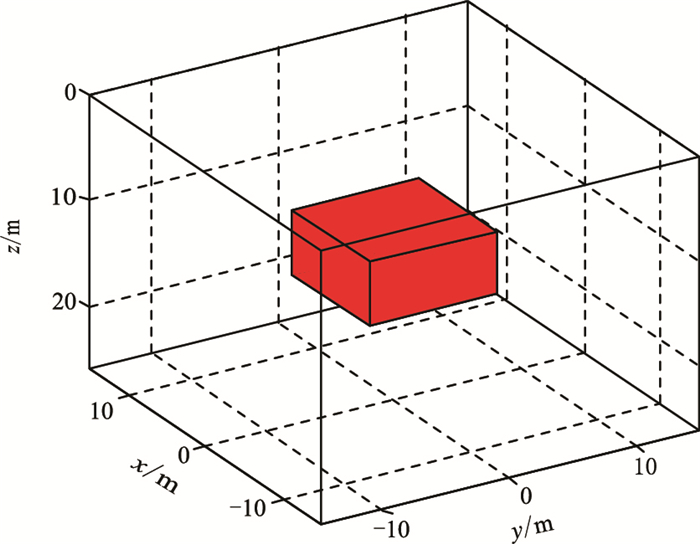
2 仿真分析 2.1 长方体模型为了证明本文方法的有效性,建立图 3所示的长方体模型进行仿真分析。假设观测面的深度为0(即地面),观测点距为2m,观测区域为26m×26m,中心点与坐标原点重合。长方体模型的长、宽、高分别为10、10、6m,中心位置坐标为(0,0,12m)。磁性体的磁化强度为40A/m,磁倾角I=70°,磁偏角D=20°,背景磁化方向与感应磁化方向相同。
|
图 3 长方体模型示意图 |
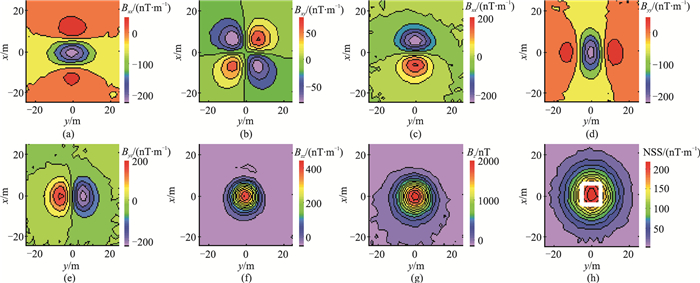
加入信噪比为40%的高斯噪声,该模型观测面上的磁测数据如图 4所示。利用本文方法对长方体的磁性参数和几何参数进行反演,结果如图 5所示。由图 5可知,计算得到的磁性体中心位置为(1m,1m,12m),磁倾角I=65°,磁偏角D=19°。将此计算结果作为反演的初始种子参数值。按照前文叙述,在不同观测数据组合条件下对磁性目标进行反演。设磁化强度为40A/m,分别利用不同的数据组合,即Bzz、Bxx/Bxy/Bxz/Byy/Byz/Bzz、Bz/Bzz以及Bz/Bxx/Bxy/Bxz/Byy/Byz/Bzz进行反演,反演结果如图 6所示。
|
图 4 长方体模型加噪磁张量及NSS计算结果 (a)Bxx;(b) Bxy;(c)Bxz;(d)Byy;(e)Byz;(f)Bzz;(g)Bz;(h)NSS(白线方框为磁性体的水平位置) |

|
图 5 长方体模型参数估计结果 (a)磁化方向;(b)水平位置;(c)深度 |
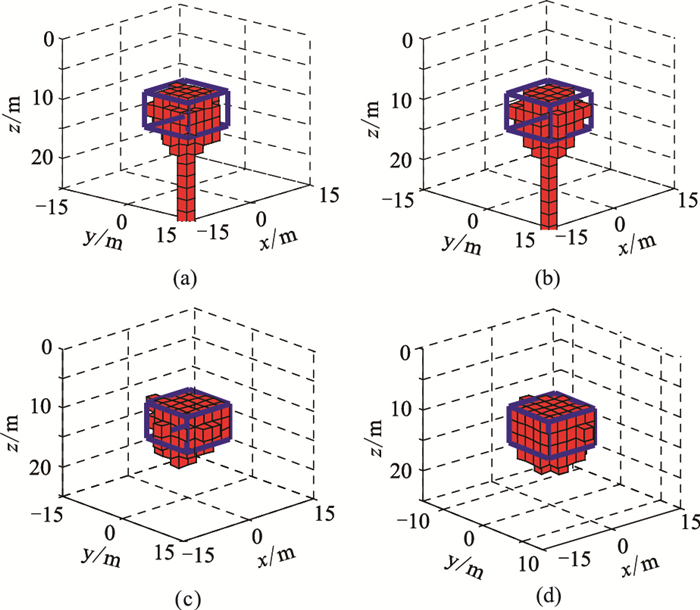
对比利用四种不同的组合数据反演结果(图 6),可以看出,相较于加入Bz数据的反演结果(图 6c、图 6d),单独利用Bzz数据(图a)或Bxx/Bxy/Bxz/Byy/Byz/Bzz(图b)数据组合获得的反演结果,其垂直分辨率较低。
|
图 6 不同数据组合条件下的磁性体形态反演结果 (a)Bzz;(b) Bz/Bxx/Bxy/Bxz/Byy/Byz/Bzz;(c)Bz/Bzz;(d)Bz/Bxx/Bxy/Bxz/Byy/Byz/Bzz。蓝色轮廓表示异常体边界,红色块体表示反演模型,图 7、图 11、图 12、图 16、图 20同 |
对不同数据获得的反演模型进行正演计算,计算结果的RMSE见表 1。可以看出,若反演数据组合中包含Bz,反演模型的正演张量数据精度稍有下降。根据图 6和表 1可以看出,虽然加入Bz数据后反演模型的正演数据精度稍有下降,但是利用Bz/Bzz数据组合和Bz/Bxx/Bxy/Bxz/Byy/Byz/Bzz数据组合能够获得更加准确的三维反演结果。同时,与Bxx/Bxy/Bxz/Byy/Byz/Bzz数据组合相比,利用Bz/Bzz数据组合的反演效率更高。
|
|
表 1 不同数据组合条件下反演结果的正演数据RMSE统计 |
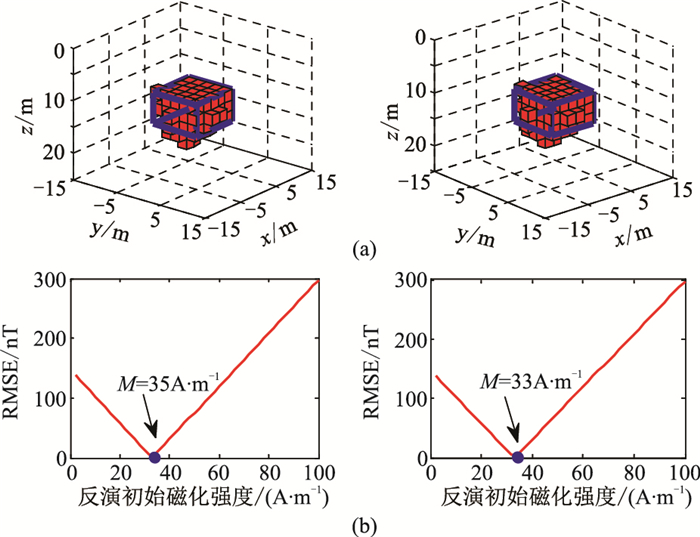
利用获得的中心位置作为种子的初始位置,分别假设初始磁化强度为1、200A/m,利用Bz/Bzz进行反演,得到不同初始磁化强度下模型的反演结果(图 7a)。利用本文的磁化强度估计方法计算图 7a模型的磁化强度,获得的磁化强度结果如图 7b所示。可以看出,即便设置不同的磁化强度作为初始种子,反演获得的磁化强度与实际值均比较接近,说明初始磁化强度的大小对反演结果影响不大。
|
图 7 初始磁化强度为1A/m(左)和200A/m(右)条件下模型三维反演结果(a)及设定不同初始磁化强度下反演模型的正演误差(b) |
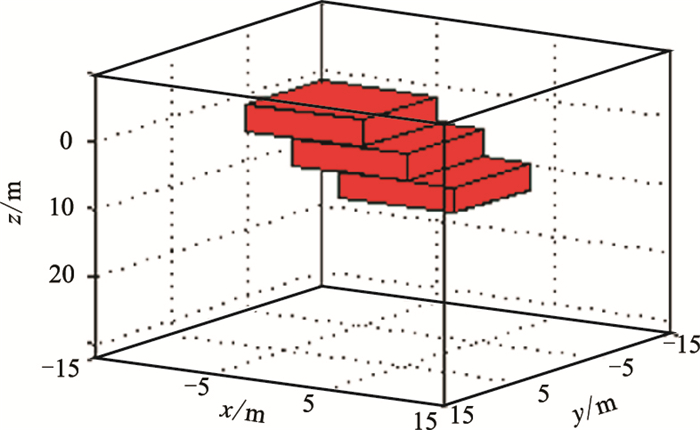
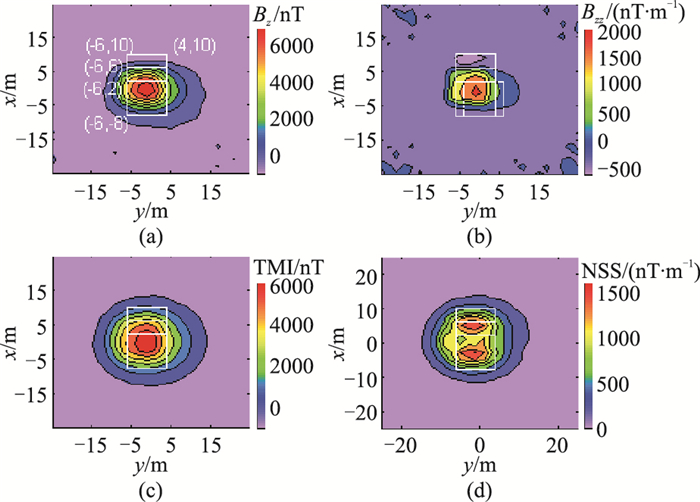
建立一个倾斜板状体模型验证本文方法的正确性。模型的空间参数如图 8所示。观测面深度为0(即地面),观测范围为26m×26m,中心点位于坐标原点,观测点间距为2m。磁性体沿x轴方向范围为-4~6m,沿y轴为-8~8m,中心点坐标为(0,1m,6m),磁化强度为40A/m,I=70°,D=20°,背景磁化方向与感应磁化方向相同。在正演数据中加入信噪比为40%的高斯噪声,观测面上的Bz、Bzz、总磁场模量
|
图 8 倾斜板状磁性体模型空间示意图 |
|
图 9 倾斜板状磁性体模型正演磁测数据(加噪) (a)Bz;(b)Bzz;(c)TMI;(d)NSS。图中白线为磁性目标水平位置 |
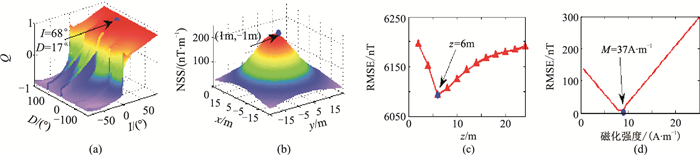
|
图 10 倾斜板状磁性体模型本文方法参数估计结果 (a) 磁化方向;(b)水平位置;(c)深度;(d) 磁化强度 |
为了分析估计的位置参数对反演结果的影响,分别设定三个不同初始位置,利用Bz/Bzz数据进行反演计算。初始位置1位于上顶面边缘的中心位置,初始位置2即本文方法获得的位置,初始位置3位于下底面边缘的中心位置(图 11上)。图 11(下)为对应的反演结果。可以看出,本文方法在不同的初始位置条件下都能够对磁性目标的形态进行有效反演。但是,当初始位置设定在上顶面边缘(图 11a)时,反演结果更集中于上顶层部分;而初始位置位于下底面边缘(图 11c)时,反演结果更集中于底层。分别对这三种反演结果进行正演计算,计算结果的均方根误差RMSE如表 2所示。根据表 2可以看出,相较于NSS和TMI,以本文方法获得的位置(图 11b)作为模型初始种子位置进行反演时,结果具有更高的计算精度。

|
图 11 倾斜板状磁性体模型种子点初始位置1(a)、2(b)、3(c)的反演结果 上图为种子点位置,下图为对应的反演结果 |
|
|
表 2 不同初始位置条件下不同数据组合反演模型的不同参数正演结果RMSE统计 |
进一步地,对NSS数据和TMI数据的反演能力进行讨论。分别利用NSS数据和TMI数据进行形态反演,结果如图 12所示。对反演模型进行正演计算,其结果与原始模型正演数据RMSE统计如表 2所示。由图 12可知,相较于TMI,NSS反演结果在深度方向上的分辨率较低,这是由于NSS数据与距离呈4次方衰减,深度信息衰减较快,而TMI数据与距离呈3次方衰减。此外,相较于Bz/Bzz组合数据,由于NSS和TMI数据仅包含振幅信息,反演模型的分辨率较低。
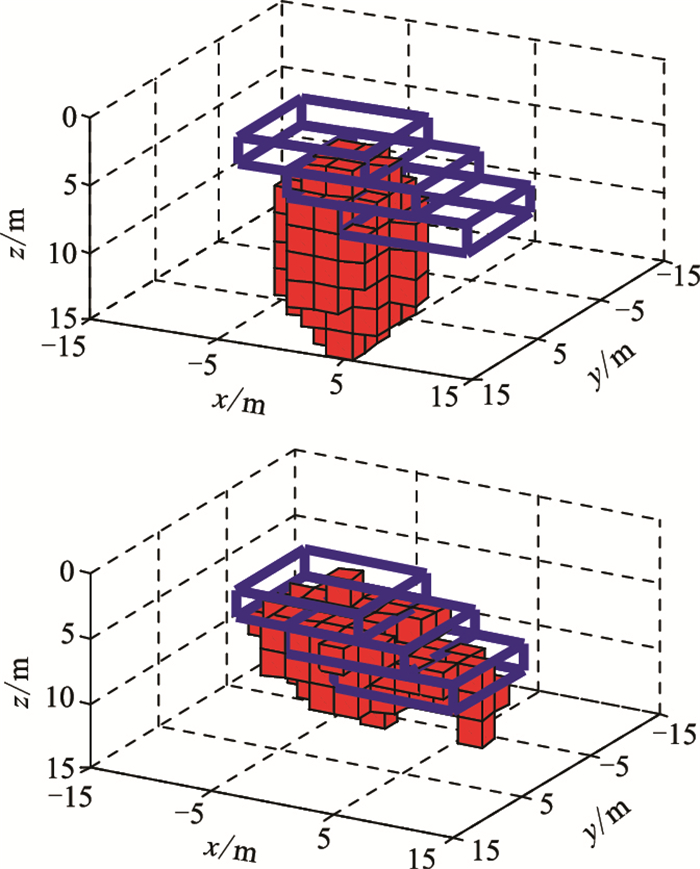
|
图 12 倾斜板状磁性体模型NSS(上)和TMI(下)反演结果 |
在实际计算过程中,模型会受剩余磁化的影响,导致实际磁化方向与背景磁化方向不同。因此,若直接利用背景场的磁化方向进行计算,会对计算结果产生一定的影响,进而影响反演结果[3]。为了解决这一问题,常使用弱敏感于磁化方向的NSS以及TMI进行反演。
建立一个倾斜板状体和长方体的组合模型(图 13,表 3),对剩磁条件下不同磁测数据的反演能力进行分析。背景磁化方向为I=60°,D=20°。观测面深度为0(即位于地面),观测点间距为2m,观测区域大小为26m×26m。观测数据中加入40%的高斯噪声,观测面上的正演磁测数据如图 14所示。
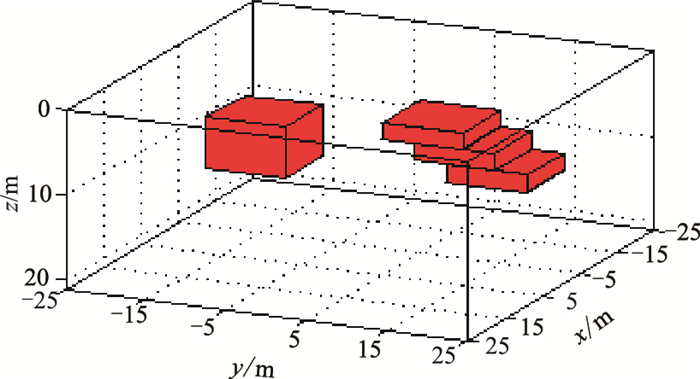
|
图 13 组合模型示意图 |
|
|
表 3 多磁性体模型参数 |

|
图 14 组合模型磁测数据 (a)Bz;(b)Bzz;(c)TMI;(d)NSS。图中白色方框为磁性目标体实际水平范围,黑色方框为划定的反演区域 |
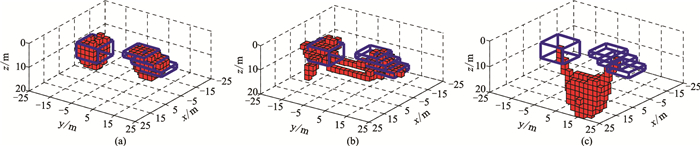
基于NSS主正极值分布范围与磁性目标的垂直分布范围基本一致,且受剩余磁化影响较小的特点,分别研究分析长方体目标和倾斜板状目标,其对应的区域如图 14d中黑线所示。利用本文的磁性目标多参数反演方法对模型初始参数进行计算,获得的初始位置、磁化方向和磁化强度如图 15所示。根据图 15上可知,计算得到的长方体模型中心位置坐标为(1m,-10m,10m),磁化方向为I=74°,D=21°,磁化强度为38A/m;根据图 15下,倾斜板模型的中心位置坐标为(1m,13m,8m),磁化方向为I=44°,D=31°,磁化强度为22A/m。对比实际模型参数可知,对于多目标体模型的参数估计,由于各磁性体的相互影响,模型的参数估计精度有所下降。利用本文方法估计组合模型的初始位置、磁化方向及磁化强度(图 15),分别利用Bz/Bzz、TMI以及NSS对此模型的空间位置进行反演,结果如图 16所示。可以看出,在剩余磁化条件下,与TMI和NSS相比,基于Bz/Bzz数据的反演结果受相邻磁性目标的影响最小,具有更高的水平及垂向反演精度。
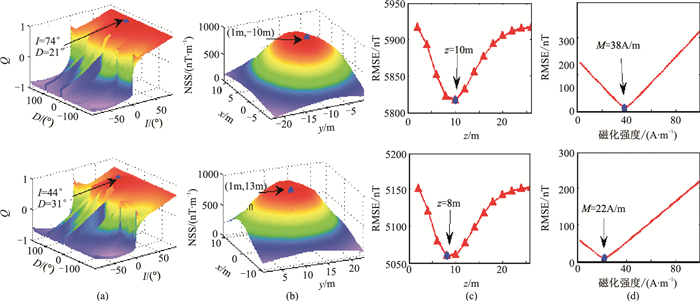
|
图 15 利用本文方法得到的区域1(上)和区域2(下)的磁化方向(a)、水平位置(b)、深度(c)和磁化强度(d)估计结果 |
|
图 16 剩磁条件下利用Bz/Bzz(a)、TMI(b)和NSS(c)反演的多目标体模型空间形态 |
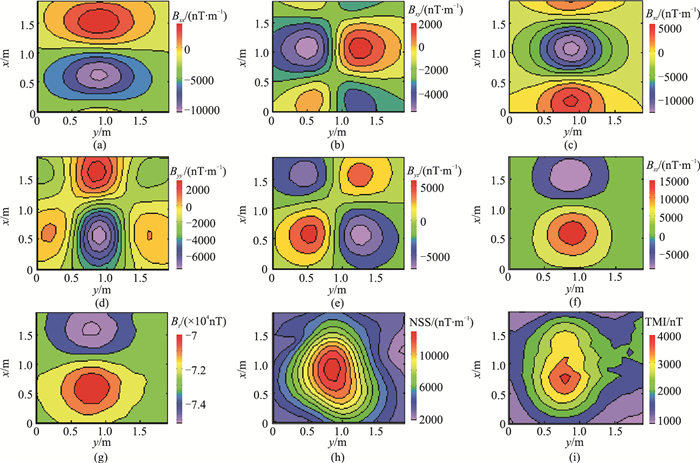
在河北省石家庄市某地对一圆柱状磁性体目标进行实测,以验证本文方法。装置系统(图 17)主要包括Mag-03传感器、数字采集模块及软件操作终端。实验中,传感器固定在无磁实验台架上,采用扫描方式对待测区域内的每一测点进行测量。测区大小为1.9m×1.9m,测点间隔为0.1m。在测区内放置一个南北走向的水平圆柱体铁块(磁性体)。背景磁化方向为I=56°,D=-16°;圆柱体底面直径为0.10m,轴长为1.05m,中心位置坐标为(0.80m,0.95m,0.45m)。观测面的实际磁测数据如图 18所示。

|
图 17 试验装置及待测模型 |
|
图 18 实验实测数据 (a)Bxx;(b) Bxy;(c)Bxz;(d)Byy;(e) Byz;(f)Bzz;(g)Bz;(h)NSS;(i)TMI |
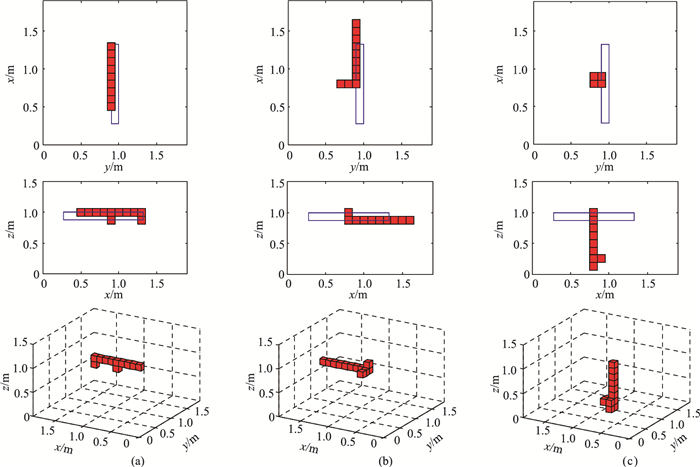
利用本文方法对模型初始参数进行计算,获得的异常体初始位置、磁化方向和磁化强度结果如图 19所示。基于实测数据计算得到的模型中心点坐标为(0.8m,0.9m,0.4m),磁化方向为I=21°,D=-1°,磁化强度为960A/m。利用这些模型磁性参数和几何参数,分别基于Bz/Bzz、TMI以及NSS对待测模型进行反演,结果如图 20所示。再对这些反演模型进行正演,其RMSE数据统计如表 4所示。根据表 4及图 20可以看出,基于Bz/Bzz数据获得的计算结果与模型实际位置最接近,具有较高的计算精度。

|
图 19 基于实测数据的模型参数估计结果 (a)磁化方向;(b)水平位置;(c)深度;(d)磁化强度 |
|
图 20 基于Bz/Bzz(a)、TMI(b)和NSS(c)反演的磁性体空间形态 上图为鸟瞰图,中图为侧视图,下图为三维显示 |
|
|
表 4 不同数据反演模型的正演数据RMSE统计 |
本文针对磁性目标三维形态反演中存在的问题,提出了一种磁性目标三维形态反演方法,即根据实测磁数据,对磁性目标的水平位置、深度、磁化方向和磁化强度进行初步估计,确定初始种子的磁性参数和几何参数;然后利用形态反演迭代计算方法,通过确定待增长区域中的最优增长模块,反演得到模型空间分布形态。仿真和实验结果证明了本文方法的正确性和实用性。具体得到如下结论。
(1) 对于磁性体的形态反演,联合Bz与磁张量,能够改善磁张量在深度上反演分辨率低的问题。
(2) 本文方法无需先验信息,只需通过观测数据就可以直接计算磁性目标体的中心位置、磁化方向和磁化强度,提高了形态反演方法的适用性,减小了人为经验确定反演初始值所引入的误差。
(3) 在剩余磁化条件下,本文方法能够直接利用Bz/Bzz数据组合对多目标模型进行反演,与基于NSS和TMI的反演结果相比,明显提高了反演分辨率。
利用NSS数据对磁性目标的水平位置进行估计时,临近叠加异常会产生混叠,影响计算精度;对于台阶等复杂模型,向上延拓的中心可能与磁性目标的中心位置不一致。因此,在下一步工作中需要对上述问题进一步研究。
| [1] |
郑建拥, 范红波, 张琪, 等. 利用磁梯度张量识别地下小型目标体[J]. 石油地球物理勘探, 2019, 54(3): 692-699. ZHENG Jianyong, FAN Hongbo, ZHANG Qi, et al. Underground small target recognition using magnetic gradient tensor[J]. Oil Geophysical Prospecting, 2019, 54(3): 692-699. |
| [2] |
李青竹, 李志宁, 张英堂, 等. 基于二阶磁张量欧拉反褶积的磁源单点定位方法[J]. 石油地球物理勘探, 2019, 54(4): 915-924. LI Qingzhu, LI Zhining, ZHANG Yingtang, et al. Magnetic source single-point positioning based on se-cond-order magnetic tensor Euler deconvolution[J]. Oil Geophysical Prospecting, 2019, 54(4): 915-924. |
| [3] |
李华东, 于鹏, 刘振友. 基于随机分布共网格模型的重磁电震联合反演技术及应用[J]. 石油地球物理勘探, 2015, 50(4): 742-748. LI Huadong, YU Peng, LIU Zhenyou. Joint inversion of gravity, magnetotelluric and seismic data based on common gridded model with random distributions[J]. Oil Geophysical Prospecting, 2015, 50(4): 742-748. |
| [4] |
习宇飞, 刘天佑, 刘双. 井中磁测三分量联合反演[J]. 石油地球物理勘探, 2012, 47(2): 344-352. XI Yufei, LIU Tianyou, LIU Shuang. A joint inversion method for borehole magnetic three-component data[J]. Oil Geophysical Prospecting, 2012, 47(2): 344-352. |
| [5] |
Schneider M, Stolz R, Linzen S, et al. Inversion of geo-magnetic full-tensor gradiometer data[J]. Journal of Applied Geophysics, 2013, 92: 57-67. DOI:10.1016/j.jappgeo.2013.02.007 |
| [6] |
李金朋, 张英堂, 范红波, 等. 基于χ2准则的磁梯度张量3D聚焦反演方法[J]. 武汉大学学报(信息科学版), 2018, 43(2): 255-261. LI Jinpeng, ZHANG Yingtang, FAN Hongbo, et al. Three-dimensional focusing inversion of magnetic gradient tensor data based on the χ2 principle[J]. Geomatics and Information Science of Wuhan University, 2018, 43(2): 255-261. |
| [7] |
索奎, 张贵宾, 梅岩辉, 等. 重磁三维反演伊犁盆地中部密度和磁性结构[J]. 地球物理学报, 2018, 61(8): 3410-3419. SUO Kui, ZHANG Guibin, MEI Yanhui, et al. Density and magnetic susceptibility distribution of central Yili Basin by three-dimensional of gravity and magnetic data[J]. Chinese Journal of Geophysics, 2018, 61(8): 3410-3419. |
| [8] |
Li S L, Li Y. Inversion of magnetic anomaly on rugged observation surface in the presence of strong re-manent magnetization[J]. Geophysics, 2014, 79(2): J11-J19. DOI:10.1190/geo2013-0126.1 |
| [9] |
Antonio G, Camacho, Fuensanta G, et al. A 3-D gra-vity inversion tool based on exploration of model possibilities[J]. Computer & Geosciences, 2002, 28(1): 191-204. |
| [10] |
Uieda L, Barbosa V C F. Use of the "shape-of-ano-maly" data misfit in 3D inversion by planting anomalous densities[C]. SEG Technical Program Expanded Abstracts, 2012, 31: 3160-3164.
|
| [11] |
曹书锦, 朱自强, 鲁光银. 重力梯度张量种植反演[J]. 中国有色金属学报, 2017, 27(5): 997-1005. CAO Shujin, ZHU Ziqiang, LU Guangyin. Planting inversion of tensor gravity data[J]. The Chinese Journal of Nonferrous Metals, 2017, 27(5): 997-1005. |
| [12] |
Uieda L, Barbosa V C F. Robust 3D gravity gradient inversion by planting anomalous densities[J]. Geophysics, 2012, 77(4): G55-G66. |
| [13] |
Cardarelli E, Fischanger F. 2D data modelling by electrical resistivity tomography for complex subsurface geology[J]. Geophysical Prospecting, 2006, 54(2): 121-133. |
| [14] |
Zhdanov M S, Liu X, Wilson G A, et al. 3D migration for rapid imaging of total-magnetic-intensity data[J]. Geophysics, 2012, 77(2): J1-J5. |
| [15] |
Zhdanov M S, Liu X, Wilson G A, et al. Potential field migration for rapid imaging of gravity gradiometry data[J]. Geophysical Prospecting, 2011, 59: 1052-1071. |
| [16] |
尹刚, 张林. 基于形态反演的小尺度磁性目标三维重建方法[J]. 上海交通大学学报, 2019, 53(9): 1074-1083. YIN Gang, ZHANG Lin. Three-dimensional reconstruction method for small scale magnetic target based on shape inversion[J]. Journal of Shanghai Jiao Tong University, 2019, 53(9): 1074-1083. |
| [17] |
Beiki M, Clark D A, Austin J R, et al. Estimating source location using normalized magnetic source strength calculated from magnetic gradient tensor data[J]. Geophysics, 2012, 77(6): J23-J37. |
| [18] |
Zhou J, Meng X. Three-dimensional cross-gradient joint inversion of gravity and normalized magnetic source strength data in the presence of remanent magnetization[J]. Journal of Applied Geophysics, 2015, 119: 51-60. |
| [19] |
Guo L, Meng X, Zhang G. Three-dimensional correlation imaging for total amplitude magnetic anomaly and normalized source strength in the presence of strong remanent magnetization[J]. Journal of Applied Geophysics, 2014, 111: 121-128. |
| [20] |
李金朋, 张英堂, 范红波, 等. 基于磁传感器阵列的多磁源参数反演方法[J]. 仪器仪表学报, 2019, 40(10): 28-37. LI Jinpeng, ZHANG Yingtang, FAN Hongbo, et al. Multi-magnetic source parameter inversion method based on magnetic sensor array[J]. Chinese Journal of Scientific Instrument, 2019, 40(10): 28-37. |
| [21] |
谢汝宽, 王平, 刘浩军. 基于最小反演拟合差的重磁场源深度计算方法[J]. 地球物理学报, 2016, 59(2): 711-720. XIE Rukuan, WANG Ping, LIU Haojun. Depth estimation of potential field by minimum inversion fitting error[J]. Chinese Journal of Geophysics, 2016, 59(2): 711-720. |
| [22] |
Blakely R J. Potential Theory in Gravity and Magne-tic Applications[M]. Cambridge: Cambridge University Press, 1996.
|
| [23] |
Yatong C, Lianghui G. A wavenumber-domain iterative approach for 3D imaging of magnetic anomalies and gradients with depth constraints[J]. Journal of Geophysics and Engineering, 2019, 16(6): 1-16. |



 范红波, 河北省石家庄市新华区和平西路97号陆军工程大学石家庄校区, 050003。Email:
范红波, 河北省石家庄市新华区和平西路97号陆军工程大学石家庄校区, 050003。Email: 