识别流体性质是油气田勘探、开发的一项重要任务,最基本的方法就是综合测井与地质、岩心以及中途测试等信息,利用不同流体的测井响应特征优选对流体敏感的参数,从而识别流体。
东方X气田位于莺歌海盆地,随着勘探目标转向中深层高温、高压领域,储层孔隙结构复杂、非均质性强,导致气、水关系复杂,使气层、水层、气水同层和干层的测井响应特征差异不明显。目前,流体识别方法主要基于测井曲线之间的差异,利用常规图板法定性识别,但识别结果过于依赖地区经验判断,且没有考虑测井曲线与储层含气性之间的非线性关系。特别是在高温、高压储层,储层电性参数复杂,往往难以找准气、水间的电性界限,导致常规方法识别储层流体性质时精度较低或方法失效。
近年来,机器学习作为一种高效的数据挖掘方法,能够挖掘测井响应特征之间的非线性关系,已经广泛用于测井解释,因此基于测井资料的机器学习算法成为流体识别的重要手段。目前储层流体识别大多采用单一的机器学习模型,常见的有神经网络[1-3]、决策树[4-5]、支持向量机[6-8]、贝叶斯网络[9-11]、随机森林[12-13]和梯度提升树[14]等。
在理论和实际应用中,每种机器学习算法各有优缺点,因此利用单一模型很难全面挖掘高温、高压储层的测井响应信息。随着模型融合技术的快速发展,模型融合算法很好地用于工业实践[15-21],但是未被用于测井解释领域。因此,本文提出利用Stacking模型融合方法(Stacked Generalization Ensemble,简称Stacking)建模,集成了流体识别效果较好的机器学习算法(决策树、支持向量机、随机森林和极端梯度提升),并利用Stacking识别莺歌海盆地高温、高压储层流体。结果发现,Stacking的预测精度明显高于各个单模型,表明该算法可有效提高流体识别精度。
1 高温、高压储层测井响应特征莺琼盆地中深层地温梯度较高(4.6℃/100m),普遍发育异常高压(压力梯度高达18~22kPa/m),储层受多期成岩作用改造,微观孔隙类型多样,具有较强的非均质性,严重影响测井流体识别精度。分析东方X气田关键探井的测井曲线发现,测井曲线与地层中含气量有如下关系:当储层从水层向气水同层过渡时,中子和密度曲线呈明显交会的“挖掘效应”,部分井的电阻率发生明显变化,部分井的电阻率差别较小,无明显台阶型变化;当含气饱和度继续增加,从气水同层向气层过渡时,中子密度曲线变化较小,但电阻率曲线明显变化,且干层普遍呈高自然伽马值。
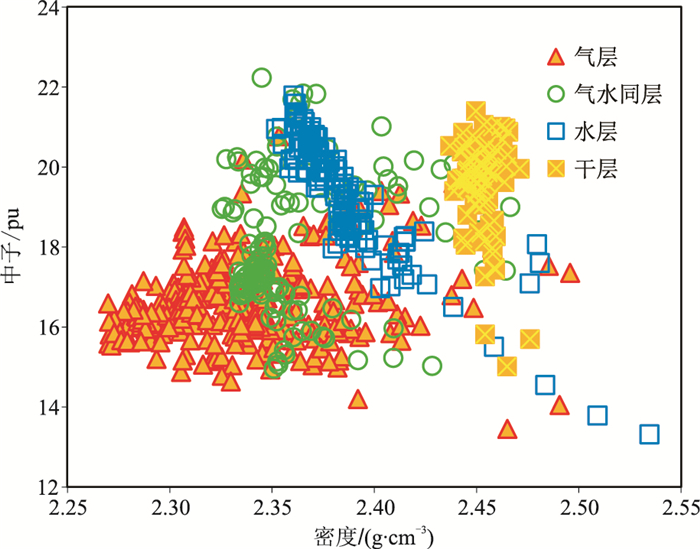
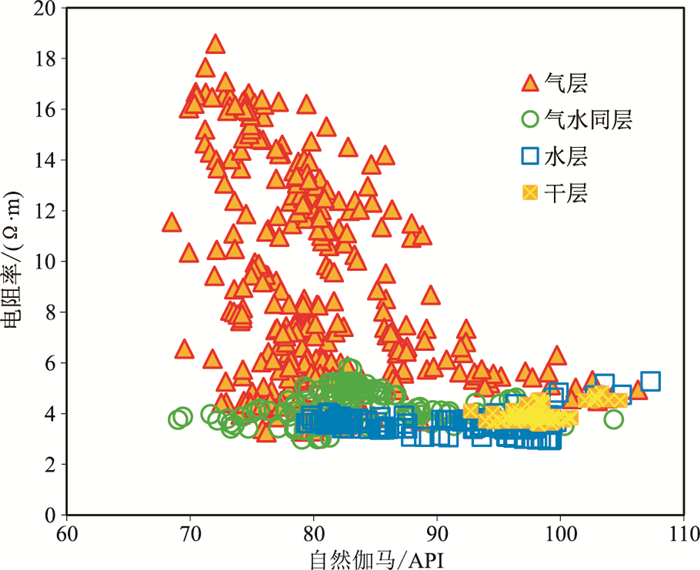
根据上述分析,绘制了东方X气田中子—密度交会图(图 1)和自然伽马—电阻率交会图(图 2)。由图 1可见:由于补偿中子测井的“挖掘效应”,气层、水层、气水同层、干层数据点分别位于图板左下方、上方、中部、右上方,这种分布符合气层和水层的测井响应特征,但是由于不同流体性质样本物性存在一定相似性,因此不同流体性质的样本数据点交叠范围明显,故无法直接应用中子—密度交会图识别流体。由图 2可见:与图 1相比,气层和气水同层的界限相对明显,但分界线附近气层和气水同层的数据点依然很密集,在气层电阻率普遍较低的背景下,容易造成误判;气水同层和水层的数据点存在一定重叠,难以找准高温、高压储层的电性界限。
|
图 1 东方X气田中子—密度交会图 |
|
图 2 东方X气田自然伽马—电阻率交会图 |
综合分析上述图板可知:东方X气田不同流体性质储层的测井响应差异不明显,尤其难以确定不同流体的电阻率下限;利用孔隙度测井曲线识别流体(图 1)易受物性因素干扰,不同流体性质的样本数据点存在重叠区域。故需要找到一种用于多参数综合识别的机器学习模型,能够综合多种因素,尽量消除流体性质以外影响因素的干扰,尽可能区分不同流体性质的数据点。
2 Stacking基于测井资料,利用机器学习算法研究储层流体性质是流体识别的重要方法。本文主要采用决策树、支持向量机、随机森林和极端梯度提升树等机器学习算法,并最终用Stacking集成。
Stacking的本质是一种堆栈集成算法,其模型融合的策略是使用“学习法”,即通过一个次级学习器结合其余几个初级学习器,然后使用次级学习器“改正”几个初级学习器的错误,主动提升集成后性能。通常将初级学习器称为基学习器,结合基学习器的次级学习器称为元学习器。首先,Stacking将原始数据集划分成若干子数据集,输入到第1层预测模型的各个基学习器中,每个基学习器输出各自的预测结果。然后,第1层的输出再作为第2层的输入,训练第2层预测模型的元学习器,再由第2层的模型输出最终预测结果。Stacking通过泛化多个模型的输出结果,以提升整体预测精度(图 3)。

|
图 3 基于Stacking的集成学习方式示意图 |
在训练阶段,若利用初级学习器的训练集产生次级训练集,则过拟合风险较大。因此,通过交叉验证的方式,利用训练初级学习器未使用的样本产生次级学习器的训练样本,使用k折交叉验证方法,将初始训练集S随机划分为k个大小相似的集合S1,S2,…,Sk。令Sj和Sj=S-Sj分别表示第j折的测试集和训练集,给定T个初级学习算法,初级学习器ht(j)通过在Sj上使用第t个学习算法而得。对Sj中每个样本xi,令zi(t)=ht(j)(xi),则由xi产生的次级训练样例的实例部分为zi=(zi1,zi2,…,ziT),标记部分为yi,于是在整个交叉验证过程结束后,从T个初级学习器产生的次级训练集是Snew={(zi,yi)}i=1m,Snew将用于训练次级学习器。
若Stacking采用分类与回归树(CART)、支持向量机(SVM)和随机森林(RF)作为基学习器,极端梯度提升树(Extreme Gradient Boosting,XGBoost)作为元学习器,则伪代码如下:
输入:初始训练集
S1,S2,…,Sk=CV(3,k)
Snew={ }
FOR EACH Sk in S1,S2,…,Sk;
CARTModelj=CART(Sj)
SVMModelj=SVM(Sj)
RFModelj=RF(Sj)
FOR EACH xi in Sj
zi1=CARTModelj.predict(xi)
zi2=SVMModelj.predict(xi)
zi3=RFj.predict(xi)
Snew.append(zi1,zi2,zi3,yi)
END FOR
END FOR
XGBoostModel=XGBoost(Snew)
输出:Stacking学习系统的预测结果。
伪代码注释如下:CV(Cross Validation)为交叉验证;append函数表示在列表末尾添加新的对象;predict函数表示用某个机器学习算法对输入数据进行预测。
3 模型优化及参数选取分别以自然伽马、深电阻率(A40H)、浅电阻率(P16H)、中子、密度曲线值为样本点,并将模型识别结果输出为:气层设定为“4”,干层设定为“3”,气水同层设定为“2”,水层设定为“1”。样本数据来自DST(Drill-stem Testing,油气井中途测试)或MDT(Modular Formation Dynamics Tester,模块式地层动态测试器)测试层段。由于DST测试段不多,MDT测试段多但只反映单点特征,因此样本数据严重不足。为了获取足够多的样本数据分析流体的测井响应特征,在MDT测试层段根据测井响应特征和气、水分布规律,在测井曲线稳定段适当扩大了样本点选取范围。选取东方X气田共10口井、22个层段(气层、气水同层、水层和干层的层数分别为8、4、5和5)共813个样本点(气层、气水同层、水层和干层的样本数分别为267、135、353和58),将其中60%用于训练集,并在训练集中用10折交叉验证法得到每个模型的最优参数,用40%作为测试集评估最终模型,分别建立CART、RF、SVM、XGBoost、Stacking模型。由于不同测井信息具有不同的量纲和数量级,影响数据分析结果,因此在建模前要进行数据标准化处理。对于线性刻度的测井曲线x(自然伽马、密度和中子),在训练时进行线性归一化处理
| $ {x_{{\rm{norm}}}} = \frac{{x - {x_{{\rm{min}}}}}}{{{x_{{\rm{max}}}} - {x_{{\rm{min}}}}}} $ | (1) |
对于非线性对数特征曲线X,如地层电阻率和冲洗带电阻率,在输入模型之前要进行对数变换
| $ {x_{{\rm{stand}}}} = \frac{{{\rm{lg}}X - {\rm{lg}}{X_{{\rm{min}}}}}}{{{\rm{lg}}{X_{{\rm{max}}}} - {\rm{lg}}{X_{{\rm{min}}}}}} $ | (2) |
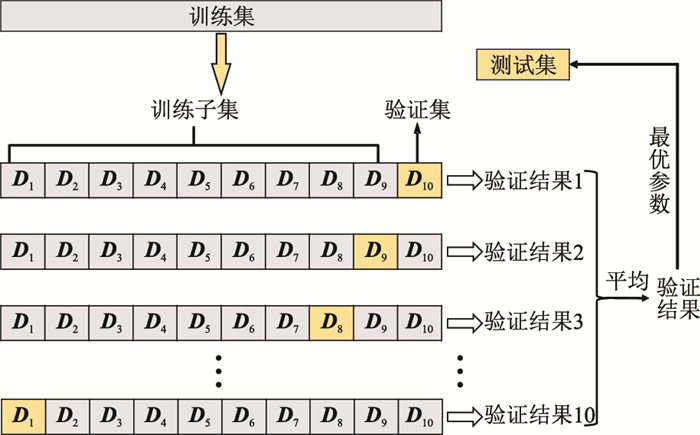
经过数据标准化后,将数据集分为训练集和测试集,再利用10折交叉验证法(图 4)将训练集分为训练子集和验证集,利用训练子集训练模型、验证集验证模型,根据验证结果不断调整模型参数,并选择最好的模型。最后,利用测试集评估最优模型,既能防止测试集信息泄露,又能用验证集优化模型。
|
图 4 10折交叉验证法示意图 |
决策树是一种常用的数据挖掘方法,类似于流程图的树型结构。决策树算法主要包括构造和分类二个过程。构造决策树分为建树和剪枝两个阶段,前者归纳出决策树,后者防止过度拟合。本文采用最常用的决策树算法CART。
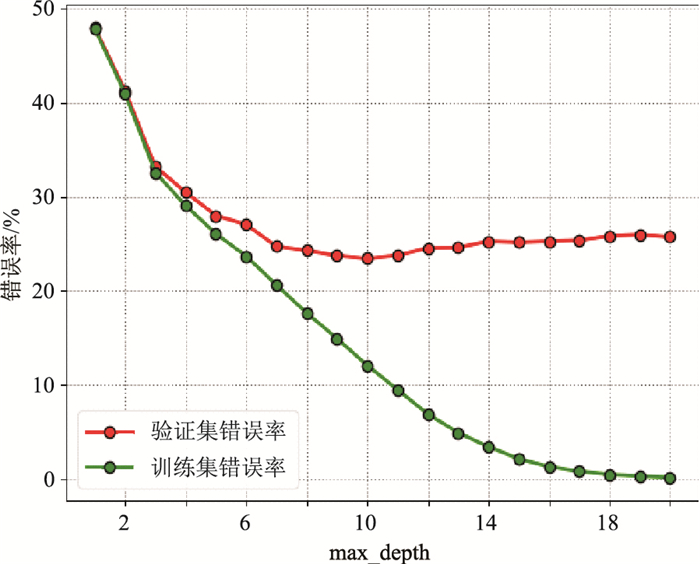
基于CART的决策树一般需要调整的参数为树的最大深度max_depth,树越深,分裂越多,越能捕获有关数据的信息,但同时越容易过拟合,使模型泛化能力变弱。因此,利用10折交叉验证法观测决策树模型的训练集和验证集在树的不同深度的表现(图 5):当max_depth不断增大时,模型训练集的错误率不断降低,但是模型验证集错误率呈先减小、后增大的趋势,说明当max_depth较小时,模型偏差较大,决策树学习能力较差;当max_depth较大时,模型方差较大,出现过拟合,导致模型过于复杂,泛化能力差;当max_depth=10时,模型在验证集上表现最好,此时模型达到最优,错误率为23.57%。
|
图 5 不同决策树max_depth与模型错误率关系 |
SVM由线性可分情况下的最优分类面发展而来,其基本思想是寻找一个满足分类要求的超平面,在保证精度的同时使超平面两侧的空白区域最大化,并且使分类间隔最大。
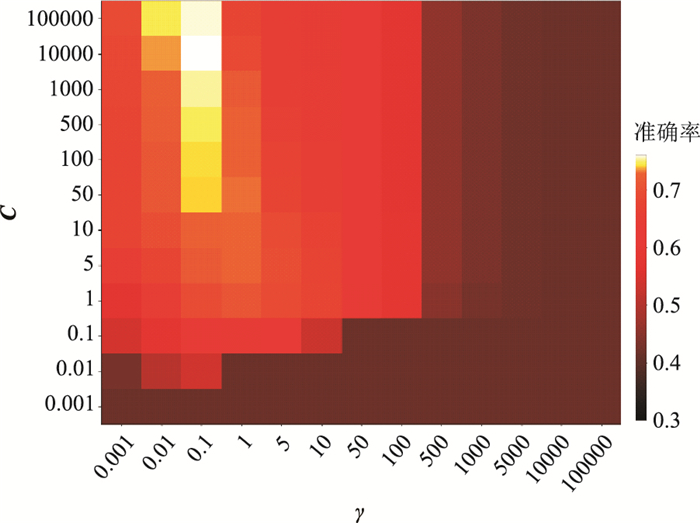
利用SVM识别流体时,需要选择转换数据维度的核函数,本文为了解决流体识别的线性不可分问题,选用径向基函数(RBF),其中惩罚系数C、γ(RBF作为核函数自带的一个参数)是基于RBF的SVM模型的两个非常重要的参数。C表征对误差的宽容度,C越大,越容易过拟合,模型的方差越大;C越小,越容易欠拟合,模型的偏差越大。γ越小,方差越大,高斯分布曲线越尖峭,越容易过拟合。因此需要选取合适的C与γ值。利用10折交叉验证方法,由验证集评价各个参数的训练模型,从而列出不同的C和γ值的流体识别准确率热图(图 6)。可见,当C=10000、γ=0.1时模型达到最优,迭代优化后的模型在验证集中的流体识别准确率为77.89%。
|
图 6 SVM的C值、γ值与判别准确率热图 颜色越浅表示模型预测能力越强 |
RF是一种集成式的有监督学习算法,同时生成多个决策树,并将模型的结果汇总以提升预测准确率,而且能提升模型的鲁棒性。
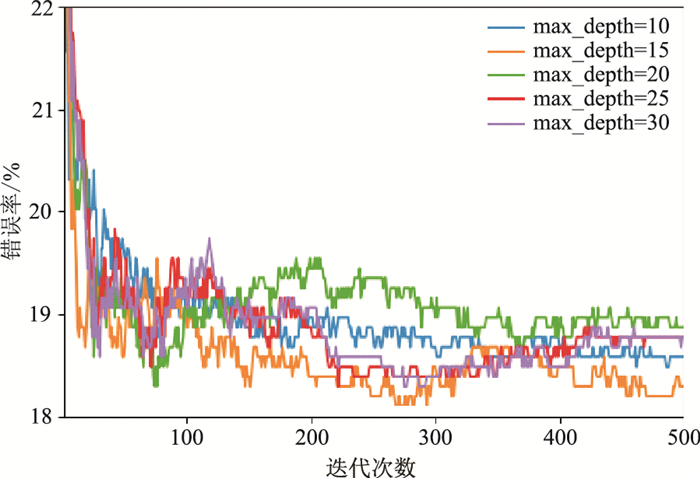
本文所用的RF模型是基于CART的引导聚集(Bagging)算法,需要调节的参数包括Bagging框架参数和CART参数,所以需要调节的参数主要是弱学习器的最大迭代次数n_estimators以及决策树的最大深度max_depth。通过10折交叉验证方法,用验证集评估不同决策树深度的模型错误率随迭代次数的变化(图 7)。可见,当n_estimators=273、max_depth=15时模型达到最优,迭代优化后的模型在验证集中的流体识别错误率为19.57%。
|
图 7 不同max_depth的RF判别错误率随迭代次数变化 |
XGBoost[22]是经过优化的集成模型,由梯度提升树模型改进和扩展而来。利用该算法构建流体性质预测模型,需要优化的参数主要有:控制模型复杂度的决策树的最大深度max_depth;子节点中最小样本权重和min_child_weight;正则项中的惩罚系数gamma;每一步迭代的步长learning_rate;弱学习器的最大迭代次数n_estimators。
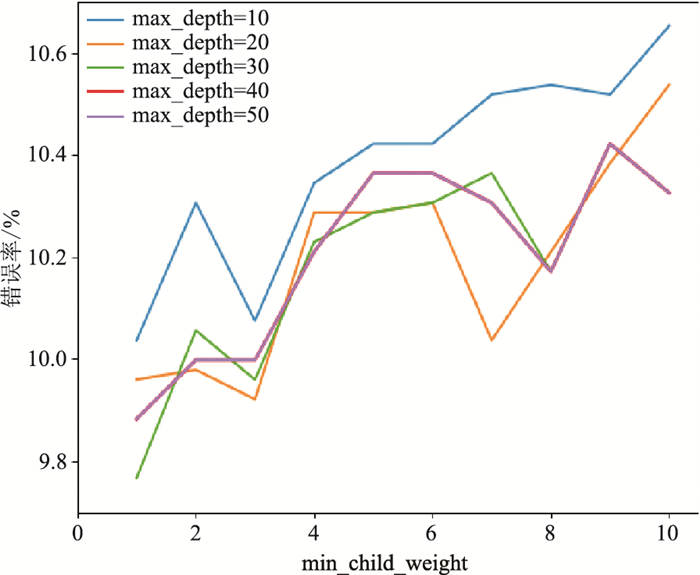
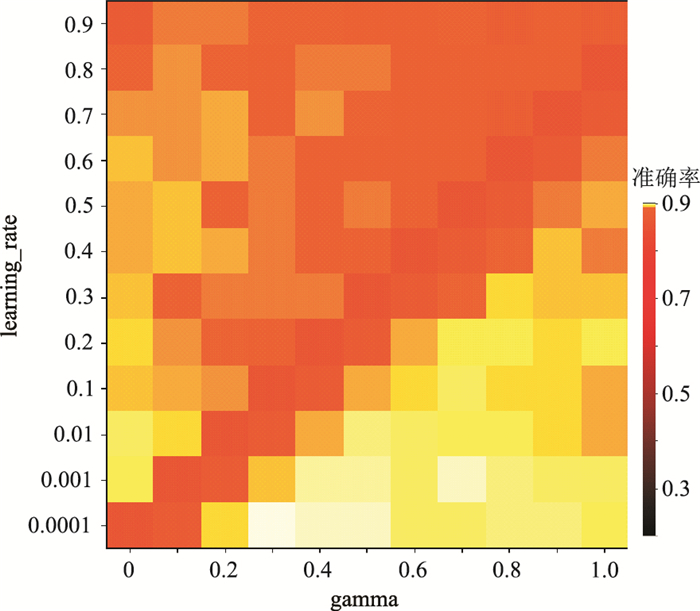
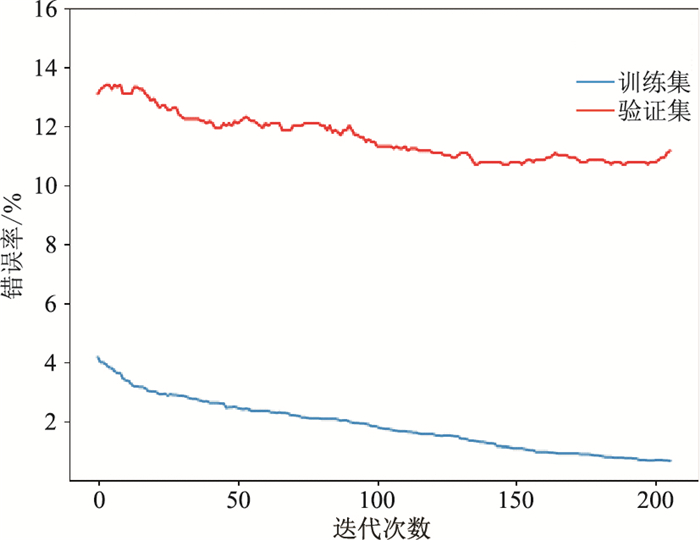
因此使用交叉验证法先优化调整对整个模型影响最大的参数max_depth和min_child_weight,得到模型在验证集上的错误率随min_child_weight和max_depth的变化关系(图 8)。可见,将模型错误率最低时的min_child_weight=1、max_depth=30确定为模型最优参数。然后调节gamma和lear-ning_rate,得到验证集的准确率随gamma和lear-ning_rate变化热图(图 9)。可见,将模型表现最优时的gamma=0.3、learning_rate=0.0001确定为模型最优参数。最后在确定以上参数的情况下,统计迭代次数与模型错误率的关系(图 10)。可见,随着迭代次数增加,模型训练集的错误率不断降低,且当n_estimators=135时验证集的错误率最低。因此最终确定模型的n_estimators=135,迭代优化后的模型在验证集中的错误率为13.26%。
|
图 8 不同max_depth的XGBoost判别 错误率随min_child_weight变化 |
|
图 9 XGBoost的learning_rate、gamma值与判别准确率热图 颜色越浅表示模型预测能力越强 |
|
图 10 XGBoost迭代次数与模型错误率关系 |
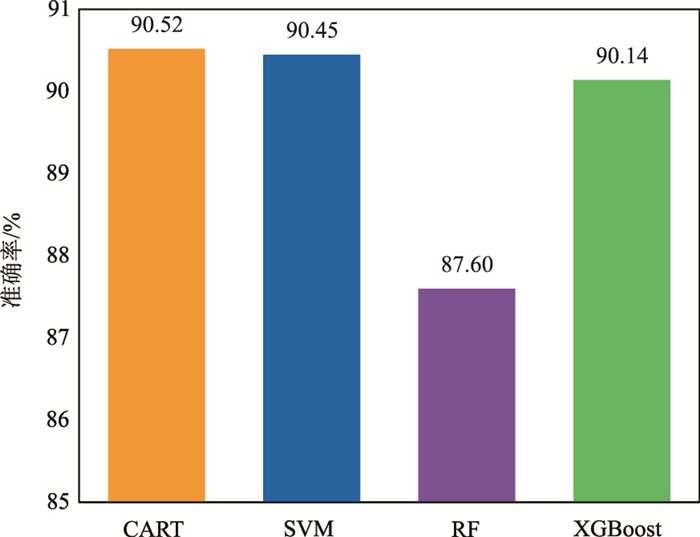
Stacking能够结合每个基模型的优点,忽略基模型本身的缺点,因此Stacking的预测精度明显高于各个单模型。当基模型预测效果不同且各有优、缺点时,需要选择合适的元学习器才能使最终模型堆叠达到最优,因此本文利用已经训练好的四个模型(CART、SVM、RF和XGBoost)依次作为元学习器,其余三个模型作为基学习器,并用交叉验证法在验证集上检验这四种模型堆叠方法的准确率,最终得到不同元学习器验证集准确率柱状图(图 11)。可见,当选用CART作为元学习器时,模型融合在验证集的效果最好,准确率达到90.52%。
|
图 11 不同元学习器验证集准确率柱状图 |
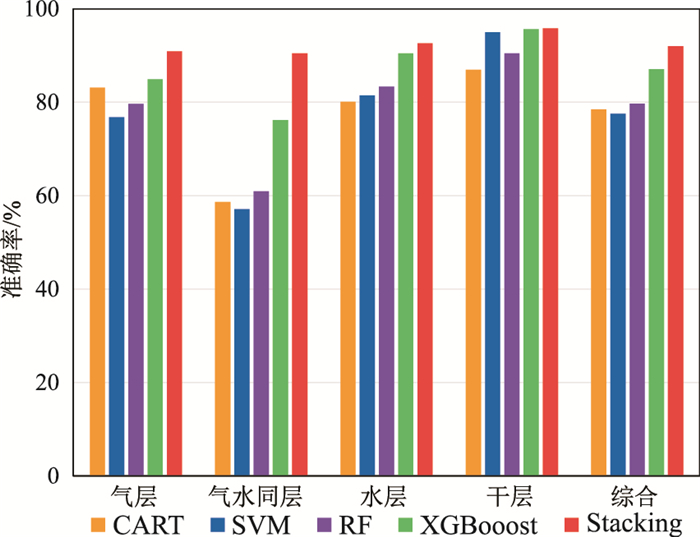
利用上述各个优化后模型评估最终模型。分别利用CART、SVM、RF和XGBoost判别测试集样本点,并与Stacking的判别结果对比(图 12),可见,CART、SVM、RF和XGBoost的准确率分别为78.46%、77.54%、79.69%、87.08%,而Stacking的准确率达到92%。由于高温、高压储层的气、水关系复杂,导致各个单模型对气水同层的识别效果一般,如XGBoost的准确率只有76.19%,而Stacking识别气水同层、气层、水层和干层的准确率分别为90.48%、90.91%、92.62%及95.83%。因此Stacking的流体识别效果较好。
|
图 12 不同流体识别方法的准确率柱状图 |
图 13为X-1井测井解释成果图。由图可见,根据测压回归资料分别证实,第6~第9层分别为干层、气层、气水同层和水层,而CART、SVM、RF和XGBoost对第6~第8层出现识别错误,如RF和XGBoost以及人工解释都误将第8层识别为气层,只有Stacking判别第8层为气水同层。因此无论是总体的识别准确率,还是识别气层、气水同层、水层以及干层的准确率,Stacking的预测效果明显优于各个单模型,说明基于模型融合策略构建模型的流体识别准确率高于单一模型,并且模型的鲁棒性更强,在每个分类上的表现也更稳定。

|
图 13 X-1井测井解释成果图 |
本文借鉴了人工智能领域的前沿算法,提出了一种基于模型融合算法的高温、高压储层流体识别技术——Stacking,将原始测井数据标准化处理生成训练样本,并选择流体识别效果较好的机器学习算法(SVM、RF和XGBoost作为Stacking的基分类器,CART作为Stacking的元分类器)建模,充分利用不同算法从不同角度观测数据空间与结构,获得了最优预测结果。
与CART、SVM及RF相比,XGBoost对高温、高压储层的流体识别效果较好。与其他机器学习算法相比,Stacking的流体识别效果更好,说明模型融合算法具有较高的应用价值,可为测井解释建模提供新思路。但是Stacking算法的复杂度导致计算时间急剧增加,因此,未来研究中有必要布置分布式计算环境,对不同基模型分别建模,有效减少计算时间。
| [1] |
吴磊, 徐怀民, 季汉成. 基于交会图和多元统计法的神经网络技术在火山岩识别中的应用[J]. 石油地球物理勘探, 2006, 41(1): 81-86. WU Lei, XU Huaimin, JI Hancheng. Application of neural networks technique based on crossplot and multielement statistics to recognition of volcanic rocks[J]. Oil Geophysical Prospecting, 2006, 41(1): 81-86. |
| [2] |
梁丽梅, 喻高明, 黎明, 等. 神经网络模拟交会图在H油田低阻油层流体识别中的应用[J]. 石油地质与工程, 2011, 25(1): 39-40, 43. LIANG Limei, YU Gaoming, LI ming, et al. Application of neural network simulated rendezvous graph in fluid identification of low-resistance reservoir in H oilfield[J]. Petroleum Geology and Engineering, 2011, 25(1): 39-40, 43. |
| [3] |
何旭, 李忠伟, 刘昕, 等. 应用卷积神经网络识别测井相[J]. 石油地球物理勘探, 2019, 54(5): 1159-1165. HE Xu, LI Zhongwei, LIU Xin, et al. Log facies re-cognition based on convolutional neural network[J]. Oil Geophysical Prospecting, 2019, 54(5): 1159-1165. |
| [4] |
王礼常, 王志章, 陶果. 样本分解交汇图法与决策树方法识别苏丹某油田流体性质[J]. 科技导报, 2012, 30(2): 22-27. WANG Lichang, WANG Zhizhang, TAO Guo. Fluid nature identification of an oil-gas field in Sultan using stylebook hierarchical decomposition cross-plot and decision tree methods[J]. Science & Technology Review, 2012, 30(2): 22-27. |
| [5] |
赵倩, 杨斌, 李星, 等. 基于图版法决策树在流体识别中的应用[J]. 测井技术, 2018, 42(6): 641-646. ZHAO Qian, YANG Bin, LI Xing, et al. Application of cross-plot-based decision tree template method in fluid identification[J]. Well Logging Technology, 2018, 42(6): 641-646. |
| [6] |
于代国, 孙建孟, 张振城, 等. 支持向量机方法识别储集层流体性质[J]. 新疆石油地质, 2005, 26(6): 675-677. YU Daiguo, SUN Jianmeng, ZHANG Zhencheng, et al. Reservoir fluid property identification with support vector machine method[J]. Xinjiang Petroleum Geology, 2005, 26(6): 675-677. |
| [7] |
赵学松, 高强山, 唐传章, 等. 基于支持向量回归机与井导向的三角洲岩性油气藏储层参数预测[J]. 石油地球物理勘探, 2016, 51(5): 976-982. ZHAO Xuesong, GAO Qiangshan, TANG Chuan-zhang, et al. Delta stratigraphic reservoir parameter estimation based on support vector regression machine and well logging data[J]. Oil Geophysical Prospecting, 2016, 51(5): 976-982. |
| [8] |
王丽, 袁伟, 丁磊, 等. 基于常规测井资料的储层流体识别方法[J]. 地质科技情报, 2018, 37(2): 241-245. WANG Li, YUAN Wei, DING Lei, et al. Reservoir fluid identification based on normal logging data[J]. Geological Science and Technology Information, 2018, 37(2): 241-245. |
| [9] |
田时芸, 刘子云. 利用测井资料判别油水层时几种判别分析方法的判别效果比较[J]. 江汉石油学院学报, 1983, 5(1): 37-46. TIAN Shiyun, LIU Ziyun. Comparison of discriminant effects of several discriminant analysis methods when using logging data to discriminate oil and water layers[J]. Journal of Jianghan Petroleum Institute, 1983, 5(1): 37-46. |
| [10] |
陈军, 范晓敏, 莫修文. 火山碎屑岩岩性的测井识别方法[J]. 吉林大学学报(地球科学版), 2007, 37(增刊): 99-101, 113. CHEN Jun, FAN Xiaomin, MO Xiuwen. The resrarch of volcaniclastic rock lithologic identification based logging[J]. Journal of Jilin University(Earth Science Edition), 2007, 37(S): 99-101, 113. |
| [11] |
袁少阳, 张占松, 李权, 等. 利用贝叶斯判别法识别岩性基础上的孔隙度评价[J]. 测井技术, 2016, 40(3): 281-285. YUAN Shaoyang, ZHANG Zhansong, LI Quan, et al. Porosity evaluation based on lithology indentification using Bayesian classifier[J]. Well Logging Technology, 2016, 40(3): 281-285. |
| [12] |
何健, 文晓涛, 聂文亮, 等. 利用随机森林算法预测裂缝发育带[J]. 石油地球物理勘探, 2020, 55(1): 161-166. HE Jian, WEN Xiaotao, NIE Wenliang, et al. Fracture zone prediction based on random forest algorithm[J]. Oil Geophysical Prospecting, 2020, 55(1): 161-166. |
| [13] |
苏瑞. 基于随机森林的F区块水淹层测井定性识别[D]. 黑龙江大庆: 东北石油大学, 2019. SU Rui. Qualitative Logging Identification of Water- Flooded Zones in F Block Based on Random Forest[D]. Northeast Prtroleum University, Daqing, Heilongjiang, 2019. |
| [14] |
陈钢花, 梁莎莎, 王军, 等. 机器学习AdaBoost.M2算法在砂砾岩流体识别中的应用[J]. 石油地球物理勘探, 2019, 54(6): 1357-1362. CHEN Ganghua, LIANG Shasha, WANG Jun, et al. Fluid identification in glutenites with the machine learning AdaBoost.M2 algorthm[J]. Oil Geophysical Prospecting, 2019, 54(6): 1357-1362. |
| [15] |
周志华. 机器学习[M]. 北京: 清华大学出版社, 2016. ZHOU Zhihua. Machine Learning[M]. Beijing: Tsinghua University Press, 2016. |
| [16] |
Huang X, Zhang L. An SVM ensemble approach combining spectral, structural, and semantic features for the classification of high-resolution remotely sensed imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(1): 257-272. |
| [17] |
De-la-Torre M, Granger E, Sabourin R, et a1. An adaptive ensemble-based system for face recognition in person re-identification[J]. Machine Vision and Applications, 2015, 26(6): 741-773. |
| [18] |
Zhang L, Zhang L, Zhang D, et al. Ensemble of local and global information for finger-knuckle-print recognition[J]. Pattern Recognition, 2011, 44(9): 1990-1998. |
| [19] |
Kavitha B, Karthi K S, Maybell P S. An ensemble design of intrusion detection system for handling uncertainty using neutrosophic logic classifier[J]. Know-ledge-Based Systems, 2012, 28(1): 88-96. |
| [20] |
Cai Z, Xu D, Zhang Q, et al. Classification of lung cancer using ensemble-based feature selection and machine learning methods[J]. Molecular BioSystems, 2015, 11(3): 791-800. |
| [21] |
方育柯. 集成学习理论研究及其在个性化推荐中的应用[D]. 四川成都: 电子科技大学, 2011. FANG Yuke. Research of Ensemble Learning Theory and Its Application in Personalized Recommendation[D]. University of Electronic Science and Technology of China, Chengdu, Sichuan, 2011. |
| [22] |
Chen T, Guestrin C. XGBoost: A scalable tree boosting system[C]. ACM SIGKDD International Confe-rence on Knowledge Discovery and Data Mining, 2016, 785-794.
|



 秦敏, 海南省海口市秀英区西海岸御府国际中海石油(中国)海南分公司南海西部石油研究院, 524057。Email:
秦敏, 海南省海口市秀英区西海岸御府国际中海石油(中国)海南分公司南海西部石油研究院, 524057。Email: 