② 中国石化西北油田分公司勘探开发研究院, 新疆乌鲁木齐 830011
② Research Institute of Exploration and Development, Northwest Oilfield Branch Co, SINOPEC, Urumqi, Xinjiang 830011, China
深层缝洞型碳酸盐岩储层中缝洞空间分布散乱,不同缝洞的规模、形态和内部结构等特征差异明显,并且由于储层埋深较大,造成地震信号信噪比低。因此由缝洞引起的“串珠状”地震响应与背景分离度差,储层识别困难[1-2]。碳酸盐岩地层中的裂缝、溶洞往往是良好的油气聚集空间[3-4],因此缝洞体储层预测具有十分重要的意义。
油气的存在导致地震信号频率和能量异常,通过谱分解技术,容易发现隐藏的特定频段的异常信息,目前已经被广泛用于储层预测、烃类检测等方面[5-8]。近年来,在经典谱分析方法的基础上,涌现出经验小波变换[9]、稀疏时频分析[10]、同步压缩变换[11]等多种有效算法。作为一种时频分析手段,联合经验模态分解(Empirical Mode Decomposition,EMD)与希尔伯特变换的希尔伯特—黄变换(HHT)方法由Huang等[12]提出,能够自适应地将信号分解为一系列的固有模态函数(Intrinsic Mode Function,IMF),继而分析各IMF的瞬时频率、瞬时振幅等[13]。EMD具有更高的时频分辨能力,但也存在模态混叠、端点效应等问题[14]。为了解决模态混叠问题,人们相继提出引入噪声辅助的集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)、完备集合经验模态分解(Complete Ensemble Empirical Mode Decomposition,CEEMD)等方法[15-16],在一定程度上消除了模态混叠,已被用于地震资料处理[17]及烃类检测[18-20],但由于其本质上缺乏完备的理论支撑,在实际应用中存在一定局限性。Dragomiretskiy等[21]提出了变分模态分解(Variational Mode Decomposition,VMD)方法,具有完善的理论基础[22],能够将多分量信号自适应、非递归地分解为一系列具有带限性质的IMF,有效控制了模态混叠问题。由于VMD的本质是维纳滤波的推广,因而具有良好的抗噪性,在地震资料去噪[23-24]及时频分析领域[25]取得了良好的效果。
Teager等[26]提出了Teager能量算子,Kaiser[27]给出了其离散形式——Teager-Kaiser(TK)算子,因具有良好的局部分析能力及考虑了频率特性,de Matos等[28]最早将其引入地震勘探邻域,用于分析碳酸盐岩储层。陈学华等[29]、唐湘蓉等[30]在时频域进行储层预测及流体识别。Xue等[31]在EMD的基础上,利用TK算子代替希尔伯特变换获得瞬时属性进行联合时频分析,解决了希尔伯特变换的端点效应问题,然而TK算子对噪声敏感的特性限制了其应用。O′Toole等[32]提出了具有良好非负特性的包络导数算子(Envelope Derivative Operator,EDO),与TK算子相比,同为具有良好的追踪信号瞬时变化能力的非线性能量算子,但EDO抗噪性和稳定性更好[33],已经被用于轴承故障检测等方面[34]。在本文中,为了满足该类非线性能量算子的应用条件,利用VMD技术将地震信号分解为包含低频、高频有效信息的IMF,再引入EDO获取瞬时振幅、瞬时频率,克服了希尔伯特变换的端点效应且具有更高的时频分辨率,最终形成一种高精度时频分析方法,并应用于中国西部N区缝洞型碳酸盐岩储层预测,取得了良好的效果。
1 方法原理 1.1 VMDVMD的目标是将输入信号分解为一系列子信号,分解后得到的模态分量具有稀疏特性并且可以重建原始信号。与EMD相比,VMD具有完备的理论基础,从本质上看,VMD是维纳滤波的推广。
VMD非递归地将多分量信号自适应地分解为具有特定稀疏属性的带限模态分量,首先定义具有中心频率的有限带宽的IMF
| $ u(t)=A(t) \cos \phi(t) $ | (1) |
式中:信号的相位ϕ(t)需满足其对时间t的一阶偏导数ϕ′(t)≥0;A(t)为包络。
定义了式(1)的IMF之后,VMD过程包括变分问题的构造和求解,若将分析信号分解成K个IMF,则对应的约束变分模型为
| $ \begin{array}{c} \mathop {\min }\limits_{\left\{ {{u_k}} \right\}\{ {\omega _k}\} } = \left\{ {\sum\limits_k {\left\| {{\partial _t}\left[ {\left[ {\delta (t) + \frac{{\rm{j}}}{{\pi t}}} \right]*{u_k}(t)} \right]{{\rm{e}}^{ - {\rm{j}}{\omega _k}t}}} \right\|_2^2} } \right\}\\ {\rm{s}}{\rm{. t}}{\rm{. }}\quad \sum\limits_k {{u_k}} = f \end{array} $ | (2) |
式中:uk为分解得到的IMF;ωk为各分量的中心角频率,分解得到的每个uk分布在以ωk为中心的窄带范围内且具有稀疏性;f为原始信号。因此
为了求解式(2)的最优解,引入二次惩罚因子α和Lagrange乘法算子λ(t),则约束变分问题转换为非约束变分问题。增广Lagrange公式为
| $ \begin{array}{*{20}{c}} {L\left( {{u_k},{\omega _k},\lambda } \right) = \alpha \sum\limits_k {\left\| {{\partial _t}\left[ {\left[ {\delta (t) + \frac{{\rm{j}}}{{\pi t}}} \right]*{u_k}(t)} \right]{{\rm{e}}^{ - {\rm{j}}{\omega _k}t}}} \right\|_2^2} }\\ { + \left\| {f - \sum\limits_k {{u_k}} } \right\|_2^2 + \left\langle {\lambda ,f - \sum\limits_k {{u_k}} } \right\rangle } \end{array} $ | (3) |
式中α控制维纳滤波器的宽度,是控制IMF保真度和正则项的平衡参数,使IMF具有较好的抗噪性,将在后文进一步讨论。利用交替方向乘子算法(Alternate direction method of multipliers,ADMM)求取式(3)的最优解,原始信号f被分解成K个窄带IMF,求解过程不断更新ukn+1、ωkn+1、λkn+1,IMF的迭代过程为
| $ \begin{array}{l} \hat{u}_{k}^{n+1}(\omega)= \\ \qquad \frac{\hat{f}(\omega)-\sum\limits_{i<k} \hat{u}_{i}^{n+1}(\omega)-\sum\limits_{i>k} \hat{u}_{i}^{n}(\omega)+\frac{\hat{\lambda}^{n}(\omega)}{2}}{1+2 \alpha\left(\omega-\omega_{k}^{n}\right)^{2}} \end{array} $ | (4) |
式中n为迭代次数。对应的中心角频率为
| $ \omega_{k}^{n+1}=\frac{\int_{0}^{\infty} \omega\left|\hat{u}_{k}^{n+1}(\omega)\right|^{2} \mathrm{~d} \omega}{\int_{0}^{\infty}\left|\hat{u}_{k}(\omega)\right|^{2} \mathrm{~d} \omega} $ | (5) |
通过
| $ \hat{\lambda}^{n+1}=\hat{\lambda}^{n}+\tau\left(\hat{f}-\sum\limits_{k} \hat{u}_{k}^{n+1}\right) $ | (6) |
更新λ。重复迭代更新ukn+1、ωkn+1、λkn+1,直至k=K,若满足迭代停止条件
| $ \sum\limits_{k} \frac{\left\|\hat{u}_{k}^{n+1}-\hat{u}_{k}^{n}\right\|_{2}^{2}}{\left\|\hat{u}_{k}^{n}\right\|_{2}^{2}}<\varepsilon $ | (7) |
则迭代结束,得到K个IMF。
由VMD分解信号时,需要预先设定IMF的个数K,在测试模拟信号时发现K取l +1(l为合成信号分量的个数)时效果最好。由于实际信号复杂多变,吴文轩等[35]、刘尚坤[36]分别利用峭度及互信息准则等方法确定K值,文中利用经验方法,确定当K=3时可取得最佳的分解效果。
1.2 包络导数算子 1.2.1 TK算子对于连续信号x(t),TK算子被定义为二阶微分方程的形式[26]
| $ \psi[x(t)]=\dot{x}^{2}(t)-x(t) \ddot{x}(t) $ | (8) |
式中:ẋ(t)=dx(t)/dt;(t)=d2x(t)/dt2。对于一个离散的调幅调频(AM-FM)信号
| $ x(m)=a(m) \cos \phi(m) $ | (9) |
式中a(m)为调幅信号,m为采样点号。x(m)的离散形式的TK算子为[27]
| $ \psi_{\mathrm{d}}[x(m)]=x^{2}(m)-x(m-1) x(m+1) $ | (10) |
TK算子是仅利用差分运算计算瞬时能量的非线性算子,考虑了信号的频率特性,最明显的优势是良好的局域特性及计算的简洁、高效性。
1.2.2 EDO对于信号瞬时能量的求取,典型的方法是以振幅值的平方进行量化,或者以包络的形式
| $ S[x(t)]=|x(t)+\mathrm{j} \mathrm{H}[x(t)]|^{2} $ | (11) |
表征。式中H[·]为希尔伯特变换。为了引入频率域的信息,可以在式(11)中以导函数的形式引入加权滤波器。根据傅里叶变换(FT)的性质,有
| $ \left\{\begin{array}{l} \frac{\mathrm{d} x(t)}{\mathrm{d} t} \stackrel{\mathrm{FT}}{\longrightarrow} \mathrm{j} \omega X(\omega) \\ x(t) \stackrel{\mathrm{FT}}{\longrightarrow} X(\omega) \end{array}\right. $ | (12) |
则包络导数算子为[32]
| $ \begin{aligned} \varGamma[x(t)] &=|\dot{x}(t)+\mathrm{j} \mathrm{H}[\dot{x}(t)]|^{2} \\ &=\dot{x}^{2}(t)+\mathrm{H}^{2}[\dot{x}(t)] \end{aligned} $ | (13) |
式(13)结合了信号的频率变化信息与随时间变化的包络,称为包络导数算子(EDO)。EDO的定义形式与TK算子较相似,只有第二项存在区别。O′Toole等[32]详细对比了TK算子、EDO用于x(t)=Acos(ω0t+ϕ)(A为振幅,ω0为初始角频率,ϕ为相位)或x(t)=Aertcos(ω0t+ϕ)(r为调节系数,用于描述振幅的变化)形式的简单信号时的特性,均取得较好效果。对于线性组合信号y(t)=x1(t)+x2(t)
其中
| $ \left\{\begin{array}{l} x_{1}(t)=A_{1} \cos \left(\omega_{1} t+\phi_{1}\right) \\ x_{2}(t)=A_{2} \cos \left(\omega_{2} t+\phi_{2}\right) \end{array}\right. $ | (14) |
将TK算子、EDO应用于y(t),分别得到
| $ \begin{array}{l} \psi[y(t)]=\psi\left[x_{1}(t)\right]+\psi\left[x_{2}(t)\right]+ \\ \frac{1}{2} A_{1} A_{2}\left(\omega_{1}-\omega_{2}\right)^{2}\left\{\cos \left[\left(\omega_{1}+\omega_{2}\right) t+\phi_{1}+\phi_{2}\right]+\right. \\ \left.\cos \left[\left(\omega_{1}-\omega_{2}\right) t+\phi_{1}-\phi_{2}\right]\right\} \end{array} $ | (15) |
| $ \begin{aligned} \varGamma[y(t)]=& \varGamma\left[x_{1}(t)\right]+\varGamma\left[x_{2}(t)\right]+\\ & a\left[\sin \left(\omega_{1} t+\phi_{1}\right) \sin \left(\omega_{2} t+\phi_{2}\right)+\right.\\ &\left.\cos \left(\omega_{1} t+\phi_{1}\right) \cos \left(\omega_{2} t+\phi_{2}\right)\right] \\ =& \varGamma\left[x_{1}(t)\right]+\varGamma\left[x_{2}(t)\right]+\\ & a \cos \left[\left(\omega_{1}-\omega_{2}\right) t+\phi_{1}-\phi_{2}\right] \end{aligned} $ | (16) |
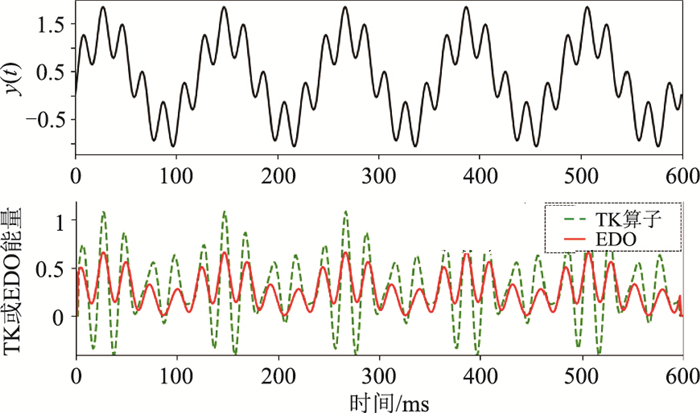
式中a=2A1A2ω1ω2。由式(15)、式(16)可见:Γ[y(t)]包含一个等于信号y(t)两个分量频率之差的项;ψ[y(t)]则包含了额外的附加项,这将在TK能量计算时出现负值。图 1为信号y(t)及TK算子、EDO能量计算结果。由图可见:对于能量的变化特征,TK算子、EDO均取得了良好的追踪结果,但在部分极值点处TK算子出现负值,这将在进一步分离能量时出现奇异值;EDO则具有良好的非负特性。
|
图 1 信号y(t)(上)及TK算子、EDO能量(下)计算结果 |
TK算子采用向前差分法获得离散形式,为了得到EDO的离散形式,定义以下中心差分形式
| $ \dot{x}(m)=\frac{x(m+1)-x(m-1)}{2} $ | (17) |
因此,离散形式的EDO为
| $ \begin{aligned} \varGamma_{\mathrm{d}}[x(m)]=& \frac{1}{4}\left[x^{2}(m+1)+x^{2}(m-1)+\right.\\ &\left.h^{2}(m+1)+h^{2}(m-1)\right]+\\ & \frac{1}{2}[x(m+1)+x(m-1)+\\ &h(m+1)+h(m-1)] \end{aligned} $ | (18) |
式中h(·)=Η[x(·)]。
1.2.3 基于VMD-EDO的时频分析方法基于VMD-EDO的时频分析方法如图 2所示。

|
图 2 基于VMD-EDO的谱分解算法 |
首先,将地震信号进行VMD,原始数据中的有效信息将主要由一个或几个IMF所反映,选取包含储层信息最多的IMF进行分析。
然后,采用能量分离(ESA)算法获得各分量信号EDO能量的瞬时频率和瞬时振幅[37]。由于ESA算法只适用于单分量信号,不能直接用于地震信号,而VMD方法将地震信号分解为一系列窄带信号,近似满足非线性能量算子的计算条件,可获得EDO能量。通过三点对称差分运算,得
| $ {\omega (m) \approx \frac{1}{2}{\mathop{\rm arc}\nolimits} {\kern 1pt} {\kern 1pt} \cos \left\{ {1 - \frac{{{\varGamma _{\rm{d}}}[x(m + 1) - x(m - 1)]}}{{2{\varGamma _{\rm{d}}}[x(m)]}}} \right\}} $ | (19) |
| $ {|A(m)| \approx \frac{{2{\psi _{\rm{d}}}[x(m)]}}{{\sqrt {{\varGamma _{\rm{d}}}[x(m + 1) - x(m - 1)]} }}} $ | (20) |
这里,瞬时频率ω(m)和瞬时振幅A(m)都是时间的函数,因此可以定义一个三维空间[t,A(t),ω(t)][38]
| $ R(\omega ,t) = {\mathop{\rm Re}\nolimits} \left[ {\sum\limits_{i = 1}^n {{A_i}} (t){{\rm{e}}^{{\rm{j}}\int {{\omega _i}(t){\rm{d}}t} }}} \right] $ | (21) |
最终可以获得IMF的时频分布,进一步可以分离得到不同频段的高精度瞬时谱。
2 模型验证为了验证VMD-EDO时频分析方法的效果,建立了地质模型(图 3a、表 1)。采用主频30Hz的雷克子波作为震源进行模拟,并添加7%的随机噪声。基于模型的VMD-EDO谱分解结果表明:在合成地震记录上缝洞体呈“串珠状”响应(图 3b);在VMD-EDO低频剖面上缝洞体呈强能量体特征(图 3c);相对于地层信息,在VMD-EDO高频剖面上缝洞体能量衰减明显(图 3d)。因此VMD-EDO谱分解结果总体体现了“低频能量加强、高频能量衰减”的特征,证明了方法的有效性。
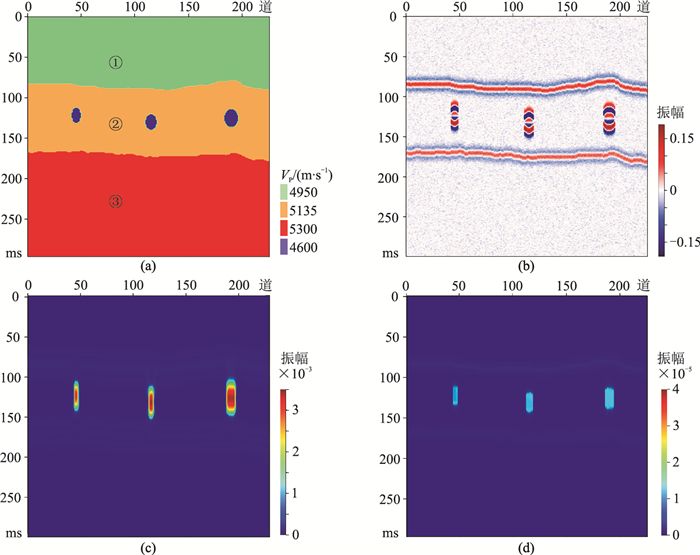
|
图 3 基于模型的VMD-EDO谱分解 (a)地质模型;(b)合成地震记录;(c)低频剖面;(d)高频剖面。图a从上至下分为3层,在第②层存在3个不同规模的缝洞体(第④层,蓝色区域) |
|
|
表 1 模型参数 |
为进一步验证VMD-EDO时频分析方法的效果,选取中国西部N区的叠后地震资料进行测试。N区位于顺托果勒低隆的北部,处于阿瓦提、满加尔坳陷与沙雅隆起的结合部,紧邻南部海相烃源岩灶,同时发育本地寒武系烃源岩,构造位置有利,油源充足,是油气长期运移、聚集的有利区。目前研究表明,N区奥陶系油气成藏条件优越,储层地震响应主要以同相轴错断、异常弯曲和“串珠状”为主。由于缝洞储层自身的规模、形态和内部结构差异明显以及埋深较大,对于时频分析精度提出了更高的要求。
图 4为A井井旁地震道CDP105及VMD结果,图 5为IMF2振幅谱及由TK算子、EDO得到的瞬时振幅。由图可见:①IMF1为超低频信息(图 4b上),而中低频及高频有效信息主要分别包含在IMF2(图 4b中)与IMF3(图 4b下)中。②整体来看,对于4600~4700ms层段的油气异常特征,分别采用TK算子(图 5b上)与EDO(图 5b下)得到的瞬时振幅相近,并且均避免了希尔伯特变换的端点问题。③由于TK能量计算时出现负值,在部分极值点附近瞬时振幅出现部分奇异值,需要采用取绝对值才能避免此问题(图 5b上);EDO计算结果更平滑,且EDO良好的非负特性有效避免了奇异值(图 5b下)。
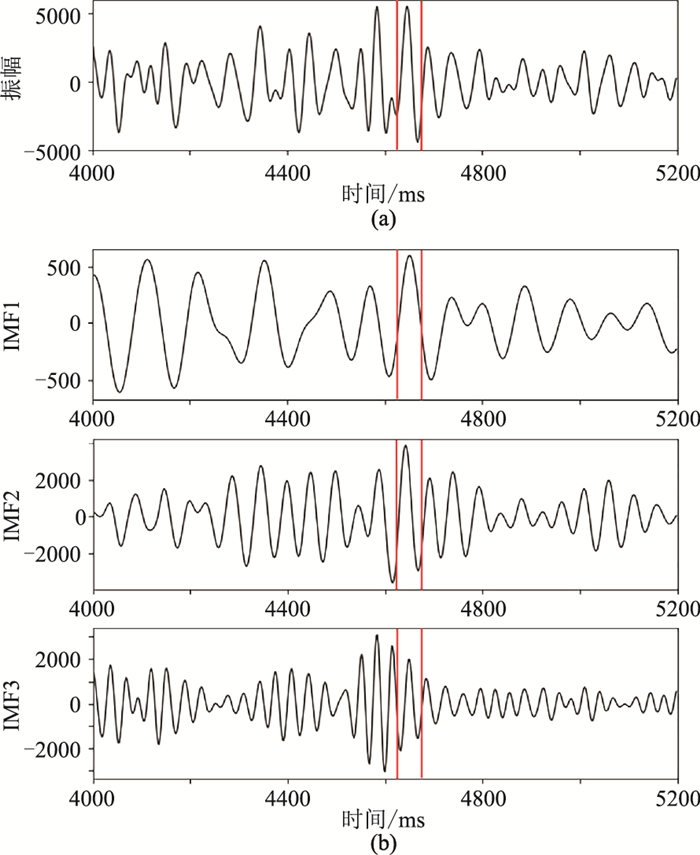
|
图 4 A井井旁地震道CDP105(a)及VMD结果(b) A井为良好的产油井,4600~4700ms(红线围成的区域)为油层 |
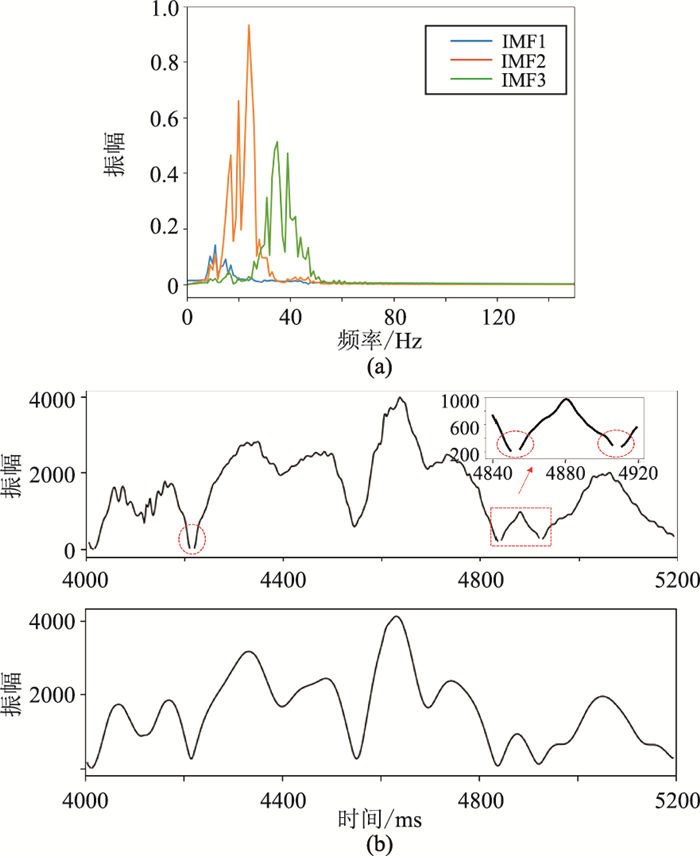
|
图 5 IMF2振幅谱(a)及由TK算子(上)、EDO(下)得到的瞬时振幅(b) |
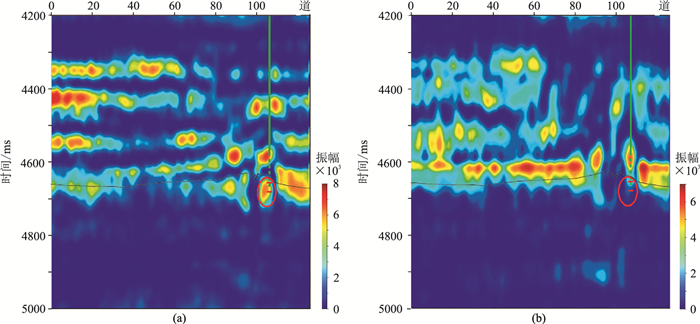
图 6为A井井旁道CDP109时频谱。由图可见,有效信息主要分布在15~40Hz频段,在4650ms附近出现强能量异常,VMD-EDO时频谱(图 6a)的时频分辨率高于连续小波变换(CWT)时频谱(图 6b)。
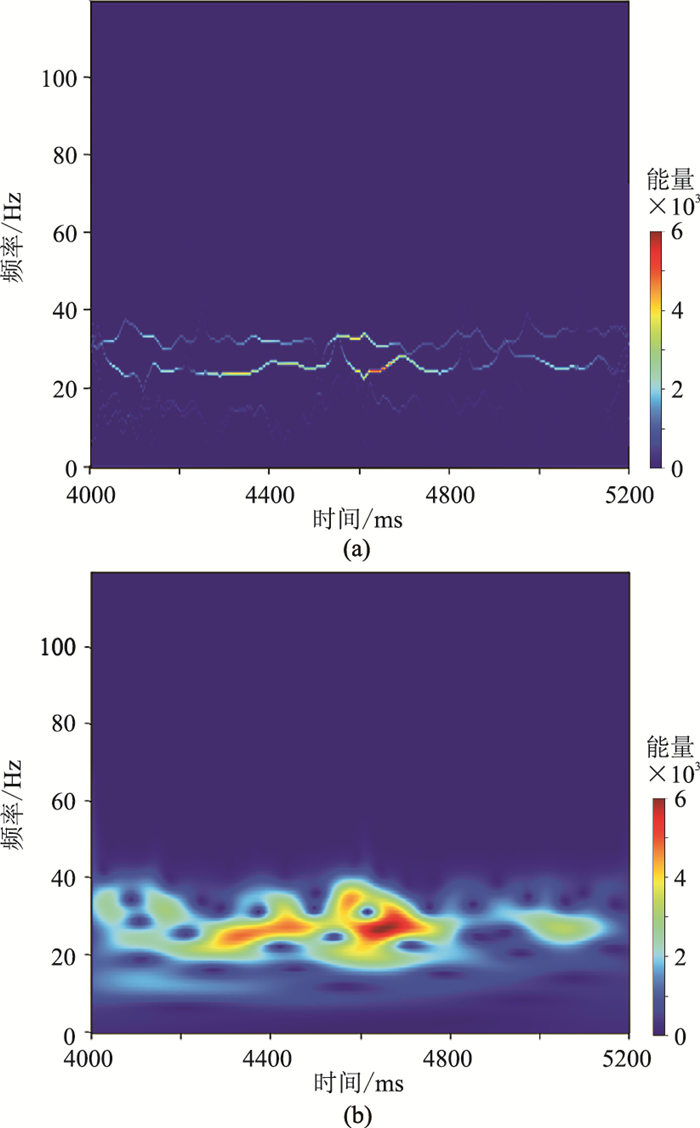
|
图 6 A井井旁道CDP109时频谱 (a)VMD-EDO;(b)CWT |
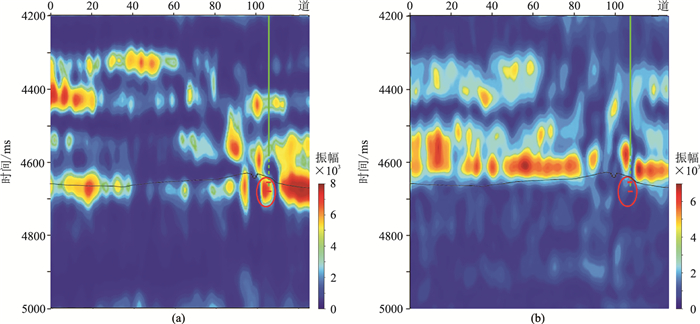
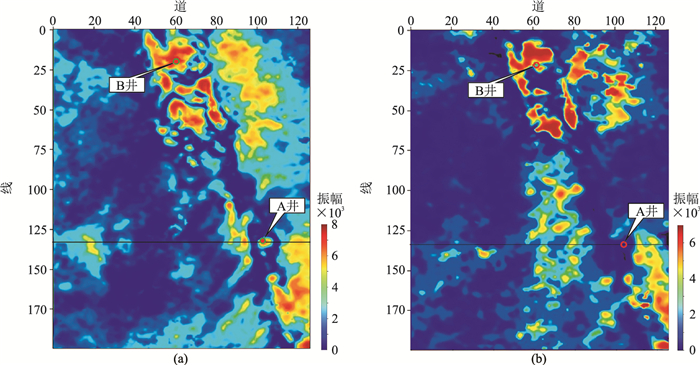
撒利明等[39]采用“低频共振、高频衰减”特征检测油气,薛雅娟等[18]分别讨论了低频(14~18Hz)、高频(26~30Hz)的时频特征,并预测了鄂尔多斯盆地海相碳酸盐岩储层(频带范围为12~30Hz)。图 7为过A井地震剖面及VMD结果。由图可见:在过A井地震剖面的CDP105、4650ms附近钻遇油气,呈小“串珠状”地震响应(图 7a);IMF2(图 7c)、IMF3(图 7d)分别反映了中低频、高频有效信息。图 8、图 9分别为VMD-EDO、CWT-EDO的低频、高频剖面。由图可见:①在含油气区域(红圈位置),两种方法都取得了良好的检测结果,具体表现为:在低频剖面上呈不连续的强亮点及周边存在弱能量团(图 8a、图 9a);随着频率升高,在高频剖面上含油气区域(红圈位置)的能量衰减明显(图 8b、图 9b)。②VMD-EDO方法检测结果的分辨率更高,能更好地区分不同深度的能量异常。图 10为对应图 7c、图 7d的VMD-EDO低频、高频目的层沿层切片。由图可见,A井、B井均为良好的产油井,两口井所在区域均明显表现为低频段强能量异常(图 10a)、高频能量衰减(图 10b)特征,进一步验证了方法的有效性。因此,在缝洞型碳酸盐岩储层中,基于VMD-EDO的高精度时频分析算法的储层预测效果较好。
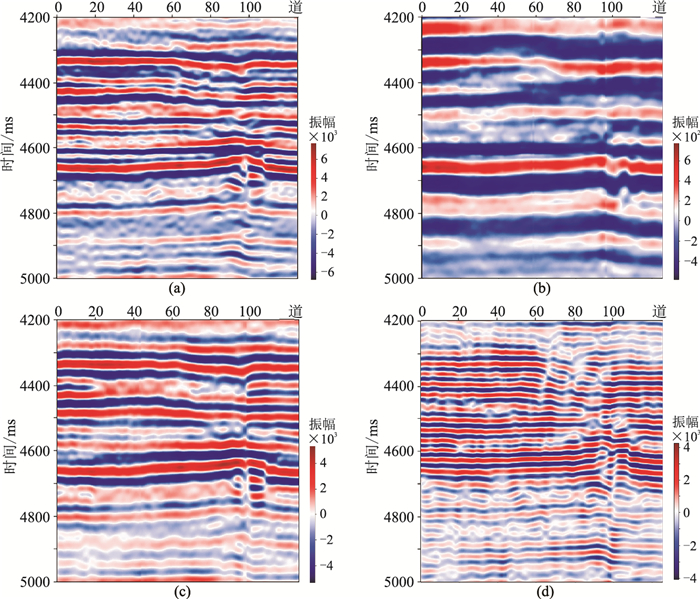
|
图 7 过A井地震剖面及VMD结果 (a)过A井地震剖面;(b)IMF1;(c)IMF2;(d)IMF3 |
4 结论与认识
本文在HHT的理论基础上,提出了一种结合VMD与EDO能量算子的高精度时频分析方法,并将其应用于中国西部N区的缝洞储层预测,获得了较好效果。
在VMD获得IMF的基础上,运用TK/EDO方法求取瞬时振幅、瞬时频率可以避免希尔伯特变换引起的端点效应,其中EDO的结果更平滑,且具有良好的抗噪性及稳定性,性能优于TK算子。
实际资料应用效果表明,与经典时频分析方法相比,基于VMD-EDO的时频分析方法具有更高的时频分辨率,能有效识别隐藏在宽频地震数据中的能量异常。结合含油气储层“低频能量加强、高频能量衰减”的特点,VMD-EDO的时频分析方法具备良好的油气检测能力。
| [1] |
文山师, 李海英, 洪才均, 等. 顺北油田断溶体储层地震响应特征及描述技术[J]. 断块油气田, 2020, 27(1): 45-49. WEN Shanshi, LI Haiying, HONG Caijun, et al. Technology of seismic response characteristics and description of fault-karst reservoir in Shunbei Oilfield[J]. Fault-Block Oil and Gas Field, 2020, 27(1): 45-49. |
| [2] |
李京昌, 陈元壮, 何宏, 等. 塔里木盆地泥盆系东河砂岩油气分布规律[J]. 新疆石油地质, 2017, 38(5): 505-511. LI Jingchang, CHEN Yuanzhuang, HE Hong, et al. Oil and gas distribution in Devonian Donghe sandstone of Tarim Basin[J]. Xinjiang Petroleum Geology, 2017, 38(5): 505-511. |
| [3] |
鲁新便, 蔡忠贤. 缝洞型碳酸盐岩油藏古溶洞系统与油气开发——以塔河碳酸盐岩溶洞型油藏为例[J]. 石油与天然气地质, 2010, 31(1): 22-27. LU Xinbian, Cai Zhongxian. A study of the paleo-cavern system in fractured-vuggy carbonate reservoirs and oil/gas development: taking the reservoirs in Tahe oilfield as an example[J]. Oil & Gas Geology, 2010, 31(1): 22-27. |
| [4] |
程洪, 汪彦, 鲁新便. 塔河地区深层碳酸盐岩断溶体圈闭类型及特征[J]. 石油学报, 2020, 41(3): 301-309. CHENG Hong, WANG Yan, LU Xinbian. Classifications and characteristics of deep carbonate fault-karst trap in Tahe area[J]. Acta Petrolei Sinica, 2020, 41(3): 301-309. |
| [5] |
Castagna J P, Sun S, Siegfried R W. Instantaneous spectral analysis: Detection of low-frequency shadows associated with hydrocarbons[J]. The Leading Edge, 2003, 22(2): 120-127. DOI:10.1190/1.1559038 |
| [6] |
de Matos M C, Marfurt K J, Johann P R S, et al. Wavelet transform Teager-Kaiser energy applied to a carbonate field in Brazil[J]. The Leading Edge, 2009, 28(6): 708-713. DOI:10.1190/1.3148413 |
| [7] |
Huang Y P, Geng J H, Zhong G F, et al. Seismic attribute extraction based on HHT and its application in a marine carbonate area[J]. Applied Geophysics, 2011, 8(2): 125-133. DOI:10.1007/s11770-010-0279-z |
| [8] |
胡瑞卿, 王彦春, 尹志恒, 等. 结合CEEMDAN和主成分分析的低信噪比微地震初至信号检测[J]. 石油地球物理勘探, 2019, 54(1): 45-53. HU Ruiqing, WANG Yanchun, YIN Zhiheng, et al. A first arrival detection method in low SNR microseismic signals based on CEEMDAN-PCA[J]. Oil Geophysical Prospecting, 2019, 54(1): 45-53. |
| [9] |
Gilles J. Empirical wavelet transform[J]. IEEE Transactions on Signal Processing, 2013, 61(16): 3999-4010. DOI:10.1109/TSP.2013.2265222 |
| [10] |
Hou T Y and Shi Z Q. Data-driven time-frequency analysis[J]. Applied and Computational Harmonic Analysis, 2013, 35(2): 284-308. DOI:10.1016/j.acha.2012.10.001 |
| [11] |
Daubechies I, Lu J, Wu H T. Synchrosqueezed wavelet transforms: An empirical mode decomposition-like tool[J]. Applied and Computational Hammonic Ana-lysis, 2011, 30(2): 243-261. DOI:10.1016/j.acha.2010.08.002 |
| [12] |
Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Procecdings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995. DOI:10.1098/rspa.1998.0193 |
| [13] |
Huang N E, Wu M L, Long S R, et al. A confidence limit for the empirical mode decomposition and Hilbert spectral analysis[J]. Procecdings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2003, 459(2037): 2317-2345. DOI:10.1098/rspa.2003.1123 |
| [14] |
曹思远, 邴萍萍, 路交通, 等. 利用改进希尔伯特-黄变换进行地震资料时频分析[J]. 石油地球物理勘探, 2013, 48(2): 246-254. CAO Siyuan, BING Pingping, LU Jiaotong, et al. Seismic data time-frequency analysis by the improved Hilbert-Huang transform[J]. Oil Geophysical Prospecting, 2013, 48(2): 246-254. |
| [15] |
Wu Z, Huang N E. Ensemble empirical mode decomposition: A noise-assisted data analysis method[J]. Advances in Adaptive Data Analysis, 2009, 1(1): 1-41. DOI:10.1142/S1793536909000047 |
| [16] |
Torres M E, Colominas M A, Schlotthauer G, et al. A complete ensemble empirical mode decomposition with adaptive noise[C]. IEEE International Conference on Acoustics, Speech and Signal Processing, 2011, 4144-4147.
|
| [17] |
乐友喜, 杨涛, 曾贤德. CEEMD与KSVD字典训练相结合的去噪方法[J]. 石油地球物理勘探, 2019, 54(4): 729-736. YUE Youxi, YANG Tao, ZENG Xiande. Seismic denoising with CEEMD and KSVD dictionary combined training[J]. Oil Geophysical Prospecting, 2019, 54(4): 729-736. |
| [18] |
薛雅娟, 曹俊兴. 聚合经验模态分解和小波变换相结合的地震信号衰减分析[J]. 石油地球物理勘探, 2016, 51(6): 1148-1155. XUE Yajuan, CAO Junxing. Seismic attenuation analy-sisusing ensemble empirical mode decomposition and wavelet transform[J]. Oil Geophysical Prospecting, 2016, 51(6): 1148-1155. |
| [19] |
鄢高韩, 杨午阳, 杨庆, 等. CEEMD高分辨率时频分析方法研究与应用[J]. 地球物理学进展, 2016, 31(4): 1709-1715. YAN Gaohan, YANG Wuyang, YANG Qing, et al. Study and application of CEEMD high resolution time-frequency analysis method[J]. Progress in Geophysics, 2016, 31(4): 1709-1715. |
| [20] |
邬蒙蒙. 改进的完备经验模态分解与WVD变换相结合在油气检测中的应用[J]. 油气地球物理, 2020, 18(1): 72-76. WU Mengmeng. Improved complete empirical mode decomposition and WVD transformation method and its application in oil and gas detection[J]. Petroleum Geophysics, 2020, 18(1): 72-76. |
| [21] |
Dragomiretskiy K, Zosso D. Variational mode decomposition[J]. IEEE Transaction on Signal Processing, 2014, 62(3): 531-544. |
| [22] |
Upadhyay A, Pachori R B. Instantaneous voiced/non-voiced detection in speech signals based on variational mode decomposition[J]. Journal of the Franklin Institute, 2015, 352(7): 2679-2707. |
| [23] |
Liu W, Cao S Y, Wang Z M. Application of variational mode decomposition to seismic random noise reduction[J]. Journal of Geophysics & Engineering, 2017, 14(4): 888-899. |
| [24] |
方江雄, 温志平, 顾华奇, 等. 基于变分模态分解的地震随机噪声压制方法[J]. 石油地球物理勘探, 2019, 54(4): 757-767. FANG Jiangxiong, WEN Zhiping, GU Huaqi, et al. Seismic random noise attenuation based on variational mode decomposition[J]. Oil Geophysical Prospecting, 2019, 54(4): 757-767. |
| [25] |
龙丹, 牛聪, 周怀来, 等. 基于VMD算法在地震数据时频分析中的应用[J]. 地球物理学进展, 2020, 35(1): 166-173. LONG Dan, NIU Cong, ZHOU Huailai, et al. Application of VMD algorithm in time-frequency analysis of seismic data[J]. Progress in Geophysics, 2020, 35(1): 166-173. |
| [26] |
Teager H M, Teager S M. Evidence for nonlinear production mechanisms in the vocal tract[J]. Speech Production & Speech Modeling, 1990. DOI:10.1007/978-94-009-2037-8_10 |
| [27] |
Kaiser J F. On a simple algorithm to calculate the e-nergy of a signal[C]. IEEE International Conference on Acoustics, Speech and Signal Processing, 1990, 381-384.
|
| [28] |
de Matos M C, Marfurt K J, Johann P, et al. Brazilian deep water carbonate reservoir study using the wavelet transform Teager-Kaiser energy[C]. SEG Technical Program Expanded Abstracts, 2008, 27: 1516-1520.
|
| [29] |
陈学华, 钟文丽, 贺振华. 基于时频域Teager主能量的储层检测[J]. 石油地球物理勘探, 2011, 46(3): 434-437. CHEN Xuehua, ZHONG Wenli, HE Zhenhua. Reservoir characterization based on Teager dominant energy in time-frequency domain[J]. Oil Geophysical Prospecting, 2011, 46(3): 434-437. |
| [30] |
唐湘蓉, 石战战, 彭真明, 等. 基于分数阶Gabor变换的Teager-Kaiser能量提取及应用[J]. 石油物探, 2014, 53(5): 595-602. TANG Xiangrong, SHI Zhanzhan, PENG Zhenming, et al. Application and extraction of Teager-Kaiser e-nergy based on the fractional Gabor transform[J]. Geophysical Prospecting for Petroleum, 2014, 53(5): 595-602. |
| [31] |
Xue Y J, Cao J X, Tian R F. EMD and Teager-Kaiser energy applied to hydrocarbon detection in a carbo-nate reservoir[J]. Geophysical Journal International, 2014, 197(1): 277-291. |
| [32] |
O'Toole J M, Temko A, Stevenson N. Assessing instantaneous energy in the EEG: a non-negative, frequency-weighted energy operator[C]. Annual International Conference of the IEEE Engineering in Medicine and Biology Society, 2014, doi: 10.1109/EMBC.2014.6944325.
|
| [33] |
Cai Z Y, Xu Y B, Duan Z S. An alternative demodulation method using envelope-derivative operator for bearing fault diagnosis of the vibrating screen[J]. Journal of Vibration and Control, 2017. DOI:10.1177/1077546317739117 |
| [34] |
任学平, 李攀, 王朝阁, 等. 基于改进VMD与包络导数能量算子的滚动轴承早期故障诊断[J]. 振动与冲击, 2018, 37(15): 6-13. REN Xueping, LI Pan, WANG Chaoge, et al. Rolling bearing early fault diagnosis based on improved VMD and envelope derivative operator[J]. Journal of Vibration and Shock, 2018, 37(15): 6-13. |
| [35] |
吴文轩, 王志坚, 张纪平, 等. 基于峭度的VMD分解中k值的确定方法研究[J]. 机械传动, 2018, 42(8): 153-160. WU Wenxuan, WANG Zhijian, ZHANG Jiping, et al. Research of the method of determining k value in VMD based on Kurtosis[J]. Journal of Mechanical Transmission, 2018, 42(8): 153-160. |
| [36] |
刘尚坤. 基于振动信号处理的旋转机械故障诊断方法研究[D]. 河北保定: 华北电力大学(保定), 2017. LIU Shangkun. Research on Fault Diagnosis Method of Rotating Machinery Based on Vibration Signal Processing[D]. North China Electric Power University (Baoding), Baoding, Hebei, 2017. |
| [37] |
Maragos P, Kaiser J F, Quatieri T. On separating amplitude from frequency modulations using energy o-perators[C]. IEEE International Conference on Acoustics, Speech and Signal Processing, 1992, 1-4.
|
| [38] |
Maragos P, Kaiser J F, Quatieri T. Energy separation in signal modulations with application to speech ana-lysis[J]. IEEE Transaction on Signal Processing, 1993, 41(10): 3024-3051. |
| [39] |
撒利明, 梁秀文, 刘全新. 一种基于多相介质理论的油气检测方法[J]. 勘探地球物理进展, 2002, 25(6): 32-35. SA Liming, LIANG Xiuwen, LIU Quanxin. A multi-phase theory based hydrocarbon detection method[J]. Progress in Exploration Geophysics, 2002, 25(6): 32-35. |



 武迪, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
武迪, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: