地层中的断层、裂隙、尖灭和孔洞等小尺度地质体对油气勘探具有重要意义,这些小尺度地质体在地震记录上的响应主要为能量较弱的绕射波。Klem等[1]指出地震数据中的绕射能量通常比反射能量弱1~2个数量级。在常规的地震数据处理流程中,来自反射界面以外的绕射波同相轴常被视作干扰噪声而被滤除。即使同时将绕射波和反射波准确偏移归位,弱绕射能量仍会被大尺度地质体反射能量淹没。为了充分利用地震数据中的绕射信息,可从全波场中提取绕射波,实现绕射波单独成像,进而提高绕射目标的成像分辨率。
早在二十世纪五十年代,Krey[2]就利用绕射波信息研究断层、断点等,但直到二十世纪八十年代,学者们才真正意识到绕射波分离成像的重要性,并相继提出不同的绕射波场分离方法。根据地震数据处理阶段的不同,可以将绕射波分离与成像方法归纳为以下三类:
(1) 基于叠前数据的绕射波分离与成像。该类方法是利用叠前道集中绕射波与反射波的运动学特征差异,从全波场中提取绕射波,进而实现绕射波单独成像。Landa等[3]提出在共炮检距道集上利用相位校正和定性分析检测小尺度绕射体。Khaidu-kov等[4]在叠前共炮点道集中利用反射波与绕射波的运动学特征差异,即反射波聚焦于震源点的镜像位置而绕射波仍保持发散的状态,通过反射波聚焦、切除、再反聚焦方法成功分离出绕射波场。Nowak等[5]根据共炮点道集中反射波与绕射波同相轴横向位置差异,借助于加权Radon变换分离反射绕射波场。Bansal等[6]讨论了多种利用叠前数据压制反射信号、增强绕射能量的方法,主要包括共炮检距倾角滤波、正常时差校正倾角滤波、特征向量滤波、Radon滤波等,并且对比、分析了不同方法的优缺点,认为特征向量法是较为有效的绕射波场分离方法。Taner等[7]利用平面波分解(Plan Wave Decomposition,PWD)滤波器生成平面波记录,依据绕射波与反射波在平面波记录中的同相轴差异,在叠前道集中分离绕射波场。黄建平等[8]对PWD解构滤波器的使用方法和在叠前、叠后道集上分离成像绕射波的流程进行了系统总结。孔雪等[9]和刘玉金等[10]证实了平面波记录具有区分绕射波与反射波的特性,并利用平面波解构滤波技术分离获得绕射波场。朱生旺等[11]解决了PWD滤波器中绕射波场的低倾角信息估计不足问题,提高了绕射波成像结果的横向分辨率。
(2) 在叠加过程中进行绕射波分离与成像。Kanasewich等[12]直接对地震信号沿着绕射波走时曲线进行叠加,获得了共炮检距道集和共断层点道集上的绕射波时间剖面。Berkovich等[13]、Dell等[14]分别利用绕射波多聚焦和共反射面的绕射走时计算方法,将选取的绕射波同相轴进行最优叠加,得到包含绕射波的叠加剖面。Asgedom等[15]利用修正的共反射面(Common Reflection Surface,CRS)技术讨论了相似度和多信号分类两种方法在分离反射波与绕射波时的优势。
(3) 在偏移过程中进行绕射波分离与成像。Landa等[16]推导了深度偏移倾角域共成像点道集(Common Imaging Gathers,CIGs)中反射波和绕射波的形态,并分析了偏移速度对两者的影响。Zhu等[17]在小波束偏移过程中,利用角度域局部成像矩阵中反射与绕射能量的分布差异,即反射能量沿着倾角方向呈线性分布而绕射能量弥散分布在整个矩阵中,分离出绕射能量并对其单独成像。Klokov等[18]将相似度扫描反射顶点去除与混合Radon变换方法相结合,在倾角域CIGs上进行绕射波场分离。Decker等[19]在偏移倾角道集中,对每个固定倾角的成像剖面应用PWD解构滤波技术,获得单独的绕射波成像剖面。Zhang等[20]提出在单炮的反射角域CIGs中通过切除菲涅耳带提取绕射波场。黄建平等[21]和李振春等[22]将逆时偏移与最小二乘偏移的优势相结合,分别发展了适用于复杂构造的保幅成像处理方法。刘梦丽等[23]提出一种满足能量守恒的逆散射成像条件,并将其与最小二乘逆时偏移(Reverse Time Migration,RTM)相结合,实现了角度滤波成像。汪天池等[24]在倾角域中利用逆时偏移提取倾角道集,然后采用中值滤波方法实现反射波与绕射波的分离。
近些年来,大量学者尝试在倾角域CIGs上进行绕射波与反射波的分离。根据倾角域CIGs中反射波响应曲线呈双曲规律而绕射波呈现拟线性规律的差异,发展了平面波解构滤波、扫描相似度顶点去除与混合Radon变换相结合[18]、相似谱能量分析等绕射波分离方法。同时,由于在倾角域CIGs中绕射波同相轴对速度误差的敏感性,Landa等[16]、Reshef等[25]、Li等[26]将其用于偏移速度分析以提高速度提取精度。
鉴于传统混合域Radon变换采用迭代重加权算法进行求解,每一步迭代常常涉及到大规模矩阵的求逆问题,计算量巨大。为此,本文引入迭代收缩阈值算法(Iterative Shrinkage Thresholding Algorithm,ISTA),发展了一种基于迭代收缩高分辨率Radon变换的绕射波分离与成像方法。首先采用迭代收缩阈值算法,通过时间域简单的模型收缩步骤获得Radon域模型的稀疏性,以解决常规Radon变换中反射波与绕射波在Radon域中能量团聚焦性差、绕射波场分离效果不理想的问题;然后在编程实现算法的基础上,通过模型数据验证了该方法的有效性和适用性。
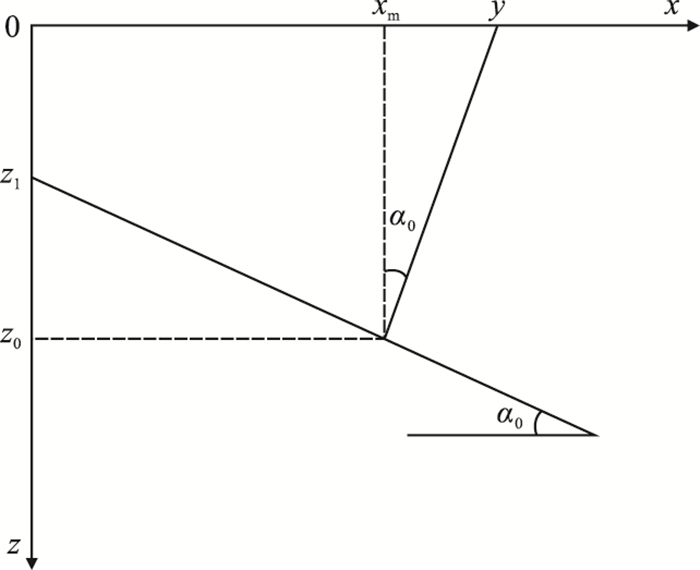
1 方法原理 1.1 倾角域共成像点道集波场特征常速介质叠后偏移(图 1)反射面的深度z(x)可以表示为[17]
| $ z(x)=z_{1}+x \tan \alpha_{0} $ | (1) |
|
图 1 零炮检距反射示意图 |
式中:z1为倾斜反射界面与z轴的交点深度;α0为反射界面的倾角;x为横坐标。在地表y处的自激自收地震响应可表示为
| $ w(y)=\frac{2\left(z_{1} \cos \alpha_{0}+y \sin \alpha_{0}\right)}{v} $ | (2) |
式中:v是介质速度;w为旅行时间。
由模型坐标(x,z)和数据坐标(y,w)之间的映射关系可得偏移公式,即
| $ x_{\mathrm{m}}=y-\frac{v_{\mathrm{m}} w}{2} \sin \alpha $ | (3) |
| $ \tau=w \cos \alpha $ | (4) |
式中:vm表示偏移速度;α为偏移倾角;τ表示截距时间。将式(2)代入式(3)和式(4)中,消去y可得倾斜反射界面在倾角域的成像表达式,即
| $ \tau\left(x_{\mathrm{m}}, \alpha\right)=\frac{2 \cos \alpha}{v} \times \frac{x_{\mathrm{m}} \sin \alpha_{0}+z_{1} \cos \alpha_{0}}{1-\gamma \sin \alpha_{0} \sin \alpha} $ | (5) |
式中γ=vm/v。根据式(1)所定义的横坐标xm处的反射面深度为z0,可得
| $ x_{\mathrm{m}} \sin \alpha_{0}+z_{1} \cos \alpha_{0}=z_{0} \cos \alpha_{0} $ | (6) |
将式(6)代入式(5),可得倾角域CIGs中固定横向位置的反射波响应表达式,即
| $ \tau(\alpha)=\tau_{0} \frac{\cos \alpha_{0} \cos \alpha}{1-\gamma \sin \alpha_{0} \sin \alpha} $ | (7) |
式中τ0=2z0/v为反射点处的双程垂直旅行时。
将式(7)对α求偏导可得到
| $ \frac{\partial \tau(\alpha)}{\partial \alpha}=\tau_{0} \cos \alpha_{0} \frac{\gamma \sin \alpha_{0}-\sin \alpha}{\left(1-\gamma \sin \alpha_{0} \sin \alpha\right)^{2}} $ | (8) |
从式(8)可以看出,当偏移速度正确,即γ=1时,反射响应为具有稳相顶点的“笑脸”状曲线,且稳相顶点位于α=α0处。
类似地,可以得到地下绕射点的倾角域响应表达式
| $ \tau(\alpha)=\tau_{0} \cos \alpha \frac{\xi \gamma \sin \alpha+\sqrt{\xi^{2}+1-\gamma^{2} \sin ^{2} \alpha}}{1-\gamma^{2} \sin ^{2} \alpha} $ | (9) |
式中ξ=(x-x0)/z0,ξ是绕射点x0和成像点x之间的横向距离与绕射点深度z0的比值。当偏移速度准确(vm=v)且成像点在绕射点处(ξ=0),式(9)简化为
| $ \tau(\alpha)=\tau_{0} $ | (10) |
由式(10)可以看出,此时绕射响应为一水平直线。
对于式(7)和式(9),利用τ(α)=2z(α)/vm和τ0=2z0/v,即可从时间域转换到伪深度域。深度域反射界面在倾角域的响应表达式为
| $ z(\alpha)=z_{0} \gamma \frac{\cos \alpha_{0} \cos \alpha}{1-\gamma \sin \alpha_{0} \sin \alpha} $ | (11) |
地下绕射点在倾角域的响应表达式为
| $ z(\alpha)=\gamma \cos \alpha \frac{\rho \gamma \sin \alpha+\sqrt{\rho^{2}+z_{0}^{2}\left(1-\gamma^{2} \sin ^{2} \alpha\right)}}{1-\gamma^{2} \sin ^{2} \alpha} $ | (12) |
式中ρ=x-x0。
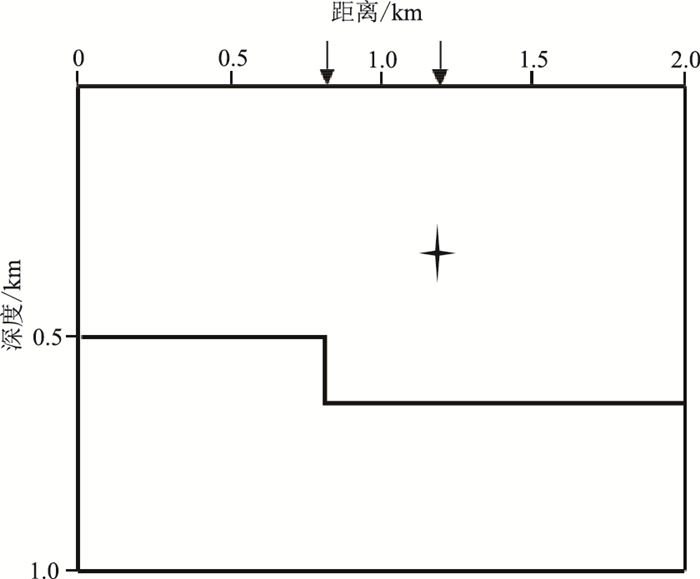
通过一个简单的常速介质模型(图 2)可直观地阐明倾角域CIGs响应曲线的特点,并且可以进一步分析两者之间的差异。该模型由一个垂直断层和一个绕射体组成,记录共150炮,最大炮检距为500m,时间采样间隔为1ms,检波点间距为10m。
|
图 2 常速介质模型 垂直断层和绕射体分别位于0.8km和1.2km的横向位置;“十”字符号示意绕射目标体 |
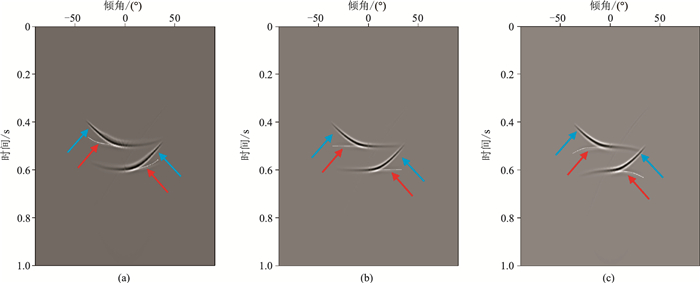
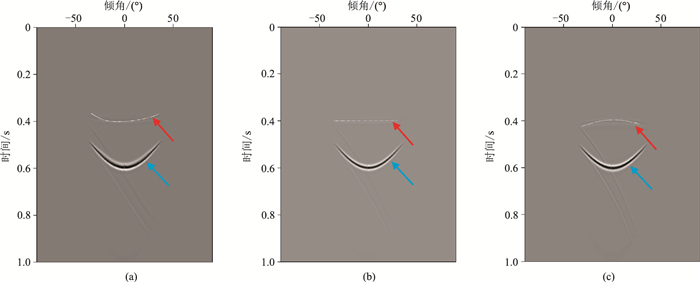
图 3和图 4分别显示了0.8km处断层和1.2km处绕射体在不同偏移速度下产生的倾角道集。可以看出,在倾角域CIGs上,位于绕射点正上方的绕射响应可分为三种情况:当偏移速度小于准确的介质速度时,绕射波表现为向上弯曲的“笑脸”状(凹形)(图 3a、图 4a);当偏移速度准确时,绕射波同相轴表现为线性形态(图 3b、图 4b);当偏移速度大于准确的介质速度时,绕射波同相轴则为向下弯曲的“哭脸”状(凸形)(图 3c、图 4c)。而反射界面响应曲线无论偏移速度准确与否,始终保持为具有稳相顶点的“笑脸”状,且稳相顶点横坐标指示界面的倾角。
|
图 3 不同偏移速度误差时断层处的倾角域CIGs (a)偏移速度为介质速度的90%;(b)偏移速度等于介质速度;(c)偏移速度为介质速度的110%蓝色和红色箭头分别指示反射波和绕射波同相轴,图 4同 |
|
图 4 不同偏移速度误差时绕射体处的倾角域CIGs (a)偏移速度为介质速度的90%;(b)偏移速度等于介质速度;(c)偏移速度为介质速度的110% |
综上所述,在倾角域CIGs中,反射响应与绕射响应曲线之间存在着明显的几何形态差异,因而可以利用两者之间形态差异作为波场分离的依据。
1.2 常规Radon变换二维抛物线Radon变换的定义式可以表示为
| $ d(t, u)=\int_{-\infty}^{+\infty} m\left(\tau=t-q u^{2}, q\right) \mathrm{d} q $ | (13) |
式中:d(t,u)为时间—空间域地震数据,其中t为时间,u为炮检距;m(τ,q)为Radon域数据,其中q表示曲率参数。
因此,抛物线Radon正变换的离散形式可以表示为
| $ \boldsymbol{D}\left(\omega, u_{k}\right)=\sum\limits_{r=0}^{n-1} \boldsymbol{M}\left(\omega, q_{r}\right) \mathrm{e}^{-\mathrm{i} \omega q_{r} u_{k}{}^{2}} $ | (14) |
式中:D(ω,u)和M(ω,q)分别为d(t,u)和m(τ,q)的傅里叶变换结果,其中ω为频率;n为Radon域的曲率个数。
由式(14)可知,Radon变换可以表示为一个线性方程组的求解问题,即
| $ \mathit{\boldsymbol{d}} = \mathit{\boldsymbol{Lm}} $ | (15) |
式中:d为地震数据;m为模型数据;L是Radon变换算子,由地震数据的采集参数和Radon变换参数共同确定。
求式(15)的反问题,不能完全满足存在性、唯一性和稳定性,故该反问题是不适定的。对于不适定问题,为获得唯一且稳定的解,最直接方法就是在反问题中引入与模型信息相关的正则化项以求解稀疏正则解,即高分辨率Radon模型解。
对于式(15),可构造如下目标函数,即
| $ J=\|\boldsymbol{d}-\boldsymbol{L} \boldsymbol{m}\|_{s}^{s}+\beta\|\boldsymbol{m}\|_{p}^{p} $ | (16) |
式中:‖m‖为正则项;‖d-Lm‖为误差项;β为正则化参数,用于调节‖d-Lm‖与‖m‖之间的权重;下标p和s分别表示向量的Lp和Ls范数,且p>0,s≤2。当正则项和误差项都采用L2范数时,则上式对应最小二乘Radon变换,即
| $ J=\|\boldsymbol{d}-\boldsymbol{L m}\|_{2}^{2}+\beta\|\boldsymbol{m}\|_{2}^{2} $ | (17) |
对式(17)求极小值,可以得到m的常规最小二乘解,即
| $ \boldsymbol{m}=\left(\boldsymbol{L}^{\mathrm{T}} \boldsymbol{L}+\boldsymbol{\beta} \boldsymbol{I}\right)^{-1} \boldsymbol{L}^{\mathrm{T}} \boldsymbol{d} $ | (18) |
式中I为单位矩阵。由式(18)可以看出,在传统最小二乘意义下求得的Radon模型解分辨率较低。由于对每一个频率所采用的阻尼因子相同,且阻尼因子的实际作用是对Radon模型数据进行平滑,导致模型空间的能量团无法较好地聚焦,降低了Radon变换的分辨率。因此,常规最小二乘Radon变换不能满足绕射波场分离的高分辨率需求。
1.3 迭代收缩高分辨率Radon变换为了获得稀疏的高分辨率Radon模型解,一般为正则项选用L1范数、数据误差项选用L2范数,即p=1、s=2,则式(18)可转换为
| $ J=\|\boldsymbol{d}-\boldsymbol{L} \boldsymbol{m}\|_{2}^{2}+\beta\|\boldsymbol{m}\|_{1}^{1} $ | (19) |
在求解稀疏反演问题(式(19))时,本文利用Lu[27]提出的混合频率—时间域迭代收缩阈值算法,即在时间域通过模型收缩步骤获得Radon模型的稀疏性,矩阵与向量的乘积操作在频率域实现。具体来说,在第k步迭代过程中,更新的模型解为
| $ \begin{array}{l} {\mathit{\boldsymbol{m}}_k} = {T_\sigma }\left\{ {{\mathit{\boldsymbol{m}}_{k - 1}} + 2{t_0}{{\rm{F}}^{ - 1}}\left\{ {{{({\mathit{\boldsymbol{L}}^{\rm{T}}}\mathit{\boldsymbol{L}})}^{ - 1}}{\mathit{\boldsymbol{L}}^{\rm{T}}}\left[ {{\rm{F}}(\mathit{\boldsymbol{d}}) - } \right.} \right.} \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\left. {\mathit{\boldsymbol{L}}{\rm{F}}\left( {{\mathit{\boldsymbol{m}}_{k - 1}}} \right)} \right]} \right\} \end{array} $ | (20) |
式中:k为当前迭代次数;t0是迭代步长;F、F-1分别表示正、反傅里叶变换;Tσ是一个收缩算子,定义为
| $ T_{\sigma}\{\boldsymbol{m}, k\}_{i j}=\left(\left|m_{i j}\right|-\alpha \frac{K-k}{K} \tilde{m}_{i j}\right)_{+} \operatorname{sgn}\left(m_{i j}\right) $ | (21) |
式中:σ为阈值,且0 < σ < 1;K为总迭代次数;sgn表示阶跃函数;二维模型m={mij},
| $ (X)_{+}=\left\{\begin{array}{ll} X & X \geqslant 0 \\ 0 & X<0 \end{array}\right. $ | (22) |
本文基于迭代收缩算法的高分率Radon变换处理步骤如下。
(1) 给定阈值σ、最大迭代次数K和二维中值滤波器的大小以及初始迭代步长t1,将当前迭代次数k设置为0。
(2) 选取Radon模型的最小二乘解作为模型迭代的初始值,m0=F-1(LTL)-1LTd,同时设置k=1。
(3) 在迭代变量k=1,2,...,K时,执行下述迭代过程:
① 将上次的模型值mk-1傅里叶变换到频率域得到F(mk-1);
② 计算Radon算子L与频率域模型值的乘积即LF(mk-1);
③ 计算频率域中数据拟合误差F(d)-LF(mk-1);
④ 计算算子的伪逆矩阵(LTL)-1LT与数据拟合误差的乘积,即(LTL)-1LT[F(d)-LF(mk-1)];
⑤ 利用傅里叶反变换将频率域数据变换到时间域,即F-1{(LTL)-1LT[F(d)-LF(mk-1)]};
⑥ 利用带有收缩运算的方程Tσ计算模型更新值mk。
(4) 循环增加迭代次数k,检查是否达到了最大迭代次数,如果“否”,则转到第(3)步。
(5) 输出Radon模型的高分辨率解。
利用上述迭代收缩高分辨Radon变换算法,在求解过程中仅需计算一次伪逆矩阵,相比于传统的迭代重加权最小二乘(Iterative Reweighted Least Squares,IRLS)求解算法,极大地降低了计算量,更适用于实际地震资料处理。
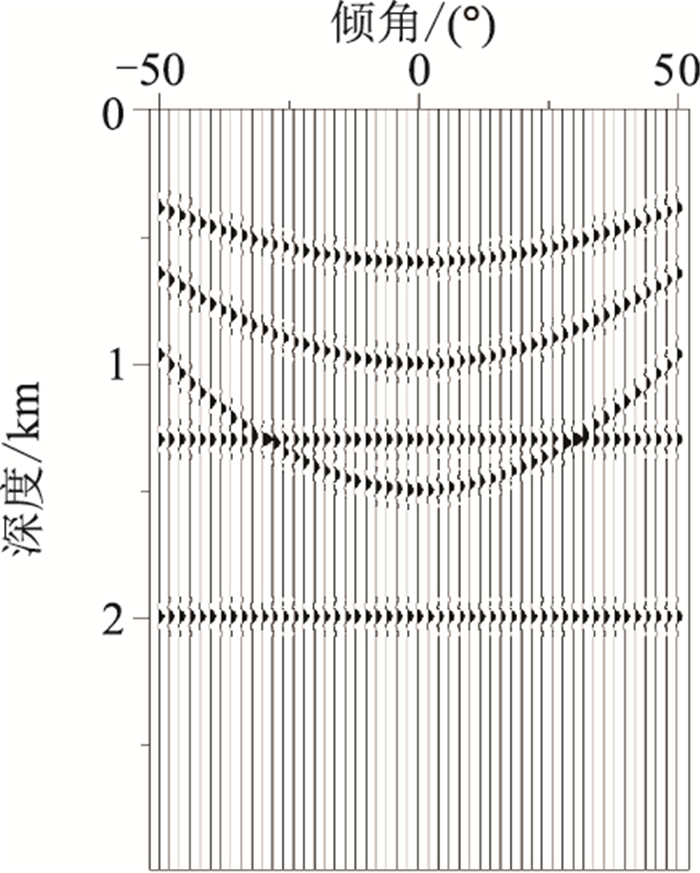
2 模型试算 2.1 有效性下面用模型试算验证本文算法的有效性。模拟CIGs中包含三条反射波和两条绕射波同相轴(图 5),反射波顶点分别位于深度600、1000、1500m处,两条绕射波同相轴则分别处于深度1300、2000m的位置。
|
图 5 模拟数据的CIG记录 |
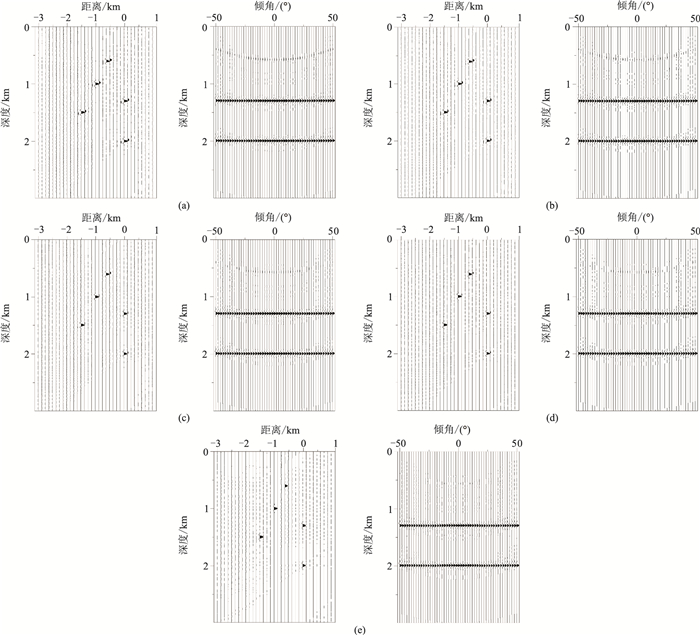
图 6为模型数据在不同迭代次数下的试算结果。测试过程中,设置最大迭代次数K=20、步长t0=0.5、阈值算子σ=0.05,二维均值滤波器的大小与模型相同。
|
图 6 不同迭代次数下迭代收缩高分辨率Radon变换结果 (a)1;(b)5;(c)10;(d)15;(e)20。左为Radon域全波场,右为时空域绕射波波场 |
从图 6可以看出,随着迭代次数的增加,Radon域模型的分辨率逐渐提高,即反射波和绕射波能量团聚焦性逐渐变好,剪刀状拖尾能量逐渐变弱,分离后的绕射波场也越来越干净。在此模拟数据的测试过程中,当迭代次数K=20时,Radon域中的反射波和绕射波能量聚焦性很好,分辨率高,切除反射后的绕射波场中几乎不存在残余反射能量。
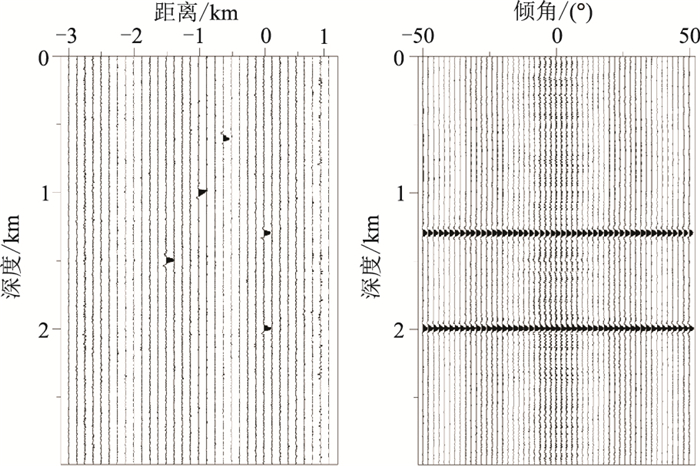
2.2 抗噪能力为了测试本文方法的抗噪能力,在图 5的模拟数据中加入了高斯白噪,得到如图 7所示数据。图 8左为图 7的常规最小二乘Radon变换结果,包含大量随机噪声,图 8右为分离后得到的时空域绕射波波场,由于在Radon域对噪声的压制不足,严重影响分离后的绕射波场质量。图 9为迭代收缩高分辨率Radon变换结果。可以看出:迭代收缩高分辨率Radon变换方法能够压制原始数据中的随机噪声,有效提高原始数据的信噪比(图 9左);本文方法从低信噪比的数据中提取绕射波的能力较强,可很好地压制模拟数据中的随机噪声(图 9右)。

|
图 7 包含高斯白噪的模拟CIG记录 |

|
图 8 常规最小二乘Radon变换结果 左为Radon域全波场,右为时空域绕射波波场 |
|
图 9 迭代收缩高分辨率Radon变换结果 左为Radon域全波场,右为时空域绕射波波场 |
为了说明本文方法的计算效率相较于IRLS算法的优势,不同迭代次数下本文方法和IRLS算法在模拟数据上的运算时间如表 1所示。从表中可以看出,IRLS算法的运算时间与迭代次数具有紧密的联系。当迭代1次时,本文方法运算时间比IRLS算法略大,这是由于基于迭代收缩算法的高分辨率Radon变换需要在迭代前对变换算子L进行一次广义逆(LTL)-1LT的计算,并将其储存于内存中,使后续迭代只需要计算矩阵向量相乘以及向量之间的运算即可,这一特性也是本文方法能够实现快速运算的核心所在。随着迭代次数的增加,本文方法运算所需时间变化平缓,而IRLS算法的运算时间随迭代次数的增加而陡然变化。通过对比可以看出,针对此模拟数据,当迭代次数超过20次后,本文方法的计算效率是常规IRLS算法的两倍左右。
|
|
表 1 两种Radon变换方法运算时间 |
选取中国西部M探区实际地震资料测试本文方法。M探区溶蚀孔洞和裂缝储层十分发育,利用传统的成像处理流程难以对储层内部的多种绕射目标体精确成像。
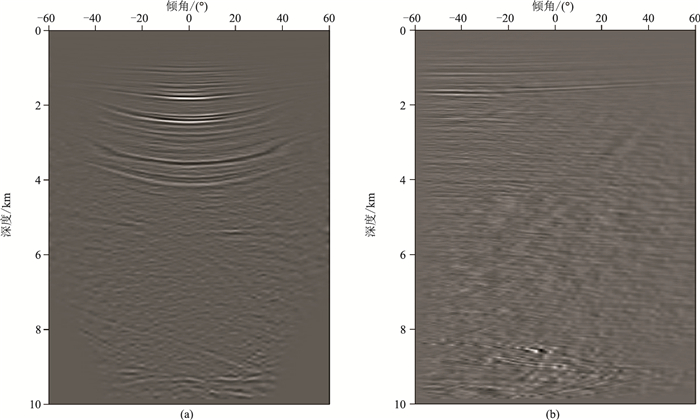
首先,利用本文方法对某一成像点下Kirchhoff叠前深度偏移(PSDM)产生的倾角域CIGs进行反射波与绕射波的分离测试,如图 10所示。
|
图 10 基于迭代高收缩分辨率Radon变换的CIGs波场分离 (a)实际地震资料的全波场CIGs;(b)波场分离后的绕射波CIGs |
图 10a和10b分别为分离前实际地震资料的倾角域CIGs和经过本文方法分离后的绕射波CIGs。从图中可以看出,全波场CIGs中的强反射能量被明显压制,尽管在分离后的绕射波CIGs中(图 10b)无法清晰地观察到分离出的弱绕射能量,但是强能量的反射同相轴被明显削弱,说明了本文方法分离反射波与绕射波是有效的。
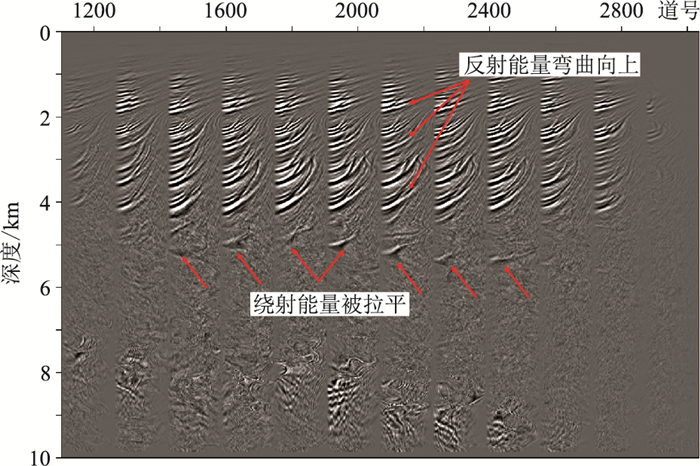
进一步将本文方法应用于该地区Inline1320测线的倾角域CIGs,图 11显示了测线Inline1320的0~60°倾角域CIGs。由图可见,强反射波能量呈双曲线形态,绕射能量则呈水平直线或者曲率较小的拟线性同相轴。
|
图 11 Inline1320测线倾角域CIGs(0~60°) |
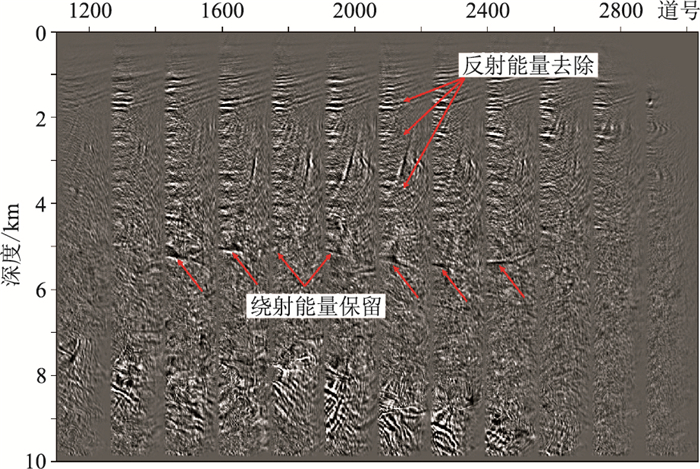
图 12为经过Radon变换压制反射波后分离得到的绕射波倾角域CIGs。由图可见,经过本文方法处理后,大部分强反射能量同相轴被去除,而同一深度点的绕射波被较好地保留。
|
图 12 Inline1320测线Radon变换后的倾角域CIGs(0~60°) |
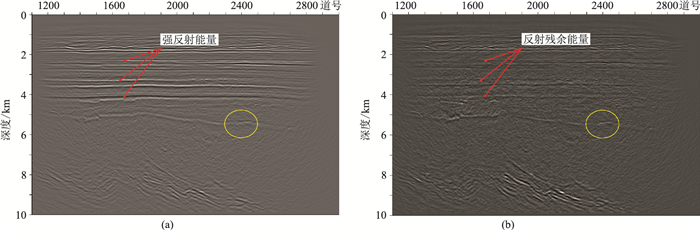
该测线波场分离前的PSDM剖面如图 13a所示,利用本文方法分离的绕射波成像剖面如图 13b所示。在原始叠加剖面(图 13a)中,由于强反射能量的干扰,绕射体的位置难以识别。从图 13b中可以看出,上覆地层反射能量残余多,中深层反射残余较弱(几乎全部去除),主要原因在于上覆地层采集脚印明显,前期CDP道集预测去除反射能量不多,而下伏地层反射波能量得到准确压制。相较于原始偏移剖面,经过绕射分离后得到的绕射波成像剖面(图 13b)中,强反射同相轴被滤除,淹没的绕射体位置凸显出来(图 13b中黄色圆圈所示)。因此,经过迭代收缩高分辨率Radon变换方法的处理,绕射体的成像结果被凸显出来,说明本文方法适用于地下小尺度非均质体的识别和精确定位。
|
图 13 中国西部M探区实际资料(Inline1320测线)处理结果 (a)波场分离前PSDM剖面;(b)波场分离后绕射波成像剖面 |
本文基于迭代收缩高分辨率Radon变换的绕射波分离成像方法,利用反射波与绕射波在倾角域CIGs中的的运动学特征差异,并通过构建一个常速介质模型以说明两者之间的差异,进一步利用反射波与绕射波的形态差异在倾角域CIGs中分离绕射波场。根据模拟数据和实际地震资料处理结果得出以下结论:
(1) 在倾角域CIGs中,反射波同相轴总是呈现开口向上的“笑脸”状曲线,绕射同相轴则表现为拟线性,根据两者曲线形态的差异可以实现波场分离;
(2) 迭代收缩高分辨率Radon变换对反射和绕射波同相轴在Radon域的聚焦能力强,分辨率高,且在计算过程中采用收缩阈值算法,不仅提高了反演的收敛速度,而且较常规方法具有更好的抗噪性;
(3) 本文方法虽然能够有效分离反射波与绕射波,并利用绕射信息揭示了地下小规模绕射体,可提高地震资料解释的精度,但由于算法中需要较多的人工干预(如迭代步长、阈值算子等的选取),存在一定的局限性。
| [1] |
Klem K, Kovalevsky G. On the intensity of waves diffracted on the edge[J]. Geology and Geophysics, 1972, 5: 82-92. |
| [2] |
Krey T. The significance of diffraction in the investigation of faults[J]. Geophysics, 1952, 17(4): 843-858. DOI:10.1190/1.1437815 |
| [3] |
Landa E, Shtivelman V, Gelchinsky B. A method for diffracted waves on common-offset sections[J]. Geophysical Prospecting, 1987, 35(4): 359-373. DOI:10.1111/j.1365-2478.1987.tb00823.x |
| [4] |
Khaidukov V, Landa E, Moser T J. Diffraction imaging by focusing-defocusing: An outlook on seismic superresolution[J]. Geophysics, 2004, 69(6): 1478-1490. DOI:10.1190/1.1836821 |
| [5] |
Nowak E J, Imhof M G. Diffractor localization via weighted Radon transforms[J]. SEG Technical Program Expanded Abstracts, 2004, 23: 2108-2111. |
| [6] |
Bansal R, Imhof M G. Diffraction enhancement in pre-stackseismic data[J]. Geophysics, 2005, 70(3): V73-V79. DOI:10.1190/1.1926577 |
| [7] |
Taner M T, Fomel S, Landa E. Separation and imaging of seismic diffractions using plane-wave decomposition[J]. SEG Technical Program Expanded Abstracts, 2006, 25: 2401-2405. |
| [8] |
黄建平, 李振春, 孔雪, 等. 基于PWD的绕射波波场分离成像方法综述[J]. 地球物理学进展, 2012, 27(6): 2499-2510. HUANG Jianping, LI Zhenchun, KONG Xue, et al. The review of the wave filed separation method about reflection and diffraction based on the PWD[J]. Progress in Geophysics, 2012, 27(6): 2499-2510. |
| [9] |
孔雪, 李振春, 黄建平, 等. 基于平面波记录的绕射目标成像方法研究[J]. 石油地球物理勘探, 2012, 47(4): 674-681. KONG Xue, LI Zhenchun, HUANG Jianping, et al. Research of diffraction imaging based on plane-wave record[J]. Oil Geophysical Prospecting, 2012, 47(4): 674-681. |
| [10] |
刘玉金, 李振春, 黄建平, 等. 绕射波叠前时间偏移速度分析及成像[J]. 地球物理学进展, 2013, 28(6): 3022-3029. LIU Yujing, LI Zhenchun, HUANG Jianping, et al. Time migration velocity analysis and imaging before diffraction wave stack[J]. Progress in Geophysics, 2013, 28(6): 3022-3029. |
| [11] |
朱生旺, 李佩, 宁俊瑞. 局部倾角滤波和预测反演联合分离绕射波[J]. 地球物理学报, 2013, 56(1): 280-288. ZHU Shengwang, LI Pei, NING Junrui. Local dip filtering and predictive inversion combined with a separate diffraction wave[J]. Chinese Journal of Geophy-sics, 2013, 56(1): 280-288. |
| [12] |
Kanasewich E R, Phadke S M. Imaging discontinuities on seismic sections[J]. Geophysics, 1988, 53(3): 334-345. DOI:10.1190/1.1442467 |
| [13] |
Berkovitch A, Belfer I, Hassin Y, et al. Diffraction ima-ging by multifocusing[J]. Geophysics, 2009, 74(6): : WCA75-WCA81. DOI:10.1190/1.3198210 |
| [14] |
Dell S, Gajewski D. Common-reflection-surface-based workflow for diffraction imaging[J]. Geophysics, 2011, 76(5): S187-S195. DOI:10.1190/geo2010-0229.1 |
| [15] |
Asgedom E, Gelius J, Austeng A, et al. A new approach to post-stack diffraction separation[J]. SEG Technical Program Expanded Abstracts, 2011, 30: 3861-3865. |
| [16] |
Landa E, Fomel S, Reshef M. Separation, imaging, and velocity analysis of seismic diffractions using migrated dip-angle gathers[J]. SEG Technical Program Expanded Abstracts, 2008, 27: 2176-2180. |
| [17] |
Zhu X, Wu R S. Imaging diffraction points using the local image matrices generated in prestack migration[J]. Geophysics, 2010, 75(1): S1-S9. DOI:10.1190/1.3277252 |
| [18] |
Klokov A, Fomel S. Separation and imaging of seismic diffractions using migrated dip-angle gathers[J]. Geophysics, 2012, 77(6): S131-S143. DOI:10.1190/geo2012-0017.1 |
| [19] |
Decker L, Klokov A. Diffraction extraction by plane-wave destruction of partial images[J]. SEG Technical Program Expanded Abstracts, 2014, 33: 3862-3867. |
| [20] |
Zhang J F, Zhang J J. Diffraction imaging using shot and opening-angle gathers: A prestack time migration approach[J]. Geophysics, 2014, 79(2): S23-S33. DOI:10.1190/geo2013-0016.1 |
| [21] |
黄建平, 曹晓莉, 李振春, 等. 最小二乘逆时偏移在近地表高精度成像中的应用[J]. 石油地球物理勘探, 2014, 49(1): 107-112. HUANG Jianping, CAO Xiaoli, LI Zhenchun, et al. Least square reverse time migration in high resolution imaging of near surface[J]. Oil Geophysical Prospecting, 2014, 49(1): 107-112. |
| [22] |
李振春, 李闯, 黄建平, 等. 基于先验模型约束的最小二乘逆时偏移方法[J]. 石油地球物理勘探, 2016, 51(4): 738-744. LI Zhenchun, LI Chuang, HUANG Jianping, et al. Regularized least-squares reverse time migration with prior model[J]. Oil Geophysical Prospecting, 2016, 51(4): 738-744. |
| [23] |
刘梦丽, 黄建平, 李闯, 等. 基于角度滤波成像的最小二乘逆时偏移[J]. 石油地球物理勘探, 2018, 53(3): 469-477. LIU Mengli, HUANG Jianping, LI Chuang, et al. Least-squares reverse time migration based on the angular filtering imaging condition[J]. Oil Geophysical Prospecting, 2018, 53(3): 469-477. |
| [24] |
汪天池, 刘少勇, 顾汉明, 等. 倾角域逆时偏移绕射波成像方法[J]. 石油地球物理勘探, 2020, 55(3): 591-598. WANG Tianchi, LIU Shaoyong, GU Hanming, et al. Seismic diffraction imaging by reverse time migration in dip angle domain[J]. Oil Geophysical Prospecting, 2020, 55(3): 591-598. |
| [25] |
Reshef M, Landa E. Post-stack velocity analysis in the dip-angle domain using diffractions[J]. Geophysical Prospecting, 2009, 57(5): 811-821. DOI:10.1111/j.1365-2478.2008.00773.x |
| [26] |
Li X F, Huang J P, Li Z C, et al. The research of diffraction migration velocity analysis method[C]. Extended Abstracts of 75th EAGE Conference and Exhibition, 2013.
|
| [27] |
Lu W K. An accelerated sparse time-invariant Radon transform in the mixed frequency-time domain based on iterative 2D model shrinkage[J]. Geophysics, 2013, 78(4): V147-V155. DOI:10.1190/geo2012-0439.1 |



 罗腾腾, 北京市海淀区学院路20号中国石油勘探开发研究院, 100083。Email:
罗腾腾, 北京市海淀区学院路20号中国石油勘探开发研究院, 100083。Email: 