② 青岛海洋科学与技术试点国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266061;
③ 浙江大学地球科学学院, 浙江杭州 310027;
④ 自然资源部第二海洋研究所海底科学重点实验室, 浙江杭州 310012;
⑤ 东方地球物理公司物探技术研究中心, 河北涿州 072751;
⑥ 东方地球物理公司研究院, 河北涿州 072751
② Functional Laboratory for Marine Mineral Resources Assessment and Prospecting, Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266061, China;
③ School of Earth Sciences, Zhejiang University, Hangzhou, Zhejiang 310027, Chian;
④ Key laboratory of Submarine Geosciences, Second Institute of Oceanography, Ministry of Natural Resoures, Hangzhou, Zhejiang 310012, China;
⑤ BGP Recearch & Development Center, CNPC, Zhuozhou, Hebei 072751, China;
⑥ Geophysical Research Institute, BGP, CNPC, Zhuozhou, Hebei 072751, China
全波形反演(Full Waveform Inversion,FWI)是利用地震记录的全波形信息,通过匹配模拟记录与实际记录反演地下介质参数的一种高分辨率建模方法。Tarantola[1-2]最先提出了时间域全波形反演方法,该方法基于广义最小二乘理论,使用理论记录与实际记录的残差来构建目标函数。此后,全波形反演得到了全面的发展。Bunks等[3]提出了时间域多尺度反演,降低了反演的非线性影响;Pratt[4]提出了在频率域进行全波形反演,不需要对地震记录进行预处理,且使用有限个频率信息即可得到高精度的反演结果;Sirgue等[5]综合时间域反演和频率域反演的优势,提出了时间—频率混合域反演方法,避免了因时间域求梯度所需要的震源波场重构以及频率域正演所需计算机内存过大等问题。
全波形反演是强非线性问题,在初始模型不准的情况下很容易陷入局部极小。实际生产中,采集资料由于种种原因,往往缺少低频信息,导致构建宏观反演模型十分困难。解决该问题最直接的办法就是通过其他方法或者使用额外的数据为全波形反演提供一个精确的初始模型[6-8],但许多情况下这不现实。为此,许多学者从全波形反演本身出发,提出了诸多改进策略。Bozda等[9]首次将希尔伯特变换应用于全波形层析成像,构建了基于观测记录与模拟记录之间包络比和瞬时相位差值的失配函数,有效降低了反演的非线性;基于包络的性质,Chi等[10]和Wu等[11]完善和发展了基于包络的全波形反演方法;Huang等[12]和Song等[13]将其应用于弹性波,发展了包络弹性波全波形反演。之后,该方法被得到进一步发展[14-17]。Shin等[18-19]首次提出在拉普拉斯域进行全波形反演,利用经过衰减的信号包含更高比重的低频信息这一特性,有效解决了低频缺失时的初始模型建立问题,并比较了不同的目标函数在频率域和拉普拉斯域中各自的特性;其后,Shin等[20]在拉普拉斯域反演的基础上,提出了拉普拉斯—频率域全波形反演;Ha等[21]对比了在频率域和拉普拉斯域的反演结果,再次证实了在缺失低频的情况下,在拉普拉斯域可以反演出模型的大尺度构造,进而为频率域反演提供良好的初始模型。Ha等[22-23]将拉普拉斯域声波全波形反演应用于陆地合成资料和海洋实际资料,并展示了信号经过衰减处理后存在零频率和低频率的证据,证明了这种低频信息的有效性。在此基础上,Kim等[24]提出了时间—拉普拉斯—频率域声波全波形反演,Jun等[25]将该方法用于弹性波;近年来,国内其他学者对该方法也做了一些相应的研究[26-27]。
另外,还有一种研究思路是降低全波形反演的非线性,降低陷入局部极小值的可能性,从而在缺失低频或者初始模型不准确的情况下,反演依然能逼近正确结果。Choi等[28]提出的基于全局互相关全波形反演可有效降低反演的非线性,其强调的是记录之间整体的相关程度,并非是记录中点与点的匹配程度;Liu等[29]详细对比了全局互相关目标函数与L2范数目标函数之间的差异,说明了互相关目标函数的优势;Tao等[30]将全局互相关应用到了全波形层析,其反演结果同样优于基于旅行时的层析成像;李青阳等[31]将互相关与反射波波形反演相结合降低了反演的非线性。Luo等[32]建立了反褶积目标函数,与互相关目标函数类似,降低了陷入局部极小值的可能性,但相对而言对带限或非脉冲源的灵敏度降低。Warner等[33-35]建立了自适应波形反演理论,通过将维纳滤波器引入目标函数,寻找将两种记录相匹配的滤波器,再建立滤波器的目标函数,使其逐渐逼近零延迟的单位脉冲函数;Guasch等[36]将该方法推广到三维,并且在缺失低频的情况下得到了较好的反演结果。van Leeuwen等[37]提出了波形重构反演,将波动方程本身作为惩罚项引入到目标函数中,通过重构波场更新模型参数,将解空间扩展到了数据空间和模型空间,有效减小了局部极小值的影响;Li等[38]将该方法引入时间域,提出了时间域波形重构法,相比于频率域可有效减少计算成本。
针对如何在缺失低频信息的情况下建立较高精度的初始模型这一难题,本文建立了一种基于时域加权的拉普拉斯—频率域弹性波全波形反演方法(Time-Weighted Laplace-Frequency Domain Elastic Full Waveform Inversion,TWLF-EFWI)。该方法在时间—频率域弹性波全波形反演的基础上,通过引入拉普拉斯阻尼因子,降低了全波形反演对于初始模型的依赖程度,形成了时间—拉普拉斯—频率域的混合域全波形反演方法。TWLF-EFWI方法仍使用传统的L2范数作为目标函数,为消除因引入拉普拉斯阻尼因子带来的地震道能量不均衡、远炮检距地震道能量衰减严重的影响,在目标函数中引入了时域加权因子,消除了拉普拉斯阻尼因子的负面影响。Marmousi 2部分模型测试结果表明,在缺失低频信息以及初始模型精度较低的情况下,本文方法可得到含有模型宏观构造的反演结果,足以满足后续反演对初始模型的精度要求。
1 全波形反演基本理论 1.1 频率域弹性波全波形反演全波形反演可以描述为一个基于地震全波场模拟的数据拟合过程,目的是实现正演记录和实际观测记录的完全拟合,也可以将全波形反演重新转换为线性化的最小二乘问题。
在频率域,波动方程矩阵形式可以表示为
| $ \mathit{\boldsymbol{AU}} = \mathit{\boldsymbol{S}} $ | (1) |
式中:A为阻抗矩阵;U为全部网格点的波场值所组成的列向量;S为震源项。
基于广义最小二乘的全波形反演目标函数定义为
| $ E(\boldsymbol{m})=\frac{1}{2} \sum\limits_{i=1}^{N_{\mathrm{s}}} \Delta \boldsymbol{d}_{i}^{\mathrm{T}} \Delta \boldsymbol{d}_{i}^{*} $ | (2) |
式中:m为模型参数;Ns为总炮数;Δd=dcal-dobs,为模拟地震记录dcal与实际地震记录dobs的差;上标“*”表示矩阵的伴随形式。全波形反演就是从目标函数出发,求解模型的更新量,然后通过对模型的迭代更新,使目标函数达到最小,或者使前后两次的目标函数的相对误差达到限定值,进而得到与其对应的模型参数的最优解。
将式(2)中的目标函数对m求导,可以导出目标函数在频率域关于模型参数的梯度为
| $ \begin{aligned} \nabla E(\boldsymbol{m}) &=\sum\limits_{i=1}^{N_{\mathrm{s}}} \operatorname{Re}\left[\left(\frac{\partial \boldsymbol{d}^{\mathrm{cal}}}{\partial \boldsymbol{m}}\right)^{\mathrm{T}} \Delta \boldsymbol{d}^{*}\right] \\ &=\sum\limits_{i=1}^{N_{\mathrm{s}}} \operatorname{Re}\left[\boldsymbol{J}^{\mathrm{T}} \Delta \boldsymbol{d}^{*}\right] \end{aligned} $ | (3) |
式中J为Fréchet导数矩阵,可由波动方程两边同时对参数m求导得到
| $ \boldsymbol{J}=\boldsymbol{R} \frac{\partial \boldsymbol{U}}{\partial \boldsymbol{m}}=-\boldsymbol{R} \boldsymbol{A}^{-1} \frac{\partial \boldsymbol{A}}{\partial \boldsymbol{m}} \boldsymbol{U} $ | (4) |
式中R表示波场U到接收记录d的映射关系。则频率域梯度可表示为
| $ \nabla E(\boldsymbol{m})=\sum\limits_{i=1}^{N_{\mathrm{s}}} \operatorname{Re}\left(-\boldsymbol{U}^{\mathrm{T}} \frac{\partial \boldsymbol{A}}{\partial \boldsymbol{m}} \boldsymbol{A}^{-1} \boldsymbol{R}^{\mathrm{T}} \Delta \boldsymbol{d}^{*}\right) $ | (5) |
上式表明目标函数的梯度由正演波场U、阻抗矩阵对模型参数的导数∂A/∂m和以地震记录残差共轭为震源的正演波场A-1RTΔd*三部分组成。
对于二维弹性波方程,在频率域表达式为
| $ \left\{\begin{aligned} -\rho \omega^{2} U_{\mathrm{f} x}=& \frac{\partial}{\partial x}\left[(\lambda+2 \mu) \frac{\partial U_{\mathrm{f} x}}{\partial x}+\lambda \frac{\partial U_{\mathrm{f}z}}{\partial z}\right] \\ &+\frac{\partial}{\partial z}\left[\mu\left(\frac{\partial U_{\mathrm{f}z}}{\partial x}+\frac{\partial U_{\mathrm{f} x}}{\partial z}\right)\right]+F_{x} \\ -\rho \omega^{2} U_{\mathrm{f}z}=& \frac{\partial}{\partial z}\left[(\lambda+2 \mu) \frac{\partial U_{\mathrm{f}z}}{\partial z}+\lambda \frac{\partial U_{\mathrm{f} x}}{\partial x}\right] \\ &+\frac{\partial}{\partial x}\left[\mu\left(\frac{\partial U_{\mathrm{f}z}}{\partial x}+\frac{\partial U_{\mathrm{f} x}}{\partial z}\right)\right]+F_{z} \end{aligned}\right. $ | (6) |
式中:Ufx和Ufz分别为频率域速度波场的水平和垂直分量;Fx和Fz为对应的频率域震源项;ω为角频率;ρ为密度;λ和μ为拉梅常数。
联合式(5)和式(6),可得目标函数关于拉梅常数的梯度在频率域的表达式
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial E}}{{\partial \lambda }} = - {\mathop{\rm Re}\nolimits} \left[ {\left( {\frac{{\partial {U_{{\rm{f}}x}}}}{{\partial x}} + \frac{{\partial {U_{{\rm{f}}z}}}}{{\partial z}}} \right)\left( {\frac{{\partial {{\tilde U}_{{\rm{f}}x}}}}{{\partial x}} + \frac{{\partial {{\tilde U}_{{\rm{f}}z}}}}{{\partial z}}} \right)} \right]}\\ {\frac{{\partial E}}{{\partial \mu }} = - {\mathop{\rm Re}\nolimits} \left[ {\left( {\frac{{\partial {U_{{\rm{f}}x}}}}{{\partial z}} + \frac{{\partial {U_{{\rm{f}}z}}}}{{\partial x}}} \right)\left( {\frac{{\partial {\rm{ }}{{\tilde U}_{{\rm{f}}x}}}}{{\partial z}} + \frac{{\partial {{\tilde U}_{{\rm{f}}z}}}}{{\partial x}}} \right) + } \right.}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {2\left( {\frac{{\partial {U_{{\rm{f}}x}}}}{{\partial x}}\frac{{\partial {{\tilde U}_{{\rm{f}}x}}}}{{\partial x}} + \frac{{\partial {U_{{\rm{f}}z}}}}{{\partial z}}\frac{{\partial {\rm{ }}{{\tilde U}_{{\rm{f}}z}}}}{{\partial z}}} \right)} \right]} \end{array}} \right. $ | (7) |
式中:
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial E}}{{\partial {v_{\rm{P}}}}} = 2\rho {v_{\rm{P}}}\frac{{\partial E}}{{\partial \lambda }}}\\ {\frac{{\partial E}}{{\partial {v_{\rm{S}}}}} = 2\rho {v_{\rm{S}}}\frac{{\partial E}}{{{\partial _\mu }}} - 4\rho {v_{\rm{S}}}\frac{{\partial E}}{{\partial \lambda }}} \end{array}} \right. $ | (8) |
式中vP和vS分别为纵波速度和横波速度。
1.2 拉普拉斯—频率域弹性波全波形反演拉普拉斯—频率域的二维弹性波方程与频率域的二维弹性波方程极其相似,为
| $ \left\{\begin{aligned} -\rho \ s^{2} U_{\mathrm{L} x}=& \frac{\partial}{\partial x}\left[(\lambda+2 \mu) \frac{\partial U_{\mathrm{L} x}}{\partial x}+\lambda \frac{\partial U_{\mathrm{L} z}}{\partial z}\right]+\\ & \frac{\partial}{\partial z}\left[\mu\left(\frac{\partial U_{\mathrm{L} z}}{\partial x}+\frac{\partial U_{\mathrm{L} x}}{\partial z}\right)\right]+L_{x} \\ -\rho \ s^{2} U_{\mathrm{L} z}=& \frac{\partial}{\partial z}\left[(\lambda+2 \mu) \frac{\partial U_{\mathrm{L} z}}{\partial z}+\lambda \frac{\partial U_{\mathrm{L} x}}{\partial x}\right]+\\ & \frac{\partial}{\partial x}\left[\mu\left(\frac{\partial U_{\mathrm{L} z}}{\partial x}+\frac{\partial U_{\mathrm{L} x}}{\partial z}\right)\right]+L_{z} \end{aligned}\right. $ | (9) |
式中:ULx和ULz分别为拉普拉斯—频率域波场的水平和垂直分量;Lx和Lz为对应的拉普拉斯—频率域震源;s=σ+iω,其中σ为拉普拉斯衰减常数。
对比式(9)与式(6)可以发现,二者的唯一区别是ω与s,所以拉普拉斯—频率域也可以看作是“复频率域”。两个域的目标函数梯度也具有相同的形式,在拉普拉斯—频率域具体形式为
| $ \left\{\begin{array}{l} \frac{\partial E}{\partial \lambda}=-\operatorname{Re}\left[\left(\frac{\partial U_{\mathrm{L} x}}{\partial x}+\frac{\partial U_{\mathrm{L} z}}{\partial z}\right)\left(\frac{\partial \widetilde{U}_{\mathrm{L} x}}{\partial x}+\frac{\partial \tilde{U}_{\mathrm{L} z}}{\partial z}\right)\right] \\ \frac{\partial E}{\partial \mu}=-\operatorname{Re}\left[\left(\frac{\partial U_{\mathrm{L} x}}{\partial z}+\frac{\partial U_{\mathrm{L} z}}{\partial x}\right)\left(\frac{\partial \widetilde{U}_{\mathrm{L} x}}{\partial z}+\frac{\partial \widetilde{U}_{\mathrm{L} z}}{\partial x}\right)+\right. \\ \ \ \ \ \ \ \ \ \ \ \ \ \left.2\left(\frac{\partial U_{\mathrm{L} x}}{\partial x} \frac{\partial \tilde{U}_{\mathrm{L} x}}{\partial x}+\frac{\partial U_{\mathrm{L} z}}{\partial z} \frac{\partial \tilde{U}_{\mathrm{L}}}{\partial z}\right)\right] \end{array}\right. $ | (10) |
式中:
同样,根据式(8),可得目标函数关于纵波速度和横波速度的梯度。
1.3 混合域弹性波全波形反演全波形反演在时间域和频率域里的基本理论是相通的,二者并无差异。时间—频率混合域全波形反演就是在时间域模拟正、反传波场,然后转换到频率域计算梯度。两种域的结合只需使用离散傅里叶变换(DFT)即可实现,即在时间域求取波场时,在时间循环中加入DFT,当循环结束时也就得到了对应的频率域的单频波场,之后再用频率域单频波场计算梯度。混合域反演结合了时间域模拟波场的高效性和频率域计算梯度的灵活性,其流程如图 1所示。
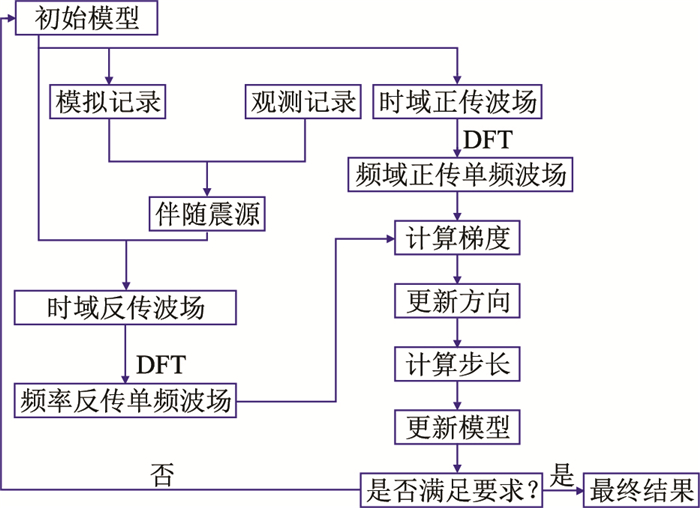
|
图 1 时间—频率域全波形反演流程 |
DFT和逆离散傅里叶变换(IDFT)的表达式为
| $ \left\{\begin{array}{l} U_{\mathrm{F}}\left(\omega_{n}\right)=\sum\limits_{k=0}^{N_{\mathrm{T}}} \mathrm{e}^{-\omega_{n} k \Delta t} u(k \Delta t) \\ u(k \Delta t)=\sum\limits_{n=0}^{N_{\mathrm{F}}} \mathrm{e}^{\omega_{n} k \Delta t} U_{\mathrm{F}}\left(\omega_{n}\right) \end{array}\right. $ | (11) |
式中:u(kΔt)和UF(ωn)分别为时间域波场和频率域波场;Δt为时间采样间隔;NT为时间域序列长度;NF为频率域序列长度。
在上述混合域的基础上,使用拉普拉斯—频率域代替频率域,形成了时域—拉普拉斯—频率域的全波形反演(图 2)。与图 1流程不同的是,需要将DFT改为离散拉普拉斯变换(DLT)进行时域与拉普拉斯—频率域间的转换,并且在求取伴随震源时需要做一次DLT和逆离散拉普拉斯变换(IDLT)。另外本文将伴随震源在时域中进行了加权处理,后文会对此进行详细描述。DLT和IDLT的表达式为
| $ \left\{\begin{array}{l} U_{\mathrm{L}}\left(s_{n}\right)=\sum\limits_{k=0}^{N_{\mathrm{T}}} \mathrm{e}^{-s_{n} k \Delta t} u(k \Delta t) \\ u(k \Delta t)=\sum\limits_{n=0}^{N_{\mathrm{L}}} \mathrm{e}^{s_{n} k \Delta t} U_{\mathrm{L}}\left(s_{n}\right) \end{array}\right. $ | (12) |
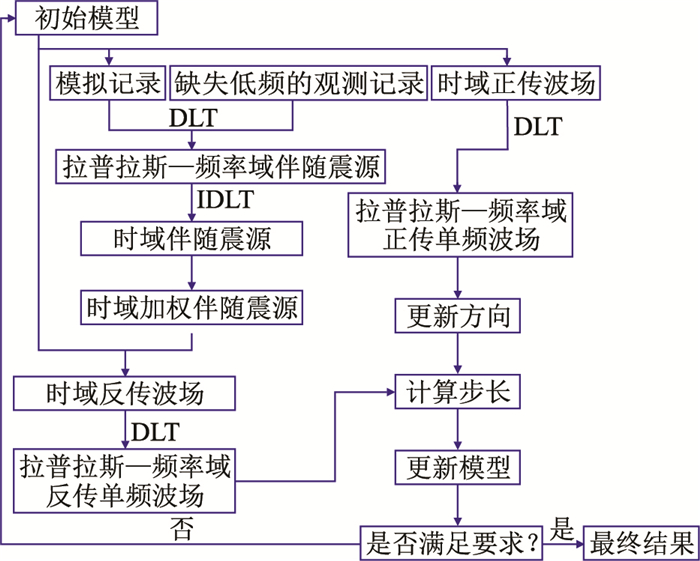
|
图 2 时间—拉普拉斯—频率域全波形反演流程 |
式中:UL(sn)为拉普拉斯—频率域波场;NL为拉普拉斯—频率域序列长度。
2 时域指数衰减波场相对于傅里叶变换,拉普拉斯变换只是增加了一个时间指数衰减项。正是这一指数衰减项,在拉普拉斯—频率域反演降低了对低频信息的依赖。
时间域信号u(t)的拉普拉斯变换为
| $ U(s)=\int_{0}^{\infty} u(t) \mathrm{e}^{-s t} \mathrm{~d} t=\int_{0}^{\infty} u(t) \mathrm{e}^{-\sigma t} \mathrm{e}^{-\mathrm{i} \omega t} \mathrm{~d} t $ | (13) |
将拉普拉斯变换中的衰减项单独取出,在时间域分析该项对信号频率的影响。时间域信号衰减可表示为
| $ \tilde{u}(t)=u(t) \mathrm{e}^{-\sigma t} $ | (14) |
在时间域的乘积等价于频率域的卷积,衰减后信号的离散傅里叶变换与原始信号和阻尼因子在频域的循环卷积相同,所以衰减后信号的零频、低频分量是原始信号频率分量的加权和。Shin等[20]曾描述衰减波场中包含“mirage-like”(海市蜃楼式)低频成分;Ha等[23]详细证明了这种衰减波场中确实存在零频和低频信息,并证明了这些信息的有效性,指出这些信息可以看作是原始信号的模糊处理结果。
为展示阻尼因子对低频成分的作用和效果,分别用地震子波及其振幅谱、地震记录及其相位谱加以说明。图 3对比了子波经不同阻尼因子衰减后的结果。原始子波(图 3a)是雷克子波经过切比雪夫滤波,去除了0~3Hz低频信息。阻尼因子为2、8和20的衰减子波如图 3b~图 3d所示。原始子波的最高波峰在中间,两侧分别有两个较小的波峰(图 3a);当阻尼因子为20时,子波的第一个波峰已经超过了中间的波峰值,第三个波峰几乎消失(图 3d)。子波衰减是随着时间变化的,到达时间越早振幅增益作用越强,到达时间越晚振幅抑制作用越强,而且阻尼因子越大,作用强度越大。
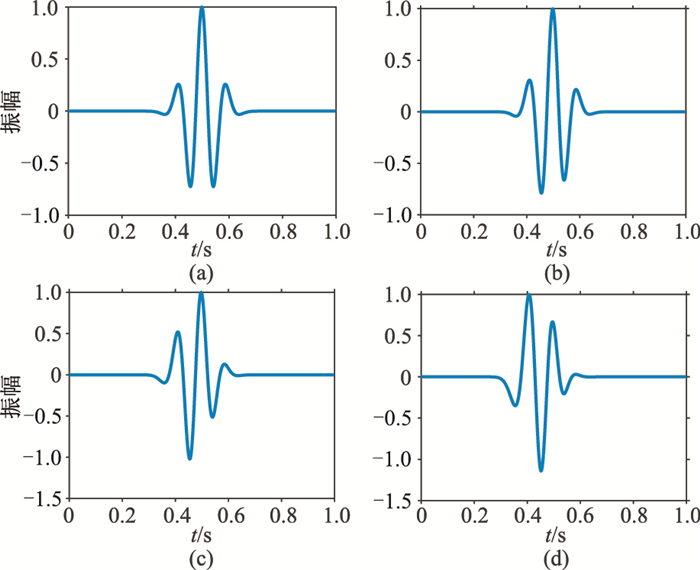
|
图 3 不同阻尼因子衰减后的子波归一化对比 (a)原始;(b)σ=2;(c)σ=8;(d)σ=20 |
图 4为图 3四个子波的振幅谱,可以看出,随着阻尼因子的增大,子波中不存在的0~3Hz低频信息慢慢出现,当阻尼因子为20时,频谱中0~3Hz频率成分已十分明显。所以,对信号进行阻尼衰减可以重构出低频信息。
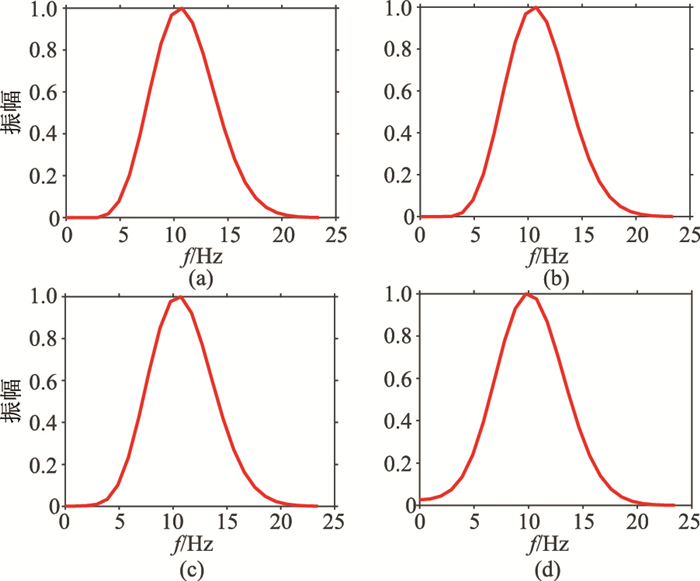
|
图 4 不同阻尼因子衰减后的子波归一化振幅谱对比 (a)原始;(b)σ=2;(c)σ=8;(d)σ=20 |
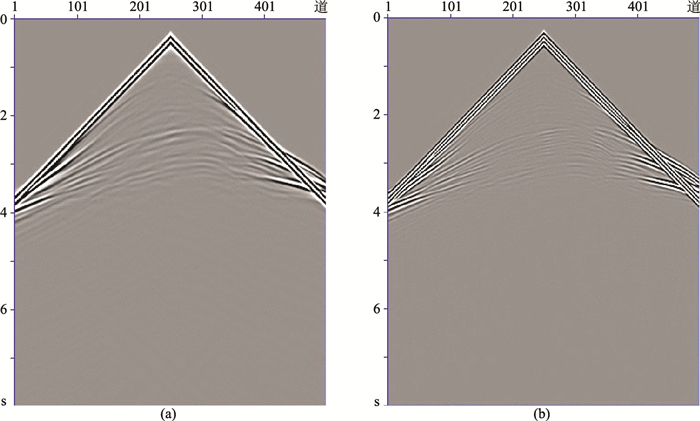
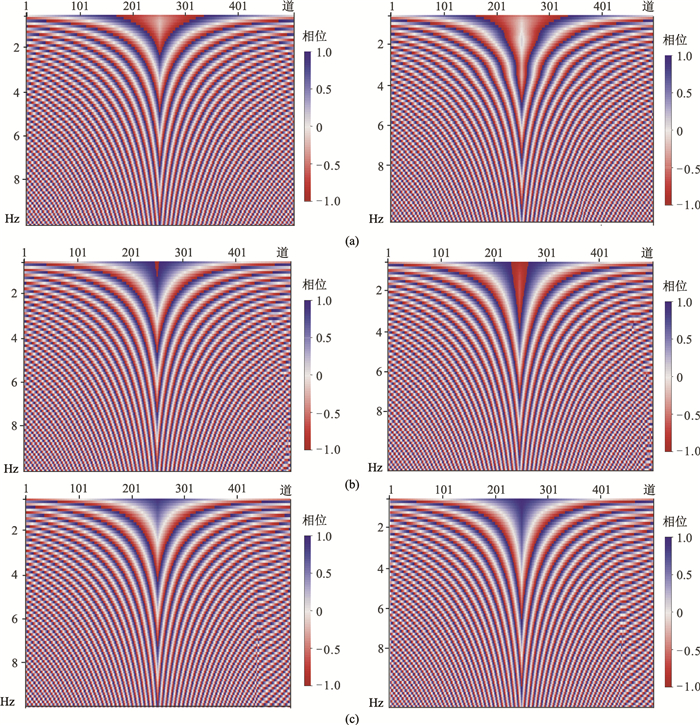
图 5a为单炮地震记录,图 5b为滤除3Hz以下频率成分后的记录,图 6为两个记录的相位谱。相比于原始记录,滤波后记录的相位谱(图 6b)中,0~3Hz的部分已经扭曲畸变。然后将两个记录分别进行阻尼因子为2、8和20的衰减,其相位谱如图 7所示。滤波记录经过衰减后的相位谱(图 7右),0~3Hz部分不再扭曲,与原始记录衰减后的相位谱(图 7左)明显相似。可以认为,经过衰减后的低频成分包含有地下介质的有效信息,可以使用该低频成分进行反演。
|
图 5 原始地震记录(a)及其滤除0~3Hz低频成分后的记录(b) |

|
图 6 原始地震记录(a)及其滤波后记录(b)的归一化相位谱 |
|
图 7 原始地震记录(左)及其滤波后记录(右)经不同阻尼因子衰减后的归一化相位谱 (a)σ=2;(b)σ=8;(c)σ=20 |
当地震记录中引入时间阻尼因子后,远炮检距地震道的能量会被衰减得很小。Shin等[20]为了消除阻尼因子产生的这一负面影响,采用了对数目标函数,即
| $ E_{\mathrm{L}}(\boldsymbol{m})=\frac{1}{2} \sum\limits_{i=1}^{N_{\mathrm{s}}}\left\|\ln \frac{\left(\boldsymbol{d}_{\mathrm{L}}^{\mathrm{cal}}\right)_{i}}{\left(\boldsymbol{d}_{\mathrm{L}}^{\mathrm{obs}}\right)_{i}}\right\|^{2} $ | (15) |
式中dLcal和dLobs分别为拉普拉斯—频率域的模拟和观测记录。
虽然对数目标函数可以消除指数衰减的负面影响,但对数目标函数本身存在固有的缺陷,即对小功率谱波场以及波场的振幅变化十分敏感,反演稳定性较差。为此,Jun等[39]提出了加权的L2目标函数,史才旺[27]提出了基于L1范数的对数目标函数。基于前人的研究,本文使用了基于时间域加权的L2目标函数。
本文的目标函数首先还是以传统的L2差值目标函数为核心,但是与前人不同的是,本方法在时间域进行加权处理,因为相较于频率域来说,时间域对于记录的操作更加方便和直观。时间域目标函数为
| $ E(\boldsymbol{m})=\frac{1}{2} \sum\limits_{i=1}^{N_{\mathrm{s}}} \sum\limits_{j=1}^{N_{\mathrm{r}}} \sum\limits_{t=1}^{T} W_{i, j, t}\left(d_{i, {j}, t}^{\mathrm{obs}}-d_{i, j, t}^{\mathrm{cal}}\right)^{2} $ | (16) |
式中:Nr为每炮道数;T每道样点数;Wi,j,t为加权系数。需要注意的是,此时的di,j,tcal、di,j,tobs不是初始的时间域记录,而是经过了拉普拉斯正、反变换后得到的时间域记录。该目标函数的梯度为
| $ \nabla E_{\mathrm{L}}(\boldsymbol{m})=\sum\limits_{i=1}^{N_{\mathrm{s}}} \sum\limits_{j=1}^{N_{\mathrm{t}}} \sum\limits_{t=1}^{T}\left[\frac{\partial d_{i, j, t}^{\mathrm{cal}}}{\partial \boldsymbol{m}}\right]^{\mathrm{T}} W_{i, j, t}\left(d_{i, j, t}^{\mathrm{obs}}-d_{i, j, t}^{\mathrm{col}}\right)^{*} $ | (17) |
不论是用对数目标函数还是加权系数目标函数,其目的都是消除阻尼因子的负面影响,增强远炮检距地震道的能量,使其在反演中发挥更大的作用。本文应用地震道差值模的倒数作为加权系数,即
| $ W_{i, j, t}=\frac{1}{\left|d_{i, j, t}^{\mathrm{cal}}-d_{i, j, t}^{\mathrm{obs}}\right|} $ | (18) |
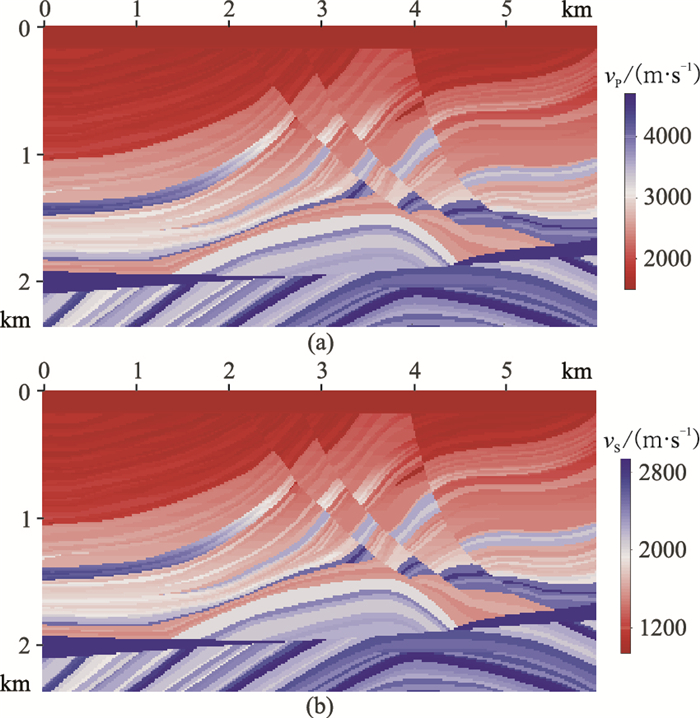
使用Marmousi 2部分模型测试本文的反演方法。为节约反演运算时间,将Marmousi 2纵波速度模型进行了截取和抽稀,得到了网格节点数为401×160、网格尺寸为15m×15m的模型作为真实纵波速度模型(图 8a);纵横波速度比设为1.7,获得其横波速度模型(图 8b);密度设为常数2000kg/m3。为提高反演效率,默认陆地浅部水平层的速度已知(vP=1500m/s)。
|
图 8 Marmousi 2部分模型 (a)纵波速度;(b)横波速度 |
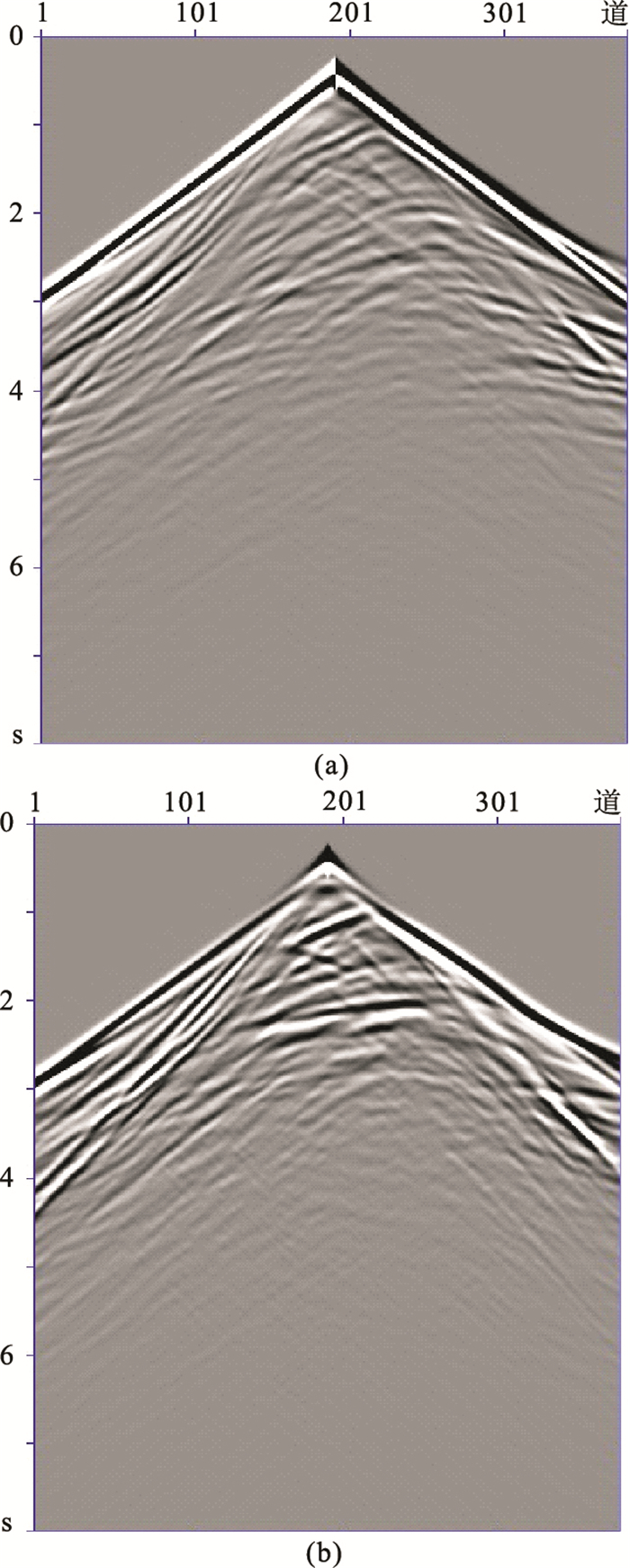
正演采用主频为6Hz的雷克子波作为激发震源,记录长度为6s,采样间隔为1.5ms。炮点和检波点均匀布置在地面,炮点范围为0~6km,共41炮;检波点范围为0.15~5.85km,每炮381道。图 9为模拟的第20炮两分量记录。
|
图 9 第20炮观测记录 (a)水平分量;(b)垂直分量 |
使用了如图 10所示的一维线性梯度模型作为初始模型,模型中不包含任何构造信息。采用多尺度反演策略,参照激发子波的主频,选取了4个频率组(表 1),前两组的频率低于3Hz,后两组的频率高于3Hz,每组分别迭代40次。

|
图 10 初始速度模型 (a)纵波速度;(b)横波速度 |
|
|
表 1 反演频率分组参数 |
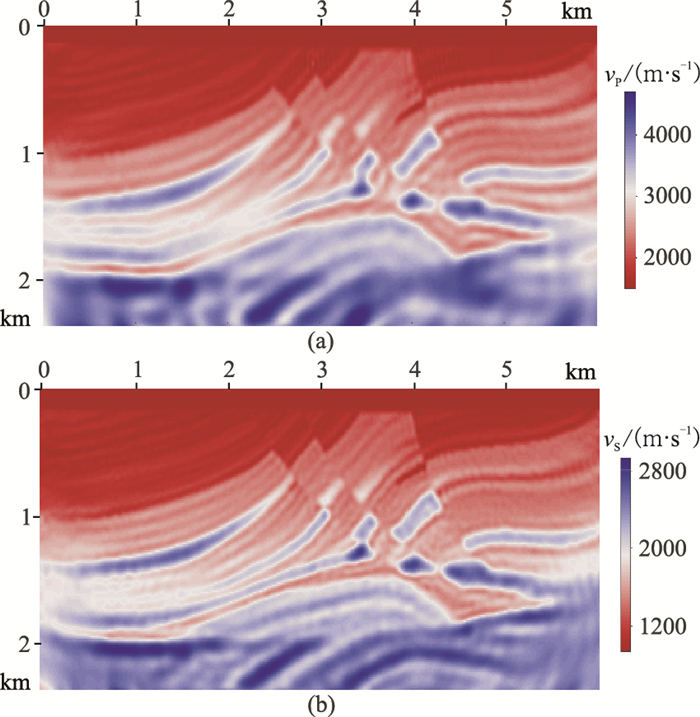
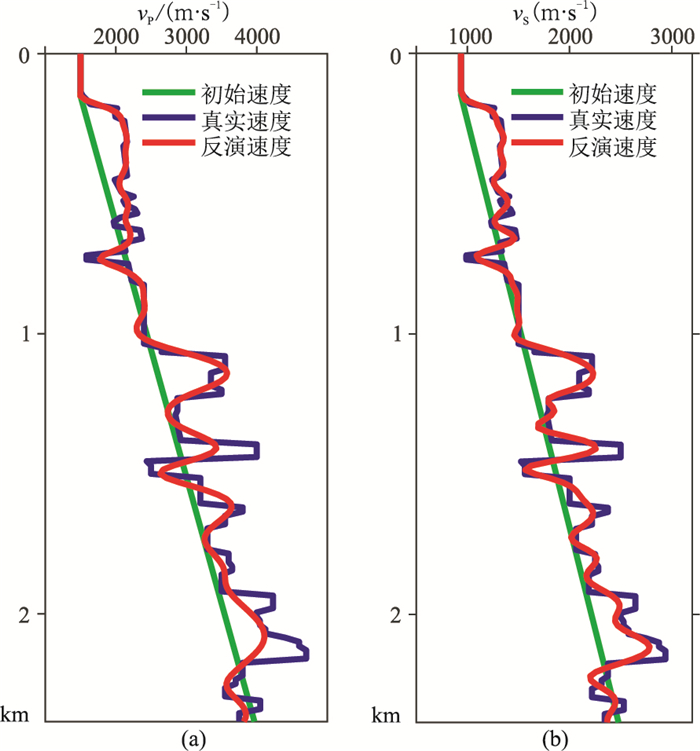
全频带数据常规时间—频率域反演最终结果如图 11所示。与图 8对比可以看出,反演结果十分接近真实模型,两侧层状介质、中部的异常体、深部的断裂和背斜构造都得到了精确重构。为了更为直观、定量地反映反演效果,抽取x=3.9km处(中部隆起处)的纵、横波速度曲线(图 12),可以发现,反演结果十分接近真实值。滤除模拟记录3Hz以下的成分,以图 10的一维线性梯度模型作为初始模型进行常规时域—频率域反演。因记录中的可用频率成分全部在3Hz以上,所以选取表 1中的后两组频率进行反演。
|
图 11 全频带常规时间—频率域反演结果 (a)纵波速度;(b)横波速度 |
|
图 12 x=3.9km处全频带常规时间—频率域反演速度曲线与真实及初始速度曲线的对比 (a)纵波速度;(b)横波速度 |
缺失低频成分的常规时间—频率域反演结果如图 13所示。因没有精确的低波数更新,所以很难避免周波跳跃现象,以至于陷入局部极值。与真实模型(图 8)对比可见,模型的大尺度构造几乎没有得到重构,只得到了一些小尺度的细节更新,并且产生了一些构造假象;断层、断块和模型深部的不整合面都不可识别。对比图 13与图 11可见,低频信息对常规反演的重要性。在初始模型精度不高的情况下,就需要使用记录中的低频信息重构出模型的大尺度构造,进而得到最终的高精度反演结果。若记录中缺失低频信息,反演就会极易陷入局部极小,导致反演失败。

|
图 13 缺失低频成分时的常规时间—频率域反演结果 (a)纵波速度;(b)横波速度 |
应用图 10的初始模型对缺失0~3Hz低频的模拟记录进行时间—拉普拉斯—频率域全波形反演。因低频已经通过拉普拉斯变换重构,所以可以使用0~3Hz的频率成分,经测试后选择了5个尺度,每个尺度进行10次迭代,具体参数如表 2所示。
|
|
表 2 复频率域反演频率分组及参数 |
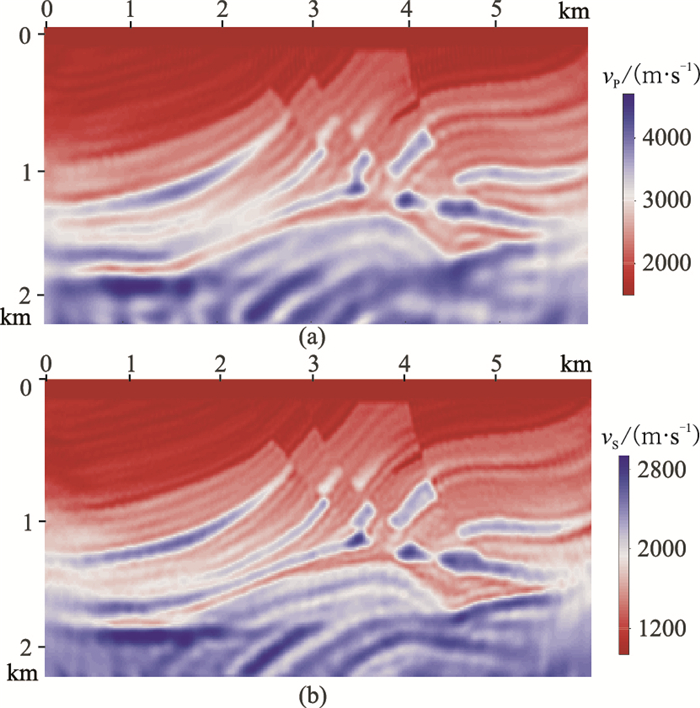
图 14为时间—拉普拉斯—频率域反演的结果,可以看到,模型中大尺度的构造已经得到恢复,其形状与真实模型的轮廓十分相近。然后将该反演结果作为初始模型,进行常规时间—频率域反演,反演尺度参数与表 1中的后两组相同。由图 15的反演结果可以看出,与真实模型十分接近,各个层位都得到了精确的反演,断层、断块等构造也十分清晰。与图 11相比,两种结果相差无几,说明该方法可以在缺失低频信息的情况下,达到含低频信息时的反演精度。为了测试本文方法对密度反演的适用性,将常密度修改为空间变化(图 16),与纵、横波速度同时参与反演。其他正、反演参数与以上相同。

|
图 14 缺失低频成分时的时间—拉普拉斯—频率域反演结果 (a)纵波速度;(b)横波速度 |
|
图 15 以时间—拉普拉斯—频率域反演结果为初始模型的常规时间—频率域反演结果 (a)纵波速度;(b)横波速度 |

|
图 16 密度模型 (a)真实密度;(b)初始密度 |
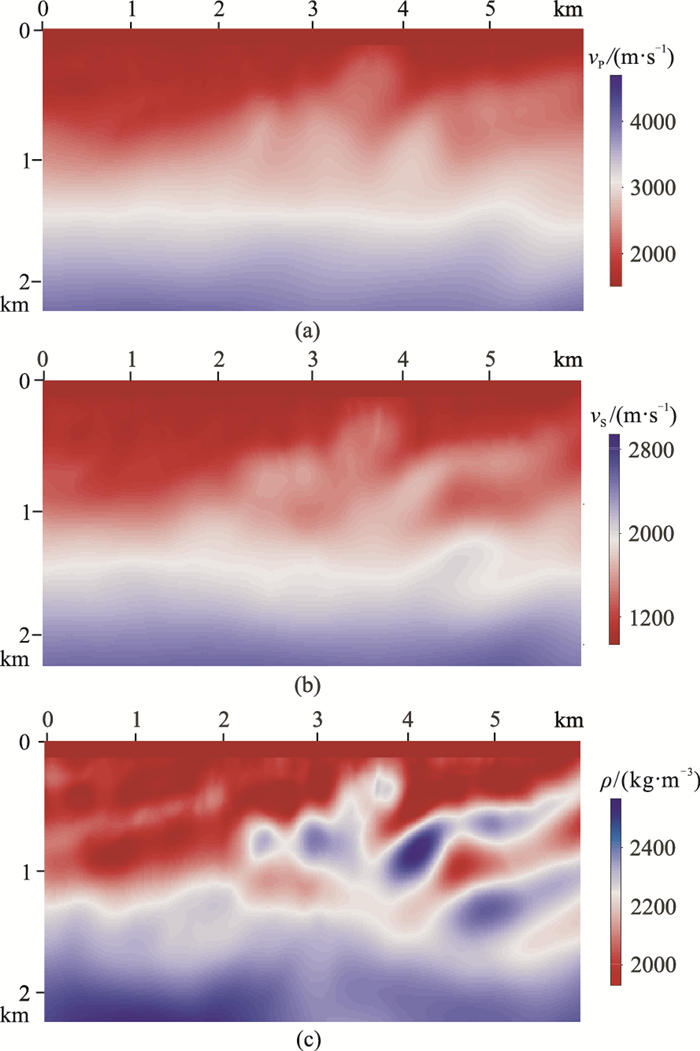
对缺失0~3Hz低频成分的记录进行时间—拉普拉斯—频率域全波形反演,结果如图 17所示,可以看出,纵、横波速度和密度模型的大尺度构造同样得到了比较好的恢复。将该反演结果作为初始模型,进行时间—频率域反演,结果如图 18所示。
|
图 17 缺失低频成分时的时间—拉普拉斯—频率域纵波速度(a)、横波速度(b)和密度(c)反演结果 |
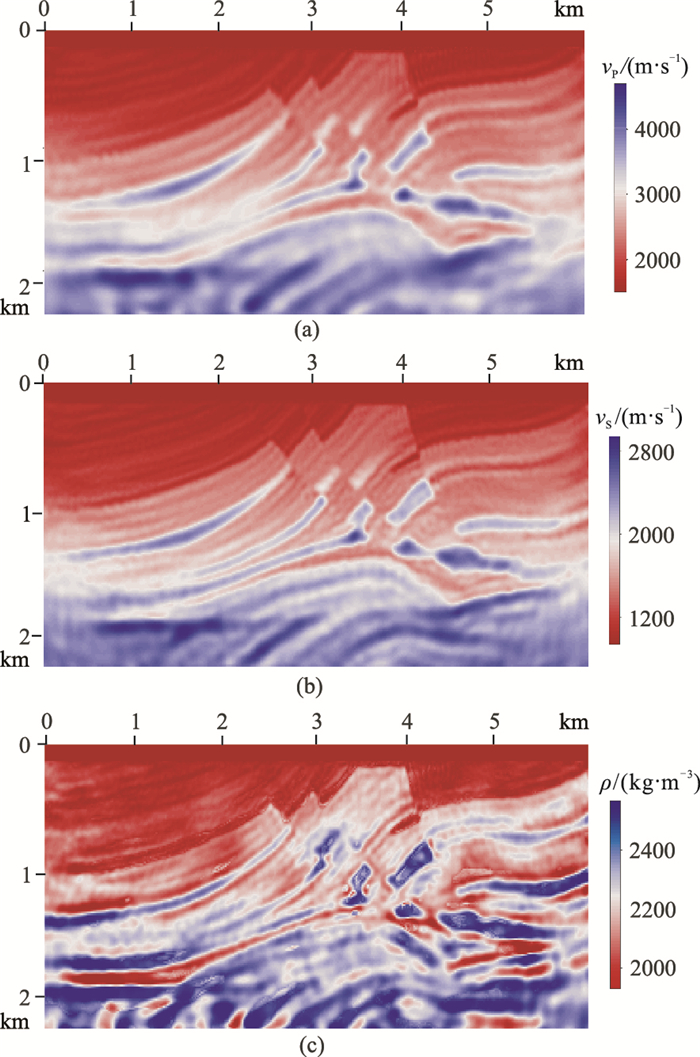
|
图 18 以时间—拉普拉斯—频率域反演结果为初始模型的纵波速度(a)、横波速度(b)和密度(c)常规时间—频率域反演结果 |
从图 18可以看出,纵、横波速度的反演结果同样十分接近真实模型。根据Ben-Hadj-Ali等[40]的模型误差公式,计算图 15的纵、横波速度相对误差分别为0.2437、0.2355,图 18的纵、横波速度相对误差分别为0.2497、0.2380,说明密度是否参与反演对纵、横波速度的反演结果几无影响,同时也说明本文方法同样适用于密度反演。对于密度项,由于与其他参数的耦合作用,其最终反演结果比速度反演略差,但是可以看出本文方法的密度反演结果仍有较高的可信度,可以体现出真实密度模型的构造形态与数值大小。上述测试结果表明,在缺失低频信息的情况下,本文方法仍然可以重构宏观构造模型,然后以此反演结果作为初始模型,进行常规时间—频率域反演,就可避免陷入局部极小,得到精确的反演结果。
5 结束语本文建立了一种基于时域加权的拉普拉斯—频率域的弹性波全波形反演方法。该方法在结合时域和频率域各自优势的基础上,通过引入拉普拉斯阻尼因子,降低了全波形反演对于低频信息的依赖性。改进的目标函数,通过时域加权的形式消除了拉普拉斯阻尼因子对地震记录能量的衰减影响,构建形式方便、灵活。另外在变密度情况下,该方法仍能得到较高精度的纵、横波速度反演结果,密度反演结果由于受到其他参数的串扰,使得其精度略低于速度反演结果,因此如何改善该方法的密度反演精度应是继续研究的方向。
| [1] |
Tarantola A. Inversion of seismic data in acoustic approximation[J]. Geophysics, 1984, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
| [2] |
Tarantola A. A strategy for nonlinear elastic inversion of seismic reflection data[J]. Geophysics, 1986, 51(5): 1893-1903. |
| [3] |
Bunks C, Saleck F M, Zaleski S, et al. Multiscale seismic waveform inversion[J]. Geophysics, 1995, 60(5): 1457-1473. DOI:10.1190/1.1443880 |
| [4] |
Pratt R G. Seismic waveform inversion in the frequency domain, Part 1: Theory and verification in a physical scale model[J]. Geophysics, 1999, 64(3): 888-901. DOI:10.1190/1.1444597 |
| [5] |
Sirgue L, Etgen J T, Albertin U. 3D frequency domain waveform inversion using time domain finite difference methods[C]. Extended Abstracts of 70th EAGE Conference & Exhibition, 2008, F022.
|
| [6] |
罗亚能, 黄捍东, 王玉梅, 等. 地震波形反演与测井联合的三维建模方法[J]. 石油地球物理勘探, 2016, 51(5): 947-954. LUO Yaneng, HUANG Handong, WANG Yumei, et al. Three-dimensional modeling based on integration of full wave inversion and well logging data[J]. Oil Geophysical Prospecting, 2016, 51(5): 947-954. |
| [7] |
刘定进, 胡光辉, 蔡杰雄, 等. 高斯束层析与全波形反演联合速度建模[J]. 石油地球物理勘探, 2019, 54(5): 1046-1056. LIU Dingjin, HU Guanghui, CAI Jiexiong, et al. A joint velocity model building method with Gaussian beam tomography and full waveform inversion for land seismic data[J]. Oil Geophysical Prospecting, 2019, 54(5): 1046-1056. |
| [8] |
张子良, 李振春, 张凯, 等. 地质模型约束的全波形速度建模反演及在复杂断块区的应用[J]. 石油地球物理勘探, 2020, 55(3): 599-606. ZHANG Ziliang, LI Zhenchun, ZHANG Kai, et al. Research of geological model-constrained FWI and application in complex fault-block zones[J]. Oil Geophysical Prospecting, 2020, 55(3): 599-606. |
| [9] |
Bozda E, Trampert J, Tromp J. Misfit functions for full waveform inversion based on instantaneous phase and envelope measurements[J]. Geophysical Journal International, 2011, 185(2): 845-870. DOI:10.1111/j.1365-246X.2011.04970.x |
| [10] |
Chi B, Dong L, Liu Y. Full waveform inversion me-thod using envelope objective function without low frequency data[J]. Journal of Applied Geophysics, 2014, 109(1): 36-46. |
| [11] |
Wu R S, Luo J, Wu B. Seismic envelope inversion and modulation signal model[J]. Geophysics, 2014, 79(3): WA13-WA24. DOI:10.1190/geo2013-0294.1 |
| [12] |
Huang C, Dong L, Chi B. Elastic envelope inversion using multicomponent seismic data with filtered-out low frequencies[J]. Applied Geophysics, 2015, 12(3): 362-377. DOI:10.1007/s11770-015-0499-8 |
| [13] |
Song J, Shi Y, Xu J, et al. Elastic full waveform inversion with envelope based misfit function[J]. SEG Technical Program Expanded Abstracts, 2015, 34: 1479-1484. |
| [14] |
敖瑞德, 董良国, 迟本鑫. 不依赖子波、基于包络的FWI初始模型建立方法研究[J]. 地球物理学报, 2015, 58(6): 1998-2010. AO Ruide, DONG Liangguo, CHI Benxin. Source-independent envelope-based FWI to build an initial model[J]. Chinese Journal of Geophysics, 2015, 58(6): 1998-2010. |
| [15] |
罗静蕊, 吴如山, 高静怀. 地震包络反演对局部极小值的抑制特性[J]. 地球物理学报, 2016, 59(7): 2510-2518. LUO Jingrui, WU Rushan, GAO Jinghuai. Local mi-nima reduction of seismic envelope inversion[J]. Chinese Journal of Geophysics, 2016, 59(7): 2510-2518. |
| [16] |
司道军. 基于包络目标函数的波形反演[D]. 山东青岛: 中国石油大学(华东), 2016.
|
| [17] |
陈俊霓. 基于全局相关与波场包络目标函数的全波形反演方法研究[D]. 陕西西安: 长安大学, 2019.
|
| [18] |
Shin C, Cha Y H. Waveform inversion in the Laplace domain[J]. Geophysical Journal International, 2008, 173(3): 922-931. DOI:10.1111/j.1365-246X.2008.03768.x |
| [19] |
Shin C, Ha W. A comparison between the behavior of objective functions for waveform inversion in the frequency and Laplace domains[J]. Geophysics, 2008, 73(5): 119-133. DOI:10.1190/1.2953978 |
| [20] |
Shin C, Cha Y H. Waveform inversion in the Laplace-Fourier domain[J]. Geophysical Journal Internatio-nal, 2009, 177(3): 1067-1079. DOI:10.1111/j.1365-246X.2009.04102.x |
| [21] |
Ha W, Cha Y H, Shin C. A comparison between Laplace domain and frequency domain methods for inverting seismic waveforms[J]. Exploration Geophy-sics, 2010, 41(3): 189-197. DOI:10.1071/EG09031 |
| [22] |
Ha W, Pyun S, Yoo J, et al. Acoustic full waveform inversion of synthetic land and marine data in the Laplace domain[J]. Geophysical Prospecting, 2010, 58(6): 1033-1047. |
| [23] |
Ha W, Shin C. Proof of the existence of both zero- and low-frequency information in a damped wavefield[J]. Journal of Applied Geophysics, 2012, 83(4): 96-99. |
| [24] |
Kim Y, Shin C, Calandra H, et al. An algorithm for 3D acoustic time-Laplace-Fourier-domain hybrid full waveform inversion[J]. Geophysics, 2013, 78(4): R151-R166. DOI:10.1190/geo2012-0155.1 |
| [25] |
Jun H, Kim Y, Shin J, et al. Laplace-Fourier-domain elastic full-waveform inversion using time-domain modeling[J]. Geophysics, 2014, 79(5): R195-R208. DOI:10.1190/geo2013-0283.1 |
| [26] |
陈浩. Laplace-Fourier域标量波全波形反演方法研究[D]. 山东青岛: 中国石油大学(华东), 2017.
|
| [27] |
史才旺. 二维混合域弹性波全波形反演研究[D]. 山东青岛: 中国海洋大学, 2018.
|
| [28] |
Choi Y, Alkhalifah T. Application of multi-source waveform inversion to marine streamer data using the global correlation norm[J]. Geophysical Prospecting, 2012, 60(4): 748-758. DOI:10.1111/j.1365-2478.2012.01079.x |
| [29] |
Liu Y, Teng J, Xu T, et al. Robust time-domain full waveform inversion with normalized zero-lag cross-correlation objective function[J]. Geophysical Journal International, 2016, 209(1): 106-122. |
| [30] |
Tao K, Grand S P, Niu F. Full-waveform inversion of triplicated data using a normalized-correlation-coefficient-based misfit function[J]. Geophysical Journal International, 2017, 210(3): 1517-1524. DOI:10.1093/gji/ggx249 |
| [31] |
李青阳, 吴国忱, 段沛然, 等. 基于互相关目标函数的反射波波形反演[J]. 石油地球物理勘探, 2020, 55(4): 754-765. LI Qingyang, WU Guochen, DUAN Peiran, et al. Reflection waveform inversion based on cross-correlation misfit function[J]. Oil Geophysical Prospecting, 2020, 55(4): 754-765. |
| [32] |
Luo S, Sava P. A deconvolution-based objective function for wave-equation inversion[J]. SEG Technical Program Expanded Abstracts, 2011, 30: 2788-2792. |
| [33] |
Warner M R, Guasch L. Adaptive waveform inversion-FWI without cycle skipping: Theory[C]. Extended Abstracts of 76th EAGE Conference & Exhibition, 2014, doi: 10.3997/2214-4609.20141093.
|
| [34] |
Warner M R, Guasch L. Robust adaptive waveform inversion[J]. SEG Technical Program Expanded Abstracts, 2015, 34: 1059-1063. |
| [35] |
Warner M R, Guasch L. Adaptive waveform inversion: Theory[J]. Geophysics, 2016, 81(6): R429-R445. DOI:10.1190/geo2015-0387.1 |
| [36] |
Guasch L, Warner M R, Ravaut C. Adaptive waveform inversion: Practice[J]. Geophysics, 2019, 84(3): R447-R461. DOI:10.1190/geo2018-0377.1 |
| [37] |
van Leeuwen T, Herrmann F J. Mitigating local minima in full-waveform inversion by expanding the search space[J]. Geophysical Journal International, 2013, 195(1): 661-667. DOI:10.1093/gji/ggt258 |
| [38] |
Li Z C, Lin Y Z, Zhang K, et al. Time-domain wavefield reconstruction inversion[J]. Applied Geophysics, 2017, 14(4): 523-528. DOI:10.1007/s11770-017-0629-6 |
| [39] |
Jun H, Kwon J, Shin C, et al. Regularized Laplace-Fourier-domain full waveform inversion using a weighted l2 objective function[J]. Pure and Applied Geophysics, 2016, 174(3): 1-26. |
| [40] |
Ben-Hadj-Ali H, Operto S, Virieux J. An efficient frequency-domain full waveform inversion method using simultaneous encoded sources[J]. Geophysics, 2011, 76(4): R109-R124. DOI:10.1190/1.3581357 |



 童思友, 山东省青岛市松岭路238号中国海洋大学海洋地球科学学院, 266100。Email:
童思友, 山东省青岛市松岭路238号中国海洋大学海洋地球科学学院, 266100。Email: 