② 中国石油大学(北京)油气资源与探测国家重点实验室, 北京 102249;
③ 中国石油大学(北京)CNPC物探重点实验室, 北京 102249
② State Key Laboratory of Petroleum Resources and Prospecting, China University of Petroleum, Beijing 102249, China;
③ CNPC Key Laboratory of Geophysical Prospecting, China University of Petroleum, Beijing 102249, China
为了解决油气勘探中薄储层的识别问题,地球物理学家们尝试了许多提高地震资料分辨率的处理方法。Portniaguine等[1-2]和Chopra等[3-5]最早基于地层反射系数奇、偶分解原理提出了谱反演方法;Puryear等[6]将反射系数对分解成奇、偶两个分量,根据奇、偶分量对薄层的分辨能力不同,首先构建了地震数据谱反演方法模型,合成数据测试和实际地震数据反演验证了方法的正确性,为提高地震数据分辨率提供了一种新方法。在随后的几年,谱反演方法得到了快速的发展和完善[7-8]。
Zhang等[9]介绍了一种反射系数基追踪反演方法,该方法通过建立反映反射模式的函数字典,将地震道数据看成是这些函数的叠加,并在反演过程中引入先验信息进行反演约束。柴新涛等[10]提出基于最小二乘奇异值分解(LSQR)算法与模拟退火算法相结合的方法,完成了稀疏谱与非稀疏谱两种假设条件下的反演,同时分析了谱反演结果的影响因素。Yuan等[11]将反射系数反演与稀疏贝叶斯学习相结合实现了谱反演,通过添加、删除或重新估计等方式检索稀疏反射系数序列,无需预先设置非零反射系数的个数,并在合成数据、物理模型数据和实际数据中验证了该方法,结果表明谱反演方法能较好地识别地下薄层。刘万金等[12]利用谱反演法有效地提高了地震数据的分辨率,并将其应用于地震属性分析。田立新等[13]基于贝叶斯理论框架,将测井等信息转换为地质统计先验信息,引入到谱反演过程,提出地质统计学谱反演法。张华等[14]及刘洁等[15]在实际地震资料处理中应用谱反演,均取得不错的效果。张军华等[16]实现了基于Moore-Penrose算法的谱反演;陈祖庆等[17]实现了基于压缩感知的谱反演算法。
地震数据谱反演的假设条件是反射系数为稀疏序列,而稀疏性也是信号分析中压缩感知算法的条件之一。因此,将压缩感知算法引入地震数据谱反演,可以很好地实现地震数据谱反演方法的求解。另外,针对实际地震数据反演过程中地震子波谱难以估算的问题,唐文博等[18]提出利用地震数据二次谱估算子波谱的方法,直接将频率域的地震子波谱用于谱反演。
本文提出联合地震数据二次谱计算方法及基于压缩感知算法的谱反演方法,试算结果表明,可以很好地解决实际数据谱反演中的稳定性问题。
1 方法原理 1.1 谱反演方法在地震数据时间域,利用脉冲函数的性质,将时间间隔为T的地层顶、底反射系数对(r1,r2)表示为[7]
| $ g(t) = {r_1}\delta \left( {t - {t_1}} \right) + {r_2}\delta \left( {t - {t_1} - T} \right) $ | (1) |
式中:r1、r2分别是地层顶、底界面的反射系数;t为时间序列采样;t1、t2分别是顶、底界面的反射时间,T=t2-t1;δ(·)为脉冲函数。如果零时间设置到地层中点,则有
| $ g(t) = {r_1}\delta \left( {t + \frac{T}{2}} \right) + {r_2}\delta \left( {t - \frac{T}{2}} \right) $ | (2) |
对式(2)进行傅里叶变换得到
| $ g(t,f) = {r_1}{{\rm{e}}^{{\rm{j}}2{\rm{ \mathsf{ π} }}f\frac{T}{2}}} + {r_2}{{\rm{e}}^{ - {\rm{j}}2{\rm{ \mathsf{ π} }}f\frac{T}{2}}} $ | (3) |
式中:f为频率;
根据反射系数对的奇偶分解原理[6]可得
| $ g(t,f) = 2{r_{\rm{e}}}\cos ({\rm{ \mathsf{ π} }}fT) + {\rm{j}}2{r_{\rm{o}}}\sin ({\rm{ \mathsf{ π} }}fT) $ | (4) |
其中re、ro为地层反射系数对(r1,r2)的偶分量和奇分量,且2re=r1+r2,2ro=r1-r2。
频率域反射系数对的实部Re[·]和虚部Im[·]为
| $ {{\mathop{\rm Re}\nolimits} [g(t,f)] = 2{r_{\rm{e}}}\cos ({\rm{ \mathsf{ π} }}fT)} $ | (5) |
| $ {{\mathop{\rm Im}\nolimits} [g(t,f)] = 2{r_{\rm{o}}}\sin ({\rm{ \mathsf{ π} }}fT)} $ | (6) |
则单一层的顶、底反射系数对Δt=t1+T/2的时延谱为
| $ \begin{array}{*{20}{l}} {{\mathop{\rm Re}\nolimits} \left[ {{{\rm{e}}^{ - {\rm{j}}2{\rm{ \mathsf{ π} }}f\Delta t}}g(t,f)} \right] = 2{r_{\rm{e}}}\cos ({\rm{ \mathsf{ π} }}fT)\cos (2{\rm{ \mathsf{ π} }}f\Delta t) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2{r_{\rm{o}}}\sin ({\rm{ \mathsf{ π} }}fT)\sin (2{\rm{ \mathsf{ π} }}f\Delta t)} \end{array} $ | (7) |
| $ \begin{array}{*{20}{l}} {{\mathop{\rm Im}\nolimits} \left[ {{{\rm{e}}^{ - {\rm{j}}2{\rm{ \mathsf{ π} }}f\Delta t}}g(t,f)} \right] = 2{r_{\rm{o}}}\sin ({\rm{ \mathsf{ π} }}fT)\cos (2{\rm{ \mathsf{ π} }}f\Delta t) - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2{r_{\rm{e}}}\cos ({\rm{ \mathsf{ π} }}fT)\sin (2{\rm{ \mathsf{ π} }}f\Delta t)} \end{array} $ | (8) |
根据以上推导可得到N个稀疏反射系数序列r(ti),i=1,2,…,N,其频率域反射系数的奇、偶分量形式如下
| $ \begin{array}{*{20}{l}} {{\mathop{\rm Re}\nolimits} [g(t,f)] = \sum\limits_{i = 1}^{N - 1} {\left[ {2{r_{{\rm{e}}(i,i + 1)}}\cos \left( {{\rm{ \mathsf{ π} }}f{T_i}} \right)\cos \left( {2{\rm{ \mathsf{ π} }}f\Delta {t_i}} \right) + } \right.} }\\ {\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2{r_{{\rm{o}}(i,i + 1)}}\sin \left( {{\rm{ \mathsf{ π} }}f{T_i}} \right)\sin \left( {2{\rm{ \mathsf{ π} }}f\Delta {t_i}} \right)} \right]} \end{array} $ | (9) |
| $ \begin{array}{*{20}{l}} {{\mathop{\rm Im}\nolimits} [g(t,f)] = \sum\limits_{i = 1}^{N - 1} {\left[ {2{r_{{\rm{o}}(i,i + 1)}}\sin \left( {{\rm{ \mathsf{ π} }}f{T_i}} \right)\cos \left( {2{\rm{ \mathsf{ π} }}f\Delta {t_i}} \right) - } \right.} }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {2{r_{{\rm{e}}(i,i + 1)}}\cos \left( {{\rm{ \mathsf{ π} }}f{T_i}} \right)\sin \left( {2{\rm{ \mathsf{ π} }}f\Delta {t_i}} \right)} \right]} \end{array} $ | (10) |
式中:
式(9)和式(10)表明,可以利用地震记录和地震子波的部分谱信息进行反演进而得到反射系数序列,该方法即地震数据谱反演[7]。因此,目标函数式为
| $ \begin{array}{l} {O_{{\rm{obj }}}} = \sum\limits_{{f_i} = {f_1}}^{{f_M}} {\left\{ {{\mathop{\rm Re}\nolimits} \left[ {\frac{{S\left( {{f_i}} \right)}}{{W\left( {{f_i}} \right)}}} \right]} \right.} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - \sum\limits_{i = 1}^{N - 1} {\left[ {2{r_{{\rm{e}}(i,i + 1)}}\cos \left( {{\rm{ \mathsf{ π} }}f{T_i}} \right)\cos \left( {2{\rm{ \mathsf{ π} }}f\Delta {t_i}} \right) + } \right.} \\ \left. {\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2{r_{{\rm{o}}(i,i + 1)}}\sin \left( {{\rm{ \mathsf{ π} }}f{T_i}} \right)\sin \left( {2{\rm{ \mathsf{ π} }}f\Delta {t_i}} \right)} \right]} \right\} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{{f_i} = {f_1}}^{{f_M}} {\left\{ {{\mathop{\rm Im}\nolimits} \left[ {\frac{{S\left( {{f_i}} \right)}}{{W\left( {{f_i}} \right)}}} \right] - } \right.} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{i = 1}^{N - 1} {\left[ {2{r_{{\rm{o}}(i,i + 1)}}\sin \left( {{\rm{ \mathsf{ π} }}f{T_i}} \right)\cos \left( {2{\rm{ \mathsf{ π} }}f\Delta {t_i}} \right) - } \right.} \\ \left. {\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2{r_{{\rm{e}}(i,i + 1)}}\cos \left( {{\rm{ \mathsf{ π} }}f{T_i}} \right)\sin \left( {2{\rm{ \mathsf{ π} }}f\Delta {t_i}} \right)} \right]} \right\} \end{array} $ | (11) |
式中:S(f)、W(f)分别是地震记录和地震子波的频谱;fi=f1,f2,…,fM是反演选取的部分谱的频率, M为选取的频率个数。
谱反演目标函数求解过程是利用部分地震信息求解整个时间域内稀疏反射系数的过程,压缩感知的基本思想是在满足有效等距条件(RIP)下,利用少量采样信号重构出完整的原信号。二者思路不谋而合,因此本文选用压缩感知算法解决谱反演问题。假设反射系数为稀疏信号,可将谱反演目标函数重写为最优化目标函数公式
| $ \mathit{\boldsymbol{r}} = \arg \mathop {\min }\limits_\mathit{\boldsymbol{r}} \left\| {\mathit{\boldsymbol{b}} - \mathit{\boldsymbol{Ar}}} \right\|_2^2{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}}.{\rm{t}}.{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left\| \mathit{\boldsymbol{r}} \right\|_1} \le \tau $ | (12) |
式中:r是待求解的反射系数;b是地震记录频谱与地震子波频谱之比;A是构建的测量矩阵;τ表示反射系数的最大幅值,一般取0.2。
可将式(12)的约束优化条件改写为无约束优化条件
| $ \mathop {\min }\limits_\mathit{\boldsymbol{r}} \frac{1}{2}\left\| {\mathit{\boldsymbol{b}} - \mathit{\boldsymbol{Ar}}} \right\|_2^2 + \lambda {\left\| \mathit{\boldsymbol{r}} \right\|_1} $ | (13) |
其中λ是用于平衡二次项和稀疏项结果权重的正则化参数。上述最优化过程为带边界约束的二次规划问题,正则化参数用于控制稀疏解。为了将非凸优化问题转化为凸优化问题,采用梯度投影稀疏重构(Gradient Projection for Sparse Reconstruction,GPSR)算法[19]进行求解。
1.2 地震子波谱的求取式(11)表明,地震数据谱反演目标函数与地震子波谱相关。因此,地震子波谱估算的准确度直接影响谱反演结果的准确性。本文通过地震数据二次谱求取地震子波谱,具体方法如下。
首先,根据地震数据褶积模型,得到频率域的地震数据振幅谱关系式
| $ {A_S}(f) = {A_W}(f){A_\mathit{\boldsymbol{r}}}(f) $ | (14) |
式中AS(f)、AW(f)和Ar(f)分别为地震记录、地震子波和反射系数的振幅谱。
然后,设法提取地震子波振幅谱。在频率域,地震信号中同时包含反射系数与地震子波的频谱信息,无法将其有效分离。而在谱模拟假设条件下,地震子波的振幅谱主要为地震记录频谱中光滑的低频分量,因此,对式(14)两边同时进行傅里叶变换,可得到地震数据的二次谱,即地震子波二次谱与反射系数二次谱的褶积,表达式为
| $ A_S^{(2)}(f) = A_W^{(2)}(f)*A_\mathit{\boldsymbol{r}}^{(2)}(f) $ | (15) |
式中AS(2)(f)、AW(2)(f)与Ar(2)(f)分别为各自振幅谱的二次谱,为实数对称序列,其傅里叶正、反变换的虚部和相位都为零。谱反演时可以通过傅里叶正变换并取模提取非时间域地震子波的振幅谱,并且在二次谱中,地震子波的信息主要集中在低频部分,反射系数信息主要分布在高频部分。因此,先对二次谱进行低通滤波,保留低频部分信息,再对低频部分进行反傅里叶变换即可得到地震子波的振幅谱。
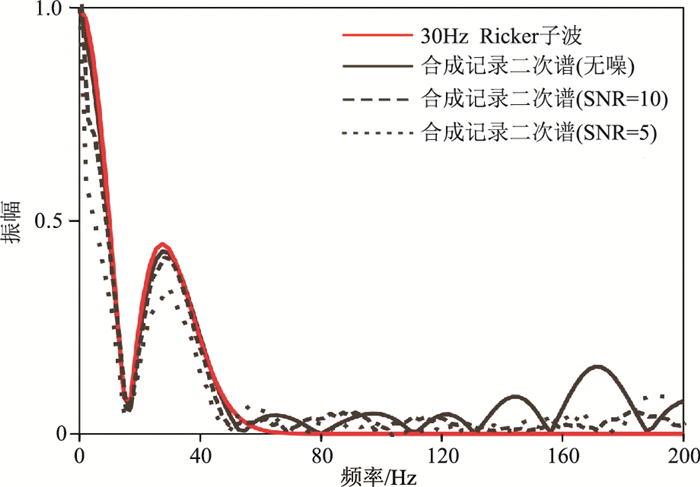
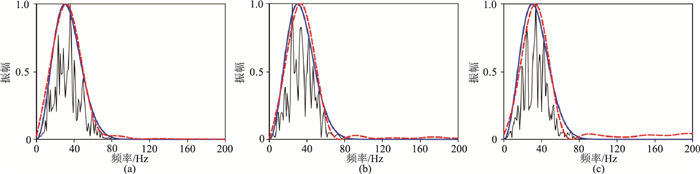
2 合成数据测试进行合成数据测试时,首先利用合成地震道数据验证由地震记录二次谱求取地震子波谱方法的准确性。图 1显示了30Hz Ricker子波和三种不同信噪比的合成地震记录的二次谱曲线,可以看出:在0~45Hz频率范围内,合成地震记录的二次谱可以很好地模拟地震子波的振幅谱。图 2显示合成地震记录振幅谱(黑线)、利用二次谱得到的子波谱(红线)和已知的地震子波谱(蓝线)。对比表明,利用地震记录二次谱可以计算得到最吻合的地震子波频谱,为实际地震数据谱反演中的地震子波谱估算提供了实用且有效的方法。
|
图 1 地震子波与合成地震记录二次谱对比 |
|
图 2 合成地震记录振幅谱(黑线)、地震子波振幅谱(蓝线)和计算得到的地震子波振幅谱(红线)对比 (a)无噪声;(b)SNR=10;(c)SNR=5 |
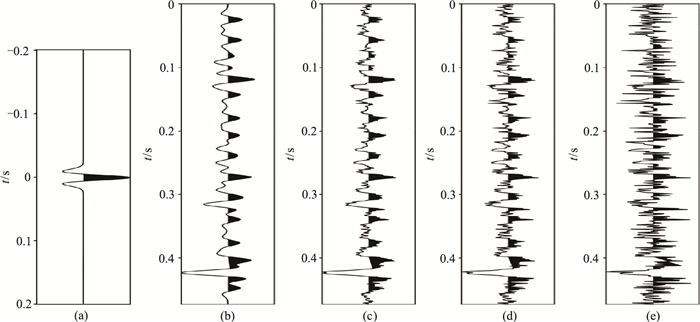
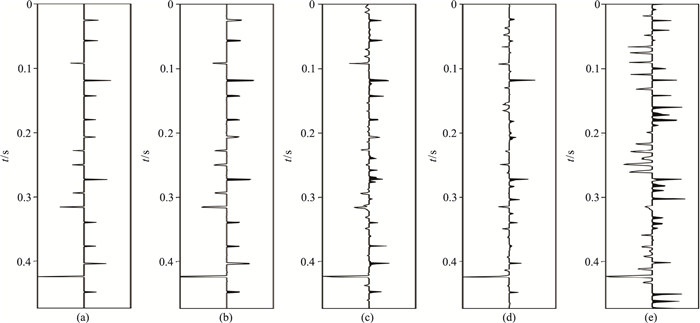
利用地震记录二次谱估算得到较准确的地震子波谱后,通过GPSR算法对合成地震记录进行谱反演试算。图 3分别展示了30Hz地震Ricker子波(图 3a)、无噪声的合成地震记录(图 3b)以及信噪比SNR分别为10、5、2的合成地震记录(图 3c~图 3e)。谱反演结果如图 4所示。对比表明,对于信噪比较高的地震数据,通过谱反演可以得到准确的反射系数。但是当SNR < 5时,反演结果受信噪比影响较大,低信噪比(如SNR=2)地震数据反演结果与实际反射系数的偏差较大。因此,谱反演输入地震数据的信噪比不能太低。
|
图 3 地震子波及合成地震记录对比 (a)Ricker子波;(b)无噪;(c)SNR=10;(d)SNR=5;(e)SNR=2 |
|
图 4 原始反射系数与谱反演结果对比 (a)原始反射系数序列;(b)无噪;(c)SNR=10;(d)SNR=5;(e)SNR=2 |
地震数据谱反演最终得到的是反射系数序列,之后,可以进一步反演波阻抗,也可以将反射系数与宽频地震子波合成高分辨率地震记录。本文利用基于压缩感知算法的谱反演结果进行实际地震数据提高分辨率处理的应用,以验证该反演算法的稳定性和有效性。处理流程包括:
(1) 对地震数据进行频谱分析,确定反演的频率范围;
(2) 计算地震记录的二次谱,进行低通滤波处理;
(3) 求取地震子波谱;
(4) 利用式(11)求解反射系数序列;
(5) 利用宽频带子波合成地震数据,得到提高分辨率后的处理结果。
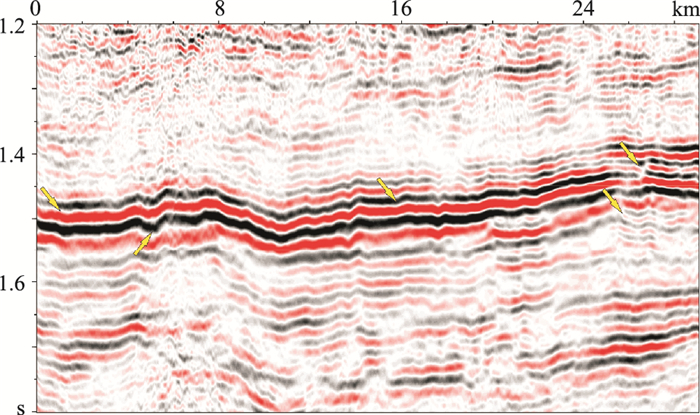
所选实际地震工区的目的层为奥陶系风化壳气藏储层,由于受上覆煤层影响,目的层的地震资料分辨率较低,后续进行高精度储层预测难度很大。图 5为工区内一条地震剖面,图中的强反射同相轴为煤层反射信号。
|
图 5 实际地震数据剖面 |
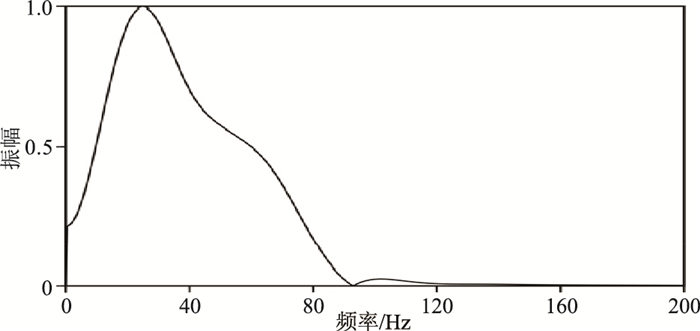
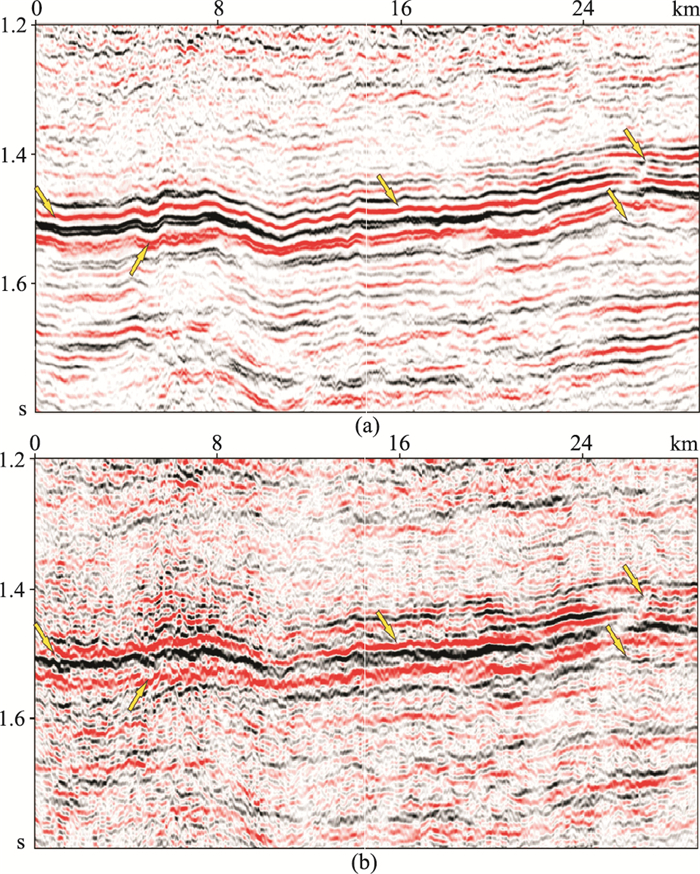
根据上述处理流程,首先通过地震数据频谱分析选取合适的反演频率范围,结合反演测试,最终选取的频率范围为10~70Hz。其次,利用地震资料的二次谱进行地震子波谱估计。针对该实际数据,采用多道平均谱估算地震子波谱。图 6为地震数据的二次谱(蓝色)与低通滤波后的二次谱(红色)对比,图 7为计算得到的地震子波谱。利用本文提出的谱反演方法对地震数据进行反演,并将反演得到的反射系数序列与宽频子波合成,输出提高分辨率处理后的结果(图 8a)。

|
图 6 实际地震数据二次谱(蓝色)与滤波后的二次谱(红色)对比 |
|
图 7 计算得到的地震子波振幅谱 |
|
图 8 实际数据反演提高分辨率处理(a)及谱白化处理(b)结果对比 |
为了验证本文方法针对实际地震数据的处理效果,同时对地震数据进行了谱白化处理,结果如图 8b所示。对比两种方法处理后的地震剖面可以看到:本文方法处理后的地震数据信噪比更高,剖面信息更加丰富,视分辨率得到明显提高;而利用谱白化处理得到的地震剖面,分辨率提高不明显,并且信噪比偏低。
对原始地震数据及处理后数据进行分频扫描,可更好地分析不同方法处理效果。图 9对比了原始数据、谱白化处理及本文方法处理结果的分频扫描结果,扫描频率分别为10~40Hz、40~80Hz和80~120Hz。可以看到,在10~40Hz扫描频段,谱白化处理(图 9d)及本文方法处理(图 9g)结果均能很好地保持原始数据的信息;40~80Hz扫描时谱白化处理结果信噪比明显降低(图 9e);在80~120Hz的扫描结果中,原始数据中80Hz以上的信息不足(图 9c),谱白化处理结果的信噪比更低(图 9f),只有本文方法处理结果恢复得到了高频段的有效信号(图 9i)。三个频段的扫描结果均表明,本文方法处理后的地震剖面的信噪比最高。

|
图 9 数据分频扫描剖面对比 (a~c)原始数据;(d~f)谱白化处理结果;(g~i)本文方法处理结果 |
本文结合地震记录的二次谱估算地震子波谱的方法,提出了一种基于压缩感知算法的地震数据谱反演方法,形成了利用谱反演结果提高地震资料分辨率的数据处理流程。实际地震资料应用结果表明,该处理流程计算步骤和参数选取均较简单,在实际数据处理中可以很好地恢复高频段有效信号,而且经过处理后的地震数据信噪比高、横向连续性好。合成数据测试表明,该方法受原始地震数据信噪比的影响较大,因此对于低信噪比资料的数据反演还需要进一步完善。
| [1] |
Portniaguine O, Castagna J P. Inverse spectral decomposition[J]. SEG Technical Program Expanded Abstracts, 2004, 23: 1786-1789. |
| [2] |
Portniaguine O, Castagna J P. Spectral inversion: lessons from modeling and Boonesville case study[J]. SEG Technical Program Expanded Abstracts, 2005, 24: 1638-1641. |
| [3] |
Chopra S, Castagna J P, Portniaguine O. Thin-bed reflectivity inversion[J]. SEG Technical Program Expanded Abstracts, 2006, 25: 2057-2061. |
| [4] |
Chopra S, Castagna J P, Portniaguine O. Seismic resolution and thin-bed reflectivity inversion[J]. CSEG Recorder, 2006, 31(1): 19-25. |
| [5] |
Chopra S, Castagna J P, Xu Y. Thin-bed reflectivity inversion and seismic interpretation[J]. SEG Technical Program Expanded Abstracts, 2007, 26: 1923-1927. |
| [6] |
Puryear C I, Castagna J P. Layer-thickness determination and stratigraphic interpretation using spectral inversion: Theory and application[J]. Geophysics, 2008, 73(2): R37-R48. DOI:10.1190/1.2838274 |
| [7] |
Chopra S, Castagna J P, Xu Y. Thin-bed reflectivity inversion and some applications[J]. First Break, 2009, 27(5): 17-24. |
| [8] |
Chopra S, Castagna J P, Xu Y. Relative acoustic impedance application for thin-bed reflectivity inversion[J]. SEG Technical Program Expanded Abstracts, 2009, 28: 3554-3558. |
| [9] |
Zhang R, Castagna J P. Seismic sparse-layer reflectivity inversion using basis pursuit decomposition[J]. Geophysics, 2011, 76(6): R147-R158. DOI:10.1190/geo2011-0103.1 |
| [10] |
柴新涛, 李振春, 韩文功, 等. 基于LSQR算法的谱反演方法研究[J]. 石油物探, 2012, 51(1): 11-18. CHAI Xintao, LI Zhenchuan, HAN Wengong, et al. Spectral inversion method analysis based on the LSQR algorithm[J]. Geophysical Prospecting for Petroleum, 2012, 51(1): 11-18. |
| [11] |
Yuan S Y, Wang S X. Spectral sparse Bayesian learning reflectivity inversion[J]. Geophysical Pro-specting, 2013, 61(4): 735-746. DOI:10.1111/1365-2478.12000 |
| [12] |
刘万金, 周辉, 袁三一, 等. 谱反演在地震属性解释中的应用[J]. 石油地球物理勘探, 2013, 48(3): 423-428. LIU Wanjin, ZHOU Hui, YUAN Sanyi, et al. Applications of spectral inversion in the attribute interpretation[J]. Oil Geophysical Prospecting, 2013, 48(3): 423-428. |
| [13] |
田立新, 王波, 张志军. 基于地质统计信息的谱反演法[J]. 石油地球物理勘探, 2015, 50(5): 967-972. TIAN Lixin, WANG Bo, ZHANG Zhijun. A spectral inversion method based on geostatistical information[J]. Oil Geophysical Prospecting, 2015, 50(5): 967-972. |
| [14] |
张华, 贺振华, 李亚林, 等. 基于ADM谱反演的高分辨率裂缝技术研究及应用[J]. 石油物探, 2016, 55(5): 737-745. ZHANG Hua, HE Zhenhua, LI Yalin, et al. Research and application of high-resolution fracture prediction technology based on ADM spectral inversion[J]. Geophysical Prospecting for Petroleum, 2016, 55(5): 737-745. DOI:10.3969/j.issn.1000-1441.2016.05.013 |
| [15] |
刘洁, 张建中, 孙运宝, 等. 基于地震谱反演地层速度估算方法及应用[J]. 石油地球物理勘探, 2016, 51(5): 909-915. LIU Jie, ZHANG Jianzhong, SUN Yunbao, et al. Seismic velocity estimation method based on spectral inversion[J]. Oil Geophysical Prospecting, 2016, 51(5): 909-915. |
| [16] |
张军华, 张晓辉, 张秋, 等. 基于Moore-Penrose算法的谱反演方法研究[J]. 地球物理学进展, 2017, 32(6): 2596-2601. ZHANG Junhua, ZHANG Xiaohui, ZHANG Qiu, et al. Research on spectral inversion method based on Moore-Penrose algorithm[J]. Progress in Geophy-sics, 2017, 32(6): 2596-2601. |
| [17] |
陈祖庆, 王静波. 基于压缩感知的稀疏脉冲反射系数谱反演方法研究[J]. 石油物探, 2015, 54(4): 459-466. CHEN Zuqing, WANG Jingbo. A spectral inversion method of sparse-spike reflection coefficient based on compressed sensing[J]. Geophysical Prospecting for Petroleum, 2015, 54(4): 459-466. |
| [18] |
唐博文, 赵波, 吴艳辉, 等. 一种实现谱模拟反褶积的新途径[J]. 石油地球物理勘探, 2010, 45(增刊1): 66-70. TANG Bowen, ZHAO Bo, WU Yanhui, et al. A new way to realize spectral modeling deconvolution[J]. Oil Geophysical Prospecting, 2010, 45(S1): 66-70. |
| [19] |
Figueiredo M A T, Nowak R D, Wright S J. Gradient projection for sparse reconstruction: Application to compressed sensing and other inverse problems[J]. IEEE Journal of Selected Topics in Signal Processing, 2007, 1(4): 586-597. |



 陈双全, 北京市昌平区府学路18号中国石油大学(北京)地球物理学院物探系, 102249。Email:
陈双全, 北京市昌平区府学路18号中国石油大学(北京)地球物理学院物探系, 102249。Email: 