② 中国石油大学(华东)山东省油藏地质重点实验室, 山东青岛 266580;
③ 中海石油(中国)有限公司湛江分公司南海西部石油研究院, 广东湛江 524000
② Shandong Provincial Key Laboratory of Reservoir Geology, China University of Petroleum(East China), Qingdao, Shandong 266580, China;
③ Nanhai Western Petroleum Research Institute, Zhanjiang Branch, CNOOC, Zhanjiang, Guangdong 524000, China
随着石油行业的快速发展,地震勘探面临的地表条件越来越复杂、地质构造也越来越复杂,地质目标也多为隐蔽的油气藏。在此条件下,实际采集的地震数据信噪比往往较低,常规处理手段难以满足高精度的成像要求。共反射面元(Common Reflection Surface,CRS)叠加技术在经过长期的研究、发展后,是低信噪比地区地震数据成像的可选方法,得到了认可和推广。
CRS叠加技术最早由德国的Hurbal[1]提出,是一种与宏观速度模型无关的地震成像方法。用于描述CRS时距公式的算子有双曲CRS算子、隐式CRS算子、非双曲CRS算子和多聚焦算子等[2]。这些算子在速度横向变化较小时相差不大,但在速度横向变化剧烈时存在一定的差异。CRS叠加的理论基础是几何地震学,考虑了反射层的局部特征和第一菲涅耳带内的全部反射。CRS叠加引入反射段及反射面理论,在几何地震学基础上研究第一菲涅耳带范围内的反射,叠加次数得到提高,在提高信噪比的同时满足高分辨率的成像要求,是低信噪比、低覆盖次数地震资料的主要处理手段[3-7]。
二维CRS叠加处理中,除了得到零炮检距剖面,同时也得到了三个波场属性参数。三参数反映了波场的运动学属性,进行部分CRS叠加时对三参数进行分析,可以使叠前数据更加规则,得到高质量的叠前数据,便于下一步常规处理。
近年来,CRS叠加理论逐步从二维拓展到了三维。三维CRS叠加中,包含八个参数:零炮检距(ZO)射线在地表的出射角(包括倾角和方位角)、法向入射点波(NIP波)和法向波(N波)在地面的波前曲率矩阵(均为2×2的对称矩阵)。因为计算成本问题,常规的三维CRS叠加分多步依次求取8个属性参数,这种方法计算成本较低,但是它在求取属性参数的过程中会系统地累积误差,降低CRS属性参数的准确性,从而影响CRS叠加的效果。
二维、三维CRS叠加技术已经在实际地震数据处理中得到了成功的应用,证明其能够显著提高叠加剖面质量尤其是深层的信噪比[8-11]。CRS叠加在复杂、含噪、叠加速度难以准确获取的陆上地震资料中取得较好效果,还被视为重要的深层地震资料处理方法,并在很多探区有成功的应用实例[12-14]。
三维CRS叠加参数的增多增加了处理的计算难度。但正因为复杂参数约束,CRS叠加结果才更加准确,也更能适用于低信噪比的复杂构造区。通过相干分析求取的八参数之间存在耦合关系,高效的参数搜索策略是非常必要的。基于三维叠前地震数据做CRS多参数搜索需要庞大的存储空间及计算量,于是便引入了许多全局优化算法,如模拟退火(Simulated Annealing,SA)算法、Powell共轭梯度算法、遗传(GA)算法、差分进化算法及粒子群优化算法等[15-19]。全局优化算法的引入可以实现共反射面元运动学波场参数的同时搜索,并避免其陷入局部极值。
本文提出了一种GA和SA算法混合的多种群分层式混合并行算法,实现一步法对三维CRS波场八参数的搜索,显著降低了计算成本,提高了计算效率。算法结构从实现两种算法互补作为出发点,在功能上实现了局部搜索与全局搜索的分离,在一定程度上既保证算法的收敛速度,又避免陷入局部极值,有效地解决了单一算法的局限性,使GA算法和SA算法融合为一体。
1 三维CRS叠加算子及波场参数借助旁轴射线理论,Bergler等[13]推导了非均匀各向同性介质条件下的三维零炮检距共反射面叠加双曲型旅行时近似公式
| $ \begin{aligned} &t_{\mathrm{hyp}}^{2}\left(\boldsymbol{m}_{\mathrm{D}}, \boldsymbol{h}\right)=\left[t_{0}\left(\boldsymbol{m}_{0}, 0\right)+\frac{2 \sin \alpha}{v_{0}} \boldsymbol{\varPhi} \boldsymbol{m}_{\mathrm{D}}\right]^{2}+\\ &\frac{2 t_{0}\left(\boldsymbol{m}_{0}, 0\right)}{v_{0}} \times\left(\boldsymbol{m}_{\mathrm{D}}^{\mathrm{T}} \boldsymbol{\varTheta}^{\mathrm{T}} \boldsymbol{\varPhi}^{\mathrm{T}} \boldsymbol{K}_{\mathrm{N}} \boldsymbol{\varPhi} \boldsymbol{\varTheta} \boldsymbol{m}_{\mathrm{D}}+\right.\\ &\left.\boldsymbol{h}^{\mathrm{T}} \boldsymbol{\varTheta}^{\mathrm{T}} \boldsymbol{\varPhi}^{\mathrm{T}} \boldsymbol{K}_{\mathrm{NIP}} \boldsymbol{\varPhi} \boldsymbol{\varTheta} \boldsymbol{h}\right) \end{aligned} $ | (1) |
式中:
为了获得更简洁的三维共反射面叠加算子,令
| $ \boldsymbol{W}_{\mathrm{Z}}=\frac{2}{v_{0}} \sin \alpha \boldsymbol{\varPhi} $ | (2) |
| $ \boldsymbol{N}_{\mathrm{H}}=\frac{2 t_{0}\left(\boldsymbol{m}_{0}, 0\right)}{v_{0}} \boldsymbol{\varTheta}^{\mathrm{T}} \boldsymbol{\varPhi}^{\mathrm{T}} \boldsymbol{K}_{\mathrm{N}} \boldsymbol{\varPhi} \boldsymbol{\varTheta} $ | (3) |
| $ \boldsymbol{M}_{\mathrm{H}}=\frac{2 t_{0}\left(\boldsymbol{m}_{0}, 0\right)}{v_{0}} \boldsymbol{\varTheta}^{\mathrm{T}} \boldsymbol{\varPhi}^{\mathrm{T}} \boldsymbol{K}_{\mathrm{NIP}} \boldsymbol{\varPhi} \boldsymbol{\varTheta} $ | (4) |
将式(2)~式(4)代入式(1),可得
| $ \begin{aligned} t_{\text {hyp }}^{2}\left(\boldsymbol{m}_{\mathrm{D}}, \boldsymbol{h}\right)=&\left[t_{0}\left(\boldsymbol{m}_{0}, 0\right)+\boldsymbol{W}_{\mathrm{Z}} \boldsymbol{m}_{\mathrm{D}}\right]^{2}+\\ &\boldsymbol{m}_{\mathrm{D}}^{\mathrm{T}} \boldsymbol{N}_{\mathrm{H}} \boldsymbol{m}_{\mathrm{D}}+\boldsymbol{h}^{\mathrm{T}} \boldsymbol{M}_{\mathrm{H}} \boldsymbol{h} \end{aligned} $ | (5) |
在共中心点CMP道集和零炮检距ZO道集中,对CRS旅行时进行简化,将优化问题分为三个步骤。在双曲CMP搜索的第一步中,得到有关NIP波波前曲率的三个参数。第二步是ZO搜索,求取ZO中心射线的方位角和倾角。第三步是在ZO搜索中得到有关N波波前曲率的三个参数。最后,对得到的八参数初值进行优化,进行CRS叠加。在该搜索策略中,Bergler等[13]采用网格搜索方法,分三步确定这八个参数,具体过程如下。
(1) 仅考虑CMP道集,即令mD=0,式(5)可写为
| $ t_{\mathrm{hyp}}^{2}(\boldsymbol{h})=t_{0}^{2}\left(\boldsymbol{m}_{0}, 0\right)+\boldsymbol{h}^{\mathrm{T}} \boldsymbol{M}_{\mathrm{H}} \boldsymbol{h} $ | (6) |
利用上式,可以实现在CMP道集数据体中对矩阵MH中的三个独立变量进行逐步搜索和叠加(称为双曲叠加或自动CMP叠加),同时得到的ZO数据体还可以作为后两步的输入数据。
(2) 设KN=0,并且在零炮检距数据体中设h=0,由式(5)可得
| $ t_{\mathrm{hyp}}\left(\boldsymbol{m}_{\mathrm{D}}\right)=t_{0}\left(\boldsymbol{m}_{0}, 0\right)+\boldsymbol{W}_{\mathrm{Z}} \boldsymbol{m}_{\mathrm{D}} $ | (7) |
式(7)用于对WZ的两参数搜索,称为线性ZO叠加,可得WZ属性体。该属性体有两个用途:一方面可以联立MH,计算出KNIP;另一方面作为输入,搜寻NH(等价于KN)参数。
(3) 在零炮检距情况下,即h=0时,式(5)可写为
| $ t_{\mathrm{hyp}}^{2}\left(\boldsymbol{m}_{\mathrm{D}}\right)=\left[t_{0}\left(\boldsymbol{m}_{0}, 0\right)+\boldsymbol{W}_{\mathrm{Z}} \boldsymbol{m}_{\mathrm{D}}\right]^{2}+\boldsymbol{m}_{\mathrm{D}}^{\mathrm{T}} \boldsymbol{N}_{\mathrm{H}} \boldsymbol{m}_{\mathrm{D}} $ | (8) |
利用上式,可以实现在叠后数据体中逐步搜索矩阵NH中的三个独立变量(称为双曲ZO搜索),得到NH属性体。这样就得到式(6)中最后的参数。
这样八个波场参数全部确定,接下来就可以利用叠加算子式(6)进行三维CRS叠加。将之前搜寻到的八参数,代入式(6)得到初始三维CRS叠加数据体,再通过对参数的优化,获得最终的三维CRS叠加结果。三维CRS叠加除了得到最终叠加数据体外,还可得到十一个数据体:八个参数数据体,两步搜索各自得到的相干数据体和最终CRS叠加的相干数据体。
通常,三步法的计算成本较低,但是会系统地累积误差,降低CRS属性参数的准确性,从而影响CRS叠加效果[20-22]。
3 一步法实现三维CRS叠加为了克服常规三步法求取三维CRS叠加八参数的局限性,本文提出一种同时确定所有CRS参数的方法,称为一步法,旨在求取更为精确的三维CRS中的八个属性参数,提高叠加效果。
要实现一步法求取八个参数,需要一种搜索精度高、效率高的全局优化策略。目前常用的全局优化算法(例如:SA法、GA算法、Powell共轭梯度算法、粒子群算法等)在搜索精度以及搜索效率方面各有优劣。这类全局优化算法在结构上具有并行性,可以根据算法的特点进行有效组合,取长补短,从而设计出性能更优的混合算法。目前应用于全局优化算法的混合模式可大致分为并联和串联。其特点多为将两种算法以同等的地位进行结合,这就导致了两种算法的结合方式固化,不能根据自身特点进行有机的结合,不能充分发挥这两种算法在参数寻优方面的特点及优势。
GA算法和SA算法都属于群体智能型全局寻优算法,在面对小规模的优化问题时,不管是参数优化效率还是参数求解质量方面,都有着成功的表现。但是随着地震勘探转向更复杂的区域,实际地震资料处理也逐渐由二维扩展到三维,需要处理的地震数据体越来越大,单纯的GA算法或SA算法在面对三维CRS叠加中八参数的求解问题时,无论是参数求解的效率还是精度均不理想[6, 8-13]。
GA算法在算法运行初期,收敛速度很快,可以在短时间内收敛到局部最优解,但随着算法中种群的进化,算法的收敛速度开始变缓,无法精确地收敛到全局最优解,即出现了“早熟收敛”现象。这也印证了GA算法简单易实现,但搜索精度不高,且算法得出的解并不一定是全局最优的特点。而且标准的GA算法是随机产生初始群体,没有约束条件,可能出现:一是初始群体中会产生一些远离最优解的个体,导致求解用时长、精度低;二是初始群体的多样性过低,容易收敛到局部极小值。而在三维CRS叠加中八参数寻优过程中,每个参数的精度都非常重要,直接影响叠加的效果。SA算法虽然收敛速度缓慢,但在理论上已经证明其搜索过程是不断接近最优解直至以概率1最终收敛于全局最优解。SA法在处理复杂且庞大的全局寻优问题时,前期的求解速度十分缓慢,因此在面对复杂的三维地震数据体时显得更加乏力。
GA算法具有快速寻优能力,SA算法有很好的全局收敛特性,两者有着几乎互补的优势。本文结合分层混合的思想,根据全局优化算法的并行性及二者的算法特点,提出GA与SA混合的多种群精英分层式混合并行寻优(简称GA-SAHP)算法,其种群个体组织方式从上到下总体可以分为三层:
(1) 顶层是根据SA算法中的热槽法,通过概率分布函数随机产生三维CRS叠加中八个相关参数的若干个候选值,这些值随机分配到中层n个GA算法中形成的每个种群的初始状态,形成初始种群;
(2) 中层则是n个独立运行的遗传迭代过程,可以在一定程度上保证解的多样性,每个种群独立交叉、变异、选择形成新解,这些局部最优解将组成精英种群,为算法底层SA算法提供初始值;
(3) 底层采用SA算法对中层选出的精英种群进行迭代,对全局最优解进行搜索,迭代一定次数之后,判断是否满足SA算法中的外循环停止准则,若满足则输出全局最优解;否则,中层的GA算法在SA算法产生的解中随机抽取一定数量的解放入中层的种群中继续进化,直至得出全局最优解,输出相干值最大的八个参数。

|
图 1 GA-SAHP算法的流程 |
整个混合寻优算法中,中上层是提高计算效率的重要步骤,先是利用热槽法增加了GA算法种群个体之间的相关性,GA算法弥补了下层SA算法在前期全局收敛效率方面的不足,在提升计算效率降低计算成本的同时,也为下层的SA算法提供局部最优解作为初始值(即初始温度T0)。中下层是算法的主体,是影响三维CRS叠加中八参数寻优质量的关键[13]。算法结构从实现两种算法互补作为出发点,实现了局部搜索与全局搜索的分离,增强了GA算法逃逸局部解的能力,提高了SA算法的搜索效率,使算法具有了收敛速度快和全局寻优能力强的特点。
4 实际地震资料处理CRS叠加适用于低信噪比、低覆盖次数地震数据的处理。为比较常规CRS叠加与基于GA-SAHP算法搜索参数的一步法CRS叠加效果,对实际海上三维地震数据进行CRS叠加处理。
图 2是实际低信噪比地震数据的CMP道集,已做过去噪、振幅补偿等前期处理,但是深层反射同相轴并不清晰。
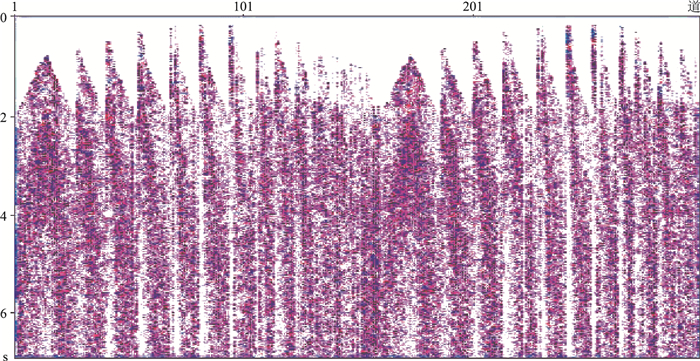
|
图 2 实际低信噪比地震数据的CMP道集 |
图 3a为实际三维数据的常规CRS叠加剖面,图 3b为基于GA-SAHP算法参数搜索的CRS叠加剖面。对比可见,在低信噪比条件下,基于GA-SAHP算法参数搜索的一步法三维CRS叠加剖面的深层反射同相轴更加清晰、效果更好,明显强于常规CRS叠加。
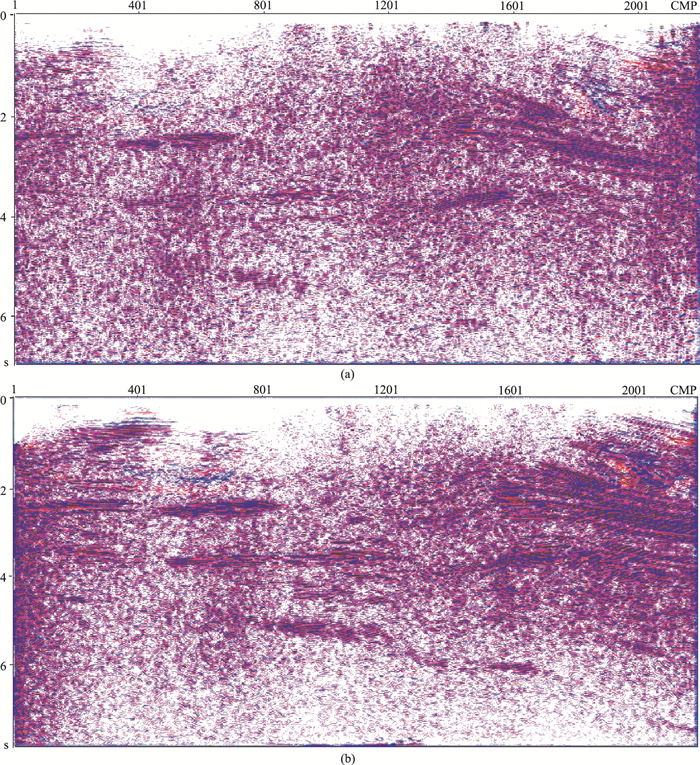
|
图 3 常规(a)与基于GA-SAHP算法(b)的CRS叠加剖面对比 |
海上实际资料的数据量大约30G。程序运行时使用具有28个节点的机群,每一个节点有8个CPU并且共享16G的内存。基于GA-SAHP算法进行参数搜索实现一步法CRS叠加时,每个进程大约需1.6G内存进行计算,总耗时为10h。常规CRS叠加中,三步法的第一步和第二部内存使用不多,每个进程大约占用1.2G内存,计算用时较短,但在第三步处理时约需1.6G内存,总用时超过17h。可见,与常规CRS叠加相比,基于GA-SAHP算法参数搜索的一步法三维CRS叠加的运算耗时及内存占用都在可承受范围内,但明显提高了参数搜索质量和成像效果。
5 结束语针对实际地震资料的基于GA-SAHP算法参数搜索的一步法三维CRS叠加与常规三步法三维CRS叠加相比具有较大优势。
(1) 改进后的CRS叠加,对低信噪比的深层成像效果更好,中深层的反射同相轴连续性增强。
(2) 在参数搜索效率方面,基于GA-SAHP算法参数搜索的一步法高于常规三步法。
因此,基于混合寻优算法的一步法三维CRS叠加适合大型三维勘探区块海量低信噪比地震数据的处理,具有推广价值。
| [1] |
Hubral P. Computing true amplitude reflections in a laterally inhomogeneous earth[J]. Geophysics, 1983, 48(8): 1051-1062. DOI:10.1190/1.1441528 |
| [2] |
Jäger R, Mann J, H cht G, et al. Common-reflection-surface stack: Image and attributes[J]. Geophysics, 2001, 66(1): 97-109. DOI:10.1190/1.1444927 |
| [3] |
Barros T, Ferrari R, Krummenauer R, et al. Differential evolution based optimization procedure for automatic estimation of the common reflection surface traveltime parameters[J]. Geophysics, 2015, 80(6): WD189-WD200. DOI:10.1190/geo2015-0032.1 |
| [4] |
Bruno P. High-resolution seismic imaging in complex environments: A comparison among common-reflection-surface stack, common-midpoint stack, and pre-stack depth migration at the Ilva-Bagnoli brownfield site[J]. Geophysics, 2015, 80(6): B203-B214. DOI:10.1190/geo2014-0488.1 |
| [5] |
陈宝书, 杨锴, 汪小将. 基于两步弥散算子的共反射面元射线束成像方法研究[J]. 地球物理学报, 2020, 63(1): 270-286. CHEN Baoshu, YANG Kai, WANG Xiaojiang, et al. The CRS-BEAM-PSDM based on two-step-smearing operator[J]. Chinese Journal of Geophysics, 2020, 63(1): 270-286. |
| [6] |
杨锴, 马在田, 罗卫东. 输出道成像方式的共反射面元叠加方法Ⅱ——实践[J]. 地球物理学报, 2006, 49(3): 895-902. YANG Kai, MA Zaitian, LUO Weidong. Common reflection surface stack by the outplan, Ⅱ: Practice[J]. Chinese Journal of Geophysics, 2006, 49(3): 895-902. DOI:10.3321/j.issn:0001-5733.2006.03.035 |
| [7] |
王华忠, 杨锴, 马在田. 共反射面元叠加的应用理论——从共反射点到共反射面元[J]. 地球物理学报, 2004, 47(1): 137-142. WANG Huazhong, YANG Kai, MA Zaitian. An applied theory on common reflection surface stack: from common reflection point to common reflection surface[J]. Chinese Journal of Geophysics, 2004, 47(1): 137-142. DOI:10.3321/j.issn:0001-5733.2004.01.021 |
| [8] |
Garabito G. Global optimization strategies for implementing 3D common reflection surface stack using the very fast simulated annealing algorithm: Application to real land data[J]. Geophysics, 2018, 83(4): V253-V261. DOI:10.1190/geo2017-0836.1 |
| [9] |
Xie Y J, Gajewski D. 3D wavefront attribute determination and conflicting dip processing[J]. Geophysics, 2018, 83(6): V325-V343. DOI:10.1190/geo2017-0792.1 |
| [10] |
Rad P, Schwarz B, Gajewski D, et al. Common reflection surface based prestack diffraction separation and imaging[J]. Geophysics, 2018, 83(1): S47-S55. DOI:10.1190/geo2016-0445.1 |
| [11] |
倪瑶, 杨锴. 基于GPU计算平台实现三维输出道方式的共反射面元(3D-CRS-OIS)叠加[J]. 石油地球物理勘探, 2013, 48(1): 49-57. NI Yao, YANG Kai. 3D common reflection surface stack algorithm based on GPU with the output imaging scheme[J]. Oil Geophysical Prospecting, 2013, 48(1): 49-57. |
| [12] |
Dell S, Gajewski D. Common-reflection-surface-based workflow for diffraction imaging[J]. Geophysics, 2011, 76(5): S187-S195. DOI:10.1190/geo2010-0229.1 |
| [13] |
Bergler S, Hubral P, Marchetti P, et al. 3D common reflection surface stack and kinematic wavefield attri-butes[J]. The Leading Edge, 2002, 21(10): 1010-1015. DOI:10.1190/1.1518438 |
| [14] |
Duveneck E. Velocity model estimation with data-derived wavefront attributes[J]. Geophysics, 2004, 69(1): 265-274. DOI:10.1190/1.1649394 |
| [15] |
Martina G, Sergius D. Velocity-estimation improvements and migration/demigration using the common-reflection surface with continuing deconvolution in the time domain[J]. Geophysics, 2019, 84(4): S229-S238. DOI:10.1190/geo2018-0173.1 |
| [16] |
Marcelo J. Velocity inversion by global optimization using finite-offset common-reflection-surface stacking applied to synthetic and Tacutu Basin seismic data[J]. Geophysics, 2019, 84(2): R165-R174. DOI:10.1190/geo2017-0117.1 |
| [17] |
Yin J H, Nakata N. Diffraction imaging using geometric-mean reverse time migration and common-reflection surface[J]. Geophysics, 2019, 84(4): S355-S364. DOI:10.1190/geo2018-0455.1 |
| [18] |
孙小东, 贾延睿, 李振春, 等. 粒子群算法参数搜索的共反射面元叠加[J]. 石油地球物理勘探, 2019, 54(4): 782-786. SUN Xiaodong, JIA Yanrui, LI Zhenchun, et al. Common reflection surface stack based on parameter searching by PSO[J]. Oil Geophysical Prospecting, 2019, 54(4): 782-786. |
| [19] |
陈汉明, 周辉, 田玉昆. 分数阶拉普拉斯算子黏滞声波方程的最小二乘逆时偏移[J]. 石油地球物理勘探, 2020, 55(3): 616-626. CHEN Hanming, ZHOU Hui, TIAN Yukun. Seismic diffraction imaging by reverse time migration in dip angle domain[J]. Oil Geophysical Prospecting, 2020, 55(3): 616-626. |
| [20] |
Bauer A, Schwarz B, Gajewski D. Utilizing diffractions in wavefront tomography[J]. Geophysics, 2017, 82(2): R65-R73. DOI:10.1190/geo2016-0396.1 |
| [21] |
Walda J, Gajewski D. Determination of wavefront attri-butes by differential evolution in the presence of confli-cting dips[J]. Geophysics, 2017, 82(4): V229-V239. DOI:10.1190/geo2016-0346.1 |
| [22] |
王征, 杨锴, 董水利, 等. 应用叠前时间偏移/反偏移与CRS-OIS叠加削弱倾角歧视影响[J]. 石油地球物理勘探, 2015, 50(5): 839-847. WANG Zheng, YANG Kai, DONG Shuili, et al. Dip discrimination reduction with CRS-OIS[J]. Oil Geophysical Prospecting, 2015, 50(5): 839-847. |



 侯孟睿, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
侯孟睿, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: 