众所周知,地震波在地下介质中传播时,由于大地滤波作用,会导致地震波能量衰减、速度频散,降低分辨薄层的能力。目前已提出了许多地层吸收衰减模型(Q模型)描述这一现象,其中常Q模型是地震勘探领域使用最多的地层吸收衰减模型[1]。地震波的衰减效应破坏了地震子波在时间方向的稳态特征,导致传统的反褶积方法很难从非稳态地震记录中准确地恢复反射系数序列。因此,基于吸收补偿的提高分辨率方法具有明确的物理意义和较大应用潜力[2-8]。
反Q滤波是吸收补偿的主要方法,有多种实现方式,其中,波场延拓和稀疏反演是两类应用最为广泛的方法。由于波场延拓方法在外推过程中存在放大函数,极易放大高频噪声,结果不稳定。因此,稀疏反演类反Q滤波方法应运而生[9-10]。Zhang等[11]将衰减补偿看作基于反演的最小二乘问题,并用贝叶斯理论进行正则化约束;Braga等[12]在小波域实现了L2范数约束的反Q滤波;Oliveira等[13]在频率域实现了L1范数约束的衰减补偿,Wang等[14]对其进行改进,在时间域实现了L1范数约束的衰减补偿。以上方法都只考虑了地震道纵向上的信息,而没有考虑相邻道之间的相关性,即都是单道补偿方法,因而结果往往会出现横向不连续问题。为了解决这一问题,将相邻道之间的相关性作为先验信息加入反演系统进行多道反演补偿的方法逐渐发展起来。
Zhang等[15]提出了一种多道反演方法,该算法将横向约束融入反演算法中,反演的结果较常规单道算法具有更好的横向连续性。Kazemi等[16]假设反射系数序列稀疏分布,提出了一种非线性多道盲源反褶积方法,主要优点是抗噪性较强且不需要子波的先验信息。Yuan等[17]先将数据转化到变换域,然后在变换域数据上加一个约束项,实现了多道波阻抗反演,在一定程度上缓解了单道反演算法的横向不连续性问题;在此基础上,Yuan等[18]提出了一种在频率—波数域的多道衰减补偿方法,增强了地震同相轴横向连续性,提高了吸收补偿的稳定性和抗噪性。
f-x域预测滤波是描述线性事件空间预测特性的有用工具,主要被用于数据插值和去噪领域[19-22]。为提高地层吸收补偿的稳定性和抗噪性,本文提出了一种基于反演的全局约束吸收补偿方法。该方法首先在f-x域计算信号预测算子[23-25],用于表征地震信号在空间上的结构关系和能量变化;然后,将该算子作为横向正则化约束引入到纵向吸收补偿系统,建立具有双向(纵向和横向)即全局约束的反演目标函数;最后应用模型数据和实际数据验证了方法的有效性。
1 地层吸收模型 1.1 Q的定义当平面波通过均匀的黏弹性介质时,其振幅衰减和速度频散可以用一个无量纲的参数Q描述
| $ Q(\omega ) = \frac{1}{2}\left[ {\frac{{|\omega |}}{{\alpha (\omega )v(\omega )}} - \frac{{\alpha (\omega )v(\omega )}}{{|\omega |}}} \right] $ | (1) |
式中:ω为圆频率;α(ω)和v(ω)分别为衰减系数和相速度。由于品质因子Q必须为正数,所以
| $ {\left[ {\frac{{\alpha (\omega )v(\omega )}}{\omega }} \right]^2} < 1 $ | (2) |
进一步假设
| $ {\left[ {\frac{{\alpha (\omega )v(\omega )}}{\omega }} \right]^2} \ll 1 $ | (3) |
则式(1)可以近似为
| $ Q(\omega ) \approx \frac{{|\omega |}}{{2\alpha (\omega )v(\omega )}} $ | (4) |
Kolsky[26]假设在测量频带范围内衰减系数α(ω)与频率呈严格的线性关系,即
| $ \alpha (\omega ) = \frac{{|\omega |}}{{2v\left( {{\omega _0}} \right)Q\left( {{\omega _0}} \right)}} $ | (5) |
式中ω0为参考圆频率。同时,Kolsky定义其相速度为
| $ \frac{1}{{v(\omega )}} = \frac{1}{{v\left( {{\omega _0}} \right)}}\left[ {1 - \frac{1}{{{\rm{ \mathsf{ π} }}Q\left( {{\omega _0}} \right)}}\ln \left| {\frac{\omega }{{{\omega _0}}}} \right|} \right] $ | (6) |
将式(5)和式(6)代入式(4),可得
| $ Q(\omega ) = Q\left( {{\omega _0}} \right)\left[ {1 - \frac{1}{{{\rm{ \mathsf{ π} }}Q\left( {{\omega _0}} \right)}}\ln \left| {\frac{\omega }{{{\omega _0}}}} \right|} \right] $ | (7) |
对于较大的品质因子,即Q(ω0)
| $ \mathop {\lim }\limits_{\gamma \to 0} \left( {1 - \gamma \ln \left| {\frac{\omega }{{{\omega _0}}}} \right|} \right) = {\left| {\frac{\omega }{{{\omega _0}}}} \right|^{ - \gamma }} $ | (8) |
式中
| $ \frac{1}{v(\omega)} \approx \frac{1}{v\left(\omega_{0}\right)}\left|\frac{\omega}{\omega_{0}}\right|^{-\gamma} $ | (9) |
| $ Q(\omega) \approx Q\left(\omega_{0}\right)\left|\frac{\omega}{\omega_{0}}\right|^{-\gamma} $ | (10) |
其中自由选择的参考频率ω0小于最低的测量频率。
Wang等[27]指出,式(6)相速度仅仅是对于ω
| $ \begin{array}{l} \frac{1}{{v(\omega )}} = \frac{1}{{v\left( {{\omega _0}} \right)}}\left[ {1 - \frac{1}{{{\rm{ \mathsf{ π} }}Q\left( {{\omega _0}} \right)}}\ln \left| {\frac{{\omega {\kern 1pt} h}}{{{\omega _0}}}} \right|} \right]\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{1}{{v\left( {{\omega _0}} \right)}}{\left| {\frac{\omega }{{{\omega _h}}}} \right|^{ - \gamma }} \end{array} $ | (11) |
式中:h是一个频率不相关的常数;ωh为重新定义的调谐参数。
对于修正的相速度模型,其相应的修正Q模型为
| $ \begin{array}{l} Q(\omega ) = Q\left( {{\omega _0}} \right)\left[ {1 - \frac{1}{{{\rm{ \mathsf{ π} }}Q\left( {{\omega _0}} \right)}}\ln \left| {\frac{\omega }{{{\omega _h}}}} \right|} \right]\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = Q\left( {{\omega _0}} \right){\left| {\frac{\omega }{{{\omega _h}}}} \right|^{ - \gamma }} \end{array} $ | (12) |
本文所用的地层吸收模型即为上述模型。
2 基于反演的纵向约束吸收补偿方法在完全弹性介质中,可以用褶积模型简单描述地震数据采集过程,即地震记录可由地震子波和反射系数序列褶积外加噪声得到
| $ \begin{aligned} d(t) &=r(t) * w(t)+n(t) \\ &=\int r(\tau) w(t-\tau) \mathrm{d} \tau+n(t) \end{aligned} $ | (13) |
式中:d(t)为地震记录;r(t)为反射系数;w(t)为震源子波;n(t)为噪声。
在黏弹性介质中,由于地层的吸收衰减作用,导致震源子波会随着传播时间而变化。因此,需要将稳态的褶积模型推广到非稳态
| $ d(t)=\int w(\tau, t) r(\tau) \mathrm{d} \tau+n(t) $ | (14) |
式中w(τ,t)为时变子波,且有w(0,t)=w(t)。
根据平面波在黏弹介质中的衰减函数,震源子波传播中的衰减可表示为
| $ w(\tau, t)=\int_{-\infty}^{+\infty} \hat{\omega}(\omega) \alpha(\omega, \tau) \exp (-\mathrm{j} \omega t) \mathrm{d} \omega $ | (15) |
将式(14)离散可改写为矩阵向量形式,有
| $ \left[\begin{array}{c} d_{1} \\ d_{2} \\ \vdots \\ d_{N} \end{array}\right]=\left[\begin{array}{cccc} w\left(t_{1}, \tau_{1}\right) & w\left(t_{1}, \tau_{2}\right) & \cdots & w\left(t_{1}, \tau_{N}\right) \\ w\left(t_{2}, \tau_{1}\right) & w\left(t_{2}, \tau_{2}\right) & \cdots & w\left(t_{2}, \tau_{N}\right) \\ & & \vdots & \\ w\left(t_{N}, \tau_{1}\right) & w\left(t_{N}, \tau_{2}\right) & \cdots & w\left(t_{N}, \tau_{N}\right) \end{array}\right]\left[\begin{array}{c} r_{1} \\ r_{2} \\ \vdots \\ r_{N} \end{array}\right]+\left[\begin{array}{c} n_{1} \\ n_{2} \\ \vdots \\ n_{N} \end{array}\right] $ | (16) |
式中N为地震道的样点数。
式(16)的加入纵向约束的L2范数最优化问题可用目标函数表示为
| $ \varPhi_{1}=\|\boldsymbol{W} \boldsymbol{r}-\boldsymbol{d}\|_{2}^{2}+\mu_{t}\|\boldsymbol{r}\|_{2}^{2} $ | (17) |
式中:W为时变子波矩阵;r为反射系数向量;d为地震记录向量;μt为纵向约束因子,主要作用为调节数据残差项(第一项)与正则化项(第二项)的权重,使得反演结果更合理。通过极小化目标函数,式(17)的解可表示为
| $ \boldsymbol{r}=\left(\boldsymbol{W}^{\mathrm{T}} \boldsymbol{W}+\mu_{t} \boldsymbol{I}\right)^{-1} \boldsymbol{W}^{\mathrm{T}} \boldsymbol{d} $ | (18) |
假设地震剖面S(t,x)只有一个振幅为常数、斜率为p的线性同相轴,转换到频率域,可表示为
| $ S(f,x) = A(f)\exp ({\rm{j}}2{\rm{ \mathsf{ π} }}fxp) $ | (19) |
式中A(f)是同相轴子波的频谱。假设道间隔Δx为常数,有x=(k-1)Δx,k=1,2,…,K,K为地震剖面的道数。对于任意频率f,有
| $ {S_k}(f) = A\exp ({\rm{j}}\theta k) $ | (20) |
式中
| $ {S_k}(f) = {a_1}(f){S_{k - 1}}(f) $ | (21) |
式中a1(f)=exp(jθ)。式(21)递归方程是一阶差分方程,也称为一阶自回归(AR)模型。通过该模型,可以沿着空间方向递归地预测有效信号。
类似地,假设在时空域有M条线性同相轴,则可以用一个M阶的差分方程表示为
| $ S_{k}(f)=\sum\limits_{i=-M, i \neq 0}^{M} a_{i}(f) S_{k-i}(f) $ | (22) |
式中ai(f)表示信号预测算子,主要用于预测无噪声的叠加复谐波。式(22)也可写成预测误差形式
| $ \sum\limits_{i=-M}^{M} g_{i}(f) S_{k-i}(f)=0 $ | (23) |
式中:g0=1;gi=-ai。
在实际数据中,噪声是不可避免的。假设地震数据由有效信号和噪声叠加而成,即
| $ D_{k}=S_{k}+N_{k} $ | (24) |
将上式代入式(23),可得
| $ \sum\limits_{i=-M}^{M} g_{i}(f) D_{k-i}(f)=\sum\limits_{i=-M}^{M} g_{i}(f) N_{k-i}(f) $ | (25) |
上式为自回归滑动平均(ARMA)模型,其自回归分量和滑动平均分量相等。
实际中,经常用一个长AR模型代替ARMA模型,则
| $ \sum\limits_{i=-M}^{M} g_{i}(f) D_{k-i}(f)=D_{k}-\sum\limits_{i=-M, i \neq 0}^{M} a_{i}(f) D_{k-i}(f)=N_{k} $ | (26) |
为了更加准确地预测有效信号,AR模型中的参数M一般需大于实际同相轴的条数,而且M的确定需要应用统计准则。
假设M=2,式(26)可以写成线性方程组
| $ \left(\begin{array}{l}D_{3} \\ D_{4} \\ D_{5}\end{array}\right)-\left(\begin{array}{lllll}D_{5} & D_{4} & D_{3} & D_{2} & D_{1} \\ D_{6} & D_{5} & D_{4} & D_{3} & D_{2} \\ D_{7} & D_{6} & D_{5} & D_{4} & D_{3}\end{array}\right)\left(\begin{array}{l}a_{-2} \\ a_{-1} \\ 0 \\ a_{1} \\ a_{2}\end{array}\right)=\left(\begin{array}{c}N_{3} \\ N_{4} \\ N_{5}\end{array}\right) $ | (27) |
其矩阵表达式为
| $ \boldsymbol{D}-\boldsymbol{Ya} =\boldsymbol{N} $ | (28) |
为了最小化噪声能量,建立目标函数
| $ J=\|\boldsymbol{D}-\boldsymbol{Y} \boldsymbol{a}\|_{2}^{2} $ | (29) |
| $ \boldsymbol{Y}^{\mathrm{H}} \boldsymbol{Y} \boldsymbol{a}=\boldsymbol{Y}^{\mathrm{H}} \boldsymbol{D} $ | (30) |
式中上标“H”表示共轭转置。需要注意的是,矩阵YHY为Toeplitz矩阵,因此可用Levinson递归法快速求解。为了获得稳定的滤波器系数,通常需要在Toeplitz矩阵的对角线上增加一个小的扰动μ1,则式(30)改写为
| $ \left(\boldsymbol{Y}^{\mathrm{H}} \boldsymbol{Y}+\mu_{1} \boldsymbol{I}\right) \boldsymbol{a}=\boldsymbol{Y}^{\mathrm{H}} \boldsymbol{D} $ | (31) |
那么待求的信号预测算子为
| $ \boldsymbol{a}=\left(\boldsymbol{Y}^{\mathrm{H}} \boldsymbol{Y}+\mu_{1} \boldsymbol{I}\right)^{-1} \boldsymbol{Y}^{\mathrm{H}} \boldsymbol{D} $ | (32) |
每一个频率的预测算子是相互独立的,将每个频率的一维预测算子依次排列,可得一维预测算子
| $ \tilde{\boldsymbol{Q}}=\left[\begin{array}{ccccc} a_{-2}\left(f_{1}\right) & a_{-1}\left(f_{1}\right) & 0 & a_{1}\left(f_{1}\right) & a_{2}\left(f_{1}\right) \\ a_{-2}\left(f_{2}\right) & a_{-1}\left(f_{2}\right) & 0 & a_{1}\left(f_{2}\right) & a_{2}\left(f_{2}\right) \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ a_{-2}\left(f_{I}\right) & a_{-1}\left(f_{I}\right) & 0 & a_{1}\left(f_{I}\right) & a_{2}\left(f_{I}\right) \end{array}\right] $ | (33) |
式中I为频点数。将每个频率的一维预测算子作用于含随机噪声的数据,可预测出有效信号
| $ \mathit{\boldsymbol{\hat D}} = \mathit{\boldsymbol{Ya}} $ | (34) |
在频率空间域,对于地震信号的预测过程,为求得预测误差
| $ \tilde{\boldsymbol{P}}=\left[\begin{array}{ccccc} a_{-2}\left(f_{1}\right) & a_{-1}\left(f_{1}\right) & -1 & a_{1}\left(f_{1}\right) & a_{2}\left(f_{1}\right) \\ a_{-2}\left(f_{2}\right) & a_{-1}\left(f_{2}\right) & -1 & a_{1}\left(f_{2}\right) & a_{2}\left(f_{2}\right) \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ a_{-2}\left(f_{I}\right) & a_{-1}\left(f_{I}\right) & -1 & a_{1}\left(f_{I}\right) & a_{2}\left(f_{I}\right) \end{array}\right] $ | (35) |
可见,该信号预测误差算子除了在输出位置的系数为-1以外,其他系数与信号预测算子的系数完全相同。地震信号的空间可预测性主要来源于地震同相轴的空间展布特征(即构造特征),信号预测误差算子直接反映了地震反射结构特征。需要注意的是,预测误差算子作用于地震数据的结果不是有效信号,而是预测误差。
现有的纵向约束吸收补偿并未考虑到地震道横向之间的关系。为了弥补这一缺陷,将地震信号的反射结构特征(即信号预测误差算子)也作为一种约束引入到吸收补偿算法。基于反演的全局约束吸收补偿方法具体计算过程如下。
(1) 通过解最小二乘的问题
| $ \begin{aligned} \varPhi_{2}=& D_{k}(f)-\sum\limits_{i=1}^{M} a_{i} D_{k-i}(f)-\sum\limits_{i=-1}^{-M} a_{i} D_{k-i}(f) \|_{2}^{2}+\\ & \lambda \sum\limits_{i=-M, i \neq 0}^{M}\left\|a_{i}\right\|_{2}^{2} \end{aligned} $ | (36) |
获得预测算子
(2) 由预测算子可得到预测误差算子
| $ \boldsymbol{P}=\left(a_{-M}, \cdots, a_{-2}, a_{-1},-1, a_{1}, a_{2}, \cdots, a_{M}\right) $ | (37) |
由所有频率的预测误差算子P组成全频段预测误差算子矩阵
(3) 通过反演
| $ \varPhi_{3}=\|\hat{\boldsymbol{D}}-\boldsymbol{D}\|_{2}^{2}+\mu_{2}\|\tilde{\boldsymbol{P}} \hat{\boldsymbol{D}}\|_{2}^{2} $ | (38) |
计算去噪地震数据。式中μ2为权衡参数。通过多次迭代求解式(38),可得频率域去噪数据。
(4) 根据频率域去噪后数据重新计算一个新预测误差算子
(5) 将重新计算的算子
| $ \varPhi_{4}=\|\boldsymbol{W} \boldsymbol{r}-\boldsymbol{d}\|_{2}^{2}+\mu_{t}\|\boldsymbol{r}\|_{2}^{2}+\mu_{x}\|\tilde{\boldsymbol{P}} \boldsymbol{W} \boldsymbol{r}\|_{2}^{2} $ | (39) |
式中μx为横向约束因子。新的目标函数的解可表示为
| $ \boldsymbol{r}=\left[\boldsymbol{W}^{\mathrm{T}} \boldsymbol{W}+\mu_{t} \boldsymbol{I}+\mu_{x}(\tilde{\boldsymbol{P}} \boldsymbol{W})^{\mathrm{T}}(\tilde{\boldsymbol{P}} \boldsymbol{W})\right]^{-1} \boldsymbol{W}^{\mathrm{T}} \boldsymbol{d} $ | (40) |
本文提出的基于反演的全局约束多道吸收补偿方法的横向约束算子由原始的地震剖面求得,包含了原始数据的反射结构信息,能够较明显地提高吸收补偿结果的稳定性和抗噪性,同时还保持了同相轴的横向连续性。
4 应用 4.1 Marmousi模型试算为验证本文方法相对于纵向约束吸收补偿方法的优越性,利用Marmousi模型进行测试。
图 1a是原始反射系数与主频为30Hz的Ri-cker子波褶积得到的Marmousi模型模拟数据,可以看出,Marmousi模型构造复杂,既有平滑的同相轴,也有大型的背斜构造和一些小型断裂。图 1b是Marmousi模型的衰减数据,其中Q设为50。图 1c和图 1d是信噪比(SNR)分别为5和20的加噪衰减数据,可以看出,由于地层吸收的影响,地震资料的分辨率降低,原有的构造反射特征变模糊。另外,随机噪声污染了地震反射信号。

|
图 1 Marmousi模型数据 (a)原始模拟数据;(b)衰减模拟数据;(c)SNR=5的加噪衰减数据;(d)SNR=20的加噪衰减数据 |
分别采用传统的纵向约束方法和本文的全局约束方法对图 1b所示的无噪衰减数据进行补偿,结果如图 2所示。其中纵向约束吸收补偿过程中μt=0.1,本文方法中μt=0.1,μx=1.0。比较图 2a与图 2b可以看出,在无噪情况下,纵向约束吸收补偿方法和本文方法均能很好地恢复地震波能量,提高地震资料的分辨率。对比图中红色箭头处可知,本文方法的结果横向更加连续、平滑,构造结构更清晰,弱反射得到了较好的恢复,证明了本文方法的效果更好。图 3为无噪衰减数据两种方法补偿前、后单道频谱对比,可以看出,两种方法都有效补偿了中高频的振幅衰减,并且拓宽了原始数据的地震频带,但本文方法补偿结果的频带略宽,包含更丰富的高频有效信息。
|
图 2 无噪衰减数据两种方法补偿结果 (a)纵向约束补偿;(b)本文方法 |

|
图 3 无噪数据两种方法补偿前、后单道频谱对比 (a)第100道;(b)第103道;(c)第123道 |
对于含噪衰减数据,纵向约束吸收补偿结果虽然恢复了地震波能量,提高了地震资料的分辨率,但是吸收补偿结果的信噪比较低,地震同相轴的横向连续性较差(图 4a)。本文方法的补偿结果不仅能够提高地震资料的分辨率,使得构造反射结构更清晰,同时也能保证补偿结果的信噪比,横向上更加连续(图 4b),如图中红色箭头所示,本文方法恢复出了更多的细节,表明本文方法比纵向约束吸收补偿方法具有更强的稳定性和抗噪性。
|
图 4 SNR=5(左)和SNR=20(右)含噪数据两种方法补偿结果对比 (a)纵向约束方法;(b)本文方法 |
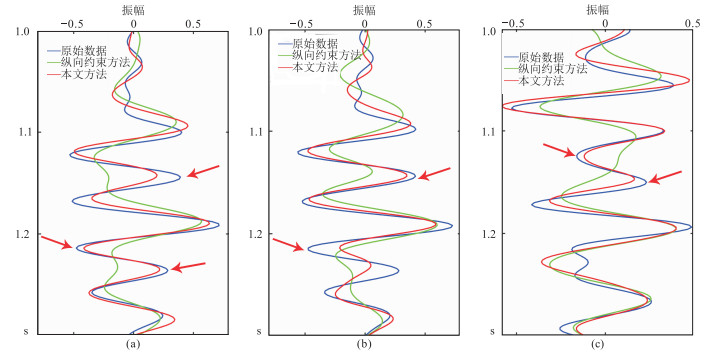
图 5为SNR=5含噪衰减数据利用两种方法补偿结果的单道对比,可以看出,本文方法补偿后与原始数据更相似,无论振幅还是相位,纵向补偿效果均较好(红色箭头所示)。图 6为图 5结果的频谱对比,可以看出,在含噪情况下,两种方法均能补偿中高频的振幅衰减,并且拓宽了补偿前数据的地震频带。此外,纵向约束补偿结果的高频部分略微强于本文方法补偿结果,有可能是前者对高频噪声的过度放大所致。
|
图 5 SNR=5含噪数据两种方法补偿结果单道对比 (a)第100道;(b)第103道;(c)第123道 |
|
图 6 SNR=5含噪数据两种方法补偿结果单道频谱对比 (a)第100道;(b)第103道;(c)第123道 |
以均方根振幅为衡量地震剖面横向连续性,图 7为SNR=5含噪衰减数据两种方法补偿结果的横向连续性对比,可见本文方法补偿结果横向上与补偿前数据更加接近,横向上抖动较小(红色箭头所示),体现了本文方法在保持剖面横向连续性和稳定性方面的优势。
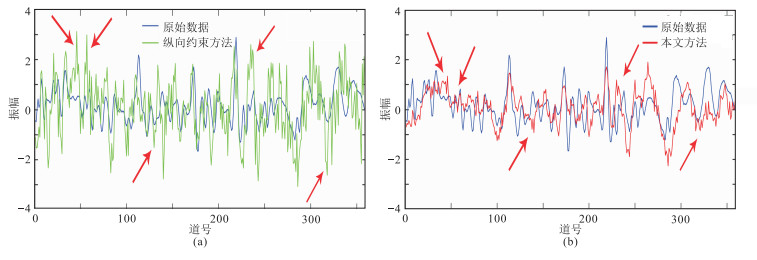
|
图 7 SNR=5含噪数据两种方法补偿结果的横向连续性对比 (a)纵向约束方法;(b)本文方法 |
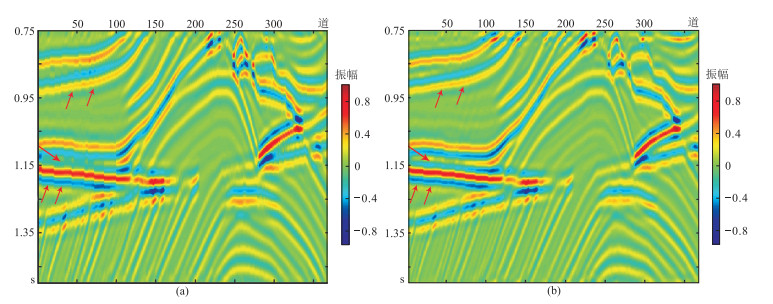
图 8a为二维实际地震叠加剖面,采用纵向约束吸收补偿方法和本文方法的处理结果分别如图 8b、图 8c所示。可以看出,纵向约束补偿方法虽然可以提高地震资料的分辨率,但补偿后地震剖面中的噪声被放大,信噪比较低;经本文方法处理后,地震资料的能量衰减得到有效补偿,地震分辨率得到一定提升,而且补偿后地震记录信噪比较高,噪声得到有效压制,地震剖面的同相轴更连续。由此可见,本文提出的基于反演的全局约束吸收补偿方法比传统的纵向约束吸收补偿方法具有更强的稳定性和抗噪性,其结果更利于后续的解释和反演。
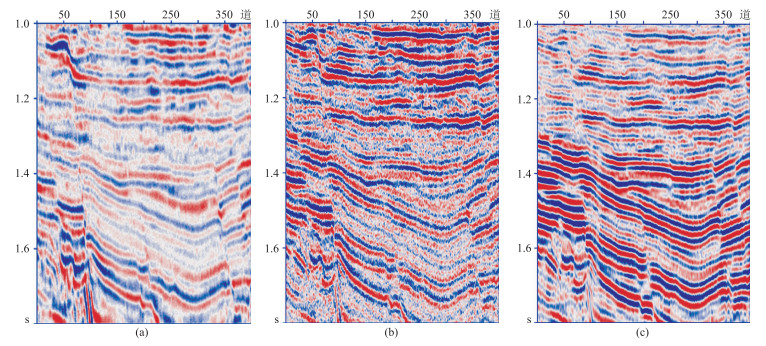
|
图 8 实际地震剖面两种方法补偿结果对比 (a)原始;(b)纵向约束方法;(c)本文方法 |
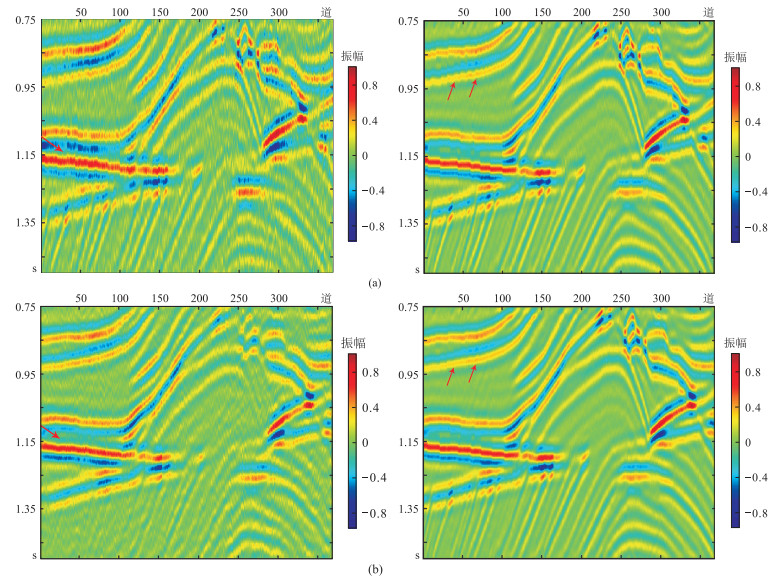
图 9为图 8数据的局部放大对比,可以看出,相较于原始剖面(图 9a),本文方法补偿剖面(图 9c)同相轴增多、更加清晰,提高了分辨率和信噪比,构造更加清楚可辨;相较于纵向约束方法补偿结果(图 9b),本文方法补偿结果信噪比较高,横向更连续。
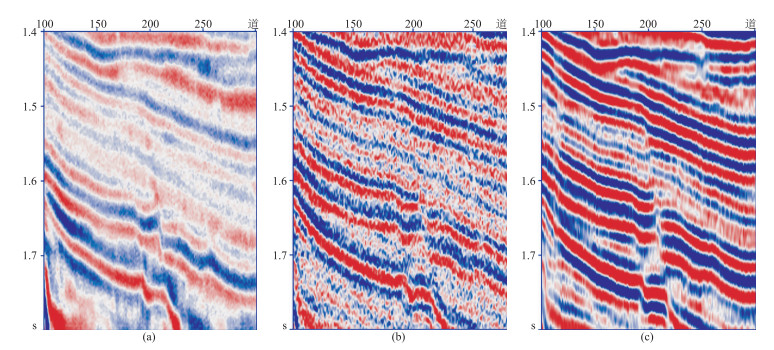
|
图 9 实际地震剖面两种方法补偿结果放大对比 (a)原始剖面;(b)纵向约束补偿剖面;(c)全局约束补偿剖面 |
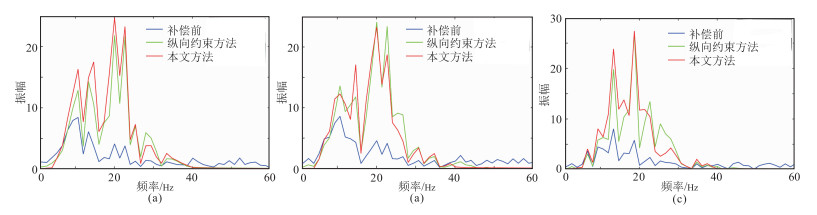
图 10为实际地震剖面两种方法补偿后的单道频谱对比,可以看出,两种方法均能有效补偿地震数据中高频振幅衰减,一定程度上拓宽了数据的地震频带,其中纵向约束方法处理结果高频部分相对较强,是高频噪声放大效应的体现。
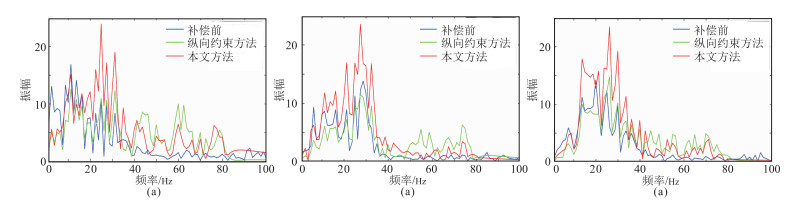
|
图 10 实际地震剖面两种方法补偿结果的单道频谱对比 (a)第100道;(b)第200道;(c)第300道 |
(1) 本文将传统的单道吸收补偿方法拓展到了多道吸收补偿,由地震信号的可预测表达计算信号预测误差算子,并将其作为横向约束算子引入多道反演框架中,提出了一种基于反演的全局约束多道吸收补偿方法。
(2) 本文方法的目标函数表达式包含了纵向和横向两个方向上的约束信息,既考虑了纵向上的地震道稀疏分布信息,又考虑了横向上的地震道间的连续性。
(3) 模型数据和实际数据补偿结果表明,本文提出的基于反演的全局约束多道吸收补偿方法具有更强的抗噪性和更高的稳定性,可有效减小补偿对于高频噪声的放大效应,提高了地震记录分辨率和信噪比,同相轴横向上更连续。
(4) 由于基于反演的全局约束多道吸收补偿方法属于多道反演算法,运算量大,计算效率较低,以后可从数值解法和矩阵运算等方面进行优化以提高计算效率。
| [1] |
Kjartansson E. Constant Q wave propagation and attenuation[J]. Journal of Geophysical Research, 1979, 84(B9): 4737-4748. DOI:10.1029/JB084iB09p04737 |
| [2] |
苏勤, 曾华会, 田彦灿, 等. 表层Q值确定性求取与空变补偿方法[J]. 石油地球物理勘探, 2019, 54(5): 988-996. SU Qin, ZENG Huahui, TIAN Yancan, et al. Near-surface Q value estimation and quantitative amplitude compensation[J]. Oil Geophysical Prospecting, 2019, 54(5): 988-996. |
| [3] |
陈增保, 陈小宏, 李景叶, 等. 一种带限稳定的反Q滤波算法[J]. 石油地球物理勘探, 2014, 49(1): 68-75. CHEN Zengbao, CHEN Xiaohong, LI Jingye, et al. A band-limited and robust inverse Q filtering algorithm[J]. Oil Geophysical Prospecting, 2014, 49(1): 68-75. |
| [4] |
凌云, 高军, 吴琳. 时频空间域球面发散与吸收补偿[J]. 石油地球物理勘探, 2005, 40(2): 176-182, 189. LING Yun, GAO Jun, WU Lin. Compensation for spherical dispersion and absorption in time-frequency-space domain[J]. Oil Geophysical Prospecting, 2005, 40(2): 176-182, 189. DOI:10.3321/j.issn:1000-7210.2005.02.018 |
| [5] |
冯玮, 胡天跃, 常丁月, 等. 基于时变子波的品质因子估计[J]. 石油地球物理勘探, 2018, 53(1): 136-146. Feng Wei, Hu Tianyue, Chang Dingyue, et al. Quality factor Q estimation based on time-varying wavelet[J]. Oil Geophysical Prospecting, 2018, 53(1): 136-146. |
| [6] |
吴吉忠, 左虎. 叠前衰减补偿时间偏移及GPU实现[J]. 石油地球物理勘探, 2019, 54(1): 84-92. WU Jizhong, ZUO Hu. Attenuation compensation in prestack time migration and its GPU implementation[J]. Oil Geophysical Prospecting, 2019, 54(1): 84-92. |
| [7] |
张壹, 王赟, 陈本池, 等. 强衰减介质中地震波场的频率—空间域特征[J]. 石油地球物理勘探, 2020, 55(5): 1016-1028, 1046. ZHANG Yi, WANG Yun, CHEN Benchi, et al. Cha-racteristics of seismic wave field in frequency-space domain in strong attenuation media[J]. Oil Geophysical Prospecting, 2020, 55(5): 1016-1028, 1046. |
| [8] |
蒋立, 陈勇, 肖艳玲, 等. 地表过渡带近地表Q补偿与地表一致性反褶积处理效果对比研究[J]. 石油物探, 2018, 57(6): 870-877. JINAG Li, CHEN Yong, XIAO Yanling, et al. A comparison of near-surface Q compensation and surface-consistent deconvolution in the near-surface transition zone[J]. Geophysical Prospecting for Petroleum, 2018, 57(6): 870-877. DOI:10.3969/j.issn.1000-1441.2018.06.009 |
| [9] |
Chai X, Wang S, Yuan S, et al. Sparse reflectivity inversion for nonstationary seismic data[J]. Geophy-sics, 2014, 79(3): V93-V105. |
| [10] |
Li G F, Liu Y, Zheng H, et al. Absorption decomposition and compensation via a two step scheme[J]. Geophysics, 2015, 80(6): V145-V155. DOI:10.1190/geo2015-0038.1 |
| [11] |
Zhang C, Ulrych T J. Seismic absorption compensation: A least squares inverse scheme[J]. Geophysics, 2007, 72(6): R109-R114. DOI:10.1190/1.2766467 |
| [12] |
Braga S, Moraes S. High-resolution gathers by inverse Q filtering in the wavelet domain[J]. Geophy-sics, 2013, 78(2): V53-V61. |
| [13] |
Oliveira S, Lupinacci W M. L1 norm inversion method for deconvolution in attenuating media[J]. Geophysical Prospecting, 2013, 61(4): 771-777. DOI:10.1111/1365-2478.12002 |
| [14] |
Wang S, Chen X. Absorption-compensation method by L1-norm regularization[J]. Geophysics, 2014, 79(3): V107-V114. DOI:10.1190/geo2013-0206.1 |
| [15] |
Zhang R, Sen M K, Srinivasan S. Multi-trace basis pursuit inversion with spatial regularization[J]. Journal of Geophysics & Engineering, 2013, 10(3): 12-35. |
| [16] |
Kazemi N, Sacchi M D. Sparse multichannel blind deconvolution[J]. Geophysics, 2014, 79(5): V143-V152. DOI:10.1190/geo2013-0465.1 |
| [17] |
Yuan S, Wang S, Luo C, et al. Simultaneous multitrace impedance inversion with transform-domain sparsity promotion[J]. Geophysics, 2015, 80(2): R71-R80. DOI:10.1190/geo2014-0065.1 |
| [18] |
Yuan S, Wang S, Tian N, et al. Stable inversion-based multitrace deabsorption method for spatial continuity preservation and weak signal compensation[J]. Geophysics, 2016, 81(3): V199-V212. DOI:10.1190/geo2015-0247.1 |
| [19] |
Soubaras R. Signal-preserving random noise attenuation by the F-x projection[J]. SEG Technical Program Expanded Abstracts, 1994, 13: 1576-1579. |
| [20] |
李国发. f-k域与f-x域联合实现道内插[J]. 石油地球物理勘探, 1995, 30(5): 693-701. LI Guofa. Joint trace interpolation in f-k and f-x domains[J]. Oil Geophysical Prospecting, 1995, 30(5): 693-701. DOI:10.3321/j.issn:1000-7210.1995.05.001 |
| [21] |
蔡加铭, 周兴元, 吴律. F-x域算子外推去噪技术研究[J]. 石油地球物理勘探, 1999, 34(3): 325-331. CAI Jiaming, ZHOU Xingyuan, WU Lü. A technique for noise elimination using operator extrapolation F-x domain[J]. Oil Geophysical Prospecting, 1999, 34(3): 325-331. |
| [22] |
魏海涛, 陆文凯, 郑晓东. 基于F-X域预测和全变分的串行滤波器[J]. 石油地球物理勘探, 2011, 46(5): 700-704. WEI Haitao, LU Wenkai, ZHENG Xiaodong. Cascaded filter based on F-X prediction and total variation filter[J]. Oil Geophysical Prospecting, 2011, 46(5): 700-704. |
| [23] |
康冶, 于承业, 贾卧, 等. f-x域去噪方法研究[J]. 石油地球物理勘探, 2003, 38(2): 136-138. KANG Ye, YU Chengye, JIA Wo, et al. A study on noise-suppression method in f-x domain[J]. Oil Geophysical Prospecting, 2003, 38(2): 136-138. DOI:10.3321/j.issn:1000-7210.2003.02.007 |
| [24] |
Liu G. F-x nonstationary seismic data interpolation using complex nonstationary autoregression[J]. Extended Abstracts of 76th EAGE Conference and Exhibition, 2014, 1-5. |
| [25] |
Spitz S. Seismic trace interpolation in the F-X domain[J]. Geophysics, 1991, 56(6): 785-794. DOI:10.1190/1.1443096 |
| [26] |
Kolsky H. The propagation of stress pulses in visco-elastic solids[J]. Philosophical Magazine, 1956, 1(8): 693-710. DOI:10.1080/14786435608238144 |
| [27] |
Wang Y, Guo J. Modified Kolsky model for seismic attenuation and dispersion[J]. Journal of Geophysics and Engineering, 2004, 1(3): 187-196. DOI:10.1088/1742-2132/1/3/003 |



 刘金涛, 甘肃省兰州市城关区雁儿湾路535号中国石油勘探开发研究院西北分院, 730030。Email:
刘金涛, 甘肃省兰州市城关区雁儿湾路535号中国石油勘探开发研究院西北分院, 730030。Email: 