② 北京京能油气资源开发有限公司, 北京 100022;
③ 东方地球物理公司研究院地质研究中心, 河北涿州 072751;
④ 中国石油川庆钻探公司地质勘探开发研究院, 四川成都 610051
② Beijing Jingneng Oil & Gas Resources Development Co. Ltd, Beijing 100022, China;
③ BGP Geological Research Center, CNPC, Zhuo-zhou, Hebei 072751, China;
④ CCDC Geological Exploration & Development Research Institute, CNPC, Chengdu, Sichuan 610051, China
可控震源地震勘探采用变频的正弦信号激发,产生一个持续较久的非线性带限信号,再通过脉冲压缩将信号转成幅度大、有效持续时间短的脉冲信号[1-2]。
自20世纪60年代以来,可控震源已逐渐成为地震勘探领域重要的激发源之一,与炸药震源相比具有经济、安全的优点。在全球范围内,可控震源采集约占陆地勘探总工作量的70%[3-4]。
谐波干扰降低了地震资料的分辨率和品质[5],因此谐波压制是可控震源数据处理的研究重点。谐波产生的原因主要有三个:一是因为可控震源的震动装置和机械装置的非线性振动产生谐振,导致可控震源的输出信号本身就存在谐波干扰;二是因为地质或地表条件较为复杂,震源平板与地面的耦合状况通常不好[6-7];三是可控震源施工参数的不合理很容易产生谐波干扰。
可控震源地震采集效率长期受扫描时间和记录时长的限制。为此,Rozemond[8]提出了滑动扫描(Slip-sweep)技术。该技术使用一种快捷的可控多源激发方式,其特点为前一炮扫描未结束下一炮即开始,时间上多组震源重叠扫描,大大提高了采集效率[9]。但记录为多组震源共同产生的混叠记录,后炮产生的谐波畸变足以干扰前一炮甚至前几炮的数据,致使其畸变愈加严重。如今压制滑动扫描谐波干扰较多使用“依次消去法”,即从最后一炮的信号开始往前计算,将每一炮的信号减去后一炮的信号,经过大量迭代计算再进行谐波压制,该方法时间成本较高。
Schrodt[10]、Martin等[11]和Reust[12]讨论了震源谐波畸变和相位变化问题,认为输出力信号越大、地面越坚硬,可控震源的谐波畸变也就愈发严重;Lebedev等[13-14]认为可控震源平板与大地接触而产生的谐波畸变是非线性的;Okaya等[15]在时频域设计滤波器可以压制可控震源与地面耦合产生的谐波畸变;Ras等[16]采用差异叠加技术可以较好地消除可控震源滑动扫描方式的谐波畸变;Dal Moro等[17]基于遗传算法将地震道中高阶谐波能量最小化。最近几年,谐波压制的方法与理论飞速发展,所有谐波去除方法也都各有利弊[18-23]。针对线性扫描方式,Li等[24-25]提出纯相移滤波压制谐波法,利用改变各次谐波的相位,将基波信号与高次谐波信号在坐标轴上分开,通过充零处理达到消除谐波畸变信号的目的。该方法既直观又高效,但实际中却很少使用,原因在于应用条件较为严苛,一旦信号受到白噪声的影响或在滑动扫描中受到来自邻炮的干扰,传统纯相移法将无法滤除全部干扰信号。
本文在纯相移法的基础上,提出一种经历两次相移变换的“双相移”滤波谐波压制方法,以克服传统纯相移法的不足。
1 原理以可控震源线性升频扫描信号为例,参考信号可以表示为
| $ s(t) = a(t)\sin \left[ {2{\rm{ \mathsf{ π} }}\int_0^t f (\tau ){\rm{d}}\tau } \right] $ | (1) |
式中:a为振幅;f为频率。令
| $ a(t) = \left\{ {\begin{array}{*{20}{l}} {\frac{A}{2}\left[ {1 + \cos \left( {{\rm{ \mathsf{ π} }}\frac{{{T_0} + t}}{{{T_0}}}} \right)} \right]}&{0 \le t \le {T_0}}\\ A&{{T_0} < t < T - {T_0}}\\ {\frac{A}{2}\left[ {1 + \cos \left( {{\rm{ \mathsf{ π} }}\frac{{T - t}}{{{T_0}}}} \right)} \right]}&{T - {T_0} \le t \le T} \end{array}} \right. $ | (2) |
式中:A为固定振幅值;T为信号的扫描长度;为防止Gibbs效应中的振幅突变,扫描信号的起、止点处要设置两个过渡,T0为扫描信号的过渡时间。
在传统的纯相移法设计的k次谐波滤波器的基础上,再设计一个m次谐波滤波器,其中1 < k < 2,0 < m < 1,构造相应的相移算子和反相移算子。其中k和m取值不接近1会导致大量白噪无法去除,而过于接近1会导致基波本身的信号被过滤掉,因此k和m取值较接近1为最佳,本文在模型试算和实际数据处理中取k=1.1、m=0.9,得到的滤波结果较理想。
构造假想的k次谐波,可表示为
| $ {s_k}(t) = {a_k}(t)\sin \left[ {2{\rm{ \mathsf{ π} }}k\int_0^t f (\tau ){\rm{d}}\tau } \right] $ | (3) |
对上式进行Fourier变换,有
| $ {S_k}(f) = \left| {{S_k}(f)} \right|\exp \left[ { - {\rm{i}}{\mathit{\Phi }_k}(f)} \right] $ | (4) |
式中Φk为k阶谐波的相位。
当|Sk(f)|=1时,构造的k次相移算子及反相移算子分别为
| $ {S_k^*(f) = \exp \left[ {{\rm{i}}{\mathit{\Phi }_k}(f)} \right]} $ | (5) |
| $ {S_k^ \cdot (f) = \exp \left[ { - {\rm{i}}{\mathit{\Phi }_k}(f)} \right]} $ | (6) |
同理构造m次相移算子及反相移算子为
| $ S_m^*(f) = \exp \left[ {{\rm{i}}{{\rm{\Phi }}_m}(f)} \right] $ | (7) |
| $ S_m^ \cdot (f) = \exp \left[ { - {\rm{i}}{{\rm{\Phi }}_m}(f)} \right] $ | (8) |
利用相移算子旋转信号,使谐波畸变信号的基波和谐波作相移分离。
谐波畸变信号可表示为
| $ s(t) = \sum\limits_{l = 1}^L {{s_l}} (t) = \sum\limits_{l = 1}^L {{a_l}} (t)\sin \left[ {2{\rm{ \mathsf{ π} }}l\int_0^t f (\tau ){\rm{d}}\tau } \right] $ | (9) |
式中L为最高谐波次数。
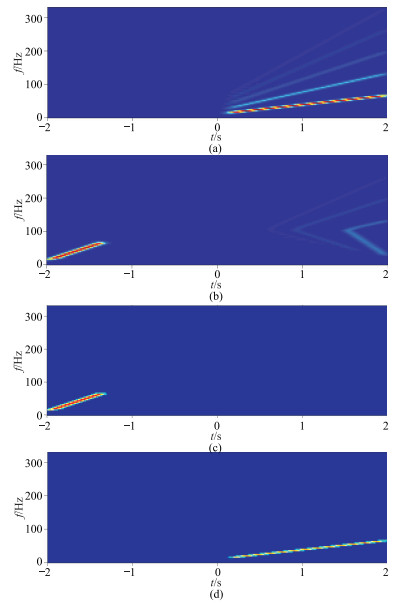
图 1a为模拟谐波畸变信号s(t)的时频谱。需要注意的是,信号的相移变换是由时域经Fourier变换在频率域中进行。而本文为了形象化展示,对过程的分析则是通过短时Fourier变换在时频域中进行。
|
图 1 纯相移法还原基波信号具体步骤的时频分析 (a) 模拟畸变信号s(t)时频谱;(b)经相移之后的信号s′(t)时频谱;(c)滤波后信号s″(t)时频谱;(d)纯相移法还原的基波信号st(t)时频谱 |
利用Fourier变换将谐波畸变信号从时间域变换到频率域,应用相移算子对谐波信号S(f)进行第一次相移处理
| $ S^{\prime}(f)=S(f) \cdot S_{k}^{*}(f) $ | (10) |
对其进行反Fourier变换回时间域。图 1b为信号s(t)经相移之后的信号s′(t)的时频谱,可见基波信号和高次谐波得到分离。设计一个去掉正时间轴区的高次谐波滤波器,使正时间轴区谐波信号振幅值为零
| $ \left\{\begin{array}{ll} s^{\prime \prime}(t)=s^{\prime}(t) & t \leqslant 0 \\ s^{\prime \prime}(t)=0 & t>0 \end{array}\right. $ | (11) |
滤波后信号s″(t)的时频谱如图 1c所示。再用Fourier变换将信号变到频率域,用k次反相移算子对信号进行反相移
| $ S_{\mathrm{t}}(f)=S^{\prime \prime}(f) S_{k}^ \cdot(f) $ | (12) |
直接对St(f)进行反Fourier变换,则获得传统纯相移法的滤波结果。纯相移法还原的基波信号st(t)时频谱如图 1d所示,可见,理想情况下,传统的纯相移滤波法可以较为精确地去除高次谐波。
双相移法区别之处在于使用m次相移算子进行第二次相移
| $ \hat S(f) = {S_{\rm{t}}}(f)S_m^*(f) $ | (13) |
将第二次相移信号反Fourier变换时间域信号
| $ \left\{ {\begin{array}{*{20}{l}} {{{\hat s}^\circ }(t) = \hat s(t)}&{t \le 0}\\ {{{\hat s}^\circ }(t) = 0}&{t > 0} \end{array}} \right. $ | (14) |
将
| $ {S^\circ }(f) = {{\hat S}^\circ }(f)S^ \cdot_m (f) $ | (15) |
将S°(f)反变换回时间域,就得到两次相移、滤波后的最终基波信号s°(t)。
上述即为基于纯相移法、将信号进行两次相移和滤波的双相移滤波谐波压制法,以达到去除信号中高次谐波、白噪、相邻炮信号以及其他界面的反射信号的目的。
2 模型测试 2.1 谐波及白噪压制测试 2.1.1 测试信号以可控震源线性升频扫描为例,扫描长度T=2s,起始频率和终止频率分别为10Hz和70Hz,5次以上的谐波分量忽略不计。令基波信号的振幅为8,2~5次谐波信号的振幅分别是基波信号的60%、40%、20%和10%。将五个信号叠加可得模拟的谐波畸变信号s。为了突出双相移法与传统纯相移法在处理白噪方面的差别,在谐波畸变信号中加入较强随机噪声(噪声能量约为有效信号的3倍,信噪比约为-4.7dB),得到含噪的谐波畸变信号(图 2)。

|
图 2 含噪谐波畸变信号的时频谱 |
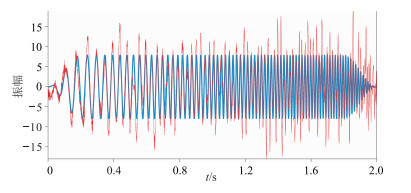
令纯相移法中的k=1.5,使用传统纯相移法处理含噪的谐波畸变信号
|
图 3 纯相移法还原的基波(红色)与原始基波信号(蓝色)的对比 |
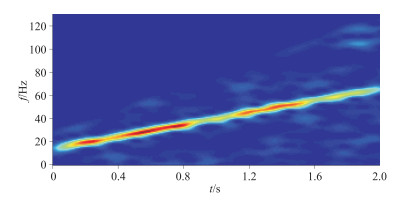
|
图 4 纯相移法还原的基波信号时频谱 |
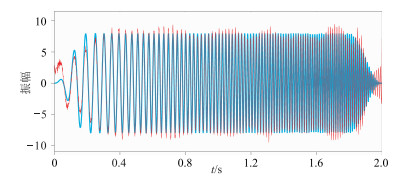
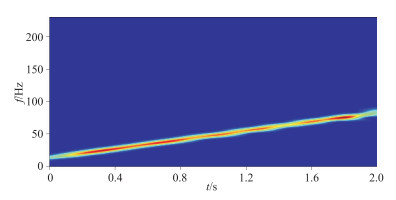
在实际力信号中,白噪声在时频图中的频率分布是完全随机的,且双相移法保留的是两条相移频率曲线之间的信号,因此为了更有效地去除基波以外其他信号的干扰,k和m的取值须接近1,使得两条频率曲线的夹角较小,以去除更大频率范围的干扰。取k=1.1、m=0.9,对图 2的含噪谐波畸变信号进行双相移滤波谐波压制,还原的基波信号与真实基波信号的对比如图 5所示,还原的基波信号时频谱如图 6所示。由图 5、图 6可见,双相移法不仅压制了谐波畸变信号中的高次谐波,白噪声也基本被滤除。
|
图 5 双相移法还原的基波(红色)与原始基波信号(蓝色)的对比 |
|
图 6 双相移法还原的基波信号时频谱 |
对比图 5、图 6与图 3、图 4可知,双相移法相对于传统的纯相移滤波法,可以更为有效地去除包含白噪等频率低于基波的信号。此外,强噪声也影响了双相移法的还原结果,还原的基波信号出现了畸变,随着信噪比的升高而畸变会逐渐减小。
2.2 滑动扫描信号应用在滑动扫描的记录中,当前炮的信号会受到来自上一炮和下一炮信号的干扰。在压制基于滑动扫描畸变信号的谐波干扰时,传统的方法为“依次消去法”,即从最后一炮的信号开始从后往前计算,将每一炮的信号减去后一炮的信号,最终经过大批次的计算得到本炮的畸变信号,再对该畸变信号进行谐波压制。该方法较为费时。
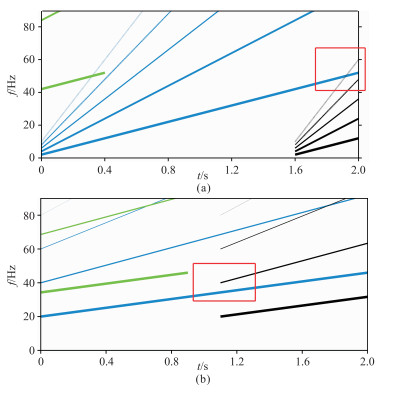
本文使用双相移法进行滑动扫描的记录谐波压制,其做法大体分为两种:第一,令下一炮信号中振幅过大、必须滤除的所有阶次谐波的频率均低于本炮基波信号频率,即“避让式”滤波,如图 7a所示;第二,令后一炮信号的二阶及以上高次谐波的频率高于本炮基波信号,即“穿插式”滤波,如图 7b所示。两种方法都需保证基波信号的扫描起止频率和滑动时间具有特定的关系。
|
图 7 滑动扫描信号用双相移法谐波压制示意图 (a)“避让式”;(b)“穿插式”。绿线为来自上一炮的信号;蓝线为本炮信号;黑线为来自下一炮的信号;红框内本炮基波信号频率与下一炮谐波信号频率交叠 |
由于高阶谐波的振幅是随着阶数升高而逐渐减小,定义N为下一炮信号中振幅过大、必须滤除的谐波的最高阶次,即N+1次以上的谐波振幅很小或可以忽略不计。在升频信号中,由于高阶谐波的斜率大于基波,因此只需在t=T时来自下一炮的N次谐波频率低于本炮基波频率即可,即
| $ N \times f(T-\Delta t)<f(T) $ | (16) |
式中Δt为滑动扫描的时间间隔。令f0为可控震源起始扫描频率,f1为终止扫描频率,将
| $ \Delta t>T \times \frac{1-\frac{1}{N}}{1-\frac{f_{0}}{f_{1}}} $ | (17) |
因滑动扫描有个隐含条件Δt < T,因此只需
同时,由于可控震源升频扫描时f0/f1恒小于1,因此应满足Δt/T>(1-1/N),该条件为Δt应满足的条件。
假定实际生产中N=4,则滑动时间条件满足Δt/T>3/4。但由于Δt越小采集效率越高,因此在Δt/T>3/4的情况下采集效率无法得到保证。实际作业中线性基波信号中的f1/f0通常较大(≥3),因此“避让式”双相移滤波谐波压制法只有不需要保证高采集效率的情况下才推荐使用,这大大减小了“避让式”的适用范围。
2.2.2 “穿插式”滤波为了应用双相移法压制高效滑动扫描采集资料的谐波干扰,本文提出了“穿插式”谐波去除法。
假设在当前炮的持续时间范围内,最晚一炮的二次谐波在时频图上完全位于本炮的基波之上,即
| $ \frac{f_{1}}{f_{0}}<\frac{\frac{T}{\Delta t}}{\operatorname{ceil}\left(\frac{T}{\Delta t}-1\right)}+1=c $ | (18) |
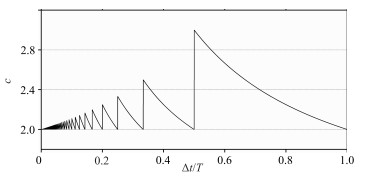
c随Δt/T的变化曲线如图 8所示,c的变化范围为2~3,由此可将可控震源信号的f1/f0分三种情况,分别讨论其滑动时间间隔Δt的取值范围。
|
图 8 Δt/T与c关系曲线 |
(1) 当f1/f0≥3时,无论滑动时间Δt如何取值,当前炮基波的频率谱始终会与来自后炮高次谐波产生交点,此时无法满足“穿插式”双相移法的频率条件,该情况下不推荐构筑“穿插式”频率模型使用双相移法进行滤波。
(2) 当f1/f0<2时,无论滑动时间Δt如何取值,本炮基波的频率谱始终不会与任何谐波产生交点,即此时可以使用双相移法去除任意滑动扫描时间间隔资料中的谐波;
(3) 2≤f1/f0<3时,Δt的取值范围如图 9所示,图中蓝线为可控震源基波信号f1/f0的值,为保证f1/f0 < c,Δt/T的取值范围应如图 9中红线所示。

|
图 9 当f1/f0确定时“穿插式”条件下滑动时间的取值范围(红线所示) |
因此,当基于滑动扫描的地震采集需要追求更高的生产效率时,如基波的信号频率刚好满足条件,或可以自主选择基波的频率大小时,“穿插式”去除谐波法是一个可以尝试的全新方法,理论上可以和双相移法有效结合压制谐波。
2.3 双相移法处理地下多反射模型以上正演模拟试算均是建立在地下为单一反射面的前提之下,然而实际上地震数据往往由各种强弱不等、时间间隔不等的反射组成,且每个反射都可以产生相应强度的谐波,使用双相移法处理诸如此类的数据时,优先考虑“穿插式”。
因为这些反射波的基波与目标信号基波频率变化一致,在时频图上表现为相互平行,因此这些基波不会与目标信号相交,可能干扰到目标信号的就只有这些反射波的高次谐波。因此,只需要让可控震源的起止扫描频率比f1/f0<2,那么无论这些反射波信号的“滑动时间”如何取值,这些反射波信号的基波还是高次谐波都不会与目标基波信号相交。
以可控震源线性升频扫描为例,扫描长度T=2s,起始频率和终止频率分别为10Hz和19Hz,模拟目标基波及其高次谐波,最高谐波次数为5。令该目标基波起震时间为0,振幅为8,2~5次谐波振幅分别为基波的60%、40%、20%和10%。
同时,在信号中添加起震时间分别为-1.5、-0.8、0.9和1.7s四个来自不同界面的反射基波信号及其谐波。四个信号扫描长度均为T=2s,起始频率和终止频率均为10和19Hz,振幅分别为目标基波的1.2、1.4、0.8、0.9倍,其2~5次谐波振幅分别是各基波振幅的60%、40%、20%和10%。
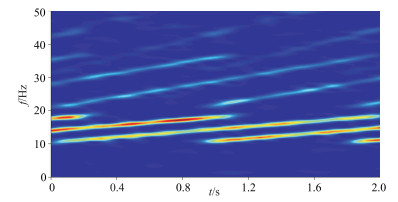
添加了目标基波、目标高次谐波、来自四个不同反射面的基波以及每个基波所对应高次谐波的信号时频谱如图 10所示(为了使模型更贴合实际地震数据,在其中加入了适量的白噪声,白噪能量约为有效信号的2倍)。由于可控震源的起止频率比f1/f0<2,目标基波信号不与任何来自其它反射面的信号有频率交叠。双相移法处理得到的目标基波信号时频谱如图 11所示,与真实基波信号的时间域波形对比如图 12所示。可以看出,在该起止频率下,白噪声和来自不同反射面的反射波及高次谐波经由双相移法的去除效果极佳。
|
图 10 含多个反射及谐波的模拟信号时频谱 |
|
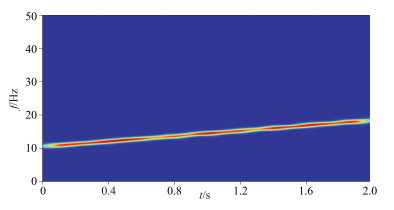
图 11 多反射模拟信号双相移法获得的目标基波信号时频谱 |
|
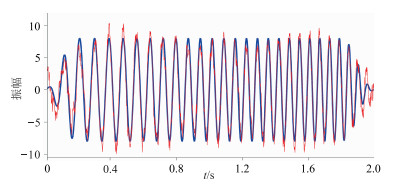
图 12 双相移法得到目标基波信号(红色) 与真实基波信号(蓝色)的对比 |
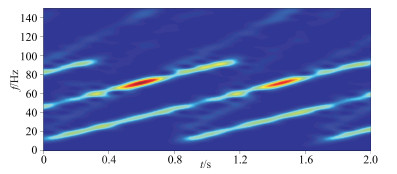
然而实际工业生产中,很多情况下基波信号的f1/f0远远大得多,因此必须考虑更实际的起止扫描频率,测试双相移法的适用性。将上述可控震源线性升频扫描多界面反射信号起止扫描频率调整为5和100Hz,其时频图如图 13所示,可以明显看出目标基波被来自其它反射面的高次谐波所干扰,不满足条件f1/f0<2,不利于使用双相移法进行谐波压制。该信号的双相移法处理得到的基波信号时频谱如图 14所示,获得的基波信号与真实基波信号的对比如图 15所示,可以看出,由于受到来自其它信号高次谐波的干扰,在干扰处有较为明显的畸变,但大部分的基波有效信号还是被保留下来。由此可知,即使起止频率比最不利的情况下,双相移法依旧可以还原大部分的基波信号,误差在可接受的范围之内。
|
图 13 起止频率不可控的多反射及其谐波模拟信号时频谱 |

|
图 14 起止频率不可控的多反射模拟信号双相移法得到的基波信号时频谱 |

|
图 15 起止频率不可控的多反射模拟信号双相移法得到的基波信号(红色)与真实基波信号(蓝色)对比 |
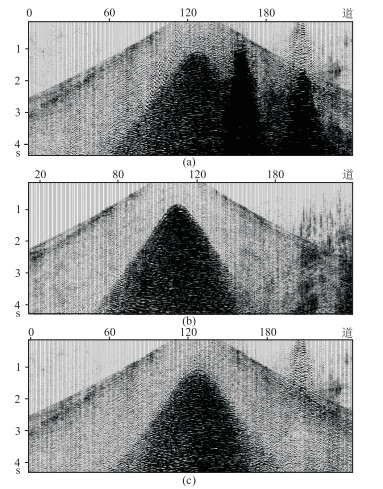
图 16a为采用线性升频滑动扫描方式采集的实际单炮地震记录,可见谐波干扰非常严重。应用纯相移滤波法对该记录进行滤波,结果如图 16b所示,谐波干扰得到了一定的去除,但由于白噪声和来自上下炮的信号所造成的干扰依旧有很大残留,干扰去除效果较为一般。应用双相移滤波法对该记录进行滤波,结果如图 16c所示,由图可知双相移法滤除了大部分谐波干扰,滤波效果明显好于纯相移法,大幅提高了信噪比。
|
图 16 原始(a)、纯相移法滤波后(b)、双相移法滤波后(c)的相关炮记录 |
纯相移滤波法是去除可控震源高次谐波的一种简洁、高效的方法,但在处理白噪声、滑动扫描等复杂信号时显得乏力。为此,本文提出双相移谐波压制滤波法,不仅解决了抗噪问题,还探讨了双相移法在滑动扫描信号谐波压制中的应用。与此同时,文中讨论了更偏向于实际的地下多反射模型中双相移法的应用,以及当信号起止频率比更偏向于实际生产的数据时双相移法的适用性问题,结果表明双相移滤波法较好地适用于各个模型结构。需要注意的是,双相移法用于滑动扫描信号需要可控震源起止扫描频率与滑动时间之间满足一定的关系。将双相移滤波法用于实际资料,并与纯相移法对比,结果显示双相移法的滤波效果更能令人满意。
当可控震源的扫描信号为非线性时,双相移法的适用性及适用条件将是下一步的研究方向。
| [1] |
陈祖斌, 林君, 于生宝. 浅层地震可控震源系统的设计[J]. 电子测量与仪器学报, 2002, 16(1): 43-48. CHEN Zubin, LIN Jun, YU Shengbao. The development of shallow seismic vibrator system[J]. Journal of Electronic Measurement and Instrument, 2002, 16(1): 43-48. |
| [2] |
凌云, 高军, 孙德胜, 等. 可控震源在地震勘探中的应用前景与问题分析[J]. 石油物探, 2008, 47(5): 425-438. LING Yun, GAO Jun, SUN Desheng, et al. Vibroseis prospects and problems analysis in seismic exploration[J]. Geophysical Prospecting for Petroleum, 2008, 47(5): 425-438. DOI:10.3969/j.issn.1000-1441.2008.05.001 |
| [3] |
南文海, 丁志淦. 可控震源发展中有关问题的探讨[J]. 物探装备, 1999, 9(2): 26-29. NAN Wenhai, DING Zhigan. Discussion on the developing of vibroseis[J]. Equipment for Geophysical Prospecting, 1999, 9(2): 26-29. |
| [4] |
佟训乾, 林君, 姜弢, 等. 陆地可控震源发展综述[J]. 地球物理学进展, 2012, 27(5): 1912-1921. TONG Xunqian, LIN Jun, JIANG Tao, et al. Summary of development of land vibrator[J]. Progress in Geophysics, 2012, 27(5): 1912-1921. |
| [5] |
曹务祥. 谐波畸变特性分析[J]. 石油物探, 2004, 43(5): 441-444. CAO Wuxiang. Character analysis of harmonic distortion[J]. Geophysical Prospecting for Petroleum, 2004, 43(5): 441-444. DOI:10.3969/j.issn.1000-1441.2004.05.006 |
| [6] |
Seriff A J, Kim W H. The effect of harmonic distortion in the use of vibratory surface sources[J]. Geophysics, 1970, 35(2): 234-246. DOI:10.1190/1.1440087 |
| [7] |
魏铁, 于世东, 于敏杰, 等. 可控震源噪声分析[J]. 石油地球物理勘探, 2008, 43(增刊2): 38-43. WEI Tie, YU Shidong, YU Minjie, et al. Analysis of noise in vibroseis[J]. Oil Geophysical Prospecting, 2008, 43(S2): 38-43. |
| [8] |
Rozemond H J. Slip sweep acquisition[C]. SEG Technical Program Expanded Abstracts, 1996, 15: 64-67.
|
| [9] |
肖虎, 唐东磊, 杨国平, 等. 可控震源动态扫描技术及应用[J]. 石油地球物理勘探, 2019, 54(3): 493-499. XIAO Hu, TANG Donglei, YANG Guoping, et al. Vibroseis dynamic sweep[J]. Oil Geophysical Prospecting, 2019, 54(3): 493-499. |
| [10] |
Schrodt J K. Techniques for improving vibroseis data[J]. Geophysics, 1987, 52(4): 469-482. DOI:10.1190/1.1442318 |
| [11] |
Martin J E, White R E. Two methods for continuous monitoring of harmonic distortion in vibroseis signals[J]. Geophysical Prospecting, 1989, 37(7): 851-872. DOI:10.1111/j.1365-2478.1989.tb02237.x |
| [12] |
Ruest D K. Vibrator force control: how simple can it get?[J]. The Leading Edge, 1995, 14(11): 1129-1133. DOI:10.1190/1.1437085 |
| [13] |
Lebedev A V, Beresnev L A. Nonlinear distortion of signals radiated by vibroseis sources[J]. Geophysics, 2004, 69(4): 968-977. DOI:10.1190/1.1778240 |
| [14] |
Lebedev A V, Beresnev L A, Vermeer P L. Model parameters of the nonlinear stiffness of the vibrator-ground contact determined by inversion of vibrator accelerometer data[J]. Geophysics, 2006, 71(3): H25-H32. DOI:10.1190/1.2196870 |
| [15] |
Okaya D A, Karageorgi E, McEvilly T V. Removing vibrator-induced correlation artifacts by filtering in frequency-uncorrelated time space[J]. Geophysics, 1992, 57(7): 916-926. DOI:10.1190/1.1443304 |
| [16] |
Ras P, Daly M, Baeten G, et al. Harmonic distortion in slip sweep records[C]. SEG Technical Program Expanded Abstracts, 1999, 18: 609-612.
|
| [17] |
Dal Moro G, Scholtz P, Iranpour K. Harmonic noise attenuation for vibroseis data[J]. GNGTS, 2007, 3(2): 511-513. |
| [18] |
伍建, 王润秋, 魏加明, 等. 可控震源地震数据谐波滤除方法[J]. 石油地球物理勘探, 2014, 49(1): 47-52. WU Jian, WANG Runqiu, WEI Jiaming, et al. A method for vibroseis data harmonic filtering[J]. Oil Geophysical Prospecting, 2014, 49(1): 47-52. |
| [19] |
张连群, 陈宝书, 李松康, 等. 白云凹陷陆架—陆坡区多次波压制技术[J]. 石油地球物理勘探, 2018, 53(2): 236-242. ZHANG Lianqun, CHEN Baoshu, LI Songkang, et al. Multiple suppression in continental shelf and slope a-reas of Baiyun Depression[J]. Oil Geophysical Pro-specting, 2018, 53(2): 236-242. |
| [20] |
陈泓竹, 王彦春. 频率域拉东变换加权约束反演压制层间多次波[J]. 石油地球物理勘探, 2018, 53(4): 666-673. CHEN Hongzhu, WANG Yanchun. Peg-leg multiple suppression with the weight-constrain inversion of Radon transform in the frequency domain in Songliao Basin[J]. Oil Geophysical Prospecting, 2018, 53(4): 666-673. |
| [21] |
刘语, 刘建红, 刘国峰, 等. 陆上地震资料多次波识别与压制技术[J]. 石油地球物理勘探, 2018, 53(增刊1): 24-28. LIU Yu, LIU Jianhong, LIU Guofeng, et al. Multiple identification and suppression on land seismic data[J]. Oil Geophysical Prospecting, 2018, 53(S1): 24-28. |
| [22] |
戴晓峰, 徐右平, 甘利灯, 等. 川中深层—超深层多次波识别和压制技术——以高石梯—磨溪连片三维区为例[J]. 石油地球物理勘探, 2019, 54(1): 54-64. DAI Xiaofeng, XU Youping, GAN Lideng, et al. Deep & ultra-deep multiple suppression in Central Sichuan: an example of Gaoshiti-Moxi[J]. Oil Geophysical Pro-specting, 2019, 54(1): 54-64. |
| [23] |
毕丽飞, 秦宁, 李钟晓, 等. 应用逆散射级数波场预测和2D卷积盲分离压制层间多次波[J]. 石油地球物理勘探, 2020, 55(3): 521-529. BI Lifei, QIN Ning, LI Zhongxiao, et al. Wavefield prediction with inverse scattering series and 2D blind separation of convolved mixtures for suppressing internal multiples[J]. Oil Geophysical Prospecting, 2020, 55(3): 521-529. |
| [24] |
Li X P. Decomposition of vibroseis data by multiple filter technique[C]. SEG Technical Program Expan-ded Abstracts, 1994, 13: 711-714.
|
| [25] |
Li X P, Sollner W, Hubral P. Elimination of harmonic distortion in vibroseis data[J]. Geophysics, 1995, 60(2): 503-516. DOI:10.1190/1.1443787 |



 王彦春, 北京市海淀区学院路29号中国地质大学(北京)地球物理与信息技术学院, 100083。Email:
王彦春, 北京市海淀区学院路29号中国地质大学(北京)地球物理与信息技术学院, 100083。Email: 