② 西安石油大学地球科学与工程学院, 陕西西安 710065
② College of Earth Science and Engineering, Xi'an Shiyou University, Xi'an, Shaanxi 710065, China
目前地震资料随机噪声常规压制方法主要包括空间域压制和变换域压制。前者有中值滤波、各向异性扩散滤波等;后者有小波阈值法、曲波变换阈值法等。其本质都是利用在特定域中有效信号与噪声具有可区分的特征进行信噪分离。
时频分析类方法主要根据时频域中有效信号与噪声的能量分布,进行噪声的分析和定位及剔除或压制[1-3],主要有基于短时傅里叶变换、连续小波变换和S变换等方法[4]。Morlet[5]提出的改进小波变换可在时频域中寻找目标信号的局部特征。但基于小波变换的一系列延伸方法对具有复杂同相轴的地震资料,效果并不理想。针对该问题,Candès等[6]提出了具有多方向、多尺度的曲波变换。包乾宗等[7]将曲波变换与奇异值分解方法相结合,对地震资料中的不同成分进行分离;Neelamani等[8]将曲波变换用于三维地震数据的随机噪声的压制;孟阁阁等[9]基于曲波变换,设计了一种自适应阈值去噪方法,效果比较明显;张恒磊等[10-11]采用非线性阈值法基于曲波变换对叠前资料进行了去噪处理,随后提出了适用于曲波域和空间域的倾角扫描去噪技术,并在复杂区块资料中取得了较好的效果;张之涵等[12]提出一种基于三维曲波变换的噪声压制方法,通过改进非线性阈值,更好地保护了有效信号;姚振岸等[13]将曲波变换与各向异性扩散滤波相结合,改善了常规曲波变换降噪方法的过度平滑与环绕效应,实现了数据边界和有效信号振幅的保护。
近几年,诸如奇异值分解、稀疏表征等新方法也逐步应用于地震资料的噪声压制。它们通过构建适用于目标资料的字典,替代小波变换、曲波变换中的确定性基函数,其本质是将去噪的过程转化为优化问题。基于该思路,Sanchis等[14]通过独立分量分析算法构建基函数,但该方法需要有效成分的统计估计;李海山等[15]采用形态分量分析方法进行字典设计,通过求解表征目标函数达到去噪的效果,但测试结果显示仍存在一定的伪影现象;Tang等[16]通过引入学习型过完备字典实现最优稀疏表征,并采用字典训练与总变差量的最小化共同抑制伪吉布斯效应,避免了伪影的干扰,但该方法需要已知噪声的统计信息,在实际应用中需要前期统计与实验;徐彦凯等[17]提出了基于自适应奇异值分解的局部正交压制方法,通过将残余信号从随机噪声中的二次分离,提高了资料的信噪比。
以上时频分析方法受不确定准则限制,只能在时间分辨率与频率分辨率之间采取折中处理[18]。针对这一缺陷,有学者提出了用于处理时序非稳态信号的经验模态分解(EMD)方法[19-20]。基于该方法的时频分析可以在时间、频率尺度上均达到较高的分辨率。EMD方法在地震资料噪声压制和属性分析中均获得了较好效果[21-23]。而对于复杂的时序非平稳信号,仅在时间域进行分解往往效果不佳,或出现假频等现象,而采用EMD方法,将单道地震记录或剖面在合适的域内分解为一系列本征模态分量(IMF),可以表征不同频段内的局部能量异常。传统EMD方法的适用条件可参见文献[21-24]。Bekara等[23]率先将EMD方法用于频率—空间域中的各频率切片数据,将分解得到的第一模态作为噪声剔除,重构之后得到噪声压制后的信号,取得一定效果。
EMD方法不需要设置针对性的参数,具有较强的泛化能力。但如果在频率—空间域的频率切片体上进行EMD处理,边界效应等现象常常导致分解过程精度低或不稳定[25]。在EMD方法的基础上发展的变分模态分解(VMD)方法,通过将地震数据进行解析化,在时频域内将地震信号分解为各个模态分量。对于时频域中带限频率切片的处理,VMD方法[26]明显优于传统EMD方法,是一种自适应、完全非递归的模态变分方法。基于奇异值分解的VMD方法通过确定模态分解个数,自适应地匹配每种模态的最优中心频率和有限带宽,最终得到变分问题的最优解,实现IMF的高效分离。该方法克服了传统EMD的端点效应与模态分量混叠问题,求解过程具有更高的稳定性。
本文通过希尔伯特-黄变换(HHT)将地震数据解析化,在时频域进行变分模态分解。通过分频分解的思路,分析每个模态分量各频段上的噪声和有效信号的能量分布,设置合适的分量数,分频段压制噪声,再将有效信号模态分量重构回时频域。实际资料测试结果表明,相较于常规RNA随机噪声压制方法,该方法有效地压制了随机背景噪声,同时对陡倾角的线性干扰有明显的压制效果。
1 算法原理对于地震剖面中的线性同相轴,可将其描述为空间坐标x和时间t的函数
| $ u(t, x)=w\left(t-\frac{x}{c}\right) $ | (1) |
式中:w为地震子波;c为波的视速度。在频率域可由Fourier变换表示为
| $ \hat{u}(f, x)=W(f) \exp \left(\frac{\mathrm{i} 2 \pi f x}{c}\right) $ | (2) |
式中W(f)为子波的频谱。
上式表明
| $ \begin{array}{*{20}{c}} &\mathop {\min }\limits_{\left\{ {{u_k}} \right\}\langle {\omega _k}\} } \sum\limits_{k=1}^{K}\left\|\partial x\left\{\left[\delta(x)+\frac{\mathrm{i}}{\pi x}\right] u_{k}(x) \exp \left(-\mathrm{j} \omega_{k} x\right)\right\}\right\|_{2}^{2}\\ &\text { 满足 } \;\;\; \sum\limits_{k=1}^{K} u_{k}=u \end{array} $ | (3) |
| $ \begin{array}{l} L\left(\left\{u_{k}\right\},\left\{\omega_{k}\right\}, \lambda\right)=\alpha \sum\limits_{k=1}^{K} \| \partial_{x}\left[u_{k}(x)\right] \times \\ \;\;\;\;\; \exp \left(-\mathrm{j} \omega_{k} x\right)\left\|_{2}^{2}+\right\| u(x)-\sum\limits_{k=1}^{K} u_{k}(x) \|_{2}^{2}+ \\ \;\;\;\;\; \left\langle\lambda(x), u(x)-\sum\limits_{k=1}^{K} u_{k}(x)\right\rangle \end{array} $ | (4) |
式中:α为权重系数,调节目标函数中的变分项与保真项;λ(x)为拉格朗日算子;
| $ \begin{aligned} u_{k}^{n+1}=& \arg \min _{u_{k}} L\left(\left\{u_{i<k}^{n+1}\right\},\left\{u_{i \geqslant k}^{n}\right\},\left\{\omega_{i}^{n}\right\}, \lambda^{n}\right) \\ =& \arg \min _{u_{k}} \alpha\left\|\partial_{x}\left[u_{k}(x) \mathrm{e}^{-\mathrm{j} \omega_{k} x}\right]\right\|_{2}^{2}+\\ &\left\|(x)-\sum\limits_{i} u_{i}(x)+\frac{\lambda(x)}{2}\right\|_{2}^{2} \end{aligned} $ | (5) |
对上式进行傅里叶变换后,可得频率域解
| $ {\hat u_k^{n + 1}(\omega ) = \frac{{\hat u(\omega ) - \sum\limits_{i \ne k} {{{\hat u}_i}} (\omega ) + \frac{{\hat \lambda (\omega )}}{2}}}{{1 + \frac{\alpha }{2}{{\left( {\omega - {\omega _k}} \right)}^2}}}} $ | (6) |
| $ {\omega _k^{n + 1} = \arg \mathop {\min }\limits_{{\omega _k}} L\left( {\left\{ {u_i^{n + 1}} \right\},\left\{ {\omega _{i < k}^n} \right\},\left\{ {\omega _{ik}^n} \right\},{\lambda ^n}} \right)}\\ \;\;\;\; { = \frac{{\int_{ - \infty }^\infty \omega {{\left\| {{{\hat u}_k}(\omega )} \right\|}^2}{\rm{d}}\omega }}{{\int_{ - \infty }^\infty {{{\left\| {{{\hat u}_k}(\omega )} \right\|}^2}} {\rm{d}}\omega }}} $ | (7) |
式中:
算法基本流程如下:
(1) 应用合适时窗选取部分目标数据,进行VMD参数初始化;
(2) 应用HHT将目标数据从时间域变换到时频域;
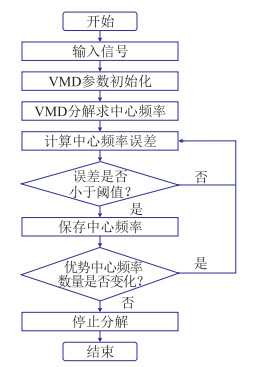
(3) 对各个频率切片进行VMD分解,确定各模态分量的中心频率(图 1);
|
图 1 VMD流程 |
(4) 按能量强弱对VMD分解后得各模态分量(记为VMDIMF)排序,保留前若干个有效VMD-IMF,重构得到滤波后的频率切片;
(5) 将滤波后的所有频率切片反变换回时空域;
(6) 移动时窗,重复上述步骤,直到完成所有数据的处理。
对于三维数据体,仅增加一项正交空间坐标基即可,整体算法流程不变。
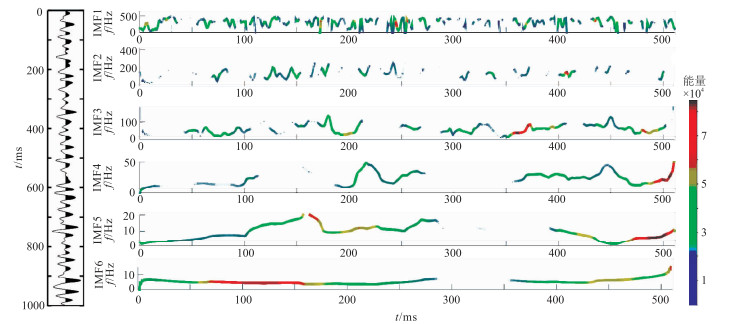
对地震数据进行HHT,可分析含噪非平稳信号在不同频率段内能量沿时间轴的分布。图 2为原始单道地震记录及其前半段(1~500ms)时频谱,其中IMF1~IMF6依次对应信号的从高频至低频信息(对于单道数据,频率切片简化为IMF)。由图 2可见,高频端和低频端主要由噪声构成,有效信息集中在IMF3~IMF5。以IMF5的时频谱为例,对其进行VMD处理,分解得到各阶VMDIMF,如图 3所示。图中将各VMDIMF的能量进行归一化,方便对比分析。若分量中存在异常值,可对图 2进行综合分析,决定是将其作为异常噪声进行剔除,还是作为局部有效信号予以保留。
|
图 2 单道地震记录及其各阶IMF的时频谱 |

|
图 3 图 2中IMF5的VMDIMF结果 |
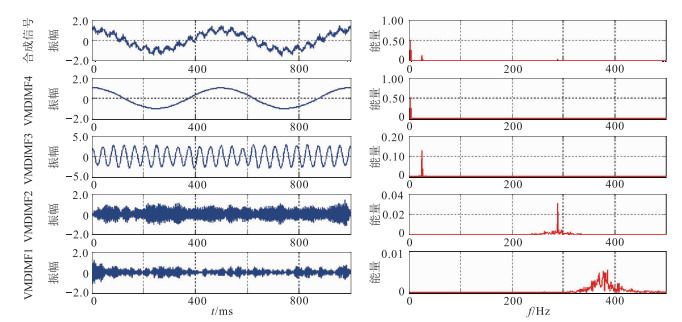
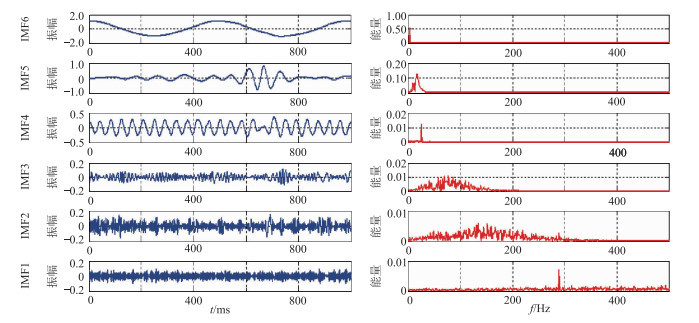
用2、25、288Hz谐波合成信号对比VMD法与传统EMD法分解效果(图 4和图 5)。在分解效率方面,由于VMD递归确定最优中心频率,仅3个VMD-IMF即分解出三个频率成分,而传统EMD方法需要6个IMF才分解出288Hz成分;在精度方面,VMD法分解得到的VMDIMF2、VMDIMF3、VMDIMF4均准确定位了合成信号的各频率成分(图 4),而EMD法分解结果中IMF2、IMF3与IMF5均为无效分量(图 5)。可见,对谐波合成信号的分解,VMD法具有明显的效率和精度优势。
|
图 4 谐波合成信号的VMD法分解结果(左)及其频谱(右) |
|
图 5 谐波合成信号的EMD法分解结果(左)及其频谱(右) |
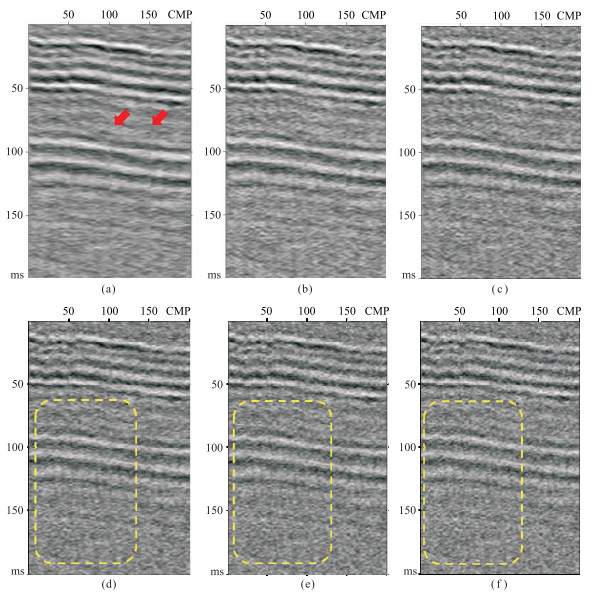
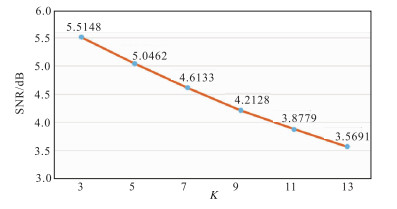
使用VMD法对地震资料进行处理时,首先需要指定总的模态个数K,该参数直接影响去噪效果。在实际应用前,首先对小块资料(比如200×200个样点)进行测试。对模型数据(图 6a)加入频带为8~55Hz的高斯随机噪声,噪声平均能量大于有效信号能量的50%,其信噪比为3.09dB(图 6b)。该加噪数据不同K值的VMD法去噪结果如图 7所示。当K=3时背景噪声压制效果最好,但有效成分出现较为明显的割裂痕迹(图 7a红色箭头所示),是由时窗截取的边缘效应被过低K值放大所致,可根据实际情况,调整时窗长度。在K为5或7时,去噪结果的割裂痕迹明显得到改善;随着K值增大,更多的背景噪声被保留,当K值过大时(该例K大于7时),出现纵向高倾角处理痕迹(图 7d~图 7f黄框所示)。图 8为图 7去噪后数据的时频谱,图 9为去噪结果信噪比(SNR)随K值的变化曲线,可见:K值较小时,处理结果的信噪比更高;随着K值的增大,更多噪声成分被保留,信噪比逐渐下降。
|
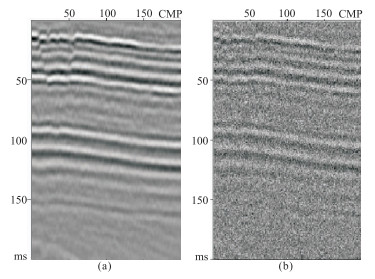
图 6 模型(a)及其加噪(b)数据 |
|
图 7 含噪模型数据不同K时的VMD法去噪结果 (a)K=3;(b)K=5;(c)K=7;(d)K=9;(e)K=11;(f)K=13 |

|
图 8 含噪模型数据不同K时的VMD法去噪后的时频谱 (a)K=3;(b)K=5;(c)K=7;(d)K=9;(e)K=11;(f)K=13 |
|
图 9 模态数K与处理结果信噪比相关趋势 |
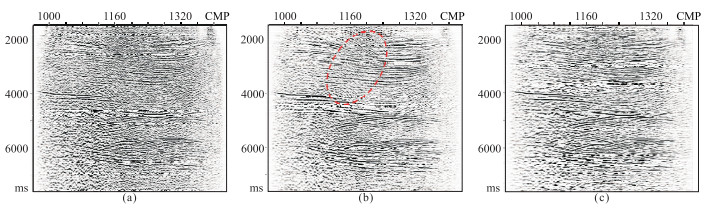
实际地震剖面如图 10a所示,采样间隔为2ms,记录长度为8s,道间距为12.5m,具有较强的随机噪声干扰,还有部分线性相关噪声,中深层同相轴连续性较差。本文方法去噪结果如图 10b所示,与原始剖面相比,浅层水平同相轴和深层低伏度同相轴的质量得到明显提升,连续性得到明显加强,构造形态更加清晰。与常规RNA去噪方法的处理结果(图 10c)相比,本文方法去噪结果未出现轻微类似斜干扰的人为痕迹(红色椭圆所示)。通过局部放大对比(图 11、图 12),处理前浅层水平同相轴背景有残留的面波成分(图 11a)经处理后得到明显的压制(图 11b);中深层的低幅度构造,在处理前受到线性噪声和高频背景噪声干扰(图 12a),处理后线性噪声痕迹几乎消失,背景随机噪声能量得到较强压制,与有效同相轴的能量不在同一数量级(图 12b)。由处理前、后的频谱(图 13)可见,由于压制了低频面波和高频背景噪声能量,低频能量和高频能量有所减弱。
|
图 10 实际地震数据去噪结果 (a)原始剖面;(b)本文方法处理剖面;(c)RNA去噪方法处理剖面 |
|
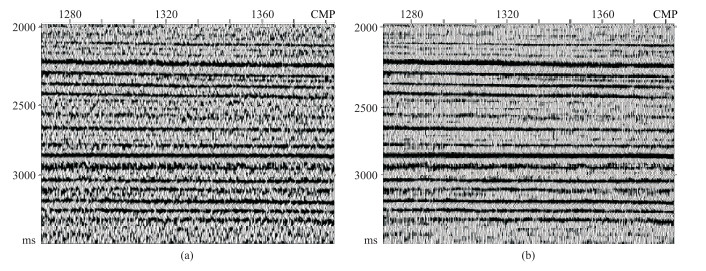
图 11 实际地震资料本文方法处理前(a)、后(b)浅层局部放大对比 |
|
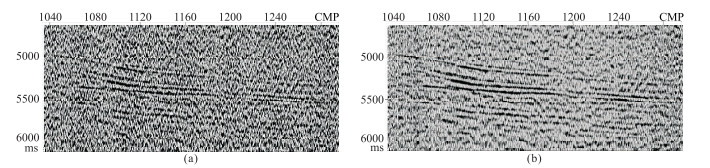
图 12 实际地震资料本文方法处理前(a)、后(b)深层局部放大对比 |
|
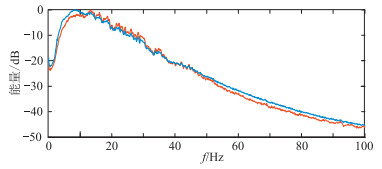
图 13 实际地震资料处理前(蓝线)、后(红线)频谱对比 |
本文通过HHT得到地震资料在各频率切片上的能量分布,然后通过VMD对各频率切片进行分解;分析有效信号与噪声在时频切片上的能量分布,在此基础上优选出有效信号模态分量重构时频切片;最后反变换回时空域,达到噪声压制的目的。分频处理可以在不同频率段内对二维信号,甚至单道信号进行有效信息的筛选,从而对局部异常噪声进行更精细的压制。模型数据测试和实际资料应用结果表明,与常规RNA方法相比,本文方法可有效压制线性干扰和随机背景噪声,处理后资料信噪比更高。
| [1] |
Han J, van der Baan M. Empirical mode decomposition for seismic time-frequency analysis[J]. Geophy-sics, 2013, 78(2): O9-O19. |
| [2] |
Liu J, Marfurt K J. Instantaneous spectral attributes to detect channels[J]. Geophysics, 2007, 72(2): P23-P31. DOI:10.1190/1.2428268 |
| [3] |
Liu Y, Fomel S. Seismic data analysis using local time-frequency decomposition[J]. Geophysical Prospecting, 2013, 61(3): 516-525. DOI:10.1111/j.1365-2478.2012.01062.x |
| [4] |
Tary J B, Herrera R H, Han J, et al. Spectral estimation: What is new? What is next?[J]. Reviews of Geo-physics, 2014, 52(4): 723-749. DOI:10.1002/2014RG000461 |
| [5] |
Morlet J. Wave propagation and sampling theory[J]. Geophysics, 1982, 47(2): 222-236. DOI:10.1190/1.1441329 |
| [6] |
Candès E J, Donoho D L. Ridgelets: A key to higher-dimensional intermittency[J]. Philosophical Transac-tions of the Royal Society A, 1999, 357(1760): 2495-2509. DOI:10.1098/rsta.1999.0444 |
| [7] |
包乾宗, 高静怀, 陈文超. Curvelet域垂直地震剖面波场分离[J]. 西安交通大学学报, 2007, 41(6): 650-654. BAO Qianzong, GAO Jinghuai, CHEN Wenchao. Wavefield separation in vertical seismic profiles in Curvelet domain[J]. Journal of Xi'an Jiaotong University, 2007, 41(6): 650-654. DOI:10.3321/j.issn:0253-987X.2007.06.005 |
| [8] |
Neelamani R, Baumstein A I, Gillard D G, et al. Coherent and random noise attenuation using the curvelet transform[J]. The Leading Edge, 2008, 27(2): 240-248. DOI:10.1190/1.2840373 |
| [9] |
孟阁阁, 王德利, 陈鑫. 基于三维曲波变换的地震数据去噪方法研究[J]. 石油物探, 2014, 53(3): 313-323. MENG Gege, WANG Deli, CHEN Xin. Research on the denoising method of seismic data based on 3D curvielet transform[J]. Geophysical Prospecting for Petroleum, 2014, 53(3): 313-323. DOI:10.3969/j.issn.1000-1441.2014.03.009 |
| [10] |
张恒磊, 张云翠, 宋双, 等. 基于Curvelet域的叠前地震资料去噪方法[J]. 石油地球物理勘探, 2008, 43(5): 508-513. ZHANG Henglei, ZHANG Yuncui, SONG Shuang, et al. Denoising method for pre-stack seismic data based on Curvelet domain[J]. Oil Geophysical Prospecting, 2008, 43(5): 508-513. DOI:10.3321/j.issn:1000-7210.2008.05.004 |
| [11] |
张恒磊, 刘天佑, 张云翠. 基于高阶相关的Curvelet域和空间域的倾角扫描噪声压制方法[J]. 石油地球物理勘探, 2010, 45(2): 208-214. ZHANG Henglei, LIU Tianyou, ZHANG Yuncui. Inclination scanning noise suppression method based on high-order correlation in Curvelet domain and spatial domain[J]. Oil Geophysical Prospecting, 2010, 45(2): 208-214. |
| [12] |
张之涵, 孙成禹, 姚永强, 等. 三维曲波变换在地震资料去噪处理中的应用研究[J]. 石油物探, 2014, 53(4): 421-430. ZHANG Zhihan, SUN Chengyu, YAO Yongqiang, et al. Research on the application of 3D curvelet transform to seismic data denoising[J]. Geophysical Prospecting for Petroleum, 2014, 53(4): 421-430. DOI:10.3969/j.issn.1000-1441.2014.04.007 |
| [13] |
姚振岸, 孙成禹, 石小磊, 等. 基于曲波变换和各向异性扩散滤波的联合去噪技术[J]. 石油学报, 2016, 37(4): 490-498. YAO Zhen'an, SUN Chengyu, SHI Xiaolei, et al. Joint denoising technique based on curvelet transform and anisotropic diffusion filtering[J]. Acta Petrolei Sinica, 2016, 37(4): 490-498. |
| [14] |
Sanchis C, Hanssen A. Sparse code shrinkage for signal enhancement of seismic data[J]. Geophysics, 2011, 76(6): V151-V167. DOI:10.1190/geo2010-0128.1 |
| [15] |
李海山, 吴国忱, 印兴耀. 形态分量分析在去除地震资料随机噪声中的应用[J]. 吉林大学学报(地球科学版), 2012, 42(2): 554-561. LI Haishan, WU Guochen, YIN Xingyao. Application of morphological component analysis in removing random noise from seismic data[J]. Journal of Jilin University(Earth Science Edition), 2012, 42(2): 554-561. |
| [16] |
Tang G, Ma W J, Yang H Z. Seismic data denoising based on learning-type overcomplete dictionaries[J]. Applied Geophysics, 2012, 9(1): 27-32. DOI:10.1007/s11770-012-0310-z |
| [17] |
徐彦凯, 曹思远, 潘晓, 等. 随机噪声的局部正交压制方法[J]. 石油地球物理勘探, 2019, 54(2): 280-287. XU Yankai, CAO Siyuan, PAN Xiao, et al. Local orthogonal suppression method for random noise[J]. Oil Geophysical Prospecting, 2019, 54(2): 280-287. |
| [18] |
Gabor D. Theory of communication, Part 1:The ana-lysis of information[J]. Journal of the Institution of Electrical Engineers-Part Ⅲ: Radio and Communication Engineering, 1946, 93(26): 429-441. |
| [19] |
Huang N, Shen Z, Long S, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Procee-dings of the Royal Society of London Series A, 1998, 454(1971): 903-995. DOI:10.1098/rspa.1998.0193 |
| [20] |
Klügel N. Practical empirical mode decomposition for audio synthesis[C]. International Conference on Di-gital Audio Effects, 2012, 15-18.
|
| [21] |
Barnhart B L, Eichinger W E. Empirical mode decomposition applied to solar irradiance, global temperature, sunspot number, and CO2 concentration data[J]. Journal of Atmospheric and Solar-Terrestrial Phy-sics, 2011, 73(13): 1771-1779. DOI:10.1016/j.jastp.2011.04.012 |
| [22] |
Chen W, Wang S, Zhang Z, et al. Noise reduction based on wavelet threshold filtering and ensemble empirical mode decomposition[C]. SEG Technical Program Expanded Abstracts, 2012, 31: 1-5.
|
| [23] |
Bekara M, van der Baan M. Random and coherent noise attenuation by empirical mode decomposition[J]. Geophysics, 2009, 74(4): V89-V98. |
| [24] |
徐智, 唐刚, 刘伟, 等. 基于变分模态分解参数优化的地震随机噪声去除方法[J]. 北京化工大学学报(自然科学版), 2019, 46(5): 60-68. XU Zhi, TANG Gang, LIU Wei, et al. Seismic random noise removal method based on optimization of variational modal decomposition parameters[J]. Journal of Beijing University of Chemical Technology(Natural Science Edition), 2019, 46(5): 60-68. |
| [25] |
Liu Y, Li Y, Lin H, et al. An amplitude-preserved time- frequency peak filtering based on empirical mode decomposition for seismic random noise reduction[J]. IEEE Geoscience and Remote Sensing Letters, 2014, 11(5): 896-900. DOI:10.1109/LGRS.2013.2281202 |
| [26] |
Dragomiretskiy K, Zosso D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531-544. DOI:10.1109/TSP.2013.2288675 |
| [27] |
Chen Y, Ma J. Random noise attenuation by f-x empirical mode decomposition predictive filtering[J]. Geophysics, 2014, 79(3): V81-V91. DOI:10.1190/geo2013-0080.1 |



 胡瑞卿, 河北省涿州市华阳东路东方地球物理公司科技园库尔勒分院处理室, 072750。Email:
胡瑞卿, 河北省涿州市华阳东路东方地球物理公司科技园库尔勒分院处理室, 072750。Email: 