众所周知,零相位地震子波具有旁瓣少、峰值时刻与地层反射界面相对应等优点,能保证零相位地震资料不仅具有较高分辨率,还有利于地震资料的解释[1-9]。确保地震资料的零相位性,无疑对构造精细解释、储层综合研究具有重要意义。在现今实际地震数据处理中,一般基于地震子波为最小相位的假设,从地震道的相位谱中消去子波的相位谱。然而从现场采集到室内处理的各个环节,均可能对地震数据的子波相位特性产生影响,因此最小相位子波的假设条件通常是很难满足的,混合相位假设的子波更符合实情。虽然混合相位地震子波假设能在某些特定条件下取得一定效果,但基于此假设的一些算法在计算量、实用性以及稳定性等方面大多还存在不足。因此,实际地震数据处理中仍大多基于最小相位假设制订处理流程。混合相位子波经最小相位反褶积处理后必然存在剩余相位,即并不是真正的零相位,尚需通过其他技术手段估算出剩余相位并进行校正处理[10-14]。
若认为地震子波相位谱不随频率发生变化,可采用常相位扫描法进行剩余相位估计,该类方法处理结果的好坏很大程度上取决于判别准则的选取。Levy等[15]提出采用最大方差模准则估算剩余相位,有效提高地震剖面的解释能力;但最大方差模准则也存在诸如计算效率低、对弱反射信息不灵敏、不能反映尖脉冲的极性和时移等不足。Sacchi等[16]、Lu等[17]分别对最大方差模准则进行局部改进,减弱传统最大方差模准则对较强反射信息的敏感性。针对最大方差模准则对噪声的不敏感性,Ooe等[18]提出指数变换准则,调节噪声压制与恢复小反射系数序列之间的平衡。Claerbout[19]提出的Parsimony准则用降低幂次的方法削弱强反射信息的作用,对强、弱反射信息都有较高灵敏度。单联瑜等[20]改进了常用相位校正判别准则,提出一种新的相位校正方法,实现精确的相位校正。徐刚等[4]通过以离散信息熵作为量化标准,对无井地震记录进行相位扫描,进而求取剩余相位。Fomel等[21]、刘俊州等[22]使用偏斜度准则实现子波剩余相位的估计。此外,在具有可靠的测井数据情况下,可采用零相位子波制作合成记录,并将其当作标准道,用相似系数作为判别准则[23-24]。
本文通过研究Ricker子波的相移特性,发现主频不同的Ricker子波在相同相位旋转下,峰值时刻存在时差,且该时差与相位旋转量具有线性关系。在常相位假设下,通过该线性关系可实现地震资料剩余相位的估计。该方法不需判别准则的约束,具有精度高、实现过程简捷等优点。
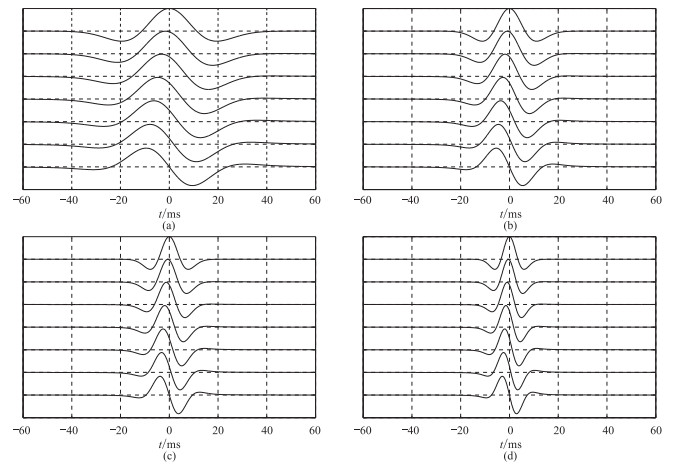
1 方法原理分别对主频为20、35、50及65Hz的零相位Ricker子波进行相位旋转,旋转角度依次为15°、30°、45°、60°、75°及90°,得到图 1所示结果。可见不同主频零相位Ricker子波波峰位置始终位于零时刻处;随着相位旋转,波峰逐渐偏离零时刻。表 1统计不同主频Ricker子波相位旋转量与波峰时移量的关系,可见波峰时移量与主频及相位旋转量有关:①同一主频Ricker子波随相位旋转量的增加其波峰时移量也增加;②在相同相位旋转量下,主频越高波峰时移量越小。换而言之,Ricker子波相位与主频、峰值时刻有关,若能定量求出三者的关系,就可通过主频和峰值时刻求取相应相位值。
|
图 1 不同主频Ricker子波随相位角旋转的变化 (a)20Hz;(b)35Hz;(c)50Hz;(d)65Hz。相位角从上到下依次为0°、15°、30°、45°、60°、75°及90° |
|
|
表 1 Ricker子波在不同相位旋转下的波峰时移量 |
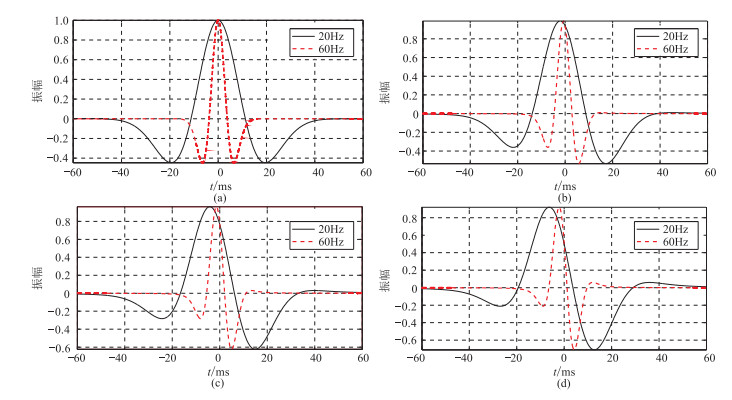
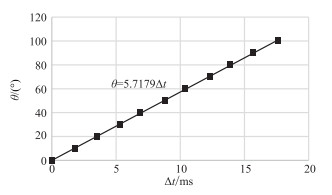
主频不同的Ricker子波在相同相位角旋转量下,其峰值时刻存在差异,可尝试通过峰值时刻的差异求取相位旋转量。以主频为20Hz和60Hz的Ricker子波为例。首先将其进行相位旋转(图 2),然后求取相同相位角下的峰值时差,将峰值时差与相位旋转量进行拟合,结果表明峰值时差与相位旋转量存在线性关系(图 3)。改变Ricker子波主频,峰值时差与相位旋转量仍然存在线性关系,只是比例系数不同而已,主频差异越大,比例系数越小(图 4)。此分析结果表明,利用Ricker子波的主频和峰值时差求取相位旋转量是可行的。
|
图 2 主频为20Hz和60Hz的Ricker子波在不同相位旋转量的波形对比 (a)0°;(b)20°;(c)40°;(d)60° |

|
图 3 主频为20Hz和60Hz的Ricker子波峰值时差Δt与相位旋转量θ的关系 |
|
图 4 主频为10Hz和60Hz的Ricker子波峰值时差Δt与相位旋转量θ的关系 |
基于以上研究结果,本文提出一种新的剩余相位估计方法:①首先对相位未知的地震数据进行频谱分析,确定出有效频带;②在有效频带的低频和高频两个区域分别选取相应滤波主频,滤波因子为Ricker子波,得到低通和高通两个数据;③对低通和高通数据做频谱分析,确定各自主频,记为f1和f2;④求出Ricker子波主频分别为f1和f2时峰值时差与相位旋转量的关系;⑤求出同一反射界面在低通和高通数据上的峰值时差;⑥将⑤中峰值时差代入④中的线性关系,得到地震数据剩余相位。
为提高剩余相位估计精度,需注意以下两点:①在有效频带范围内,两次滤波所选主频差异尽可能大;②为减小求峰值时差的偶然误差,在实际应用中需用多道求取峰值时差,然后取其平均作为最终的峰值时差。
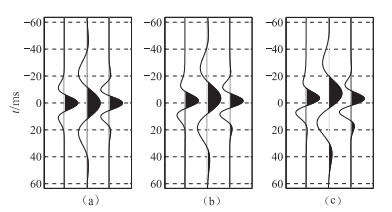
2 理论模型试算对主频为35Hz,相位角为0°、30°、60°的Ricker子波做滤波处理,滤波主频分别为15Hz和60Hz,得到图 5所示结果。对滤波后数据进行频谱分析(图 6),主频为35Hz的Ricker子波经过主频为15Hz和60Hz的Ricker子波滤波处理后,主频分别变为20Hz和43Hz。经过统计分析,峰值时差与相位旋转量的拟合关系式为θ=17.064Δt(图 7)。
|
图 5 主频为35Hz、相位角依次为0°(a)、30°(b)、60°(c)的Ricker子波滤波后峰值时刻的变化 滤波主频分别为15Hz(中)和60Hz(右) |
|
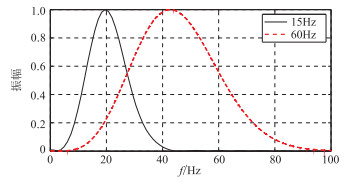
图 6 主频为35Hz的Ricker子波经过主频分别为15Hz和60Hz的Ricker子波滤波后的频谱 |
|
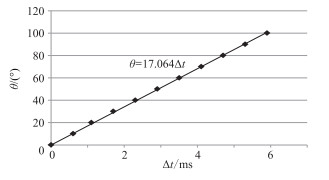
图 7 主频为20Hz和43Hz的Ricker子波峰值时差Δt与相位旋转量θ的关系 |
从图 5中可见,当相位角为0°时,峰值时差为0,由拟合关系得出的相位角为0°;当相位角为30°时,峰值时差为1.7ms,由拟合关系得出的相位角为29.0°,与实际相位值仅差1.0°;当相位角为60°时,峰值时差为3.5ms,由拟合关系得出的相位角为59.7°,与实际相位值基本一致。
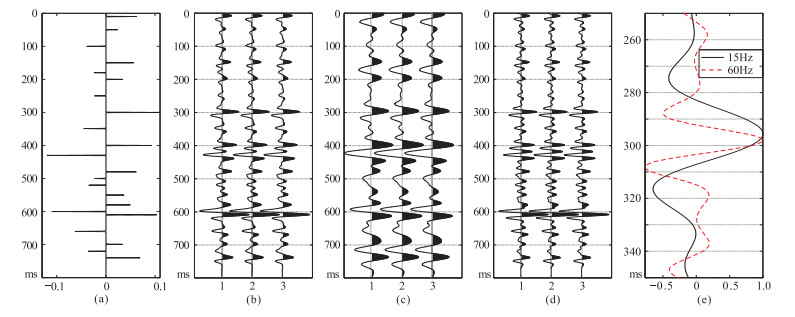
采用反射系数序列(图 8a)与35Hz主频、40°相位Ricker子波进行褶积运算,得到合成地震记录(图 8b),分别采用主频为15Hz和60Hz的Ricker子波对其做滤波处理(图 8c、图 8d)。为避免干涉效应的影响,选取300ms处的波峰计算峰值时差,对300ms附近滤波后数据进行放大(图 8e),可见15Hz滤波结果峰值时间为295.6ms、60Hz滤波结果峰值时间为298.1ms,对应峰值时差Δt=2.5ms。将该峰值时差代入图 7中关系式,计算出剩余相位为42.6°。采用该剩余相位角对原始记录进行零相位校正,所得结果(图 9a)与主频相同的零相位Ricker子波合成记录(图 9b)相一致。
|
图 8 反射系数、40°相位角Ricker子波合成地震记录及滤波结果 (a)反射系数;(b)40°相位角Ricker子波合成记录;(c)15Hz滤波结果;(d)60Hz滤波结果;(e)300ms附近图c与图d放大对比 |
|
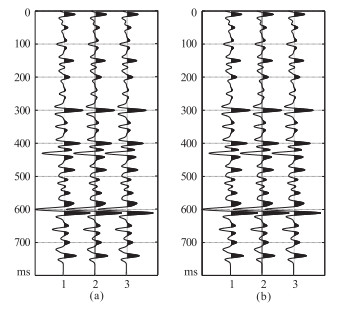
图 9 基于本文方法零相位化处理结果(a) 及零相位Ricker子波合成记录(b) |
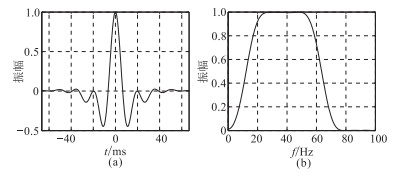
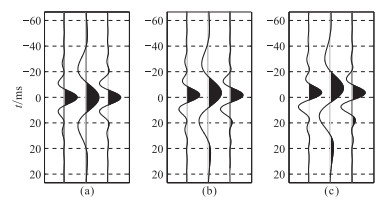
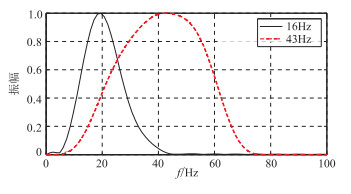
为进一步验证本文方法的适用性,用带通子波(图 10)替换上述的Ricker子波。将该带通子波分别进行30°、60°相位角旋转,采用主频分别为16Hz和43Hz的Ricker子波进行滤波处理,得到如图 11所示结果。对滤波后的数据进行频谱分析(图 12),该带通子波经过主频为16Hz和43Hz的Ricker子波滤波处理后,主频变为20Hz和43Hz,因此峰值时差与相位旋转量的拟合关系式为:θ=17.064Δt(图 7)。从图 11中可看出:当相位角为0°时,峰值时差为0,由拟合关系得出的相位角为0°;当相位角为30°时,峰值时差为1.8ms,拟合得出的相位角为30.7°;当相位角为60°时,峰值时差为3.6ms,拟合得出的相位角为61.4°。
|
图 10 带通子波(a)及其频谱(b) |
|
图 11 相位角依次为0°(a)、30°(b)、60°(c)的带通子波滤波后峰值时刻的变化 滤波主频分别为16Hz(中)和43Hz(右) |
|
图 12 带通子波分别经过主频为16Hz和43Hz的Ricker子波滤波后的频谱 |
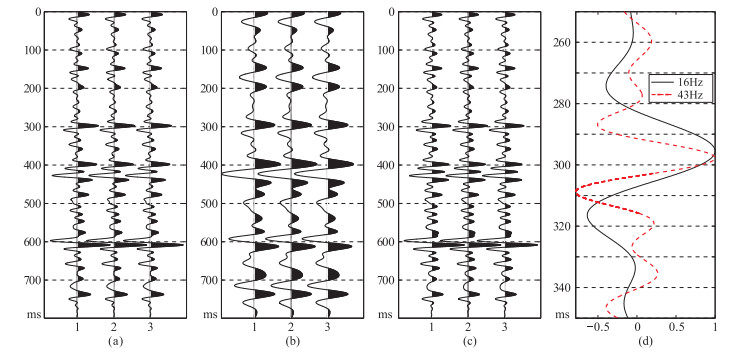
采用图 8a的反射系数与40°相位角的带通子波进行模拟,得到图 13a所示的合成地震记录;分别用主频为16Hz和43Hz的Ricker子波对其做滤波处理(图 13b、图 13c)。对300ms附近滤波后数据进行放大显示(图 13d),16Hz滤波结果的峰值时间为295.5ms,43Hz滤波结果的峰值时间为297.8ms,对应峰值时差Δt=2.3ms,将该峰值时差代入图 7中关系式,计算出剩余相位角为39.2°,较准确地估计出地震记录的剩余相位角。可见本文方法对带通子波也具有较强适用性。
|
图 13 40°相位角带通子波合成地震记录及滤波结果 (a)40°相位角带通子波合成记录;(b)16Hz滤波结果;(c)43Hz滤波结果;(d)300ms附近图b与图c放大对比 |
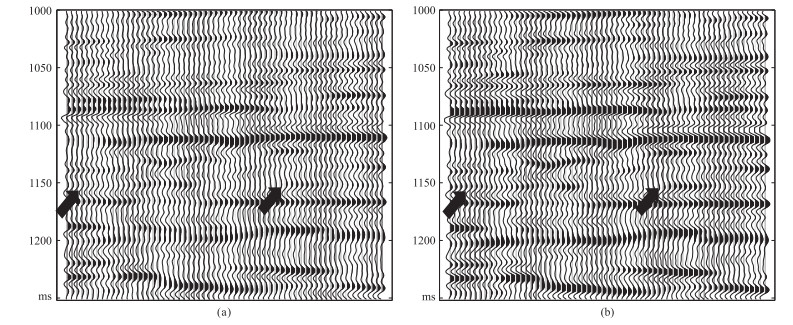
图 14a为渤海M区实际叠后地震剖面,采用本文方法对其进行剩余相位估计并做零相位化处理,得到图 14b所示结果。可见经零相位化处理后剖面上弱反射同相轴能量得到增强,分辨率有一定改善(黑色箭头所指)。
|
图 14 实际地震资料基于本文方法零相位化处理前(a)、后(b)剖面对比 |
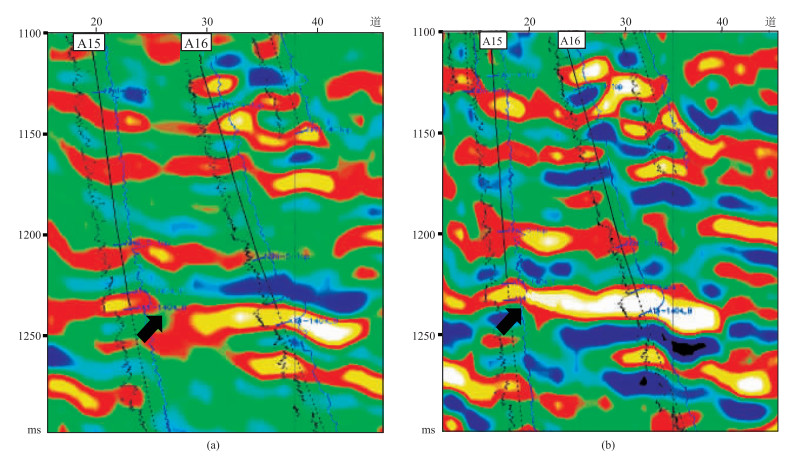
为验证本文方法的可靠性,运用本文方法求得该实际地震资料的剩余相位角是40°。为更好地研究储层的发育特征,对该资料做-40°相移后再进行反演(图 15)。原始地震资料反演结果认为目的层处A15井与A16井不连通(黑色箭头所指),而经相位校正后的资料反演结果认为目的层处A15井与A16井是连通的。油气开采动态资料表明,A15井注水后,A16井很快有反应,表明A15井与A16井之间的储层的确是连通的。这也证实基于本文方法得到的剩余相位角是可信的。
|
图 15 基于本文方法零相位化处理前(a)、后(b)反演剖面对比 |
对地震数据剩余相位的估计,前人研究成果大多是建立在一定判别准则上进行的,判别准则选取的合理性,直接影响最终结果。本文通过研究Ricker子波的相移特性,发现主频不同的Ricker子波在相同相位旋转下,峰值时差与相位旋转量具有线性关系,通过该线性关系实现地震资料剩余相位角的估计。该方法不需要判别准则的约束,原理简单、运算量小、精度高,具有较强实用性。模型试算和实际资料处理结果表明,本文方法能有效地估计出地震数据的剩余相位角,从而实现地震资料的零相位化。
| [1] |
刘金俊, 王修田, 徐世浙. 实现地震道零相位化的子波相位谱消去法[J]. 海洋地质与第四纪地质, 1999, 19(4): 89-95. LIU Jinjun, WANG Xiutian, XU Shizhe. The method of eliminating wavelet phase spectrum of zero-phase seismic traces[J]. Marine Geology & Quaternary Geology, 1999, 19(4): 89-95. |
| [2] |
苏贵仕, 沈克非, 丁学垠. 地震数据处理中关于地震子波相位特性的探讨[J]. 石油地球物理勘探, 2008, 43(增刊2): 121-124. SU Guishi, SHEN Kefei, DING Xueyin. Discussion on phase character of seismic wavelet in seismic data processing[J]. Oil Geophysical Prospecting, 2008, 43(S2): 121-124. |
| [3] |
李强, 何晓松, 王立. 一种实现井约束零相位化的处理方案[J]. 石油地球物理勘探, 2009, 44(增刊1): 76-78. LI Qiang, HE Xiaosong, WANG Li. Introducing a processing technique to realize well constrained zero phasizing[J]. Oil Geophysical Prospecting, 2009, 44(S1): 76-78. |
| [4] |
徐刚, 王静, 黄卫, 等. 一种基于信息熵理论的地震子波相位校正方法[J]. 石油地球物理勘探, 2014, 49(2): 239-243, 251. XU Gang, WANG Jing, HUANG Wei, et al. A me-thod for seismic wavelet zero-phasing based on information entropy theory[J]. Oil Geophysical Prospecting, 2014, 49(2): 239-243, 251. |
| [5] |
王守君, 方中于, 史文英, 等. 海洋地震资料子波零相位化技术研究与应用[J]. 石油物探, 2015, 54(5): 551-559. WANG Shoujun, FANG Zhongyu, SHI Wenying, et al. Marine seismic wavelet zero-phasing technology and its application[J]. Geophysical Prospecting for Petroleum, 2015, 54(5): 551-559. DOI:10.3969/j.issn.1000-1441.2015.05.008 |
| [6] |
吕磊, 黄云峰, 田彦灿, 等. 零相位反褶积在不整合接触关系保真处理中的应用[J]. 石油地球物理勘探, 2018, 53(增刊2): 20-23. LYU Lei, HUANG Yunfeng, TIAN Yancan, et al. Zero-phase deconvolution applied in unconformity contact relation processing[J]. Oil Geophysical Pro-specting, 2018, 53(S2): 20-23. |
| [7] |
刘书亭, 张宪国, 任丽华, 等. 利用地震沉积学定量刻画辫状河三角洲砂体——以委内瑞拉MPE-3区块为例[J]. 石油地球物理勘探, 2019, 54(6): 1348-1356. LIU Shuting, ZHANG Xianguo, REN Lihua, et al. Quantification of braided river-delta sand body based on seismic sedimentology: an example of the Block MPE-3 in Venezuela[J]. Oil Geophysical Prospecting, 2019, 54(6): 1348-1356. |
| [8] |
张波, 郭平, 高树生, 等. 高分辨率处理技术在辽河雷家地区碳酸盐岩储层中的应用[J]. 石油地球物理勘探, 2018, 53(增刊1): 43-50. ZHANG Bo, GUO Ping, GAO Shusheng, et al. High- resolution processing techniques applied for carbonate reservoirs in Leijia Area, Liaohe[J]. Oil Geophysical Prospecting, 2018, 53(S1): 43-50. |
| [9] |
周东红, 谭辉煌, 王伟. 相位校正S域反褶积方法及应用[J]. 石油地球物理勘探, 2020, 55(6): 1245-1252. ZHOU Donghong, TAN Huihuang, WANG Wei. Deconvolution in S domain with phase correction and its application[J]. Oil Geophysical Prospecting, 2020, 55(6): 1245-1252. |
| [10] |
郭向宇, 周兴元, 董敏煜. 混合相位子波的相位估算及校正[J]. 石油地球物理勘探, 1998, 33(2): 214-221. GUO Xiangyu, ZHOU Xingyuan, DONG Minyu. Phase estimate and correction of mixed-phase wavelet[J]. Oil Geophysical Prospecting, 1998, 33(2): 214-221. |
| [11] |
王君, 周兴元. 子波相位校正及效果分析[J]. 石油地球物理勘探, 2008, 43(增刊2): 142-145. WANG Jun, ZHOU Xinyuan. Wavelet phase correction and analysis of effect[J]. Oil Geophysical Pro-specting, 2008, 43(S2): 142-145. |
| [12] |
刘玉金, 李振春, 郭恺. 基于局部相似度的非稳态相位校正方法[J]. 石油地球物理勘探, 2012, 47(6): 887-893. LIU Yujin, LI Zhenchun, GUO Kai. Non-stationary phase correction based on local similarity[J]. Oil Geo-physical Prospecting, 2012, 47(6): 887-893. |
| [13] |
高少武, 赵波, 李桂芳, 等. 纯相位因子估算与剩余子波相位校正[J]. 石油地球物理勘探, 2014, 49(3): 463-467. GAO Shaowu, ZHAO Bo, LI Guifang, et al. Estimation of pure phase factor and phase correction of residual wavelet[J]. Oil Geophysical Prospecting, 2014, 49(3): 463-467. |
| [14] |
李合群, 周兴元. 时差、常相位校正及加权叠加[J]. 石油地球物理勘探, 2000, 35(4): 415-418. LI Hequn, ZHOU Xingyuan. Moveout and constant phase corrections, along with weighted stacking[J]. Oil Geophysical Prospecting, 2000, 35(4): 415-418. DOI:10.3321/j.issn:1000-7210.2000.04.002 |
| [15] |
Levy S, Oldenburg D W. Automatic phase correction of common-midpoint stacked data[J]. Geophysics, 1987, 52(1): 51-59. DOI:10.1190/1.1442240 |
| [16] |
Sacchi M D, Velis D R, Cominguez A H. Minimum entropy deconvolution with frequency-domain constraints[J]. Geophysics, 1994, 59(6): 938-945. DOI:10.1190/1.1443653 |
| [17] |
Lu W K, Liu D Q. Frequency recovery of band-limited seismic data based on sparse spike train deconvolution[C]. SEG Technical Program Expanded Abstracts, 2007, 26: 1977-1981.
|
| [18] |
Ooe M, Ulrych T J. Minimum entropy deconvolution with an exponential transformation[J]. Geophysical Prospecting, 1979, 27(2): 458-473. DOI:10.1111/j.1365-2478.1979.tb00979.x |
| [19] |
Claerbout J F. Parsimonious deconvolution[J]. Stanford Exploration Project, 1977, 13: 1-9. |
| [20] |
单联瑜, 王希萍, 李振春, 等. 相位校正判别准则的改进及应用效果分析[J]. 石油物探, 2008, 47(3): 219-224. SHAN Lianyu, WANG Xiping, LI Zhenchun, et al. Improvement of discriminant criteria for phase correction and its application effect[J]. Geophysical Pro-specting for Petroleum, 2008, 47(3): 219-224. DOI:10.3969/j.issn.1000-1441.2008.03.002 |
| [21] |
Fomel S, van der Baan M. Local skewness attribute as a seismic phase detector[J]. Interpretation, 2014, 2(1): 49-56. |
| [22] |
刘俊州, 马铭, 时磊, 等. 基于偏斜度准则的地震子波相位估计方法特征研究[J]. 地球物理学进展, 2017, 32(1): 210-216. LIU Junzhou, MA Ming, SHI Lei, et al. Characteristics study of seismic wavelet phase estimation based on the skewness criterion[J]. Progress in Geophy-sics, 2017, 32(1): 210-216. |
| [23] |
姚逢昌. 振幅谱补偿和相位校正[J]. 石油物探, 1990, 29(3): 46-59. YAO Fengchang. Amplitude spectra compensation and phsse correction[J]. Geophysical Prospecting for Petroleum, 1990, 29(3): 46-59. |
| [24] |
陈春继, 冯世民, 莫阿玲, 等. 90°相移技术在岩性解释中的应用[J]. 石油地球物理勘探, 2012, 47(1): 95-99. CHEN Chunji, FENG Shimin, MO Aling, et al. Application of 90° phase data in lithologic interpretation[J]. Oil Geophysical Prospecting, 2012, 47(1): 95-99. |



 刘传奇, 天津市滨海新区海川路2121号海洋石油大厦B座中海油天津分公司渤海石油研究院, 300459。Email:
刘传奇, 天津市滨海新区海川路2121号海洋石油大厦B座中海油天津分公司渤海石油研究院, 300459。Email: 