② 中国石油化工股份有限公司江汉石油管理局物探处物探研究中心, 湖北潜江 433100
② Geophysical Research Center, Geophysical Department, Jianghan Petroleum Administration Bureau, Sinopec, Qianjiang, Hubei 433100, China
在地震勘探中,受现场施工条件限制或因地下传播路径复杂,所采集到的地震数据往往信噪比较低,有效信号常淹没在强大噪声背景中,致使依赖于较高信噪比的一些处理技术的应用效果受到影响,如速度分析、静校正量计算、地震建模及偏移成像等。因此,亟待通过采用各种更有效去噪技术提高地震资料的信噪比。
在传统去噪技术中,常用减小噪声或增强信号,或两者兼顾的方法。这些方法(如随机噪声衰减、F-X decon、奇异值分解、多项式拟合等)都建立在信号占优的前提下,否则难以达到应用目的。许多学者持续研究并改进各自提出的方法,以期进一步提高或拓展这些技术对不同地区、不同资料的有效性和普适性[1-6]。
小波技术的出现给解决此类难题带来了新途径,其最成功的应用是小波变换阈值去噪。由于其算法简捷、去噪效果明显而成为去噪环节乃至整个地震数据处理领域应用最广泛的方法之一[7-10]。然而,经典小波阈值去噪算法采用设定全局阈值方式,而地震资料中的噪声具有明显时空变性质,采用全局阈值去噪方法易产生过扼杀/过保留现象。尽管人们在阈值计算上进行了大量尝试,提出了一些计算局部阈值的算法[11-12]。但由于方法本身所限,求取的阈值只能是相对准确;加上小波阈值去噪技术中所用去噪算法本身在数学机理上不尽严谨[13-14],因此人们逐渐试用其他技术取代小波阈值去噪方法[15-21],并取得了显著成效。这些方法[15-21]考虑了去噪过程的相关细节,均有严格的应用条件,并要求待处理地震资料具有一定信噪比。
对于低信噪比资料而言,现阶段苛求对其准确无误地去噪只是一种奢望,能有效提取信号(包容一定的去噪误差)是目前可供努力的方向之一。这就要求去噪方法一定要具有强大的噪声压制能力。小波阈值去噪方法持续活跃于信号处理领域达20余年,亦主要缘于此。为此,本文依然借用这种方法从低信噪比地震资料中提取信号。当然,上已述及小波阈值去噪方法仍存有诸多缺陷,应对其进行必要的修正、完善。
文献[22]提出了时空变阈值去噪,且成功地应用于可控震源地震资料。该项技术巧妙利用在同一震点上多道相关未叠加可控震源资料(同一震点,不同震次形成的道集)满足叠加三条件,以相邻道的叠加结果作为小波去噪过程中的初始标准值,采用迭代方法求取方差,进而求取时空变阈值,实现时空变小波阈值去噪。但非可控震源地震资料不具备上述条件,应用上述思路及方法则需要对其进行必要的修正和改进。
目前,任何去噪技术都不可能彻底去除噪声,小波阈值去噪也不例外。若能对去噪结果再应用叠加技术,才能更准确地从低信噪比资料中提取信号。多个小波基函数的出现,给这一思路的实现带来了可能。应用多个小波对同一地震记录道分别进行时空变小波阈值去噪,得到多道去噪记录。这些去噪后的多道记录具有信号同相、噪声相关性差或不相关的特点,为应用叠加技术创造了条件。
基于上述分析,本文所提方法的实现思路为:通过改进的小波阈值技术进行去噪,并采用多个不同小波重复上述处理,得到多道去噪后地震记录;将所得多道去噪地震记录进行叠加。两种技术中,前者为后者的基础,后者是前者的完善,两者紧密结合实现低信噪比资料中的信号提取。
1 方法原理 1.1 时空变小波阈值去噪 1.1.1 经典小波阈值去噪小波变换具有很强的数据相关性,它不仅能使信号能量在小波域集中到一些大的有限的系数中,而且可使噪声的能量分布于整个小波域。因此经小波分解后,信号的小波变换系数大于噪声的小波变换系数,可认为幅值较大的小波系数一般以信号为主,而幅值较小的小波系数在很大程度上是噪声。于是找到一个合适的λ作为阈值,当第j层第k个小波系数wj,k小于该阈值时,可认为这时的wj,k主要是由噪声引起,则将系数wj,k减小至零;当wj,k大于该阈值时,认为此时的wj,k主要是由信号引起,则将该系数予以保留,从而实现了信噪分离。
从上述分析可见,小波阈值去噪是通过压制噪声、保留有效信号实现的。
经典的小波阈值去噪公式为
| $ \hat{w}_{j, k}=\left\{\begin{array}{cl} \operatorname{sign}\left(w_{j, k}\right) \cdot \sqrt{w_{j, k}^{2}-a \lambda^{2}} & \left|w_{j, k}\right| \geqslant \lambda \\ 0 & \left|w_{j, k}\right|<\lambda \end{array}\right. $ | (1) |
式中:
由式(1)可知,去噪是否彻底取决于阈值λ的准确求取、权系数a的适当选用及噪声处理细节的严谨。显然,基于地震资料中噪声具有明显的时空变性,只有时空变地求取λ、实时调节a,并对去噪处理方式进行必要修正,才能较彻底地压制噪声。
1.1.2 改进的时空变小波阈值去噪方法文献[22]已初步实现了时空变阈值去噪,本文沿用这一思路。但非可控震源资料中有效信号并非一定呈水平排列,在利用文献[22]方法时,需进行相邻道信号同相轴方向扫描,然后沿同相轴方向求叠加结果作为初始标准值,并通过迭代方法修正方差,进而求取时空变阈值。但因式(1)中a并无时空变化,故该方法去噪结果仍有误差。a是为调节去噪强度而设,若存有某种依据实时对阈值作出过大还是过小的判断,并对其进行必要的修正,就可较好地控制阈值的大小以减小去噪误差,即实现了a的时空变。事实上,根据单道信息无法判别求取的阈值是否适当,但多道地震记录的存在,且相邻道信号具有相关性,给判断阈值是否准确提供了依据。
地震数据处理中,中值、叠加结果常被用作评判处理结果是否准确。同样,可将处理点作为中心,选择左右各N道记录沿信号方向求取中值和叠加结果,将去噪结果限制在以上述两结果为上、下限的局部值域中,进而在去噪过程中减少过扼杀/过保留现象。具体实施方案:若待去噪样点值大于阈值,取中值、叠加结果和利用式(1)得到的去噪结果三者之间的中值为去噪结果;对于小于阈值的样点去噪结果也以中值、叠加结果和0三者的中值取代“充零”处理。即改进的小波阈值去噪公式为
| $ \hat{w}_{j, k}=\left\{\begin{array}{ll} \text { median(med,stack, thre) } & \left|w_{j, k}\right| \geqslant \lambda \\ \text { median(med, stack, 0) } & \left|w_{j, k}\right|<\lambda \end{array}\right. $ | (2) |
式中:median表示以括号内三个数的中值为去噪结果;med表示以处理道为中心,沿信号方向2N+1个样点的中值;stack为上述2N+1个样点叠加结果;thre为式(1)中的
式(2)隐含了应用中值和叠加结果对式(1)中a进行了实时修正这一事实。当thre为式(2)中的中值时,表示此时a较准确,不需实时修改;若中值为med或stack,暂令其为b,式(1)中a为待定系数,有
| $ \operatorname{sign}\left(w_{j, k}\right) \cdot\left(w_{j, k}^{2}-a \lambda^{2}\right)^{1 / 2}=b $ | (3) |
通过式(3)可反求a,实现实时修正的目的(实施中没必要多此一举),即改进的小波阈值去噪是通过实时调节a实施。这种修正既限定了阈值大小,修正了加权系数的不变性,也完善了去噪方式。
从另一角度看,将式(1)修改为式(2)是将经典小波阈值去噪由单道去噪改为多道去噪,当式(2)中用于计算中值的道数N取0时,式(2)退化为式(1)。这种变化可满足同一工区不同区域的去噪需求。
去噪可采用多道或单道方式。多道方式的优势是利用相邻道信号相关的特点,增加识别噪声的准确度及去噪的稳定性,缺陷是可能会模糊突变点信息;而单道方式的优劣正好与之相反。对式(2)两次应用相邻道信息,保证了去噪结果的准确性。同时,应用求中值的方法对去噪中的减法和充零进行修正,减小了该去噪方法对去噪结果的损害。
当然,这种修改程度随阈值的准确度而变化。当阈值准确且待处理样点的绝对值大于阈值时,利用式(2)求取的中值大多为阈值,此时实际上是应用式(1)进行去噪处理,但阈值的求取过程中依然应用了多道的信息;当阈值存有较大误差时,则应用中值/叠加结果进行修正,进而减小去噪过程中的过扼杀/过保留现象。当待处理样点的绝对值小于阈值,将充零处理修正为求中值。这种处理缓解了充零处理后引起的信号重构畸变。
由式(2)可知,阈值的准确求取依赖于信号同相轴方向的准确度,因此方向扫描是该方法的重要环节。由于小波变换后各小波尺度下的小波系数信噪比高低不同,为提高信号扫描的准确度,宜选用信噪比最高的小波尺度进行方向扫描,本文即采用此方法。限于篇幅,文中未对此内容展开讨论。
1.2 多个小波去噪结果的叠加取多个不同小波,分别应用改进的小波阈值去噪技术对某道地震记录进行去噪处理,一道地震记录通过多次处理可得到与所应用小波个数一样的多道地震记录。由式(2)可知,对同一地震道应用不同小波去噪的结果上,信号位置不会移动,即这些地震道在同一位置具有类似的信号信息,但有幅度大小及形态差异。因所用小波的不同,导致其分解、阈值计算、去噪及重构方面的差异,致使去噪后的地震记录残留不同的随机噪声。简言之,去噪后的多道地震记录在同一位置信号强相关,而噪声特征为弱相关/不相关。这一特殊特征使叠加技术中最重要的应用条件“信号时间对齐”得以满足。
设
| $ \hat{S}_{m}(t)=S_{m}(t)+N_{m}(t) $ | (4) |
式中
| $ \bar S(t) = \sum\limits_{m = 1}^M {{{\hat S}_m}} (t) = \sum\limits_{m = 1}^M {{S_m}} (t) + \sum\limits_{m = 1}^M {{N_m}} (t) $ | (5) |
该式右边第一项信号同相叠加,能量增强;第二项噪声同相性差,相加后有一定程度互相抵消。
需要说明的是,不同的小波具有不同的特征,适应不同类型的噪声。理论上,应选用尽可能多的小波以适应地震资料中噪声的多变性。但在实际应用中,面对各种不同的噪声,很难选取最适用的小波。本文选用Morlet、Marr及Sym2三种小波进行去噪,其适用性及有效性基本符合要求。
2 理论模型测试及实际资料处理 2.1 理论模型测试 2.1.1 改进的小波阈值去噪方法应用效果影响经典小波阈值去噪效果的三个因素(λ、a及去噪方式)中,前两个因素上文已述及,此处主要测试第三个因素对去噪结果的影响及改进后的去噪效果。为使测试因素单一,这里选择信号同相轴呈水平层状,以避开信号方向扫描不准影响阈值计算结果;减小外加噪声,使求取阈值更准确,并突显去噪处理方式对去噪结果的影响。
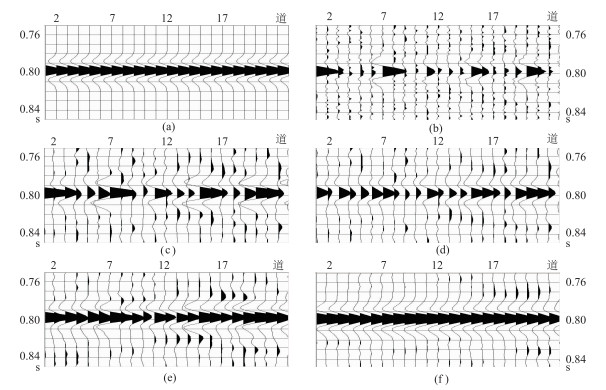
图 1a是由22道40Hz雷克子波构成的记录,对该记录各道加入不同的随机噪声(信噪比为0.6),得到相差迥异的含噪记录(图 1b)。应用Morlet小波通过经典小波变换公式进行去噪,所得结果(图 1c)中噪声显著衰减,淹没于噪声背景的有效信号突显出来。但因仍采用减法运算和充零处理,致使提取的记录产生了明显形变,有些道(第8道和第9道的0.8s处)甚至严重失真。
|
图 1 改进的时空变小波阈值去噪效果分析 (a)22道40Hz雷克子波;(b)对图a各道加上不同随机噪声;(c)经典小波阈值去噪结果;(d)小波系数小于阈值时应用式(1)去噪结果;(e)小波系数大于阈值时应用式(1)去噪结果;(f)应用式(2)小波阈值去噪结果 |
为进一步分析经典小波阈值去噪产生误差的原因,以两种方案进行测试:①小波系数不小于小波阈值时,用经典公式计算;而当小波系数小于小波阈值时,采用“求中值”方法取代充零实施去噪处理;②小波系数不小于小波阈值时,采用求中值方式;而当其小于小波阈值时,采用充零方法实施去噪处理。这两种测试可清楚观察到经典小波阈值压制噪声技术中减去阈值和充零处理两种方式对噪声的压制效果。从第一种测试方案处理结果(图 1d)可见,其效果优于图 1c(第8道和第9道在0.8s处有改善),尽管其记录形态也存在明显失真,但失真程度远低于图 1c,且在信号同相轴的上、下方噪声明显减少,有效地减小了因充零处理而导致的畸变。这表明通过对式(1)充零处理方式的改进可克服待处理样点小于阈值时简单采用充零处理导致的有效信号损失。再观察第二种测试方案处理结果(图 1e),虽也可见记录道形变,但总体效果优于图 1d(第8道和第9道在0.8s处有明显改善)。这表明对式(1)中减法处理的改进明显减弱了对信号的损害。图 1f是利用式(2)的去噪结果,可见随机噪声得到有效压制,并成功地提取了有效信号,产生的形变比图 1e显著减弱,且信号上方和下方的噪声也得到有效压制,与图 1a非常接近。
实际上,经典小波阈值去噪存有的三项缺陷对处理结果的影响是一个综合效应,特别是应用于低信噪比资料。此例仅用于直观观测经典小波阈值去噪中去噪方法存有的去噪误差。
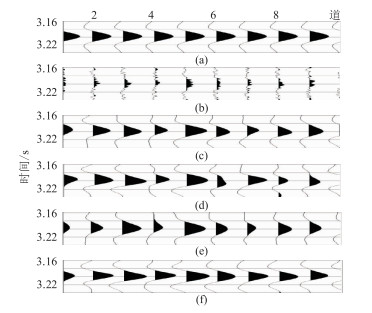
2.1.2 不同小波去噪效果及叠加技术增强效果类似于图 1,此算例依然选择水平状信号。通过商用软件对由主频为16Hz的雷克子波构成的原始模型(图 2a)加入信噪比为0.4的噪声(图 2b),加噪后有效信号完全淹没于噪声之中。分别应用Morlet、Marr、Sym2三种小波进行改进的小波阈值去噪,从处理结果(图 2c~图 2e)可见,信号大体显露,位置相同,但形态稍有差异,且不同小波所得到的去噪结果呈现较明显差异,第4、6、8道尤为突出。图 2f为图 2c~图 2e的加权叠加,可见多个小波去噪结果叠加增强了有效信号,形变信号得以恢复,弥补了单小波阈值压制噪声缺陷,波形很接近图 2a,叠加技术的作用一目了然。
|
图 2 不同小波去噪结果及叠加技术增强有效信号效果分析 (a)10道16Hz雷克子波理论模型;(b)对图a加入随机噪声;(c)~(e)分别为对图b应用Morlet、Marr、Sym2小波用本文方法去噪结果;(f)对图c~图e的加权叠加结果 |
有效信号淹没于噪声背景的实际资料无法直观观察信号提取是否真实,本文采用对合成单炮加噪的方式测试本文方法的有效性及适应性。
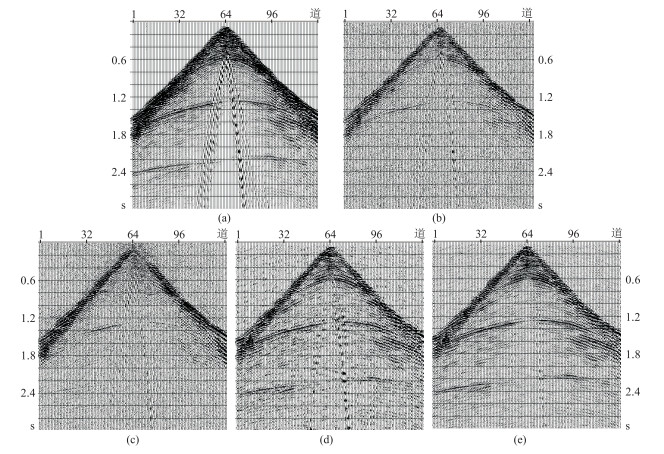
采用简单平层地质模型,通过商用软件GX2D进行正演模拟,得到原始单炮记录(图 3a)。该记录共有128道,道长为3s,采样率为2ms;由加噪软件对图 3a做加噪处理(图 3b,信噪比为0.1)。选用已广泛应用的增强信号软件F-X decon做测试处理,所得处理结果(图 3c)中未呈现有效波同相轴,可见常规软件难以有效提取低信噪比资料中的信号。分别应用Morlet、Marr、Sym2三种小波做经典小波阈值去噪及加权叠加,将处理结果(图 3d)与图 3c进行对比,可见小波阈值法去噪能力明显优于F-X decon。另外,虽然强同相轴显露出来,但提取的信号不太清晰,层间噪声依然存在,同相轴的连续性、光滑性存有明显缺陷,表明经典小波阈值去噪因自身存有的缺陷,处理效果仍有很大改进空间。图 3e是本文方法(即分别应用Morlet、Marr、Sym2三种小波进行改进的小波阈值去噪并叠加)的处理结果,可见强同相轴更连续光滑,弱同相轴的连续性也有所改善,层间噪声基本消除干净,也没有出现遗漏和新增的同相轴,与图 3a非常接近,充分展现了本文方法的优势。
|
图 3 模拟单炮资料处理效果对比 (a)原始单炮;(b)加噪后单炮;(c)F-X decon处理;(d)经典小波阈值(应用Morlet、Marr、Sym2三种小波)去噪+叠加;(e)本文小波阈值去噪(应用Morlet、Marr、Sym2三种小波)+叠加 |
同时从图 3e可以看出,应用本文方法后面波也得以有效压制,而经典小波阈值去噪结果仍存有较强的面波干扰(图 3d),这是由于本文方法对面波的处理采用了先假设面波为信号,在面波所在的小波尺度下进行面波方向扫描,并沿面波方向计算小波阈值,应用式(3)求取面波,再从该尺度下原始小波系数减去该值,从而达到消除面波的目的。
此例表明,本文方法同样适用于信号同相轴为非水平排列的炮集记录。
2.2 实际数据处理人工模拟单炮、人工加噪模拟与实际单炮记录存在诸多不同。针对实际单炮,将常规信号增强软件、经典小波阈值去噪与本文方法进行比较,以测试本文方法对实际地震资料的有效性和适用性。
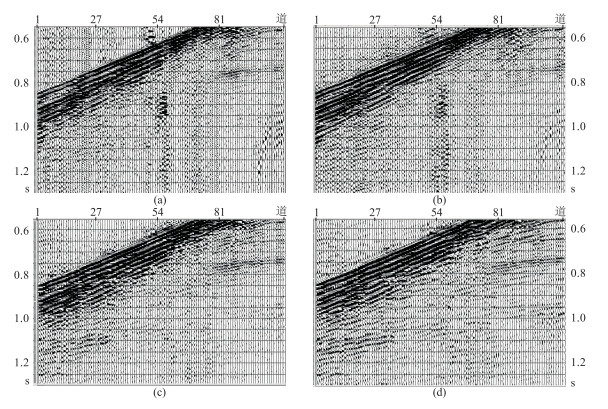
图 4a为原始单炮,信号淹没于随机噪声、强能量环境噪声、面波、50Hz工频干扰等多种背景噪声中。观察F-X decon方法处理结果(图 4b),由于用该方法去噪时利用了多道信息,而其中噪声能量占优,去噪结果中隐藏在噪声中的信号难以仅通过应用该技术得以显露。在应用Morlet小波的经典小波阈值去噪结果(图 4c)中,显露出图 4a中仅能隐约可见的同相轴,并大体上可连续追踪。图 4d是本文方法(应用了Morlet、Marr、Sym2三种小波及叠加)的处理结果,与图 4c相比有效信号更清晰,同相轴的连续性、光滑性均增强,剖面清晰度大幅度地提高,整个剖面面貌得到较明显的改观,达到了预期的处理效果。另外,图 4a中的随机噪声、强能量环境噪声、面波等经处理后均得到有效压制。与图 3e算例类似,图 4d的良好处理效果主要归功于在去噪阈值的求取过程中采用了多道技术,增强了小波阈值去噪技术的噪声识别能力。
|
图 4 实际单炮资料试处理效果对比 (a)原始单炮;(b)F-X decon处理;(c)经典小波阈值(应用Morlet小波)去噪;(d)本文方法(应用Morlet、Marr、Sym2三种小波+叠加)去噪 |
本文采用去噪与叠加相结合的方法实现从低信噪比地震记录中提取信号,取得了较好应用效果。通过理论分析、数据测试处理,得到如下认识。
(1) 采用改进的小波阈值去噪方法实施去噪。即用实时修正去噪系数a的方式对经典小波阈值去噪技术进行改进;将小波阈值去噪由单道计算改进为多道计算,以提高噪声识别和压制的准确性和稳定性。
(2) 采用叠加技术进一步增强信号。以多个小波进行小波阈值去噪处理,达到一道地震记录变多道的效果,为叠加技术的应用创造了条件。
(3) 先后应用去噪技术和叠加技术提高地震资料的信噪比,将这两种不同思路的去噪方法有机结合并成功地从低信噪比资料中提取信号。
(4) 虽仍依赖于原始资料的信噪比,但本文方法将多道思想应用于小波阈值去噪,去噪结果对信噪比的适应性远超同类常规处理方法。
| [1] |
张军华. 地震资料去噪方法——原理、算法、编程及应用[M]. 山东东营: 石油大学出版社, 2011.
|
| [2] |
Canales L L. Random noise reduction[C]. SEG Technical Program Expanded Abstracts, 1984, 3: 525-527.
|
| [3] |
李振春, 张军华. 地震数据处理方法[M]. 山东东营: 石油大学出版社, 2004.
|
| [4] |
徐彦凯, 曹思远, 何元. 双曲Radon ASVD方法压制叠前地震数据随机噪声研究[J]. 石油地球物理勘探, 2017, 52(3): 451-457. XU Yankai, CAO Siyuan, HE Yuan. Prestack seismic random noise attenuation with a hyperbolic Radon-ASVD[J]. Oil Geophysical Prospecting, 2017, 52(3): 451-457. |
| [5] |
刘志鹏, 赵伟, 陈小宏, 等. 局部频率域SVD压制随机噪声方法[J]. 石油地球物理勘探, 2012, 47(2): 202-206. LIU Zhipeng, ZHAO Wei, CHEN Xiaohong, et al. Local SVD for random noise suppression of seismic data in frequency domain[J]. Oil Geophysical Prospecting, 2012, 47(2): 202-206. |
| [6] |
刘志刚, 谢言光, 陈峰. 地震数据处理中噪声衰减方法的探讨[J]. 石油地球物理勘探, 2009, 44(增刊1): 67-71. LIU Zhigang, XIE Yanguang, CHEN Feng. Discussion on noise attenuation methods in seismic data processing[J]. Oil Geophysical Prospecting, 2009, 44(S1): 67-71. |
| [7] |
Mallat S. A theory for multiresolution signal decomposition: The wavelet representation[J]. IEEE Tran-sactions on Pattern Analysis and Machine Intelligence, 1989, 11(7): 674-693. DOI:10.1109/34.192463 |
| [8] |
Donoho D L, Johnstone I M. Ideal spatial adaptation via wavelet shrinkage[J]. Biometrika, 1994, 81(3): 425-455. DOI:10.1093/biomet/81.3.425 |
| [9] |
Donoho D L. Ten-minute tour[J]. Progress in Wavelet Analysis and Application, 1993, 338(2): 639-654. |
| [10] |
Donoho D L. Denoising by soft thresholding[J]. IEEE Transactions on Information Theory, 2002, 41(3): 613-627. |
| [11] |
王坤明. 自动选取阈值方法比较研究[J]. 抚顺石油学院学报, 2002, 27(2): 70-73. WANG Kunming. Comparative study on automatic selection threshold[J]. Journal of Fushun Petroleum University, 2002, 27(2): 70-73. |
| [12] |
董永生, 羿旭明. 基于四种改进阈值的小波去噪方法[J]. 数学杂志, 2006, 26(6): 473-477. DONG Yongsheng, YI Xuming. Wavelet denoising method based on four improved thresholds[J]. Journal of mathematics, 2006, 26(6): 473-477. |
| [13] |
余江奇, 曹思远, 陈红灵, 等. 改进阈值的Curvelet变换稀疏反褶积[J]. 石油地球物理勘探, 2017, 52(3): 426-433. YU Jiangqi, CAO Siyuan, CHEN Hongling, et al. Sparse deconvolution based on Curvelet transform of improved threshold[J]. Oil Geophysical Prospecting, 2017, 52(3): 426-433. |
| [14] |
彭玉华. 一种改进的小波变换阈值去噪方法[J]. 通信学报, 2004, 25(8): 119-123. PENG Yuhua. An improved thresholding method in wavelet transform domain for denoising[J]. Journal on Communications, 2004, 25(8): 119-123. DOI:10.3321/j.issn:1000-436X.2004.08.016 |
| [15] |
贾瑞生, 赵同彬, 孙红梅, 等. 基于经验模态分解及独立成分分析的微震信号降噪方法[J]. 地球物理学报, 2015, 58(3): 1013-1023. JIA Ruisheng, ZHAO Tongbin, SUN Hongmei, et al. Micro-seismic signal denoising method based on empirical mode de-composition and independent component analysis[J]. Chinese Journal of Geophysics, 2015, 58(3): 1013-1023. |
| [16] |
赵天姿, 宋炜, 王尚旭. 基于匹配追踪算法的时频滤波去噪方法[J]. 石油物探, 2008, 47(4): 367-371. ZHAO Tianzi, SONG Wei, WANG Shangxu. Time-frequency filtering denoising method based on ma-tching pursuit algorithm[J]. Geophysical Prospecting for Petroleum, 2008, 47(4): 367-371. DOI:10.3969/j.issn.1000-1441.2008.04.009 |
| [17] |
孙苗苗, 李振春, 曲英铭, 等. 基于曲波域稀疏约束的OVT域地震数据去噪方法研究[J]. 石油物探, 2019, 58(2): 208-218. SUN Miaomiao, LI Zhenchun, QU Yingming, et al. A seismic denoising method based on curvelet transform with sparse constraint in OVT domain[J]. Geophysical Prospecting for Petroleum, 2019, 58(2): 208-218. |
| [18] |
曹静杰, 杨志权, 孙秀丽. 一种基于曲波变换的自适应地震随机噪声消除方法[J]. 石油物探, 2018, 57(1): 72-78. CAO Jingjie, YANG Zhiquan, SUN Xiuli. An adaptive seismic random noise elimination method on Curvelet transform[J]. Geophysical Prospecting for Petroleum, 2018, 57(1): 72-78. DOI:10.3969/j.issn.1000-1441.2018.01.010 |
| [19] |
徐彦凯, 曹思远, 潘晓, 等. 随机噪声的局部正交压制方法[J]. 石油地球物理勘探, 2019, 54(2): 280-287. XU Yankai, CAO Siyuan, PAN Xiao, et al. A local orthogonalization for seismic random noise suppression[J]. Oil Geophysical Prospecting, 2019, 54(2): 280-287. |
| [20] |
孙成禹, 刁俊才, 李文静. 基于曲波噪声估计的三维块匹配地震资料去噪[J]. 石油地球物理勘探, 2019, 54(6): 1188-1194. SUN Chengyu, DIAO Juncai, LI Wenjing. 3D Block matching seismic data denoising based on Curvelet noise estimation[J]. Oil Geophysical Prospecting, 2019, 54(6): 1188-1194. |
| [21] |
张入化, 黄建平, 国运东, 等. 基于Seislet域分数阶阈值去噪算法的地震资料去噪[J]. 石油物探, 2020, 59(1): 40-50. ZHANG Ruhua, HUANG Jianping, GUO Yundong, et al. Fractional threshold denoising algorithm in seislet domain for seismic data denoising[J]. Geophysical Prospecting for Petroleum, 2020, 59(1): 40-50. |
| [22] |
夏洪瑞, 葛川庆, 彭涛. 小波时空变阈值去噪方法在可控震源资料处理中的应用[J]. 石油地球物理勘探, 2010, 45(1): 23-27. XIA Hongrui, GE Chuanqing, PENG Tao. Application of wavelet time-space-varying threshold denoising method in vibroseis seismic data processing[J]. Oil Geophysical Prospecting, 2010, 45(1): 23-27. |



 许自龙, 江苏省南京市江宁区上高路219号石油物探技术研究院, 211103。
许自龙, 江苏省南京市江宁区上高路219号石油物探技术研究院, 211103。