世界油气需求量的持续增长与常规油气产量的不断下降使得非常规油气成为近年全球油气资源勘探开发新亮点[1]。在油气开采过程中,采出、注水、注气、水力压裂等作业都会诱发地震。目前很多油田采用压裂方法以提高油气采收率,该方法同样适用于低渗透性的非常规油气田[2]。为了促进油气藏开采的高产、高效,可利用现今广泛应用的“微地震监测”技术研究压裂诱发的微地震效应,绘制压裂裂缝空间图像获取裂缝产状等相关信息[3-4]。
通常由压裂导致的微地震事件产生的地震波较弱,且压裂施工现场噪声较强,因此微地震数据一般呈现“弱信号、强干扰”特征,影响初至拾取、发震时刻计算、震源定位等分析。微地震数据中有效信号能量极其微弱、噪声类型复杂,其信噪比远低于常规地震记录,如何压制其中噪声是微地震数据处理的关键[5]。经过去噪处理后,微地震数据的信噪比、分辨率及保真度等都能得到不同程度的提高,有利于后续的地震资料综合解释,对油气及其他矿藏的开采具有重要的指导意义。
微地震数据去噪方法很多,根据微地震监测方式可分为井中和地面两种微地震数据去噪。前者的信噪比相对较高,常用去噪方法为偏振滤波、F-K变换[6]等;后者的信噪比较低,现行去噪方法主要包括基于小波变换、曲波变换、剪切波变换等变换域去噪方法、单道奇异值分解(SVD)及改进的K-L变换法。其中:传统傅里叶变换对非平稳信号去噪效果不理想[7];变换域方法能很好地区分非平稳信号的突变部分[8],但去噪结果受基函数影响,且会出现吉布斯效应;而SVD及K-L变换限制条件多,仅适用于水平及倾斜同相轴。由于地面微地震数据具有噪声能量强、有效信号能量弱、非平稳等特点,很多常规去噪方法难以获得较好去噪效果,因此亟待研发地面微地震数据去噪方法。
Huang等[9-11]的经验模态分解(EMD)方法是一种信号自适应分解方法,无需先验信息就能突显系统的物理特性。CEEMDAN(Complete ensemble EMD with adaptive noise)[12]方法是对EMD方法的改进,利用白噪声均匀分布的统计特性,通过对目标信号多次添加一定幅值的白噪声来克服模态混叠的影响。但基于EMD的阈值去噪方法对于低信噪比地震记录滤波效果不佳[13]。即使在信噪比为-9dB情况下,时频峰值滤波(TFPF)算法也可有效压制噪声[14]。这两种方法现广泛应用于机器故障监测、信号处理、地震探测等领域。
武安绪等[15]通过EMD对实际地震波形信号进行时频分析。吴琛等[16]利用EMD方法提取地震信号动力特征。方江雄等[17]提出基于VMD的地震随机噪声压制方法,提高了计算效率和保幅性能。胡瑞卿等[18]结合CEEMDAN和主成分分析法检测低信噪比微地震初至信号。金雷等[19-20]利用TFPF消除合成地震数据随机噪声。林红波等[21-22]指出TFPF时窗长度随时间变化能在压制噪声的同时更好地保护有效信号。李月等[23-24]系统地分析了TFPF时窗长度和窗型对压制随机噪声的影响,并给出TFPF时窗长度的选取规则。秦桓等[25]对微地震数据进行EMD,利用同步压缩提取高频段有效信号,并与低频部分重构,成功消除了微地震中的混叠噪声。瞿明岳等[26]通过EMD改进TFPF方法,有效地消除电力线通信噪声,降低了误码率。
根据微地震数据具有随机性、非平稳性和时频耦合等特性,兼顾EMD呈现的模态混叠及低信噪比去噪能力欠缺问题,本文提出基于CEEMDAN的时频峰值滤波微地震数据去噪方法。模型测试和实际数据处理结果验证了方法的有效性与实用性。
1 基本原理 1.1 自适应白噪声完整集合经验模态分解CEEMDAN通过在各阶段添加有限次的自适应白噪声,实现在较小平均次数下重构误差趋近于零。该算法在程序上实现了添加自适应白噪声,可很好地抑制模态混淆且避免原始信号失真。具体步骤如下。
(1) 在原始数据S(t)中分别多次添加自适应白噪声Bq(t),其中q表示添加噪声次数,一般取10~50,本文取q=50,则第q次信号可表示为
| ${\rm{IM}}{{\rm{F}}_1} = \frac{1}{{50}}\sum\limits_{q = 1}^{50} {{\rm{IMF}}_1^{(q)}} $ | (1) |
式中IMF1(q)表示Sq(t)分解的一阶IMF。余项
(2) 构造新的待分解信号
| $ {\rm{IM}}{{\rm{F}}_2} = \frac{1}{{50}}\sum\limits_{q = 1}^{50} {{\rm{IMF}}_2^{(q)}} $ | (2) |
余项
(3) 重复步骤(1)和步骤(2),到程序终止,共产生w个IMF,最后的余项为
| $ \boldsymbol{R}=\boldsymbol{S}(t)-\sum\limits_{p=1}^{w} \mathrm{IMF}_{p} $ | (3) |
样本熵是一种与近似熵类似但精度更高的数据复杂度衡量指标,可对数据的复杂度进行量化分析。样本熵的物理意义是表征信号中产生新模式的概率大小,以衡量时间序列复杂性。即新模式产生概率越小——样本熵越小,序列自我相似度就越高;样本熵越大,样本序列就越复杂。本文中样本熵越大,IMFs中各个频率越多,具体体现为噪声含量高;样本熵越小,IMFs越趋向于有效信号。
通常,N个数据点组成的时间序列
(1) 按序号组成1组m维的向量序列:
(2) 将向量
| $ d\left[\boldsymbol{X}_{m}(i), \boldsymbol{X}_{m}(j)\right]=\max [|x(i+k)-x(j+k)|] $ | (4) |
其中:
(3) 设相似容限(Tolerance for accepting matches)为r,通常取值为0.10~0.25个时间序列标准差。向量
| $ \boldsymbol{B}_{i}^{m}(r)=\frac{\boldsymbol{B}_{i}}{N-m-1} \quad 1 \leqslant i \leqslant N-m $ | (5) |
(4) 对所有
| $ \boldsymbol{B}^{m}(r)=\frac{1}{N-m} \sum\limits_{i=1}^{N-m} \boldsymbol{B}_{i}^{m}(r) $ | (6) |
(5) 将维数m增至m+1,重复以上步骤,可得
(6) 当N为有限值时,定义样本熵
| $\operatorname{SampEn}(m, r, N)=-\ln \frac{\boldsymbol{B}^{m+1}(r)}{\boldsymbol{B}^{m}(r)} $ | (7) |
TFPF的本质是基于Wigner-Ville分布(WVD)的瞬时频率估计。待处理的含噪数据可表示为
| $ \boldsymbol{s}(t)=\boldsymbol{x}(t)+\boldsymbol{n}(t) $ | (8) |
式中:x(t)是有效信号;n(t)是加性随机噪声。滤波的目的就是从含噪数据s(t)中恢复有效信号x(t)。TFPF可在不需假设条件的情况下很好地恢复有效信号,其具体步骤为:
(1)对含噪数据进行编码,将其变为解析信号的形式;对含噪数据s(t)进行频率调制,得到单位幅度的解析信号
| $ \boldsymbol{z}_{s}(t)=\exp \left[\mathrm{j} 2 \pi \mu \int_{0}^{t} \boldsymbol s(\lambda) \mathrm{d} \lambda\right] $ | (9) |
式中μ是频率调制指数。
(2) 取解析信号z(t)的伪Wigner-Ville分布(PWVD)的峰值,对解析信号进行瞬时频率估计,作为有效信号x(t)的估计值
| $ \hat{x}=\hat{f}(t)=\frac{\arg \max \left[W_{z}(t, f)\right]}{\mu} $ | (10) |
式中Wz(t,f)是解析信号z(t)的PWVD。
1.3.2 窗长选择对TFPF滤波的影响为了说明窗长选择对TFPF算法在信号保幅和噪声压制上存在的问题,通过合成理论波形,用不同的窗长滤波,对比分析滤波结果。图 1a为有效信号,对其加入-1dB的噪声,可见在噪声背景下,该含噪数据(图 1b)中原始有效信号已极难辨别。

|
图 1 有效信号(a)及其含噪数据(b) |
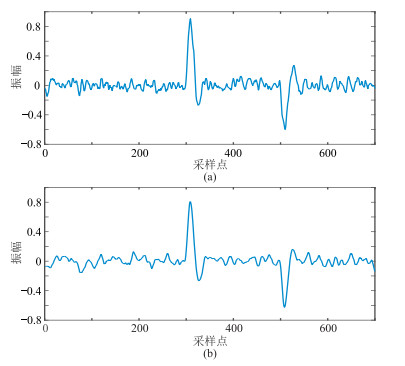
选用不同窗长的TFPF算法对s(t)进行滤波,从处理结果(图 2)可看出,各窗长的该算法均削减了噪声,验证了TFPF算法对噪声压制的有效性。进一步对比分析发现,长窗长具有更强的噪声压制能力,但信号幅度损失极大。
|
图 2 窗长分别为9(a)和13(b)的滤波结果 |
本文提出基于CEEMDAN的TFPF去噪方法,可灵活选择窗口长度,精准识别噪声位置。详细流程(图 3)如下。
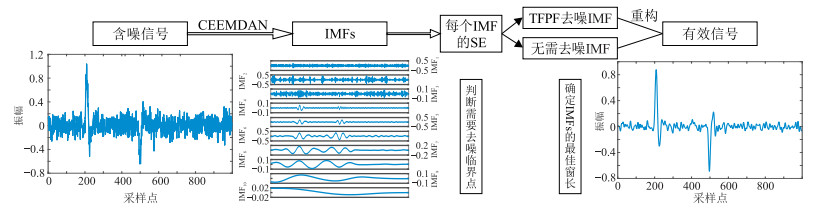
|
图 3 本文方法处理流程图 |
(1) 利用CEEMDAN分解信号,能使信号按从高到低频率分解,得到若干个IMF分量。
(2) 通过计算IMFs的样本熵判断含噪临界点,高于此临界值的IMFs需进行滤波。
(3) 在选定需进行TFPF的IMFs后,根据地震数据的经验公式对各个IMF选择合适窗长
| $ W_{L} \leqslant \frac{0.384 f_{\mathrm{s}}}{f_{\mathrm{d}}} $ | (11) |
式中:fs为地震波的采样频率;fd为主频。从该式可见,若fs增大或fd减小,则窗长相应变大。对于高频IMFs,采用长窗长;对于低频IMFs,适用短窗长。这样,就能达到保持有效信号幅度与压制随机噪声间的平衡。
(4) 最后将滤波后的IMFs与保留的IMFs重构,即可得到有效信号。
3 数值实验结果与分析 3.1 理论模型试算选用两个主频分别为30Hz和25Hz的Ricker子波组成的波形进行实验。采样率为1ms,共计1000个采样点。向该信号中加入高斯白噪声,使信噪比(SNR)达到约5dB,有效信号基本被噪声淹没。
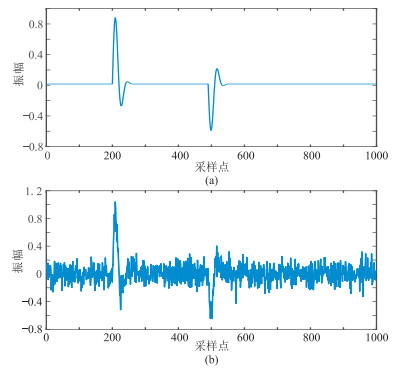
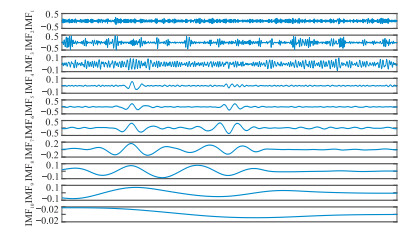
分别对原始的和加噪的理论模型数据(图 4)做CEEMDAN处理,得到分解后的多个IMFs(图 5)及其对应的样本熵(图 6)。通过此样本熵,可选择需进行TFPF的IMFs;再根据各个IMFs的频率特性灵活地选择窗长。选取该信号的前五个IMFs进行滤波。根据式(11),对前五个IMFs分量分别选择窗长为13、11、9、9、7,再将经TFPF滤波的信号与残留IMFs构成完整滤波信号。传统EMD去噪方法是舍弃前三个含大量噪声的IMFs,以其余的IMFs重构信号。而固定窗长TFPF去噪方法,根据式(11)选定窗口长度为13。
|
图 4 理论数据模型 (a)原始数据;(b)加噪信号 |
|
图 5 理论模型数据经CEEMDAN分解后的IMFs |
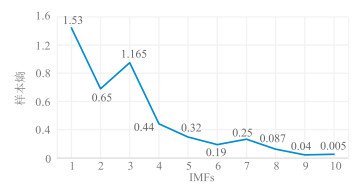
|
图 6 图 5各个IMFs对应的样本熵 |
分别应用传统EMD、固定窗长TFPF和本文CEEMDAN-TFPF三种去噪方法针对上述理论模型进行随机噪声压制处理。可见传统EMD去噪方法所得去噪结果(图 7a)中随机噪声得到一定程度压制(相对于图 4b),但仍有较多残留噪声;固定窗长TFPF方法的去噪结果(图 7b)中噪声得到较好压制,但振幅与图 4a相差较大;而CEEMDAN-TFPF方法的去噪结果(图 7c)不仅更彻底地压制了随机噪声,且很好地保持了有效信号的振幅,兼顾了“保幅”与“去噪”。
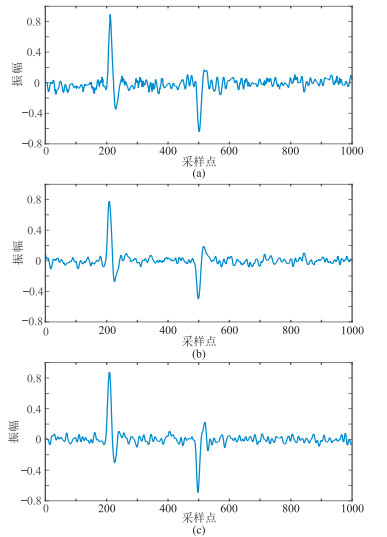
|
图 7 理论模型数据不同方法去噪结果 (a)传统EMD;(b)固定窗长TFPF;(c)CEEMDAN-TFPF |
为更充分、直观地展示实验结果,将原始数据、加噪信号和上述三种方法去噪结果置于同一坐标系下做波形对比(图 8),并将其波峰、波谷局部放大(图 9)显示,可见本文方法去噪结果更贴近原始数据。
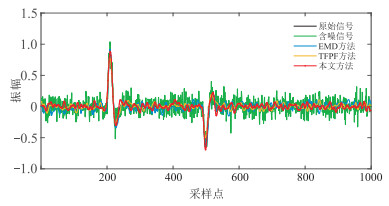
|
图 8 不同方法去噪结果波形对比 |
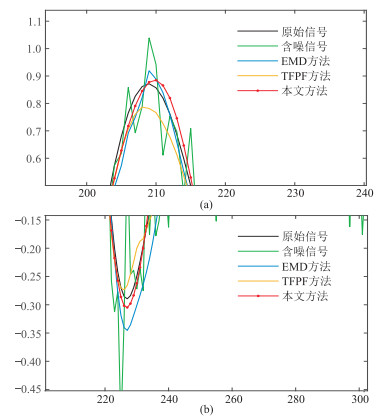
|
图 9 对应图 8波峰(a)、波谷(b)波形的放大显示 |
选自M地区实际矿山微地震数据(图 10a)中包含大量随机噪声,严重影响后续监测分析与微地震源定位。对该数据做傅里叶变换,分析频谱特征得知其主频集中于10Hz附近(图 10a中),信号在高频部分分布较宽。因矿山微地震数据具低频特性,故高频部分的贡献基本为随机噪声,应予压制及去除。
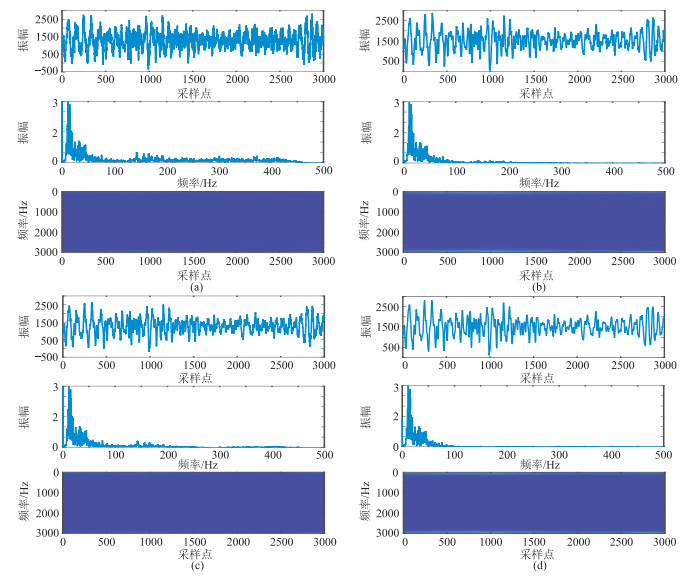
|
图 10 针对实际微地震数据应用不同方法去噪所得波形、频谱及时频对比 (a)实际原始微地震数据;(b)传统EMD方法;(c)固定窗长TFPF方法;(d)本文(CEEMDAN-TFPF)方法 |
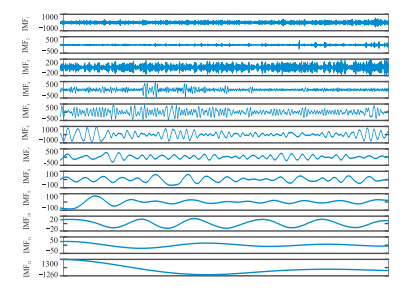
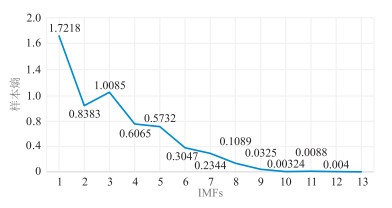
对上述数据做CEEMDAN处理,得到分解后的各个IMFs(图 11)及其对应的样本熵(图 12),据此样本熵可选择需进行TFPF的IMFs,且能由各个IMFs的频率特性灵活地选择窗长。选取该信号前六个IMFs进行滤波,根据式(11)对前六个IMFs分量分别选定窗长为9、9、7、7、5、5,最后将经TFPF滤波后的信号与残留IMFs重构为完整滤波信号。对于传统EMD去噪方法,也是舍弃前三个含大量噪声的IMFs,以剩余IMFs重构信号;固定窗长的TFPF去噪方法,据式(11)选定窗口长度为9。
|
图 11 实际微地震数据经CEEMDAN分解后的IMFs |
|
图 12 实际微地震数据各IMF对应的样本熵 |
分别应用传统EMD、固定窗长TFPF和CEEMDAN-TFPF三种去噪方法对实际数据进行随机噪声压制处理。可见传统EMD方法所得去噪结果(图 10b上)中随机噪声得到一定程度的压制,但仍残留较多噪声;固定窗长TFPF方法所得去噪结果(图 10c上)中可看出噪声得到了较好的压制,但振幅与图 10a相差较大;而本文方法去噪结果(图 10d上)中,不仅更彻底地(对比前两种方法)压制了随机噪声,且充分地保持了有效信号振幅,能达到保持有效信号幅度和压制随机噪声间的平衡。
对比分析三种方法去噪后频谱,可见传统EMD去噪方法(图 10b中)能很好压制高频噪声,但几乎未压制低频噪声;固定窗长TFPF去噪方法(图 10c中)的中低频噪声未能很好地去除;而本文方法对于全频段噪声都有很强压制能力。从其时频分布图(图 10下)可见,去噪后数据中干扰信息减弱。
4 结论传统TFPF方法是选择一个固定时窗进行滤波,不能同时兼顾信号去噪和幅值保持,过度压制噪声会造成有效信号幅值的严重衰减。而EMD存在模态混叠问题,且传统EMD方法通过舍弃噪声分量的处理方式不能有效压制噪声。本文提出一种基于CEEMDAN-TFPF的压制随机噪声方法,利用EMD的尺度分解特性将原数据按频率高低分解成一系列IMFs,再计算这些模态分量的样本熵,确定滤波模态分量,然后对这些分量做自适应时窗长度的TFPF处理,最后将滤波后的分量与剩余分量相加得到最终滤波信号。通过对模拟数据和实际微地震数据的处理,得到以下认识和结论:
(1) CEEMDAN-TFPF去噪方法是自适应的,对参数的选择无严格限制,能提高数据分析的效率。
(2) 该方法能有效克服EMD的模态混叠问题,且可更精准地判别噪声分量,对需滤波的IMF灵活选择窗长,达到信号保幅与噪声压制间的平衡,提高微地震数据信噪比。
(3) 与传统EMD和定窗长TFPF两种去噪方法相比,本文方法能在有效压制随机噪声的同时,也很好地保护有效信号幅值,准确识别有效微地震信号,提高定位精度,保留原始微地震事件的数据特征,给后续微地震数据研究提供可靠基础数据。
| [1] |
邹才能, 杨智, 朱如凯, 等. 中国非常规油气勘探开发与理论技术进展[J]. 地质学报, 2015, 89(6): 979-1007. ZOU Caineng, YANG Zhi, ZHU Rukai, et al. Progress in China's unconventional oil & gas exploration and development and theoretical technologies[J]. Acta Geologica Sinica, 2015, 89(6): 979-1007. DOI:10.3969/j.issn.0001-5717.2015.06.001 |
| [2] |
董世泰, 高红霞. 微地震监测技术及其在油田开发中的应用[J]. 石油仪器, 2004, 18(5): 5-8. DONG Shitai, GAO Hongxia. Microseismic moni-tering technology and its application to oilfield deve-lopment[J]. Oil Equipment, 2004, 18(5): 5-8. |
| [3] |
刘振武, 撒利明, 巫芙蓉, 等. 中国石油集团非常规油气微地震监测技术现状及发展方向[J]. 石油地球物理勘探, 2013, 48(5): 843-853. LIU Zhenwu, SA Liming, WU Furong, et al. Microseismic monitor technology status for unconventional resource E & P and its future development in CNPC[J]. Oil Geophysical Prospecting, 2013, 48(5): 843-853. |
| [4] |
孙龙德, 撒利明, 董世泰. 中国未来油气新领域与物探技术对策[J]. 石油地球物理勘探, 2013, 48(2): 317-324. SUN Longde, SA Liming, DONG Shitai. New challenges for the future hydrocarbon in China and geophysical technology strategy[J]. Oil Geophysical Prospecting, 2013, 48(2): 317-324. |
| [5] |
邵婕, 孙成禹, 唐杰, 等. 基于字典训练的小波域稀疏表示微地震去噪方法[J]. 石油地球物理勘探, 2016, 51(2): 254-260. SHAO Jie, SUN Chengyu, TANG Jie, et al. Micro-seismic data denoising based on sparse representations over learned dictionary in the wavelet domain[J]. Oil Geophysical Prospecting, 2016, 51(2): 254-260. |
| [6] |
张旭亮, 桂志先, 王鹏, 等. 基于K-L变换的微地震资料去噪的分析及应用[J]. 工程地球物理学报, 2013, 10(1): 81-84. ZHANG Xuliang, GUI Zhixian, WANG Peng, et al. The analysis and application of micro-seismic data denoising based on K-L transform[J]. Chinese Journal of Engineering Geophysics, 2013, 10(1): 81-84. |
| [7] |
Alvanitopoulos P F, Papavasileiou M, Andreadis I, et al. Seismic intensity feature construction based on the Hilbert-Huang transform[J]. IEEE Transactions on Instrumentation & Measurement, 2012, 61(2): 326-337. |
| [8] |
盛冠群, 李振春, 王维波, 等. 基于小波分解与高阶统计量的微地震初至拾取方法研究[J]. 石油物探, 2015, 54(4): 388-395. SHENG Guanqun, LI Zhenchun, WANG Weibo, et al. A new automatic detection method of microseismic events based on wavelet decomposition and high-order statistics[J]. Geophysical Prospecting for Petroleum, 2015, 54(4): 388-395. |
| [9] |
Huang N E, Long S R, Wu M L C, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society A — Mathematical, Physical and Engineering Sciences, 1998, 454(1971): 903-995. DOI:10.1098/rspa.1998.0193 |
| [10] |
Huang N E. Introduction to the Hilbert-Huang Trans-form and Its Related Mathematical Problems[M]. USA: World Scientific Publishing Co Private Ltd, 2005: 1-26.
|
| [11] |
Huang N E, Wu M L C, Qu W, et al. Applications of Hilbert-Huang transform to non-stationary financial time series analysis[J]. Applied Stochastic Models in Business & Industry, 2010, 19(3): 245-268. |
| [12] |
Maria E T, Macelo A C, Gaston S, et al. A complete ensemble empirical mode decomposition with adaptive noise[C]. Prague, Czech Republic: IEEE International Conference on Acoustics, Speech and Signal Pro-cessing (ICASSP), 2011.
|
| [13] |
刘彦萍. 时空二维时频峰值滤波方法压制地震勘探随机噪声的研究[D]. 吉林长春: 吉林大学, 2013. LIU Yanping. The Research of Spation Temporal 2-D Time-Frequency Peak Filtering for Seismic Random Noise Suppression[D]. Jilin University, Changchun, Jilin, 2013. |
| [14] |
Boashash B, Mesbah M. Signal enhancement by time-frequency peak filtering[J]. IEEE Transactions on Signal Processing, 2004, 52(4): 929-937. |
| [15] |
武安绪, 吴培稚, 兰从欣, 等. Hilbert-Huang变换与地震信号的时频分析[J]. 中国地震, 2005, 21(2): 207-215. WU Anxu, WU Peizhi, LAN Congxin, et al. Hilbert-Huang transform and time-frequency analysis of seismic signal[J]. Earthquake Research in China, 2005, 21(2): 207-215. |
| [16] |
吴琛, 周瑞忠. Hilbert-Huang变换在提取地震信号动力特性中的应用[J]. 地震工程与工程振动, 2006, 26(5): 41-46. WU Chen, ZHOU Ruizhong. Application of Hilbert-Huang transform in extracting dynamic properties of seismic signals[J]. Earthquake Engineering and Engineering Vibration, 2006, 26(5): 41-46. |
| [17] |
方江雄, 温志平, 顾华奇, 等. 基于变分模态分解的地震随机噪声压制方法[J]. 石油地球物理勘探, 2019, 54(4): 757-767. FANG Jiangxiong, WEN Zhiping, GU Huaqi, et al. Seismic random noise attennuation based on variation-al mode decomposition[J]. Oil Geophysical Prospecting, 2019, 54(4): 757-767. |
| [18] |
胡瑞卿, 王彦春, 尹志恒, 等. 结合CEEMDAN和主成分分析的低信噪比微地震初至信号检测[J]. 石油地球物理勘探, 2019, 54(1): 45-53. HU Ruiqing, WANG Yanchun, YIN Zhiheng, et al. A first arrival detection method in low SNR micro-seismic signals based on CEEMDAN-PCA[J]. Oil Geophysical Prospecting, 2019, 54(1): 45-53. |
| [19] |
金雷. 时频峰值滤波在地震勘探资料中随机噪声压制的研究[D]. 吉林长春: 吉林大学, 2006. JIN Lei. Time-Frequency Peak Filtering and Its Application on Random Noise Attenuation for Seismic Exploration Data[D]. Jilin University, Changchun, Jilin, 2006. |
| [20] |
金雷, 李月, 杨宝俊. 用时频峰值滤波方法消减地震勘探资料中随机噪声的初步研究[J]. 地球物理学进展, 2005, 20(3): 724-728. JIN Lei, LI Yue, YANG Baojun. Reduction of random noise for seismic data by time-frequency peak filtering[J]. Progress in Geophysics, 2005, 20(3): 724-728. |
| [21] |
林红波. 时频峰值滤波随机噪声消减技术及其在地震勘探中的应用[D]. 吉林长春: 吉林大学, 2007. LIN Hongbo. Time-Frequency Peak Filtering De-noise Technique and Its Application in Seismic Exploration[D]. Jilin University, Changchun, Jilin, 2007. |
| [22] |
林红波, 李月, 叶文海, 等. 时频峰值滤波去噪技术及其应用[J]. 地球物理学进展, 2008, 23(6): 1953-1957. LIN Hongbo, LI Yue, YE Wenhai, et al. Denoising technique based on Time-Frequency Peak Filtering and its application[J]. Progress in Geophysics, 2008, 23(6): 1953-1957. |
| [23] |
Wu N, Li Y, Yang B. Noise attenuation for 2-D seismic data by radial-trace time-frequency peak filtering[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(5): 874-878. |
| [24] |
李月, 林红波, 杨宝俊, 等. 强随机噪声条件下时窗类型局部线性化对TFPF技术的影响[J]. 地球物理学报, 2009, 52(7): 1899-1906. LI Yue, LIN Hongbo, YANG Baojun, et al. The influence of limited linearization of time window on TFPT under the strong noise background[J]. Chinese Journal of Geophysics, 2009, 52(7): 1899-1906. |
| [25] |
秦晅, 蔡建超, 刘少勇, 等. 基于经验模态分解互信息熵与同步压缩变换的微地震信号去噪方法研究[J]. 石油物探, 2017, 56(5): 658-666. QIN Heng, CAI Jianchao, LIU Shaoyong, et al. Microseismic data denoising method based on EMD mutual information entropy and synchrosqueezing transform[J]. Geophysical Prospecting for Petroleum, 2017, 56(5): 658-666. |
| [26] |
翟明岳, 苏岭东. 基于EMD-TFPF算法的电力线通信噪声消除技术研究[J]. 电力系统保护与控制, 2015, 43(7): 51-56. ZHAI Mingyue, SU Lingdong. A noise mitigation method based on EMD-TFPF in powerline communication system[J]. Power System Protection and Control, 2015, 43(7): 51-56. |



 程浩, 辽宁省沈阳市和平区文化路三号巷11号东北大学资源与土木工程学院, 110819。Email:
程浩, 辽宁省沈阳市和平区文化路三号巷11号东北大学资源与土木工程学院, 110819。Email: 