② 中国石油化工股份有限公司油田勘探开发事业部, 北京 100728
② Exploration & Development Affairs Department, Sinopec, Beijing 100728, China
中国西部复杂山前带地区地表高程和近地表速度结构变化剧烈,给近地表建模带来巨大挑战,且严重影响激发井深设计、静校正等[1-2],也吸引许多学者针对该类地区特点开展各种近地表建模及静校正方法研究[3-5]。马晶晶等[6]利用折射静校正的中、长波长静校正优势,在沙丘为主的准噶尔盆地山前带取得较好效果。蓝益军[7]提出基于连续介质理论的空变时深曲线静校正方法,并成功应用于近地表以沙丘和巨厚砾石为主的山前带地区。方勇等[8]将菲涅耳层析静校正技术应用于库车地区,郭振波等[9]将回转波层析静校正应用于西部复杂地区,但层析静校正不能解决激发井深设计问题,且需耗费大量时间拾取初至,不适用于地震数据快速处理。
本次研究区位于乌鲁木齐市东北部、博格达山西北缘,区内总体地势呈西北低、东南高,地形高差较大,最大可达约3000m。该区近地表主要为黄土、砾石二元结构,低速层为表层黄土,厚度较小,降速层为泥质砾石或黏土质砾石,厚度一般较大。这类近地表分布广泛,且为该区各种近地表中最复杂的类型,构建精确的近地表黄土和砾石厚度模型及查清近地表地球物理特征,是解决该区近地表问题的关键。尚新民等[10]曾在该区联合利用露头、岩性录井、微测井与浅层二维地震等信息建立了全区近地表模型,基于该模型逐点设计激发井深。
已有的研究成果为解决山前带黄土砾石区静校正问题奠定了基础。本文基于山前带黄土砾石区近地表特征研究,应用地质统计学方法建立了黄土层底界面和砾石层底界面,分别根据黄土层和砾石层的时深曲线计算静校正量,从而实现了一种高效的山前带黄土砾石区静校正方法,为该类地区激发井深设计及静校正提供了新思路。
1 方法原理 1.1 近地表调查方法为了查清工区近地表岩性分布及速度结构,共布设了173口微测井和3条二维浅层地震测线。微测井采用井中激发、井口接收,以1km×1km间隔均匀布设,钻井过程中根据上返岩屑做岩性录井,井深大于50m的微测井比例超过25%。全区还部署了3条针对近地表浅层调查的地震测线,采用中间激发双边接收观测方式,两边各有501道,道距为2m,最大炮检距为1000m,炮点距为6m,激发井深为2.5m。藉此二维测线层析反演以全面了解该工区近地表速度结构。
1.2 基于微测井的近地表特征研究近地表特征主要包括近地表岩性分布、垂向速度变化规律、近地表介质与速度的关系、近地表介质时深对应关系及近地表介质空间分布特征等。
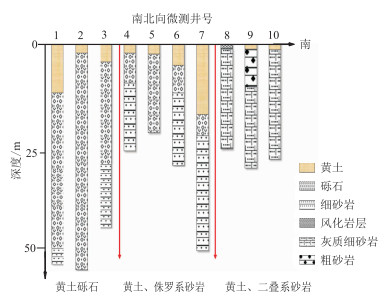
1.2.1 近地表岩性分布沿南北向抽取一条线上的微测井(数据),绘制出岩性剖面(图 1)。可见在工区北部和中部地表高程较低,黄土层和砾石层均较厚,为巨厚连续沉积;向南随着地表高程增加,黄土、砾石厚度逐渐变薄,砾石分布逐渐消失。
|
图 1 近地表岩性探测南北向剖面 |
该区近地表速度分层性较差,常规微测井资料解释方法存在较大人为误差。利用微测井初至信息做层析反演可获得可靠性更高的井筒速度模型[11]。
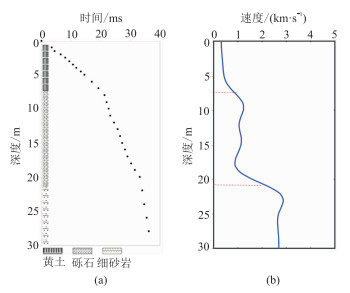
图 2为区内一口微测井初至、岩性剖面及层析反演的井周速度模型,该微测井初至层析反演的速度与岩性录井数据较吻合。统计全区微测井层析反演结果后得知:表层黄土的速度在1000m/s以下,砾石层速度分布于1000~2000m/s范围,高于2000m/s的介质大多为基岩。据此可将近地表的速度模型转化为岩性模型。
|
图 2 典型微测井初至、岩性剖面(a) 及初至层析反演的速度曲线(b) |
已有研究成果表明,与大沙漠区近地表相似,巨厚砾石区近地表呈连续介质特征,利用时深曲线静校正方法可有效解决静校正问题,尤其对于中、长波长静校正具有一定的优势[12, 13]。
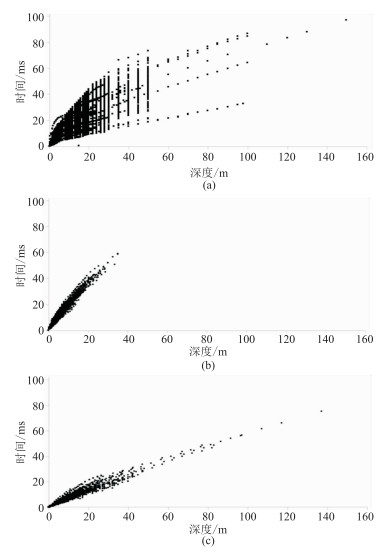
为了验证该类方法是否同样适用于山前带黄土砾石区,进一步分析了该区近地表微测井时深关系。图 3a是全区所有微测井的时深散点图,可见时深关系规律性差。分别按照0~1000m/s和1000~ 2000m/s速度区间,将每一口微测井分成黄土层段(图 3b,深度0点为地表)和砾石层段(图 3c,深度0点为黄土层与砾石层的分界面),在相同介质层内时深散点规律性较强,都呈现明显的连续介质特征。可见黄土层和砾石层内部速度随深度变化的规律性很强,这一结果为时深曲线静校正方法的应用提供了依据,也提示近地表建模的关键是建立分层结构模型,亦即黄土层与砾石层的厚度模型。
|
图 3 不同层段范围微测井时深散点图 (a)全井段;(b)黄土层段;(c)砾石层段 |
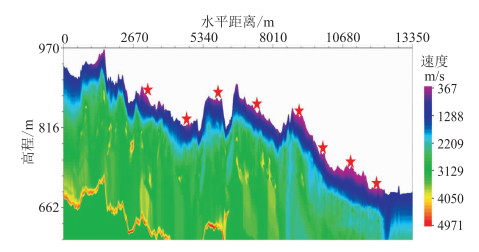
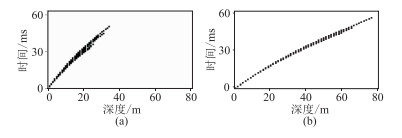
为了从其他资料进一步佐证以上观点,选取一条二维浅层地震测线的大炮初至进行层析反演得到近地表模型(图 4)。在该测线上均匀选取多个样点,提取这些样点的近地表速度曲线,将速度曲线转为时深曲线,分别按照0~1000m/s和1000~ 2000m/s速度区间提取数据,绘制时间—深度散点图(图 5)。层析反演结果转换的时深关系具有明显的连续介质特征,与微测井结果基本一致。
|
图 4 工区二维测线大炮初至层析反演结果 |
|
图 5 二维层析反演结果转换的时深散点 (a)0~1000m/s速度区间;(b)1000~2000m/s速度区间 |
近地表建模是以微测井测量结果作为控制点,基于空间插值得到近地表黄土和砾石底界面模型。由于已知炮点和检波点高程,岩性界面模型和厚度模型本质上是相同的,知道其中一个模型即可得到另一个模型。在地表起伏较大、近地表变化剧烈地区,岩性界面高程和厚度的插值结果可能会有很大差异,需从中选取最适合的。
所有空间插值算法都基于待插值数据的空间自相关,它表示变量在同一分布区内观测数据之间潜在的相互依赖性,若变量空间不相关,则插值结果可靠性无法保证。变量的空间自相关一般用莫兰(Moran)指数、P值和z得分三个参数表征[14]。莫兰指数是一个归一化的有理数,取值范围是[-1.0,1.0]。该指数表征空间相关性大小:大于0时,表示数据呈现空间正相关,其值越大空间相关性越明显;小于0时,表示数据呈空间负相关,其值越小空间差异越大;等于0时,空间呈随机性。P值表示观测值呈随机分布的概率,P值越小说明观测值随机分布的概率越小,如P=0.05表示观测值只有5%的可能性是随机生成的结果。z得分表示观测值标准差的倍数,z得分越高表示数据聚集性越强。
分别按0~1000m/s和1000~2000m/s速度区间提取每口微测井处黄土层、砾石层的厚度和界面高程,计算两种介质层高程和厚度分布的莫兰指数、P值和z得分(表 1)。结合图 3可知:山前带近地表黄土、砾石层厚度和界面高程的莫兰指数均大于0.2、P值均小于0.05、z得分均大于3.5,具有明显的空间正相关和高聚集特征,故可通过空间插值建立全区模型。黄土、砾石层厚度的莫兰指数和z得分均明显大于界面高程的,P值明显小于界面高程的(表 1),说明对厚度的空间插值结果更可靠。
|
|
表 1 空间自相关分析结果 |
空间插值方法主要有以反距离加权插值为代表的确定性插值和基于数据测量统计特征的地质统计学插值法。通过设定待测点周围控制点的权重,进行加权求和,得到待测点的值
| $ Z\left( {{x_0}} \right) = \sum\limits_{i = 1}^m {{\lambda _i}} Z\left( {{x_i}} \right) $ | (1) |
式中:Z(x0)为待测点x0的值;Z(xi)为控制点i的测量值;m为控制点个数;λi为控制点i的权系数
| $ {\lambda _i} = \frac{{{{\left[ {d\left( {{x_0},{x_i}} \right)} \right]}^{ - \alpha }}}}{{\sum\limits_{i = 1}^m {{{\left[ {d\left( {{x_0},{x_i}} \right)} \right]}^{ - \alpha }}} }} $ | (2) |
式中:d(x0, xi)为控制点i到待测点的距离;α为正实数,该值越大插值结果受最近点影响越大,一般取2。显然,此算法简捷、实用,当采样点较密集且均匀分布时精度更高。
克里金插值的原理是利用区域化变量的已知测量数据及其变异函数,对待测点进行线性无偏最优估计,也可用式(1)表示,但其权系数的计算不同,除与距离有关外,还与区域化变量的方向变化有关。以无偏为前提,克里金方差为最小可得到求解待定权系数λi的方程组[12]
| $ \left\{ {\begin{array}{*{20}{l}} {\sum\limits_{i = 1}^n {{\lambda _i}} C\left( {{x_i},{x_j}} \right) + \mu = C\left( {{x_0},{x_j}} \right)\quad j = 1,2, \cdots ,n}\\ {\sum\limits_{i = 1}^n {{\lambda _i}} = 1} \end{array}} \right. $ | (3) |
式中犆C(xi, xj)是Z(xi)与Z(xj)的协方差函数。
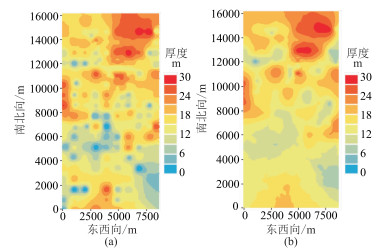
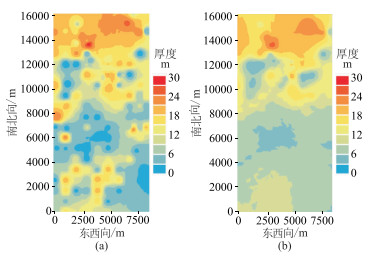
1.3.2 不同插值方法效果对比分别利用反距离加权和普通克里金插值建立工区近地表黄土和砾石层厚度模型(图 6、图 7)。结果表明:反距离加权插值法简捷高效,但易产生“牛眼”现象;普通克里金插值法考虑了测量数据相关性在不同方向的差异,结果更平滑、自然。
|
图 6 黄土层厚度模型 (a)反距离加权插值;(b)普通克里金插值 |
|
图 7 砾石层厚度模型 (a)反距离加权插值;(b)普通克里金插值 |
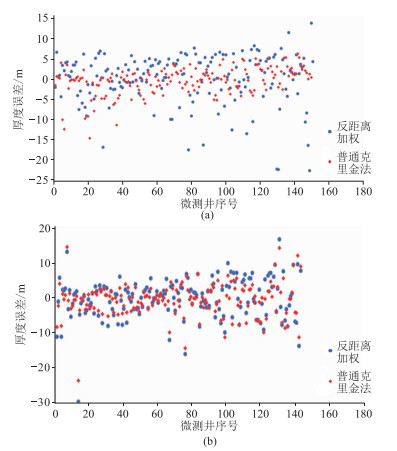
进一步对插值结果做交叉验证,图 8中以普通克里金插值法所得黄土和砾石厚度误差总体上均明显小于反距离加权插值结果,克里金插值法所得黄土厚度误差约为-5~5m、砾石厚度误差大致为-10~ 10m,克里金插值法效果优于反距离加权插值法。
|
图 8 交叉验证对比 (a)黄土厚度模型;(b)砾石层厚度模型 |
研究区地形起伏较大,控制点相对稀少且呈均匀分布,起伏较大的局部区域无控制点或控制点密度不够,降低了黄土和砾石层厚度插值结果的可靠性。根据已有的研究成果[15-17],利用地表与近地表岩性界面之间的相似性可进一步提高建模的精度。根据给定半径内的控制点信息计算出每个插值点岩性界面与地表的相似系数
| $ K(S, N)=\frac{\operatorname{Cov}(S, N)}{\sqrt{\operatorname{Var}(S) \operatorname{Var}(N)}} $ | (4) |
式中:K(S, N)为地表高程S与界面(黄土层底或砾石层底)高程N的相似系数;Cov(S,N)为S与N的协方差;Var(·)为方差。
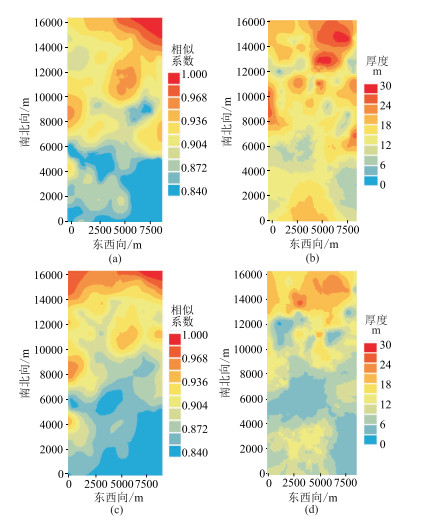
从利用式(4)计算的岩性界面与地表高程的相似系数(图 9a、图 9c)看,整体上工区南部黄土界面和砾石界面与地表高程相似系数较小,北部的较大,这是由于东南部属于地表起伏剧烈的陡坡区,近地表物性不稳定,而北部属于冲积扇,地表起伏较小,近地表沉积物规律性较好。
|
图 9 地表相似系数及校正后厚度模型 (a)黄土界面与地表相似系数;(b)黄土层厚度;(c)砾石界面与地表相似系数;(d)砾石层厚度 |
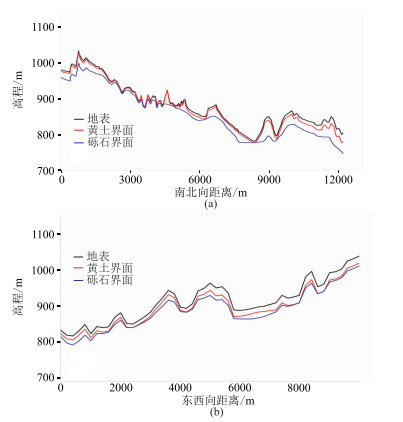
对图 6和图 7模型进行校正,得到校正后的模型(图 9b、图 9d),再结合图 10可知,本区黄土层厚度和砾石层厚度均呈现出由东南向西北部增加的趋势,与工区地表地形和高程分布基本一致。进一步通过交叉验证对校正效果进行评价
| ${H^{^\prime }} = H + (S - N)(1 - K) $ | (5) |
|
图 10 校正后模型的二维剖面 (a)东西向5000m处南北向剖面;(b)南北向10000m处东西向剖面 |
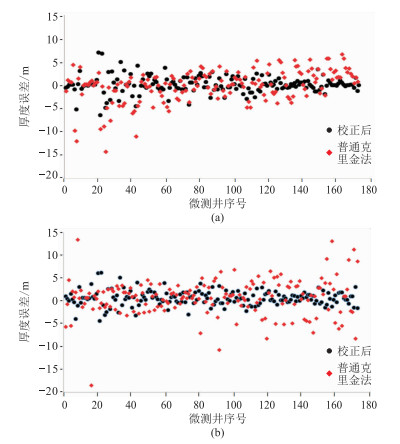
式中:H′为校正后厚度;H为插值后所得厚度;N为插值后所得界面高程。可见经过相似系数校正后,黄土和砾石层厚度误差基本分布在-5~5m (图 11),即误差进一步减小,模型精度有所提高。
|
图 11 校正后黄土层(a)和砾石层(b)厚度模型的交叉验证 |
时深曲线静校正主要用于大沙漠区,基本原理是对低降速带内的微测井时深散点进行拟合,得到一条自变量为深度、因变量为时间的时深关系曲线,再根据建立的低降速带厚度模型,利用时深关系公式求取地震波在低降速带的传播时间,进一步计算静校正量[7, 12, 18]。与其他静校正方法相比,此方法不需反演详细的近地表速度结构,也不需拾取大炮初至信息,在近地表满足连续介质假设条件下,能高效地解决静校正问题,特别是对中、长波长静校正具有一定优势,在大沙漠和巨厚砾石区应用较多。
据该区微测井资料,时深散点在黄土层内和砾石层内呈现明显的规律性(图 3),在此提出分层时深曲线静校正方法。该方法采取“两步法”计算:地表到高速层顶界的时间根据黄土厚度和砾石厚度分别用黄土层和砾石层时深曲线计算后相加得到,此为“剥去量”;再通过替换速度计算高速层顶界到基准面的时间,此为“充填量”。任意炮点或检波点静校正量依据不同高程/厚度从下式选择计算
| $ {\Delta t = \left\{ {\begin{array}{l} { - {f_1}\left( {{h_1}} \right) - {f_2}\left( {{h_2}} \right) + \frac{{{E_{{\rm{base}}}} - {E_{{\rm{hvlt}}}}}}{{{v_{\rm{R}}}}},}\\ \;\;\;\;\;\;{{E_{{\rm{station }}}} = {E_{{\rm{surface }}}}}\\ { - {f_1}\left( {{h_1}} \right) + {f_1}\left( {{s_{{\rm{depth}}}}} \right) - {f_2}\left( {{h_2}} \right) + \frac{{{E_{{\rm{base}}}} - {E_{{\rm{hvlt}}}}}}{{{v_{\rm{R}}}}},}\\ \;\;\;\;\;\;{{E_{{\rm{surface }}}} - {h_1} \le {E_{{\rm{station }}}} < {E_{{\rm{surface }}}}}\\ { - {f_2}\left( {{h_2}} \right) + {f_2}\left( {{s_{{\rm{depth}}}} - {h_1}} \right) + \frac{{{E_{{\rm{base}}}} - {E_{{\rm{hvlt}}}}}}{{{v_{\rm{R}}}}},}\\ \begin{array}{l} \;\;\;\;\;\;{E_{{\rm{surface }}}} - {h_1} - {h_2} \le {E_{{\rm{station }}}} < {E_{{\rm{surface }}}} - {h_1}\\ \frac{{{s_{{\rm{depth}}}} - {h_1} - {h_2}}}{{{v_{\rm{H}}}}} + \frac{{{E_{{\rm{base}}}} - {E_{{\rm{hvlt}}}}}}{{{v_{\rm{R}}}}},\\ \;\;\;\;\;\;{E_{{\rm{station }}}} < {E_{{\rm{surface }}}} - {h_1} - {h_2} \end{array} \end{array}} \right.}\\ $ | (6) |
式中:f1、f2分别为待计算点黄土层和砾石层时深曲线;h1、h2分别为该点黄土层和砾石层厚度;EstationEsurface、Ebase、Ehvlt分别为待计算点高程、地表高程、基准面高程、高速层顶高程;sdepth为待计算点深度;vH、vR分别为待计算点高速层速度和替换速度。检波点一般位于地表,采用式(6)中的第一种情况进行计算。
2 实际应用效果针对图 3中黄土层和砾石层段时深散点,用最小二乘法拟合出黄土层和砾石层时深关系分别为
| $ f_{1}(x)=-0.0459 x^{2}+2.6958 x $ | (7) |
| $ f_{2}(x)=-0.0012 x^{2}+0.6607 x $ | (8) |
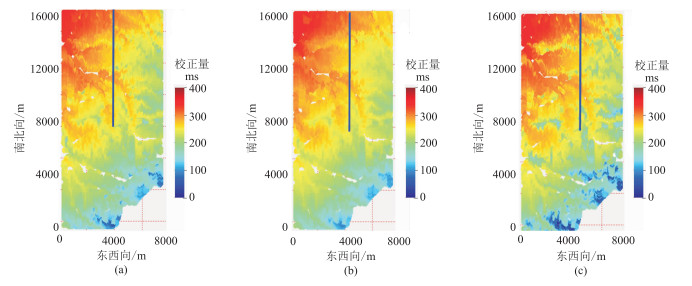
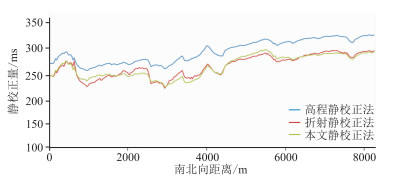
利用式(6)计算校正后厚度模型(图 9b、图 9d) 的静校正量(图 12c),与高程静校正、某商业软件的折射静校正结果进行对比(图 12),可见不同方法计算的静校正量的总体趋势较一致。对比沿图 12中蓝色直线抽取的一条检波线上不同方法的静校正量(图 13),看到本文方法与折射静校正法计算的静校正量总体分布一致,但在局部有明显差别。
|
图 12 不同静校正方法计算的静校正量平面图 (a)高程静校正;(b)折射静校正;(c)本文方法 |
|
图 13 不同静校正方法的检波点静校正量对比 |
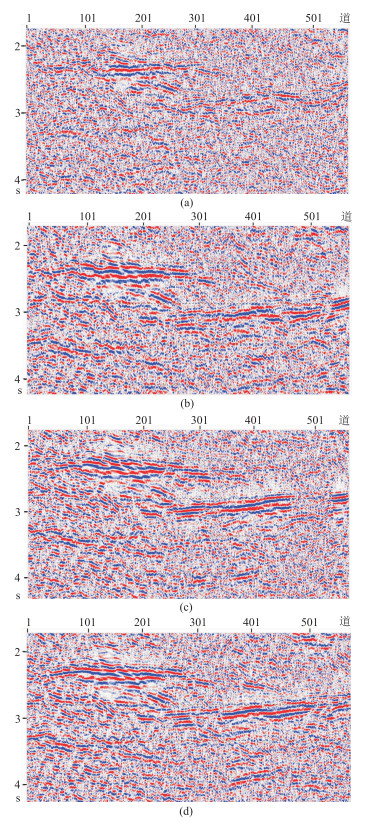
进一步对比叠加剖面(图 14)效果,且(三种方法)采用同一叠加速度以消除其影响。可见本文方法明显优于高程静校正,总体上也优于折射波静校正,同时在计算效率上具有明显优势,证明本文的近地表建模及静校正方法的正确性。
|
图 14 不同静校正方法局部叠加剖面对比 (a)未做静校正(b)高程静校正(c)折射静校正(d)本文方法 |
通过对中国西部山前带近地表黄土、砾石结构展开系统研究,得出以下认识和结论。
(1) 研究区地表黄土层速度在1000m/s以下,砾石层速度为1000~2000m/s,山前带近地表黄土层和砾石层内时深关系具有较好规律性,近似为连续介质,可以用时深关系曲线描述。
(2) 黄土层和砾石层厚度分布均具有较强空间相关性,可通过对微测井测量的黄土层和砾石层厚度做空间插值建立整个工区厚度模型;普通克里金插值效果好于反距离加权插值法,利用介质界面与地表面的相似性调整厚度模型可进一步提高精度。
(3) 本文的近地表建模与分层时深关系曲线静校正方法具有较高计算效率,避免了基于初至的静校正方法需耗费大量时间做初至拾取,更适合当前高密度地震勘探现场处理的需求,同时建立的岩性界面还可用于激发井深设计。
(4) 受限于施工成本及难度,本区仅有几口微测井井深超过100m,在砾石层较厚区域未能探测到砾石底界位置。建议在该区尽量采用更多数量的超深微测井,以更准确地落实砾石底界分布。条件允许情况下,也可采用大排列的折射法加以补充,这样将使本文方法取得更好效果。
| [1] |
臧胜涛, 苏勤, 王建华, 等. 山地复杂构造带地震资料处理方法[J]. 石油地球物理勘探, 2018, 53(增刊1): 62-68. ZANG Shengtao, SU Qin, WANG Jianhua, et al. Seismic data processing methods for complex mountainous areas[J]. Oil Geophysical Prospecting, 2018, 53(S1): 62-68. |
| [2] |
宋桂桥, 于世焕. 山前带地震勘探技术进展与对策研究[J]. 石油物探, 2012, 51(6): 539-547. SONG Guiqiao, YU Shihuan. Progress and strategy of the seismic exploration in foothill area[J]. Geophysical Prospecting for Petroleum, 2012, 51(6): 539-547. DOI:10.3969/j.issn.1000-1441.2012.06.001 |
| [3] |
王振宇, 杨勤勇, 李振春, 等. 近地表速度建模研究现状及发展趋势[J]. 地球科学进展, 2014, 29(10): 1138-1148. WANG Zhenyu, YANG Qinyong, LI Zhenchun, et al. Research status and development trend of near-surface velocity modeling[J]. Advances in Earth Science, 2014, 29(10): 1138-1148. DOI:10.11867/j.issn.1001-8166.2014.10.1138 |
| [4] |
黄鹏, 殷厚成, 薛维忠, 等. 山前带复杂浅表层建模研究[J]. 石油物探, 2019, 58(6): 837-845. HUANG Peng, YIN Houcheng, XUE Weizhong, et al. Modeling of complex near-surface in piedmont zone[J]. Geophysical Prospecting for Petroleum, 2019, 58(6): 837-845. DOI:10.3969/j.issn.1000-1441.2019.06.006 |
| [5] |
沈鸿雁, 王鑫, 李欣欣. 近地表结构调查及参数反演综述[J]. 石油物探, 2019, 58(4): 471-485. SHEN Hongyan, WANG Xin, LI Xinxin. Near surface structure survey and parameter inversion review[J]. Geophysical Prospecting for Petroleum, 2019, 58(4): 471-485. |
| [6] |
马晶晶, 苏艳丽, 王晓涛, 等. 折射波静校正技术在准噶尔盆地山前带的应用[J]. 石油地球物理勘探, 2018, 53(增刊1): 19-23. MA Jingjing, SU Yanli, WANG Xiaotao, et al. Refraction static corrections applied in the piedmont belt, Junggar Basin[J]. Oil Geophysical Prospecting, 2018, 53(S1): 19-23. |
| [7] |
蓝益军. 一种解决巨厚表层问题的新思路[J]. 勘探地球物理进展, 2009, 32(2): 107-111. LAN Yijun. A new method of data acquisition in area of huge thick near surface[J]. Progress in Exploration Geophysics, 2009, 32(2): 107-111. |
| [8] |
方勇, 罗文山, 姜翠苹, 等. 库车山地地震资料层析静校正方法的应用[J]. 石油地球物理勘探, 2017, 52(增刊1): 23-27, 33. FANG Yong, LUO Wenshan, JIANG Cuiping, et al. Tomo-statics for Kuqa seismic data[J]. Oil Geophysical Prospecting, 2017, 52(S1): 23-27, 33. |
| [9] |
郭振波, 孙鹏远, 钱忠平, 等. 快速回转波近地表速度建模方法[J]. 石油地球物理勘探, 2019, 54(2): 261-267. GUO Zhenbo, SUN Pengyuan, QIAN Zhongping, et al. Fast near-surface model building with turning wave[J]. Oil Geophysical Prospecting, 2019, 54(2): 261-267. |
| [10] |
尚新民, 王延光, 崔庆辉, 等. 准南缘山前带精细近地表建模技术研究[J]. 地球物理学进展, 2019, 34(5): 1887-1892. SHANG Xinmin, WANG Yanguang, CUI Qinghui, et al. Research on fine near surface modeling in south foothill belt of Jungar basin[J]. Progress in Geophy-sics, 2019, 34(5): 1887-1892. |
| [11] |
金昌昆, 王延光, 尚新民, 等. 微测井与方位加权插值精细近地表速度建模技术[J]. 石油地球物理勘探, 2020, 55(2): 257-265. JIN Changkun, WANG Yanguang, SHANG Xinmin, et al. Near-surface velocity modeling based on micro-log and azimuth-weighted interpolation[J]. Oil Geophysical Prospecting, 2020, 55(2): 257-265. |
| [12] |
潘树林, 陈凯, 崔庆辉, 等. 基于地质统计学的沙漠地区逐点时深曲线静校正方法[J]. 石油物探, 2019, 58(5): 709-715. PAN Shulin, CHEN Kai, CUI Qinghui, et al. A point-by-point time-depth curve static correction method based on geostatistics[J]. Geophysical Prospecting for Petroleum, 2019, 58(5): 709-715. |
| [13] |
祖云飞, 王珂, 倪宇东, 等. 时深曲线法静校正在复杂山地三维中的应用[C]. 中国石油学会2017年物探技术研讨会, 天津, 2017, 250-254. ZU Yunfei, WANG Ke, NI Yudong, et al. Application of time-depth curve 3D static correction in complex mountain areas[C]. 2017 Geophysical Technology Seminar (Hosted by Chinese Petroleum Society), Tianjin, 2017, 250-254. |
| [14] |
Nguyen Tien Thanh, 刘修国, 任泽. 局部空间自相关及其在勘探地球化学中的空间聚集研究[J]. 物探与化探, 2014, 38(2): 370-376. Nguyen Tien Thanh, LIU Xiuguo, REN Ze. A study of geochemical exploration spatial cluster indentification based on local spatial autocorrelation[J]. Geophysical and Geochemical Exploration, 2014, 38(2): 370-376. |
| [15] |
张新东, 吕景峰, 蔡明, 等. 一种适用于复杂地貌山前带的表层调查方法[J]. 天然气勘探与开发, 2015, 38(2): 35-37, 42. ZHANG Xindong, LYU Jingfeng, CAI Ming, et al. A method to investigate the surface conditions in complex mountain front[J]. Natural Gas Exploration & Development, 2015, 38(2): 35-37, 42. |
| [16] |
葛利华, 姜弢, 徐学纯, 等. 辽西葫芦岛东部表层结构调查及速度建模[J]. 吉林大学学报(地球科学版), 2014, 44(3): 1039-1047. GE Lihua, JIANG Tao, XU Xuechun, et al. Surface survey and velocity model building in eastern Huludao of Western Liaoning Province[J]. Journal of Jilin University(Earth Science Edition), 2014, 44(3): 1039-1047. |
| [17] |
潘家智. 相关系数在松北地区表层建模中的应用分析[J]. 西南石油大学学报(自然科学版), 2018, 40(3): 76-86. PAN Jiazhi. Application of correlation coefficients for surface modeling in the Songbei Area[J]. Journal of Southwest Petroleum University (Science & Techno-logy Edition), 2018, 40(3): 76-86. |
| [18] |
王建民, 初海红, 刘国友. 基于近地表结构分析的静校正方法与应用[J]. 大庆石油地质与开发, 2016, 35(5): 136-140. WANG Jianmin, CHU Haihong, LIU Guoyou. Static correction method and application based on the near surface structures analysis[J]. Petroleum Geology and Oilfield Development in Daqing, 2016, 35(5): 136-140. |



 崔庆辉, 山东省东营市东营区北一路210号中国石化胜利油田物探研究院物探方法室, 257022。Email:
崔庆辉, 山东省东营市东营区北一路210号中国石化胜利油田物探研究院物探方法室, 257022。Email: 