② 同济大学海洋高等研究院, 上海 200092;
③ Modeling and Imaging Laboratory, University of California, Santa Cruz, CA 95060, USA
② Institute for Advanced Study, Tongji University, Shanghai 200092 China;
③ Modeling and Imaging Laboratory, University of California, Santa Cruz, California 95060, USA
地震波旅行时常用于反演地下速度结构。在射线层析中,由于引入了高频近似假设,旅行时只与连接炮检对的几何射线上的速度扰动有关。对于有限频带的地震波,若速度非均匀体的尺度小于菲涅耳体的宽度时,地震波散射起主导作用。由此发展了绕射层析理论[1-2],可以较好地处理地震波的一阶绕射效应。基于Born近似,Luo等[3]给出了地震波旅行时Fréchet导数(旅行时敏感度核函数),可以定量描述速度扰动对地震波旅行时扰动的影响。通过波动方程线性化近似(Born近似或Rytov近似),Woodward[4]提出了“波路径”的概念,作为无限高频假设下的射线路径向有限频地震波传播的推广。借助伴随状态理论,可以实现(波形、旅行时、振幅等)Fréchet导数的高效计算[5-11]。
通常旅行时Fréchet导数由Born近似导出[12-18],但Born近似成立条件较为苛刻。相比于Born近似,Rytov近似可以更好地描述由于速度扰动引起的前向散射波的相位扰动[19],因而更适用于旅行时反演。基于Rytov近似也可以构造相应的旅行时敏感度核函数[20-27]。
然而,Born近似与Rytov近似均属于弱散射近似,要求速度扰动远小于背景速度[28-29]。为克服弱散射近似的制约,Feng等[30]提出了可以适用于强扰动模型的广义Rytov近似理论(Generalized Rytov approximation,GRA)。对于前向散射及小角度传播,GRA可以较为准确地预测地震波的相位扰动,因而更适用于旅行时反演。本文将GRA理论应用于传统的有限频层析,构造一种适用范围更广的旅行时敏感度核函数并用于初至旅行时层析。模型数据测试结果表明,本文提出的广义Rytov近似旅行时层析可以建立高精度的近地表速度模型,且收敛速度较快。
1 理论 1.1 广义Rytov近似有限频旅行时敏感度核函数频率域标量声波方程可以表示为
| $ ({\nabla ^2} + {k^2}){u_0} = 0 $ | (1) |
式中:k(x)=ω/v0(x),为背景速度场v0(x)中的地震波数;u0(x,ω)为背景波场;▽2为Laplace算子。
记扰动后的速度场为v(x),波场(总场)为u(x,ω),总场与背景场的关系为
| $ u(\mathit{\boldsymbol{x}},\omega ) = {u_0}(\mathit{\boldsymbol{x}},\omega ){\rm{exp}}[\psi (\mathit{\boldsymbol{x}},\omega )] $ | (2) |
式中ψ(x,ω)为复相位。
在前向散射(散射角定义如图 1所示)及小角度传播假设下,复相位可以用广义Rytov近似[31]表示为
| $ \begin{array}{l} {\psi ^{{\rm{GRA}}}}(\mathit{\boldsymbol{x}},\omega ) = \int {\Delta s } ({\mathit{\boldsymbol{x}}^\prime }) \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{2{\omega ^2}{s_0}({\mathit{\boldsymbol{x}}^\prime }){G_0}({\mathit{\boldsymbol{x}}^\prime },\omega ;\mathit{\boldsymbol{x}}){u_0}({\mathit{\boldsymbol{x}}^\prime },\omega )}}{{{u_0}(\mathit{\boldsymbol{x}},\omega )}}{\rm{d}}{\mathit{\boldsymbol{x}}^\prime } \end{array} $ | (3) |
|
图 1 散射角定义:地震波入射方向与散射方向的夹角 前向散射对应小散射角,背向散射对应大散射角 |
式中:G0(x′, ω; x)为v0(x)中从x′到x的格林函数;Δs(x)=s(x)-s0(x)为慢度扰动,其中s0(x)=v0-1(x)、s(x)=v-1(x)分别为背景慢度和扰动后的慢度。
式(3)引起的相位延迟可以表示为
| $ \Delta {t_{\rm{p}}}(\omega ) = - \frac{{{\rm{Im}}[\psi (\omega )]}}{\omega } $ | (4) |
有限频带地震信号的旅行时扰动可以表示为单频谐波的相位延迟的加权叠加[23-26, 32],有
| $ \Delta t = \int W (\omega )\Delta {t_{\rm{p}}}(\omega ){\rm{d}}\omega $ | (5) |
式中
结合式(3)~式(5),可以建立带限信号旅行时扰动与慢度扰动的线性关系
| $ \Delta t({\mathit{\boldsymbol{x}}_{\rm{r}}},{\mathit{\boldsymbol{x}}_{\rm{s}}}) = \int \Delta s(\mathit{\boldsymbol{x}}){K^{{\rm{GRA}}}}(\mathit{\boldsymbol{x}};{\mathit{\boldsymbol{x}}_{\rm{r}}},{\mathit{\boldsymbol{x}}_{\rm{s}}}){\rm{d}}\mathit{\boldsymbol{x}} $ | (6) |
式中:xs和xr分别为源和检波点坐标;KGRA(x; xr, xs)为广义Rytov近似旅行时敏感度核函数(Generalized Rytov approximation based traveltime sensitivity kernel,简称为GRA核函数),可表示为
| $ \begin{array}{l} {K^{{\rm{GRA}}}}(\mathit{\boldsymbol{x}};{\mathit{\boldsymbol{x}}_{\rm{r}}},{\mathit{\boldsymbol{x}}_{\rm{s}}}) = \int {W(\omega )} \frac{1}{\omega } \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{Im}} [ - 2{\omega ^2}{s_0}(\mathit{\boldsymbol{x}})\frac{{{G_0}(\mathit{\boldsymbol{x}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{r}}}){u_0}(\mathit{\boldsymbol{x}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}})}}{{{u_0}({\mathit{\boldsymbol{x}}_{\rm{r}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}})}}]{\rm{d}}\omega \end{array} $ | (7) |
显然,显式计算式(7)需要计算频率域格林函数[25],因而计算量较大,尤其是对于三维问题。为了避免显式计算核函数,本文采用冯波等[26]给出的方法,通过引入如下辅助函数
| $ q({\mathit{\boldsymbol{x}}_{\rm{r}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}) = {\left[ {\frac{{W(\omega )}}{{ {\rm{i}}\omega {u_0} ({\mathit{\boldsymbol{x}}_{\rm{r}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}})}}} \right]^*} $ | (8) |
利用Parseval定理,将式(7)中对角频率的积分转化为对时间积分,则
| $ \begin{array}{*{20}{l}} {{K^{{\rm{GRA}}}}\left( {\mathit{\boldsymbol{x}};{\mathit{\boldsymbol{x}}_{\rm{r}}},{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\mathop{\rm Re}\nolimits} \left\{ {\int {{q^*}} \left( {{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)\left[ { - 2{\omega ^2}{s_0}(\mathit{\boldsymbol{x}}){u_0}\left( {\mathit{\boldsymbol{x}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right) \times } \right.} \right.}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\left. {\quad {G_0}\left( {\mathit{\boldsymbol{x}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{r}}}} \right)} \right]{\rm{d}}\omega } \right\}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = 2{\rm{ \mathsf{ π} }}{\mathop{\rm Re}\nolimits} \left\{ {\int_0^T 2 {s_0}(\mathit{\boldsymbol{x}})\partial _t^2{u_0}\left( {\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right) \times } \right.}\\ {\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \quad {{\left[ {{g_0}\left( {\mathit{\boldsymbol{x}}, - t\mid {\mathit{\boldsymbol{x}}_{\rm{r}}},0} \right) * q\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)} \right]}^*}{\rm{d}}t} \right\}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \int_0^T 2 {s_0}(\mathit{\boldsymbol{x}})\partial _t^2{u_0}\left( {\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)\left\{ {{g_0}\left( {\mathit{\boldsymbol{x}}, - t\mid {\mathit{\boldsymbol{x}}_{\rm{r}}},0} \right) * } \right.}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {{\mathop{\rm Re}\nolimits} \left[ {2{\rm{ \mathsf{ π} }}{q^*}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)} \right]} \right\}{\rm{d}}t} \end{array} $ | (9) |
式中:T表示地震记录时长;g0表示时间域格林函数;“*”表示褶积(与上标“*”表示复共轭不同)。
若定义旅行时伴随场为
| $ \begin{array}{l} {{\tilde u}_{\rm{r}}}(\mathit{\boldsymbol{x}},T - t;{\mathit{\boldsymbol{x}}_{\rm{r}}})\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {g_0}(\mathit{\boldsymbol{x}}, - t|{\mathit{\boldsymbol{x}}_{\rm{r}}},0) * {\rm{Re}}[2{\rm{ \mathsf{ π} }}{q^*}({\mathit{\boldsymbol{x}}_{\rm{r}}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}})]\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {g_0}(\mathit{\boldsymbol{x}},T - t|{\mathit{\boldsymbol{x}}_{\rm{r}}},T) * {\rm{Re}}[2{\rm{ \mathsf{ π} }}{q^*}({\mathit{\boldsymbol{x}}_{\rm{r}}}{\rm{,}}t;{\mathit{\boldsymbol{x}}_{\rm{s}}})] \end{array} $ | (10) |
式(9)可以重写为
| $ \begin{array}{*{20}{l}} {{K^{{\rm{GRA}}}}(\mathit{\boldsymbol{x}};{\mathit{\boldsymbol{x}}_{\rm{r}}},{\mathit{\boldsymbol{x}}_{\rm{s}}}) = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int_0^T 2 {s_0}(\mathit{\boldsymbol{x}})\partial _t^2{u_0}(\mathit{\boldsymbol{x}}{\rm{,}}t;{\mathit{\boldsymbol{x}}_{\rm{s}}}){{\tilde u}_{\rm{r}}}(\mathit{\boldsymbol{x}},T - t;{\mathit{\boldsymbol{x}}_{\rm{r}}}){\rm{d}}t} \end{array} $ | (11) |
式中旅行时伴随场由旅行时伴随震源
基于旅行时残差L2范数的误差泛函可表示为
| $ \mathop {{\rm{min}}}\limits_{\mathit{\boldsymbol{m}} \in \mathit{\boldsymbol{M}}} J(\mathit{\boldsymbol{m}}) = \frac{1}{2}\sum\limits_{l = 1}^{{N_{\rm{d}}}} \Delta t_l^2 = \frac{1}{2}\Delta {\mathit{\boldsymbol{t}}^{\rm{T}}}\Delta \mathit{\boldsymbol{t}} $ | (12) |
式中:m=(m1, m2, …, mNv)T∈M,为模型空间M中的向量,本文为慢度模型(采用网格参数化方式),其中Nv为网格点数;Δt=(Δt1, Δt2, …, ΔtNd)T∈D,为数据空间D中的向量(旅行时残差),其中Nd为炮检对数。
利用Gauss-Newton反演算法,式(12)可以迭代求解
| $ {\mathit{\boldsymbol{m}}^{k + 1}} = {\mathit{\boldsymbol{m}}^k} - {\alpha ^k}P[\mathit{\boldsymbol{H}}_{\rm{a}}^{ - 1}({\mathit{\boldsymbol{m}}^k})\nabla J]({\mathit{\boldsymbol{m}}^k})] $ | (13) |
式中:k为迭代次数;α为步长,可以通过线性搜索方法计算;▽J为目标函数梯度;
根据式(12),泛函梯度可表示为
| $ \Delta J({\mathit{\boldsymbol{m}}^k}) = \frac{{\partial J}}{{\partial {\mathit{\boldsymbol{m}}^k}}} = {\left( {\frac{{\partial \Delta {\mathit{\boldsymbol{t}}^k}}}{{\partial {\mathit{\boldsymbol{m}}^k}}}} \right)^{\rm{T}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta {\mathit{\boldsymbol{t}}^k} = {\mathit{\boldsymbol{K}}^{\rm{T}}}\Delta {\mathit{\boldsymbol{t}}^k} $ | (14) |
基于广义Rytov近似,∂Δt/∂m即为式(11)给出的核函数。将式(11)代入式(14),则泛函数梯度可表示为
| $ \begin{array}{l} \nabla J\left( {{\mathit{\boldsymbol{m}}^k}} \right)(\mathit{\boldsymbol{x}}) = \left( {{\mathit{\boldsymbol{K}}^{\rm{T}}}\Delta {\mathit{\boldsymbol{t}}^k}} \right)(\mathit{\boldsymbol{x}})\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \sum\limits_{{\mathit{\boldsymbol{x}}_{\rm{s}}}} {\sum\limits_{{\mathit{\boldsymbol{x}}_{\rm{r}}}} {{K^{{\rm{GRA}}}}} } \left( {\mathit{\boldsymbol{x}};{\mathit{\boldsymbol{x}}_{\rm{r}}},{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)\Delta {t^k}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}},{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \sum\limits_{{\mathit{\boldsymbol{x}}_{\rm{s}}}} {\int_0^T 2 } {s_k}(\mathit{\boldsymbol{x}})\partial _t^2{u_0}\left( {\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right) \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \tilde u\left( {\mathit{\boldsymbol{x}},T - t;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right){\rm{d}}t \end{array} $ | (15) |
式中
考虑到显式计算Hessian矩阵需要巨大的计算量及存储量,且求逆困难,因此,将对Hessian矩阵的求逆转化为求解如下法方程的近似解
| $ {\mathit{\boldsymbol{H}}_{\rm{a}}}({\mathit{\boldsymbol{m}}^k})\Delta {\mathit{\boldsymbol{m}}^k} = \nabla J({\mathit{\boldsymbol{m}}^k}) $ | (16) |
本文用共轭梯度(Conjugate gradient,CG)法求解式(16)获得模型更新方向,并采用隐式矩阵向量乘方法[26]直接计算Hessian矩阵与向量的乘,因而无需显式计算及存储Hessian矩阵。具体计算公式详见附录A。
2 数值试验 2.1 高斯扰动模型图 2为一个含有高斯异常体的二维10km×5km速度模型,网格间距为10m。其背景速度v0=3000m/s,异常体的速度扰动可表示为
| $ \Delta v (x,z) = \varepsilon {v_0} {\rm{exp}} \left( { - \frac{{{r^2}}}{{2{a^2}}}} \right) $ | (17) |

|
图 2 含有高斯扰动(ε= 50%)的速度模型及观测系统红色倒三角为检波点位置 |
式中:ε为速度扰动百分比;a=1km为高斯异常体的尺度参数;
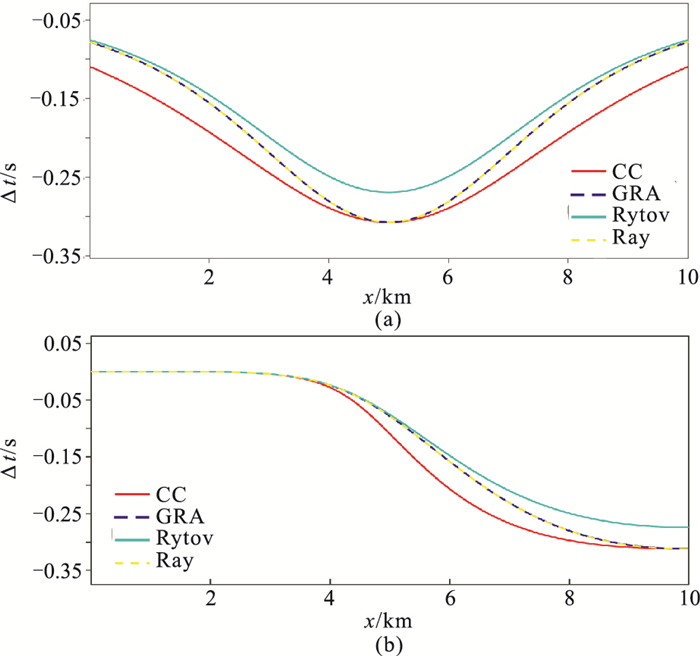
首先,用时—空域高阶有限差分求解声波方程,用真实模型(包含高斯异常体的速度模型)和背景模型(即均匀背景速度模型)进行正演(震源是主频为15Hz的Ricker子波),得到的地震记录分别作为观测数据和模拟数据。然后,用互相关(Cross-correlation,简记为CC)函数测量观测数据和模拟数据的时差,作为真实时差的测量值(即观测时差)。随后,分别用射线(Ray)核函数(速度网格内的射线长度)、Rytov近似旅行时敏感度核函数[26]及本文提出的GRA旅行时敏感度核函数预测旅行时扰动(即核函数与模型扰动做内积)。图 3为震源在地表(5.0km,0)和(0,0)处、201个检波器均匀分布在z=5.0km处(图 2中红色倒三角所示)旅行时扰动对比。由图 3可以看出:①射线和GRA核函数的预测时差完全重合,但与Rytov近似预测结果有较大偏差。②对于小角度前向散射(图 3a中对应为:震源位于地表(5.0km,0),检波器横坐标在(5.0km,5.0km)附近),GRA核函数的预测时差与观测时差基本一致。证明了GRA核函数在前向小角度散射时具有较好的线性特征,克服了传统波动方程线性化近似中的速度小扰动假设的制约。这与GRA理论预测相符(GRA理论指出,对于小角度前向散射,GRA可以较为精确地预测地震波的相位扰动)。③随着散射角增大,GRA核函数的预测时差逐渐偏离观测时差,并逐渐与Rytov近似预测结果趋于一致。根据GRA理论推导可知[30],Rytov近似为GRA的一阶近似,本质上都隐含了小角传播假设。因此,随着散射角增大,GRA的成立条件(即前向小角散射)不再成立,导致预测时差偏离观测值。对于图 3b中的震源位置(左上角(0,0)处),前向小角度散射对应检波器横坐标在10km附近,三类核函数预测结果与图 3a一致。
|
图 3 震源在地表不同位置三种旅行时敏感度核函数的预测时差与测量时差对比 (a)(xs,zs)=(5.0km,0);(b)(xs,zs)=(0,0) |
上述测试表明:GRA核函数精度与散射角密切相关。对于前向小角度散射,GRA可以较为准确地预测地震波的旅行时扰动。随着散射角不断增大,GRA核函数精度逐渐降低,但仍好于Rytov近似。虽然对于大角度散射,GRA核函数的预测结果并不准确,甚至与观测时差偏离较远,但并不会导致层析反问题求解失败。原因在于:层析反问题通过最优化算法迭代求解时差目标函数,而非直接对线性方程组直接求逆。即使正问题的线性化近似不严格成立,只要反问题的凸性较好,依然可以采用最优化算法求解目标泛函。
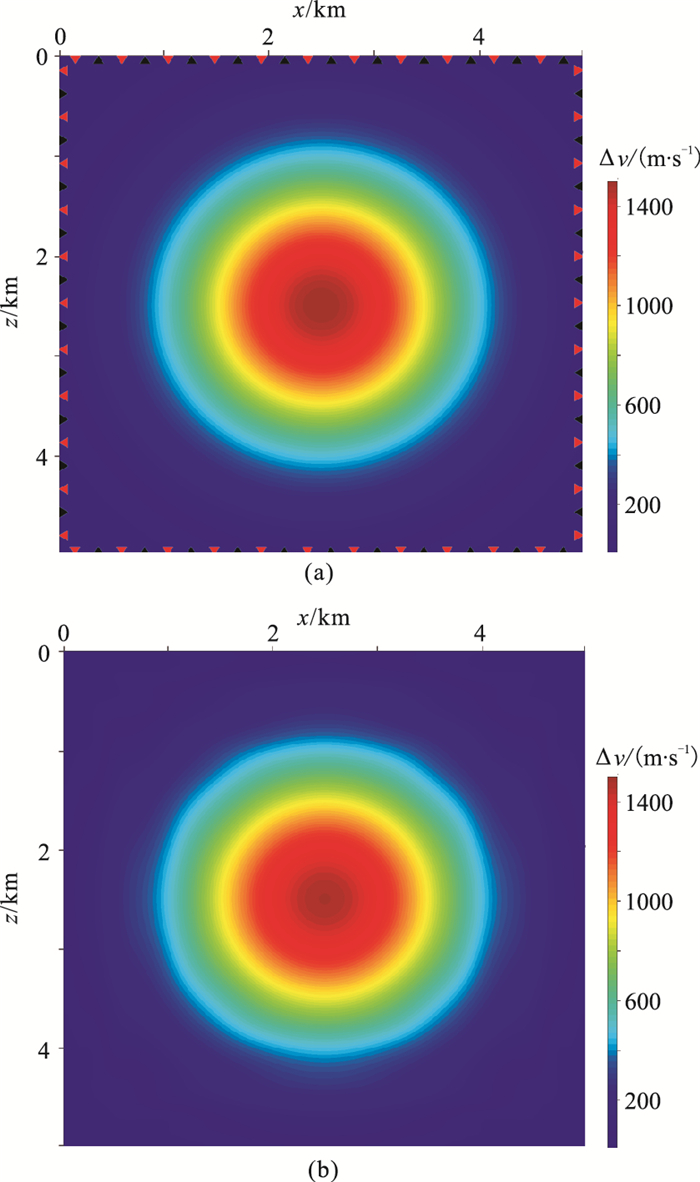
为了验证GRA初至层析方法的有效性、尽可能消除观测系统对反演结果的影响,设计了一个理想观测系统如图 4a所示,100个检波器均匀分布高斯异常体模型的四周,围绕模型四周激发100次,震源是主频为15Hz的Ricker子波(对应波长λ0=0.2km,与高斯异常体尺度参数关系为a = 5λ0)。
|
图 4 高斯模型观测系统(a)及GRA旅行时反演结果(b) 黑色正三角形表示震源位置;红色倒三角形表示检波点位置 |
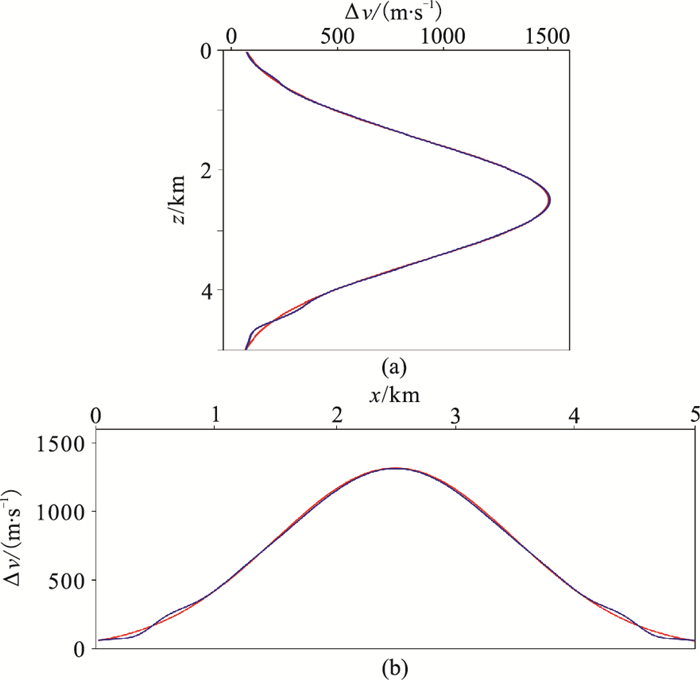
反演采用的初始模型为均匀背景速度场(v0=3000m/s),并用互相关方法测量观测数据和模拟数据的时移量作为初至旅行时残差。反演采用SEIS-COPE数值优化软件包(SEISCOPE optimization toolbox)中的截断牛顿算法(对于旅行时层析,截断牛顿算法退化为高斯牛顿算法)实现最优化,其中,梯度和Hessian矩阵与向量乘由附录A中给出的隐式矩阵与向量乘方法计算。在迭代反演中,采用2次CG内迭代求解式(16),获得模型更新方向,并用线性搜索方法计算迭代步长。反演收敛准则为判断相对旅行时误差(J(mk)/J(m0))是否小于预设的阈值(σ=1.0×10 -4)。经过10次迭代(图 5为反演收敛曲线),反演结果如图 4b所示,与真实速度模型在视觉上几乎没有差别。为定量对比反演结果,对反演的扰动模型(反演结果减去初始模型)与真实的高斯异常体进行横向和纵向抽线对比(图 6),反演的速度扰动与真实的高斯扰动基本吻合,证明了对于完备的观测系统及简单高斯速度模型,GRA初至层析可以得到高精度的反演结果,证实了方法的有效性。

|
图 5 GRA初至层析的收敛曲线 |
|
图 6 高斯模型层析(蓝色)与真实(红色)速度扰动曲线 (a)x=2.5km; (b)z=2.5km |
应用Marmousi-2模型验证GRA初至层析对复杂速度模型及不完备的观测系统的有效性。为模拟陆上地震采集,切除了原始速度模型中上覆的水体部分,并在模型右侧扩边3km(图 7a)。x和z方向网格数目分别为2001和301,网格间距均为10m。

|
图 7 Marmousi-2模型(a)及GRA初至层析的速度更新量(b) |
设计了一个单边观测系统:震源和检波器均放置在地表,起始炮点位于x=0,炮间距为100m,共171炮;最小和最大炮检距分别为400m和5000m,道间距为20m(每炮共231道)。最大炮检距较大,因此可以用初至波旅行时反演近地表速度。采用有限差分求解波动方程正演地震信号,震源是主频为15Hz的Ricker子波。由于观测地震记录较为复杂,采用自动方法[31]拾取初至,作为观测记录的初至旅行时。
初始模型采用随深度线性递增的速度场(z=0,v=1000m/s;z=3.5km,v=3000m/s)。为降低计算量,采用20m×20m网格剖分进行速度反演,并用相同的初至拾取方法拾取模拟数据的旅行时,进而计算初至时差。反演实现框架与高斯模型一致(相对旅行时误差阈值σ=1.0×10-2)。经过5次迭代反演收敛,得到的速度更新量如图 7b所示,浅层的高速异常得到了较好的恢复。其收敛曲线如图 8所示,可以看出,高斯—牛顿算法收敛速度较快。
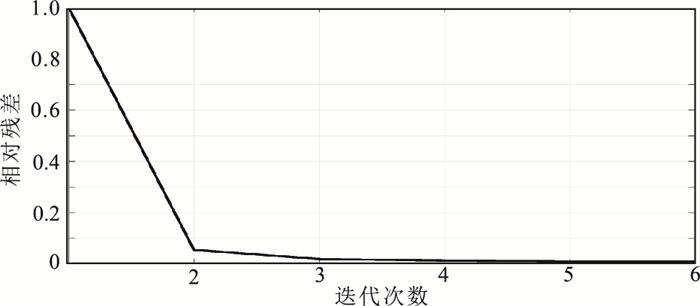
|
图 8 GRA初至层析的收敛曲线 |
为定量对比反演结果,抽取z=0.1、0.2、0.4、0.6km处速度横向变化曲线,如图 9所示。可以看出,在近地表(z=0.1、0.2km),反演结果(蓝色曲线)逼近真实的高速隆起,反演精度较高(图 9a和图 9b)。随着深度增加,反演精度逐渐降低(图 9c和图 9d),但反演结果仍然与真实速度模型的整体趋势相吻合。

|
图 9 不同深度处初始(绿色)、真实(红色)、GRA层析(蓝色)速度横向变化曲线对比 (a)z=0.1km;(b)z=0.2km;(c)z=0.4km;(d)z=0.6km |
Marmousi-2模型实验结果表明,利用中、小炮检距的初至波旅行时信息,GRA初至层析可以建立高精度的近地表速度模型。
3 讨论旅行时(差)的精确测量是所有旅行时反演类方法所共有的问题。本文的重点为讨论如何将广义Rytov近似方法与有限频层析理论的结合,是笔者过去研究工作[26]的理论推广和应用,因而没有讨论如何准确测量初至波时差。若震源子波已知且模拟数据与观测数据的初至波形基本一致,此时测量初至波时差相对简单。反之,若震源子波未知或由于地下介质复杂导致初至波形畸变严重,此时需要采用与震源无关的反演类算法消除子波波形畸变对旅行时测量的影响,如双差旅行时(double-difference traveltime)[33-34]测量等。
4 结论本文提出了一种基于广义Rytov近似的有限频旅行时敏感度核函数,克服了传统有限频层析方法中弱速度扰动假设的制约。对于前向散射及小角度传播,广义Rytov近似旅行时敏感度核函数可以较为准确地预测地震波的旅行时扰动,从而可以提高反演精度并加速反演收敛。在计算方面,本文采用了隐式矩阵向量乘方法直接计算Hessian矩阵与向量的乘,无需显式计算及存储Hessian矩阵,进而可以提高高斯—牛顿迭代反演算法的效率。复杂的Marmousi-2模型测试结果表明,GRA初至层析可以建立高精度的近地表速度模型。
附录A 隐式矩阵向量乘Hessian矩阵与向量积可表示为
| $ {\mathit{\boldsymbol{H}}_{\rm{a}}}\mathit{\boldsymbol{p}} = {\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{Kp}} = {\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{h}} $ | (A-1) |
式中:p=p(x)为模型空间中的向量;h=h(xr, xs)为数据空间中的向量。因此需要计算两次矩阵向量积。
首先,∀(xr, xs),Kp可以表示为
| $ \begin{array}{l} (\mathit{\boldsymbol{Kp}})\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}},{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right) = \int p (\mathit{\boldsymbol{x}}){\mathop{\rm Re}\nolimits} \left\{ {\int - 2{\omega ^2}{s_0}(\mathit{\boldsymbol{x}}){u_0}\left( {\mathit{\boldsymbol{x}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right) \times } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\left[ {{G_0}\left( {\mathit{\boldsymbol{x}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{r}}}} \right){q^*}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)} \right]{\rm{d}}\omega } \right\}{\rm{d}}\mathit{\boldsymbol{x}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\mathop{\rm Re}\nolimits} \left[ {\int {{q^*}} \left( {{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right){u_{\rm{p}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right){\rm{d}}\omega } \right] \end{array} $ | (A-2) |
式中up(xr, ω; xs)满足如下Born近似
| $ \begin{array}{*{20}{l}} {{u_{\rm{p}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right) = \int - 2{\omega _{s0}}(\mathit{\boldsymbol{x}})\mathit{\boldsymbol{p}}{|_\mathit{\boldsymbol{x}}} \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {G_0}\left( {\mathit{\boldsymbol{x}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{r}}}} \right){u_0}\left( {\mathit{\boldsymbol{x}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right){\rm{d}}\mathit{\boldsymbol{x}}} \end{array} $ | (A-3) |
利用Parseval定理,式(A-2)可改写为
| $ \begin{array}{l} (\mathit{\boldsymbol{Kp}})\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}},{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right) = 2{\rm{ \mathsf{ π} Re}}\left[ {\int_0^T {{q^*}} \left( {{\mathit{\boldsymbol{x}}_{\rm{r}}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right){u_{\rm{p}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right){\rm{d}}t} \right] \\ {\kern 1pt} = \int_0^T u_{\rm{q}}{\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right){u_{\rm{p}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right){\rm{d}}t} \end{array} $ | (A-4) |
式中
| $ \begin{array}{*{20}{l}} {{u_{\rm{q}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right) = 2{\rm{ \mathsf{ π} Re}}[{q^*}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)]}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = 2{\rm{ \mathsf{ π} Re}}{{[{\rm{F}}{{\rm{T}}^{ - 1}}q\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)]}^*}} \end{array} $ | (A-5) |
| $ {{u_{\rm{p}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right) = {\rm{F}}{{\rm{T}}^{ - 1}}{u_{\rm{p}}}\left( {{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega ;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)} $ | (A-6) |
同时,式(A-3)在时—空域满足如下方程组
| $ \left\{ \begin{array}{l} [\partial _t^2m(\mathit{\boldsymbol{x}}) - {\nabla ^2}]{u_0}\left( {\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right) = f(t)\delta (\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_{\rm{s}}})\\ [\partial _t^2m(\mathit{\boldsymbol{x}}) - {\nabla ^2}]{u_{\rm{p}}}\left( {\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right) = 2{s_0}(\mathit{\boldsymbol{x}})p(\mathit{\boldsymbol{x}})\partial _t^2{u_0}\left( {\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right) \end{array} \right. $ | (A-7) |
式中f为震源函数。
其次,根据式(15),对于空间任意一点x,KTh可以表示为
| $ \begin{array}{l} ({\mathit{\boldsymbol{K}}^{\rm{T}}}\mathit{\boldsymbol{p}})(\mathit{\boldsymbol{x}}) = \sum\limits_{{\mathit{\boldsymbol{x}}_{\rm{s}}}} {\sum\limits_{{\mathit{\boldsymbol{x}}_{\rm{r}}}} {{k^{{\rm{GRA}}}}} } \left( {\mathit{\boldsymbol{x}};{\mathit{\boldsymbol{x}}_{\rm{r}}},{\mathit{\boldsymbol{x}}_{\rm{s}}}} \right)h({\mathit{\boldsymbol{x}}_{\rm{r}}},{\mathit{\boldsymbol{x}}_{\rm{s}}})\\ {\kern 1pt} = \sum\limits_{{\mathit{\boldsymbol{x}}_{\rm{s}}}} {\int_0^T 2 {s_0}(\mathit{\boldsymbol{x}})\partial _t^2{u_0}(\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}){{\tilde u}_h}(\mathit{\boldsymbol{x}},T - t;{\mathit{\boldsymbol{x}}_{\rm{s}}}){\rm{d}}t} \end{array} $ | (A-8) |
式中
| $ \begin{array}{l} {{\tilde u}_h}(\mathit{\boldsymbol{x}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}}) = \sum\limits_{{\mathit{\boldsymbol{x}}_{\rm{r}}}} {\{ {g_0}(} \mathit{\boldsymbol{x}}, - t|{\mathit{\boldsymbol{x}}_{\rm{r}}},0) * \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [\tilde f({\mathit{\boldsymbol{x}}_{\rm{r}}},t;{\mathit{\boldsymbol{x}}_{\rm{s}}})h({\mathit{\boldsymbol{x}}_{\rm{r}}},{\mathit{\boldsymbol{x}}_{\rm{s}}})]\} \end{array} $ | (A-9) |
为单炮旅行时伴随波场。
| [1] |
Slaney M, Kak A C, Larsen L. Limitations of imaging with first-order diffraction tomography[J]. IEEE Transactions On Microwave Theory and Techniques, 1984, 32(8): 860-873. DOI:10.1109/TMTT.1984.1132783 |
| [2] |
Wu R S, Toksöz M N. Diffraction tomography and multisource holography applied to seismic imaging[J]. Geophysics, 1987, 52(1): 11-25. DOI:10.1190/1.1442237 |
| [3] |
Luo Y, Schuster G T. Wave-equation travel time inversion[J]. Geophysics, 1991, 56(5): 645-653. DOI:10.1190/1.1443081 |
| [4] |
Woodward M J. Wave-equation tomography[J]. Geo-physics, 1992, 57(1): 15-26. |
| [5] |
Lailly P. The seismic inverse problem as a sequence of before stack migrations[C]. Expanded Abstracts of Conference on Inverse Scattering, Theory and Application, 1983, 206-220.
|
| [6] |
Liu Q, Tromp J. Finite-frequency kernels based upon adjoint methods[J]. Bulletin of the Seismological Society of America, 2006, 96(6): 2383-2397. DOI:10.1785/0120060041 |
| [7] |
Liu Q, Tromp J. Finite-frequency sensitivity kernels for global seismic wave propagation based upon adjoint methods[J]. Geophysical Journal International, 2008, 174(1): 265-286. DOI:10.1111/j.1365-246X.2008.03798.x |
| [8] |
Tape C, Liu Q, Tromp J. Finite frequency tomography using adjoint methods-methodology and examples using membrane surface waves[J]. Geophysical Journal International, 2007, 168(3): 1105-1129. DOI:10.1111/j.1365-246X.2006.03191.x |
| [9] |
Tarantola A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 1984, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
| [10] |
Tromp J, Tape C, Liu Q. Seismic tomography, adjoint methods, time reversal, and banana-doughnut kernels[J]. Geophysical Journal International, 2005, 160(1): 195-216. |
| [11] |
李海山, 杨午阳, 雍学善. 三维一阶速度-应力声波方程全波形反演[J]. 石油地球物理勘探, 2018, 53(4): 730-736. LI Haishan, YANG Wuyang, YONG Xueshan. Three-dimensional full waveform inversion based on the first-order velocity-stress acoustic wave equation[J]. Oil Geophysical Prospecting, 2018, 53(4): 730-736. |
| [12] |
Marquering H, Dahlen F A, Nolet G. Three-dimensional sensitivity kernels for finite-frequency traveltimes:The banana-doughnut paradox[J]. Geophysical Journal International, 1999, 137(3): 805-815. DOI:10.1046/j.1365-246x.1999.00837.x |
| [13] |
Dahlen F A, Hung S H, Nolet G. Fréchet kernels for finite-frequency traveltimes, I:Theory[J]. Geophy-sical Journal International, 2000, 141(1): 157-174. DOI:10.1046/j.1365-246X.2000.00070.x |
| [14] |
Hung S H, Dahlen F A, Nolet G. Fréchet kernels for finite-frequency traveltime, Ⅱ:Examples[J]. Geophysical Journal International, 2000, 141(1): 175-203. DOI:10.1046/j.1365-246X.2000.00072.x |
| [15] |
Zhao L, Jordan T H, Chapman C H. Three-dimensional Fréchet differential kernels for seismic delay times[J]. Geophysical Journal International, 2000, 141(3): 558-576. DOI:10.1046/j.1365-246x.2000.00085.x |
| [16] |
崔超, 黄建平, 王自颖, 等. 基于双差的波动方程反射波旅行时反演方法[J]. 石油地球物理勘探, 2017, 52(4): 734-742. CUI Chao, HUANG Jianping, WANG Ziying, et al. Double difference wave-equation reflection traveltime inversion[J]. Oil Geophysical Prospecting, 2017, 52(4): 734-742. |
| [17] |
付继有, 李振春, 杨国权, 等. 声介质波动方程反射旅行时反演方法[J]. 石油地球物理勘探, 2015, 50(6): 1134-1140. FU Jiyou, LI Zhenchun, YANG Guoquan, et al. Wave equation reflection travel-time inversion in acoustic media[J]. Oil Geophysical Prospecting, 2015, 50(6): 1134-1140. |
| [18] |
谢春, 刘玉柱, 董良国, 等. 基于声波方程的有限频伴随状态法初至波旅行时层析[J]. 石油地球物理勘探, 2015, 50(2): 274-282. XIE Chun, LIU Yuzhu, DONG Liangguo, et al. First arrival tomography with finite frequency adjoint-state method based on acoustic wave equation[J]. Oil Geophysical Prospecting, 2015, 50(2): 274-282. |
| [19] |
Wu R S. Wave propagation, scattering and imaging using dual-domain one-way and one-return propagators[J]. Pure and Applied Geophysics, 2003, 160(3-4): 509-539. |
| [20] |
Spetzler J, Snieder R. The effects of small-scale he-terogeneity on the arrival time of waves[J]. Geo-physical Journal International, 2001, 145(3): 786-796. DOI:10.1046/j.1365-246x.2001.01438.x |
| [21] |
Spetzler J, Snieder R. The Fresnel volume and transmitted waves[J]. Geophysics, 2004, 69(3): 653-663. DOI:10.1190/1.1759451 |
| [22] |
Jocker J, Spetzler J, Smeulders D, et al. Validation of first-order diffraction theory for the traveltimes and amplitudes of propagating waves[J]. Geophysics, 2006, 71(6): T167-T177. DOI:10.1190/1.2358412 |
| [23] |
Xie X B, Yang H. The finite-frequency sensitivity kernel for migration residual moveout and its applications in migration velocity analysis[J]. Geophysics, 2008, 73(6): S241-S249. DOI:10.1190/1.2993536 |
| [24] |
刘玉柱, 董良国, 李培明, 等. 初至波菲涅尔体地震层析成像[J]. 地球物理学报, 2009, 52(9): 2310-2320. LIU Yuzhu, DONG Liangguo, LI Peiming, et al. Fresnel volume tomography based on the first arrival of the seismic wave[J]. Chinese Journal of Geophy-sics, 2009, 52(9): 2310-2320. DOI:10.3969/j.issn.0001-5733.2009.09.015 |
| [25] |
Xu W, Xie X B, Geng J. Validity of the Rytov approximation in the form of finite-frequency sensitivity kernels[J]. Pure and Applied Geophysics, 2015, 172(6): 1409-1427. DOI:10.1007/s00024-014-0991-8 |
| [26] |
冯波, 罗飞, 王华忠. 一阶Rytov近似有限频旅行时层析[J]. 地球物理学报, 2019, 62(6): 2217-2226. FENG Bo, LUO Fei, WANG Huazhong. Wave equation traveltime tomography using Rytov approximation[J]. Chinese Journal of Geophysics, 2019, 62(6): 2217-2226. |
| [27] |
刘定进, 胡光辉, 蔡杰雄, 等. 高斯束层析与全波形反演联合速度建模[J]. 石油地球物理勘探, 2019, 54(5): 1046-1056. LIU Dingjin, HU Guanghui, CAI Jiexiong, et al. A joint velocity model building method with Gaussian beam tomography and full waveform inversion for land seismic data[J]. Oil Geophysical Prospecting, 2019, 54(5): 1046-1056. |
| [28] |
Beydoun W B, Tarantola A. First Born and Rytov approximations:Modeling and inversion conditions in a canonical example[J]. The Journal of the Acoustical Society of America, 1988, 83(3): 1045-1055. DOI:10.1121/1.396537 |
| [29] |
罗飞, 王华忠, 冯波, 等. 透射波旅行时Beam层析成像方法[J]. 石油物探, 2019, 58(3): 356-370. LUO Fei, WANG Huazhong, FENG Bo, et al. Beam tomography based on transmission traveltime[J]. Geo-physical Prospecting for Petroleum, 2019, 58(3): 356-370. |
| [30] |
Feng B, Wu R S, Wang H. A generalized Rytov approximation for small scattering-angle wave propagation and strong perturbation media[J]. Geophysical Journal International, 2019, 219(2): 968-974. DOI:10.1093/gji/ggz338 |
| [31] |
Snieder R, Lomax A. Wavefield smoothing and the effect of rough velocity perturbations on arrival times and amplitudes[J]. Geophysical Journal International, 1996, 125(3): 796-812. DOI:10.1111/j.1365-246X.1996.tb06024.x |
| [32] |
Luo F, Wang H, et al. Automatic traveltime picking using structure-enhanced high-dimensional time-frequency transform[C]. Extended Abstracts of 81st EAGE Conference and Exhibition, 2019, 1-5.
|
| [33] |
Yuan Y O, Simons F J, Tromp J. Double-difference adjoint seismic tomography[J]. Geophysical Journal International, 2016, 206(3): 1599-1618. DOI:10.1093/gji/ggw233 |
| [34] |
Zhang H, Thurber C H. Double-difference tomography:The method and its application to the Hayward Fault, California[J]. Bulletin of the Seismological Society of America, 2003, 93(5): 1875-1889. DOI:10.1785/0120020190 |



 罗飞, 上海市四平路1239号同济大学海洋与地球科学学院, 200092。Email:
罗飞, 上海市四平路1239号同济大学海洋与地球科学学院, 200092。Email: