2 东北石油大学人工智能能源研究院, 黑龙江大庆 163318
2 Artificial Intelligence Energy Research Institute, Northeast Petroleum University, Daqing, Heilongjiang 163318, China
噪声压制是地震资料处理的基础工作[1-2],旨在提升地震数据的信噪比,以提高后续地震资料处理和解释的效率及精度。现有的地震数据随机噪声压制方法可以划分为基于模型的去噪和基于数据驱动的去噪两大类。
基于模型的地震数据去噪方法是通过建立数据的分布模型预测包含噪声数据的真实情况。该方法又可进一步划分为时域和变换域两类,其中时域去噪方法中,具有代表性的是滤波法[3-4],基本原理是利用地震数据时域分布的特点构建滤波函数以去除噪声数据;变换域去噪方法中常用的有Fourier变换[5]、Radon变换[6]、Wavelet变换[7-9]等,基本原理是利用数据在某个基函数空间中具有比较好的分布特征,先将数据投影到变换域,然后分析变换系数中有效信号和噪声分布的特点,建立相应的分布模型,预测变换域去除噪声的系数,最后反变换回时域以达到去噪的目的。
基于数据驱动的地震数据去噪方法则是根据大量样本数据的特点,通过自适应学习的方式获得样本数据的特征,利用学习得到的主要特征表示地震数据。该方法又可进一步划分为浅层学习和深度学习两类。
在浅层学习中,具有代表性的是学习型超完备字典方法,如基于K-奇异值分解(K-Singular Value Decomposition,K-SVD)的超完备字典学习的去噪方法[10],通过对待处理数据的学习和训练,自适应地调整变换基函数,以适应特定数据本身,可以更充分地稀疏表示地震数据。Tang等[11]、张岩等[12]将该方法引入地震数据处理,利用超完备字典学习技术,根据地震数据的本身特点,自适应构造超完备字典,稀疏表示地震数据,从而恢复数据的主要特征,取得了较好的去噪效果。此类方法学习得到的特征是一种表示数据的基函数(或者叫原子),是一种浅层的特征,待处理的数据可以转化为字典中若干个原子的线性组合。
近年来,随着大数据、人工智能的发展和GPU等硬件计算能力的提升,深度学习方法通过增加神经网络的层数,得到样本数据更深层次的特征,在计算机视觉领域得到了突破性的进展,同时在地震数据处理中也逐渐得到关注[13-15]。当前基于深度学习的去噪方法通常采用残差学习[16-17]、生成对抗网络[18]、降噪自编码[19-21]等技术,基本原理是利用大量的样本覆盖待处理数据的特征,通过多层卷积的方式提取数据时域的特征,然后采用深度学习的非线性逼近能力调整网络参数,从而建立一个复杂的去噪模型,用于去除待处理数据的噪声。该类方法较传统方法去噪效果有大幅提升,但仍然存在两个方面主要问题。
(1) 通常仅关注单一时域或者传统变换域(如傅里叶变换域、小波变换域等)的特征提取。如韩卫雪等[22]提出的用于地震数据去噪的网络模型,与常规地震数据去噪算法相比,具有更好的去噪效果,但由于仅考虑时域提取特征,导致去噪过程中出现细节的丢失。Zhang等[16]提出的基于残差学习的卷积去噪网络(Residual Learning of Deep CNN for Image Denoising,DnCNN)算法,采用卷积残差学习框架,从函数回归角度出发,用卷积神经网络(Convolutional Neural Networks,CNN)将噪声从含噪图像中分离出来。Yu等[23]系统地介绍了DnCNN算法用于地震数据压制的过程并讨论了CNN的超参数设置问题。Wang等[24]也将DnCNN模型应用于地震数据噪声压制,取得了较好的效果。Zhao等[25]从图像块大小、卷积核大小、网络深度、训练集等方面对原始DnCNN进行了改进,使其适用于低频和沙漠区地震资料非高斯噪声的抑制。Dong等[26]在此基础上,采用自适应DnCNN算法对沙漠地震资料进行去噪处理,有效提高了低频资料的信噪比。Yang等[17]扩展了原有的DnCNN模型,构造了地震数据随机噪声衰减的卷积神经网络(CNN for Randon Noise Attenuation of Seismic Data, SDACNN),将激活函数替换为指数线性单元(Exponential Linear Units,ELU)以增强网络的鲁棒性。以上方法均可以归结为基于DnCNN模型及其改进的去噪方法,而DnCNN仅关注时域的特征提取,忽略了数据在频域的特征,导致去噪地震数据中纹理特征损失较大。地震数据中同相轴的纹理特征是判断油气贮藏位置的关键,若考虑结合频域的特征,可在一定程度上抑制假频、使纹理保持效果得到较大的提升。Zhang等[19]和Chen等[20]基于无监督学习中自编码的概念,采用自编码的方式将地震数据降维以提取主要特征,再通过上采样层恢复到原尺寸,自适应地学习有效信号,实现无监督的地震数据随机噪声抑制,取得了较好的效果,但也忽略了地震数据在频域的特征,性能仍存在较大的提升空间。
Liu等[27]提出的多级小波卷积神经网络(Multi-level Wavelet CNN,MWCNN)模型考虑图像的小波域分布特性,提出一种多级小波CNN框架,将离散小波变换与卷积网络结合,充分考虑了图像的频域特征。Zhu等[28]利用短时傅里叶变换(Short-time Fourier Transform,STFT)将时域数据转化为频域数据,将实部和虚部传入卷积神经网络,网络根据输入数据产生信号和噪声掩膜,再利用相关掩膜进行估计,得到地震信号和噪声的频域系数,最后利用逆STFT得到时域去噪信号和噪声。以上两种方法的卷积处理过程仅在频域中进行,忽略了时域的特征,因此在地震数据能量较弱的区域,无法仅根据有限的特征判别真实数据和噪声数据,从而导致局部纹理模糊的现象。
(2) 使用的卷积核通常为较小的固定尺寸,提取地震数据的特征信息不充分,影响感受野大小。相同条件下,如果想得到相同范围的感受野就只能增加网络深度,但网络深度的增加会使提取的特征越来越高级,导致地震数据丢失较多的细节信息。例如Zhang等[16]、韩卫雪等[22]和其他部分学者基于DnCNN模型的改进[23-26]均使用固定大小为3×3的卷积核,学习到的噪声不充分,且具有较深的层数,容易造成过拟合现象。由于没有充分权衡卷积核大小与网络深度之间的关系,容易出现训练时间较长和细节信息丢失的问题。李传朋等[29]的去噪卷积神经网络模型采用3×3与5×5的卷积核相结合的方法,去噪效果明显提高。
针对上述问题,本文提出基于联合深度学习的地震数据随机噪声压制方法。首先,地震数据随机噪声压制模型结合时域和频域特征,利用联合误差定义损失函数,综合描述不同空间中地震数据的特征;其次,考虑到地震数据中包含复杂的地质结构和较强的非局部自相似性,采用一种扩充卷积的方式,利用多种尺寸的卷积核提取特征,增加地震数据特征提取的多样性,增大感受野,减少网络过拟合,提高收敛速度;再次,模型利用残差网络不断提取每层网络的噪声特征, 将噪声从含噪数据中分离出来;最后,网络利用批归一化(Batch Normalization,BN)算法实行归一化,进一步提高地震数据去噪效果。
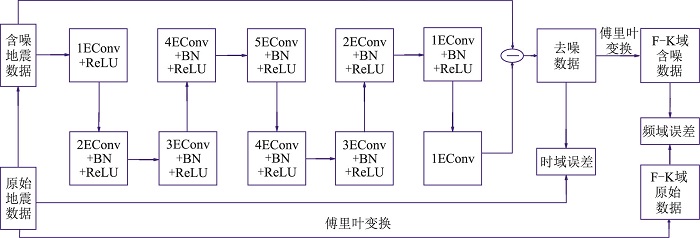
1 方法原理 1.1 网络模型结构本文提出的网络模型结构如图 1所示,输入含噪地震数据y=x+v,其中x为不含噪地震数据,v为随机噪声。引入残差学习的思想,通过训练得到原始地震数据的估计
|
图 1 网络模型结构图 |
模型中还包括BN(Batch Normalization,批量归一化)层和修正线性单元(Rectified Linear Unit,ReLU)。模型的深度为10层,第1层由EConv和ReLU组成,EConv扩充因子为1,即卷积核大小为3×3,用于提取含噪地震数据的特征,卷积处理后得到128个特征映射。ReLU激活函数用于执行非线性映射,去除地震数据中的冗余,尽可能保留噪声数据的主要特征。第2层至第9层分别由EConv、BN和ReLU组成,EConv扩张因子依次为2、3、4、5、4、3、2、1,对应卷积核大小分别为5×5、7×7、9×9、11×11、9×9、7×7、5×5、3×3,每层卷积处理后都得到128个特征映射,用于加快并稳定训练过程, 提升去噪性能。第10层由EConv组成,扩充因子为1,卷积核大小为3×3,卷积操作后得到1个特征映射,即为残差网络学习到的噪声。
针对地震数据去噪的特点,模型具体思路及设计如下:
(1) 联合时、频域的损失函数。由于当前大多数基于深度学习的去噪模型忽略时域与频域的联系,导致数据纹理细节损失较大。本文充分考虑时域和频域的特征,将傅里叶变换与卷积神经网络相结合,利用时域和频域联合误差定义损失函数,改善去噪效果,消除假频。
(2) 扩充卷积。为了平衡卷积核大小与网络深度之间的关系,采用扩充卷积的方式,在保留了传统3×3卷积优点的基础上,通过调整扩充因子增加感受野。从第1层至第10层,扩充因子分别设置为1、2、3、4、5、4、3、2、1、1,网络各层感受野大小分别为3、7、13、21、31、39、45、49、51、53。相同条件下,Dn-CNN模型如果达到大小为53的感受野,则需要26层的网络深度,但网络层数过多会导致丢失较多的细节信息。
(3) 残差网络学习。由于网络的输入与输出具有很强的相似性,残差学习更适合于地震数据的去噪。网络模型通过提取大量含噪数据样本学习噪声的特征,将含噪数据与所学到的噪声相减,得到去噪后地震数据。
(4) 输入、输出尺寸保持一致。在卷积操作过程中,由于卷积计算的特点,逐层卷积会使特征图越来越小,特征表示能力也越来越弱,还会导致最后的数据边界引入噪声。本文提出的模型在每次卷积操作前,均对待处理数据用0扩充边界,确保每层输出的特征图与输入保持相同尺寸。
1.2 联合损失函数的构造目前基于深度学习的图像去噪优化函数往往采用均方误差(Mean Squared Error,MSE)损失函数。本文在时域MSE的基础上,引入傅里叶域MSE联合设计损失函数,其中MSE定义为去噪数据与原始不含噪声数据的均方误差,即
| $ {\rm{MSE}} = \frac{1}{n}\sum\limits_{i = 1}^n {{\rm{ sum }}} {({\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{\hat x}}_i})^2} $ | (1) |
式中:n为样本数量;xi为第i个原始不含噪地震数据,即为时域训练目标;
神经网络模型的目标函数为联合时域和频域的最小化损失函数,即
| $ {\rm{loss}} = \frac{1}{n}\sum\limits_{i = 1}^n {{{({\mathit{\boldsymbol{x}}_i} - {{\mathit{\boldsymbol{\hat x}}}_i})}^2}} + \frac{1}{n}\sum\limits_{i = 1}^n {{{(\mathit{\boldsymbol{x}}_i^{\rm{f}} - \mathit{\boldsymbol{\hat x}}_i^{\rm{f}})}^2}} $ | (2) |
式中:xif为xi经过傅里叶变换后的频域训练目标;
卷积神经网络特征提取的核心在于通过卷积核与图像卷积运算提取特征。传统二维卷积运算的数学定义为
| $ \mathit{\boldsymbol{s}}(i,j) = \sum\limits_p {\sum\limits_q \mathit{\boldsymbol{z}} } (i - p,j - q)\mathit{\boldsymbol{\omega }} (p,q) $ | (3) |
卷积操作需经过180°旋转,然后对应位置相乘并求和。卷积神经网络中的二维卷积运算与传统二维卷积的算法原理相同,在实现的方式上略有不同,不需要旋转,直接对相应位置相乘并求和,即
| $ \mathit{\boldsymbol{s}}(i,j) = \sum\limits_p {\sum\limits_q \mathit{\boldsymbol{z}} } (i + p,j + q)\mathit{\boldsymbol{\omega }}(p,q) $ | (4) |
式(3)和(4)中:z是卷积层的输入数据矩阵;ω是卷积核;p、q分别表示卷积核的高度和宽度;i、j代表卷积操作后像素点的位置。
为了增加特征信息提取的多样化,采用扩充卷积的方式获得更多特征信息,并为网络提供更大的感受野,从而在噪声压制过程中充分利用地震数据的非局部自相似性,保留更多地震数据内部的有效信息。扩充卷积通过增加每层的卷积核尺寸以增加感受野,定义卷积核的宽和高均为(2r+1)。结合扩充卷积后的卷积操作表示为
| $ \begin{array}{l} \mathit{\boldsymbol{s}}(i,j) = \sum\limits_{2r + 1} {\sum\limits_{2r + 1} \mathit{\boldsymbol{z}} } (i + 2r + 1,j + 2r + 1) \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{\omega }}(2r + 1,2r + 1) \end{array} $ | (5) |
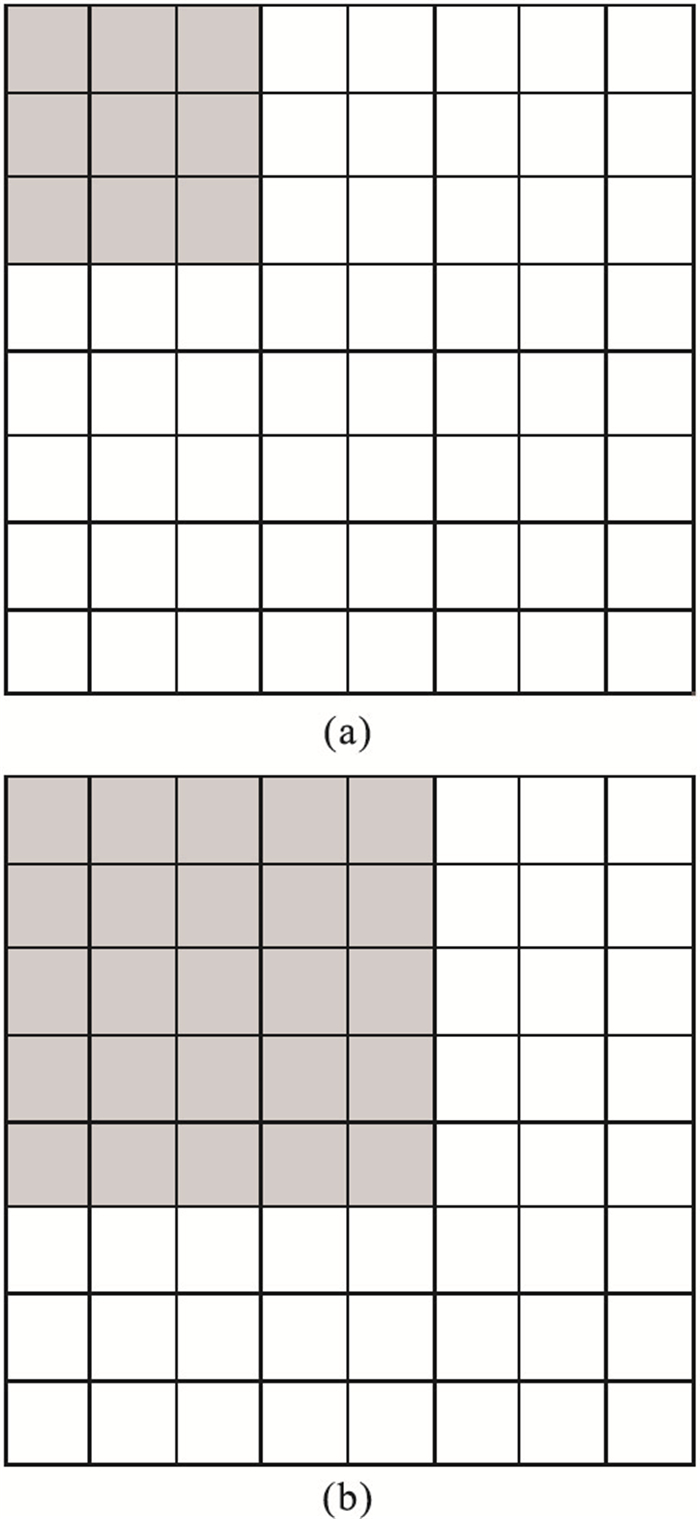
传统卷积与扩充卷积的操作对比如图 2所示,扩充卷积每层的感受野大小为
| $ G(i) = [G(i - 1) - 1] \times {\rm{stride}}(i) + c(i) $ | (6) |
|
图 2 经典卷积(a,卷积核大小为3×3)与扩充卷积(b,扩充因子为2,卷积核大小增至5×5)对比 |
式中:stride(i)为第i层卷积操作的步长;c(i)为第i层卷积核尺寸大小。
2 模型测试选择Marmousi模型数据测试本文方法。将Marmousi模型数据裁剪得到10000个300个采样点×207道的切片数据x,将数据集分别按照80%、10%、10%的比例划分为训练集、验证集、测试集。地震数据的随机噪声通过0均值正态分布的高斯随机噪声仿真,噪声的标准差与原始地震数据的标准差成正相关。噪声标准差定义为
| $ \sigma = l\sqrt {\frac{1}{{MN}}\sum\limits_{i = 1}^M {\sum\limits_{s = 1}^N {{{({\mathit{\boldsymbol{x}}_{t,s}} - u)}^2}} } } $ | (7) |
式中:M为切片时间采样总数;N为切片地震道采样总数;xt, s为x中坐标为(t, s)的元素,t为时间采样序号;s为地震道记录序号;u为地震数据x的均值;l为噪声强度的比例因子。
去噪效果的衡量指标可采用峰值信噪比(Peak Signal to Noise Ratio,PSNR)、信噪比(Signal Noise Ratio,SNR)或结构相似性(Structural Similarity Index,SSIM),对应表达式为
| $ {\rm{PSNR}} = 10\lg \frac{{{\rm{max}}({\mathit{\boldsymbol{x}}^2})}}{{{\rm{MSE}}}} $ | (8) |
| $ {\rm{SNR}} = 10{\rm{lg}}\frac{{\sum\limits_{t = 1}^M {\sum\limits_{s = 1}^N {{{({\mathit{\boldsymbol{x}}_{t,s}})}^2}} } }}{{\sum\limits_{t = 1}^N {\sum\limits_{s = 1}^N {{{({\mathit{\boldsymbol{x}}_{t,s}} - {{\mathit{\boldsymbol{\hat x}}}_{t,s}})}^2}} } }} $ | (9) |
| $ {\rm{SSIM}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{\hat x}}) = \frac{{(2{u_\mathit{\boldsymbol{x}}}{u_{\mathit{\boldsymbol{\hat x}}}} + {C_1})(2{\sigma _{\mathit{\boldsymbol{x\hat x}}}} + {C_2})}}{{({u_\mathit{\boldsymbol{x}}}^2 + {u_{\mathit{\boldsymbol{\hat x}}}}^2 + {C_1})({\sigma _\mathit{\boldsymbol{x}}}^2 + {\sigma _{\mathit{\boldsymbol{\hat x}}}}^2 + {C_2}){\rm{ }}}} $ | (10) |
式(8)~式(10)中:max(x2)表示求取矩阵x2中最大的元素;ux和
在训练过程中,学习率初始设定为0.001,采用Adam算法优化学习目标,根据前一次迭代的误差调整学习率的大小,提高收敛速度与逼近效果。Epoch设置为50次,批大小设置为20,网络的输入、输出尺寸均为300×207。实验硬件平台采用Intel I7、8核CPU,内存为32G,GPU为GeForce RTX 2080 SUPER。操作系统为64位Ubuntu 18.04 LTS,软件平台采用Python 3.6环境,联合深度学习框架使用Pytorch1.2搭建。
2.1 网络层次结构分析为证明本文提出网络模型的有效性,分别对时频域联合损失函数、扩充卷积、残差学习策略、BN层的作用进行测试。
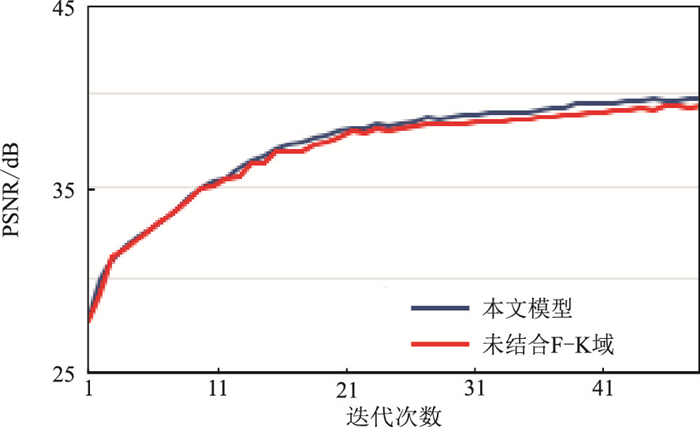
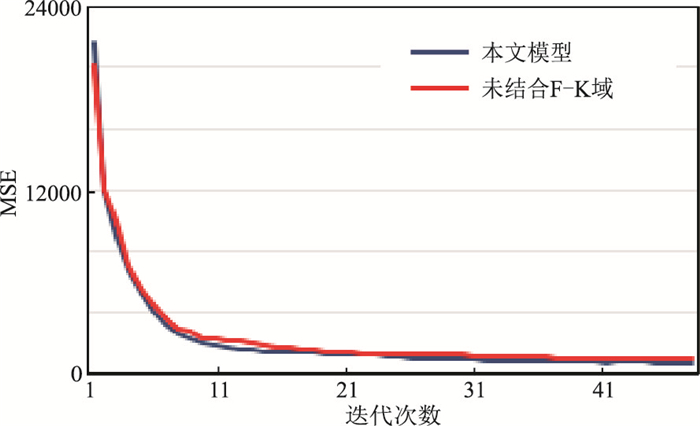
2.1.1 时频域联合损失函数将未结合F-K域损失函数的模型与本文模型(结合F-K域损失函数)对比测试(迭代50次)。本文模型的PSNR稍高于未结合F-K域损失函数(图 3);两个模型的训练过程均具有稳定的收敛性能,且本文模型的MSE略低于未结合F-K域损失函数模型,去噪效果的误差更小(图 4)。
|
图 3 不同模型计算误差函数的PSNR对比 |
|
图 4 不同模型计算误差函数的MSE对比 |
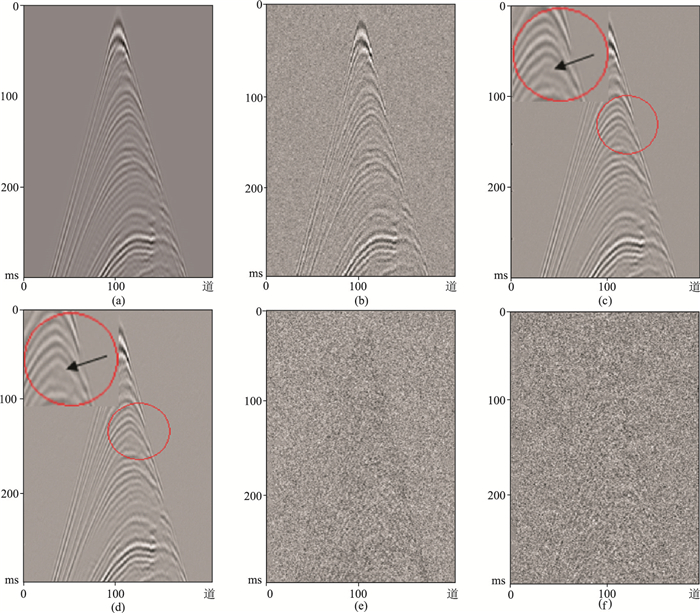
图 5为同一样本在两种模型下的去噪效果图。对比图 5c与图 5d可见,结合F-K域误差模型的去噪结果,在图中圆形区域内同相轴更光滑,表明联合F-K域计算损失函数模型的纹理保持效果优于单一时域的误差模型。另外,测试集的去噪效果(图 5d)与图 3中训练集稳定时的PSNR很接近,拟合效果较好。从PSNR、SSIM、SNR的评价指标来看,也说明本文模型较单一时域的误差模型噪声压制效果更好。图 5e和图 5f分别为未结合F-K域计算损失函数的残差剖面和本文模型的残差剖面,前者的残差还保留部分原始地震数据的纹理,而本文算法的残差更接近真实的随机噪声。
|
图 5 不同模型去噪效果对比图 (a)原始地震数据;(b)加入l为0.05的高斯随机噪声后的地震数据;(c)未结合F-K域计算损失函数的去噪结果;(d)结合F-K域计算损失函数的去噪结果;(e)未结合F-K域计算损失函数的残差剖面;(f)结合F-K域计算损失函数的残差剖面图c和图d的左上方较大圆形区域为中间较小圆形区域的放大展示。图c中:PSNR=39.0700dB,SNR=33.1892dB,SSIM=0.8553。图d中:PSNR=39.6300dB,SNR=33.7171dB,SSIM=0.8920 |
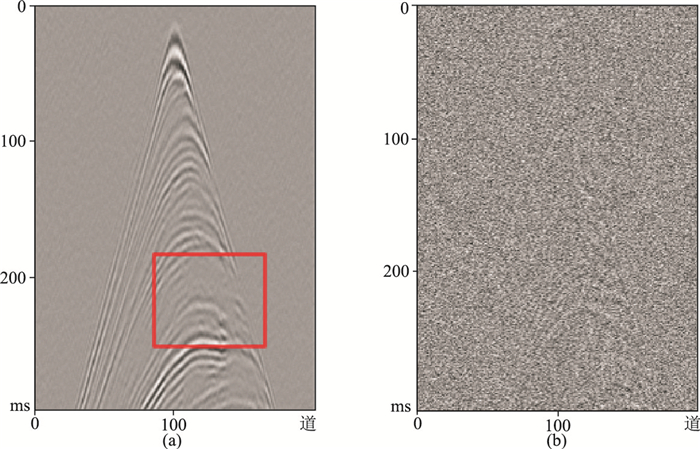
此外,将仅含F-K域损失函数的模型与本文模型对比实验,含噪地震数据如图 5b所示,图 6a为仅含F-K域计算目标函数的噪声压制效果,可见其PSNR、SNR和SSIM值均低于联合目标函数。由于无法仅根据有限的特征判别真实数据和噪声数据,导致地震数据能量较弱的区域(矩形标记区域)中的同相轴信息的丢失。相比本文模型的残差剖面(图 5f),仅含F-K域计算目标函数的残差剖面(图 6b)包含较强的有效信号,说明对有效信号的保护效果不够理想。
|
图 6 仅含F-K域计算目标函数的去噪结果(a)和残差剖面(b) 图a中:PSNR=36.6800dB,SNR=29.3225dB,SSIM=0.8130 |
将3×3的经典卷积核与本文所提出的模型对比测试。在网络深度均为10层的前提下,扩充卷积的感受野大小为53×53,传统3×3卷积的感受野大小则为21×21。若欲使传统的3×3卷积得到相同范围的感受野,则需要将网络深度扩展到26层。因此采用三种不同的策略对比实验,策略A为卷积核大小为3×3的10层网络模型;策略B为本文所提出的网络模型;策略C为卷积核大小为3×3的26层网络模型。
在l为0.03的条件下,训练过程中PSNR收敛情况如图 7a所示,策略A和策略B模型分别训练23和30次达到收敛状态,而策略C需要训练37次才能达到收敛状态。相比之下,前两者的训练时间效率更高。另外,通过对比三者PSNR,发现本文网络模型在训练集上最终收敛的PSNR为44dB,比策略A的PSNR约提高3dB。在测试集上,本文模型的平均PSNR为42.3dB,比策略A的PSNR平均约提高2.4dB。

|
图 7 不同网络结构模型训练PSNR (a)和MSE(b)对比 |
在l为0.03的条件下,训练过程中MSE收敛情况如图 7b所示,可见相比于策略A和策略B,策略C的MSE曲线波动更剧烈且不稳定。相比于策略A,本文网络模型的MSE曲线在训练达到稳定时的误差更小,去噪效果更好。
实验表明,扩充卷积的优势在于通过设置扩充因子增大感受野。从扩充因子的设定方面考虑,对比4组不同的扩充因子设置方案,包括对称的扩充因子设置(r=1、2、3、4、5、4、3、2、1、1,记为策略D;r=3、3、2、2、1、1、2、2、3、3,记为策略E)和非对称的扩充因子设置(r=1、1、2、2、3、3、4、4、5、5,记为策略F;r=1、2、3、4、5、6、7、8、9、10,记为策略H),收敛情况的对比结果如图 8所示。由图可见,对称式扩充因子的设置明显优于非对称设置,扩充因子的对称设置使模型收敛较快,并且训练趋于稳定时的PSNR也较高,表明对称式的特征提取更适用于地震数据的去噪。此外,在两组对称式的扩充因子设置方案中,策略D优于策略E,原因在于不同的扩充因子决定了不同尺度的卷积核大小,多种类的扩充因子增加了特征提取的多样性,使地震数据中的噪声提取更充分。

|
图 8 各组扩充因子模型的收敛情况对比 |
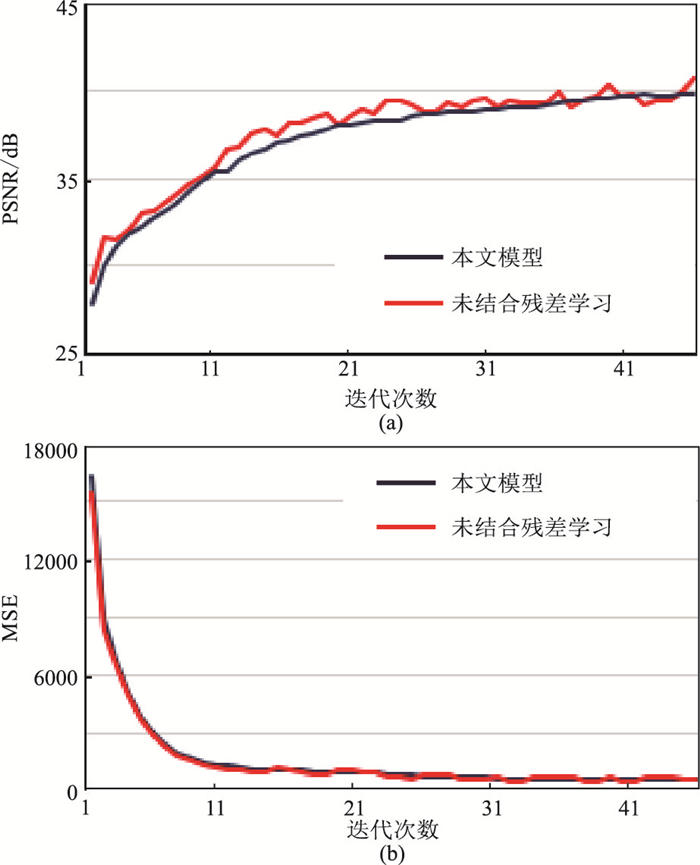
将不含残差学习的模型与本文所提模型对比实验。在l为0.05的情况下,不含残差学习的模型的PSNR曲线有多处剧烈波动,呈锯齿形上升;本文模型的PSNR曲线更稳定、更快地收敛(图 9a)。
|
图 9 有、无残差学习模型的PSNR(a)与MSE(b)对比 |
图 9b为模型有、无残差学习的MSE对比图,可见随着迭代次数的增加,两模型的MSE均逐渐降低,但不含残差学习模型较本文模型波动更为剧烈且收敛更慢。
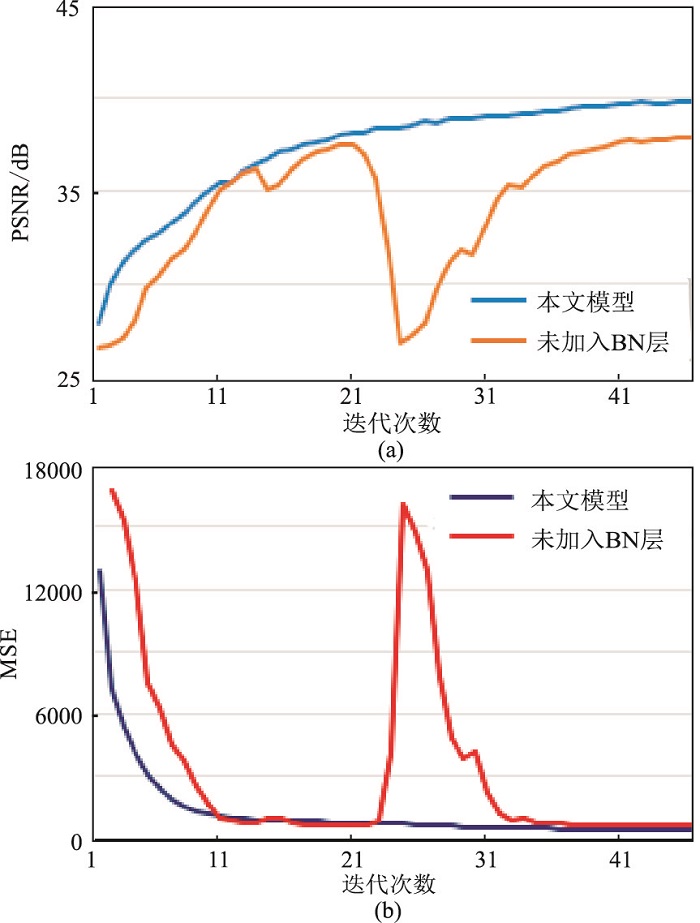
2.1.4 残差网络中加入BN层将不含BN层的模型与本文所提模型对比实验。在l为0.05的情况下,不含BN层的模型的PSNR曲线波动剧烈而且收敛较慢;相反,本文模型的PSNR曲线更稳定、收敛更快(图 10a),并且本文模型在测试集上的平均PSNR值比前者高约1.9dB。
|
图 10 有、无BN层模型的PSNR(a)与MSE(b)对比 |
图 10b为模型有、无残差学习的MSE对比,可见不含BN层模型的MSE曲线波动剧烈且不稳定,而本文模型的MSE曲线更稳定地收敛。
2.1.5 网络模型的部分特征图分析为了分析模型去噪的中间环节的运行状态,任选一批测试集中的一个样本在去噪过程中的部分特征如图 11所示。原始Marmousi地震数据切片为图 5a,加入l为0.05的高斯随机噪声后的地震数据如图 5b,图 11a为经过第1层(EConv+ReLU)中128个3×3的卷积核处理得到的特征图。可以看出每个卷积核学习到不同的特征,由于是网络第1层提取的特征,其中保留一些较为微弱且连续的原始地震数据的同相轴信息。经过第2~第9层(EConv+BN+ReLU)处理后,又分别得到128个特征图,其中EConv扩张因子分别为2、3、4、5、4、3、2、1,对应的卷积核大小分别为5×5、7×7、9×9、11×11、9×9、7×7、5×5、3×3。截取第4层和第8层提取的特征图,由图可见经过4层卷积处理后(图 11b),同相轴信息被认为是有效信号不再被提取,卷积核提取的是含有地震数据大致轮廓的含噪特征图;经过8层卷积提取(图 11c),模型得到的几乎全是噪声,不再含有原始数据的轮廓和同相轴等有效信息。为了清楚显示特征提取的效果,将第2层、4层、6层、8层的第1个卷积核提取的特征图放大展示(图 12a~图 12d),可以看出模型从浅层学习提取的特征包含有效信号到深层特征仅包含噪声的变化过程。在此基础上,经过第10层EConv处理后,得到1个特征图(图 12e),对应扩充因子为1、卷积核大小为3×3,该特征图即为残差网络学习到的所有噪声。最后将原始含噪声的地震数据与网络模型学习到的残差相减,得到该网络模型的最终输出结果(图 12f),即去噪后的地震数据。

|
图 11 网络模型去噪过程中经过不同层网络后的特征图 (a)第1层;(b)第4层;(c)第8层 |

|
图 12 部分特征图的放大展示 (a)第2层第1个卷积核提取的特征;(b)第4层第1个卷积核提取的特征;(c)第6层第1个卷积核提取的特征;(d)第8层第1个卷积核提取的特征;(e)经过第10层网络后得到的特征;(f)最终去噪结果 |
将本文提出的网络模型与Curvelet变换、DCT超完备字典、K-SVD自适应学习超完备字典、Dn-CNN的噪声压制效果进行对比。
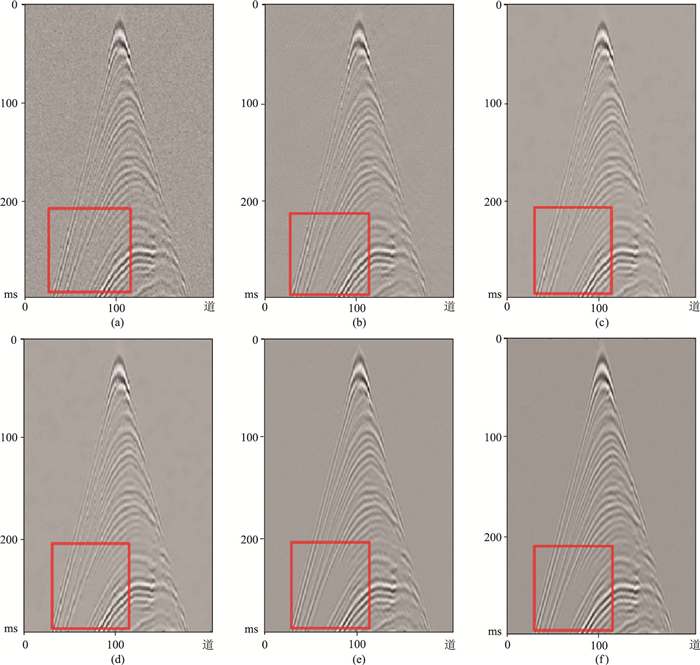
2.2.1 相同强度随机噪声情况任选一个Marmousi地震数据样本,原始数据如图 5a所示,图 13a为加入l为0.03的高斯随机噪声后的地震数据,其中矩形标记区域中的同相轴信息被噪声严重干扰。对图 13a分别运用Curvelet变换、DCT字典、K-SVD字典、DnCNN以及本文算法进行噪声压制,并对比效果。
|
图 13 不同去噪算法在相同强度高斯随机噪声下的去噪效果对比 (a)加入l为0.03的高斯随机噪声后地震数据;(b)Curvelet变换;(c)DCT超完备字典;(d)K-SVD自适应学习超完备字典;(e)DnCNN方法;(f)本文方法 |
图 13b为Curvelet变换稀疏表示后的去噪效果,由于Curvelet变换适用于分析二维信号中的曲线边缘特征,在地震数据处理领域应用比较广泛,可以看出地震数据中部分噪声得到了压制,但仍存在大量噪声。
图 13c为DCT字典学习的去噪效果,地震数据被划分成可重叠且固定大小的数据块以保持局部特征,可见去噪效果得到改善,但由于单一的DCT基不能自适应地反映图像的局部特征,因此矩形标记区域中的部分同相轴信息被当成噪声去除。
图 13d为基于K-SVD自适应学习的超完备字典稀疏表示去噪效果,在DCT变换的基础上构造的超完备冗余字典,有效地捕捉了主要特征,进一步提高了去噪效果,但K-SVD算法不考虑数据块之间的相似性,导致数据块边界与局部波形变化剧烈的地震道失真。
图 13e为基于深度学习的DnCNN去噪效果,通过利用大量的样本覆盖待处理数据的特征,采用多层卷积、非线性映射等方式提取数据时域的特征,不断调整网络模型直至找到一个使误差最小的参数。该方法虽然效果有大幅提升,但由于仅关注时域特征,在地震数据能量较弱的区域无法仅根据有限的特征判别真实数据和噪声数据,导致矩形标记区域中的同相轴信息的丢失。
图 13f为本文算法去噪效果,结合F-K域计算损失函数,从时域和频域联合考虑误差,改善噪声去除的效果,采用扩充卷积增加地震数据特征提取的多样性,减少了地震数据细节的丢失。可以看出,与DnCNN去噪算法相比,本文算法细节损失明显减弱,同相轴纹理也更加清晰。
以上不同方法去噪后的PSNR、SNR、SSIM对比如表 1所示。可见本文方法较其他同类方法去噪效果更好。另外,分析有效信号的保护效果。各种去噪方法的残差剖面如图 14所示。原始数据如图 5a所示,图 14a为加入l为0.03的高斯随机噪声后的残差剖面,图 14b~图 14d分别为Curvelet变换、DCT超完备字典、K-SVD自适应学习超完备字典噪声压制后的残差剖面,这三种方法均包含随机噪声和较强的信号,对有效信号的保护效果不理想。图 14e为DnCNN噪声压制后的残差剖面,可见信号保护的效果已有明显提升。图 14f为本文算法噪声压制后的残差剖面,较前面四种去噪方法而言,有效信号保护能力最强。
|
|
表 1 不同方法去噪效果对比 |

|
图 14 不同去噪算法在相同强度高斯随机噪声下的残差剖面对比 (a)加入l为0.03的高斯随机噪声后;(b)Curvelet变换噪声压制后;(c)DCT超完备字典噪声压制后;(d)K-SVD自适应学习超完备字典噪声压制后;(e)DnCNN噪声压制后;(f)本文方法噪声压制后 |
为对比不同算法对不同强度噪声的适应性,表 2列出了不同算法在加入较低强度高斯随机噪声(l为0.01~0.08)条件下噪声压制后的SNR对比,可见本文算法优于其他算法的噪声压制效果。
|
|
表 2 不同算法在加入较低强度高斯随机噪声下噪声压制后的SNR对比 |
表 3为不同算法在加入较高强度高斯随机噪声(l为0.1~0.8)下噪声压制后的SNR对比,可见当l小于0.3时,本文算法比其他算法的去噪效果更好;当l大于0.3时,由于噪声较强,大部分有效地震数据被噪声淹没,导致各种算法的去噪效果均不理想,尤其是Curvelet变换采用的硬阈值处理方法,去噪效果较差。本文算法与DCT、K-SVD、DnCNN的噪声压制效果比较接近。
|
|
表 3 不同算法在加入较高强度高斯随机噪声下噪声压制后的SNR对比 |
分别在原始数据加入不同强度的噪声作为训练数据,将训练保存好的模型应用于不同强度噪声的测试集上,以加入l为0.01~0.08的高斯随机噪声为例,对比训练数据不同的噪声强度对结果的影响(表 4)可以看出如下特点。
|
|
表 4 不同强度噪声的训练数据对测试数据噪声压制后的SNR对比 |
(1) 以原始数据加入l=0.03噪声等级的测试集为例(表 4中l=0.03的列),采用l=0.03强度的噪声训练的网络取得了该列中最高的SNR值,该列的其他训练噪声强度因子l=0.02、0.04、0.05的训练集得到的网络,去噪效果比较接近。
(2) 以l=0.03噪声等级的训练集为例(表 4中l=0.03的行),该模型不仅对l=0.03的噪声强度去噪有效,对l=0.02、0.04的噪声强度也表现出了较好的去噪效果。因此本文算法对于测试集噪声分布与训练集分布较为接近时具有一定的泛化能力。
3 实际资料处理 3.1 数据训练为了进一步说明本文算法的噪声压制效果,以实际地震数据为样本测试不同去噪算法(图 15)。

|
图 15 任意样本及训练效果展示 (a)原始地震数据;(b)加入强度l为0.03的高斯随机噪声后数据;(c)第50次迭代训练的去噪结果;(d)第50次迭代训练去噪后的残差剖面。图b和图c的PSNR、SNR、SSIM分别为27.4771dB、23.2793dB、0.6185和41.85162dB、37.4036dB、0.9578 |
为了提高训练效率与特征提取的精度,在原始地震数据的基础上进行了裁剪处理,得到2000个300个采样点×500道的切片数据。为了减少单个样本特征的复杂程度,在实际训练过程中,对其中1800个样本进一步处理,均以50个道为间距平移、裁剪得到7个200道×300个采样点的切片数据,共得到12600个样本,其中训练集包含11200个样本,验证集包含1400个样本,其余的200个尺寸为300个采样点、500道的切片数据作为测试集。训练过程中学习率初始设定为0.001,采用Adam算法优化学习目标,Epoch设置为50次,批量大小设置为20。
为说明本文算法对训练数据库样本去噪的训练效果,在第50次迭代中任意选取一个样本进行展示(图 15)。图 15a为原始地震数据,图 15b为加入l为0.03的高斯随机噪声后的地震数据,图 15c为第50次迭代训练后的去噪效果。通过评价指标SNR和SSIM可以看出,本文模型在实际数据的训练阶段具有较强的噪声压制效果。图 15d为第50次迭代训练去噪效果的残差剖面,可以看出本文模型具有较强的有效信号保护与随机噪声逼近能力。
3.2 数据测试为充分测试本文算法对实际地震数据的适用性,选取了两组实际数据,第一组为经过噪声压制预处理的实际数据,第二组为原始实际数据。
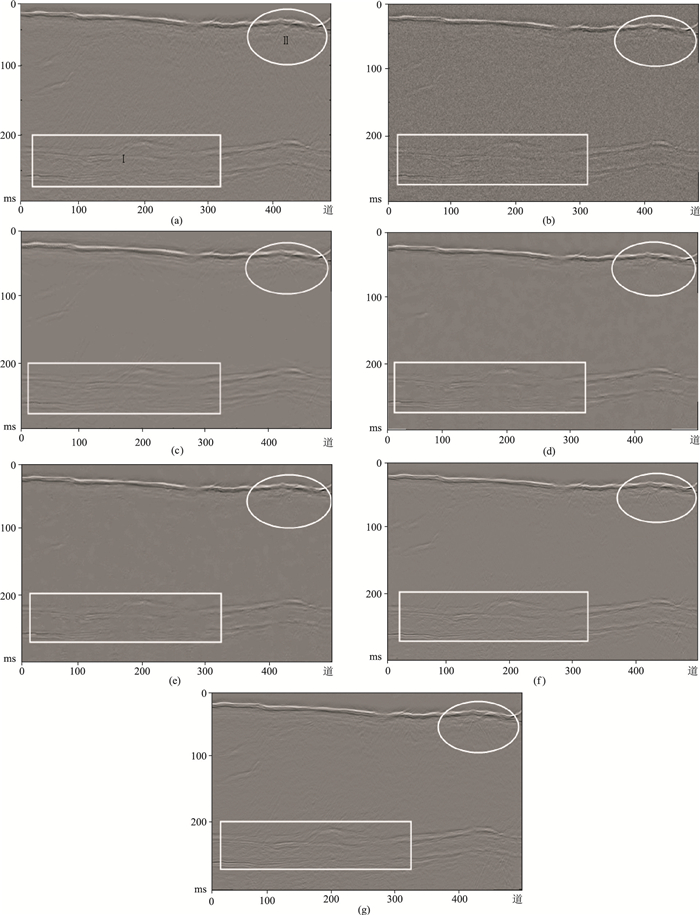
3.2.1 经过预处理的实际数据实验为了说明本文算法对测试数据库样本的去噪效果,在测试数据库中任意选取一个经过预处理的实际地震数据样本如图 16a所示,其中矩形标记区域(记为Ⅰ区域)中的数据同相轴较密集且特征明显,而椭圆形标区域(记为Ⅱ区域)中的数据能量较弱且特征不明显。加入强度l为0.03的高斯随机噪声后的地震数据如图 16b所示,受噪声的影响,Ⅰ区域同相轴变得模糊且不连续,而Ⅱ区域内能量弱的部分几乎不能直观看出原始数据的特征。图 16c为Curvelet变换噪声压制效果,可以看出Ⅰ区域同相轴的边缘得到了较好的恢复,但Ⅱ区域的特征被看成是噪声,导致有效信号和噪声一起被压制。图 16d为DCT超完备字典噪声压制效果,Ⅰ区域同相轴不密集并且Ⅱ区域的纹理细节丢失。图 16e为K-SVD自适应学习超完备字典噪声压制效果,同DCT的噪声压制效果类似。图 16f为DnCNN噪声压制效果,训练数据集的噪声强度l的覆盖范围为0.03~0.10,以提高模型在该区间的泛化能力,训练好的网络模型记为G1,可以看出Ⅰ区域同相轴连续且细节信息保持较好,Ⅱ区域出现细节丢失的现象。图 16g为本文算法噪声压制效果,采用与G1模型相同的训练数据集,训练好的网络模型记为G2,由于采用扩张卷积充分提取噪声特征,使Ⅰ区域和Ⅱ区域都保留了较好的细节信息,和原始地震数据的相似度最高。以上方法去噪后的PSNR、SNR、SSIM对比如表 5所示。
|
图 16 不同方法对预处理后实际数据的噪声压制效果对比 (a)预处理后原始叠后海洋地震数据;(b)加入l为0.03的高斯随机噪声后数据;(c)Curvelet变换方法;(d)DCT超完备字典方法;(e)K-SVD自适应学习超完备字典方法;(f)DnCNN方法;(g)本文方法 |
|
|
表 5 不同方法去噪后的PSNR、SNR、SSIM对比 |
在测试数据库中任意选取原始的实际地震数据样本如图 17a所示,红色矩形Ⅰ区域中的地震数据同相轴较密集且特征明显;红色矩形Ⅱ区域中的地震数据信息被噪声淹没,无法识别;红色矩形Ⅲ区域中的同相轴受噪声影响,连续性较差。经过Curvelet变换噪声压制后(图 17b),Ⅱ区域和Ⅲ区域同相轴的边缘得到了较好的恢复,总体上虽然抑制了一些噪声,但Ⅰ区域中仍含有大量噪声,去噪效果不够明显。经过DCT超完备字典噪声压制后(图 17c),Ⅰ区域和Ⅲ区域中同相轴信息得到了较好的恢复,去噪效果比较明显,但Ⅱ区域中的有效信号和噪声一起被压制,导致纹理细节的丢失。经过K-SVD自适应学习超完备字典噪声压制后(图 17d),同DCT的噪声压制效果类似。图 17e和图 17f分别为网络模型G1和G2应用于实际数据的噪声压制效果,因为模型G1和G2的训练数据集覆盖了强度l从0.03到0.10的噪声等级,所以两模型可以学习到该区间的噪声特征分布,进而对原始实际数据中的随机噪声进行去噪处理。从图 17e中可以看出,Ⅰ区域和Ⅲ区域同相轴连续且细节信息保持较好,Ⅱ区域中的纹理特征较DCT超完备字典和K-SVD自适应学习超完备字典噪声压制更明显,但依然存在着细节丢失的现象。从图 17f中可以看出,Ⅰ区域和Ⅲ区域中的噪声得到了很好地抑制,均保留了清晰且连续的同相轴信息,易于观测,Ⅱ区域的细节信息也得到了较好的恢复,因此模型G2的去噪效果更优于模型G1。

|
图 17 原始实际数据不同方法噪声压制结果对比 (a)原始叠后地震数据;(b)Curvelet变换方法;(c)DCT超完备字典方法;(d)K-SVD自适应学习超完备字典方法;(e)DnCNN方法;(f)本文方法 |
本文提出了一种新的基于联合深度学习的地震数据随机噪声压制方法,联合时域与频域的信息,定义损失函数,加强地震数据细节的保持,改善了噪声去除的效果。通过研究卷积核大小和网络深度对感受野大小的影响,采用扩充卷积,设置扩充因子,并通过实验确定了最优的一组扩充因子,增加了地震数据特征提取的多样性,减少复杂的地震道数据噪声压制过程中细节的丢失。此外,本文方法还考虑了网络输入与输出数据具有相似性的特点,引入残差学习策略学习噪声,在此基础上,加入BN层加快训练收敛,提高地震数据去噪效率。分别通过模型数据和实际数据与当前比较流行的随机噪声压制算法对比表明,在噪声压制效果方面,本文去噪模型可获得更高的信噪比和局部细节特征的保持能力;在噪声压制效率方面,本文模型在测试过程不需要迭代学习,运行效率较高;在算法泛化能力方面,本文模型在测试噪声强度与训练集接近的情况下具有一定的泛化能力。综上所述,该模型可有效地处理地震数据随机噪声压制问题。
| [1] |
张军华, 吕宁, 田连玉, 等. 地震资料去噪方法综合评述[J]. 石油地球物理勘探, 2005, 40(增刊1): 121-127. ZHANG Junhua, LYU Ning, TIAN Lianyu, et al. A comprehensive review of seismic data denoising me-thods[J]. Oil Geophysical Prospecting, 2005, 40(S1): 121-127. |
| [2] |
胡天跃. 地震资料叠前去噪技术的现状与未来[J]. 地球物理学进展, 2002, 17(2): 218-223. HU Tianyue. The current situation and future of seismic data prestack noise attenuation techniques[J]. Progress in Geophysics, 2002, 17(2): 218-223. DOI:10.3969/j.issn.1004-2903.2002.02.005 |
| [3] |
关新平, 赵立兴, 唐英干. 图像去噪混合滤波方法[J]. 中国图象图形学报, 2005, 10(3): 332-337. GUAN Xinping, ZHAO Lixing, TANG Yinggan. Mixed filter for image denoising[J]. Journal of Image and Graphics, 2005, 10(3): 332-337. DOI:10.3969/j.issn.1006-8961.2005.03.013 |
| [4] |
王伟, 高静怀, 陈文超, 等. 基于结构自适应中值滤波器的随机噪声衰减方法[J]. 地球物理学报, 2012, 55(5): 1732-1741. WANG Wei, GAO Jinghuai, CHEN Wenchao, et al. Random seismic noise suppression via structure-adaptive median filter[J]. Chinese Journal of Geophysics, 2012, 55(5): 1732-1741. |
| [5] |
Alsdorf D. Noise reduction in seismic data using Fourier correction coefficient filtering[J]. Geophysics, 1997, 62(5): 1617-1627. DOI:10.1190/1.1444264 |
| [6] |
Trad D, Ulrych T, Sacchi M. Latest view of sparse Radon transforms[J]. Geophysics, 2003, 68(10): 386-399. |
| [7] |
Cao S, Chen X. The second-generation wavelet transform and its application in denoising of seismic data[J]. Applied Geophysics, 2005, 2(2): 70-74. DOI:10.1007/s11770-005-0034-4 |
| [8] |
章珂, 刘贵忠, 邹大文, 等. 二进小波变换方法的地震信号分时分频去噪处理[J]. 地球物理学报, 1996, 39(2): 265-271. ZHANG Ke, LIU Guizhong, ZOU Dawen, et al. Seismic data time-frequency domain denoising based on dyadic wavelet transform[J]. Chinese Journal of Geophysics, 1996, 39(2): 265-271. DOI:10.3321/j.issn:0001-5733.1996.02.013 |
| [9] |
高静怀, 毛剑, 满蔚仕, 等. 叠前地震资料噪声衰减的小波域方法研究[J]. 地球物理学报, 2006, 49(4): 1155-1163. GAO Jinghuai, MAO Jian, MAN Weishi, et al. On the denoising method of prestack seismic data in wavelet domain[J]. Chinese Journal of Geophysics, 2006, 49(4): 1155-1163. DOI:10.3321/j.issn:0001-5733.2006.04.030 |
| [10] |
Elad M, Aharon M. Image denoising via sparse and redundant representations over learned dictionaries[J]. IEEE Transactions on Image Processing, 2006, 15(12): 3736-3745. DOI:10.1109/TIP.2006.881969 |
| [11] |
Tang G, Ma J W, Yang H Z. Seismic data denoising based on learning-type overcomplete dictionaries[J]. Applied Geophysics, 2012, 9(1): 27-32. DOI:10.1007/s11770-012-0310-z |
| [12] |
张岩, 任伟建, 唐国维. 应用结构聚类字典学习压制地震数据随机噪声[J]. 石油地球物理勘探, 2018, 53(6): 1119-1127. ZHANG Yan, REN Weijian, TANG Guowei. Random noise suppression on seismic data based on structured-clustering dictionary learning[J]. Oil Geophysical Prospecting, 2018, 53(6): 1119-1127. |
| [13] |
张玉玺, 刘洋, 张浩然, 等. 基于深度学习的多属性盐丘自动识别方法[J]. 石油地球物理勘探, 2020, 55(3): 475-483. ZHANG Yuxi, LIU Yang, ZHANG Haoran, et al. Multiattribute automatic interpretation of salt domes based on deep learning[J]. Oil Geophysical Prospecting, 2020, 55(3): 475-483. |
| [14] |
李海山, 陈德武, 吴杰, 等. 叠前随机噪声深度残差网络压制方法[J]. 石油地球物理勘探, 2020, 55(3): 493-503. LI Haishan, CHEN Dewu, WU Jie, et al. Pre-stack random noise suppression with deep residual network[J]. Oil Geophysical Prospecting, 2020, 55(3): 493-503. |
| [15] |
王钰清, 陆文凯, 刘金林, 等. 基于数据增广和CNN的地震随机噪声压制[J]. 地球物理学报, 2019, 62(1): 421-433. WANG Yuqing, LU Wenkai, LIU Jinlin, et al. Random seismic noise attenuation based on data augmentation and CNN[J]. Chinese Journal of Geophysics, 2019, 62(1): 421-433. |
| [16] |
Zhang K, Zuo W M, Chen Y J, et al. Beyond a Gaussian denoiser:Residual learning of deep CNN for image denoising[J]. IEEE Transactions on Image Processing, 2017, 26(7): 3142-3155. DOI:10.1109/TIP.2017.2662206 |
| [17] |
Yang L Q, Chen W, Liu W, et al. Random noise attenuation based on residual convolutional neural network in seismic datasets[J]. IEEE Access, 2020, 8: 30271-30286. DOI:10.1109/ACCESS.2020.2972464 |
| [18] |
曹仰杰, 贾丽丽, 陈永霞, 等. 生成式对抗网络及其计算机视觉应用研究综述[J]. 中国图象图形学报, 2018, 23(10): 1433-1449. CAO Yangjie, JIA Lili, CHEN Yongxia, et al. Review of computer vision based on generative adversarial networks[J]. Journal of Image and Graphics, 2018, 23(10): 1433-1449. DOI:10.11834/jig.180103 |
| [19] |
Zhang M, Liu Y, Chen Y K. Unsupervised seismic random noise attenuation based on deep convolutional neural network[J]. IEEE Access, 2019, 7: 179810-179822. DOI:10.1109/ACCESS.2019.2959238 |
| [20] |
Chen Y K, Zhang M, Bai M, et al. Improving the signal-to-noise ratio of seismological datasets by unsupervised machine learning[J]. Seismological Research Letters, 2019, 90(4): 1552-1564. |
| [21] |
罗仁泽, 李阳阳. 一种基于RUnet卷积神经网络的地震资料随机噪声压制方法[J]. 石油物探, 2020, 59(1): 51-59. LUO Renze, LI Yangyang. Random seismic noise attenuation based on RUnet convolutional neural network[J]. Geophysical Prospecting for Petroleum, 2020, 59(1): 51-59. |
| [22] |
韩卫雪, 周亚同, 池越. 基于深度学习卷积神经网络的地震数据随机噪声去除[J]. 石油物探, 2018, 57(6): 862-869. HAN Weixue, ZHOU Yatong, CHI Yue. Deep lear-ning convolutional neural networks for random noise attenuation in seismic data[J]. Geophysical Prospecting for Petroleum, 2018, 57(6): 862-869. DOI:10.3969/j.issn.1000-1441.2018.06.008 |
| [23] |
Yu S W, Ma J W, Wang W L. Deep learning for denoising[J]. Geophysics, 2019, 84(6): V333-V350. DOI:10.1190/geo2018-0668.1 |
| [24] |
Wang F, Chen S C. Residual learning of deep convolutional neural network for seismic random noise attenuation[J]. IEEE Geoscience and Remote Sensing, 2019, 16(8): 1314-1318. DOI:10.1109/LGRS.2019.2895702 |
| [25] |
Zhao Y X, Li Y, Dong X T, et al. Low-frequency noise suppression method based on improved DnCNN in desert seismic data[J]. IEEE Geoscience and Remote Sensing, 2019, 16(5): 811-815. DOI:10.1109/LGRS.2018.2882058 |
| [26] |
Dong X T, Li Y, Yang B J. Desert low-frequency noise suppression by using adaptive DnCNNs based on the determination of high-order statistic[J]. Geophysical Journal International, 2019, 219(2): 1281-1299. DOI:10.1093/gji/ggz363 |
| [27] |
Liu P J, Zhang H Z, Lian W, et al. Multilevel wavelet convolutional neural networks[J]. IEEE Access, 2019, 7: 74973-74985. DOI:10.1109/ACCESS.2019.2921451 |
| [28] |
Zhu W Q, Mousavi S M, Beroza G C. Seismic signal denoising and decomposition using deep neural networks[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(11): 9476-9488. DOI:10.1109/TGRS.2019.2926772 |
| [29] |
李传朋, 秦品乐, 张晋京. 基于深度卷积神经网络的图像去噪研究[J]. 计算机工程, 2017, 43(3): 253-260. LI Chuanpeng, QIN Pinle, ZHANG Jinjing. Research on image denoising based on deep convolutional neural network[J]. Computer Engineering, 2017, 43(3): 253-260. DOI:10.3969/j.issn.1000-3428.2017.03.042 |



 董宏丽, 黑龙江省大庆市高新技术开发区发展路199号东北石油大学人工智能能源研究院, 163318。Email:
董宏丽, 黑龙江省大庆市高新技术开发区发展路199号东北石油大学人工智能能源研究院, 163318。Email: