② 东方地球物理公司物探技术研究中心, 河北涿州 072750
② Research & Development Center, BGP Inc., CNPC, Zhuozhou, Hebei 072750, China
为了采集海量地震数据并控制勘探成本,Beasley[1]提出多源地震同时激发采集技术,随后Berkhout等[2]提出并发展了混合激发采集的概念,使混采技术得到迅速发展。近年来OBN高效混采(High Efficient Blended Shooting)的发展,有效推动了“两宽一高”技术在海洋地震勘探的应用,同时大大降低了勘探成本,成为目前全球海洋地震勘探的热点技术。然而多个震源同时激发,在节省采集成本的同时,也必然产生震源间的交叉干扰,因此分离混叠交叉的邻炮干扰是高效混采必不可少的环节。
混采数据分离方法基本可以分为两类,即基于直接去噪和基于稀疏反演预测噪声的分离方法。前者利用混叠干扰在共炮域外的其他域的随机分布特点直接压制干扰,如Hoover等[3]通过衰减随机噪声压制独立同步扫描(ISS)邻炮干扰,Zhang等[4]采用加权τ-p变换压制邻炮干扰,Huo等[5]在CMP域由矢量中值滤波压制混叠干扰,王文闯等[6]利用阿尔法均值(α-trimmed)矢量中值滤波去噪,周丽等[7]提出利用自适应迭代多级中值滤波法分离海上多震源混合波场,Doulgeris等[8]提出在共检波点道集上利用频率—波数域滤波消除混叠干扰的迭代算法。上述基于去噪的混采数据分离方法效率高、成本低,但在数据混叠度较高时,分离效果不理想。为此,人们广泛研究了基于稀疏反演预测噪声的混采数据分离方法。Akerberg等[9]利用稀疏Radon变换分离混采数据;Abma等[10]在傅里叶变换域由凸集投影(POCS)算法获得了高质量分离结果;Lin等[11]提出了基于Curvelet域L1约束的分离方法;Chen等[12]利用Seislet域整形正则化方法取得了理想的分离效果;Qu等[13]对比了Curvelet变换结合不同正则化约束的混采分离算法;Zu等[14]提出周期震源编码海上混采方式;宋家文等[15]基于频率—波数—波数域(FKK)变换的稀疏反演法分离三维高效混采数据。
随着混采技术的成熟以及计算集群的发展,基于稀疏反演预测噪声的混采数据分离方法逐步进入产业化进程,目前已在多个实际陆上数据混采作业中取得理想效果。陆上混采数据一般是在生产炮之间产生交叉混叠干扰,类型单一。然而,在海洋OBN高效混采过程中,由于施工方式导致非生产炮数量不可忽略,引起混叠干扰类型复杂多样,严重制约了该技术的应用效果。
本文针对A区OBN高效混采数据,在充分分析多种混叠干扰类型的基础上,研究了迭代动态映射技术以及炮点逻辑坐标预处理、稀疏反演法的技术方案,旨在成功预测各类混叠干扰,以期达到理想分离效果。
1 OBN混采数据混叠干扰分析A区实际数据为共检波点道集,对于每个OBN来说,设计的有效生产炮为23万个,但是实际记录的单炮数量一般超过30万个,即除有效生产炮之外的非生产炮的数量超过20%。非生产炮包括软启动炮(Soft Start,驱逐海洋哺乳动物)、重炮(多线束施工)、废炮(采集船偏离航线)和坏炮(由船等设备导致)等,这是由OBN混采特有的施工方式决定的。非生产炮数量过多造成逻辑坐标系统下的重炮以及严重数据变观现象,是OBN高效混采资料中产生多种类型混叠干扰的两种主要原因。
1.1 重炮引起的干扰类型图 1为重炮定义的炮类型,若仅考虑生产炮受到的混叠干扰,可将所有炮类型定义为5种。

|
图 1 重炮定义的炮类型 生产炮受到的混叠干扰来自A1、B1和B2 |
在一定观测系统下,逻辑坐标系统中炮点之间的相对方位关系和物理坐标系统保持一致。然而在变观情况下,炮点的逻辑位置之间的相对方位关系可能与物理坐标系统不一致,因此可将所有炮类型定义为3种(图 2)。

|
图 2 变观定义的炮类型 |
| $ {\mathit{\boldsymbol{d}} = \mathit{\boldsymbol{ \boldsymbol{\varGamma} m}}} $ | (1) |
式中:d为混叠记录;m为未混叠信号;Γ为混叠算子,包含所有震源的激发时间以及空间位置信息。由于观测到的样点数远少于需要反演的样点数,故混采数据的分离为欠定反演问题。为了求解分离信号,在FKK域施加L0范数稀疏约束,建立目标函数
| $ {J\left( \mathit{\boldsymbol{m}} \right) = \left\| {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{ \boldsymbol{\varGamma} m}}} \right\|_2^2 + \lambda {{\left\| {{\rm{F}}\left( \mathit{\boldsymbol{m}} \right)} \right\|}_0}} $ | (2) |
式中:F为三维傅里叶变换算子;λ为正则化参数,控制误差项和约束项权重。该目标函数极小值问题可通过迭代收缩阈值法[17]求解
| $ {{\mathit{\boldsymbol{m}}_{i + 1}} = {{\rm{F}}^{ - 1}}{\mathit{\boldsymbol{T}}_\tau }{\rm{F}}[{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{\rm{H}}}\mathit{\boldsymbol{d}} - \left( {{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{\rm{H}}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }} - \mathit{\boldsymbol{I}}} \right){\mathit{\boldsymbol{m}}_i}]} $ | (3) |
式中:上标“H”表示取共轭;Tτ为FKK变换域的阈值算子;I为单位矩阵;i为迭代次数。
式(3)表示将数据变换到FKK域并预测混叠干扰,然后在共检波点时—空域减去该混叠干扰的迭代过程。
针对A区OBN高效混采(高峰期平均能达3万单炮/日,每天数据量约7TB),选择基于FKK变换的稀疏反演法预测噪声的分离方法。采用快速傅里叶变换提高计算效率,利用指数阈值加快迭代收敛速度,从而精准、稳定、快速地分离高混叠度的海量地震数据[15]。
2.1.2 适用条件分析在FKK域预测混叠干扰受以下因素制约。
(1) 由于FKK变换存在制约条件,无法直接预测并分离重炮位置的B1类混叠干扰(图 3)。

|
图 3 混叠炮集(左)和存在B1类残留混叠干扰的分离炮集(右) |
通过炮逻辑坐标申请网格内存时,由于每个内存只允许读入一炮数据,并没有相应的网格空间容纳逻辑坐标重复的炮数据,因此无法有效预测该类混叠干扰;一般情况下,FKK分离技术只能预测并去除A1类混叠干扰,即使通过设置有效炮道头将所有非生产炮置成生产炮类型,也只能提高分离B2类混叠干扰的能力。
(2) FKK变换和混叠算子均要求炮点在逻辑坐标系统下的相对方位关系与物理坐标系统保持一致。
在变观情况下,若炮点逻辑坐标相对方位关系不能与物理坐标系统保持一致,则无法预测混叠干扰,只能预测D1类混叠干扰。此外,虽能较好地去除C2类混叠干扰(图 4红框处),但不能彻底分离C1类混叠干扰(图 4箭头处)。

|
图 4 混叠检波点道集(左)与分离后检波点道集(右) 左图右下方小图为炮点物理坐标分布,右图右下方小图为炮点逻辑坐标分布, 红色粗线为炮排列位置 |
在上述两种制约条件发生时,无法有效预测混采数据中的多种混叠干扰,导致分离效果不佳。
2.2 OBN高效混采多种混叠干扰分离分析混叠干扰类型可知,有效预测B1类和C1类混叠干扰难度较大。因此,应研究相对应的由FKK分离技术预测这两类混叠干扰的技术方案,提升分离效果。
2.2.1 迭代动态映射技术由图 1可知,B1类炮为与生产炮位置重合且产生混叠干扰的非生产炮。在实际施工中,在同一个逻辑位置上,可能存在多个B1类炮,重炮问题相当严重。识别多重B1类炮的技术是解决该问题的关键所在。通过问题分析,将B1类炮映射到新的逻辑线、点号位置,且新位置和周围炮的相对方位关系与旧位置保持一致,即可唯一识别该类炮。
本文研究了迭代动态映射技术,将多重B1类炮映射到没有重炮现象的同一个逻辑坐标系统下,在统筹、保持所有类型的炮位置相对方位关系的前提下,全局统一重新定义所有炮的逻辑线、点号,并预测所有类型的混叠干扰,在分离干扰后再恢复原始逻辑线、点号,最终达到成功分离的目的。
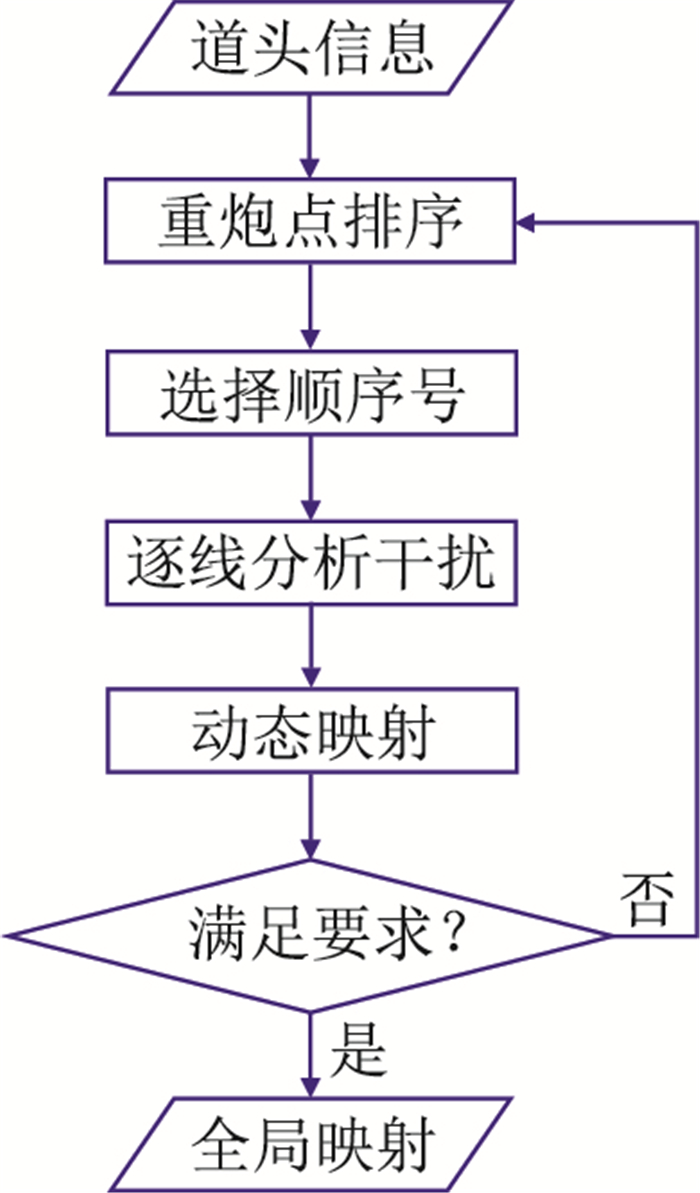
迭代动态映射技术流程(图 5)为:①通过道头信息输入,对每一个重炮点位置上的所有重炮排序,排序原则是生产炮序号始终为1,非生产炮序号从2开始;②从重炮点的序号2位置的非生产炮(B1类)开始,逐炮、线分析混叠干扰范围,分析搜索时间范围为[-7s,7s+T](7s为记录长度,T由共检波点道集的强相干噪声的延续时间确定);③根据设定的门槛值,将符合要求的所有非生产炮标记并建立映射到新逻辑坐标系统的函数,完成本轮迭代的动态映射;④再迭代至重炮点的序号3位置非生产炮(B1类),动态映射该位置的所有非生产炮、线,直至满足要求为止;⑤利用标记信息,将各轮迭代的映射函数整合成全局统一映射函数并输出。
|
图 5 迭代动态映射技术流程 |
由图 4可见,C1类炮产生的混叠干扰分离效果不理想,这主要由C1类炮逻辑坐标相对方位关系与物理坐标不一致引起。本文针对C1类炮,利用物理坐标信息对逻辑坐标做预处理,使处理后的逻辑坐标相对方位关系与物理坐标保持一致,同时在预处理过程中,尽量规避更多的重炮点现象,即
| $ {{x_{{\rm{LN}}}} = {x_{{\rm{L0}}}} + \frac{{{x_{\rm{P}}} - {x_{{\rm{P0}}}}}}{{{\rm{Int}}}} + \mathit{\Delta }} $ | (4) |
式中:xLN为计算后的逻辑坐标;xL0为参照点逻辑坐标;xP为物理坐标;xP0为参照点物理坐标;Int为逻辑坐标间隔;Δ为规避重炮的调整因子。
3 应用效果利用本文的迭代动态映射技术、炮逻辑坐标预处理、FKK稀疏反演分离技术系列,对A区OBN高效混采数据分离处理,取得了理想的分离效果。
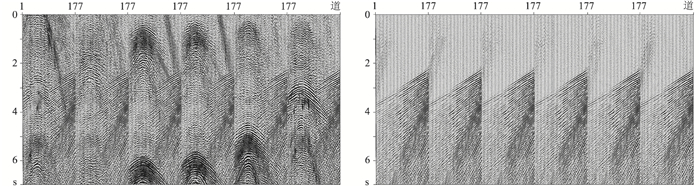
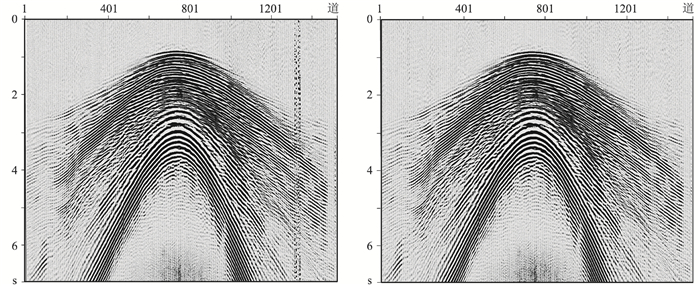
利用迭代动态映射技术可很好地识别并分离B1类炮产生的混叠干扰(图 6右),在采用炮逻辑坐标预处理后的分离道集上很好地去除了C1类炮的残留混叠干扰(图 7右)。
|
图 6 应用迭代动态映射技术前(左)、后(右)的FKK稀疏反演分离炮集 |
|
图 7 炮逻辑坐标预处理前(左)、后(右)的FKK稀疏反演分离检波点道集 |
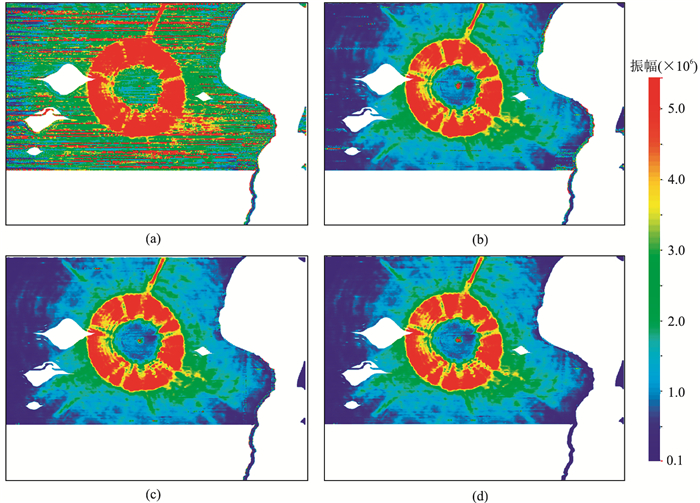
图 8为单检波点浅层(0~2300ms)的均方根振幅属性图。由图可见:在原始混叠数据(图 8a)中混叠干扰呈强能量条纹状随机分布;经FKK稀疏反演,尽管去除了大部分混叠干扰,但仍残留较多B1类混叠干扰(图 8b);经迭代动态映射技术的FKK稀疏反演,已基本分离重炮现象导致的B1类型混叠干扰(图 8c);在实施迭代动态映射技术和炮逻辑坐标预处理的FKK稀疏反演后,基本分离了B1类和C1类混叠干扰,分离效果较理想(图 8d)。
|
图 8 单检波点均方根振幅属性(0~2300ms) (a)原始混叠数据;(b)FKK稀疏反演;(c)迭代动态映射技术的FKK稀疏反演;(d)迭代动态映射技术和炮逻辑坐标预处理的FKK稀疏反演。红色圈为相干噪声 |
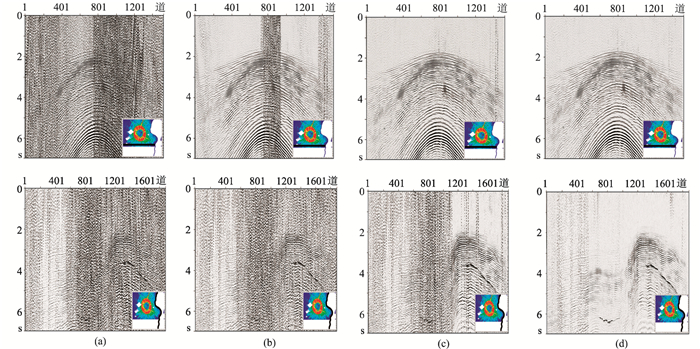
图 9为炮排列A、B共检波点道集分离效果对比。由图可见,应用迭代动态映射技术以及炮逻辑坐标预处理后的FKK稀疏反演分离数据信噪比最高,分离效果最理想(图 9d)。
|
图 9 炮排列A(上)、B(下)共检波点道集分离效果对比 (a)原始混叠道集;(b)FKK稀疏反演;(c)迭代动态映射技术的FKK稀疏反演;(d)迭代动态映射技术和炮逻辑坐标预处理的FKK稀疏反演。小图中黑色线为炮排列所在位置,炮排列A为东西向,炮排列B沿着岛屿岸线呈近南北向 |
与陆上混采数据混叠干扰类型单一相比,由于OBN高效混采施工的特殊性,OBN高效混采数据中存在多种混叠干扰类型。本文提出的迭代动态映射技术、炮点逻辑坐标预处理技术满足FKK稀疏反演分离技术的适用条件,能有效地识别、分离有效信号与两类混叠干扰——与生产炮逻辑坐标位置重叠的非生产炮产生的干扰、变观原因造成的逻辑坐标相对方位关系与物理坐标不一致的炮产生的干扰。
文中提出的迭代动态映射技术、炮点逻辑坐标预处理、FKK稀疏反演法分离技术系列,在A区的OBN高效混采海量数据中获得了良好效果,分离的单炮数据保真度高,在优化分离效率的前提下,取得了较理想的分离效果。
| [1] |
Beasley C J. A new look at marine simultaneous sources[J]. The Leading Edge, 2008, 27(7): 914-917. DOI:10.1190/1.2954033 |
| [2] |
Berkhout A J, Blacquiere G, Verschuur D J. Changing the mindset in seismic data acquisition[J]. The Lea-ding Edge, 2008, 27(7): 924-938. DOI:10.1190/1.2954035 |
| [3] |
Hoover G, Sublett V, Carter C, et al.Infield proce-ssing of an ISS dataset south-east Algeria[C].SEG Technical Program Expanded Abstracts, 2010, 29: 468-472.
|
| [4] |
Zhang C, Olofsson B.Separating simultaneous source data using weighted tau-p transform[C].Extended Abstracts of 74th EAGE Conference & Exhibition, 2012, doi: 10.3997/2214-4609.20148371.
|
| [5] |
Huo S, Luo Y, Kelamis P.Simultanueous sources se-paration via multi-directional vector-median filter[C].SEG Technical Program Expanded Abstracts, 2009, 28: 31-35.
|
| [6] |
王文闯, 李合群, 赵波, 等. 基于矢量中值滤波压制同步激发邻炮干扰[J]. 石油地球物理勘探, 2014, 49(6): 1061-1067. WANG Wenchuang, LI Hequn, ZHAO Bo, et al. Cross interference noise attenuation using alpha-trimmed vector median filtering[J]. Oil Geophysical Prospecting, 2014, 49(6): 1061-1067. |
| [7] |
周丽, 庄众, 成景旺, 等. 利用自适应迭代多级中值滤波法分离海上多震源混合波场[J]. 石油地球物理勘探, 2016, 51(3): 434-443. ZHOU Li, ZHUANG Zhong, CHENG Jingwang, et al. Multi-source blended wavefield separation for marine seismic based on an adaptive iterative multi-level median filtering[J]. Oil Geophysical Prospecting, 2016, 51(3): 434-443. |
| [8] |
Doulgeris P, Mahdad A, Blacquiere G.Iterative separation of blended marine data: discussion on the coherency-pass filter[C].SEG Technical Program Expanded Abstracts, 2011, 30: 26-31.
|
| [9] |
Akerberg P, Hampson G, Martin H, et al.Simulta-neous sources separation by sparse Radon transform[C].SEG Technical Program Expanded Abstracts, 2008, 27: 2801-2805.
|
| [10] |
Abma R, Manning T, Tanis M, et al.High quality se-paration of simultaneous sources by sparse inversion[C].Extended Abstracts of 70th EAGE Conference & Exhibition, 2008, B003.
|
| [11] |
Lin T, Herrmann F.Designing simultaneous acquisition with compressive sensing[C].Extended Abstracts of 71st EAGE Conference & Exhibition, 2009, 127-00269.
|
| [12] |
Chen Y, Fomel S, Hu J. Iterative deblending of simultaneous source seismic data using seislet-domain shaping regularization[J]. Geophysics, 2014, 79(5): V179-V189. DOI:10.1190/geo2013-0449.1 |
| [13] |
Qu S, Zhou H, Liu R, et al. Deblending of simulta-neous source seismic data using fast iterative shrinkage thresholding algorithm with firm thresholding[J]. Acta Geophysica, 2016, 64(4): 1064-1092. DOI:10.1515/acgeo-2016-0043 |
| [14] |
Zu S, Zhou H, Chen Y, et al. A periodically varying code for improving deblending of simultaneous sources in marine acquisition[J]. Geophysics, 2016, 81(3): V213-V225. DOI:10.1190/geo2015-0447.1 |
| [15] |
宋家文, 李培明, 王文闯, 等. 基于稀疏反演的高效混采数据分离方法[J]. 石油地球物理勘探, 2019, 54(2): 268-273. SONG Jiawen, LI Peiming, WANG Wenchuang, et al. High-productivity blended acquired data separation by sparse inversion[J]. Oil Geophysical Prospecting, 2019, 54(2): 268-273. |
| [16] |
李培明, 宋家文, 柳兴刚, 等. 海上高效混叠采集参数优化设计[J]. 石油地球物理勘探, 2020, 55(4): 707-715. LI Peiming, SONG Jiawen, LIU Xinggang, et al. Optimization of parameter design for high-productivity marine blending acquisition[J]. Oil Geophysical Prospecting, 2020, 55(4): 707-715. |
| [17] |
Daubechies I, Defrise M, Mol C D. An iterative thre-sholding algorithm for linear inverse problems with a sparsity constraint[J]. Communications on Pure and Applied Mathematics, 2004, 57(11): 1413-1457. DOI:10.1002/cpa.20042 |



 陈鹰鹏, 河北省涿州市华阳东路东方地球物理公司科技园研究院海外业务部, 072750。Email:
陈鹰鹏, 河北省涿州市华阳东路东方地球物理公司科技园研究院海外业务部, 072750。Email: