② 中国石化西北油田勘探开发研究院, 新疆乌鲁木齐 830011
② Research Institute of Exploration and Development, Northwest Oilfield Branch Co., SINOPEC, Urumqi, Xinjiang 830011, China
地震剖面中强反射轴的存在,对位于其内部或附近的目的层有效信号造成了较严重的影响,尤其是强反射轴附近存在隐蔽油气储层时,储层的反射信息会被强反射轴遮盖或融合而难以识别和区分。但这些储层往往又因为埋藏位置好、产量高,而成为重要勘探目标。因此消除强反射轴影响、提高油气储层刻画的精确度变得越来越重要。
经过多年探究,多子波分解与重构、匹配追踪成为强反射轴压制的两种常用技术。刘炳杨等[1]认为单一子波的假设会造成部分有用信息的丢失,由此应用多子波分解与重构技术成功剥离了目标区的强屏蔽层。佘刚等[2]利用多子波分解与重构技术去除了煤层强反射,提高了储层预测精度。
匹配追踪算法是由Mallat等[3]于1993年首次提出,并详细推导了理论公式,自此该算法开始应用于地震勘探多个领域,如薄层识别[4-5]、时频分析[6-7]、地震道缺失重建[8]等。Wang[9-10]通过改进提出了多道匹配追踪算法,将其应用于强反射轴剥离,取得较好效果。宋维琪等[11]将复数子波应用于匹配追踪算法,识别了薄层砂体。李海山等[12]对匹配追踪算法中的过完备字典进行优化,通过匹配煤层强反射信息消除了其屏蔽作用。张在金等[13]提出层位与子波约束下的匹配追踪去除强轴技术,剥离强轴后在储层下方发现明显的伴影异常。许璐等[14]针对瞬时频率的“负频率”问题,将局部频率引入匹配追踪算法,利用反射能量公式剥离了强反射轴。何峰等[15]从井旁地震道提取匹配子波,利用改进的匹配追踪算法去除了煤层强反射,凸现目标砂体。
前人的研究大多卓有成效,但鲜见针对“迭代终止”方面的研究文献,且迭代次数若选择不当,信号分解重构时就会引入噪声;其次,上述研究主要聚焦于强反射轴附近被压制的信号,却忽略或绕开了强反射轴内部含有的有效信号问题。
为此,本文利用残差比阈值约束匹配追踪算法中的迭代,避免了迭代次数选择不当引入的噪声,并在一定程度上提高了信号分解的效率。为了保留强反射轴中的有效信号,利用从多道提取的强反射信号求取能量加权系数,增加了强反射轴中有效信号的能量占比,再引入强反射轴压制参数λ,从而压制了强反射轴。理论模型和实际地震资料的处理结果表明,与常规层位约束匹配追踪强反射轴压制方法相比,本文方法具有更好效果。
1 方法原理 1.1 匹配追踪算法原理及实现方法匹配追踪算法在信号稀疏分解方面具有较好效果,常用的有单道匹配追踪算法和多道匹配追踪算法[16-17]。由于单道匹配追踪算法结果的横向连续性较差,因此本文选择多道匹配追踪算法。
假设一道地震信号x可被分解为一系列子波与随机噪声的组合,即可表达[18-19]为
| $ \mathit{\boldsymbol{x}} = \left\langle {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{\psi }}_{{\mathit{\boldsymbol{\gamma }}_1}}}} \right\rangle {\mathit{\boldsymbol{\psi }}_{{\mathit{\boldsymbol{\gamma }}_1}}} + {\mathit{\boldsymbol{R}}_1}(\mathit{\boldsymbol{x}}) $ | (1) |
式中:〈x,ψγ1〉为第1次迭代的地震信号x与其最优匹配子波ψγ1的内积,γ1表示第1次迭代后最优匹配子波的参数集合;R1(x)为第1次迭代后遗留的残差项。由于R1(x)与ψγ1是正交的,因此满足
| $ \left\| \mathit{\boldsymbol{x}} \right\|_2^2 = {\left| {\left\langle {\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{\psi }}_{{\mathit{\boldsymbol{\gamma }}_1}}}} \right\rangle } \right|^2} + \left\| {{\mathit{\boldsymbol{R}}_1}(\mathit{\boldsymbol{x}})} \right\|_2^2 $ | (2) |
K次迭代后,信号x可表示为
| $ \mathit{\boldsymbol{x}} = \sum\limits_{k = 1}^{K - 1} {\left\langle {{\mathit{\boldsymbol{R}}_k}(\mathit{\boldsymbol{x}}),{\mathit{\boldsymbol{\psi }}_{{\mathit{\boldsymbol{\gamma }}_k}}}} \right\rangle } {\mathit{\boldsymbol{\psi }}_{{\mathit{\boldsymbol{\gamma }}_k}}} + {\mathit{\boldsymbol{R}}_K}(\mathit{\boldsymbol{x}}) $ | (3) |
式中ψγk为第K次迭代出的匹配子波。由于匹配追踪算法是一个迭代过程,此过程中为了使残差项RK(x)足够小,则必须使地震信号x与其最优匹配子波ψγk∈Ψ的内积尽量大,这就需要找到与信号x最匹配的子波,最终将x分解为K-1个子波与第K次迭代后残差项的线性表示。因此,最优匹配子波的参数求取关系到信号的分解和重构精度。本文采用三步法[10]求取最优匹配子波的控制参数,具体实现过程如下。
第一步,初始参数估计。以Morlet小波作为基本原子,其表达式[20]为
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{\psi }}(t) = {\rm{exp}}\left[ { - \frac{{\ln 2{\omega ^2}{{(t - \mu )}^2}}}{{{\pi ^2}{\sigma ^2}}}} \right] \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{exp[i}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \omega (t - \mu ) + \phi ]} \end{array} $ | (4) |
式中:μ表示位移参数;ω表示子波圆频率;σ表示尺度参数;ϕ表示子波相位。
令γk={μk,ωk,σk,ϕk}构成子波参数数组,通过调整四个参数的大小就可得到子波库。设X={x1,x2,x3,…,xL}为一组相邻地震道,一般选择3道以上(L表示一组地震道的总道数)。定义该组地震道的平均道为
| $ {\mathit{\boldsymbol{\psi }}_{{\mathit{\boldsymbol{\gamma }}_k}}} = \mathop {{\rm{arg}}{\kern 1pt} {\rm{max}}}\limits_{{\mathit{\boldsymbol{\psi }}_{{\mathit{\boldsymbol{\gamma }}_k}}} \in \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}} \frac{{\left\langle {{\mathit{\boldsymbol{R}}_k}(\mathit{\boldsymbol{\bar x}}),{\mathit{\boldsymbol{\psi }}_{{\mathit{\boldsymbol{\gamma }}_k}}}} \right\rangle }}{{{{\left\| {{\mathit{\boldsymbol{\psi }}_{{\mathit{\boldsymbol{\gamma }}_k}}}} \right\|}_2}}} $ | (5) |
式中Ψ={ψγk}Γ,是子波组成的过完备字典,其中Γ表示γk的集合。
第二步,优化初始参数。得到初始参数γk={μk,ωk,σk,ϕk}后,确定最优参数的搜索范围为γ′k={[μk-nΔμ,μk+nΔμ],[ωk-nΔω,ωk+nΔω],[σk-nΔσ,σk+nΔσ],[ϕk-nΔϕ,ϕk+nΔϕ]}(n为正整数,{Δμ,Δω,Δσ,Δϕ}为各参数的邻域)。利用相邻L道地震信息联合优化初始参数
| $ {\mathit{\boldsymbol{\psi }}_{{\mathit{\boldsymbol{\gamma }}_k}}} = \mathop {{\rm{arg}}{\kern 1pt} {\rm{max}}}\limits_{{\mathit{\boldsymbol{\psi }}_{{\mathit{\boldsymbol{\gamma }}_k}}} \in \mathit{\boldsymbol{ \boldsymbol{\varPsi} }}} \frac{{\sum\limits_{l = 1}^L {\left| {\left\langle {{\mathit{\boldsymbol{R}}_k}({\mathit{\boldsymbol{x}}_l}),{\mathit{\boldsymbol{\psi }}_{{\mathit{\boldsymbol{\gamma }}_k}}}} \right\rangle } \right|} }}{{{{\left\| {{\mathit{\boldsymbol{\psi }}_{{\mathit{\boldsymbol{\gamma }}_k}}}} \right\|}_2}}} $ | (6) |
由式(6)得到的最优子波参数适用于相邻L道中的任意道。
第三步,匹配子波振幅估计。求取最优子波参数后,利用
| $ {\mathit{\boldsymbol{a}}_{l,k}} = \frac{{\left| {\left\langle {{\mathit{\boldsymbol{R}}_k}({\mathit{\boldsymbol{x}}_l}),{\mathit{\boldsymbol{\psi }}_{{\mathit{\boldsymbol{\gamma }}_k}}}} \right\rangle } \right|}}{{\left\| {{\mathit{\boldsymbol{\psi }}_{{\mathit{\boldsymbol{\gamma }}_k}}}} \right\|_2^2}} $ | (7) |
可得到相邻L道中各单道对应的振幅al,k,最后即得最优匹配子波wl,k=al,kψγk。
1.2 迭代终止条件约束下的匹配追踪法(TC-MMP)一般来说,传统的匹配追踪算法迭代终止条件主要有两类:一是给定一个硬阈值门限,如设定最大迭代次数K,那么迭代K次后的信号即可表示为K-1个匹配子波与其残差项的线性组合。但不同地震道的最佳迭代次数难以确定。最大迭代次数设置得过小,会造成残差较大,影响信号的重构精度;设置得过大时,对于较低信噪比的信号,分解到一定迭代次数时噪声方差可能比有效信号方差大,若继续迭代分解,信号重构时就会引入一定噪声,且耗时较长,因此硬阈值门限的迭代终止条件不一定可取。二是给定一个残差阈值门限,即当残差小于给定阈值时终止迭代,这种方法对于较高信噪比信号较适用,最终重构结果误差较小;当信号信噪比较低时,给定一个特定阈值,残差会以指数形式减小,但降至一定阶段残差会随迭代次数增加几乎保持不变,此时子波能量远小于残差,因此给定残差阈值门限的终止条件也不一定可取。
基于上述分析,本文采用残差比阈值作为迭代终止条件[21-22],有效保证信号分解重构的精度。
含噪声地震信号可表示为
| $ \mathit{\boldsymbol{s}} = \mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{N}}_{\Delta f}} $ | (8) |
式中:Δf为地震信号的频宽;NΔf表示Δf内的噪声;此处x为不含噪声地震信号。
根据匹配追踪算法的重构理论[3],残差项Rk(x+NΔf)以指数收敛到0,即
| $ \left\| {{\mathit{\boldsymbol{R}}_k}(\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{N}}_{\Delta f}})} \right\|_2^2 \le {\left[ {\frac{{(\alpha - 1)(\beta + 1)}}{\alpha }} \right]^k}\left\| {\mathit{\boldsymbol{x}} + {\mathit{\boldsymbol{N}}_{\Delta f}}} \right\|_2^2 $ | (9) |
式中:α为字典Ψ={ψγk}Γ中匹配子波的数量;β为过完备字典库Ψ的相关系数,可表示为
| $ \beta = \mathop {{\rm{sup}}}\limits_{i,j;i \ne j} |\left\langle {{\mathit{\boldsymbol{\psi }}_{{\mathit{\boldsymbol{\gamma }}_i}}},{\mathit{\boldsymbol{\psi }}_{{\mathit{\boldsymbol{\gamma }}_j}}}} \right\rangle | $ |
进一步可得
| $ \begin{array}{*{20}{l}} {\left\| {{\mathit{\boldsymbol{R}}_k}(\mathit{\boldsymbol{s}})} \right\|_2^2 - \left\| {{\mathit{\boldsymbol{R}}_{k + 1}}(\mathit{\boldsymbol{s}})} \right\|_2^2 \le }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\beta + 1 - \alpha \beta }}{\alpha }{{\left[ {\frac{{(\alpha - 1)(\beta + 1)}}{\alpha }} \right]}^k}\left\| \mathit{\boldsymbol{s}} \right\|_2^2} \end{array} $ | (10) |
由式(10)可知,第k次与第k+1次的迭代残差之差也会以指数形式减小,因此看似也可将残差之差作为迭代终止条件,但分析式(1)~式(3)可知,第k次与第k+1次迭代的残差之差还有如下关系
| $ \left\| {{\mathit{\boldsymbol{R}}_k}(\mathit{\boldsymbol{s}})} \right\|_2^2 - \left\| {{\mathit{\boldsymbol{R}}_{k + 1}}(\mathit{\boldsymbol{s}})} \right\|_2^2 = \left| {\left\langle {{\mathit{\boldsymbol{R}}_k}(\mathit{\boldsymbol{s}}),{\mathit{\boldsymbol{\psi }}_{{\mathit{\boldsymbol{\gamma }}_{k + 1}}}}} \right\rangle } \right|\left\| {{\mathit{\boldsymbol{\psi }}_{{\mathit{\boldsymbol{\gamma }}_{k + 1}}}}} \right\|_2^2 $ | (11) |
即当信号信噪比较低时,第k+1次迭代出的匹配子波ψγk+1在一定程度上必受噪声影响,且影响||Rk(s)||22-||RK+1(s)||22的收敛,所以认残差之差作为迭代终止条件也不太可取。
因此,为了进一步增强迭代终止条件的鲁棒性,拟将残差比q[Rk(s)]作为迭代终止条件,即有
| $ q[{\mathit{\boldsymbol{R}}_k}(\mathit{\boldsymbol{s}})] = \frac{{\left\| {{\mathit{\boldsymbol{R}}_{k + 1}}(\mathit{\boldsymbol{s}}) - \zeta {\mathit{\boldsymbol{R}}_k}(\mathit{\boldsymbol{s}})} \right\|_2^2}}{{\left\| {\zeta {\mathit{\boldsymbol{R}}_k}(\mathit{\boldsymbol{s}})} \right\|_2^2}} $ | (12) |
式中
首先将残差比阈值引入多道匹配追踪形成TC-MMP算法。为了验证残差比阈值迭代的有效性,将其与上述两种传统迭代方式进行对比(图 1),设定迭代次数为40。从图 1b可看出,当迭代次数达到20次以后,硬阈值门限和残差阈值门限曲线几乎稳定不变,两种方式迭代的用时分别为20.263s、19.931s;而残差比阈值曲线显示,在22次迭代以后就自适应地终止迭代,说明||Rk+1(s)-ζ Rk(s)||22相比于||ζ Rk(s)||22已是非常小的值(<0.005),耗时仅2.056s,且重构效果较好。因此,应用残差比阈值作为终止迭代条件,具有一定实用性。

|
图 1 传统迭代方式与残差比阈值迭代信号重构对比 (a)不同迭代方式信号重构结果;(b)残差及残差比迭代结果 |
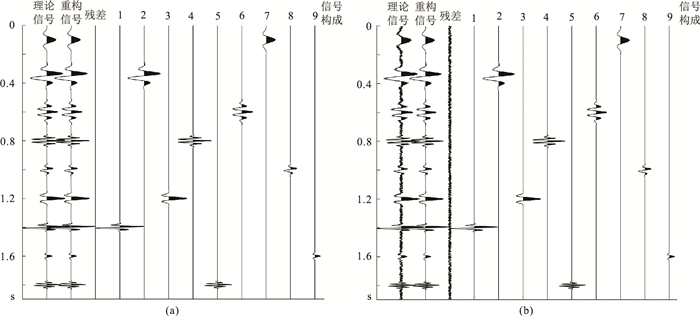
以9个不同频率、相位、尺度、时间的Morlet小波合成理论信号(图 2),验证TC-MMP算法的分解效果。对不含噪信号(图 2a)用本文算法迭代9次,每次迭代都可得到最优匹配子波,且最终重构信号与理论信号毫无差别,残差为零。对理论信号加入噪声(信噪比为5:1),再对该含噪信号进行迭代分解(图 2b),可见用本文算法迭代9次分解出的最优匹配子波都是构成理论信号的子波,重构信号与理论信号高度相似,且残差为加入的随机噪声,说明TC-MMP算法在噪声环境下依然较稳定。
|
图 2 TC-MMP算法理论信号迭代分解过程 (a)未加噪信号;(b)加噪信号 |
通常利用层位约束的匹配追踪算法识别并剥离强反射轴,但这类方法同时也压制了强反射轴中的有效信号。本文以目标强反射轴为中心,上下截取时窗,并确保时窗内强反射轴位置的振幅最强;利用TC-MMP算法对地震信号进行分解后,得到一系列匹配子波及其残差项,其中能量最强的匹配子波可视为强反射信号。针对强反射轴中被淹没的有效信号,采用多道联合压制强反射轴方法。首先通过多道提取的强反射信号求取能量加权系数ε,其作用是增加强反射轴中有效信号的能量占比,再调整压制参数λ(0~1之间),即可得到保留有效信号的强反射轴压制结果dnew
| $ \left\| {{\mathit{\boldsymbol{d}}_{{\rm{new}}}}} \right\|_2^2 = \frac{{\left\| {{\mathit{\boldsymbol{d}}_{{\rm{origin}},\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}}} - \lambda \varepsilon {\mathit{\boldsymbol{d}}_{{\rm{strong}},\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}}}} \right\|_2^2}}{p} $ | (13) |
| $ \varepsilon = \frac{{{\rm{M}}\left( {\sqrt {{\mathit{\boldsymbol{d}}_{{\rm{strong}},\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}}}} } \right)}}{{\sqrt {{\mathit{\boldsymbol{d}}_{{\rm{strong}},\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}}}} }} $ | (14) |
式中:dorigin,Λ代表原始地震信号;dstrong,Λ表示强反射轴能量集合;Λ={1,2,…,N}表示地震道编号,N为总的地震道数;p为平衡参数(一般取为1);M(·)表示取平均。
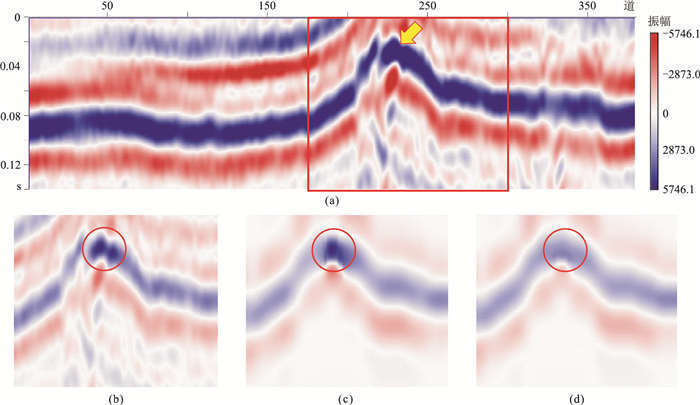
图 3a是截取的含有强反射轴的实际地震剖面,且强反射轴中存在有效信号(黄色箭头标记处)。针对该区域内特征剖面(图 3b),分别得到用常规方法(图 3c)和本文方法(图 3d)提取的强反射轴。从红色标记处看到,与常规方法相比,应用本文能量加权法后,强反射轴中的有效信号并未被提取,说明强反射轴压制以后,其中的有效信号可凸显出来,证明能量加权法确实有效。
|
图 3 不同方法强反射轴提取对比 (a)强反射轴中含有效信号的实际剖面;(b)局部剖面;(c)常规方法提取的强反射轴;(d)本文方法提取的强反射轴 |
基于上述研讨,本文方法包含如下步骤(图 4)。
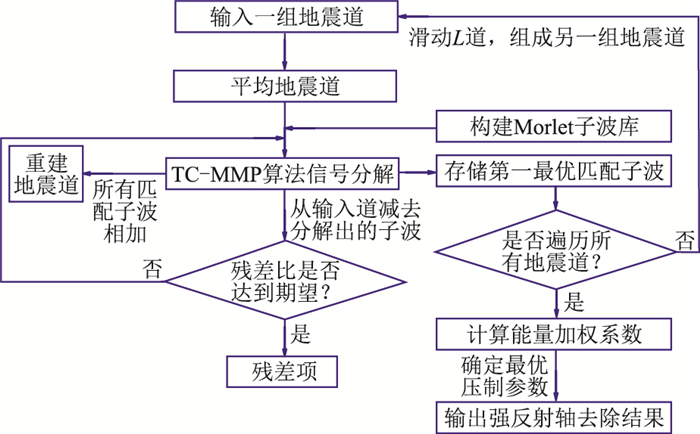
|
图 4 基于TC-MMP算法的强反射轴压制方法流程 |
(1) 选取一段含强反射轴地震剖面,以目标强反射轴为中心截取上下时窗,得到一组地震信号X={x1,x2,x3,…,xL},L一般取5。
(2) 输入平均地震道
(3) 经式(6)求取的子波参数适用于该组地震信号L道中任一道,故将从步骤(2)提取的强反射信号当作这L道信号的强反射,并存储这L道强反射。
(4) 滑动L道选择另一组地震信号X′,重复步骤(1)~步骤(3),直至遍历所有地震道(N道),可得N道强反射信号,即从多道提取的强反射信号。
(5) 利用式(13)求取能量加权系数,并确定最优压制参数,联合压制强反射轴。
2 模型验证构建一个二维速度模型(图 5),其具体参数如表 1所示,密度是由Gardner公式[23]求得。模型中溶洞②和③距高阻层顶界面(强反射轴)很近,可近似代表强反射轴中的有效信号;其他溶洞和速度异常体可近似地表征强反射轴附近的有效(反射)信息。为了确定最优的强反射轴压制参数,采用30Hz的Morlet小波作为地震子波,选取模型的第135道(强反射轴中含有溶洞②信息)进行单道模拟(对应图 6中黑色曲线)。
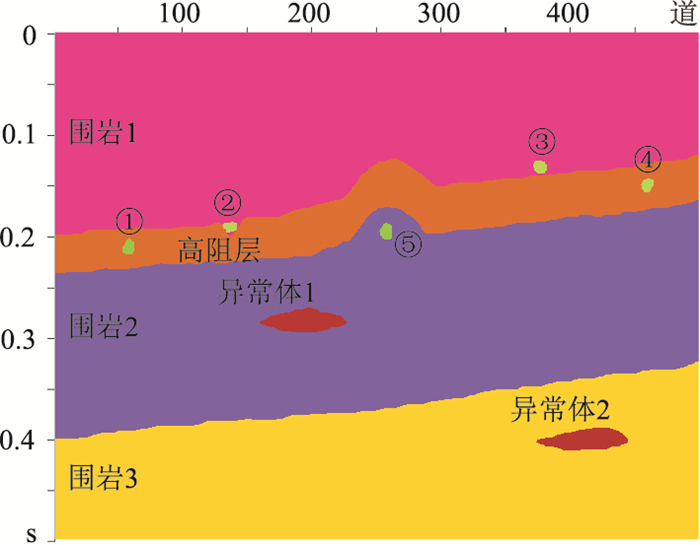
|
图 5 二维速度模型 |
|
|
表 1 速度模型参数 |
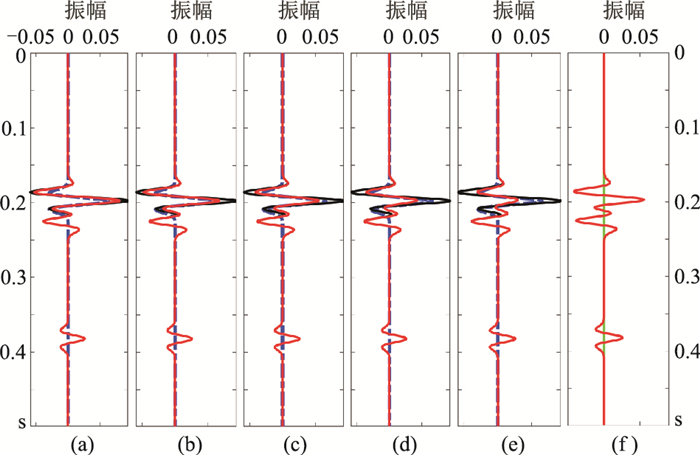
|
图 6 模型单道不同λ压制强反射轴结果 (a)λ=0.2;(b)λ=0.4;(c)λ=0.6;(d)λ=0.8;(e)λ=1.0 (a)~(e)黑线为模型第135道信号,蓝线为本文方法提取的强反射轴信号,红线为强反射轴压制后结果;(f)红线为设置于模型中的有效信号,绿线为λ=0.6时的强反射轴压制结果与有效信号之差 |
利用本文方法对模拟的单道数据做强反射轴压制处理,通过调整压制参数得到不同的λ(0.2、0.4、0.6、0.8、1.0)时模型第135道的压制结果(图 6)。对比图 6a~图 6e发现,当λ=0.6时(图 6c)强反射压制效果较理想;图 6f中λ=0.6时强反射轴压制结果与有效信号(红线)之差(绿线)几乎为0,也充分说明本文方法在压制强反射轴后还能突显被强反射轴淹没的有效信号。
对整个模型进行模拟得到图 7a所示正演记录,图中强反射轴中的有效信号几乎看不见,强反射轴下方的有效信号若隐若现。对比常规方法(图 7b)与本文方法(图 7c,λ=0.6)压制强反射轴后结果,可见经两种方法处理后强反射轴附近(红色箭头处)有效信号虽都得到凸显,但常规方法处理后强反射轴中的有效信号难以寻觅,而本文方法较充分地保留了强反射轴中的有效信号。
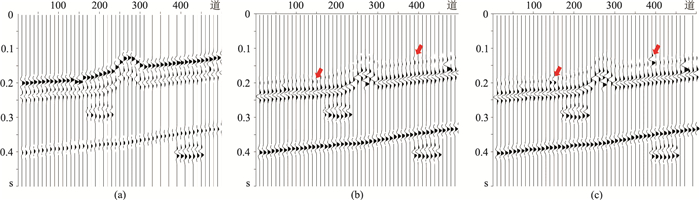
|
图 7 不含噪正演模型压制强反射轴前、后剖面 (a)未加噪正演剖面;(b)常规方法处理结果;(c)本文方法处理结果(λ=0.6) |
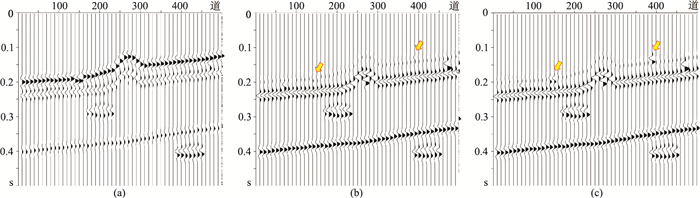
再对模型数据加入噪声(图 8a,信噪比为4:1),分析、对比常规方法(图 8b)与本文方法(图 8c)压制结果,可看出本文方法在噪声环境下依然效果明显(黄色箭头处),这无疑有助于目标区储层精细描述及后续地质综合解释。
|
图 8 加噪正演模型压制强反射轴前、后剖面 (a)加噪正演剖面;(b)常规方法处理结果;(c)本文方法处理结果(λ=0.6) |
中国新疆S区的奥陶系碳酸盐岩地层发育典型的缝洞型储集体。因碳酸盐岩内部地层界面波阻抗差异较小,奥陶系内幕反射明显较弱,发育的岩溶缝洞在地震剖面上表现为“串珠”状反射,若存在强反射轴,则会严重影响有效信号的显现,加大有效信号的识别难度。因此,亟待研发有效的强反射轴压制技术。
将本文方法应用于该区强反射轴压制,并列举两个实例验证本文方法的有效性和适用性。
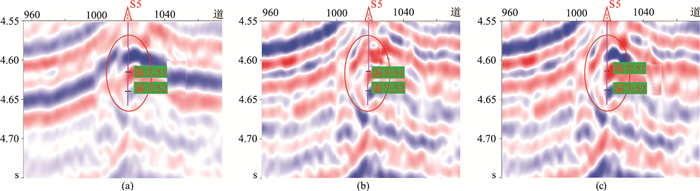
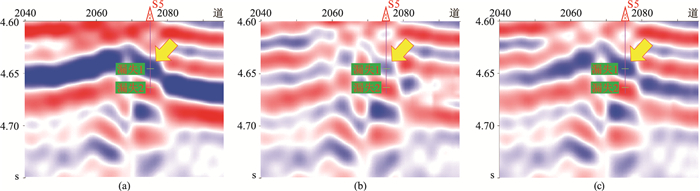
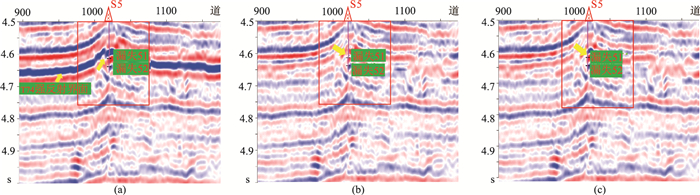
在实例1原始地震剖面(图 9a)上,受T74强反射层影响,其附近的有效信号被掩盖,若无测井资料,很难识别出有效信号。分别利用常规方法和本文方法对原始剖面进行强反射轴压制处理,发现两种方法处理结果(图 9b,图 9c)都使强反射轴附近的信号得到了一定程度凸显。进一步将图 9a中红色方框区域做局部放大显示(图 10),可见S5井漏失位置处有效信号弱,且强反射轴中也存在有效信号。对比常规方法(图 10b)与本文方法(图 10c)的强反射轴压制结果,可见本文方法使强反射轴中的有效信号得到最大程度的保留。实例2的强反射轴压制效果如图 11、图 12所示,可见S52井漏失位置处的有效信号原本被强反射轴淹没,但经本文方法处理后得以很好地凸显,再次表明本文的强反射轴压制方法确实有效且实用,可为该区缝洞储层识别研究提供技术支撑。
|
图 9 实例1压制强反射轴前、后剖面 (a)原始地震剖面;(b)常规方法处理;(c)本文方法处理 |

|
图 11 实例2压制强反射轴前、后剖面 (a)原始地震剖面;(b)常规方法处理;(c)本文方法处理 |
4 结论与认识
通过本项研究,得到如下认识和结论:
(1) 当目的层附近存在高阻层时,在地震剖面上形成强反射轴且会影响其附近有效信号的显现,更难精确识别强反射轴内部的有效信号,给储层预测带来巨大困难。
(2) 将残差比阈值作为迭代终止条件引入多道匹配追踪,即形成TC-MMP算法。通过与两种传统迭代方式进行对比,发现残差比阈值迭代终止条件可较好地实现自适应终止迭代,在一定程度上提高了信号分解的效率。
(3) 以目标强反射轴为中心建立时窗,用TC-MMP算法分解信号,将能量最强匹配子波作为强反射信号,通过多道提取的强反射信号求取能量加权系数,增大强反射轴中有效信号的能量占比,再通过试算方法选取理想强反射轴压制参数,使最终强反射轴压制结果最大程度上保留强反射轴中有效信号,同时也凸显该强反射轴附近有效信号。
(4) 模型数据和实际资料的处理结果表明,与常规层位约束匹配追踪强反射轴压制方法相比,本文方法压制强反射轴效果更佳,实用性更强。
需要指出的是:应用本文方法时需首先确保时窗内强反射位置的振幅能量最大;其次时窗的选取需根据实际资料特征确定,若取得过大就会延缓信号分解速度,进而影响其使用效率。
| [1] |
刘炳杨, 张军华, 郭迎春, 等.基于多子波分解与重构的强屏蔽层剥离技术[C].中国地球物理学会第28届学术年会论文集, 2012, 储层地球物理(17专题): 461.
|
| [2] |
佘刚, 周小鹰, 王箭波. 多子波分解与重构法砂岩储层预测[J]. 西南石油大学学报(自然科学版), 2013, 35(1): 19-27. SHE Gang, ZHOU Xiaoying, WANG Jianbo. Prediction of sand reservoir with multi-wavelet seismic trace decomposition and reconstruction[J]. Journal of Southwest Petroleum University (Science & Technology Edition), 2013, 35(1): 19-27. |
| [3] |
Mallat S, Zhang Z. Matching pursuit with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397-3415. DOI:10.1109/78.258082 |
| [4] |
朱博华, 向雪梅, 张卫华. 匹配追踪强反射层分离方法及应用[J]. 石油物探, 2016, 55(2): 280-287. ZHU Bohua, XIANG Xuemei, ZHANG Weihua. Strong reflection horizons separation based on matching pursuit algorithm and its application[J]. Geophysical Prospecting for Petroleum, 2016, 55(2): 280-287. DOI:10.3969/j.issn.1000-1441.2016.02.014 |
| [5] |
宋新武, 郑浚茂, 范兴燕, 等. 基于Ricker子波匹配追踪算法在薄互层砂体储层预测中的应用[J]. 吉林大学学报(地球科学版), 2011, 41(增刊1): 387-392. SONG Xinwu, ZHENG Junmao, FAN Xingyan, et al. Application of the thin-interbedded reservoir prediction based on ricker wavelet match tracing algorithm[J]. Journal of Jilin University (Earth Science Edition), 2011, 41(S1): 387-392. |
| [6] |
刘汉卿, 张繁昌, 王纳申, 等. 井资料约束的地震资料高频恢复[J]. 石油地球物理勘探, 2015, 50(5): 890-895. LIU Hanqing, ZHANG Fanchang, WANG Nashen, et al. Seismic high frequency information recovery constrained by well data[J]. Oil Geophysical Prospecting, 2015, 50(5): 890-895. |
| [7] |
邓世广, 王淑艳, 赵文津, 等. 基于OpenMP并行计算的匹配追踪时频分析方法[J]. 石油地球物理勘探, 2018, 53(3): 454-461. DENG Shiguang, WANG Shuyan, ZHAO Wenjin, et al. A matching pursuit time-frequency analysis method based on OpenMP parallel computing[J]. Oil Geophysical Prospecting, 2018, 53(3): 454-461. |
| [8] |
兰南英, 张繁昌, 张益明, 等. 快速结构字典学习三维地震数据重建方法[J]. 石油地球物理勘探, 2020, 55(1): 1-9. LAN Nanying, ZHANG Fanchang, ZHANG Yiming, et al. 3D seismic data reconstruction based on a fast structure dictionary learning method[J]. Oil Geophysical Prospecting, 2020, 55(1): 1-9. |
| [9] |
Wang Y H. Seismic time-frequency spectral decomposition by matching pursuit[J]. Geophysics, 2007, 72(1): V13-V20. DOI:10.1190/1.2387109 |
| [10] |
Wang Y H. Multichannel matching pursuit for seismic trace decomposition[J]. Geophysics, 2010, 72(1): V61-V66. |
| [11] |
宋维琪, 朱卫星, 孙英杰. 复数子波匹配追踪算法识别薄层砂体[J]. 地球物理学进展, 2007, 22(6): 1796-1801. SONG Weiqi, ZHU Weixing, SUN Yingjie. Identify bed layer sandbody by complex wavelet matching algorithm[J]. Progress in Geophysics, 2007, 22(6): 1796-1801. DOI:10.3969/j.issn.1004-2903.2007.06.018 |
| [12] |
李海山, 杨午阳, 田军, 等. 匹配追踪煤层强反射分离方法[J]. 石油地球物理勘探, 2014, 49(5): 866-870. LI Haishan, YANG Wuyang, TIAN Jun, et al. Coal seam strong reflection separation with matching pursuit[J]. Oil Geophysical Prospecting, 2014, 49(5): 866-870. |
| [13] |
张在金, 张军华, 李军, 等. 煤系地层地震强反射剥离方法研究及低频伴影分析[J]. 石油地球物理勘探, 2016, 51(2): 376-383. ZHANG Zaijin, ZHANG Junhua, LI Jun, et al. A method for stripping coal seam strong reflection and low-frequency shadow analysis[J]. Oil Geophysical Prospecting, 2016, 51(2): 376-383. |
| [14] |
许璐, 吴笑荷, 张明振, 等. 基于局部频率约束的动态匹配追踪强反射识别与分离方法[J]. 石油地球物理勘探, 2019, 54(3): 587-593. XU Lu, WU Xiaohe, ZHANG Mingzhen, et al. Strong reflection identification and separation based on the local-frequency-constrained dynamic matching pursuit[J]. Oil Geophysical Prospecting, 2019, 54(3): 587-593. |
| [15] |
何峰, 翁斌, 韩刚, 等. 一种基于地震约束的井控匹配追踪煤层强反射消除技术[J]. 中国海上油气, 2019, 31(1): 61-66. HE Feng, WENG Bin, HAN Gang, et al. A seismic constraint-based technology for elimination of strong coal seam reflection via well-control and matching pursuit[J]. China Offshore Oil and Gas, 2019, 31(1): 61-66. |
| [16] |
邓志文, 赵贤正, 陈雨红, 等. 自适应波形多道匹配追踪断层识别技术[J]. 石油地球物理勘探, 2017, 52(3): 532-537. DENG Zhiwen, ZHAO Xianzheng, CHEN Yuhong, et al. Fault identification based on multichannel adaptive waveforms matching pursuit[J]. Oil Geophysical Prospecting, 2017, 52(3): 532-537. |
| [17] |
李晋, 燕欢, 汤井田, 等. 基于匹配追踪和遗传算法的大地电磁噪声压制[J]. 地球物理学报, 2018, 61(7): 3086-3101. LI Jin, YAN Huan, TANG Jingtian, et al. Magnetotelluric noise suppression based on matching pursuit and genetic algorithm[J]. Chinese Journal of Geophysics, 2018, 61(7): 3086-3101. |
| [18] |
Zhang F C, Lan N Y. Seismic-gather wavelet-stretch-ing correction based on multiwavelet decomposition algorithm[J]. Geophysics, 2020, 85(5): V377-V384. DOI:10.1190/geo2018-0835.1 |
| [19] |
Xue J, Cai C G, Gu H M, et al. Matching pursuit-based sparse spectral analysis:Estimating frequency-dependent anomalies from nonstationary seismic data[J]. Geophysics, 2020, 85(5): V385-V396. DOI:10.1190/geo2018-0758.1 |
| [20] |
Liu J W, Kurt J M. Matching pursuit decomposition using Morlet wavelets[C]. SEG Technical Program Expanded Abstracts, 2005, 24: 786-789.
|
| [21] |
王珺, 李永庆. 遗传算法和正交时频原子相结合的地震记录快速匹配追踪[J]. 石油地球物理勘探, 2016, 51(5): 881-888. WANG Jun, LI Yongqing. Seismic trace fast match-ing pursuit based on genetic algorithm and orthogonal time-frequency atom[J]. Oil Geophysical Prospecting, 2016, 51(5): 881-888. |
| [22] |
梁巍, 阙沛文, 陈亮, 等. 基于残差比阈值的迭代终止条件匹配追踪稀疏分解方法[J]. 上海交通大学学报, 2010, 44(2): 171-175. LIANG Wei, QUE Peiwen, CHEN Liang, et al. Residual ratio iteration termination condition for MP method[J]. Journal of Shanghai Jiaotong University, 2010, 44(2): 171-175. |
| [23] |
Gardner G H F, Gardner L W, Gregory A R. Formation velocity and density-the diagnostic basics for stratigraphic traps[J]. Geophysics, 1974, 39(6): 770-780. DOI:10.1190/1.1440465 |



 宋维琪, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
宋维琪, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: