2 中国石油勘探开发研究院, 北京 100083
2 Research Institute of Petroleum Exploration and Development, PetroChina, Beijing 100083, China
地震记录中常常混杂着大量的随机噪声,严重降低了资料的信噪比。有效压制地震数据中的随机噪声是地震资料处理的重要环节。然而,由于其产生具有随机性且无固定频率和视速度,随机噪声压制一直是勘探地球物理界的难点之一。目前,压制随机噪声的方法可归纳为时间域滤波[1-2]、频率域滤波[3]、空间域滤波[4]和各种变换域滤波[5-9]等。Rudin等[4]于1992年首次提出空间域的全变分(Total variation,TV)模型,利用含噪数据总变分比无噪信号总变分大的性质,构造能量泛函以达到去噪的目的。鉴于其有效性,该模型被广泛应用于噪声压制[10-12]、波阻抗反演[13]和全波形反演[14]等领域。
尽管TV模型具有保护图像边缘信息的优势,但存在严重的阶梯效应,导致信号分片光滑。针对此问题,Selesnick等[15]率先将交叠组稀疏(Overlapping group sparsity,OGS)引入TV模型,指出信号的一阶差分不仅具有稀疏特性,还具有结构稀疏特性。之后Selesnick等[16]通过正则化技术有效识别出平滑区域内被强噪声污染的信号。为挖掘图像一阶梯度和二阶梯度的结构稀疏性,陈颖频等[17]将OGS与TV模型相结合,构建了一种改进的去噪模型。
上述方法[15-17]从本质上都是在寻找不同的正则项及惩罚函数,以达到最佳去噪效果。考虑到L1正则项是一种凸近似,往往使重构的非零信号比真实值小而导致过拟合,Ahlad等[18]提出组内使用L2范数和组间使用L1范数的加权方式。Lp伪范数本质是一种非凸正则项,它具有比凸核更接近秩函数的优点,能在恢复信号细节与给定残差稀疏解之间达到平衡,被广泛应用于图形修复、地震数据重建和重力反演等领域[19-21]。Adam等[22-23]基于高阶TV模型,引入非凸正则项技术,在图形去模糊方面取得一定效果;同时指出OGS与非凸高阶TV模型在去除斑块虚假信息上是互补的。然而,目前尚未见到将Lp伪范数、OGS和TV模型三者相结合应用于地震资料去噪的实例。
鉴于一阶TV模型不能有效保护信号的边缘及纹理特征,存在严重的阶梯效应,本文将高阶TV模型与OGS相结合,目的是充分挖掘和利用两者的优点,在减弱阶梯效应的同时较好地保护局部信息;同时,为解决信号重构过程中产生的斑点和块状问题,保护非零有效信号,引入非凸Lp伪范数;最后通过模拟数据和实际资料对本文方法进行验证,并与常规五种去噪方法进行对比。
1 去噪原理 1.1 传统TV去噪模型实际地震数据可表示为
| $ \mathit{\boldsymbol{y}} = \mathit{\boldsymbol{s}} + \mathit{\boldsymbol{n}} $ | (1) |
式中:y表示检波器接收到的地震数据;s表示有效信号; n为随机噪声。TV去噪模型对应如下数学极值问题[4]
| $ \mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{s}} \left\{ {\frac{1}{2}\left\| {\mathit{\boldsymbol{s}} - \mathit{\boldsymbol{y}}} \right\|_2^2 + \lambda {\rm{TV}}(\mathit{\boldsymbol{s}})} \right\} $ | (2) |
式中:||·||2为欧几里德范数;
Selesnick等[15]定义了窗尺度为K×K且中心点为(i, j)的二维矩阵
| $ {{\mathit{\boldsymbol{\tilde f}}}_{i,j,K}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{f}}_{i - {m_1},j - {m_1}}}}&{{\mathit{\boldsymbol{f}}_{i - {m_1},j - {m_1} + 1}}}& \cdots &{{\mathit{\boldsymbol{f}}_{i - {m_1},j + {m_2}}}}\\ {{\mathit{\boldsymbol{f}}_{i - {m_1} + 1,j - {m_1}}}}&{{\mathit{\boldsymbol{f}}_{i - {m_1} + 1,j - {m_1} + 1}}}& \cdots &{{\mathit{\boldsymbol{f}}_{i - {m_1} + 1,j + {m_2}}}}\\ {}&{}& \vdots &{}\\ {{\mathit{\boldsymbol{f}}_{i + {m_2} - 1,j - {m_1}}}}&{{\mathit{\boldsymbol{f}}_{i + {m_2} - 1,j - {m_1} + 1}}}& \cdots &{{\mathit{\boldsymbol{f}}_{i + {m_2} - 1,j + {m_2}}}}\\ {{\mathit{\boldsymbol{f}}_{i + {m_2},j - {m_1}}}}&{{\mathit{\boldsymbol{f}}_{i + {m_2},j - {m_1} + 1}}}& \cdots &{{\mathit{\boldsymbol{f}}_{i + {m_2},j + {m_2}}}} \end{array}} \right] $ | (3) |
式中
| $ \phi (\mathit{\boldsymbol{f}}) = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{{\left\| {{\mathit{\boldsymbol{f}}_{i,j,K}}} \right\|}_2}} } $ | (4) |
可见,OGS将邻域信息作为参考形成组合梯度,能充分挖掘信号的局部相似性。
1.3 基于OGS非凸Lp伪范数高阶TV模型考虑到OGS能有效恢复全局较大轮廓而高阶TV模型可较好地保护局部弱信号,将OGS与高阶TV模型结合,充分利用两者优点形成一个混合去噪模型;同时,引入非凸Lp伪范数以更准确地重构噪声数据中非零信号。该模型所对应的数学极值问题[22]表示为
| $ \mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{s}} \left[ {\frac{{{\lambda _1}}}{2}\left\| {\mathit{\boldsymbol{s}} - \mathit{\boldsymbol{y}}} \right\|_2^2 + \phi (\nabla \mathit{\boldsymbol{s}}) + {\lambda _2}\left\| {{\nabla ^2}\mathit{\boldsymbol{s}}} \right\|_p^p + \vartheta (\mathit{\boldsymbol{s}})} \right] $ | (5) |
式中:
改进的方法是以信号周围点的信息作为参考形成组合梯度,使孤立的噪声污染点与邻域的组合梯度下降;同时保持图像边缘点与邻域的组合梯度强度,通过设定合理的阈值,可在有效去除噪声的同时,减弱阶梯效应,较好地保护有效信号。
采用分离变量法将式(5)转化成如下受约束的极值问题
| $ \begin{array}{l} \mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{s}} \left[ {\frac{{{\lambda _1}}}{2}\left\| {\mathit{\boldsymbol{s}} - \mathit{\boldsymbol{y}}} \right\|_2^2 + \phi (\mathit{\boldsymbol{a}}) + {\lambda _2}\left\| \mathit{\boldsymbol{b}} \right\|_p^p + \vartheta (\mathit{\boldsymbol{c}})} \right]\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{a}} = \nabla \mathit{\boldsymbol{s}},\mathit{\boldsymbol{b}} = {\nabla ^2}\mathit{\boldsymbol{s}},\mathit{\boldsymbol{c}} = \mathit{\boldsymbol{s}} \end{array} $ | (6) |
该式对应的无约束增广拉格朗日极值为
| $ \begin{array}{*{20}{l}} {L\left( {\mathit{\boldsymbol{s}},\mathit{\boldsymbol{a}},\mathit{\boldsymbol{b}},\mathit{\boldsymbol{c}};{\mathit{\boldsymbol{\xi }}_1},{\mathit{\boldsymbol{\xi }}_2},{\mathit{\boldsymbol{\xi }}_3}} \right) = }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{\lambda _1}}}{2}\left\| {\mathit{\boldsymbol{s}} - \mathit{\boldsymbol{y}}} \right\|_2^2 + \phi (\mathit{\boldsymbol{a}}) + {\lambda _2}\left\| \mathit{\boldsymbol{b}} \right\|_p^p + \vartheta (\mathit{\boldsymbol{c}}) - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{\xi }}_1^{\rm{T}}(\mathit{\boldsymbol{a}} - \nabla \mathit{\boldsymbol{s}}) + \frac{\beta }{2}\left\| {\mathit{\boldsymbol{a}} - \nabla \mathit{\boldsymbol{s}}} \right\|_2^2 - \mathit{\boldsymbol{\xi }}_2^{\rm{T}}\left( {\mathit{\boldsymbol{b}} - {\nabla ^2}\mathit{\boldsymbol{s}}} \right) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{\beta }{2}\left\| {\mathit{\boldsymbol{b}} - {\nabla ^2}\mathit{\boldsymbol{s}}} \right\|_2^2 - \mathit{\boldsymbol{\xi }}_3^{\rm{T}}(\mathit{\boldsymbol{c}} - \mathit{\boldsymbol{s}}) + \frac{\beta }{2}\left\| {\mathit{\boldsymbol{c}} - \mathit{\boldsymbol{s}}} \right\|_2^2} \end{array} $ | (7) |
式中:ξ1、ξ2和ξ3为拉格朗日乘子;β表示与
为求解式(7)所示的复杂耦合问题,本文采用交替方向乘子法(Alternating direction method of multipliers,ADMM)[25],按照下式交替迭代更新
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{s}}^{k + 1}} = \mathop {{\rm{arg}}{\kern 1pt} {\kern 1pt} {\rm{min}}}\limits_\mathit{\boldsymbol{s}} \mathit{\boldsymbol{L}}\left( {\mathit{\boldsymbol{s}},{\mathit{\boldsymbol{a}}^k},{\mathit{\boldsymbol{b}}^k},{\mathit{\boldsymbol{c}}^k};\mathit{\boldsymbol{\xi }}_1^k,\mathit{\boldsymbol{\xi }}_2^k,\mathit{\boldsymbol{\xi }}_3^k} \right)}\\ {{\mathit{\boldsymbol{a}}^{k + 1}} = \mathop {{\rm{arg}}{\kern 1pt} {\rm{min}}}\limits_\mathit{\boldsymbol{a}} \mathit{\boldsymbol{L}}\left( {{\mathit{\boldsymbol{s}}^{k + 1}},\mathit{\boldsymbol{a}},{\mathit{\boldsymbol{b}}^k},{\mathit{\boldsymbol{c}}^k};\mathit{\boldsymbol{\xi }}_1^k,\mathit{\boldsymbol{\xi }}_2^k,\mathit{\boldsymbol{\xi }}_3^k} \right)}\\ {{\mathit{\boldsymbol{b}}^{k + 1}} = \mathop {{\rm{arg}}{\kern 1pt} {\rm{min}}}\limits_\mathit{\boldsymbol{b}} \mathit{\boldsymbol{L}}\left( {{\mathit{\boldsymbol{s}}^{k + 1}},{\mathit{\boldsymbol{a}}^{k + 1}},\mathit{\boldsymbol{b}},{\mathit{\boldsymbol{c}}^k};\mathit{\boldsymbol{\xi }}_1^k,\mathit{\boldsymbol{\xi }}_2^k,\mathit{\boldsymbol{\xi }}_3^k} \right)}\\ {{\mathit{\boldsymbol{c}}^{k + 1}} = \mathop {{\rm{arg}}{\kern 1pt} {\rm{min}}}\limits_\mathit{\boldsymbol{c}} \mathit{\boldsymbol{L}}\left( {{\mathit{\boldsymbol{s}}^{k + 1}},{\mathit{\boldsymbol{a}}^{k + 1}},{\mathit{\boldsymbol{b}}^{k + 1}},\mathit{\boldsymbol{c}};\mathit{\boldsymbol{\xi }}_1^k,\mathit{\boldsymbol{\xi }}_2^k,\mathit{\boldsymbol{\xi }}_3^k} \right)} \end{array}} \right. $ | (8) |
可见,式(7)所示耦合问题被分解成四个子问题。下面利用式(9)~式(13)求解相应子问题。
sk+1是一个最小平方问题,其解析解为
| $ \begin{array}{l} {\mathit{\boldsymbol{s}}^{k + 1}} = {[{\lambda _1}\mathit{\boldsymbol{I}} + \beta {\nabla ^{\rm{T}}}\nabla + \beta {({\nabla ^2})^{\rm{T}}}{\nabla ^2} + \beta \mathit{\boldsymbol{I}}]^{ - 1}}[{\lambda _1}\mathit{\boldsymbol{y}} - {\nabla ^{\rm{T}}}{\mathit{\boldsymbol{\xi }}_1} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \beta {\nabla ^{\rm{T}}}{\mathit{\boldsymbol{a}}^k} - {({\nabla ^2})^{\rm{T}}}{\mathit{\boldsymbol{\xi }}_2} + \beta {({\nabla ^2})^{\rm{T}}}{\mathit{\boldsymbol{b}}^k} - {\mathit{\boldsymbol{\xi }}_3} + \beta {\mathit{\boldsymbol{c}}^k} \end{array} $ | (9) |
ak+1的约束如下
| $ {\mathit{\boldsymbol{a}}^{k + 1}} = \mathop {{\rm{arg}}{\kern 1pt} {\rm{min}}}\limits_\mathit{\boldsymbol{a}} \left[ {\frac{\beta }{2}\left\| {\mathit{\boldsymbol{a}} - \left( {\nabla {\mathit{\boldsymbol{s}}^{k + 1}} + \frac{{\mathit{\boldsymbol{\xi }}_1^k}}{\beta }} \right)} \right\|_2^2 + \phi (\mathit{\boldsymbol{a}})} \right] $ | (10) |
式中包含了式(4)所示的OGS正则项,当K=1时式(10)退化成传统的高阶TV模型;当K>1时,式(10)表示求解OGS正则项。鉴于最大最小值(Majorization minimization,MM)算法具有高效利用函数凹凸性搜寻原函数最值的优点,当原目标函数难优化时,不直接对其求解,而是求解一个易于优化且逼近于原目标函数的替代函数[26]。本文通过二次函数替代ϕ(a)实现MM算法。
同理,bk+1的约束为
| $ {\mathit{\boldsymbol{b}}^{k + 1}} = \mathop {{\rm{arg}}{\kern 1pt} {\rm{min}}}\limits_\mathit{\boldsymbol{b}} \left[ {\frac{\beta }{2}\left\| {\mathit{\boldsymbol{b}} - \left( {{\nabla ^2}{\mathit{\boldsymbol{s}}^{k + 1}} + \frac{{\mathit{\boldsymbol{\xi }}_2^k}}{\beta }} \right)} \right\|_2^2 + {\lambda _2}\left\| \mathit{\boldsymbol{b}} \right\|_p^p} \right] $ | (11) |
式(11)是一个非凸优化问题。非凸优化算法和阈值的选取是决定去噪效果的两个重要因素。鉴于经典的加权方向迭代L1算法能有效平衡信号的正负二阶微分[27-28],因此本文采用该算法求解
| $ \begin{array}{l} {\mathit{\boldsymbol{b}}^{k + 1}} = \mathop {{\rm{arg}}{\kern 1pt} {\rm{min}}}\limits_\mathit{\boldsymbol{b}} \left[ {\frac{\beta }{2}\left\| {\mathit{\boldsymbol{b}} - \left( {{\nabla ^2}{\mathit{\boldsymbol{s}}^{k + 1}} + \frac{{\mathit{\boldsymbol{\xi }}_2^k}}{\beta }} \right)} \right\|_2^2 + } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\sum\limits_i {\frac{{{\lambda _2}p\left| {{\mathit{\boldsymbol{b}}_i}} \right|}}{{\left| {\mathit{\boldsymbol{b}}_i^k} \right| + \zeta }}} } \right]\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \max \left[ {\left| {\frac{{\beta {\nabla ^2}{\mathit{\boldsymbol{s}}^{k + 1}} + \mathit{\boldsymbol{\xi }}_2^k}}{\beta }} \right| - \frac{{\lambda _2^2p}}{{\beta \left( {\left| {\mathit{\boldsymbol{b}}_i^k} \right| + \varepsilon } \right)}},0} \right] \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathop{\rm sign}\nolimits} \left( {{\nabla ^2}{\mathit{\boldsymbol{s}}^{k + 1}} + \frac{{\mathit{\boldsymbol{\xi }}_2^k}}{\beta }} \right) \end{array} $ | (12) |
式中:ζ和ε都是较小量,用以避免分母为零;max表示求二者较大值;sign为符号函数。
类似地,ck+1的约束为
| $ {\mathit{\boldsymbol{c}}^{k + 1}} = \mathop {{\rm{arg}}{\kern 1pt} {\rm{min}}}\limits_\mathit{\boldsymbol{c}} \left[ {\frac{\beta }{2}\left\| {\mathit{\boldsymbol{c}} - \left( {{\mathit{\boldsymbol{s}}^{k + 1}} + \frac{{\mathit{\boldsymbol{\xi }}_3^k}}{\beta }} \right)} \right\|_2^2 + \vartheta (\mathit{\boldsymbol{s}})} \right] $ | (13) |
另外,求解式(7)所需的三个拉格朗日乘子可表示如下
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\xi }}_1^{k + 1} = \mathit{\boldsymbol{\xi }}_1^k + \left( {{\mathit{\boldsymbol{a}}^{k + 1}} - \nabla {\mathit{\boldsymbol{s}}^{k + 1}}} \right)}\\ {\mathit{\boldsymbol{\xi }}_2^{k + 1} = \mathit{\boldsymbol{\xi }}_2^k + \beta \left( {{\nabla ^2}{\mathit{\boldsymbol{s}}^{k + 1}} - {\mathit{\boldsymbol{b}}^{k + 1}}} \right)}\\ {\mathit{\boldsymbol{\xi }}_3^{k + 1} = \mathit{\boldsymbol{\xi }}_3^k + \left( {{\mathit{\boldsymbol{s}}^{k + 1}} - {\mathit{\boldsymbol{c}}^{k + 1}}} \right)} \end{array}} \right. $ | (14) |
至此,四个子问题已求解完成。
将整个算法流程总结如下:
(1) 输入二维地震数据y,给定参数λ1>0,λ2>0,K,p;
(2) 初始化模型:s0=y,k=0,β=0.004,si=1, 2, 3=0,模型更新率εmin=1×10-6;
(3) 更新式(9)中的sk+1;
(4) 采用MM迭代算法更新式(10)中的ak+1;
(5) 更新式(12)中的bk+1;
(6) 更新式(13)中的ck+1;
(7) 更新式(14)中的ξ1k+1、ξ2k+1和ξ3k+1;
(8) 当
信噪比通常用信号总能量与噪声总能量的比值SNR(Signal to noise ratio)表征,是评价整体去噪效果的常用指标;结构相似性参数SSIM(Structural similarity)从亮度、对比度、结构三方面度量两幅图像的相似性,常作为衡量图像失真或噪声压制情况的客观标准[29];同时,为表征高斯噪声强弱,定义零均值噪声的标准差为δ。三者的具体定义如下
| $ {\rm{SNR}} = 10{\rm{lg}}\frac{{\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{s^2}(i,j)} } }}{{\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{{[s(i,j) - y(i,j)]}^2}} } }} $ | (15) |
| $ {\rm{SSIM}} = \frac{{(2{\mu _\mathit{\boldsymbol{s}}}{\mu _\mathit{\boldsymbol{y}}} + {C_1})(2{\sigma _{\mathit{\boldsymbol{sy}}}} + {C_2})}}{{(\mu _\mathit{\boldsymbol{s}}^2 + \mu _\mathit{\boldsymbol{y}}^2 + {C_1})(\sigma _\mathit{\boldsymbol{s}}^2 + \sigma _\mathit{\boldsymbol{y}}^2 + {C_2})}} $ | (16) |
| $ \delta = \sqrt {\frac{{\sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {{{[s(i,j) - y(i,j)]}^2}} } }}{{MN}}} $ | (17) |
式中:M、N分别表示二维地震数据的行数和列数;μs、μy对应表示s、y的均值;σs、σy分别表示s、y的方差;σsy表示s与y的协方差;C1和C2是维持稳定的两个常量,一般分别取2.252和6.752。为了更全面地评判去噪效果,本文将SNR、SSIM和运算耗时作为三个客观评价指标。
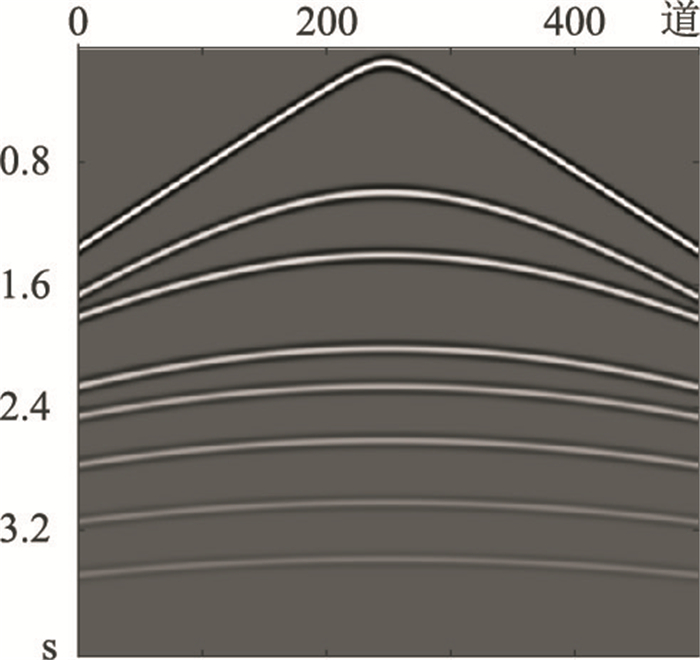
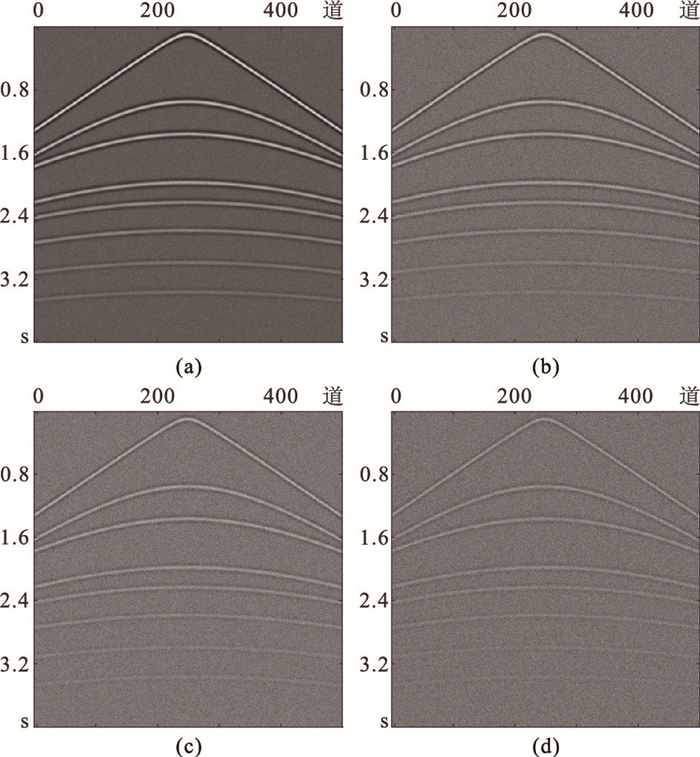
2.2 模拟数据构建一个水平层状模型,通过有限差分声波正演模拟得到图 1所示的共炮记录。模拟采用主频为20Hz的雷克子波,采样间隔为4ms,采样长度为4s,接收道数为500。为了模拟地震数据中不同强度的随机噪声,向该记录加入标准差为δ的高斯白噪声,得到图 2所示的含噪数据。由图 2可知,随着δ增大,背景噪声加强,SNR降低,SSIM变差,弱反射信号逐渐被强噪声淹没。
|
图 1 正演模拟共炮记录 |
|
图 2 不同δ的含噪数据 (a)δ=10;(b)δ=20;(c)δ=30;(d)δ=40 |
OGS从一个点向四周延伸K×K个点,可有效挖掘信号的局部相似性。为考察K值对去噪效果的影响,通过不断调整其大小,分别对图 2所示的四种不同噪声背景下的地震数据做去噪处理。
图 3展示不同K值得到的去噪结果所对应的三种指标的变化曲线。从图 3a可见,随着K值的增大,SNR先从小到大逐渐增加,达到最大值后减小。当SNR取最大值时,K值分别为3、5、7和10,说明K值的优选与背景噪声强度有关。当背景噪声较弱时,较小K值就能达到满意的去噪效果;当背景噪声增强时,应适当增大K值以提高SNR。图 3b中的SSIM表现出与SNR类似形态,区别在于当SSIM达到最大值后缓慢减小。这说明K值超过最优值后,对SSIM的影响不显著。图 3c显示,随着K值的增大运算耗时也不断增加,这是由于邻域信息的引入,导致计算量增大。

|
图 3 去噪结果的三指标随K值的变化曲线 (a)SNR;(b)SSIM;(c)耗时 |
因此,K值对本文方法去噪效果有显著影响。当K值过小时,邻域信息不足导致SNR和SSIM达不到最优,去噪效果欠佳;而当K值过大时,又会引入过多不相似的数据点,反而导致评价指标减小,去噪能力下降,这不仅会产生平滑效应,还会因使用过多邻域信息增加不必要的计算量。
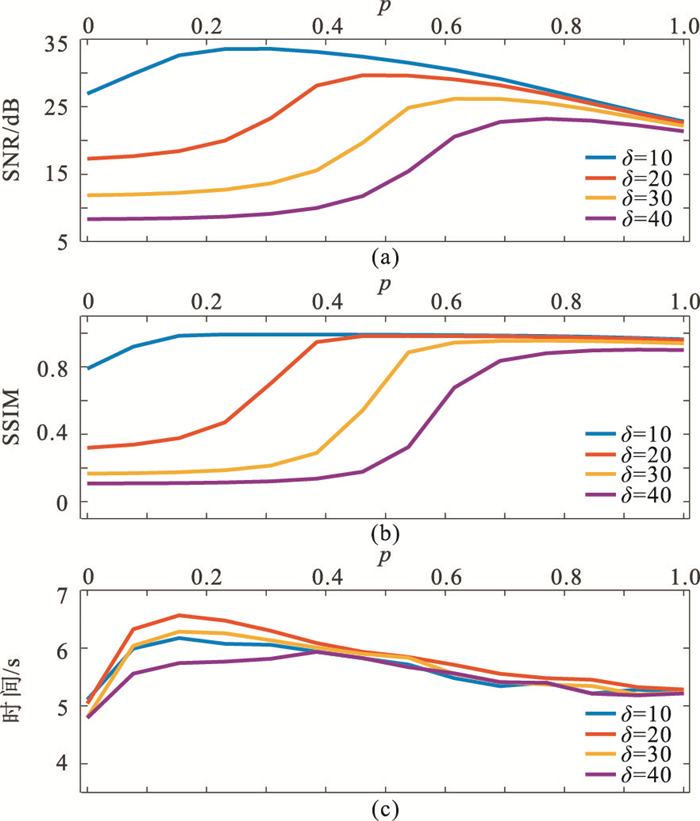
边界与局部细节的恢复主要受非凸正则化阶数p控制,对图 2含噪数据进行处理并得到图 4所示三种指标随p的变化曲线。图 4a表明,当δ=10时,SNR随p值增大而快速增至最大值,然后快速减小;当δ=20、30和40时,SNR曲线都具有平缓段、快速上升段和快速下降段。在平缓段SNR对p值不敏感,经快速上升后达到最大值。SNR取最大值时对应p值分别为0.23、0.46、0.62和0.75,这说明p值的优选与噪声强度有关。图 4b表明,弱噪声情况下SSIM曲线先上升,然后保持平缓;当背景噪声变强时,SSIM曲线呈现平缓段—快速上升段—平缓段分布。该指标取最大值时对应p值分别为0.16、0.47、0.62和0.83。图 4c表明,随着p值增大,运算耗时先增至最大值,然后逐渐减小,显然该指标与背景噪声强度无关。
|
图 4 去噪结果的三种指标随p值的变化曲线 (a)SNR;(b)SSIM;(c)耗时 |
综上,p值对本文去噪方法有同样显著的影响。高SNR资料应取较小p值;反之,低SNR资料应适当增大p值,以达到最佳去噪效果。
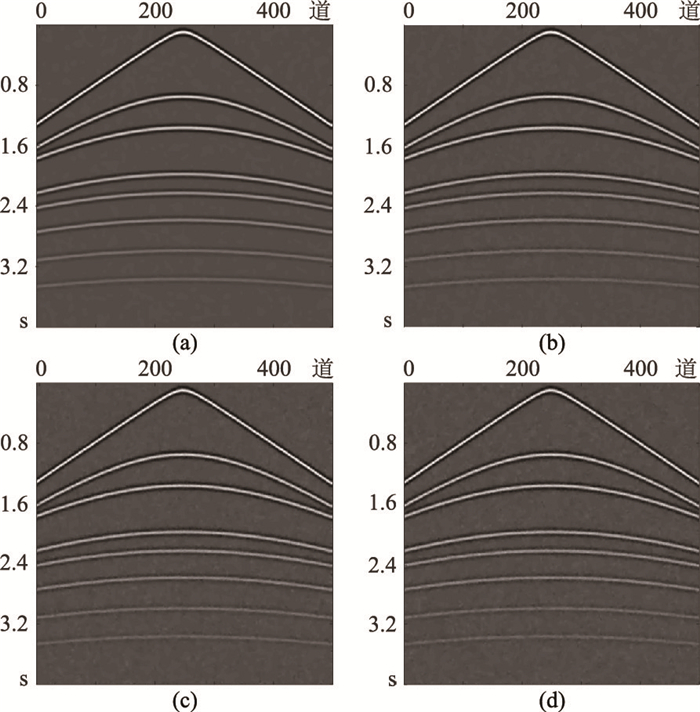
图 5展示K与p最优情形下对图 2所示四种不同强度噪声背景下地震数据的去噪效果。不同强度随机噪声均得到有效压制,剖面整体干净,反射波同相轴清晰,深层弱能量信号得到有效保护。
|
图 5 含有不同δ背景噪声数据的去噪结果 (a)δ=10;(b)δ=20;(c)δ=30;(d)δ=40 |
以上去噪试验表明,本文方法能压制阶梯效应,去除不同强度随机噪声,提高信噪比,并能有效保护弱能量信号。
2.4 方法对比为进一步验证本文方法的有效性,分别与各向异性全变分(Anisotropic total variation,ATV)、交叠组稀疏全变分(Overlapping group sparsity total variation,OGSTV)、中值滤波(Median filter,MF)、三维块匹配(Block matching 3D,BM3D)和K奇异值分解(K-singular value decomposition,KSVD)等五种方法进行对比。其中,ATV和OGSTV与本文方法属于同类,后三者为常用去噪方法。
表 1展示这些方法去噪后各项指标对比结果。从SNR和SSIM指标看,本文方法明显优于其他五种方法。从运算耗时指标看,本文方法用时虽然大于MF、ATV和OGSTV,但都未超过8s,在可接受范围内。对比后发现,用时明显小于BM3D和KSVD,这是由于最后两种方法涉及到耗时的非局部块匹配和字典训练。
|
|
表 1 针对四种含噪数据的六种方法去噪结果评价指标对比 |
图 6展示δ=40时上述六种方法去噪结果。强噪声背景下,ATV(图 6a)去噪并不理想,残留明显斑点和小块,阶梯效应严重。OGSTV(图 6b)引入邻域信息,阶梯效应得到一定压制,但仍存部分斑点伪影。MF(图 6d)去噪效果最差,存在大量残余噪声。BM3D(图 6e)产生了平滑效应,对深层弱信号的保护能力差。KSVD(图 6f)存在一定斑点,影响了最终去噪效果。图 6c所示剖面干净,阶梯效应弱,深层反射波同相轴连续性好,说明本文方法具有保护弱信号能力。

|
图 6 不同去噪方法对比 (a)ATV;(b)OGSTV;(c)本文方法;(d)MF;(e)BM3D;(f)KSVD |
从上述不同方法纵横向对比可知,本文方法能有效去除随机噪声,压制阶梯效应,更好地保护弱信号,在效率与精度上能达到良好的平衡。
3 实际资料应用将本文去噪方法应用于M工区实际地震资料。所选单炮记录(图 7a)共有240道,采样点数为700,采样间隔为2ms。由于存在大量随机噪声,反射波同相轴连续性差,弱能量信号被掩盖,信噪比较低。其叠后剖面(图 7b)共有800道,采样点数为800,采样间隔为2ms。该剖面深部地层有一定起伏,且发育微断层。随机噪声的存在致使剖面不清晰,同相轴错断,给地质解释带来诸多不便。

|
图 7 原始地震资料 (a)单炮资料;(b)叠后剖面 |
分别用上述六种方法进行去噪处理并得到图 8(单炮)和图 9(剖面)所示结果。历经多次试验并优选,针对图 7所示实际资料,本文方法参数设置为K=4、p=0.18和K=3、p=0.21。对比所得单炮记录去噪结果可知,ATV(图 8a)和MF(图 8d)去噪效果差,信号失真严重,尤其是1.2~1.5s和2.1~2.5s区间的弱信号;相对而言,OGSTV(图 8b)阶梯效应明显减少,去噪效果有一定提升,但仍存残余噪声;BM3D(图 8e)能保留强能量信号,但弱信号恢复能力差,产生了严重的平滑效应;KSVD(图 8f)和本文方法(图 8c)去噪效果相对较好,但KSVD在一些细节(弱信号)上不如本文方法。

|
图 8 不同单炮记录去噪结果对比 (a)ATV;(b)OGSTV;(c)本文方法;(d)MF;(e)BM3D;(f)KSVD |

|
图 9 叠后资料去噪结果对比 (a)ATV;(b)OGSTV;(c)本文方法;(d)MF;(e)BM3D;(f)KSVD |
对比、分析图 9及表 2可知,MF去噪效率高,但剖面(图 9d)上仍有大量噪声残留;OGSTV(图 9b)去噪效果有改善,但仍不理想;ATV(图 9a)去噪后产生的阶梯效应使部分细节丢失;同样地,BM3D(图 9e)出现平滑模糊区块,不利于微断裂等信息的恢复;KSVD(图 9f)和本文方法(图 9c)都有效压制了随机噪声,但KSVD计算效率低。
|
|
表 2 不同去噪方法的计算耗时对比 |
针对实际资料的应用结果表明,本文方法能压制不同强度随机噪声,减弱阶梯效应,有效保护信号细节特征,去噪后整个剖面同相轴具有更好清晰度和连续性,因此具有良好应用潜力。
4 结论(1) 本文去噪方法适用于不同强度的背景噪声,在有效压制随机噪声的同时兼顾计算效率,能显著提高地震资料的品质,具有广阔的应用前景。
(2) OGS考虑了信号的邻域信息,能充分挖掘局部相似性;将它与高阶TV模型和Lp伪范数结合,不仅能压制阶梯效应,提高算法去噪能力,而且能有效保护图像边缘信息,具有较高保真度。
(3) K值决定邻域信息的多少,若K值过小,则不能充分挖掘邻域信息;反之,若引入非相似信息,则不仅增大了计算量,而且导致平滑效应。p值关系到局部非零值信号的恢复,对于弱信号局部细节的保护有重要作用。
| [1] |
Liu C, Liu Y, Yang B J, et al. A 2D multistage median filter to reduce random seismic noise[J]. Geophysics, 2006, 71(5): V105-V110. DOI:10.1190/1.2236003 |
| [2] |
Liu Y, Liu C, Wang D. A 1D time-varying median filter for seismic random, spike-like noise elimination[J]. Geophysics, 2009, 74(1): V17-V24. DOI:10.1190/1.3043446 |
| [3] |
Naghizadeh M. Seismic data interpolation and denoi-sing in the frequency-wavenumber domain[J]. Geophysics, 2012, 77(2): V71-V80. DOI:10.1190/geo2011-0172.1 |
| [4] |
Rudin L I, Osher S, Fatemi E. Nonlinear total variation based noise removal algorithms[J]. Physica D:Nonlinear Phenomena, 1992, 60(1-4): 259-268. DOI:10.1016/0167-2789(92)90242-F |
| [5] |
Douglas A. Noise reduction in seismic data using Fourier correlation coefficient filtering[J]. Geophysics, 1997, 62(5): 1617-1627. DOI:10.1190/1.1444264 |
| [6] |
Shan H, Ma J W, Yang H Z. Comparisons of wavelets, contourlets and curvelets in seismic denoising[J]. Journal of Applied Geophysics, 2009, 69(2): 103-105. DOI:10.1016/j.jappgeo.2009.08.002 |
| [7] |
汪金菊, 袁力, 刘婉如, 等. 地震信号随机噪声压制的双树复小波域双变量方法[J]. 地球物理学报, 2016, 59(8): 3046-3055. WANG Jinju, YUAN Li, LIU Wanru, et al. Dual-tree complex wavelet domain bivariate method for seismic signal random noise attenuation[J]. Chinese Journal of Geophysics, 2016, 59(8): 3046-3055. |
| [8] |
程浩, 王德利, 王恩德, 等. 尺度自适应三维Shearlet变换地震随机噪声压制[J]. 石油地球物理勘探, 2019, 54(5): 970-978. CHENG Hao, WANG Deli, WANG Ende, et al. Seismic random noise suppression based on scale-adaptive 3D-Shearlet transform[J]. Oil Geophysical Prospecting, 2019, 54(5): 970-978. |
| [9] |
张华, 刁塑, 温建亮, 等. 应用二维非均匀曲波变换压制地震随机噪声[J]. 石油地球物理勘探, 2019, 54(1): 16-23. ZHANG Hua, DIAO Su, WEN Jianliang, et al. A random noise suppression with 2D non-uniform curvelet transform[J]. Oil Geophysical Prospecting, 2019, 54(1): 16-23. |
| [10] |
Tang G, Ma J W. Application of total variation based curvelet shrinkage for three-dimensional seismic data denoising[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(1): 103-107. DOI:10.1109/LGRS.2010.2052345 |
| [11] |
Kong D H, Peng Z M. Seismic random noise attenuation using shearlet and total generalized variation[J]. Journal of Geophysics and Engineering, 2015, 12(6): 1024-1035. DOI:10.1088/1742-2132/12/6/1024 |
| [12] |
Diriba G, Ma J W, Yong X S. A compound method for random noise attenuation[J]. Geophysical Prospecting, 2018, 66(8): 1548-1567. DOI:10.1111/1365-2478.12672 |
| [13] |
王治强, 曹思远, 陈红灵, 等. 基于TV约束和Toeplitz矩阵分解的波阻抗反演[J]. 石油地球物理勘探, 2017, 52(6): 1193-1199. WANG Zhiqiang, CAO Siyuan, CHEN Hongling, et al. Wave impedance inversion based on TV regularization and Toeplitz-sparse matrix factorization[J]. Oil Geophysical Prospecting, 2017, 52(6): 1193-1199. |
| [14] |
张盼, 韩立国, 巩向博, 等. 基于各项异性全变分约束的多震源弹性波全波形反演[J]. 地球物理学报, 2018, 61(2): 716-732. ZHANG Pan, HAN Liguo, GONG Xiangbo, et al. Multi-source elastic full waveform inversion based on the anisotropic total variation constraint[J]. Chinese Journal of Geophysics, 2018, 61(2): 716-732. |
| [15] |
Selesnick I, Chen P Y.Total variation denoising with overlapping group sparsity[C]. IEEE International Conference on Acoustics, Speech and Signal Proces-sing, 2013: 5696-5700.
|
| [16] |
Selesnick I, Farshchian M. Sparse signal approximation via nonseparable regularization[J]. IEEE Tran-sactions on Signal Processing, 2017, 65(10): 2561-2575. DOI:10.1109/TSP.2017.2669904 |
| [17] |
陈颖频, 彭真明, 李美慧, 等. 基于交叠组稀疏广义全变分的地震信号随机噪声衰减[J]. 石油地球物理勘探, 2019, 54(1): 24-35. CHEN Yingpin, PENG Zhenming, LI Meihui, et al. Random noise suppression based on the improved total generalized variation with overlapping group sparsity[J]. Oil Geophysical Prospecting, 2019, 54(1): 24-35. |
| [18] |
Ahlad K, Omair A M, Swamy M. An efficient denoi-sing framework using weighted overlapping group sparsity[J]. Information Sciences, 2018, 454(1): 292-311. |
| [19] |
Chen P Y, Selesnick I. Group-sparse signal denoising:non-convex regularization, convex optimization[J]. IEEE Transactions on Signal Processing, 2014, 62(13): 3464-3478. DOI:10.1109/TSP.2014.2329274 |
| [20] |
刘群, 付丽华, 张婉娟. 非凸Lp范数三维地震数据重建[J]. 石油地球物理勘探, 2019, 54(5): 979-987. LIU Qun, FU Lihua, ZHANG Wanjuan. 3D seismic data reconstruction based on non-convex Lp norm[J]. Oil Geophysical Prospecting, 2019, 54(5): 979-987. |
| [21] |
李泽林, 姚长利, 吕庆田, 等. 基于Lp范数稀疏优化算法的重力三维反演[J]. 地球物理学报, 2020, 62(10): 3699-3709. LI Zelin, YAO Changli, LU Qingtian, et al. 3D inversion of gravity data using Lp-norm sparse optimization[J]. Chinese Journal of Geophysics, 2020, 62(10): 3699-3709. |
| [22] |
Adam T, Paramesran R. Image denoising using combined higher order non-convex total variation with overlapping group sparsity[J]. Multidimensional Systems Signal Processing, 2018, 30(1): 503-527. |
| [23] |
Adam T, Paramesran R. Hybrid non-convex second-order total variation with applications to non-blind image deblurring[J]. Signal, Image and Video Processing, 2019, 14(1): 115-123. |
| [24] |
Liu G, Huang T Z, Liu J, et al. Total variation with overlapping group sparsity for image deblurring under impulse noise[J]. Plos One, 2015, 10(4): 1-23. |
| [25] |
Wu H, Li S, Chen Y P, et al. Seismic impedance inversion using second-order overlapping group sparsity with A-ADMM[J]. Journal of Geophysics and Engineering, 2020, 17(1): 97-116. DOI:10.1093/jge/gxz094 |
| [26] |
Figueiredo M A T, Bioucas-Dias J M, Nowak R D. Majorization-minimization algorithms for waveletbased image restoration[J]. IEEE Transactions on Image Processing, 2007, 16(12): 2980-2991. DOI:10.1109/TIP.2007.909318 |
| [27] |
Yang X, Karniadakis G E. Reweighted L1minimization method for stochastic elliptic differential equations[J]. Journal of Computational Physics, 2013, 248(1): 87-108. |
| [28] |
Wipf D, Nagarajan S. Iterative reweighted L1 and L2 methods for finding sparse solutions[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 317-329. DOI:10.1109/JSTSP.2010.2042413 |
| [29] |
Wang Z, Bovik A C, Sheikh H R, et al. Image quality assessment:from error visibility to structural similarity[J]. IEEE Transactions on Image Processing, 2004, 13(4): 600-612. DOI:10.1109/TIP.2003.819861 |



 胡天跃, 北京市海淀区颐和园路5号北京大学地球与空间科学学院, 100871。Email:
胡天跃, 北京市海淀区颐和园路5号北京大学地球与空间科学学院, 100871。Email: