近年来,随着高效地震采集技术的发展以及在地震勘探领域的广泛应用,陆上宽方位和高密度地震采集成为可能。高效地震采集技术的应用不仅大幅度提高了生产效率,能获得高覆盖次数的地震资料,而且极大地改善了地震资料品质。超高效混叠采集技术[1]采用多组可控震源独立激发,各组间无等待时间,对可控震源数量无特别限制;且可控震源数量越多,采集施工效率越高。但采用多组震源不同激发点位同时激发,必然在原始单炮记录上产生很强的邻炮干扰,即混叠噪声,显著降低地震数据的信噪比,影响后续地震数据处理质量。
根据超高效混叠采集的特点,相同接收排列记录了不同震源在不同点位的不同时间激发的能量。在共炮点道集上,该能量具有相干性;在共炮检距道集、共接收点道集或共中心点道集上,只有来自主激发点的能量具有相干性,而来自邻炮干扰的能量则都表现为随机性强振幅或尖脉冲干扰。因此,可通过基于信号域滤波法[2-7]和基于迭代反演[8-15]的去噪方法压制混叠噪声。基于信号域的去噪方法实现简单,计算效率高,但压制效果欠佳;基于迭代反演的方法是将混叠数据分离转化为求解最优化问题,实现混叠噪声压制,如基于稀疏域的迭代阈值法,但需较多迭代次数才能取得理想结果。
奇异值分解(SVD)方法[16]本质上是一种正交分解方法,奇异值愈大的分量对地震信号贡献(占比)也愈大。利用二维空间中信号相关性,通过去掉较小的奇异值,可压制不相关的噪声,提高地震资料的信噪比。基于此,本文设计了一种基于SVD约束迭代反演的混叠噪声压制方法。首先以选定区域混叠噪声奇异值对混叠数据的奇异值向量进行约束,然后通过迭代反演的策略逐步更新混叠数据的奇异值向量,最终在共炮检距域或做过动校正的共中心点域压制混叠噪声。通过数据测试,验证了该方法在压制混叠噪声的同时,也可很好地保护有效信号。
1 方法原理 1.1 奇异值分解SVD是将特征值或奇异值作为正交基在信号空间正交分解的特征,以增强相干能量,压制干扰。设有M×N的地震数据D,其中M为道数,N为采样点数,则该地震数据的SVD表示为
| $ \boldsymbol{D}=\boldsymbol{U} \boldsymbol{V} \boldsymbol{W}^{\mathrm{T}}=\sum\limits_{i=1}^{r} \sigma_{i} \boldsymbol{u}_{i} \boldsymbol{w}_{i}^{\mathrm{T}} $ | (1) |
式中:ui和wi分别为矩阵DDT和DTD的第i个特征向量;
地震数据经SVD后,根据能量大小可分为若干个奇异值,大奇异值主要反映原始记录中地震道与地震道间相关性强的信号,小奇异值主要对应噪声。合理选取较大奇异值可重建原始地震数据中具有相关特性的地震数据,压制不相关噪声,提高地震资料的信噪比。针对混叠采集数据,在共炮检距域或经NMO后的共中心点域,来自主激发源的能量具有很强的相关性,经SVD后对应大的奇异值;混叠噪声呈随机性,经SVD后对应较小SVD值,通过迭代反演更新的策略可压制混叠噪声。
1.2 基于迭代反演的混叠噪声分离方法混叠采集由不同空间位置的多个震源按随机编码方式激发,构成时域混叠炮集记录[17],即
| $ \boldsymbol{d}_{\mathrm{bl}}=\boldsymbol{d}_{1}+\mathit{\boldsymbol{\varGamma}} \boldsymbol{d}_{2} $ | (2) |
式中:dl和d2为来自不同炮的单炮数据;Γ表示混叠因子,包含震源激发的时间和位置,可通过震源或记录仪器获得。
求解不同炮数据的反演一般式可表示为
| $ \boldsymbol{F m}=\tilde{\boldsymbol{d}} $ | (3) |
式中
| $ \boldsymbol{m}=\left[\begin{array}{l} \boldsymbol{d}_{1} \\ \boldsymbol{d}_{2} \end{array}\right] \quad \boldsymbol{F}=\left[\begin{array}{ll} \boldsymbol{I} & \mathit{\boldsymbol{\varGamma}} \\ \mathit{\boldsymbol{\varGamma}}^{-1} & \boldsymbol{I} \end{array}\right] \quad \tilde{\boldsymbol{d}}=\left[\begin{array}{c} \boldsymbol{d}_{\mathrm{bl}} \\ \mathit{\boldsymbol{\varGamma}}^{-1} \boldsymbol{d}_{\mathrm{bl}} \end{array}\right] $ |
通过Landweber迭代算法和正则化方法,得到求解式(3)最优化问题的一般形式解[9-10]为
| $ \boldsymbol{m}_{n+1}=\mathrm{R}\left[m_{n}+\boldsymbol{B}\left(\tilde{\boldsymbol{d}}-\mathit{\boldsymbol{\varGamma}} \boldsymbol{m}_{n}\right)\right] $ | (4) |
式中:R对应S-1TτS,为整形正则化算符,其中S和S-1分别表示对地震数据求SVD及其逆运算,Tτ为阈值滤波因子,且τ为滤波阈值,本文选取目标区混叠噪声的奇异值作为滤波阈值;mn表示第n次迭代去噪结果;B为反传算子,近似看作F的逆。
在共炮检距域和NMO后的共中心点域,地震数据具有很好的相干性。经过SVD后,具有很好相干性的同相轴可由若干较大奇异值表征。但混叠噪声在共炮检距域和NMO后的共中心点域却呈现随机分布,经过SVD后,奇异值变小。通过选取部分仅含混叠噪声数据,在迭代反演过程中利用该混叠数据的奇异值对原始混叠数据进行约束,可较好地分离出混叠噪声,进而得到压制混叠噪声后的地震数据。
因此,基于SVD约束迭代反演的混叠噪声压制方法的技术思路为:①首先将原始共炮点数据筛选为共炮检距域数据,并选取仅含有混叠噪声的部分数据;②对共炮检距数据和仅含有混叠噪声数据进行SVD;③利用式(4)进行基于混叠噪声奇异值约束的混叠噪声压制,若满足输出条件则输出最终结果,若不满足输出条件,则继续循环迭代,直到满足期望输出条件。
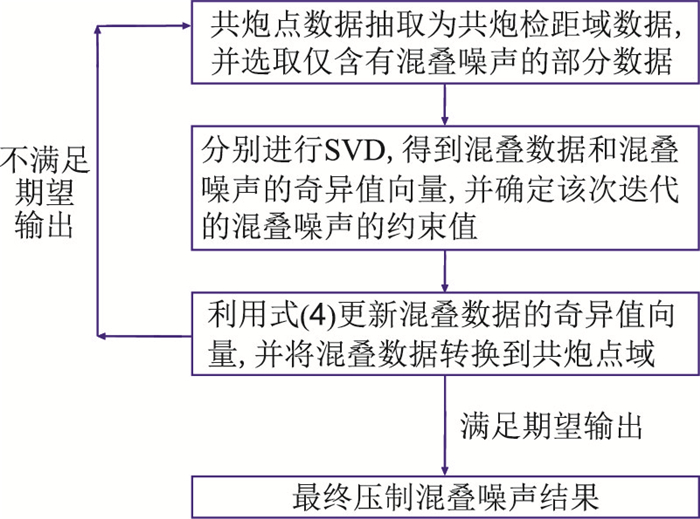
具体的实现步骤及流程(图 1)细述如下:
|
图 1 本文混叠噪声压制法简要流程 |
(1) 将混叠采集得到的共炮点域数据dbl转换到共炮检距域数据doffset,0;
(2) 抽取离激发点最近的共炮检距域数据,确定有效波最先到达的时间tb;
(3) 对共炮检距域数据进行SVD,对应式(1)即有doffset,0=Ubl,0Vbl,0Wbl,0T,从而获得该共炮检距域数据的奇异值向量Vbl,0;
(4) 选取时间tb前的不含有效波(主要是混叠噪声)的矩形窗数据dnoise,0,进行SVD,对应式(1)也有dnoise,0=Unoise,0Vnoise,0Wnoise,0T,同样获得混叠噪声数据的奇异值向量Vnoise,0,并确定该次迭代的混叠噪声的约束值λ0=max(Vnoise,0);
(5) 采用硬阈值函数,得到更新后奇异值向量V1=max(0,Vbl,0-λ0)*Vbl,0,进而获得第一次压制混叠噪声后共炮检距域数据moffset,1=Ubl,0V1Wbl,0T;
(6) 将获得第一次压制混叠噪声的共炮检距域数据moffset,1转换到共炮点域,得到对应的共炮点域数据m1;然后据混叠因子Γ计算m1的混叠数据dbl,1=Γm1;
(7) 依次重复步骤(3)~步骤(6),逐步迭代得到第n次更新的Vbl,n-1和Vnoise,n-1,以及第n次更新后压制混叠噪声的奇异值向量Vn=max(0,Vbl,n-1-λn-1)*Vbl,n-1和相应的共炮检距域数据doffset,n=Ubl,n-1VnWbl,n-1T,直到压制混叠噪声后数据的信噪比达到期望值,循环结束;
(8) 将第n次压制混叠噪声后的共炮检距域数据doffset,n转换到共炮点域,得到最终压制混叠噪声后的数据mn。
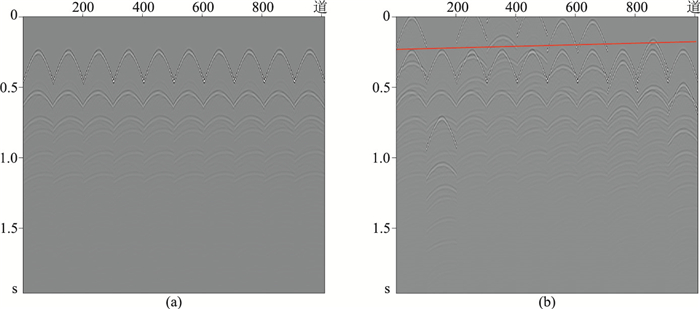
2 数据测试 2.1 正演数据模拟测试选取不含混叠噪声的正演数据(图 2a),通过加入混叠因子,模拟得到了含有混叠噪声的数据(图 2b),按本文设计的方法及流程对该数据进行处理。将图 2b中共炮点域数据转换到共炮检距域,在共炮检距域选取图 2b红线以上数据(在共炮检距域该部分数据主要为混叠噪声)进行SVD,将分解得到的奇异值矩阵的最大值作为迭代反演过程中的约束值。
|
图 2 不含混叠噪声(a)和加入混叠噪声后(b)的正演模拟数据 |
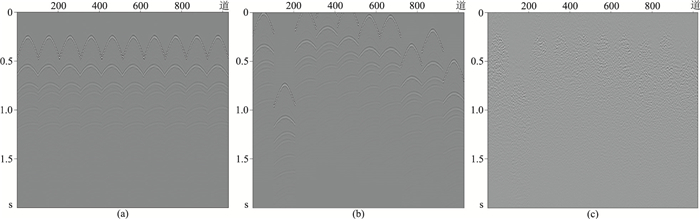
图 3a和图 3b分别为压制混叠噪声后数据和压制的混叠噪声,可见源自邻炮的混叠噪声干扰被很好压制,有效信号得以恢复,分离后信噪比达22.95dB。图 3c为原始不含混叠噪声数据与压制混叠噪声后数据的差值,对比发现两者间仅有微弱差异,主要同相轴和深部微弱能量得以充分保护。另外,在未达到期望输出要求的中间迭代结果中,仍会残留部分混叠噪声。
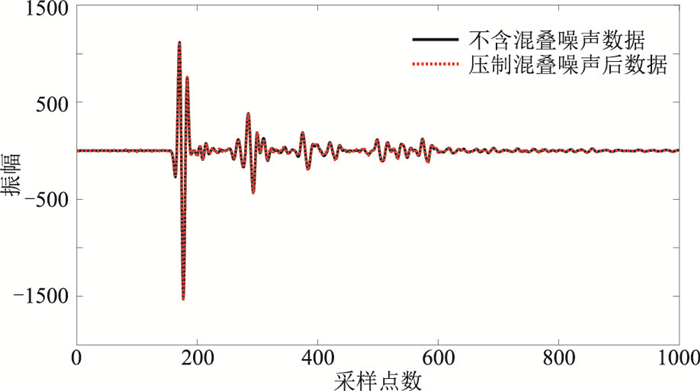
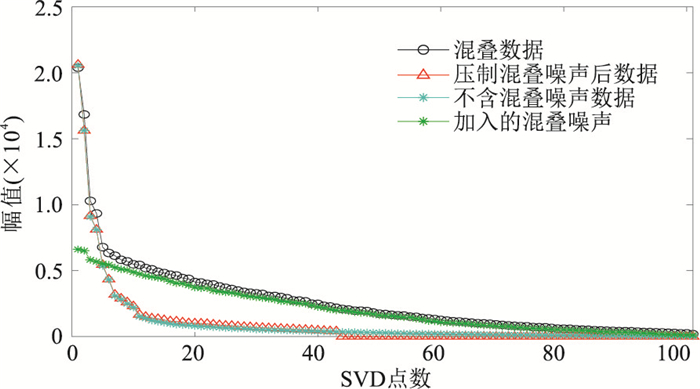
提取不含混叠噪声数据与压制混叠噪声后数据的单道(图 4),对比后可见二者基本一致;进一步分析对比原始不含混叠噪声数据与压制混叠噪声后数据的奇异值向量(图 5),可看出二者也非常接近。因此,本文方法是有效的。
|
图 4 不含混叠噪声数据与压制混叠噪声后数据的振幅对比 |
|
图 5 模拟数据压制混叠噪声前、后奇异值向量对比 |
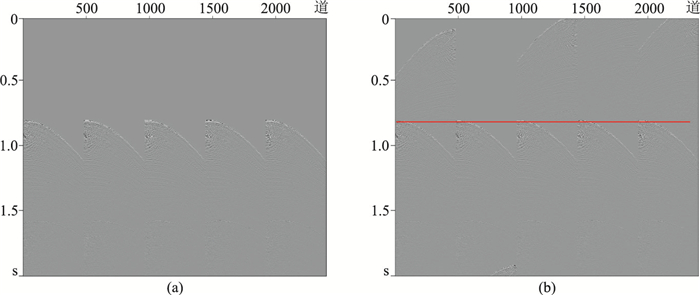
选取实际数据进行方法测试。对不含混叠噪声原始数据(图 6a)加入混叠因子,得到模拟含混叠噪声数据(图 6b)。按本文方法流程首先将共炮点域数据转换到共炮检距域,在共炮检距域选取图 6b红线对应旅行时以上混叠噪声数据进行SVD,选取所得混叠噪声奇异值矩阵的最大值作为迭代反演的混叠数据奇异值向量的约束值。
|
图 6 不含混叠噪声(a)和加入混叠噪声后(b)的实际数据 |
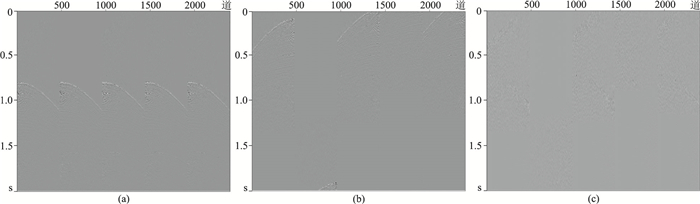
对比压制混叠噪声后的数据(图 7a)、压制的混叠噪声(图 7b)和不含混叠噪声原始数据与压制混叠噪声数据的差值(图 7c),同样可看出本文方法在压制混叠数据的同时,充分保留了主要的有效信号;另外,在未达到期望输出要求的中间迭代结果中,混叠噪声中会残留部分有效信号。
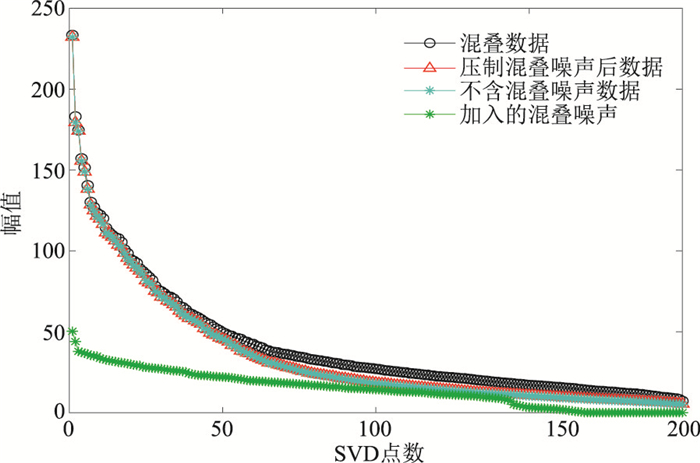
图 8为压制混叠噪声前、后奇异值向量对比,可见经迭代反演得到的压制混叠噪声后数据的奇异值向量趋近于原始不含混叠噪声数据。
该实际数据的测试结果充分证明了本文方法压制混叠噪声的有效性。
|
图 8 实际数据压制混叠噪声前、后奇异值向量对比 |
超高效混叠采集技术推动了地震采集技术的进步,有利于提高作业效率和降低生产成本。但相邻激发源之间会产生严重的混叠噪声干扰,降低地震数据的信噪比。为此,基于SVD具有优良的表征同相轴之间相干性的特性,根据混叠噪声在共炮检距域或NMO后的共中心点域呈现为随机噪声的性质,设计一种混叠噪声奇异值约束迭代反演的混叠噪声压制方法。利用混叠噪声所表征的奇异值对混叠数据的奇异值分量进行约束,通过迭代反演更新混叠数据的奇异值向量,有效压制混叠噪声。
去除混叠噪声前,必要的静校正、去面波等预处理可提升混叠噪声压制效果;复杂波场会影响常规SVD方法压制混叠噪声的效果,可选择在经过NMO的共中心点道集进行处理。
通过模型和实际数据测试,验证了本文方法压制混叠噪声的有效性。
| [1] |
Howe D, Foster M, Allen T, et al. Independent simultaneous sweeping: a method to increase the producti-vity of land seismic crews[C]. SEG Technical Program Expanded Abstracts, 2008, 27: 2826-2830.
|
| [2] |
Chen Y K. Deblending using a space-varying median filter[J]. Exploration Geophysics, 2014, 46(4): 332-341. |
| [3] |
董烈乾, 汪长辉, 李长芬, 等. 利用自适应中值滤波方法压制混叠噪声[J]. 地球物理学进展, 2018, 33(4): 1475-1479. DONG Lieqian, WANG Changhui, LI Changfen, et al. Blending noise removal utilizing an adaptive median filter[J]. Progress in Geophysics, 2018, 33(4): 1475-1479. |
| [4] |
孙哲, 王建锋, 王静, 等. 基于时空变中值滤波的随机噪声压制方法[J]. 石油地球物理勘探, 2016, 51(6): 1094-1102. SUN Zhe, WANG Jianfeng, WANG Jing, et al. Random noise elimination based on the time-space variant median filtering[J]. Oil Geophysical Prospecting, 2016, 51(6): 1094-1102. |
| [5] |
程浩, 王德利, 王恩德, 等. 自适应三维Shearlet变换地震随机噪声压制[J]. 石油地球物理勘探, 2019, 54(5): 970-978. CHENG Hao, WANG Deli, WANG Ende, et al. Seismic random noise suppression based on scale-adaptive 3D-Shearlet transform[J]. Oil Geophysical prospecting, 2019, 54(5): 970-978. |
| [6] |
Huo S, Luo Y, Kelamis P G. Simultaneous sources separation via multidirectional vector-median filtering[J]. Geophysics, 2012, 77(4): V123-V131. DOI:10.1190/geo2011-0254.1 |
| [7] |
Akerberg P, Hampson G, Rickett J, et al. Simulta-neous source separation by sparse radon transform[C]. SEG Technical Program Expanded Abstracts, 2008, 27: 2801-2805.
|
| [8] |
王坤喜, 毛伟建, 张庆臣, 等. 同时震源数据的直接反演分离[J]. 石油地球物理勘探, 2020, 55(1): 17-28. WANG Kunxi, MAO Weijian, ZHANG Qingchen, et al. A direct inversion method for deblending simultaneous-source data[J]. Oil Geophysical Prospecting, 2020, 55(1): 17-28. |
| [9] |
Dong L Q, Wang C H, Zhang M G, et al. Blended noise suppression using a hybrid median filter, normal moveout and complex curvelet transform approach[J]. Studia Geophysica et Geodaetica, 2020, 64(2): 241-254. DOI:10.1007/s11200-020-0269-9 |
| [10] |
Chen Y, Fomel S, Hu J. Iterative deblending of simultaneous-source seismic data using seislet-domain shaping regularization[J]. Geophysics, 2014, 79(5): V179-V189. DOI:10.1190/geo2013-0449.1 |
| [11] |
韩立国, 谭尘青, 吕庆田, 等. 基于迭代去噪的多源地震混合采集数据分离[J]. 地球物理学报, 2013, 56(7): 2402-2412. HAN Liguo, TAN Chenqing, LYU Qingtian, et al. Separation of multi-source blended seismic acquisition data by iterative denoising[J]. Chinese Journal of Geo-physics, 2013, 56(7): 2402-2412. |
| [12] |
朱立华. 基于稀疏反演的多震源地震混合采集数据分离技术[J]. 石油物探, 2018, 57(2): 208-212. ZHU Lihua. Deblending simultaneous-source seismic data using sparse inversion[J]. Geophysical Prospecting for Petroleum, 2018, 57(2): 208-212. DOI:10.3969/j.issn.1000-1441.2018.02.005 |
| [13] |
Zu S, Zhou H, Li Q, et al. Shot-domain deblending using least-squares inversion[J]. Geophysics, 2017, 82(4): V241-V256. DOI:10.1190/geo2016-0413.1 |
| [14] |
Chen Y. Iterative deblending with multiple constraints based on shaping regularization[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(11): 2247-2251. DOI:10.1109/LGRS.2015.2463815 |
| [15] |
宋家文, 李培明, 王文闯, 等. 基于稀疏反演的高效混采数据分离方法[J]. 石油地球物理勘探, 2019, 54(2): 268-273. SONG Jiawen, LI Peiming, WANG Wenchang, et al. High-productivity blended acquired data separation by sparse inversion[J]. Oil Geophysical Prospecting, 2019, 54(2): 268-273. |
| [16] |
Shohei M, Toshifumi M, Takeshi T. Singular-value decomposition analysis of source illumination in seismic interferometry by multidimensional deconvolution[J]. Geophysics, 2013, 78(3): Q25-Q34. DOI:10.1190/geo2012-0245.1 |
| [17] |
Berkhout A J. Changing the mindset in seismic data acquisition[J]. The Leading Edge, 2008, 27(7): 924-938. DOI:10.1190/1.2954035 |



 董烈乾, 河北省涿州市范阳中路307号中国石油集团东方地球物理公司国际勘探事业部, 072751。Email:
董烈乾, 河北省涿州市范阳中路307号中国石油集团东方地球物理公司国际勘探事业部, 072751。Email: