2 中国地质大学(北京)地球物理与信息技术学院, 北京 100083
2 School of Geophysics and Information Technology, China University of Geosciences (Beijing), Beijing 100083, China
“相”是一定岩层生成时的古地理环境及其物质表现的总和[1],而地震相是沉积相的地震响应。由于沉积环境对油气形成具有重要影响,所以准确分析地震相对油气勘探和油藏评价具有指导意义[2-4]。传统的地震相划分主要由人工直接在地震剖面上解释,俗称“相面法”,人为因素较多,具有极大的主观性和不确定性,同时受限于地震资料分辨率,无法满足精细勘探的精度需求[5]。
随着地震数字处理技术和计算机技术的发展,地震相分析进入数据分析时代,目前常用的地震相分析方法有随机模拟、神经网络[6-7]、聚类算法[8-10]和深度学习[11-12]等。随机模拟以地质统计学为基础,以已知信息为约束条件,通过随机函数产生等概率地震相模型[13-14]。但随机模拟结果易受随机模型影响,而且在地质结构复杂地区难以准确划分地震相。神经网络和深度学习具有较强的容错性和泛化能力,但需要海量训练样本数据,同时训练网络的计算开销巨大。聚类算法作为最常用的无监督学习方法之一,通过对无标记样本的学习揭示数据的内在性质和规律[15-16]。K均值聚类、C模糊聚类等经典聚类算法在简单数据集上均获得了理想的聚类结果,但对于非凸数据集并不能实现全局最优。以图论为基础的谱聚类方法能够在任意形状的数据空间实现全局最优划分[17-18]。因此本文选择谱聚类方法划分地震相,通过与井资料的标定,建立地震相与地质体间的对应关系。
地震数据中包含丰富的地质信息,但直接用地震数据划分地震相的计算量巨大,还容易造成维数灾难。常规地震属性可以提取地震数据中的特征信息,但种类繁多的地震属性往往对应不同的地质特征,人为选择地震属性划分地震相往往导致预测结果的多解性[19-20]。反射系数是地质特征的直观反映,但很难直接准确求取地层反射系数。
本文提出一种基于地震数据倒谱特征参数的谱聚类地震相分析方法。该方法以地震倒谱特征参数为谱聚类的输入变量划分地震相,然后通过井标定,建立地震相与地质体间的对应关系。其优点是:一方面能够提取反射系数信息作为地震相划分依据;另一方面可以将数据集的聚类转化为图的最优分割问题,能够适应复杂数据空间的分类。通过模型和实际数据验证了方法的可行性。
1 方法原理 1.1 倒谱特征参数地震勘探中,地层反射系数直观反映了地质特征,因此可以利用反射系数作为输入信息分析地震相。目前从地震数据中提取反射系数信息的常用方法有反褶积[21-23]、谱反演[24-25]等,但仍很难准确求取地层反射系数。Xie等[26]认为,语音信号处理中的声学模型与地震勘探中的褶积模型相近,可以借鉴语音信号的处理方法提取地震反射系数信息。因此本文从地震数据中提取反射系数的表征参数——地震倒谱特征参数,代替反射系数作为谱聚类的输入特征向量分析地震相。
假设s(n)为长度为N的一段地震信号,根据褶积理论,在时间域s(n)为子波x(n)与反射系数h(n)的褶积
| $ s(n)=x(n) * h(n) $ | (1) |
式中n表示时间域采样点。将式(1)变换到倒谱域
| $ \begin{aligned} Z^{-1}[\ln S(z)]=& Z^{-1}[\ln X(z)]+\\ & Z^{-1}[\ln H(z)] \end{aligned} $ | (2) |
式中:S(z)、X(z)、H(z)分别为s(n)、x(n)、h(n)的Z域表示,z表示Z域采样点;Z-1{·}表示逆Z变换。
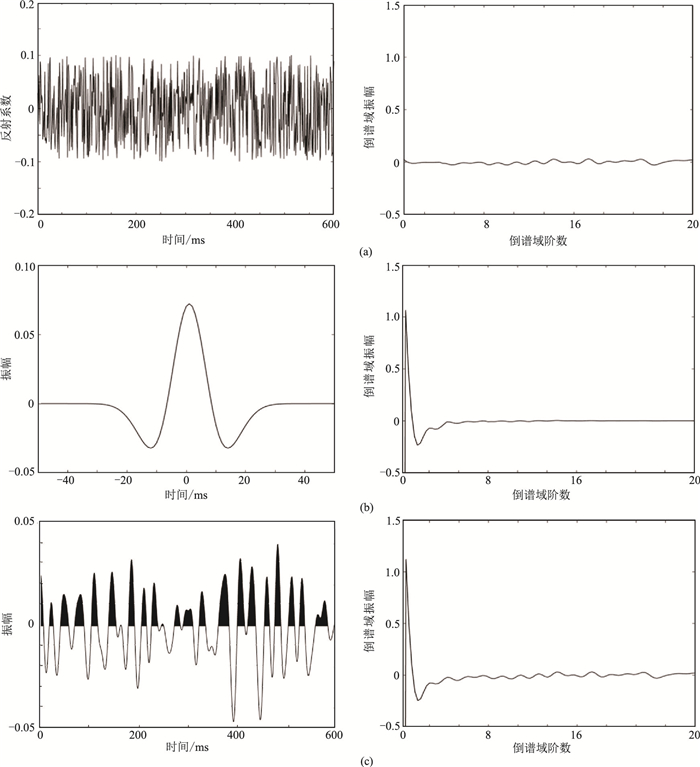
式(2)表明,对信号进行Z变换后取对数,再进行逆Z变换就得到信号的倒谱域表示。在倒谱域褶积地震信号转化为加性信号,容易分离地震子波与反射系数。利用模型数据验证式(2)的正确性(图 1)。可见,倒谱域地震记录的振幅(图 1c右)为反射系数振幅(图 1a右)与子波振幅(图 1b右)之和,实验结果验证了式(2)。根据式(2),有
| $ \hat{H}(Z)=\ln H(Z)=\sum\limits_{n=1}^{\infty} \hat{h}(n) z^{-n} $ | (3) |
|
图 1 反射系数(a)、Ricker子波(b)、地震数据(c)的时间域(左)和倒谱域(右)表示 |
式中
对于倒谱特征参数的计算,参照声纹识别技术[27],建立H(Z)的全极点模型
| $ H(Z)=\frac{G}{1-\sum\limits_{i=1}^{p} a_{i} z^{-i}} $ | (4) |
式中:ai为线性预测系数(Linear Predictive Coefficients,LPC);p为线性预测阶数;G为预测模型增益。
将式(3)两边对n求导,得到
| $ \left\{ \begin{array}{l} \hat h(0) = 0\\ \hat h(1) = {a_1}\\ \vdots \\ \hat h(n) = \left\{ {\begin{array}{*{20}{l}} {{a_n} + \sum\limits_{i = 1}^{n - 1} {\frac{i}{n}} {a_{n - i}}\hat h(i)}&{1 < n \le p}\\ {\sum\limits_{i = n - p}^{n - 1} {\frac{i}{n}} {a_{n - i}}\hat h(i)}&{n > p} \end{array}} \right. \end{array} \right. $ | (5) |
由自相关方法和Levinson-Durbin递推算法[28]计算地震数据得到ai。
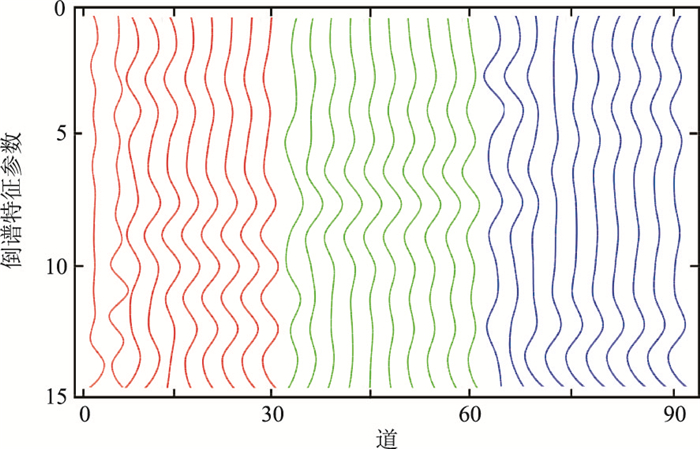
为了分析提取倒谱特征参数的有效性,建立楔形体模型(图 2a),用30Hz雷克子波正演得到合成地震记录,抽取其中三分之一(图 2b)进行分析;然后以单道地震记录为输入,提取地震数据的1~15阶倒谱特征参数(图 3)。可见,与正演地震记录30、60道位置反映的速度体边界(图 2b)相比,倒谱特征参数反映的边界(图 3)更清楚。说明地震倒谱特征参数可以充分提取反射系数信息,可作为谱聚类地震相分析的输入变量。

|
图 2 楔形体模型(a)及其正演地震记录(b) 30、60道位置对应楔形体中不同速度体边界 |
1.2 谱聚类
聚类作为一种不需要特定标签数据进行训练的无监督学习方法,已成为研究最多、应用最广的机器学习方法之一[15]。谱聚类方法能够将数据集的聚类转化为图的划分问题。图中的一个结点对应一个数据点,结点间的边权值对应数据间的相似度。图的切割就是找到一条或几条边,以这些边为切割点,将图划分为两个或多个子图,使同一个子图数据点间相似度高,不同子图数据点间相似度低[29-30]。
首先定义最小割集准则,将全部样本划分为集合A和B,目标函数Cut(A, B)为
| $ {\mathop{\rm Cut}\nolimits} (\mathit{\boldsymbol{A}}, \mathit{\boldsymbol{B}}) = \sum\limits_{{x_i} \in \mathit{\boldsymbol{A}}, {x_j} \in \mathit{\boldsymbol{B}}} {{w_{ij}}} $ | (6) |
式中
根据拉普拉斯矩阵的性质,目标函数转化为
| $ \operatorname{Cut}(\boldsymbol{A}, \boldsymbol{B})=\frac{1}{2} \boldsymbol{f}^{\mathrm{T}}(\boldsymbol{D}-\boldsymbol{W}) \boldsymbol{f}=\frac{1}{2} \boldsymbol{f}^{\mathrm{T}} \boldsymbol{L} \boldsymbol{f} $ | (7) |
式中:f为划分指示向量,
因此,可以将图的划分问题转化为寻找“全局最优”问题,即
| $ \min \limits_\boldsymbol{f} \boldsymbol{f}^{\mathrm{T}}(\boldsymbol{D}-\boldsymbol{W}) \boldsymbol{f} \quad \text { s. t. } \quad \boldsymbol{f}^{\mathrm{T}} \boldsymbol{f}=m $ | (8) |
式中m为聚类样本数。
根据瑞利商性质,式(8)可以转换为求解L的特征值问题,即使fT(D-W)f最小的解为L最小特征值对应的特征向量。将二分类问题推广到k类分类,谱聚类可表示为以下优化问题
| $ \min \limits_\boldsymbol{H} \operatorname{Tr}\left[\boldsymbol{R}^{\mathrm{T}}(\boldsymbol{D}-\boldsymbol{W}) \boldsymbol{R}\right] \quad \text { s. t. } \quad \boldsymbol{R}^{\mathrm{T}} \boldsymbol{D} \boldsymbol{R}=\boldsymbol{I} $ | (9) |
式中:Tr[·]为矩阵的迹;
在实际应用中发现,上述经典谱聚类方法存在相似度矩阵维数过大的问题。如对于10000个样本点的数据集,相似度矩阵大小为10000×10000,难以实现矩阵的存储和计算。因此本文优化了相似度矩阵计算方法,构建了稀疏相似度矩阵。首先设定稀疏系数ξ,对于某一样本点的相似度向量Wi=[wi1, wi2, …,wim],只保留相似度最大的前ξ个相似系数,其余以0值存储。通过对所有样本相似度向量的稀疏化,可以得到稀疏相似度矩阵。然后利用稀疏矩阵特征值分解的方法求取相似度矩阵的特征值和特征向量。
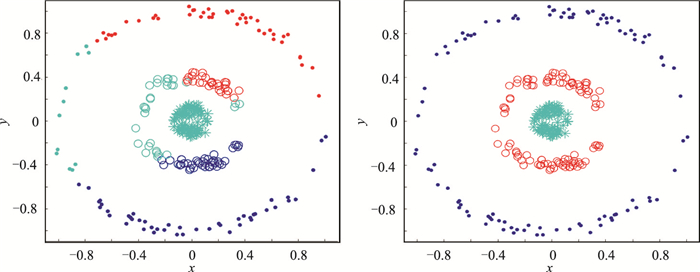
本文利用Three-circle数据集分析、对比K均值与谱聚类的效果(图 4)。可见:当相同标记的样本为同一种颜色,不同标记的样本为不同颜色时,分类精度更高;K均值的分类精度较低,这是由于其基于原型数据欧式距离进行分类,只考虑数据之间的欧式距离,因此对复杂结构数据集无法得到满意的分类结果(图 4左);谱聚类将原始数据映射到特征向量的数据空间中进行划分,因此对复杂结构数据集也能以极高的精度实现样本聚类(图 4右)。
|
图 4 Three-circle数据集K均值聚类(左)、谱聚类(右)效果 不同的标记点代表真实不同分类,颜色代表分类结果 |
根据前文的方法原理,建立方法的技术路线:
(1) 根据目标要求,按照一定大小的时窗提取每道地震记录;
(2) 以地震记录为输入,利用自相关方法和Levinson-Durbin递推算法计算线性预测系数ai;
(3) 利用式(5)通过递推方式计算地震信号倒谱特征参数
(4) 以
(5) 根据W求出相应正则化或非正则化L,并通过对L进行特征分解求出特征值及其对应特征向量;
(6) 选择特征向量构成特征向量空间,在特征向量空间采用常规聚类算法进行聚类,得到地震相自动分析结果。
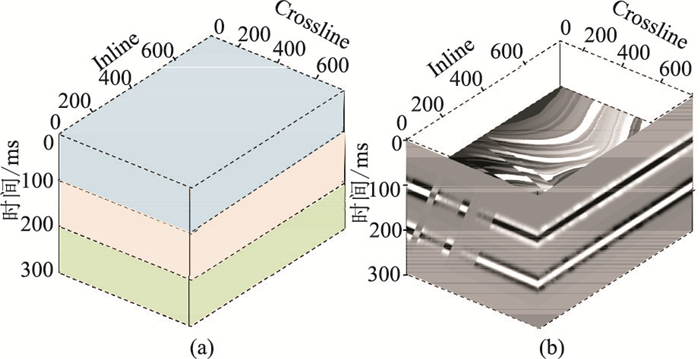
2 模型与实际数据测试 2.1 模型试验为了验证上述地震相分析方法的有效性,建立三维地质模型(图 5a),假设同一地震相具有相同或相近波阻抗数值。用30Hz雷克子波正演得到合成地震记录(图 5b)。
|
图 5 三维地质模型(a)及其正演地震记录(b) 模型尺寸为750×737×300,纵向上分为三层,每层时间厚度均为100ms,其中上、下两层为均匀层,速度为3000m/s,密度为2.2g/cm3,中间层由Marmousi模型(图 6)纵向叠置组成 |
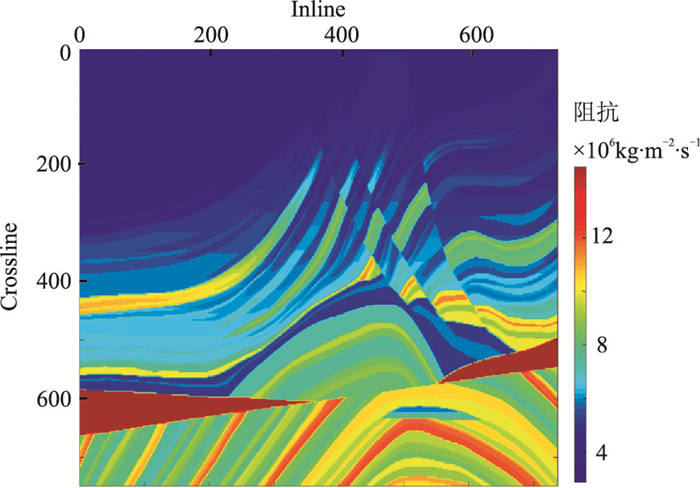
|
图 6 图 5a中间层阻抗平面图 |
按照本文方法利用正演地震记录得到聚类簇数k分别为3、6和10的地震相划分结果(图 7、图 8和图 9),倒谱特征参数阶数为1~15。

|
图 7 地震相划分结果(k=3) (a)真实地震相(根据波阻抗数据进行均分);(b)谱聚类(以地震倒谱特征参数为输入);(c)K均值聚类(以地震倒谱特征参数为输入);(d)K均值聚类(以地震记录为输入) |

|
图 8 地震相划分结果(k=6) (a)真实地震相(根据波阻抗数据进行均分);(b)谱聚类(以地震倒谱特征参数为输入);(c)K均值聚类(以地震倒谱特征参数为输入);(d)K均值聚类(以地震记录为输入) |

|
图 9 地震相划分结果(k=10) (a)真实地震相(根据波阻抗数据进行均分);(b)谱聚类(以地震倒谱特征参数为输入);(c)K均值聚类(以地震倒谱特征参数为输入);(d)K均值聚类(以地震记录为输入) |
通过直观对比、分析发现:①K均值聚类方法在原始数据空间计算距离,对于复杂数据划分能力有限,地震相划分结果(图 7c、图 7d、图 8c、图 8d、图 9c、图 9d)与真实地震相(图 7a、图 8a、图 9a)差距较大,而且随着聚类簇数增加,划分结果的随机性也逐渐增大,表现为:以地震记录为输入的K均值聚类结果(图 7d、图 8d、图 9d)存在很大的随机性,可解释性差,即使聚类簇数较低仍存在很大误差;以地震倒谱特征参数为输入的K均值聚类结果(图 7 c、图 8 c、图 9 c)可以消除地震波形的影响,充分利用反射系数划分地震相,可提高划分精度。②谱聚类方法将数据从原始数据空间映射到特征向量空间,避免直接计算数据距离,在复杂数据空间中仍有较高的划分精度,地震相划分结果(图 7b、图 8b、图 9b)与真实地震相(图 7a、图 8a、图 9a)吻合良好。为了说明聚类簇数为3、6和10的波阻抗的数值范围,统计了每一分类结果的类内波阻抗数值范围(表 1)。可见,与K均值聚类地震相划分结果(c、d)相比,谱聚类地震相划分结果(b)不同类间波阻抗数据重叠最小,与真实地震相(a)的波阻抗范围基本一致,吻合度更高。
|
|
表 1 k=3、6、10的类内波阻抗数值范围 |
为了更直观地定量评价模型划分精度,定义Rand指数
| $ \mathrm{RI}=\frac{2[\operatorname{vol}(\boldsymbol{S})+\operatorname{vol}(\boldsymbol{N})]}{m(m+1)} $ | (10) |
式中S、N为样本集合,即
| $ \left\{\begin{array}{l} \boldsymbol{S}=\left\{\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right) \mid \lambda_{i}=\lambda_{j}, \lambda_{i}^{*}=\lambda_{j}^{*}, i<j\right\} \\ \boldsymbol{N}=\left\{\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right) \mid \lambda_{i} \neq \lambda_{j}, \lambda_{i}^{*} \neq \lambda_{j}^{*}, i<j\right\} \end{array}\right. $ | (11) |
式中:λi、λj为真实划分结果簇标记;λi*、λj*为聚类结果对应的簇标记。RI∈[0, 1],其值越大,聚类精度越高。
图 10为不同方法模型划分的RI。由图可见:以地震记录为输入的K均值聚类地震相划分精度较低(RI约为0.5);以地震倒谱特征参数为输入的K均值聚类地震相划分精度明显提高(RI约为0.7);以地震倒谱特征参数为输入的谱聚类地震相划分精度最高(RI均大于0.9),再次验证了本文方法的有效性。
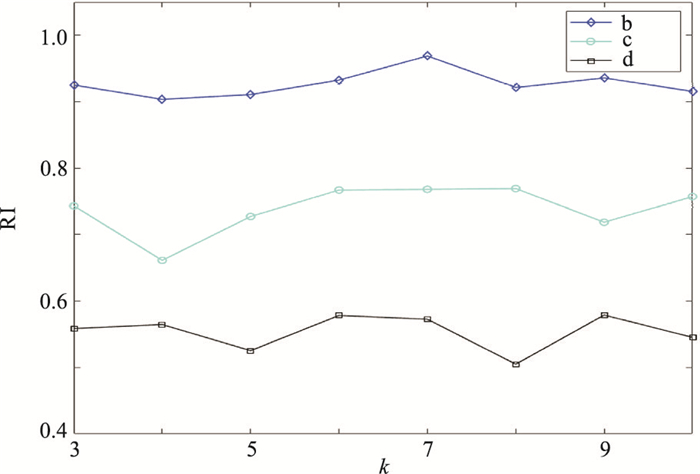
|
图 10 不同方法模型划分的RI b、c、d分别代表谱聚类(以地震倒谱特征参数为输入)、K均值聚类(以地震倒谱特征参数为输入)、K均值聚类(以地震记录为输入) |
利用实际地震资料测试本文方法的技术路线。图 11为P区Inline和Crossline地震剖面,目的层段为Es3下砂砾岩储层,层位S3为Es3下的顶。图 12为目标层段钻井资料。利用叠后三维地震数据分析地震相宏观展布,详细流程如下。
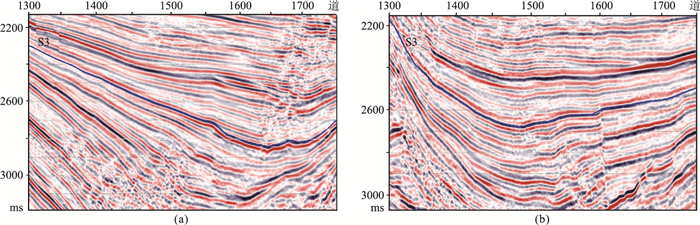
|
图 11 P区Inline(a)和Crossline(b)地震剖面 |
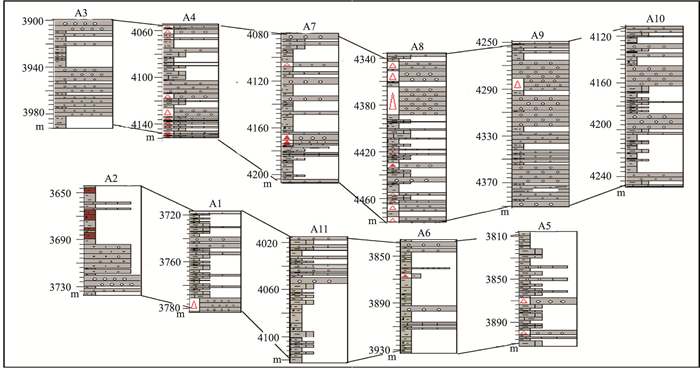
|
图 12 目标层段钻井资料 |
(1) 首先以S3为顶、向下50ms为底,截取时窗内的地震数据;
(2) 对截取的单道地震数据提取1~15阶地震倒谱特征参数,并做归一化处理;
(3) 以提取的地震倒谱特征参数为输入,采用谱聚类方法对全部地震道划分地震相。
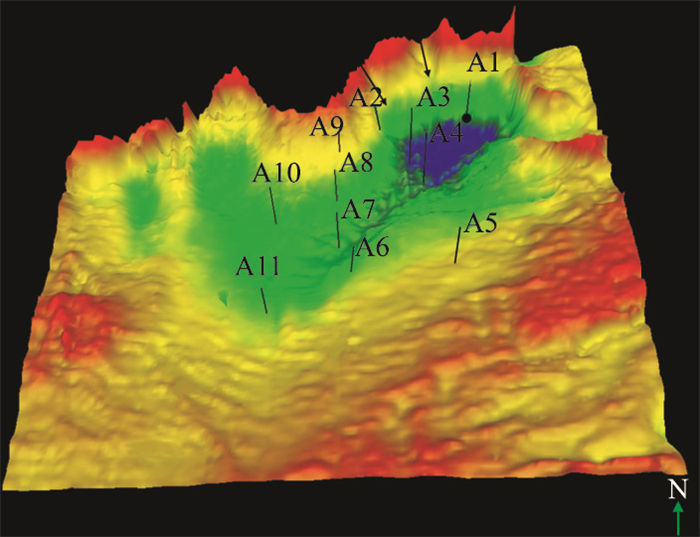
图 13为P区地震相划分结果。由图可见:①与地震瞬时振幅地震相划分结果(图 13b)相比,谱聚类地震相划分结果(图 13a)的地震相边界更清晰,可解释性更强。②与地震瞬时振幅地震相划分结果(图 13b)相比,多地震属性地震相划分结果(图 13c)的湖底扇体边界更清楚;但在湖底扇区域外,A5、A6井以南的区域仍显示大片扇体发育区(图 13c),与古地貌(图 14)不符,因此地震相划分精度低于谱聚类。钻井资料(图 12)揭示,A3、A4、A7、A8、A9、A10井位于扇体发育区,A1、A2、A5、A6、A11井位于扇体边缘或扇体不发育区。

|
图 13 P区地震相划分结果 (a)谱聚类;(b)地震瞬时振幅;(c)多地震属性聚类结果中的红色和黄色区域标定为扇体发育区,绿色和蓝色区域标定为扇体欠发育区 |
|
图 14 P区Es3下古地貌图 绿色为古地貌中的湖底部分 |
图 14为P区Es3下古地貌图。对比图 13a与图 14可见,前者的扇体发育区对应于后者的湖底区域,两者划分的边界吻合良好,验证了谱聚类地震相分析的准确性。
3 讨论本文提出一种基于地震数据倒谱特征参数的谱聚类地震相分析方法,其中倒谱特征参数阶数的选择对地震相分析结果具有重要影响。李韵[27]指出,在一定范围内,线性预测阶数与倒谱特征参数包含的信息量呈成正比,但是超过了某个值,高阶参数包含的信息量很少,而且会增加计算难度和量度,因此线性预测阶数的最佳取值范围为8~32。钟林鹏[31]通过实验论证了倒谱特征参数有效信息主要集中在前几阶。分析式(5)发现:当倒谱特征参数阶数小于线性预测阶数时,每一阶倒谱特征参数都会有新的线性预测系数加入;当倒谱特征参数的阶数大于线性预测阶数时,每一阶倒谱特征参数不再有新的线性预测系数加入,只是前几阶倒谱特征参数值的累加,因此包含的信息量有限,与文献[27, 31]结果一致。
为了在实际地震数据测试中选择合适阶数的倒谱特征参数,要在理论分析的基础上根据实际情况决定。对于大尺度目标,如目标层段为数百毫秒的地震数据,可以取较大的线性预测阶数,更利于挖掘宏观信息,相应地可取较高的倒谱特征参数阶数。对于小尺度目标,都应取较小的线性预测阶数和倒谱特征参数阶数。
4 结论与认识本文以地震倒谱特征参数为输入变量,研究了利用谱聚类分析地震相的方法。通过模型测试和实际数据应用,取得如下认识:
(1) 以图论为基础的谱聚类方法将数据的聚类转化为图的分割问题,通过图的最优分割实现数据的精确聚类。相较于传统以原型数据聚类的方法,谱聚类对复杂高维数据的划分能力更强,划分精度更高。通过优化相似度矩阵计算方法,构建稀疏相似度矩阵,可以降低矩阵维度过大引起的存储和计算量大的问题,使谱聚类更适用于划分三维空间地震相。
(2) 以地震数据的倒谱特征参数代替原始地震记录作为地震相划分的输入变量,一方面能减少数据的维数,减少计算复杂度和数据量;另一方面能消除波形的影响,提取直接反映地质情况的反射系数信息,提高划分精度。
(3) 实际数据应用表明,与地震瞬时振幅、多地震属性地震相划分结果相比,文中方法划分的地震相带与古地貌吻合更好,边界更清晰,可解释性也更强。将地震相划分结果与井资料进行标定可以划分不同的沉积单元,为油气勘探和油藏评价提供数据支撑。
| [1] |
Nivlet P. Uncertainties in seismic facies analysis for reservoir characterisation or monitoring:causes and consequences[J]. Oil & Gas Science and Technology, 2007, 62(2): 225-235. |
| [2] |
Abraham K J, Larry W L, Carlos T V, et al. Seismic facies identification and classification using simple statistics[J]. SPE Reservoir Evalution & Enginee-ring, 2008, 11(6): 984-990. |
| [3] |
Michael R, Bahk J J, Kim H S, et al. Seismic facies a-nalyses as aid in regional gas hydrate assessments, Part-I:classification analyses[J]. Marine and Petro-leum Geology, 2013, 47(1): 248-268. |
| [4] |
蔡涵鹏, 胡浩炀, 吴庆平, 等. 基于叠前地震纹理特征的半监督地震相分析[J]. 石油地球物理勘探, 2020, 55(3): 504-509. CAI Hanpeng, HU Haoyang, WU Qingping, et al. Semi-supervised seismic facies analysis based on pre-stack seismic texture[J]. Oil Geophysical Prospecting, 2020, 55(3): 504-509. |
| [5] |
朱剑兵, 赵培坤. 国外地震相划分技术研究新进展[J]. 勘探地球物理进展, 2009, 32(3): 167-171. ZHU Jianbing, ZHAO Peikun. Advances in seismic facies classification technology abroad[J]. Progress in Exploration Geophysics, 2009, 32(3): 167-171. |
| [6] |
穆星. 利用地震几何属性和自组织神经网络进行地震相的自动识别[J]. 地质科技情报, 2005, 24(3): 109-112. MU Xing. Method of seismic facies auto-classification by the seismic geometrical attribute and the self-organizing neural network[J]. Geological Science and Technology Information, 2005, 24(3): 109-112. DOI:10.3969/j.issn.1000-7849.2005.03.022 |
| [7] |
Ivan D M, Jean-Jules B, Bruce S H. A visual data-mining methodology for seismic facies analysis:Part 2:Application to 3D seismic data[J]. Geophysics, 2009, 74(1): P1-P11. DOI:10.1190/1.3046455 |
| [8] |
Thierry C, Manuel P, Kostia A. Unsupervised seismic facies classification:A review and comparison of techniques and implementation[J]. The Leading Edge, 2003, 22(10): 942-953. DOI:10.1190/1.1623635 |
| [9] |
张, 郑晓东, 李劲松, 等. 基于SOM和PSO的非监督地震相分析技术[J]. 地球物理学报, 2015, 58(9): 3412-3423. ZHANG Yan, ZHENG Xiaodong, LI Jinsong, et al. Unsupervised seismic analysis technology based on SOM and PSO[J]. Chinese Journal of Geophysics, 2015, 58(9): 3412-3423. |
| [10] |
刘仕友, 宋炜, 应明雄, 等. 基于密度的含噪声角道集波形聚类地震相分析[J]. 石油物探, 2019, 58(5): 773-782. LIU Shiyou, SONG Wei, YING Mingxiong, et al. Seismic facies analysis for angle gathers based on DBSCAN waveform clustering[J]. Geophysical Prospecting for Petroleum, 2019, 58(5): 773-782. DOI:10.3969/j.issn.1000-1441.2019.05.017 |
| [11] |
Duan Y T, Zheng X D, Hu L L, et al. Seismic facies analysis based on deep convolutional embedded clustering[J]. Geophysics, 2019, 84(6): IM87-IM97. DOI:10.1190/geo2018-0789.1 |
| [12] |
Thilo W, Indranil P, Robert L G, et al. Seismic facies analysis using machine learning[J]. Geophysics, 2018, 83(5): O83-O95. DOI:10.1190/geo2017-0595.1 |
| [13] |
刘振峰, 郝天珧, 杨长春. 沉积模型和储层随机建模[J]. 地球物理学进展, 2003, 18(3): 519-523. LIU Zhenfeng, HAO Tianyao, YANG Changchun. Sedimentation models and stochastic reservoir modeling[J]. Progress in Geophysics, 2003, 18(3): 519-523. DOI:10.3969/j.issn.1004-2903.2003.03.030 |
| [14] |
冯国庆, 李允, 林作华, 等. 应用序惯指示模拟方法模拟沉积微相[J]. 西南石油学院学报, 2001, 23(2): 1-4. FENG Guoqing, LI Yun, LIN Zuohua, et al. Application of sequential indicator simulation method to delineating sedimentary microfacies[J]. Journal of Southwest Petroleum Institute, 2001, 23(2): 1-4. DOI:10.3863/j.issn.1674-5086.2001.02.001 |
| [15] |
周志华. 机器学习[M]. 北京: 清华大学出版社, 2016: 197-199. ZHOU Zhihua. Machine Learning[M]. Beijing: Tsinghua University Press, 2016: 197-199. |
| [16] |
伍育红. 聚类算法综述[J]. 计算机科学, 2015, 42(Z6): 491-524. WU Yuhong. General overview on clustering algorithms[J]. Computer Science, 2015, 42(Z6): 491-524. |
| [17] |
南男, 杨健, 赵晶晶, 等. 基于谱聚类特征向量分析的模态划分方法[J]. 华东理工大学学报(自然科学版), 2017, 43(5): 669-676. NAN Nan, YANG Jian, ZHAO Jingjing, et al. Mode partitioning method based on eigenvector analysis in spectral clustering[J]. Journal of East China University of Science and Technology (Natural Science Edition), 2017, 43(5): 669-676. |
| [18] |
高尚兵, 周静波, 严云洋. 一种新的基于超像素的谱聚类图像分割算法[J]. 南京大学学报(自然科学版), 2013, 49(2): 169-175. GAO Shangbing, ZHOU Jingbo, YAN Yunyang. A new superpixel based spectral clustering for image segmentation[J]. Journal of Nanjing University (Na-tural Sciences), 2013, 49(2): 169-175. |
| [19] |
印兴耀, 周静毅. 地震属性优化方法综述[J]. 石油地球物理勘探, 2005, 40(4): 482-489. YIN Xingyao, ZHOU Jingyi. Summary of optimum method of seismic attributes[J]. Oil Geophysical Prospecting, 2005, 40(4): 482-489. DOI:10.3321/j.issn:1000-7210.2005.04.027 |
| [20] |
冯小英, 杨延辉, 左银卿, 等. 敏感属性与参数反演融合定量预测煤体结构[J]. 石油地球物理勘探, 2019, 54(5): 1115-1122. FENG Xiaoying, YANG Yanhui, ZUO Yinqing, et al. Coal structure quantitative prediction with sensitive-attribute and parameter-inversion fusion[J]. Oil Geophysical Prospecting, 2019, 54(5): 1115-1122. |
| [21] |
张繁昌, 刘杰, 印兴耀, 等. 修正柯西约束地震盲反褶积方法[J]. 石油地球物理勘探, 2008, 43(4): 391-396. ZHANG Fanchang, LIU Jie, YIN Xingyao. Modified Cauchy-constrained seismic blind deconvolution[J]. Oil Geophysical Prospecting, 2008, 43(4): 391-396. DOI:10.3321/j.issn:1000-7210.2008.04.006 |
| [22] |
Sui Y H, Ma J W. A nonstationary sparse spike deconvolution with anelastic attenuation[J]. Geophy-sics, 2019, 84(2): R221-R234. |
| [23] |
Du X, Li G F, Zhou Z X, et al. Band-controlled sparse deconvolution[J]. Journal of Applied Geophysics, 2018, 155(8): 53-61. |
| [24] |
张繁昌, 何晋越, 桑凯恒, 等. 稀疏反射系数频率域正余弦分量协同反演方法[J]. 石油地球物理勘探, 2018, 53(4): 778-783. ZHANG Fanchang, HE Jinyue, SANG Kaiheng, et al. A sparse reflectivity sine-cosine synergistic inversion method in the frequency[J]. Oil Geophysical Prospecting, 2018, 53(4): 778-783. |
| [25] |
Castagna J P. Spectral decomposition and high resolution reflectivity inversion[C]. SEG Technical Program Expanded Abstracts, 2004, 23: 1238-1241.
|
| [26] |
Xie T, Zheng X D, Zhang Y. Seismic facies analysis based on speech recognition feature parameters[J]. Geophysics, 2017, 82(3): O23-O35. DOI:10.1190/geo2016-0121.1 |
| [27] |
李韵.声纹识别系统中特征参数提取方法的对比分析研究[D].四川成都: 成都理工大学, 2016. LI Yun.The Comparison and Analysis of the Feature Extraction Algorithm of Voiceprint Recognition System[D]. Chengdu University of Technology, Chengdu, Sichuan, 2016. |
| [28] |
韩纪庆, 张磊, 郑铁然. 语音信号处理[M]. 北京: 清华大学出版社, 2013: 97-114. HAN Jiqing, ZHANG Lei, ZHENG Tieran. Processing of Speech Signal[M]. Beijing: Tsinghua University Press, 2013: 97-114. |
| [29] |
Francis R B, Michael I J. Learning spectral clustering, with application to speech separation[J]. Journal of Machine Learning Research, 2006, 7(6): 1963-2001. |
| [30] |
Shi J B, Malik J. Normalized cuts and image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(8): 888-905. DOI:10.1109/34.868688 |
| [31] |
钟林鹏.说话人识别系统中的语音信号处理技术研究[D].四川成都: 电子科技大学, 2013. ZHONG Linpeng.Studies on the Speech Signals Processing of the Speaker Recognitions System[D]. University of Electronic Science and Technology of China, Chengdu, Sichuan, 2013. |



 张繁昌, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Emall:
张繁昌, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Emall: