2 中国石油大学(北京), 北京 102249
2 China University of Petroleum (Beijing), Beijing 102249, China
对于致密砂岩储层,因受成岩作用和裂缝分布等多种地质因素影响,较难准确获取渗透率,因此在测井解释中渗透率预测方法始终为研究难点。渗透率预测模型主要分为物理模型[1-3]和拟合模型[4-6]。常用的物理模型有指数型[1-3]、Kozeny-Carman[2-3, 7]、Timur[2, 8-9]和Herron[2, 8-9]等。虽然上述物理模型基于测井理论,能得到可靠的渗透率预测值,但推广性较差,原因在于:难以准确获取模型的许多非测井曲线参数,如束缚水饱和度和岩石矿物含量等,导致在资料不充足的情况下无法应用;致密砂岩储层孔喉系统复杂,且易发育裂缝,使渗透率测井响应存在多解性,因此利用同一模型难以良好解释研究区所有层段。由于渗透率本质上是多种地质特征参数的综合反映,而这些参数大多与测井响应相关,因此从数学角度上讲可由测井曲线拟合渗透率[4-6]。拟合模型一般仅用于计算测井曲线,且无需过多考虑地质因素的影响,极大减少了渗透率预测的计算量,因此在测井解释中得到快速发展[10-12]。多元线性拟合和逐步迭代为经典的拟合方法。与多元线性拟合相比,逐步迭代考虑了自变量共线性问题,因此应用更广泛。刘建建等[10]利用逐步回归建立了长6储层渗透率模型。刘敏[11]以测井资料为基础,利用逐步回归估算了长庆T气田致密砂岩储层渗透率。由嘉雨[12]利用逐步回归计算了榆树林油田葡萄花油层储层参数。虽然逐步迭代能快速预测渗透率,但也存在问题,如难以确定各类测井曲线与渗透率之间的复杂关系,因此无法用解析式表示目的层渗透率最优拟合模型。
为更智能地建立拟合模型,人们尝试利用机器学习技术预测渗透率。当前,拟合性能较好的机器学习模型包括支持向量回归(support vector regression,SVR)[13-16]和梯度提升决策树(gradient boosting decision tree,GBDT)等[17-20]。邓浩阳[13]利用SVR估算高孔、低渗碳酸盐岩储层渗透率。李佳[14]利用SVR和其他机器学习模型预测多孔介质渗透率,且SVR预测效果较好。Majid等[15]、Zhang等[16]利用以径向基函数为主的SVR预测储层渗透率,取得较好效果[15-16]。Subasi等[17]使用改进GBDT模型高效预测了常规油气储层渗透率。韩启迪等[18]、谢云欣[19]、Zhang等[20]认为GBDT在测井解释方面具有发展前景。虽然上述拟合模型的预测效果较好,但仍存在一些应用问题:①由于建模时需多种经验参数(SVR需要惩罚系数等,GBDT需要回归决策树(classification and regression tree,CART)个数和学习速率等),难以优化预测结果;②由于模型没有加入正则化项,在学习过程中易出现过拟合现象;③受自身算法的限制,模型在训练大量样本时非常低效。针对上述问题,人们提出了一种性能更好的模型——XGBoost[21-23],高效地实现了GBDT算法并进行了算法和工程上的许多改进。该模型加入了正则化项,并将拟合模型精细化,因此在理论上较SVR和GBDT等拥有更强的预测能力[21-22]。闫星宇等[23]利用XGBoost较好地预测了致密砂岩含气储层参数,但其采用试错法调试参数,效率低,且无法保证所用参数为最优组合。为此,本文从优化参数角度出发,利用粒子群优化(particle swarm optimization,PSO)算法改进XGBoost[24-26],进而提出渗透率预测模型PSO-XGBoost,并阐述该模型的方法原理及相关实验。
1 方法原理因为XGBoost利用测井数据预测渗透率,所以训练样本和预测样本数据集应由测井曲线和实测渗透率数据构成,可表示为
| $ \boldsymbol{A}=\left\{\boldsymbol{X}_{m n}, \boldsymbol{Y}_{m}\right\} $ | (1) |
式中:Xmn为测井数据集,m为样本量,n为测井曲线个数;Ym为渗透率向量。在确定样本数据集后,预测模型可表示为[21-23]
| $ F\left(x_{i}\right)=f_{0}\left(\boldsymbol{x}_{i}\right)+\sum\limits_{k=1}^{K_{X}} \sum\limits_{j=1}^{T_{k}} w_{j, k} \cdot \eta $ | (2) |
式中:f0(xi)为初始模型(也称基分类器),xi为第i个样本;k=1, 2, …, KX为迭代次数;j=1, 2, …, Tk为CART叶节点,Tk为第k次迭代的CART叶节点个数;wj, k为第k次迭代的第j叶节点对应的所有样本的替代值;η为学习速率。
f0(xi)一般由损失函数确定,即
| $ f_{0}\left(\boldsymbol{x}_{i}\right)=\underset{\alpha}{\operatorname{argmin}} \sum\limits_{i=1}^{m} L\left(y_{i}, \alpha\right) $ | (3) |
式中L(yi, α)为损失函数,确定目标值与预测值之间的差值,yi为第i个样本目标值,α为使损失函数达到最小的常数。wj, k由
| $ w_{j, k}=-\frac{\sum \partial L\left(y_{i}, \hat{y}_{i, k-1}\right) / \partial \hat{y}_{i, k-1}}{\sum \partial^{2} L\left(y_{i}, \hat{y}_{i, k-1}\right) / \partial \hat{y}_{i, k-1}^{2}+\lambda} $ | (4) |
确定。式中:
XGBoost采用不同损失函数可得到不同的训练效果。考虑到平方损失函数对异常点或噪声点敏感,本文采用绝对损失函数建模[21-22]。
由于XGBoost在建模中要设定许多经验参数,如CART叶节点个数、学习速率和正则化系数等,因此需优化才能保证建模质量。PSO能解决多目标最优化问题,因此文中用该技术优化XGBoost。如设定优化种群数量为q,则XGBoost参数种群可表示为
| $ \mathit{\boldsymbol{ \boldsymbol{\varGamma} }} = \left\{ {{\mathit{\boldsymbol{\sigma }}_{i'}}\mid {\mathit{\boldsymbol{\sigma }}_{i'}} = \left( {{\sigma _{1i'}}, {\sigma _{2i'}}, \cdots , {\sigma _{zi'}}} \right)\quad i' = 1, 2, \cdots , q} \right\} $ | (5) |
式中
| $ \left\{\begin{array}{l} \mathit{\boldsymbol{\varDelta}}_{i'}^{j'}=\left\{\boldsymbol{\sigma}_{i'}^{j'} \mid \boldsymbol{\sigma}_{i'}^{j'}=\min \left(\left\|\boldsymbol{O}_{i'} \boldsymbol{-} \boldsymbol{O}_{\mathrm{std}}\right\|_{2}\right) \quad j'=1, 2, \cdots, t\right\} \\ \mathit{\boldsymbol{\varDelta}}_{g}^{j'}=\left\{\boldsymbol{\sigma}_{\mathit{\Gamma}}^{j'} \mid \boldsymbol{\sigma}_{\mathit{\Gamma}}^{j'}=\min \left(\left\|\boldsymbol{O}_{\mathit{\Gamma}}^{\prime}-\boldsymbol{O}_{\mathrm{std}}\right\|_{2}\right)\right\} \\ \boldsymbol{W}_{i'}^{j'+1}=\omega \boldsymbol{W}_{i'}^{j'}+c_{1} r_{1}\left(\mathit{\boldsymbol{\varDelta}}_{i'}^{j'}-\boldsymbol{\sigma}_{i'}^{j'}\right)+c_{2} r_{2}\left(\mathit{\boldsymbol{\varDelta}}_{g}^{j'}-\boldsymbol{\sigma}_{i'}^{j'}\right) \\ \boldsymbol{\sigma}_{i'}^{j'+1}=\boldsymbol{\sigma}_{i'}^{j'}+\boldsymbol{W}_{i'}^{j'+1} \end{array}\right. \\ \text { s. t. }\left\{\begin{array}{l} \boldsymbol{\sigma}_{i'}^{j'} \in\left[\boldsymbol{\sigma}_{\max _{-} 1}, \boldsymbol{\sigma}_{\max _{-} 2}\right] \\ \boldsymbol{W}_{i'}^{j'} \in\left[-\boldsymbol{W}_{\max }, \boldsymbol{W}_{\max }\right] \end{array}\right. $ | (6) |
式中:
为在PSO迭代前期锁定全局最优解方向,ω一般取较大值,而在迭代后期取较小值进行局部搜索。本文采用线性下降法(linear decreasing inertia weight,LDIW)优化ω[25-26]。
综合上述,图 1总结了PSO-XGBoost计算流程[21-26]。
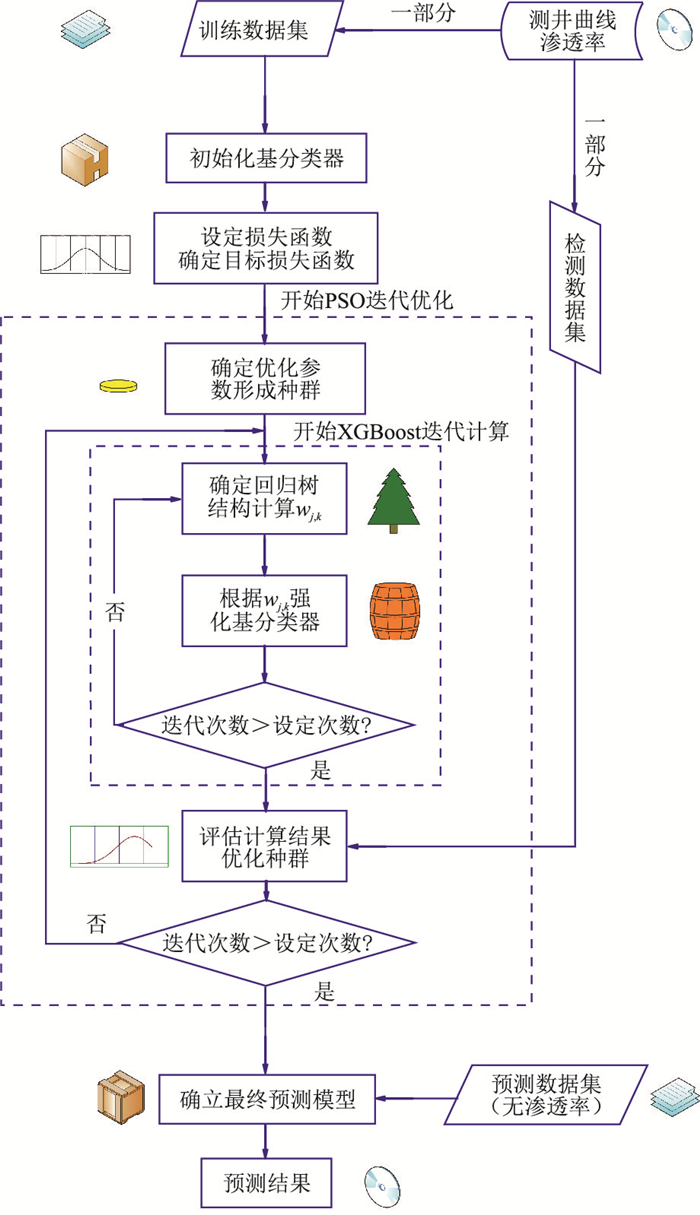
|
图 1 PSO-XGBoost计算流程 |
实验目的层为姬塬油田西部长4+5段致密砂岩储层。姬塬油田处于鄂尔多斯盆地中西部,位于天环坳陷和陕北斜坡两个一级构造单元之间(图 2a)。长4+5段是三叠系延长组主力层系之一,储层形成受控于沉积相带展布,多为水下分流河道砂体,部分为河口坝砂体[27-30]。分析现有资料可知,储层孔隙以原生粒间孔(图 2c)、粒间溶孔(图 2d)和晶间孔(图 2e、图 2f)为主,在某些井区发育微裂缝(图 2g),表明储层具有一定的储集空间和渗流通道[27-28]。然而,在成岩作用阶段,受石英次生增大和自生黏土矿物等影响,孔喉结构以细孔—细微喉道和微孔—细微喉道组合为主,在压汞曲线上多体现为Ⅲ型和Ⅳ型(图 2h),说明储层渗流性较差。因此,在评价储层时,能否获取准确渗透率数值将成为一关键研究点[29-30]。

|
图 2 工区及其储层相关资料 (a)鄂尔多斯盆地构造单元划分;(b)姬塬油田研究区长4+5顶面构造图;(c)原生粒间孔(YP1井,长4+511);(d)长石溶蚀孔隙(YP2井,长4+522);(e)高岭石晶间孔(YZ1井,长4+512);(f)绿泥石与伊利石晶间孔(YZ2井,长4+522);(g)微裂缝(YZ3井,长4+522);(h)储层压汞曲线分类 |
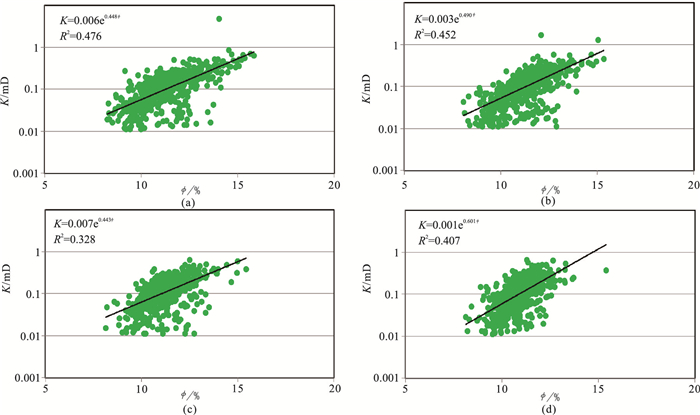
由岩心和测井等资料分析得知,目的层可划分为4个小层(长4+511、长4+512、长4+521、长4+522)。采用指数模型分析小层渗透率时,发现孔渗相关性较差(图 3),其拟合优度R2一般小于0.5。对于其他常用物理模型,如Kozeny-Carman模型等,因基础资料不充足无法应用。以上情况说明常规物理模型并不适用于预测目的层渗透率,故文中采用PSO-XGBoost进行预测。为突出验证效果,在实验中对比了逐步迭代、SVR和GBDT三种模型的验证结果。验证井共有8口,分布在研究区东、西部(图 2b),东、西部储层因受不同沉积和成岩作用影响而具有不同的品质。为综合验证PSO-XGBoost的预测能力,设计了三个实验。三个实验分别为:利用西区井资料(H1、H2、Y1)预测东区井资料(HA);利用东区井资料(L1、H3、H4)预测西区井资料(HB);利用全区井资料预测东、西区井资料(HA、HB)。前两个实验可了解不同储层品质的井区资料的相互预测效果,第三个实验考查在训练更多样本的情况下模型的预测能力。
|
图 3 不同小层的指数型孔(ϕ)—渗(K)模型 (a)长4+511;(b)长4+512;(c)长4+521;(d)长4+52 2 |
实验测井数据由H1、H2和Y1井资料组成,共534个样本。每个样本由6条测井曲线构成,包括声波时差(AC)、补偿中子测井(CNL)、补偿密度测井(DEN)、自然伽马(GR)、自然电位(SP)和原状地层电阻率(RT)。样本对应的渗透率值由气测实验得到,变化范围为0.01~7.60mD。表 1展示了部分训练样本数据。由于对比模型SVR和GBDT在计算中也涉及经验参数,因此为使验证对象都处于相同优化状态,也用PSO进行优化。对于逐步迭代,由于算法只利用自变量和因变量数据进行分析,不涉及处理其他经验参数,因此无需优化。由PSO-XGBoost计算流程(图 1)可知,因增加PSO优化流程,训练样本分为两部分,一部分用于建模,另一部分用于PSO迭代检测。为此,在实验中将训练样本以比例0.7/0.3分配给建模和优化检测,即374个样本用于建模,160个样本用于优化检测。
|
|
表 1 部分训练样本数据 |
虽然逐步迭代公式无需优化,但为防止所建模型过拟合,也采用上述训练样本分配方案进行建模和检测。应用逐步迭代之前,先要确定测井曲线与渗透率之间的关系式。由于该模型只是从数学角度出发对数据进行处理,且为加强通用性,一般不加入交叉项和幂指数项,所以设定的渗透率与所用的测井曲线的关系式一般为线性[8-10]。渗透率和RT常呈数量级变化,但目的层的RT变化不大,因此建模时将渗透率数据K以对数形式分析。由374个训练样本拟合得到的逐步迭代模型为
| $ \begin{array}{r} \lg K=0.017 \mathrm{AC}+0.028 \mathrm{CNL}-1.91 \mathrm{DEN}- \\ 0.021 \mathrm{GR}+0.013 \mathrm{SP}+0.003 \mathrm{RT}+1.746 \end{array} $ | (7) |
式(7)的调整拟合优度R2(0.68)高于常规指数模型(图 3)。因此,与常规指数模型相比,以多种测井曲线资料为基础,利用逐步迭代建立的拟合模型能更好地反映致密砂岩储层渗透率的变化趋势。采用MSE (mean squared error)评价计算误差[7-12],因此误差单位应为mD2。在下文中,为表达简便,MSE只讨论其数值。统计逐步迭代模型的160个检测样本的验证结果(图 4a)表明,72.5%的结果与目标值处于同一数量级,说明该模型在预测同一井区的数据时效果较好。

|
图 4 实验1建模验证结果统计 (a)逐步迭代;(b)PSO-SVR;(c)PSO-GBDT;(d)PSO-XGBoost 绿色点为预测渗透率K′与岩心渗透率K处于同一数量级,红色点表示两者不在同一数量级 |
预测样本为HA井数据,共50个,其构成比例与训练样本一致。利用逐步迭代模型进行预测的MSE较大(0.8744,表 2),说明逐步迭代建立的拟合模型在不同储层品质的井区资料的相互预测中效果不理想。
|
|
表 2 实验MSE统计 |
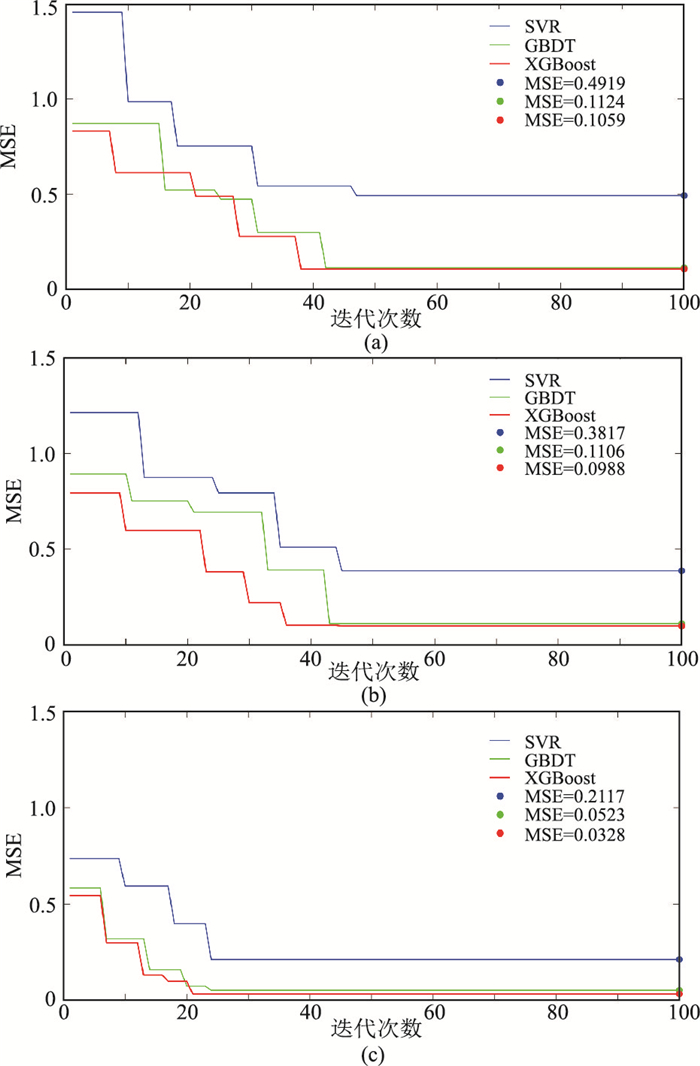
对于SVR,首先确定参数框架,之后再进行PSO优化建模,其中3个参数需要优化[13-16, 24-26]。需要说明的是,重力系数和加速系数虽为经验值,但一般不需要改动,即大幅度改动这些参数也不明显影响优化结果,侧面说明利用PSO技术进行优化可减少模型调参工作量。SVR参数优化结果与初始设定值差别较大,说明参数优化的必要性(表 3)。优化过程(图 5a)表明,在100次迭代中,MSE由1.400降至0.4919,说明了PSO的优化作用。PSO-SVR的验证结果统计(图 4b)表明,84.38%的计算结果与目标值处于同一数量级,其可靠程度较逐步迭代模型有所提升,表明PSO-SVR能更好地处理来自同一井区的数据。利用PSO-SVR的MSE较逐步迭代小(0.7212,表 2),但仍不理想,说明该模型在利用其他井区资料预测渗透率时效果不好。
|
|
表 3 预测模型参数设置和参数优化结果 |
|
图 5 PSO优化过程及其优化结果 (a)实验1;(b)实验2;(c)实验3 |
对于GBDT,表 3分别展示了初始参数设定、优化参数设定和参数优化结果[17-20]。优化过程(图 5a)表明,MSE由0.8000降至0.1124,表明PSO在参数优化方面的显著作用。PSO-GBDT验证结果统计(图 4c)表明,92.5%的结果与目标值数处于同一数量级,说明在处理检测样本时该模型的预测能力较逐步迭代、SVR强,且MSE(0.1526,表 2)远小于上述两种模型,说明该模型能有效利用其他井区资料预测目标井数据。
对于XGBoost,表 3分别展示了初始参数、PSO优化参数和参数优化结果[21-23]。优化过程(图 5a)表明,MSE由0.7000降至0.1059,充分说明XGBoost的参数优化得益于PSO技术。PSO-XGBoost验证结果统计(图 4d)表明,94.37%的结果与目标值数处于同一数量级,表明在处理来自同一井区的资料时,该模型的预测能力强于前三种模型,且MSE(0.1273,表 2)最小,证明该模型能有效利用其他井区资料高精度地完成预测任务。
图 6为实验1预测结果柱状图。由图可知,PSO-GBDT和PSO-XGBoost落在计算误差列中的数据点最多,但后者的数据点整体更偏向0线,表明PSO-XGBoost预测结果的精度最高。
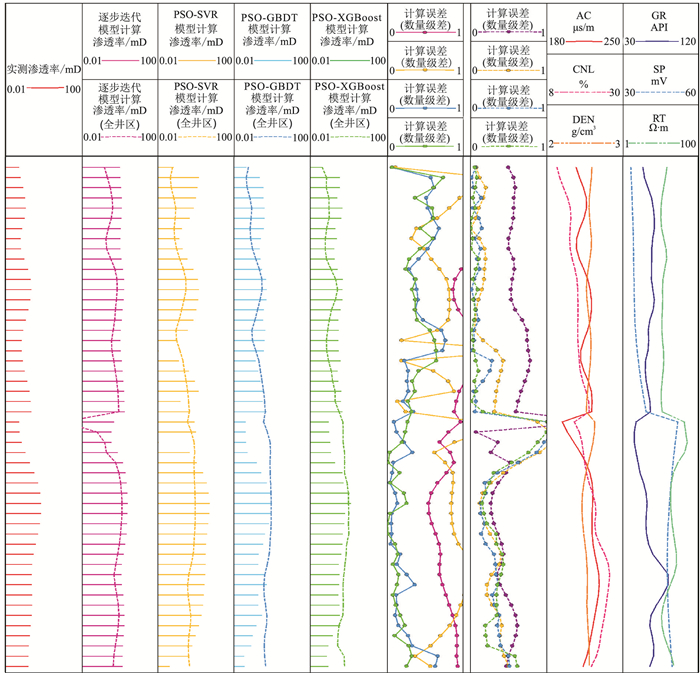
|
图 6 实验1预测结果柱状图 为更好地对比各模型预测结果的可靠度,计算误差一列只显示预测值与目标值数量级差小于一个量级的数据点(图 7同),因此数据点值越小,预测结果误差越小;不同颜色、线条对应不同的计算结果(图 7同) |
本实验训练数据由L1、H3和H4井资料构成,共505个样本,样本构成要素同实验1。渗透率值由气测实验得到。在实验中将训练样本以比例0.7/0.3分配给建模和优化检测。
对于逐步迭代,建模得到的拟合公式为
| $ \begin{aligned} \mathrm{lg} K=&-0.017 \mathrm{AC}-12.36 \mathrm{DEN}-\\ & 0.09 \mathrm{GR}-0.023 \mathrm{SP}+0.018 \mathrm{RT}+36.803 \end{aligned} $ | (8) |
式中的拟合变量缺少CNL,说明CNL曲线在实验中对于渗透率变化无影响。对比式(7)和式(8)发现,逐步迭代在处理不同井区资料时得到的拟合表达式差别较大,表明模型的推广性差,即由本井区资料所建的拟合模型不适用于预测其他井区资料。预测数据由HB井资料构成,共50个样本,其构成要素与训练样本一致。利用逐步迭代模型进行预测的MSE(0.3479,表 2)明显小于实验1,表明该模型的预测能力受建模数据影响较大,因此模型的预测稳定性非常差。
对于SVR,参数及其优化设定同实验1。优化过程(图 5b)表明,MSE由约1.2000降至0.3871,表明模型的预测能力受PSO优化而得到提升。PSO-SVR的MSE(0.1756,表 2)明显小于实验1,表明该模型的预测能力受建模资料品质影响较大,因此计算稳定性不佳而难以推广应用。
对于GBDT,参数及其优化设定同实验1。优化过程(图 5b)表明,MSE由约0.8000降至0.1106,说明PSO起到了良好的优化作用。PSO-GBDT的MSE(0.1413,表 2)与实验1相近,表明该模型能利用其他井区资料有效预测渗透率,而且预测稳定性较好,能够推广应用。
对于XGBoost,参数及其优化设定同实验1。优化过程(图 5b)表明,MSE由约0.7000降至0.0988,说明PSO技术在建模中起到了良好的优化作用。PSO-XGBoost的MSE(0.0667,表 2)最小,再次证明PSO-XGBoost能够利用其他井区资料有效预测渗透率,而且预测能力最强。
图 7为实验2预测结果柱状图。由图可见:虽然PSO-SVR的计算误差与PSO-XGBoost的相近,且都靠近0点,但在计算误差列的顶端和末段都处于0.5~1范围内,且中间有些点的误差已经大于1;PSO-XGBoost在这些区域的点都基本落在0~0.5范围内,表明PSO-XGBoost的计算结果更精确。
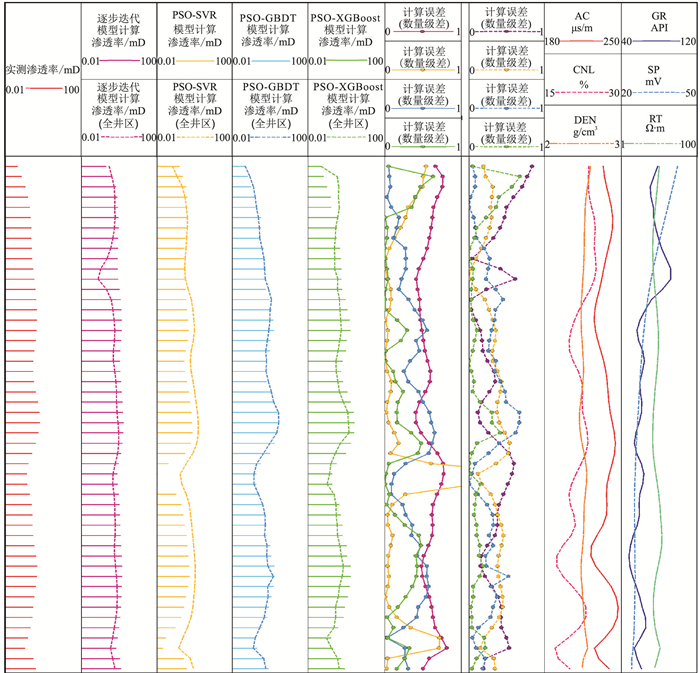
|
图 7 实验2预测结果柱状图 |
在本实验中,将由东、西井区资料合并构成的训练数据进行预测。训练样本有1039个,对于所有模型,将训练样本以比例0.7/0.3分配给建模和优化检测。
对于逐步迭代,得到的拟合公式为
| $ \begin{aligned} \mathrm{lg} K=& 0.032 \mathrm{CNL}-7.06 \mathrm{DEN}-0.014 \mathrm{GR}-\\ & 0.012 \mathrm{SP}-0.004 \mathrm{RT}+19.198 \end{aligned} $ | (9) |
模型经算法判断将AC曲线去除,形成的拟合表达式与实验1、实验2的不一致,再次说明在处理不同的建模数据时逐步迭代容易形成不同的拟合公式,难以推广应用。对于目标井的MSE(分别为0.3360和0.1581,表 2)较实验1、实验2的小,表明在训练更多学习样本的情况下,模型的预测能力得到明显提升。
对于SVR,优化过程(图 5c)表明PSO具优化作用,PSO-SVR的MSE(分别为0.1534和0.1146,表 2)小于实验1、实验2,证明该模型的预测能力在处理更多训练样本的情况下得到加强。同时,MSE与实验1的相差较大,与实验2的相差较小,也再次表明模型的预测能力受训练数据品质影响较大,反映了模型的预测稳定性差。
对于GBDT,PSO-GBDT的MSE(分别为0.1352和0.0990,表 2)小于实验1、实验2,但相差不大,说明模型不仅在训练更多学习样本后形成更强的预测能力,而且模型的预测稳定性较好,能够推广应用。
对于XGBoost,PSO-XGBoost的MSE(分别为0.1259和0.0378,表 2)小于实验1、实验2,且降幅较小,说明XGBoost的预测能力不仅在处理更多训练样本后得到提升,而且预测稳定性好。与PSO-GBDT相比,XGBoost的MSE更小,说明该模型更具备推广价值。
由图 6和图 7的计算误差列可看出,在处理更多建模样本的情况下,各验证模型的MSE较实验1、实验2有所减小,很好地说明了扩大训练样本容量是一种提升各验证模型预测能力的有效手段。同时,PSO-XGBoost的MSE最小,再一次说明该模型预测渗透率的能力最强,最具推广应用价值。
2.5 计算时间分析表 2展示了各验证模型在不同实验中的计算耗时。从整体上看,PSO-SVR耗时最少,PSO-XGBoost耗时最多。PSO-XGBoost的计算速度最慢是因为在实验中没有采用XGBoost并行计算技术。考虑到在处理大数据时,XGBoost计算耗时会随着回归树量的增加而成倍增长,为此设计了能够并行计算的数据存储方式及其处理方法[21-23]。在处理大于10万个样本或样本包含上百个变量的数据体时,才能明显体现XGBoost的并行计算效率。虽然PSO-XGBoost在处理所用的训练样本(小数据体)时耗时最长,但与其他模型的耗时差距并不大,在可接受范围之内,并且所得结果的精度更高,说明PSO-XGBoost在处理一般小型数据体时效率较高。
3 结论本文从优化参数角度出发,利用PSO算法改进XGBoost[24-26],得到渗透率预测模型PSO-XGBoost,阐述了该模型的方法原理并进行了预测致密砂岩储层渗透率实验,得到以下认识:
(1) 与物理模型相比,拟合模型涉及的储层特征参数较少,因此在建模资料不充足的情况下,适用性更好。
(2) 致密砂岩储层因孔喉系统复杂且易发育裂缝,使渗透率在测井响应上与孔隙度相关性差,导致指数模型适用性差。
(3) 与指数模型相比,逐步迭代能更好地反映渗透率与测井曲线之间的线性响应关系,但由于预测性能受建模数据品质影响很大,导致计算稳定性不佳,使其难以推广使用。
(4) SVR参数能够由PSO技术优化,且形成的PSO-SVR在处理小型数据体时能快速给出预测结果。但模型的预测性能随训练样本品质的变化而有较大的波动,导致模型预测稳定性较差,因此PSO-SVR难以推广使用。
(5) 使用PSO技术可优化GBDT参数,形成的PSO-GBDT不仅能快速给出可靠的预测结果,且模型的预测性能随训练样本品质变化的波动不大,表明具备推广应用性。
(6) 使用PSO技术可优化XGBoost参数,且形成的PSO-XGBoost预测效率高,稳定性好,具备推广使用性。与PSO-GBDT相比,PSO-XGBoost的预测精度更高,表明更具推广使用价值。
(7) 逐步迭代、PSO-SVR、PSO-GBDT、PSO-XGBoost的预测能力都可在训练更多学习样本后得到明显提升。
| [1] |
窦占斌.致密含气砂岩储层测井评价方法研究[D].北京: 中国地质大学(北京), 2014. DOU Zhanbin.Logging Evaluation Study of Tight Gas Sandstone Reservoir[D]. China University of Geosciences (Beijing), Beijing, 2014. |
| [2] |
周新波, 段迎利, 袁伟, 等. M油田渗透率计算方法研究[J]. 科技创新与应用, 2014(32): 76. ZHOU Xinbo, DUAN Yingli, YUAN Wei, et al. Permeability computation method research of M oilfield[J]. Technology Creation and Application, 2014(32): 76. |
| [3] |
张冲, 张占松, 张超谟. 基于等效岩石组分理论的渗透率解释模型[J]. 测井技术, 2014, 38(6): 690-694. ZHANG Chong, ZHANG Zhansong, ZHANG Chaomo. A permeability interpretation model based on equivalent rock element theory[J]. Well Logging Technology, 2014, 38(6): 690-694. DOI:10.3969/j.issn.1004-1338.2014.06.010 |
| [4] |
陈俊, 谢润成, 刘成川, 等. 中江气田侏罗系致密砂岩气藏测井流体识别及定量评价[J]. 天然气工业, 2019, 39(增刊1): 136-141. CHEN Jun, XIE Runcheng, LIU Chengchuan, et al. Flow Characterization and quantitative evaluation of the tight gas-bearing sandstone reservoirs in the Jurassic member of Zhongjiang gas field[J]. Natural Gas Industry, 2019, 39(S1): 136-141. |
| [5] |
柴愈坤, 冯沙沙, 王华. 致密砂岩储层物性参数建模方法探讨[J]. 中外能源, 2017, 22(5): 39-43. CHAI Yukun, FENG Shasha, WANG Hua. Discussion on the physical parameter modeling method for tight sandstone reservoir[J]. Sino-Global Energy, 2017, 22(5): 39-43. |
| [6] |
张鹏, 张小莉. 低孔低渗储层渗透率测井解释模型研究[J]. 地下水, 2014, 36(2): 74-76. ZHANG Peng, ZHANG Xiaoli. Study on the well-logging interpretation model of reservoirs of low porosity and permeability[J]. Ground Water, 2014, 36(2): 74-76. DOI:10.3969/j.issn.1004-1184.2014.02.031 |
| [7] |
苏海波, 王晓宏, 张世明, 等. 低渗透油藏油水相对渗透率模型的分形表征方法[J]. 东北石油大学学报, 2019, 43(5): 88-94. SU Haibo, WANG Xiaohong, ZHANG Shiming, et al. Fractal characterization method of oil-water relative permeability model in low permeability reservoirs[J]. Journal of Northeast Petroleum University, 2019, 43(5): 88-94. |
| [8] |
陈俊, 沙里锞, 王新海, 等. 用压覆岩心渗透率优化测井渗透率计算模型[J]. 断块油气田, 2016, 23(2): 189-192. CHEN Jun, SHA Like, WANG Xinhai, et al. Optimization of logging permeability calculation model using overburden pressure core permeability[J]. Fault-Block Oil and Gas Field, 2016, 23(2): 189-192. |
| [9] |
廖东良, 吴海燕. 基于流动单元改进的渗透率解释模型[J]. 测井技术, 2015, 39(6): 802-806. LIAO Dongliang, WU Haiyan. Modified permeability model based on flow units[J]. Well Logging Techno-logy, 2015, 39(6): 802-806. |
| [10] |
刘建建, 赵军龙, 屈晓荣. 鄂尔多斯盆地S区长6储层测井解释模型的建立及应用[J]. 中外能源, 2016, 21(8): 32-38. LIU Jianjian, ZHAO Junlong, QU Xiaorong. Establishment and application of logging interpretation model of Chang 6 reservoir in area S of Ordos Basin[J]. Sino-Global Energy, 2016, 21(8): 32-38. |
| [11] |
刘敏.长庆T气田致密砂岩气层测井评价方法[D].山东青岛: 中国石油大学(华东), 2016. LIU Min.Method Research for Well Logging Evaluation of Tight Gas-Bearing Sandstone in T Gas Field of Changqing[D]. China University of Petroleum (East China), Qingdao, Shandong, 2016. |
| [12] |
由嘉雨.榆树林油田葡萄花油层储层参数精细评价[D].黑龙江大庆: 东北石油大学, 2016. YOU Jiayu.Refined Evaluation of Reservoir Parameters of Putaohua Oil Layer in Yushulin Oil Field[D]. Northeast Petroleum University, Daqing, Heilongjiang, 2016. |
| [13] |
邓浩阳.高孔低渗碳酸盐岩储层孔隙结构及物性表征方法研究[D].四川成都: 西南石油大学, 2018. DENG Haoyang.The Evaluation Method of Pore Structure and Physical Property in Carbonate Rock Reservoir with High Porosity and Low Permeability[D]. Southwest Petroleum University, Chengdu, Sichuan, 2018. |
| [14] |
李佳.基于机器学习的多孔介质渗透率预测研究[D].浙江杭州: 浙江大学, 2019. LI Jia.A Machine Learning-Based Approach for Permeability Prediction of Porous Media[D]. Zhejiang University, Hangzhou, Zhejiang, 2019. |
| [15] |
Majid B, Hadi R. Reservoir rock permeability prediction using SVR based on radial basis function kernel[J]. Carbonates and Evaporites, 2019, 34(3): 699-707. DOI:10.1007/s13146-019-00493-4 |
| [16] |
Zhang G Y, Wang Z Z, Li H J, et al. Permeability prediction of isolated channel sands using machine lear-ning[J]. Journal of Applied Geophysics, 2018, 159(9): 605-615. |
| [17] |
Subasi A, El-Amin M F, Darwich T, et al. Permeability prediction of petroleum reservoirs using stochastic gradient boosting regression[J]. Journal of Ambient Intelligent and Human Computing, 2020, 53(2): 147-153. |
| [18] |
韩启迪, 张小桐, 申维. 基于梯度提升决策树(GBDT)算法的岩性识别技术[J]. 矿物岩石地球化学通报, 2018, 37(6): 1173-1180. HAN Qidi, ZHANG Xiaotong, SHEN Wei. Lithology identification technology based on gradient boosting decision tree(GBDT) algorithm[J]. Bulletin of Minera-logy, Petrology and Geochemistry, 2018, 37(6): 1173-1180. |
| [19] |
谢云欣.四川盆地雷口坡组油气聚集带特征及分布评价[D].四川成都: 成都理工大学, 2018. XIE Yunxin.Oil and Gas Accumulation Zones Characteristics and Distribution Evaluation of Leikoupo Formation, Sichuan Basin[D]. Chengdu University of Technology, Chengdu, Sichuan, 2018. |
| [20] |
Zhang C S, Zhang Y, Shi X J, et al. On incremental lear-ning for gradient boosting decision trees[J]. Neural Processing Letters, 2019, 50(1): 957-987. DOI:10.1007/s11063-019-09999-3 |
| [21] |
Chen T, Guestrin C.XGboost: A scalable tree boosting system[C]. ACM SIGKDD International Confe-rence on Konwledge Discovery and Data Mining, 2016, 785-794.
|
| [22] |
Torlay L, Perrone-Bertolotti M, Thomas E. Machine lear-ning-XGBoost analysis of language networks to classify patients with epilepsy[J]. Brain Informatics, 2017, 4(3): 159-169. DOI:10.1007/s40708-017-0065-7 |
| [23] |
闫星宇, 顾汉明, 肖逸飞, 等. XGBoost算法在致密砂岩气层测井解释中的应用[J]. 石油地球物理勘探, 2019, 54(2): 447-455. YAN Xingyu, GU Hanming, XIAO Yifei, et al. XGBoost algorithm applied in the interpretation of tight-sand gas reservoir on well logging data[J]. Oil Geophysical Prospecting, 2019, 54(2): 447-455. |
| [24] |
杨维, 李歧强. 粒子群优化算法综述[J]. 中国工程科学, 2004, 6(5): 87-94. YANG Wei, LI Qiqiang. Survey on particle swarm optimization algorithm[J]. Engineering Science, 2004, 6(5): 87-94. DOI:10.3969/j.issn.1009-1742.2004.05.018 |
| [25] |
刘建华.粒子群算法的基本理论及其改进研究[D].湖南长沙: 中南大学, 2009. LIU Jianhua.The Research of Basic Theory and Improvement on Particle Swarm Optimization[D]. Center South University, Changsha, Hunan, 2009. |
| [26] |
温阳东, 李龙剑. 基于LDIW-PSO算法的BP神经网络在压力传感器中的应用[J]. 化工自动化及仪表, 2014, 41(9): 1031-1034. WEN Yangdong, LI Longjian. Application of LDIW-PSO algorithm-based BP neural network in pressure sensor[J]. Control and Instruments in Chemical Industry, 2014, 41(9): 1031-1034. DOI:10.3969/j.issn.1000-3932.2014.09.011 |
| [27] |
赵冰瑶.姬塬油田王盘山地区长4+5储层成岩相微观孔隙结构及渗流特征研究[D].陕西西安: 西北大学, 2018. ZHAO Bingyao.The Study on Microscopic Pore Structure and Percolation Characteristics of Diagene-tic Facies in Chang 4+5 Reservoir of Wangpanshan Area, Jiyuan Oilfield[D]. Northwest University, Xi'an, Shaanxi, 2018. |
| [28] |
王文枫, 岳大力, 赵继勇, 等. 利用地震正演模拟方法研究地层结构——以鄂尔多斯盆地合水地区延长组三段为例[J]. 石油地球物理勘探, 2020, 55(2): 411-418. WANG Wenfeng, YUE Dali, ZHAO Jiyong, et al. Research on stratigraphic structure based on seismic forward modeling:A case study of the third member of the Yanchang Formation in Heshui area, Ordos Basin[J]. Oil Geophysical Prospecting, 2020, 55(2): 411-418. |
| [29] |
李慧琼, 张盟勃, 蒲仁海, 等. 黄257井区叠前纵波方位各向异性裂缝分布预测[J]. 石油地球物理勘探, 2017, 52(2): 350-359. LI Huiqiong, ZHANG Mengbo, PU Renhai, et al. Late Triassic fracture detection with seismic azimuth anisotropics in Huang 257 survey, Ordos Basin[J]. Oil Geophysical Prospecting, 2017, 52(2): 350-359. |
| [30] |
周荔青, 刘忠群, 蒲仁海, 等. 镇泾地区长8段三维地震强振幅异常带成因探讨[J]. 石油地球物理勘探, 2017, 52(2): 371-380. ZHOU Liqing, LIU Zhongqun, PU Renhai, et al. Strong amplitude anomaly on 3D seismic survey in the Southwestern Ordos Basin[J]. Oil Geophysical Pro-specting, 2017, 52(2): 371-380. |



 谷宇峰, 北京市西城区羊肉胡同17号自然资源部油气资源战略研究中心, 100034。Email:
谷宇峰, 北京市西城区羊肉胡同17号自然资源部油气资源战略研究中心, 100034。Email: