② 河南省瓦斯地质与瓦斯治理重点实验室——省部共建国家重点实验室培育基地, 河南焦作 454150;
③ 东方地球物理公司综合物化探处, 河北涿州 072751
② State Key Laboratory Cultivation Base for Gas Geology and Gas Control, Jiaozuo, Henan 454150, China;
③ GME & Geochemical Surveys, BGP, CNPC, Zhuozhou, Hebei 072751, China
煤层气是世界公认的三大非常规天然气之一,储层的压裂改造是提高采收率的主要手段[1]。其中,微地震监测技术可以通过储层压裂改造引发的震源点进行成像,从而为储层压裂改造提供依据。然而,煤层气水力压裂区围岩或煤层破碎严重、煤层较软,致使微地震信号微弱,资料解释困难[2]。由于电磁信号对导电流体和裂缝中的压裂剂较敏感,Beskardes等[3]采用三维直流电法对煤层气压裂效果进行了深入研究,其中高精度三维电法数值模拟是关键。
目前,三维直流电正、反演计算中应用最广的数值模拟方法主要有积分方程法[4-6]、有限差分法[7-8]和有限元法[9-13]。这三种方法各有优缺点:积分方程法计算速度快,但只能应用结构化网格处理异常体,对复杂地质体的模拟具有局限性;有限差分法精度不高,且只能应用结构化网格;有限元法精度较高,且可以结合非结构化网格[14-17]处理复杂模型,但相较于前两种方法,所需的计算内存较高。近些年来,随着计算机硬件计算能力的提高和数值计算方法的进步,有限元法得到广泛应用[18]。
在三维直流电数值模拟中,有限元法通常可通过两种策略提高解的精度,即加密网格和应用高阶形函数。为快速得到最优的网格分布,目前正演通常采用h型自适应加密算法[19-22]对网格进行加密。该算法首先固定网格单元上形函数的阶数(通常较低),然后利用后验误差估计估算每个单元的误差,最后对误差较大的单元进行加密。但是,若单元上解的光滑度较高,对单元进行加密仍无法快速提高解的精度。为解决这一问题,Grayver等[23]在求解三维地电模型时,对网格中的所有单元应用高阶形函数,提高了解的精度,并证明高阶自适应有限元法可以用最少的自由度得到最精确的有限元解。
本文基于高阶自适应有限元实现了直流电阻率模型的正演。首先阐述了有限元算法的实现步骤和关键技术,包括高阶形函数生成方法、后验误差估计技术和悬挂点上的约束条件;然后通过数值算例验证了算法的精确性,并且对比了形函数阶数不同时(p=1、2、3)的模拟结果;最后,将此方法应用于沁水盆地南部某煤气层压裂监测区的三维模型,通过三维直流电阻率模拟,验证了方法的有效性。
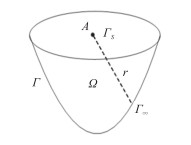
1 正演理论 1.1 控制方程假设在地面A点放置一个电流强度为I的点电源(图 1),空间电位分布满足
|
图 1 点源示意图 |
| $ \nabla \cdot (\sigma {\kern 1pt} \nabla U) = - I{\delta _A} $ | (1) |
式中:σ表示电导率;δA表示A点的Dirac delta函数;U表示电位。在地表Γs处,电流沿地表流动,所以电流密度的法向分量为0,表示为
| $ {\left. {\frac{{\partial U}}{{\partial \mathit{\boldsymbol{n}}}}} \right|_{{\varGamma _{\rm{s}}}}} = 0 $ | (2) |
式中n是边界上外法向向量。
假定区域Ω内,电性不均匀性对无穷远边界Γ∞(图 1)处的电位分布不产生影响,即Γ∞处的电位为点电源所产生的电位,表示为
| $ {\left. U \right|_{{\varGamma _\infty }}} = \frac{c}{r} $ | (3) |
式中:c是比例系数;r是A点到边界Γ∞的距离。将式(3)对n求导,消去常数c,可得
| $ \frac{{\partial U}}{{\partial \mathit{\boldsymbol{n}}}} + \frac{{\cos (\mathit{\boldsymbol{r}},\mathit{\boldsymbol{n}})}}{r}U = 0 $ | (4) |
式中r是由点A指向边界Γ∞的方向向量。
综上所述,三维直流电阻率模型边界值问题可由以下偏微分方程描述
| $ \left\{ {\begin{array}{*{20}{l}} {\nabla \cdot (\sigma \nabla U) = - I{\delta _A}}&{ \in \varOmega }\\ {\frac{{\partial U}}{{\partial \mathit{\boldsymbol{n}}}} = 0}&{ \in {\varGamma _{\rm{s}}}}\\ {\frac{{\partial U}}{{\partial \mathit{\boldsymbol{n}}}} + \frac{{\cos (\mathit{\boldsymbol{r}},\mathit{\boldsymbol{n}})}}{r}U = 0}&{ \in {\varGamma _\infty }} \end{array}} \right. $ | (5) |
将区域Ω离散为一系列非结构化六面体单元,每个单元e上电位的近似解为
| $ {U_{\rm{e}}} = \sum\limits_{i = 1}^m {{u_{\rm{i}}}} {\phi _{\rm{i}}} = \mathit{\boldsymbol{u}}_{\rm{e}}^{\rm{T}}\mathit{\boldsymbol{\phi}} = {\mathit{\boldsymbol{\phi}} ^{\rm{T}}}{\mathit{\boldsymbol{u}}_{\rm{e}}} $ | (6) |
式中:m是单元上自由度个数;ui是单元中第i个自由度上的电位;ue是由m个自由度上未知电位组成的向量;ϕi是第i个自由度上的形函数;ϕ是由m个形函数组成的向量。
对式(5)应用伽辽金有限元法[24],可得单元e上的弱解形式为
| $ \begin{array}{*{20}{c}} {\int_{{\varOmega ^{\rm{e}}}} \sigma \nabla {\phi _j} \cdot \nabla {U_{\rm{e}}}{\rm{d}}{\varOmega ^{\rm{e}}} + \int_{\varGamma _\infty ^{\rm{e}}} {\frac{{\cos (\mathit{\boldsymbol{r}},\mathit{\boldsymbol{n}})}}{r}} \cdot {\phi _j}{U_{\rm{e}}}{\rm{d}}\varGamma _\infty ^{\rm{e}} - }\\ {\int_{{\varOmega ^{\rm{e}}}} {{\phi _j}} \cdot I{\delta _A}{\rm{d}}{\varOmega ^{\rm{e}}} = 0\quad j = 1,2 \cdots ,m} \end{array} $ | (7) |
式中:Ωe是单元e所围区域;Γ∞e是无穷远边界上单元e的面。据式(7)对每个单元积分,可得
| $ {\mathit{\boldsymbol{k}}_{\rm{e}}}{\mathit{\boldsymbol{u}}_{\rm{e}}} = {\mathit{\boldsymbol{f}}_{\rm{e}}} $ | (8) |
式中:ke是m×m阶矩阵;fe是m维向量。矩阵ke中第i行、第j列元素kije和向量fe的第i行元素fie分别为
| $ k_{ij}^{\rm{e}} = \sigma \int_{{\varOmega ^{\rm{e}}}} {\nabla {\phi _i} \cdot } \nabla {\phi _j}{\rm{d}}{\varOmega ^{\rm{e}}} + \frac{{\sigma \cos (\mathit{\boldsymbol{r}},\mathit{\boldsymbol{n}})}}{r}\int_{\varGamma _\infty ^{\rm{e}}} {{\phi _i}{\phi _j}{\rm{d}}\varGamma _\infty ^{\rm{e}}} $ | (9) |
| $ f_i^{\rm{e}} = \int_{{\varOmega ^{\rm{e}}}} {{\phi _i}I{\delta _A}{\rm{d}}{\varOmega ^{\rm{e}}}} $ | (10) |
对所有单元分别组装矩阵,可以得到系统线性方程组
| $ \mathit{\boldsymbol{KU = F}} $ | (11) |
式中:K是一个n×n阶的稀疏对称正定矩阵,n是网格中自由度总数;U是网格中所有自由度上未知电位组成的n维向量;F是一个n维向量,描述源的分布。
1.3 形函数的生成任意空间中、任意阶数的形函数可由一维多项式的张量积表示[25]
| $ \phi _i^{(p)}(x) = \prod\limits_{0 \le d < {\rm{dim}}} {\theta _{{j_d}(i)}^{(p)}({x_d})} $ | (12) |
式中:θj(p)(·)是一维多项式,p表示多项式的阶数;xd表示空间中心点的坐标,下标“d”表示空间维度序号;dim表示维数;jd(i)表示将d维中按字典排序的形函数的下标映射到一维形函数中的下标。本文取dim=3,有
| $ \left\{ {\begin{array}{*{20}{l}} {{j_0}(i) = \left\lfloor {i/(p + 1)} \right\rfloor }\\ {{j_1}(i) = i \times {\rm{mod}}(p + 1)}\\ {{j_2}(i) = \left\lfloor {i/{{(p + 1)}^2}} \right\rfloor } \end{array}} \right. $ | (13) |
式中:$\left\lfloor \cdot \right\rfloor $为向下取整;mod(·)表示取模。多项式θj(p)(·)可以根据多项式阶数p动态计算得到
| $ \theta _j^{(p)}\left( {\frac{n}{p}} \right) = {\delta _{nj}};\quad 0 \le n \le p $ | (14) |
单元上形函数的个数m可由空间维度d和形函数的阶数p确定
| $ m = {(p + 1)^d} $ | (15) |
以二维形函数(p=2)在单元上的分布为例(图 2),这些自由度上形函数的数学表达式为

|
图 2 二维形函数(2阶)在单元上的分布示意图 |
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {{\phi _0} = (2x - 1)(x - 1)(2y - 1)(y - 1)}\\ {{\phi _1} = x(2x - 1)(2y - 1)(y - 1)} \end{array}\\ \begin{array}{*{20}{l}} {{\phi _2} = (2x - 1)(x - 1)y(2y - 1)}\\ {{\phi _3} = x(2x - 1)y(2y - 1)}\\ {{\phi _4} = (2x - 1)(x - 1) \times 4(1 - y)y} \end{array}\\ \begin{array}{*{20}{l}} {{\phi _5} = 4x(2x - 1)(1 - y)y}\\ {{\phi _6} = 4(1 - x)x \times (2y - 1)(y - 1)}\\ {{\phi _7} = 4(1 - x)x \times y(2y - 1)}\\ {{\phi _8} = 4(1 - x)x \times 4(1 - y)y} \end{array} \end{array} \right. $ | (16) |
根据式(16),分别绘制自由度0和自由度7上形函数在单元上的分布形态(图 3)。图中黑色区域表示z=0平面,所以形函数为负值的区域在图 3中显示不完整。可以看出,形函数所在自由度上函数值为1,在其他自由度上函数值均为0。

|
图 3 自由度0(a)和自由度7(b)上形函数在单元上的分布形态 |
后验误差估计可以无需人工干预,以最快的速度得到最优的网格分布。目前主要有两类后验误差估计方法,即基于梯度恢复[15]和基于残差[26]的后验误差估计方法。本文采用前者将单元中每个面上有限元解的梯度跳跃量[27]作为单元上的基本误差
| $ {E_{{F_w}}} = {c_{{F_w}}}\int_{\partial {K_w}} {{{\left[ {\frac{{\partial {u_{hp}}}}{{\partial \mathit{\boldsymbol{n}}}}} \right]}^2}} $ | (17) |
式中:w表示单元面的编号;EF表示一个面上的误差估计量;cF=he/24,he是单元e中最长的对角线长度;符号[·]代表在单元面上的跳跃值。单元e上的误差估计量ηe2可由公式
| $ \eta _{\rm{e}}^2 = \sum\limits_{w = 1}^l {{E_{{F_i}}}} $ | (18) |
计算,其中l是单元中面数目。
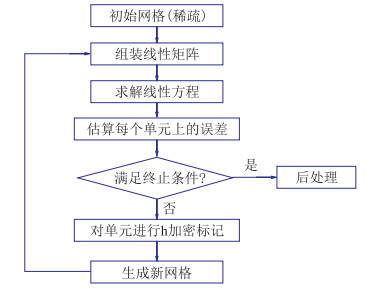
得到所有单元的误差估计后,对误差前10%的单元进行加密得到新的网格,然后在新的网格上重新计算有限元解,直到迭代次数或自由度个数达到设定值,迭代结束。h型自适应有限元算法流程如图 4所示。
|
图 4 h型自适应有限元算法流程图 |
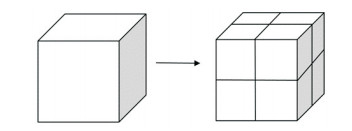
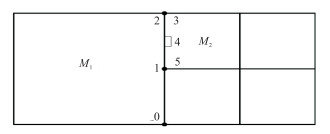
本文采用八叉树加密方法[28](图 5)对网格进行自适应加密,所以当一个单元一个面被加密时,在相邻两个单元的公共面上会出现悬挂点。为保证有限元的连续性,需要在这些悬挂点上添加一些约束条件。为方便起见,以二维网格上应用2阶形函数为例说明悬挂点上所施加的约束条件(图 6)。三维空间及其不同阶数形函数的情况与此类似。
|
图 5 八叉树加密原理 |
|
图 6 悬挂点示意图 自由度4是悬挂点 |
图 6中,自由度0、1和2属于单元M1,自由度3、4和5属于单元M2。为保证单元M1与单元M2的公共面上有限元的连续性,需满足
| $ {u_0}{\phi _0} + {u_1}{\phi _1} + {u_2}{\phi _2} = {u_3}{\phi _3} + {u_4}{\phi _4} + {u_5}{\phi _5} $ | (19) |
其中自由度2与自由度3、自由度1与自由度5表示同一自由度,即
| $ \left\{ {\begin{array}{*{20}{l}} {{u_2} = {u_3}}\\ {{u_1} = {u_5}} \end{array}} \right. $ | (20) |
当通过1.3节中的步骤求得自由度0、1和2上的形函数表达式后,可以得到
| $ {u_4} = - \frac{1}{8}{u_0} + \frac{3}{4}{u_1} + \frac{3}{8}{u_2} $ | (21) |
上式即为悬挂点4上的约束条件。
2 数值算例本文在程序实现中使用了开源有限元框架deal.II[29-30]。所使用的计算平台配备了Intel Xeon E5 2680 V4 CPU,包含14个处理器核心,主频为2.4GHz,内存为128GB。
2.1 正确性验证采用均匀半空间模型验证形函数阶数为3时算法的正确性。模型的计算区域为200m×200m×200m,点源位于原点O(0, 0, 0),沿x轴正方向以2m的间隔布置20个测点。
由于此模型较为简单,电位解析解[31]计算公式为
| $ u = \frac{I}{{2{\rm{ \mathit{ π} }}\sigma R}} $ | (22) |
式中R为测点与点源的距离。
通过有限元模拟各测点的电位,再计算得到视电阻率曲线(图 7a);通过与解析解对比,得到所有测点的相对误差(图 7b)。从图 7a可以看出:距离点源越远,有限元的解越精确;随着迭代次数的增加,有限元解快速收敛于解析解。从图 7b可以看到,随着自由度个数的增加,所有测点的相对误差大幅度降低。表 1给出了第1次、第3次以及第5次网格剖分方案下的自由度个数、计算时间和测点的最大相对误差,最大相对误差从124.8%降至0.3%,证明本文算法具有很高的精度。
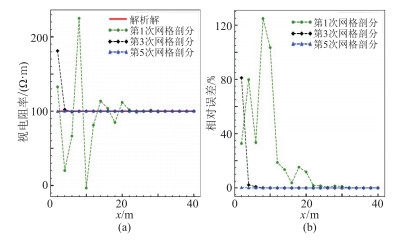
|
图 7 第1次、第3次和第5次网格剖分方案下的视电阻率曲线(a)及相对误差(b) |
|
|
表 1 第1次、第3次和第5次网格剖分方案下的自由度个数、测点视电阻率最大相对误差及耗时统计 |
应用均匀半空间模型分析形函数阶数p=1、2、3时自适应有限元解的收敛速度。计算区域为500m×500m×500m,背景电阻率为100Ω·m,初始剖分网格为8000个单元。从源点S(0, 0, 0)处向地下注入电流强度为1A的电流,沿x轴正方向100~400m范围内等间隔布置31个测点,间距为10m。对不同的网格剖分方案分别计算各测点的有限元解,然后参照解析解计算所有测点的相对误差,最终用所有测点的视电阻率平均相对误差展示有限元解的收敛速度,结果如图 8所示。表 2列出了形函数阶数p=1、2、3时最终网格上的自由度个数和所有测点的电阻率有限元解的平均相对误差。
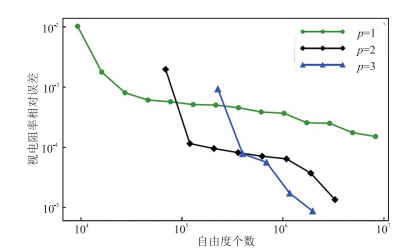
|
图 8 形函数p=1、2、3时有限元解的收敛速度对比 |
|
|
表 2 不同p值时网格自由度个数和所有测点视电阻率平均相对误差统计 |
从图 8和表 2可以看出,对于粗糙网格,形函数的阶数越高,有限元解的精度越高;有限元解的相对误差随着迭代次数的增加逐渐下降,p=1时有限元解曲线下降最慢,且最终网格上自由度个数最多为8256929,而所有测点的有限元解的平均相对误差仅降至1.5×10-4;p=2时有限元解的收敛速度有所提升,最终网格上的自由度个数为3277344,大约是p=1时最终网格上自由度个数的5/8,所有测点有限元解的平均相对误差降至1.4×10-5,即有限元解的精确度相较于p=1时提高了约11倍;p=3时有限元解的收敛性能最佳,最终网格上自由度个数为1968695,所有测点的有限元解的平均相对误差为8.8×10-6,相较于p=2时,自由度个数减少了1308649,精度提高了约1.5倍。综上所述,p=3时有限元程序可以用最少的自由度个数得到最精确的解。
图 9展示了形函数阶数p=1、2、3时最终网格剖分数目和误差分布。众所周知,在点源附近电势变化剧烈,导致解的光滑度较低,在距离点源较远的区域中解的光滑度较高。从图中可以看到,在距离点源较远、解比较光滑的区域中,形函数的阶数越高,最终网格上有限元解的误差越小;形函数的阶数p越高,最终整体误差越小。在距点源非常近的区域,p=1、2时网格得到了充分加密,而p=3时网格未得到充分加密。由于点源附近网格加密程度不同,从图 9c(右)可以清楚看到,p=3时在距离点源非常近的区域,有限元解的误差较高;而p=1、2时点源附近的误差较p=3时明显降低。

|
图 9 p=1(a)、2(b)、3(c)时最终网格剖分方案(左)及误差分布(右) |
对低阻异常体模型(图 10)进行模拟,以验证算法的有效性。异常体是一个电阻率为10Ω·m的低阻长方体,位于坐标原点正下方。背景电阻率为100Ω·m。

|
图 10 低阻异常体模型示意图 |
采用对称四极装置模拟计算沿x轴的视电阻率拟断面。x方向的计算范围为-400~400m,测点间距为20m;z方向为100~600m。供电电极的极距由200m逐渐增加到1200m,测量电极的极距为相应供电电极距的1/3。
首先,计算得到沿x轴的视电阻率拟断面(图 11a),可以清楚地看到,在x轴-100~100m范围内有一个低阻异常区,其宽度与模型异常体基本一致。
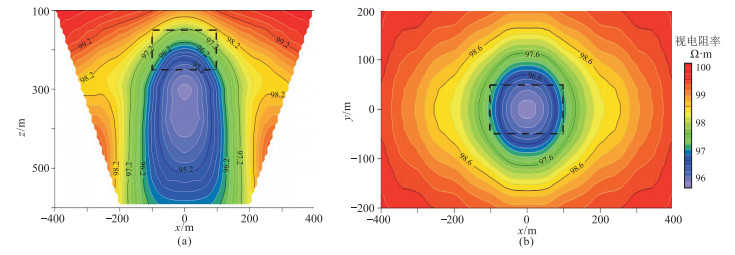
|
图 11 x轴视电阻率拟断面(a)及视深度为200m(b)的视电阻率平面图 黑色虚线为异常体边界 |
然后,在地表平行于x轴布置41条测线,测线范围为y=-200~200m,测线间距为10m,沿x方向测点的布设同图 11a。供电电极极距仍为400m。截取视深度z=200m的数据绘制视电阻率平面图(图 11b)。可以看到,大致由x轴-100~100m、y轴-50~50m所围区域是一个低阻区,其中心位置与模型异常体的中心位置吻合,覆盖范围与模型也基本一致。
2.4 合成数据模拟为验证高阶自适应有限元算法对较复杂模型的模拟效果,本文基于沁水盆地南部某煤层气压裂监测资料,建立三维电性模型验证本文算法的有效性。
沁水盆地南部煤层埋藏浅、厚度大、煤储层中煤层气含量高,且具有相对较高的渗透率,压裂后富水地层较上覆和下伏地层通常表现为低阻特征[32-33]。模型的计算区域为2000m×2000m×1000m。煤层气异常体在x、y和z轴方向的范围分别为-76~92m、-50~50m、124~190m,异常体示意图如图 12所示。模型的背景电阻率为100Ω·m,压裂前异常体电阻率设为10000Ω·m,压裂后为1Ω·m。
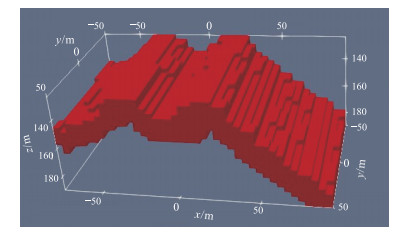
|
图 12 煤层气模型示意图 |
采用对称四极电阻率测量装置。测线沿x方向布设,测线范围y为-80~80m,测线间隔5m,测点范围x为-100~100m,间隔为5m。供电电极的极距为300m。分别计算煤层压裂前、后的视电阻率分布,并从计算结果中提取x方向-100~100m、y方向-80~80m、z=150m的视电阻率数据。通过定量计算得到压裂后的视电阻率相对异常
| $ R = \frac{{C - B}}{B} $ | (23) |
式中B、C分别为压裂前、后的视电阻率。图 13a、图 13b分别为第一次和压裂结束后的视电阻率相对异常分布。
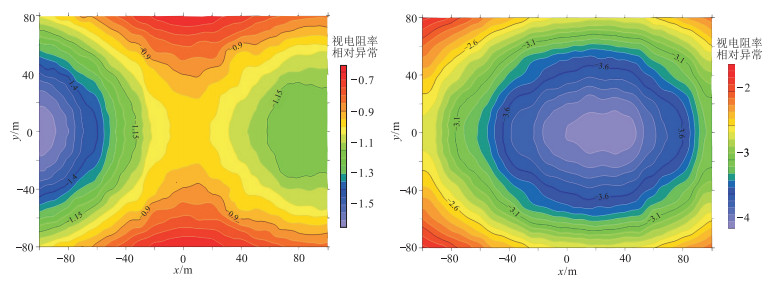
|
图 13 第一次压裂(左)及压裂完成后(右)z=150m平面视电阻率相对异常分布图 |
第一次压裂后,x方向-74~-40m范围内充满压裂剂,该区域电阻率约1Ω·m(即压裂剂的电阻率),其他范围内异常体的电阻率值仍很高,约为10000Ω·m。计算得到对称四级装置条件下z=150m平面的视电阻率后,通过定量计算得到了视电阻率相对异常图(图 13左)。因为压裂范围较小,所以图中左侧区域显示出小范围的低阻异常(图 13中蓝色的低阻区域)。
压裂结束后,异常区域内全部充满压裂剂,这些区域视电阻率主要体现为压裂液的低阻(1Ω·m)特征(图 13右)。图中的蓝色低异常区域与模型(图 12)中的煤层气分布区域基本一致。
分析图 13可知,采用本文算法并结合对称四级电阻率测量装置,可以定性地反演异常体的水平分布,计算结果与模型相吻合。因此,该方法在煤层气压裂监测领域具有重要应用价值。
3 结论本文应用高阶自适应有限元算法实现了直流电阻率模型正演,算例表明该算法具有较高的精度。
(1) 形函数阶数p=3时,数值模拟有限元解收敛最快,可以用少量的自由度个数得到精确的有限元解。
(2) 在点源附近电势剧烈变化的区域,可通过加密网格提高解的精度;在离点源较远处,解析解比较光滑,可通过提高单元上形函数的阶数提高解的精度,效果显著。
(3) 合成数据模型的模拟结果证明三维直流电阻率法是煤层气储层压裂监测的一项重要补充技术。
感谢河南理工大学对本项目提供了高性能计算资源!
| [1] |
陈海潮, 唐有彩, 钮凤林, 等. 利用微地震参数评估水力压裂改造效果研究进展[J]. 石油科学通报, 2016, 2(1): 198-208. CHEN Haichao, TANG Youcai, NIU Fenglin, et al. Recent advances in microseismic monitoring and implications for hydraulic fracturing mapping[J]. Petroleum Science Bulletin, 2016, 2(1): 198-208. |
| [2] |
Tafti T A, Sahimi M, Aminzadeh F, et al. Use of microseismicity for determining the structure of the fracture network of large-scale porous media[J]. Physical Review, 2013, 87(3): 32152. |
| [3] |
Beskardes G D, Weiss C J. Modelling to responses of 3-D complex fracture networks[J]. Geophysical Journal International, 2018, 214(3): 1901-1912. DOI:10.1093/gji/ggy234 |
| [4] |
Hvozdara M, Kaikkonen P. An integral equations solution of the forward DC geoelectric problem for a 3-D body of inhomogeneous conductivity buried in a halfspace[J]. Journal of Applied Geophysics, 1998, 39(2): 95-107. DOI:10.1016/S0926-9851(98)00007-X |
| [5] |
Mirgalikyzy T, Mukanova B, Modin I. Method of integral equations for the problem of electrical tomography in a medium with ground surface relief[J]. Journal of Applied Mathematics, 2015, 31(5): 113-123. |
| [6] |
任政勇, 陈建超, 汤井田, 等. 一种新的三维大地电磁积分方程正演方法[J]. 地球物理学报, 2017, 60(11): 4506-4515. REN Zhengyong, CHEN Janchao, TANG Jingtian, et al. A new integral equation approach for 3D magnetotelluric modeling[J]. Chinese Journal of Geophysics, 2017, 60(11): 4506-4515. DOI:10.6038/cjg20171134 |
| [7] |
Spitzer K. A 3-D finite-difference algorithm for DC resistivity modelling using conjugate gradient methods[J]. Geophysical Journal International, 1995, 123(2): 903-914. |
| [8] |
Wang T, Fang S. 3-D electromagnetic anisotropy mode-ling using finite differences[J]. Geophysics, 2001, 66(5): 1386-1398. DOI:10.1190/1.1486779 |
| [9] |
Li Y, Spitzer K. Three-dimensional DC resistivity forward modelling using finite elements in comparison with finite difference solutions[J]. Geophysical Journal International, 2002, 151(3): 924-934. DOI:10.1046/j.1365-246X.2002.01819.x |
| [10] |
Brenner S, Scott R. The Mathematical Theory of Finite Element methods[M]. Springer Science & Business Media, 2007.
|
| [11] |
任政勇, 汤井田. 基于局部加密非结构化网格的三维电阻率法有限元数值模拟[J]. 地球物理学报, 2009, 52(10): 2627-2634. REN Zhengyong, TANG Jingtian. Finite element modeling of 3-D DC resistivity using locally refined unstructured meshes[J]. Chinese Journal of Geophysics, 2009, 52(10): 2627-2634. DOI:10.3969/j.issn.0001-5733.2009.10.023 |
| [12] |
周勇, 张志勇, 张大洲, 等. 自适应网格直流电阻率三维反演[J]. 石油地球物理勘探, 2019, 54(5): 1174-1180. ZHOU Yong, ZHANG Zhiyong, ZHANG Dazhou, et al. 3D DC resistivity inversion based on inversion-oriented adaptive meshes[J]. Oil Geophysical Prospecting, 2019, 54(5): 1174-1180. |
| [13] |
郭来功, 戴广龙, 杨本才, 等. 多先验信息约束的三维电阻率反演方法[J]. 石油地球物理勘探, 2018, 53(6): 1333-1340. GUO Laigong, DAI Guanglong, YANG Bencai, et al. 3D resistivity inversion with multiple priori-information constraint[J]. Oil Geophysical Prospecting, 2018, 53(6): 1333-1340. |
| [14] |
Li Y, Pek J. Adaptive finite element modelling of two-dimensional magnetotelluric fields in general anisotropic media[J]. Geophysical Journal International, 2008, 175(3): 942-954. DOI:10.1111/j.1365-246X.2008.03955.x |
| [15] |
Ren Z Y, Tang J T. 3D direct current resistivity mode-ling with unstructured mesh by adaptive finite-element method[J]. Geophysics, 2010, 75(1): H7-H17. DOI:10.1190/1.3298690 |
| [16] |
Tang J T, Wang F, Ren Z Y. 2.5-D DC resistivity mode-ling by adaptive finite-element method with unstructured triangulation[J]. Chinese Journal of Geophysics, 2010, 55(3): 708-716. |
| [17] |
Wang W, Wu X, Spitzer K. Three-dimensional DC anisotropic resistivity modelling using finite elements on unstructured grids[J]. Geophysical Journal International, 2013, 193(2): 734-746. DOI:10.1093/gji/ggs124 |
| [18] |
司兆伟, 邓少贵, 林发武, 等. 泥浆侵入各向异性地层阵列侧向测井响应数值模拟[J]. 石油地球物理勘探, 2020, 55(1): 187-196. SI Zhaowei, DENG Shaogui, LIN Fawu, et al. Nume-rical simulation of array laterolog responses in anisotropic formation with mud invasion[J]. Oil Geophysical Prospecting, 2020, 55(1): 187-196. |
| [19] |
Franke A, Börner R U, Spitzer K. Adaptive unstructured grid finite element simulation of two-dimensio-nal magnetotelluric fields for arbitrary surface and seafloor topography[J]. Geophysical Journal International, 2007, 171(1): 71-86. DOI:10.1111/j.1365-246X.2007.03481.x |
| [20] |
Ren Z Y, Tang J T. A goal-oriented adaptive finite-element approach for multi-electrode resistivity system[J]. Geophysical Journal International, 2014, 199(1): 136-145. DOI:10.1093/gji/ggu245 |
| [21] |
Yan B, Li Y, Liu Y. Adaptive finite element modeling of direct current resistivity in 2-D generally anisotropic structures[J]. Journal of Applied Geophysics, 2016, 130: 169-176. DOI:10.1016/j.jappgeo.2016.04.018 |
| [22] |
任政勇, 邱乐稳, 汤井田, 等. 基于电流密度连续性条件的直流电阻率各向异性问题自适应有限元模拟[J]. 地球物理学报, 2018, 61(1): 331-343. REN Zhengyong, QIU Lewen, TANG Jingtian, et al. 3D modeling of direct-current anisortopic resistivity using the adaptive finite-element method based on continuity of current density[J]. Chinese Journal of Geophysics, 2018, 61(1): 331-343. |
| [23] |
Grayver A V, Kolev T V. Large-scale 3D geoelectromagnetic modeling using parallel adaptive high-order finite element method[J]. Geophysics, 2015, 80(6): E277-E291. DOI:10.1190/geo2015-0013.1 |
| [24] |
张榴晨, 徐松. 有限元法在电磁计算中的应用[M]. 北京: 中国铁道出版社, 1996.
|
| [25] |
Bangerth W, Kayser H O. Data structures and requirements for hp finite element software[J]. ACM Transactions on Mathematical Software, 2009, 36(1): 1-31. |
| [26] |
Babuška I, Rheinboldt W C. Adaptive approaches and reliability estimations in finite element analysis[J]. Computer Methods in Applied Mechanics and Engineering, 1979, 17/18(3): 519-540. |
| [27] |
Kelly D W, De J P, Zienkiewicz O C, et al. A posteriori error analysis and adaptive processes in the finite element method:Part I, error analysis[J]. International Journal for Numerical Methods in Engineering, 1983, 19(11): 1593-1619. DOI:10.1002/nme.1620191103 |
| [28] |
赵宁, 王绪本, 余刚, 等. 面向目标自适应海洋可控源电磁三维矢量有限元正演[J]. 地球物理学报, 2019, 62(2): 779-788. ZHAO Ning, WANG Xuben, YU Gang, et al. 3D MCSEM parallel goal-oriented adaptive vector finite element modeling[J]. Chinese Journal of Geophysics, 2019, 62(2): 779-788. |
| [29] |
Arndt D, Bangerth W, Clevenger T C, et al. The deal. Ⅱ. library, version 9.1[J]. Journal of Numerical Mathematics, 2019, 27(4): 203-213. DOI:10.1515/jnma-2019-0064 |
| [30] |
Bangerth W, Hartmann R, Kanschat G. The deal. Ⅱ. a general-purpose object-oriented finite element library[J]. ACM Transactions on Mathematical Software, 2007, 33(4): 24. DOI:10.1145/1268776.1268779 |
| [31] |
徐世浙. 地球物理中的有限单元法[M]. 北京: 科学出版社, 1994.
|
| [32] |
李琼, 何建军, 曹均. 沁水盆地和顺地区煤层气储层物理特征[J]. 石油地球物理勘探, 2013, 48(5): 734-739. LI Qiong, HE Jiangjun, CAO Jun. Physical characteristics of coalbed methane reservoir in Heshun Area of Qinshui Basin[J]. Oil Geophysical Prospecting, 2013, 48(5): 734-739. |
| [33] |
闫文华, 陈宗翠, 马喜梅, 等. 煤层气地震解释技术应用及效果——以沁水盆地郑庄区块三维为例[J]. 石油地球物理勘探, 2012, 47(增刊1): 66-71. YAN Wenhua, CHEN Zongcui, MA Ximei, et al. 3D seismic interpretation of coalbed methane in Zhengzhuang Block, Qinshui Basin[J]. Oil Geophysical Prospecting, 2012, 47(S1): 66-71. |



 秦策, 河南省焦作市山阳区世纪大道2001号河南理工大学物理与电子信息学院, 454150。Email:
秦策, 河南省焦作市山阳区世纪大道2001号河南理工大学物理与电子信息学院, 454150。Email: