② 东方地球物理公司综合物化探处, 河北涿州 072751;
③ 南方科技大学前沿与交叉科学研究院, 广东深圳 518055
② GME & Geochemical Surveys, BGP, CNPC, Zhuozhou, Hebei 072751, China;
③ SUSTech Academy for Advanced Interdisciplinary Studies, Shenzhen, Guangdong 518055, China
瞬变电磁法(Transient Electromagnetic Me-thod,TEM)是一种重要的可控源电法勘探方法,该方法采用不接地回线或接地导线向地下发射脉冲电流,在一次场的间歇期,观测大地中的感应电磁场(通常观测垂直方向的感应电动势),也称为二次场。通过研究二次场随时间和空间的变化规律,分析大地的电性分布特征。因采用人工源,并且观测二次场,该方法具有数据精度高、不受一次场影响等优点,已被广泛地应用于工程、水文、环境、资源等勘探领域[1-5]。
尽管当前TEM数据的二维和三维正反演解释取得了巨大进步[6-11],然而由于反演计算量大,需要大规模的计算平台,难以普遍应用于实际资料[12-16],故一维反演仍是目前实际资料处理解释主要手段之一[17-21]。然而,TEM数据的一维反演存在反演剖面连续性差的问题,且数据记录周期的晚期信号弱,单点反演的深部数据受噪声影响大。
基于大地介质电性连续变化的特点,Auken等[22]首先将横向约束反演方法用于直流电电磁数据反演;Vallée等[23]将横向约束方法应用于时间域航空电磁数据的反演,有效改善了反演效果;蔡晶等[15]、殷长春等[16]分别将该方法用于航空电磁数据频域和时域反演,明显改善了整个反演剖面的连续性,提高了解释结果的准确性。
传统的横向约束反演方法只沿测线方向进行横向约束。对于三维测网的观测数据,若只沿测线方向进行横向约束而不考虑相邻测线之间构造的关联性,会大大降低地质解释的可靠性。为此,Viezzoli等[24]提出了基于空间约束的航空电磁数据反演方法,即不仅沿测线方向,也垂直于测线方向施加横向约束。殷长春等[25]将空间约束用于航空电磁拟三维反演,通过理论和实测数据测试证明了该方法适合求解多测线航空电磁数据的最优化反演。
本文从横向约束原理出发,将横向约束引入地面三维测网的TEM数据的一维反演解释,给出了一种距离加权进行相邻点横向约束的拟三维反演方法。该方法能有效地实现横向约束,保证相邻测点模型的连续性,且不要求测网是严格规则的,实现了一般测网条件下的横向约束拟三维反演。模型正演数据和实际数据测试结果验证了该方法的正确性、有效性和实用性。
1 横向约束拟三维反演方法传统的横向约束拟二维反演方法首先集成剖面数据,再沿测线施加横向约束,同时反演测线上多测点的地电参数[16]。该方法的实质是把相邻测点地电模型的差异作为约束项加入目标函数,对模型进行横向平滑处理,以保证相邻测点间模型的连续性,进而压制因为噪声导致的单个测点地电参数突变。TEM勘探中,测点设计常采用测网方式,且通常测点分布是非完全规则的。基于横向约束的原理,本文采用一种距离加权相邻点进行横向约束的拟三维反演方法,即:对所有测点数据进行集成,对所有测点均采用半径r之内、距其最近的p个测点进行距离加权横向约束,反演测点处的地电模型,实现一种广泛适用的TEM数据横向约束拟三维反演。
距离加权相邻点横向约束的原理如图 1所示。图中测点按顺序编号,各测点的反演由距其最近的p个点进行横向约束。例如,33号测点由距其最近的24、34、25、32号测点(此时p=4)进行横向约束,这4个测点分别称为33号点的第1~4号相邻点。

|
图 1 距离加权相邻点横向约束原理示意图 |
设三维测网有l个测点,按一定顺序进行编号,并设每个测点有k个衰减延时(实际各个测点的延时数可以不一致,此处为了表述方便,都设为k)。这l个测点的电磁数据可表示为
| $ \begin{array}{l} \mathit{\boldsymbol{d}} = [{d_{11}},{d_{12}}, \cdots ,{d_{1k}}, \cdots ,{d_{i1}},{d_{i2}}, \cdots ,\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {d_{ik}}, \cdots ,{d_{l1}},{d_{l2}}, \cdots ,{d_{lk}}{]^{\rm{T}}} \end{array} $ | (1) |
假设反演模型为n层,只考虑各层的电导率σ,则l个测点的总模型可表示为
| $ \begin{array}{l} \mathit{\boldsymbol{m}} = [{\sigma _{11}},{\sigma _{12}}, \cdots ,{\sigma _{1n}}, \cdots ,{\sigma _{i1}},{\sigma _{i2}}, \cdots ,\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\sigma _{in}}, \cdots ,{\sigma _{l1}},{\sigma _{l2}}, \cdots ,{\sigma _{\ln }}{]^{\rm{T}}} \end{array} $ | (2) |
以各测点为中心,在横向约束半径r内搜索距其最近的p个测点(如果数据点不足,允许少于p个测点),并分别记录这p个点的序号及其距离。
基于吉洪诺夫正则化反演思想,反演目标函数中包含数据拟合项及正则化项。将横向约束作为正则化项加入反演目标函数,依次将各测点与其第1~p个相邻点的模型差异加入目标函数,再将各测点模型的纵向粗糙度加入目标函数,由此得到横向及纵向上均施加了平滑约束的反演目标函数。求解该反演目标函数,即可得到拟三维反演结果。距离加权横向约束的拟三维反演目标函数可写为
| $ \begin{array}{l} \phi = {[F(\mathit{\boldsymbol{m}}) - \mathit{\boldsymbol{d}}]^{\rm{T}}}{\mathit{\boldsymbol{C}}^{ - 1}}[F(\mathit{\boldsymbol{m}}) - \mathit{\boldsymbol{d}}] + {k_{\rm{v}}}{({\mathit{\boldsymbol{E}}_{\rm{v}}}m)^{\rm{T}}} \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({\mathit{\boldsymbol{E}}_{\rm{v}}}\mathit{\boldsymbol{m}}) + {k_{\rm{h}}}\sum\limits_{i = 1}^p {{{({\mathit{\boldsymbol{E}}_{{\rm{h}},i}}\mathit{\boldsymbol{m}})}^{\rm{T}}}} {\mathit{\boldsymbol{D}}_i}({\mathit{\boldsymbol{E}}_{{\rm{h}},i}}\mathit{\boldsymbol{m}}) \end{array} $ | (3) |
式中:F为正演算子;C为协方差矩阵,用于基于数据误差对观测数据拟合进行加权;kv、kh分别为纵向和横向约束因子;Ev为各测点模型的纵向一阶差分矩阵;Eh, i为各测点第i相邻点横向约束一阶差分矩阵(若某测点的第i相邻点不存在时,Eh, i中对应于该测点的行元素全为零);Di为第i相邻点横向约束距率加权矩阵;Evm和Eh, im分别表示所有测点对应模型的纵向粗糙度及其第i个相邻点的横向粗糙度。Ev、Eh, i及Di可分别表示为
| $ \begin{array}{l} {\mathit{\boldsymbol{E}}_{\rm{v}}} = \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left[ {\begin{array}{*{20}{c}} { - 1}&1&0& \cdots &{}&{}&0\\ 0&{ - 1}&1&0& \cdots &{}&0\\ {}&{}&{}& \vdots &{}&{}&{}\\ 0& \cdots &{}& \cdots &0&{ - 1}&1 \end{array}} \right]_{[l \times (n - 1)] \times (l \times n)}}\\ \end{array} $ | (4) |
| $ \begin{array}{l} {\mathit{\boldsymbol{E}}_{{\rm{h}},i}} = {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left[ {\begin{array}{*{20}{c}} { - 1}&0& \cdots &1&0& \cdots &0\\ 0&{ - 1}&0& \cdots &1& \cdots &0\\ {}&{}&{}& \vdots &{}&{}&{}\\ 0& \cdots &0&1&0& \cdots &{ - 1} \end{array}} \right]_{(l \times n) \times (l \times n)}} \end{array} $ | (5) |
| $ {\mathit{\boldsymbol{D}}_i} = {\left[ {\begin{array}{*{20}{c}} {\frac{1}{{{r_{1,i}}}}}&0& \cdots &{}&{}&0\\ 0&{\frac{1}{{{r_{1,i}}}}}&0& \cdots &{}&0\\ {}&{}& \vdots &{}&{}&{}\\ {}&{}&{}&0&{\frac{1}{{{r_{l,i}}}}}&0\\ 0& \cdots &{}&{}&0&{\frac{1}{{{r_{l,i}}}}} \end{array}} \right]_{(l \times n) \times (l \times n)}} $ | (6) |
式中rl, i表示第l个测点与其第i个相邻点的距离。在实际数据处理过程中,需要设定一个最小距离r0,当rl, i<r0时,用r0代替。式(3)中依次加入了各测点与其相邻p个测点地电模型的差异对模型进行横向约束,求该目标函数的极小,即能得到横向平滑约束的最小二乘解,从而实现了横向约束拟三维反演。
式(3)中的纵向约束及横向约束项为反演目标函数的平滑正则化项,根据吉洪诺夫正则化的思想,纵向约束因子kv及横向约束因子kh可依据工区内地层的纵向和横向变化特征初选,在保证数据拟合的前提下,以后验方式选择合理的值。
由于各测点都选取相邻测点进行横向约束,该方法不要求测网严格规则,同时对各测点的排序也不做要求,具有广泛的适应性。此外,该方法同样适用于二维数据的反演,此时该方法即为常规的横向约束拟二维反演(LCI)。
2 横向约束拟三维反演目标函数的求解高斯—牛顿法具有迭代稳定、收敛快的特点,因此本文采用高斯—牛顿迭代法求解式(3)中横向约束拟三维反演目标函数的极小。
设m0为模型初值,Δm为模型修正量,将F在m0处一阶展开,目标函数对Δm求导,并令导数为零,得到高斯—牛顿法模型修正量的求解式为
| $ \begin{array}{*{20}{l}} {\left[ {{\mathit{\boldsymbol{J}}^{\rm{T}}}{\mathit{\boldsymbol{C}}^{ - 1}}\mathit{\boldsymbol{J}} + {k_{\rm{v}}}\mathit{\boldsymbol{E}}_{\rm{v}}^{\rm{T}}{\mathit{\boldsymbol{E}}_{\rm{v}}} + {k_{\rm{h}}}\sum\limits_{i = 1}^p {\left( {\mathit{\boldsymbol{E}}_{{\rm{h}},i}^{\rm{T}}{\mathit{\boldsymbol{D}}_i}{\mathit{\boldsymbol{E}}_{{\rm{h}},i}}} \right)} } \right]\Delta \mathit{\boldsymbol{m}}}\\ {{\kern 1pt} = {\mathit{\boldsymbol{J}}^{\rm{T}}}{\mathit{\boldsymbol{C}}^{ - 1}}\left[ {\mathit{\boldsymbol{d}} - F\left( {{\mathit{\boldsymbol{m}}_0}} \right)} \right] - {k_{\rm{v}}}\mathit{\boldsymbol{E}}_{\rm{v}}^{\rm{T}}{\mathit{\boldsymbol{E}}_{\rm{v}}}{\mathit{\boldsymbol{m}}_0} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {k_{\rm{h}}}\sum\limits_{i = 1}^p {\left( {\mathit{\boldsymbol{E}}_{{\rm{h}},i}^{\rm{T}}{\mathit{\boldsymbol{D}}_i}{\mathit{\boldsymbol{E}}_{{\rm{h}},i}}{\mathit{\boldsymbol{m}}_0}} \right)} } \end{array} $ | (7) |
式中J为各测点正演函数与相应模型雅可比矩阵的集成,即顺序地以各测点一维雅可比矩阵为块的分块对角矩阵,该矩阵仅包含l×k×n个非零元素。
由式(7)可求解Δm, 得到修正后的模型m=m0+Δm,再把m赋给m0,这样反复迭代,直到达到预设的拟合误差或最大迭代次数,即得到最终反演结果。
式(7)反演迭代的关键在于求取正演函数相对于模型的雅可比矩阵。本文重点研究最常用的回线源装置瞬变电磁法。一维正演采用首先在频率域进行、再通过正弦变换转换到时间域的经典算法,雅可比矩阵的求取则采用拟正演的方法。
水平矩形回线源布设于地面,测点可位于地面上除发射导线处的任何位置,记录数据为垂直磁场的感应电动势。对于回线源频率域的响应,可将矩形线圈的四边看作是4个导线源,则回线源的响应可表示为四个导线源的叠加场,地面上的磁场垂直分量[26]为
| $ {H_{\rm{z}}} = \sum\limits_{j = 1}^4 {\frac{I}{{4{\rm{ \mathit{ π} }}}}} \int_{ - {L_j}/2}^{{L_j}/2} {\frac{y}{R}} \int_0^\infty {(1 + {r_{{\rm{TE}}}})} \frac{{{\lambda ^2}}}{{{\mu _0}}}{J_1}(\lambda R){\rm{d}}\lambda {\rm{d}}{x^\prime } $ | (8) |
式中:J1(λR)为一阶贝塞尓函数,λ为内侧积分变量,
通过正弦变换
| $ {{\dot H}_{\rm{z}}}=\frac{2}{{\rm{ \mathit{ π} }}}\int_0^\infty {{\rm{Im}}[{H_{\rm{z}}}(\omega )]\sin (\omega t){\rm{d}}\omega } $ | (9) |
可得到Hz磁场时间域的响应
根据式(8)和式(9),只有反射系数rTE中包含模型参数,因此只需要对rTE求导。本文借鉴MT Occam反演[27]中的正演函数对地层电导率的求导方法,基于反射系数递推,采用拟正演方法计算瞬变响应对于各层的偏导数。
rTE的表达式[26]为
| $ {r_{{\rm{TE}}}} = \frac{{{Y_0} - {{\hat Y}_1}}}{{{Y_0} + {{\hat Y}_1}}} $ | (10) |
| $ {{\rm{Y}}_0} = \frac{{{{\rm{u}}_0}}}{{{{{\rm{\hat z}}}_0}}} $ | (11) |
其中
| $ {{\hat Y}_1} = {Y_1}\frac{{{{\hat Y}_2} + {Y_1}\tanh ({u_1}{h_1})}}{{{Y_1} + {{\hat Y}_2}\tanh ({u_1}{h_1})}} $ | (12) |
| $ {{\hat Y}_i} = {Y_i}\frac{{{{\hat Y}_{i + 1}} + {Y_i}\tanh ({u_i}{h_i})}}{{{Y_i} + {{\hat Y}_{i + 1}}\tanh ({u_i}{h_i})}} $ | (13) |
| $ {{\hat Y}_N} = {Y_N} $ | (14) |
| $ {Y_i} = \frac{{{u_i}}}{{{{\hat z}_i}}} $ | (15) |
式中:
| $ \frac{{\partial {r_{{\rm{TE}}}}}}{{\partial {\rm{lg}}{\sigma _i}}} = \ln 10 \times {\sigma _i}\frac{{\partial {r_{{\rm{TE}}}}}}{{\partial {\sigma _i}}} = \frac{{ - 2\frac{{\partial {{\hat Y}_1}}}{{\partial {\sigma _i}}}{Y_0}}}{{{{({Y_0} + {{\hat Y}_1})}^2}}} $ | (16) |
| $ \begin{array}{l} \frac{{\partial {{\hat Y}_1}}}{{\partial {\sigma _i}}} = \frac{{\partial {{\hat Y}_1}}}{{\partial {{\hat Y}_2}}} \times \frac{{\partial {{\hat Y}_2}}}{{\partial {{\hat Y}_3}}} \times \cdots \times \\ \quad \quad {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\partial {{\hat Y}_i}}}{{\partial {{\hat Y}_{i + 1}}}} \times \cdots \times \frac{{\partial {{\hat Y}_i}}}{{\partial {\sigma _i}}}\quad j + 1 \le i \end{array} $ | (17) |
式(16)表明,计算下一层电导率的导数可以利用上一层计算的中间结果,从而减少计算量,提高计算效率。
需要注意的是,计算
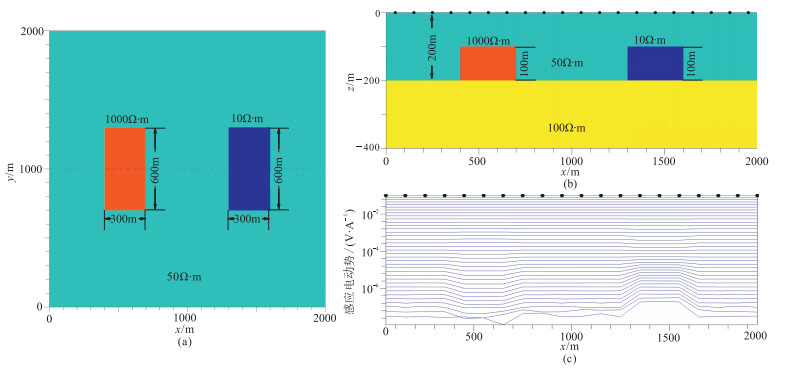
为验证上述横向约束拟三维反演方法的效果,设计包含一个高阻体及一个低阻体的模型(图 2a和图 2b)进行正演模拟,再用正演合成数据进行反演测试。模拟采用中心回线装置,设发射回线为100m×100m的正方形,电流为10A,接收线圈面积为200m2,观测时间范围为0.00001~0.00500s,测网点线距均为100m,共计21×21个测点。正演场中加入典型的1 nV/m2随机背景噪声。由于本实验的目的是验证横向约束拟三维反演的有效性,因此对各测点对应的模型采用一维正演。
|
图 2 测试模型俯视图(a)和侧视图(b)及正演加噪多测道感应电动势曲线(c) 图c中从上到下感应电动势的观测时间为0.00001~0.00500s, 对数等间距取35道数据 |
图 2c为过高阻体及低阻体中心测线(y=950m)的加噪感应电动势多测道曲线。由于TEM信号早期强、晚期弱,所以图 2c中早期段中没有明显噪声,而晚期段中噪声明显。
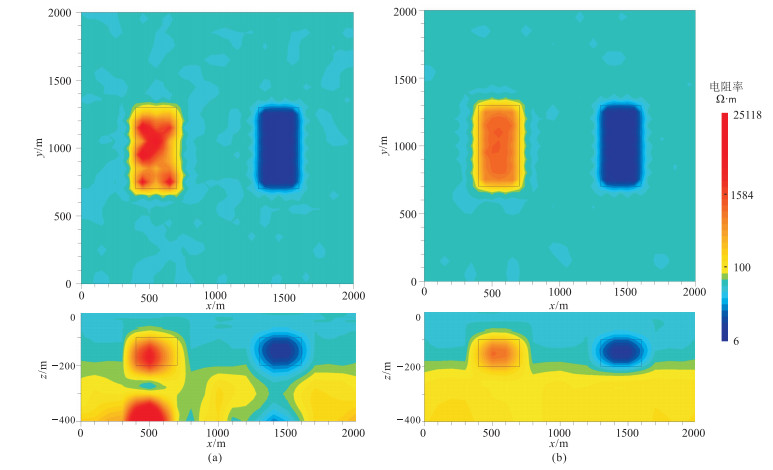
采用本文横向约束拟三维反演方法对正演数据(图 2c)进行反演,同时进行单点一维反演,以便对比分析两种方法的效果。两种方法反演的拟合误差均设为小于5%。反演结果见图 3。从图 3a可以看到,单点一维反演结果中,高阻体及低阻体的形态大致能够恢复,但高阻体内存在明显的横向不连续特征;反演剖面的下部则出现明显不合理的横向不连续现象及电阻率突变,其原因是晚期噪声的影响。从图 3b可以看出,横向约束拟三维反演对模型的恢复效果很好,低阻体及高阻体形态基本完整,边界清晰;异常体以下的区域形态也恢复较好。可见横向约束拟三维反演通过增强横向连续性,能够有效地压制单点反演造成的不合理模型突变。此外,在横向上,拟三维反演的地层界面很清晰,并没有因为横向约束导致界面模糊,原因在于地层界面产生的瞬变异常(图 2c)边界清晰,反演函数中数据拟合项的影响强于横向约束项。
|
图 3 单点一维反演(a)与横向约束拟三维反演(b)z=150m(上)和y=950m(下)电阻率切片对比 |
在中东某油田的采油区,地震资料显示在浅部(深度约200m)可能存在凹陷,但不能完全确定。这类浅部凹陷严重影响地震资料的深部成像质量。为查清该浅部结构,改善地震剖面成像效果,在该区部署了TEM勘探,调查400m深度以上地层结构。
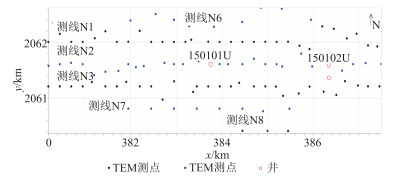
TEM采用200m×200m的中心回线装置,观测数据为垂直磁场分量。设计线距为400m,点距为250m,但由于工区位于采油区,油田设施众多,为避开油田设施的干扰,实际测点分布很不规则(图 4)。
|
图 4 中东某地TEM测点分布图 蓝、黑色圆点代表不同测线上的测点 |
由于测点分布很不规则,因此采用横向约束拟三维反演方法。为了对比分析反演方法效果,对其中一条测线(N1测线)同时进行常规单点一维反演。图 5为N1测线经面积、电流归一化后的观测感应电动势等值线剖面图,图 6为该测线单点一维反演和横向约束拟三维反演电阻率剖面及其对应的归一化感应电动势正演剖面。N2、N3测线反演电阻率剖面见图 7,图 8为全工区拟三维电阻率反演结果在不同海拔上的水平切片。

|
图 5 N1线归一化观测感应电动势剖面 |

|
图 6 N1线单点一维反演(a)和横向约束拟三维反演(b)电阻率剖面(上)及对应的模拟归一化感应电动势剖面(下) |
|
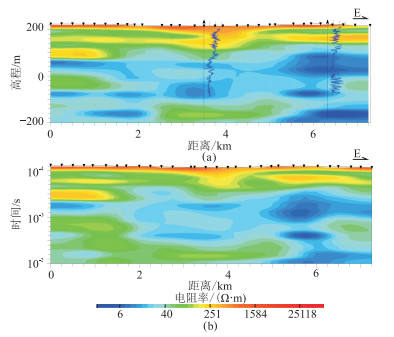
图 7 N2线(a)和N3线(b)横向约束拟三维反演电阻率剖面 图a中蓝色曲线为微测井视电阻率曲线 |

|
图 8 横向约束拟三维反演电阻率在海拔200m(a)和海平面(b)的水平切片 |
可以看出,单点一维电阻率反演剖面能大致体现沿测线的构造特征,但各测点间的连续性不好,横向上孤立异常突出,地层电性特征显示也不甚清楚;而横向约束拟三维反演的电性层横向连续性较好,地层电性特征清楚,很大程度上避免了单点反演中的不合理电性突变,有效提高了反演剖面的精度。还可以看出,相邻的N1、N2及N3测线反演剖面上电性层横向连续,电性特征清楚,电性层在各剖面上能够很好地进行追踪,中部的目标凹陷(横坐标2~4km)被清晰地勾绘了出来。图 7中反演电阻率剖面叠加了后期微测井视电阻率曲线,可见反演剖面与电测井曲线吻合较好,进一步说明本文横向约束拟三维反演结果的可靠性。图 8中,地层横向变化特征清楚,清晰地显示了中部浅层凹陷的形态及走向。
实际数据应用结果说明本文方法能够有效地实现一般测网条件下的TEM数据横向约束拟三维电阻率反演。
5 结论针对TEM数据一维电阻率反演中存在反演剖面连续性差的问题,本文将横向约束引入TEM数据反演中;考虑到实际测点分布并不严格规则的特点,构建了距离加权相邻点横向约束的拟三维反演方法,并采用高斯—牛顿法进行求解。
模型合成数据及实际数据的计算结果说明,距离加权相邻点横向约束拟三维反演可有效实现横向约束,保证相邻测点模型的连续性,提高反演解释效果,且对一般非规则测网TEM数据也是适用的,具有广泛的适用性。
| [1] |
Danielsen J E, Auken E, Jørgensen F, et al. The application of the transient electromagnetic method in hydrogeophysical surveys[J]. Journal of Applied Geo-physics, 2003, 53(4): 181-198. DOI:10.1016/j.jappgeo.2003.08.004 |
| [2] |
Zhou N N, Xue G Q, Chen W Y, et al. Large-depth hydro-geological detection in the North China-type coalfield through short-offset grounded-wire TEM[J]. Environmental Earth Sciences, 2015, 74(3): 2393-2404. DOI:10.1007/s12665-015-4240-y |
| [3] |
胡祖志, 石艳玲, 何展翔, 等. 瞬变电磁法在西部黄土层勘探中的应用[J]. 石油地球物理勘探, 2016, 51(增刊): 131-136. HU Zuzhi, SHI Yanling, HE Zhanxiang, et al. Transient electromagnetic exploration in loess layer, Wes-tern China[J]. Oil Geophysical Prospecting, 2016, 51(S): 131-136. |
| [4] |
Men Y Y, Yang Y J, Zhu Y S. The investigation of underground aquifer layer for oilfield sewage reinjection with TDEM[C]. International Geophysical Conference, Qingdao, China, 2017, 1005-1007.
|
| [5] |
邓宇, 金留青, 李万山, 等. 近地表岩溶探测方法[J]. 石油地球物理勘探, 2018, 53(2): 430-436. DENG Yu, JIN Liuqing, LI Wanshan, et al. An integrated geophysical method for near-surface karst survey[J]. Oil Geophysical Prospecting, 2018, 53(2): 430-436. |
| [6] |
Commer M. Three-dimensional Inversion of Transient Electromagnetic Data: A Comparative Study[D]. Universität zu Köln, Köln, Germany, 2003.
|
| [7] |
Haber E, Oldenburg D W, Shekhtman R. Inversion of time domain three-dimensional electromagnetic data[J]. Geophysical Journal of the Royal Astronomical Society, 2007, 171(2): 550-564. DOI:10.1111/j.1365-246X.2007.03365.x |
| [8] |
Börner R U. Numerical modeling in geo-electromagnetic:advances and challenges[J]. Surveys in Geophysics, 2010, 31(2): 225-245. DOI:10.1007/s10712-009-9087-x |
| [9] |
Yang D K, Oldenburg D W, Haber E. 3-D inversion of airborne electromagnetic data parallelized and accelerated by local mesh and adaptive soundings[J]. Geophysical Journal International, 2014, 196(3): 1492-1507. DOI:10.1093/gji/ggt465 |
| [10] |
李建慧, 刘树才, 焦险峰, 等. 地-井瞬变电磁法三维正演研究[J]. 石油地球物理勘探, 2015, 50(3): 556-564. LI Jianhui, LIU Shucai, JIAO Xianfeng, et al. Three-dimensional forward modeling for surface borehole transient electromagnetic method[J]. Oil Geophysical Prospecting, 2015, 50(3): 556-564. |
| [11] |
Liu Y H, Yin C C, Ren X Y, et al. 3D parallel inversion of time-domain airborne EM data[J]. Applied Geophysics, 2016, 13(4): 701-711. DOI:10.1007/s11770-016-0581-x |
| [12] |
薛国强, 李貅, 底青云. 瞬变电磁法正反演问题研究进展[J]. 地球物理学进展, 2008, 23(4): 1165-1172. XUE Guoqiang, LI Xiu, DI Qingyun. Research progress in TEM forward modeling and inversion calculation[J]. Progress in Geophysics, 2008, 23(4): 1165-1172. |
| [13] |
薛国强, 闫述, 陈卫营. 接地源短偏移瞬变电磁法研究展望[J]. 地球物理学进展, 2014, 29(1): 177-181. XUE Guoqiang, YAN Shu, CHEN Weiying. Research prospect to grounded-wire TEM with short-offset[J]. Progress in Geophysics, 2014, 29(1): 177-181. |
| [14] |
薛国强, 于景邨. 瞬变电磁法在煤炭领域的研究与应用新进展[J]. 地球物理学进展, 2017, 32(1): 319-326. XUE Guoqiang, YU Jingcun. New development of TEM research and application in coal mine exploration[J]. Progress in Geophysics, 2017, 32(1): 319-326. |
| [15] |
蔡晶, 齐彦福, 殷长春. 频率域航空电磁数据的加权横向约束反演[J]. 地球物理学报, 2014, 57(3): 954-960. CAI Jing, QI Yanfu, YIN Changchun. Weighted la-terally-constrained inversion of frequency-domain airborne EM data[J]. Chinese Journal of Geophysics, 2014, 57(3): 954-960. |
| [16] |
殷长春, 邱长凯, 刘云鹤, 等. 时间域航空电磁数据加权横向约束反演[J]. 吉林大学学报(地球科学版), 2016, 46(1): 254-261. YIN Changchun, QIU Changkai, LIU Yunhe, et al. Weighted laterally-constrained inversion of time-domain airborne electromagnetic data[J]. Journal of Jilin University(Earth Science Edition), 2016, 46(1): 254-261. |
| [17] |
曾庆宁, 罗瀛, 刘帅, 等. 瞬变电磁全期视电阻率的弦截无限逼近算法[J]. 石油地球物理勘探, 2019, 54(6): 1371-1375. ZENG Qingning, LUO Ying, LIU Shuai, et al. A secant infinite approximation algorithm for the full-time apparent resistivity in transient electromagnetic me-thod[J]. Oil Geophysical Prospecting, 2019, 54(6): 1371-1375. |
| [18] |
翁爱华, 王雪秋. 长偏移距瞬变电磁测深甚晚期响应及视电阻率的数值计算[J]. 地震地质, 2003, 25(4): 664-670. WENG Aihua, WANG Xueqiu. Numerical simulations of very-late time response and apparent resistivity in long-offset TEM sounding[J]. Seismology and Geology, 2003, 25(4): 664-670. DOI:10.3969/j.issn.0253-4967.2003.04.016 |
| [19] |
Farquharson C G, Oldenburg D W, Routh P S. Simultaneous 1D inversion of loop-loop electromagnetic data for magnetic susceptibility and electrical conducti-vity[J]. Geophysics, 2003, 68(6): 1857-1869. DOI:10.1190/1.1635038 |
| [20] |
陈清礼, 严良俊, 付志红, 等. 长偏移距瞬变电磁法全区视电阻率的二分搜索数值算法[J]. 石油地球物理勘探, 2009, 44(6): 779-782. CHEN Qingli, YAN Liangjun, FU Zhihong, et al. The all-time apparent resistivity bisearch numerical algorithm based on long offset transient electromagnetic method[J]. Oil Geophysical Prospecting, 2009, 44(6): 779-782. DOI:10.3321/j.issn:1000-7210.2009.06.023 |
| [21] |
Christensen N B. Fast approximate 1D modelling and inversion of transient electromagnetic data[J]. Geophysical Prospecting, 2016, 64(6): 1620-1631. DOI:10.1111/1365-2478.12373 |
| [22] |
Auken E, Christiansen A V. Layered and laterally constrained 2D inversion of resistivity data[J]. Geophysics, 2004, 69(3): 752-761. DOI:10.1190/1.1759461 |
| [23] |
Vallée M A, Smith R S. Inversion of airborne time-domain electromagnetic data to a 1D structure using lateral constraints[J]. Near Surface Geophysics, 2009, 7(1): 63-71. DOI:10.3997/1873-0604.2008035 |
| [24] |
Viezzoli A, Auken E, Munday T. Spatially constrai-ned inversion for quasi-3D modelling of airborne electromagnetic data:an application for environmental assessment in the lower Murray region of south Australia[J]. Exploration Geophysics, 2009, 40(2): 173-183. DOI:10.1071/EG08027 |
| [25] |
殷长春, 朱姣, 邱长凯, 等. 航空电磁拟三维模型空间约束反演[J]. 地球物理学报, 2018, 61(6): 2537-2547. YIN Changchun, ZHU Jiao, QIU Changkai, et al. Spatially constrained inversion for airborne EM data using quasi-3D models[J]. Chinese Journal of Geophysics, 2018, 61(6): 2537-2547. |
| [26] |
米萨克N, 纳比吉安编, 赵经祥译.勘查地球物理——电磁法[M].北京: 地质出版社, 1992.
|
| [27] |
Steven C C, Robert L P, Catherine G C. Occam's inversion:A practical algorithm for generating smooth models from electromagnetic sounding data[J]. Geophysics, 1987, 52(3): 289-300. DOI:10.1190/1.1442303 |



 杨云见, 河北省涿州市范阳西路189号东方地球物理公司, 072751。Email:
杨云见, 河北省涿州市范阳西路189号东方地球物理公司, 072751。Email: