② 有色资源与地质灾害探查湖南省重点实验室, 湖南长沙 410083;
③ 中南大学地球科学与信息物理学院, 湖南长沙 410083;
④ 自然资源部覆盖区深部资源勘查工程技术创新中心, 湖南长沙 410083;
⑤ 长沙航空职业技术学院, 湖南长沙 410124
② Hunan Key Laboratory of Nonferrous Resources and Geological Hazards Exploration, Changsha, Hunan 410083, China;
③ School of Geosciences and Info-physics, Central South University, Changsha, Hunan 410083, China;
④ Technical Innovation Center of Coverage Area Deep Resources Exploration, Ministry of Natural Resources, Changsha, Hunan 410083, China;
⑤ Changsha Aeronautical Vocational and Technical College, Changsha, Hunan 410124, China
卫星、航空、地面、井中等多维空间的磁场数据测量技术迅速发展并逐渐成熟,配套的数据处理和解释技术也在不断更新和完善,这势必拓宽磁法勘探的应用领域,提高磁法的探测能力[1-4]。磁场数据三维反演不仅能够提供磁异常体的空间位置,还能获得磁性异常体的形状、物性分布等定量信息,在磁场数据处理和解释中具有重要意义,一直是该领域的研究热点问题。
目前的磁异常反演包括磁化率和磁性界面两方面的内容。磁化率反演首先固定反演网格,假设反演单元内磁化率为常数或者线性分布,建立反演目标函数,然后最小化反演目标函数,从而获得目标的磁化率分布[5-6]。Li等[6]利用一个或多个适当的加权函数将先验信息引入目标函数;Pilkington[7]对目标函数进行平滑及深度加权; Miguel[8]通过地质统计学模型实现了岩性约束下的重磁数据联合反演;Fregoso等[9]实现了重磁数据的交叉梯度联合反演。上述方法可定量描述地质构造的磁化率分布。磁性界面反演方法一般假定已知地下异常体的磁化率,通过反演得到异常体的边界和位置。管志宁等[10]提出了频率域磁性单界面反演方法,推导了常磁性与变磁性单界面反问题解的近似表达式;Pilkington等[11]提出了利用重磁资料确定地壳界面起伏形态;Wang等[12]对多面体的顶点位置进行反演;刘沈衡等[13]利用欧拉算法反演磁性界面;Fullagar等[14]通过混合参数化反演得到目标体磁化率的分布及垂直界面的位置。赵文举等[15]通过BP神经网络预测磁性体顶面埋深;郑强等[16]基于磁梯度张量特征值成功地识别了磁性体边界。然而,由于缺乏地下异常体拓扑结构和数量信息,现有的磁边界反演算法无法灵活描述复杂地下磁性目标体的几何形状。
因此,需要一种无需过多关于异常体拓扑结构和数量的先验信息就可以直接反演地下磁异常体空间位置和边界的算法。基于水平集方法[17-21]的磁边界反演算法正好符合这一要求,该方法仅需已知目标体的平均磁化率就可以反演得到地下异常体的边界及几何形状。Isakov等[22]将水平集方法用于重力数据反演;Zheglova等[23]将水平集用于地震旅行时层析成像,实现了边界的二维重建;Li等[24]在磁性数据的反演中引入水平集,用两个水平集对地下磁性体的边界进行了三维反演;在矿产勘查中,Li等[25]在地表数据与钻孔磁资料的联合反演中引入水平集,实现了目标圈定。基于水平集的反演可以得到异常体明确的边界,将水平集引入磁边界反演,是改善磁边界反演效果的重要途径。然而,目前已发表的基于水平集的磁性目标体边界反演算法仅使用了两个水平集,而实际地球物理勘探的目标往往是多个具有不同磁化率的磁性体。
针对上述问题,本文在Li等[24]的基础上提出了一种基于多重水平集的磁边界反演算法,该算法具有抗噪性强、精度高、多目标识别的优点。首先基于多个水平集函数建立磁界面反演目标函数,并详细推导了在多重水平集反演构架下磁边界反演的实现过程;然后采用任意四面体单元磁法解析解算法[24]进行高精度正演计算,构建正演网格与反演网格的映射关系,并基于加权基本无振荡(WENO)格式对水平集函数进行更新及重新初始化;最后,通过多个理论模型算例验证本文反演算法的有效性,并分析初始模型对反演结果的影响。
1 方法与原理 1.1 基于磁化率的多重水平集表示假设非磁性背景下,区域Ω中包含N个磁性体,且每个磁性体具有恒定的磁化率,则磁化率分布可表示为
| $ \kappa (\mathit{\boldsymbol{\tilde r}}) = \left\{ {\begin{array}{*{20}{c}} {{\kappa _i}}&{\mathit{\boldsymbol{\tilde r}} \in {\mathit{\boldsymbol{D}}_i}}\\ 0&{\mathit{\boldsymbol{\tilde r}} \in \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}\backslash \cup {\mathit{\boldsymbol{D}}_i}} \end{array}i = 1, 2, \cdots , N} \right. $ | (1) |
式中:Di是第i个磁性体的区域,各个异常体区域不一定相互连通;κi表示第i个磁性体的磁化率;符号“∪”表示求并集;符号“\”表示求补集;$\mathit{\boldsymbol{\tilde r}}$表示源的空间坐标。
上述模型的磁化率可用水平集公式表示为
| $ \kappa (\mathit{\boldsymbol{\tilde r}}) = \sum\limits_{i = 1}^N {\{ {\kappa _i}H[{\phi _i}(\mathit{\boldsymbol{\tilde r}})]\prod\limits_{n = 1, n \ne i}^N {[1 - H[{\phi _n}(\mathit{\boldsymbol{\tilde r}})]\} } \} } $ | (2) |
式中:ϕ(·)表示水平集函数;H(·)表示Heaviside函数[25]。其表达式分别为
| $ {\phi _i}(\mathit{\boldsymbol{\tilde r}})\left\{ {\begin{array}{*{20}{l}} {{\rm{ > }}0}&{\mathit{\boldsymbol{\tilde r}} \in {\mathit{\boldsymbol{D}}_i}}\\ { = 0}&{\mathit{\boldsymbol{\tilde r}} \in \partial {\mathit{\boldsymbol{D}}_i}}\\ {{\rm{ < }}0}&{\mathit{\boldsymbol{\tilde r}} \in \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}\backslash {\mathit{\boldsymbol{D}}_i}} \end{array}} \right. $ | (3) |
| $ {H_\varepsilon }(\phi ) = \left\{ {\begin{array}{*{20}{c}} 0&{{\rm{ }}\phi < - \varepsilon }\\ {\frac{1}{2} + \frac{\phi }{{2\varepsilon }} + \frac{1}{{2{\rm{ \mathit{ π} }}}}\sin \frac{{{\rm{ \mathit{ π} }}\phi }}{\varepsilon }}&{ - \varepsilon \le \phi \le \varepsilon }\\ 1&{{\rm{ }}\varepsilon < \phi } \end{array}} \right. $ | (4) |
式中:∂Di表示区域Di的边界;ε是一个很小的数,用来控制边界面的厚度,ε越小,得到的边界面越尖锐,反之则越平滑。用水平集函数ϕi($\mathit{\boldsymbol{\tilde r}}$)参数化未知域Di,并通过恢复ϕi($\mathit{\boldsymbol{\tilde r}}$)重构磁化率分布κ($\mathit{\boldsymbol{\tilde r}}$)。磁源的边界由零水平集$\left\{\tilde{\boldsymbol{r}} \mid \phi_{i}(\tilde{\boldsymbol{r}})=0\right\}$表示,在数值上,水平集函数保持为源边界∂Di的带符号距离函数
| $ {\phi _i}(\mathit{\boldsymbol{\tilde r}}) = \left\{ {\begin{array}{*{20}{l}} {{\rm{dist}}(\mathit{\boldsymbol{\tilde r}}, \partial {\mathit{\boldsymbol{D}}_i})}&{\mathit{\boldsymbol{\tilde r}} \in {\mathit{\boldsymbol{D}}_i}}\\ { - {\rm{dist}}(\mathit{\boldsymbol{\tilde r}}, \partial {\mathit{\boldsymbol{D}}_i})}&{\mathit{\boldsymbol{\tilde r}} \in \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}\backslash {\mathit{\boldsymbol{D}}_i}} \end{array}} \right. $ | (5) |
式中dist($\mathit{\boldsymbol{\tilde r}}$, ∂Di)表示从源$\mathit{\boldsymbol{\tilde r}}$到边界∂Di的最短距离。符号距离属性可以通过水平集重新初始化来维护。
根据式(2),可以得到κ($\mathit{\boldsymbol{\tilde r}}$)关于更新模型参数ϕi的Fréchet导数
| $ \begin{array}{l} \frac{{\partial \kappa (\mathit{\boldsymbol{\tilde r}})}}{{\partial {\phi _i}}} = {\kappa _i}\delta ({\phi _i})\prod\limits_{n = 1, n \ne i}^N {\{ 1 - H[{\phi _n}(\mathit{\boldsymbol{\tilde r}})]\} - } \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \delta ({\phi _i})\prod\limits_{n = 1, n \ne i}^N {\left\{ {{\kappa _n}H({\phi _n})\prod\limits_{n = 1, n \ne i}^N {[1 - H({\phi _m})]} } \right\}} \end{array} $ | (6) |
式中δ(·)是Dirac delta函数。
1.2 基于多重水平集的磁边界反演算法反演的总目标函数Ei可表示为数据拟合差泛函Ed和正则化项Er的线性组合
| $ {E_{\rm{t}}} = {E_{\rm{d}}} + \alpha {E_{\rm{r}}} $ | (7) |
式中:Er有助于平滑零水平集{$\mathit{\boldsymbol{\tilde r}}$|ϕi($\mathit{\boldsymbol{\tilde r}}$)=0}表征的边界形状,且可缓解反演问题中解的非唯一性;α是正则化参数,本文参考Li等[24]的取值,选取$a{\rm{ = }}{10^{ - 12}} \times {\left({\frac{1}{{4{\rm{ \mathsf{ π} }}}}{B_0}\kappa /\bar \sigma } \right)^2}$,其中B0表示感应场强度,本文取B0=50000nT,σ表示数据误差标准差的平均值。
1.2.1 数据失配项及其导数用$\left\{d_{k}^{*}\right\}_{k=1}^{M}$表示观测数据,$\left\{d_{k}\right\}_{k=1}^{M}$表示模型正演数据,数据拟合差泛函[24]为
| $ {E_{\rm{d}}} = \frac{1}{{2M}}\sum\limits_{k = 1}^M {{{\left( {\frac{{{d_k} - d_k^ * }}{{{o_k}}}} \right)}^2}} $ | (8) |
式中:M是观测点数;σk是与第k个数据相关的误差标准偏差,数据拟合差的最优值一般为0.5。
Ed关于κ($\mathit{\boldsymbol{\tilde r}}$)的Fréchet导数为
| $ \frac{{\partial {E_{\rm{d}}}}}{{\partial \kappa (\mathit{\boldsymbol{\tilde r}})}} = \frac{1}{{4{\rm{ \mathit{ π} }}}}{B_0}\frac{1}{M}\sum\limits_{k = 1}^M {\frac{{{d_k} - d_k^*}}{{\sigma _k^2}}K} ({\mathit{\boldsymbol{r}}_k}, \mathit{\boldsymbol{\tilde r}}) $ | (9) |
式中K(rk, $\mathit{\boldsymbol{\tilde r}}$)是积分核函数,可表示为
| $ \begin{array}{l} K({\mathit{\boldsymbol{r}}_k}, \mathit{\boldsymbol{\tilde r}}) = \frac{1}{{|{\mathit{\boldsymbol{r}}_k} - \mathit{\boldsymbol{\tilde r}}{|^3}}}\left\{ {\frac{{3{{[{\mathit{\boldsymbol{B}}_0}({\mathit{\boldsymbol{r}}_k} - \mathit{\boldsymbol{\tilde r}})]}^2}}}{{|{\mathit{\boldsymbol{r}}_k} - \mathit{\boldsymbol{\tilde r}}{|^2}}} - 1} \right\}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{r}}_k} \in \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}, \mathit{\boldsymbol{\tilde r}} \le \mathit{\boldsymbol{ \boldsymbol{\varOmega} }} \end{array} $ | (10) |
其中:B0表示磁感应场的方向;r表示观测点的空间坐标;Γ表示观测面。结合式(8)与式(9),可以得到拟合差泛函Ed关于ϕi($\mathit{\boldsymbol{\tilde r}}$)的Fréchet导数
| $ \begin{array}{l} \frac{{\partial {E_{\rm{d}}}}}{{\partial {\phi _i}(\mathit{\boldsymbol{\tilde r}})}} = \frac{1}{{4{\rm{ \mathit{ π} }}}}\delta \left( {{\phi _i}} \right) \times \left\{ {{\kappa _i}\prod\limits_{n \ne i}^N {\left\{ {1 - H\left[ {{\phi _n}(\mathit{\boldsymbol{\tilde r}})} \right]} \right\}} - } \right.\\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{n \ne i}^N {{\kappa _n}} H\left( {{\phi _n}} \right)\prod\limits_{m \ne i, n}^N {\left[ {1 - H\left( {{\phi _m}} \right)} \right]} } \right\} \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {B_0}\frac{1}{M}\sum\limits_{k = 1}^M {\frac{{{d_k} - d_k^*}}{{\sigma _k^2}}} K\left( {{\mathit{\boldsymbol{r}}_k}, \mathit{\boldsymbol{\tilde r}}} \right) \end{array} $ | (11) |
使Ed最小化的必要条件是∂Ed/∂ϕi($\mathit{\boldsymbol{\tilde r}}$)=0,可通过更新模型参数ϕi恢复磁化率κ($\mathit{\boldsymbol{\tilde r}}$)。式(10)中函数δ(ϕi)在数值上可近似为${{\rm{ \mathsf{ δ} }}_\tau }\left({{\phi _i}} \right) = {{\cal L}_{\mathit{\boldsymbol{T}}_\tau ^i}} \times \left| {\nabla {\phi _i}} \right|$[21, 26-28],其中
| $ {\mathcal{L}_{T_\tau ^i}} = \left\{ {\begin{array}{*{20}{l}} 1&{\mathit{\boldsymbol{\tilde r}} \in \mathit{\boldsymbol{T}}_\tau ^i}\\ 0&{\mathit{\boldsymbol{\tilde r}} \in \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}\backslash \mathit{\boldsymbol{T}}_\tau ^i} \end{array}} \right. $ | (12) |
| $ \mathit{\boldsymbol{T}}_\tau ^i = \{ \mathit{\boldsymbol{\tilde r}} \in \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}:|{\phi _i}(\mathit{\boldsymbol{\tilde r}})| \le \tau \} $ | (13) |
式中参数τ控制函数δ(ϕi)的带宽,并在Tτi中更新水平集函数ϕi。为了有效更新,本文设置τ=0.5×min(Δx, Δy, Δz),其中Δx、Δy、Δz分别表示正演区域x、y、z方向网格大小。
令
| $ \begin{array}{l} {F_i}(\mathit{\boldsymbol{\tilde r}}) = \frac{1}{{4{\rm{ \mathit{ π} }}}}\left\{ {{\kappa _i}\prod\limits_{n = 1, n \ne i}^N {\left\{ {1 - {H_\varepsilon }\left[ {{\phi _n}(\mathit{\boldsymbol{\tilde r}})} \right]} \right\}} - } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\sum\limits_{n = 1, n \ne i}^N {{\kappa _n}} {H_\varepsilon }\left( {{\phi _n}} \right)\prod\limits_{m = 1, m \ne i, n}^N {\left[ {1 - {H_\varepsilon }\left( {{\phi _m}} \right)} \right]} } \right\} \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {B_0}{{\cal L}_{T_\tau ^i}}\frac{1}{M}\sum\limits_{k = 1}^M {\frac{{{d_k} - d_k^*}}{{\sigma _k^2}}} K\left( {{\mathit{\boldsymbol{r}}_k}, \mathit{\boldsymbol{\tilde r}}} \right) \end{array} $ | (14) |
则
| $ \frac{{\partial {E_{\rm{d}}}}}{{\partial {\phi _i}(\mathit{\boldsymbol{\tilde r}})}} = {F_i}(\mathit{\boldsymbol{\tilde r}})|\nabla {\phi _i}| $ | (15) |
为了进一步降低反演的多解性,本文在水平集反演目标函数中引入Tikhonov正则化项
| $ {E_{\rm{r}}} = \sum\limits_{i = 1}^P {\frac{1}{2}} \int_\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}^{} | \nabla {\phi _i}{|^2}{\rm{d}}\mathit{\boldsymbol{\tilde r}} $ | (16) |
式中P代表水平集个数。Er的Fréchet导数为
| $ \frac{{\partial {E_{\rm{r}}}}}{{\partial {\phi _i}}} = - {\nabla ^2}{\phi _i} $ | (17) |
式中▽2表示拉普拉斯算子。因此,得到
| $ \frac{{\partial {E_{\rm{r}}}}}{{\partial {\phi _i}}} = \frac{{\partial {E_{\rm{d}}}}}{{\partial {\phi _i}}} - \alpha {\nabla ^2}{\phi _i} = {F_i}|\nabla {\phi _i}| - \alpha {\nabla ^2}{\phi _i} $ | (18) |
对均匀网格,利用WENO格式对水平集方程和重新初始化方程进行空间离散[29-34],并利用三阶精确总变差递减龙格—库塔格式(TVD-RK3)[32]进行时间离散化。
1.3.1 水平集方程的近似对于式(18),使用TVD-RK3格式及Godunov法对H(▽ϕi)=Fi|▽ϕi|进行空间离散化,得到
| $ {H_{\rm{G}}}\left( {{\phi _i}} \right) = \left\{ {\begin{array}{*{20}{l}} {{F_i}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sqrt {\max \left( {{{\left| {{a_ + }} \right|}^2}, {{\left| {{b_ - }} \right|}^2}} \right) + \max \left( {{{\left| {{c_ + }} \right|}^2}, {{\left| {{d_ - }} \right|}^2}} \right) + \max \left( {{{\left| {{e_ + }} \right|}^2}, {{\left| {{f_ - }} \right|}^2}} \right)} }&{{F_i} \le 0}\\ {{F_i}{\kern 1pt} {\kern 1pt} {\kern 1pt} \sqrt {\max \left( {{{\left| {{a_ - }} \right|}^2}, {{\left| {{b_ + }} \right|}^2}} \right) + \max \left( {{{\left| {{c_ - }} \right|}^2}, {{\left| {{d_ + }} \right|}^2}} \right) + \max \left( {{{\left| {{e_ - }} \right|}^2}, {{\left| {{f_ + }} \right|}^2}} \right)} }&{{F_i} > 0} \end{array}} \right. $ | (19) |
式中:(·)+=max(·, 0),(·)-=min(·, 0);a=Dx-ϕi、b=Dx+ϕi、c=Dy-ϕi、d=Dy+ϕi、e=Dz-ϕi、f=Dz+ϕi,其中Dx-和Dx+、Dy-和Dy+、Dz-和Dz+分别表示WENO格式下求x、y、z方向上的向后和向前差分。
使用TVD-RK3格式进行时间离散化。例如, 对水平集方程${\phi _t} + {F_i}|\nabla \phi | = 0$,首先对ϕ(l)执行一次欧拉计算,得到t(l+1)时刻的解${\tilde \phi ^{(l + 1)}}$
| $ \frac{{{{\tilde \phi }^{(l + 1)}} - {\phi ^{(l)}}}}{{\Delta t}} + {H_{\rm{G}}}[{\phi ^{(l)}}] = 0 $ | (20) |
式中:Δt为时间步长;l表示迭代次数。然后,对$\tilde{\phi}$(l+1)再次执行欧拉计算
| $ \frac{{{{\tilde \phi }^{(l + 2)}} - {\phi ^{(l + 1)}}}}{{\Delta t}} + {H_{\rm{G}}}[{{\tilde \phi }^{(l + 1)}}] = 0 $ | (21) |
得到下一时刻t(l+2)的临时解$\tilde{\phi}$(l+2)。用平均法给出$t^ \left(l+\frac{1}{2}\right)$时刻的临时解$\tilde{\phi}^\left(l+\frac{1}{2}\right)=\frac{3}{4} \phi^{(l)}+\frac{1}{4} \tilde{\phi}^{(l+2)}$。根据下式,从$\tilde{\phi}^\left(l+\frac{1}{2}\right)$得到$t^\left(l+\frac{3}{2}\right)$时刻的临时解$\tilde{\phi}^\left(l+\frac{3}{2}\right)$
| $ \frac{{{{\tilde \phi }^{(l + \frac{3}{2})}} - {\phi ^{(l + \frac{1}{2})}}}}{{\Delta t}} + {H_{\rm{G}}}\left[ {{{\tilde \phi }^{(l + \frac{1}{2})}}} \right] = 0 $ | (22) |
通过线性平均更新ϕ(l+1)
| $ {\phi ^{(l + 1)}} = \frac{1}{3}{\phi ^{(l)}} + \frac{2}{3}{{\tilde \phi }^{(l + \frac{3}{2})}} $ | (23) |
并建立一个Courant-Friedrichs-Lewy(CFL)条件[34]
| $ \begin{array}{l} \Delta t\left\{ {\frac{{{\rm{max}}|{F_i}|}}{{{\rm{min}}(\Delta x, \Delta y, \Delta z)}}} \right. + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\frac{\alpha }{{ {\rm{min}} [{{(\Delta x)}^2}, {{(\Delta y)}^2}, {{(\Delta z)}^2}]}}} \right\} < 1 \end{array} $ | (24) |
保持更新的稳定性。在本文反演中,正则化参数α远小于max|Fi|,所以设
| $ \Delta t = 0.5\frac{{{\rm{min}}(\Delta x, \Delta y, \Delta z)}}{{{\rm{max}}|{F_i}|}} $ | (25) |
一般情况下,水平集函数在通过式(18)进行迭代时,并不保留其符号距离属性,所以Sussman等[19]引入了重新初始化方程
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial {\phi _i}}}{{\partial i}} + {\rm{sign}}[\phi _i^{(0)}](|\nabla {\phi _i}| - 1) = 0}\\ {{\phi _i}(\mathit{\boldsymbol{\tilde r}}, t = 0) = {\phi _i}(\mathit{\boldsymbol{\tilde r}})}\\ {{{\left. {\frac{{\partial {\phi _i}}}{{\partial \mathit{\boldsymbol{n}}}}} \right|}_{\partial \mathit{\boldsymbol{ \boldsymbol{\varOmega} }}}} = 0} \end{array}} \right. $ | (26) |
式中:ϕi(0)表示初始值;n表示法向;sign $\left[{\phi _i^{(0)}} \right] = \phi _i^{(0)}/\sqrt {{{\left[{\phi _i^{(0)}} \right]}^2} + {{\left| {\nabla \phi _i^{(0)}} \right|}^2}{{(\Delta h)}^2}} $,其中Δh=min(Δx, Δy, Δz)。本文应用水平集重新初始化维持ϕi的符号距离属性,即|▽ϕi|=1,可以看成是对模型参数ϕi的正则化[22, 35-36]。因为水平集函数表征的边界形状主要由零水平集确定,所以实际上只需对式(24)进行迭代,使|▽ϕi|趋近于1,并用解ϕi代替水平集函数ϕi(0)。在本文算法中,通过||▽ϕi|-1|≤γ控制水平集函数的重新初始化程度与次数,其中γ为一个很小的数。
对于重新初始化方程的离散化求解,同样使用TVD-RK3格式以及Godunov空间离散化$H\left({\nabla \phi _i^{(0)}} \right) = {\mathop{\rm sign}\nolimits} \left[{\phi _i^{(0)}} \right]\left({\left| {\nabla {\phi _i}} \right| - 1} \right)$,即
| $ {H_{\rm{G}}}\left( {{\phi _i}} \right) = \left\{ {\begin{array}{*{20}{l}} {{\rm{sign}}\left[ {\phi _i^{\left( 0 \right)}} \right]\sqrt {\max \left( {{{\left| {{a_ + }} \right|}^2}, {{\left| {{b_ - }} \right|}^2}} \right) + \max \left( {{{\left| {{c_ + }} \right|}^2}, {{\left| {{d_ - }} \right|}^2}} \right) + \max \left( {{{\left| {{e_ + }} \right|}^2}, {{\left| {{f_ - }} \right|}^2}} \right)} - 1}&{\phi _i^{\left( 0 \right)} \le 0}\\ {{\rm{sign}}\left[ {\phi _i^{\left( 0 \right)}} \right]\sqrt {\max \left( {{{\left| {{a_ - }} \right|}^2}, {{\left| {{b_ + }} \right|}^2}} \right) + \max \left( {{{\left| {{c_ - }} \right|}^2}, {{\left| {{d_ + }} \right|}^2}} \right) + \max \left( {{{\left| {{e_ - }} \right|}^2}, {{\left| {{f_ + }} \right|}^2}} \right)} - 1}&{\phi _i^{\left( 0 \right)} > 0} \end{array}} \right. $ | (27) |
分别选取两个水平集和三个水平集的模型分析该反演算法的效果。模拟计算区域为1000m(x)×1000m(y)×500m(z),并将其均匀划分为40×40×20个六面体网格,每个六面体网格均被划分为六个四面体单元;观测面为z=100m的水平面,观测点个数M=21×21。对每个模型的正演数据都加入均值为零、标准差σ=5nT的高斯白噪声,记模拟观测磁异常场为{dk*}k=1M。
2.1 反演流程本文采用任意四面体单元磁法解析解算法[24]进行高精度正演计算,利用正、反演网格之间的物性映射实现正演网格与反演网格相互独立运行,并基于WENO格式对水平集函数进行更新及重新初始化,具体反演流程如下。
(1) 初始化水平集函数ϕi;
(2) 用式(2)表示磁化率κ($\mathit{\boldsymbol{\tilde r}}$);
(3) 基于任意四面体单元磁法解析解算法[26]计算各个模型在观测面Γ的正演数据dkk=1M;
(4) 基于WENO格式计算总目标函数Et的负梯度方向-∂Et/∂ϕi,并更新水平集函数ϕi;
(5) 重新初始化水平集函数ϕi,使其保持带符号距离属性;
(6) 返回步骤(2),直至迭代收敛或达到最大迭代次数。
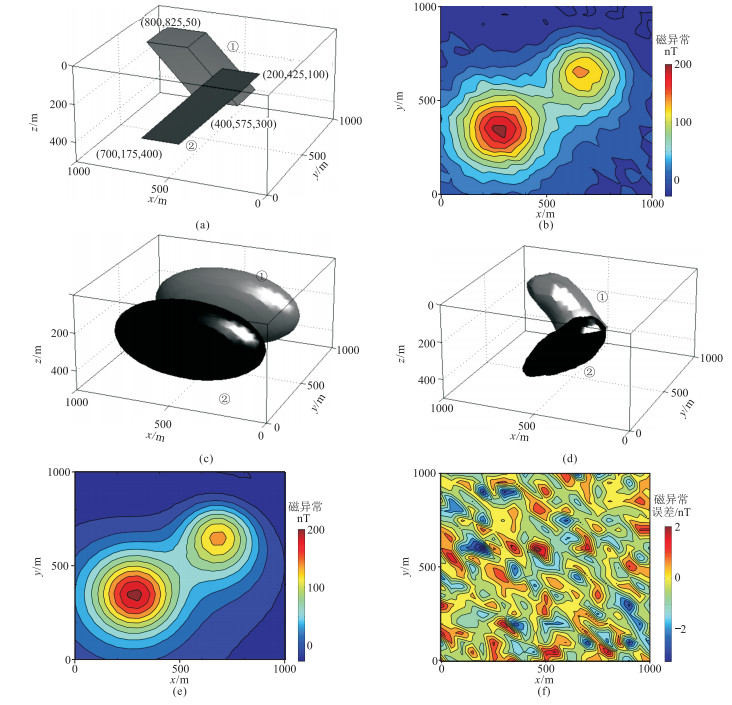
2.2 两个水平集模型设计一个由具有不同磁化率的两个倾斜棱镜体组成的模型,分析基于两个水平集公式的磁边界反演效果。首先根据先验信息确定两个不同的磁化率,并使用基于两个水平集公式的磁边界反演算法确定异常体数目并恢复磁性体边界。
设计模型如图 1a所示,由κ1=0.04SI和κ2=0.08SI的两个倾斜棱镜体组成。图 1b为加噪总磁异常图。初始猜测如图 1c所示。反演中引入两个水平集函数ϕ1和ϕ2,初始猜测分别为
|
图 1 两个不同磁化率的倾斜棱镜模型及两个水平集计算结果 (a)模型示意图;(b)加噪总磁异常图;(c)初始猜测模型;(d)两个水平集的反演模型;(e)图d正演磁异常图;(f)图e与图b的差值 |
| $ \begin{array}{l} {\phi _1} = 1 - \\ \ \ \ \ \ \ \ \ \sqrt {\frac{{{{(x - 500)}^2}}}{{{{400}^2}}} + \frac{{{{(y - 750)}^2}}}{{{{150}^2}}} + \frac{{{{(z - 250)}^2}}}{{{{200}^2}}}} \end{array} $ | (28) |
| $ \begin{array}{l} {\phi _2} = 1 - \\ \ \ \ \ \ \ \ \ \sqrt {\frac{{{{(x - 500)}^2}}}{{{{400}^2}}} + \frac{{{{(y - 250)}^2}}}{{{{150}^2}}} + \frac{{{{(z - 250)}^2}}}{{{{200}^2}}}} \end{array} $ | (29) |
图 1d是使用多水平集反演得到的模型,其数据拟合差Ed=0.5022,可见反演结果与原模型的形状和位置吻合较好。图 1e是磁场强度B0=50000nT、磁倾角为75°、磁偏角为25°的背景感应场下,反演模型(图 1d)在观测面正演的磁异常图。图 1f为反演模型的正演磁异常(图 1e)与原模型加噪磁异常(图 1b)之差。反演结果的更多细节见图 2。显然,使用两个水平集的反演结果很好地恢复了每个棱镜体的倾角、空间位置及形态,且反演误差与预期的一样,呈随机分布特征。
|
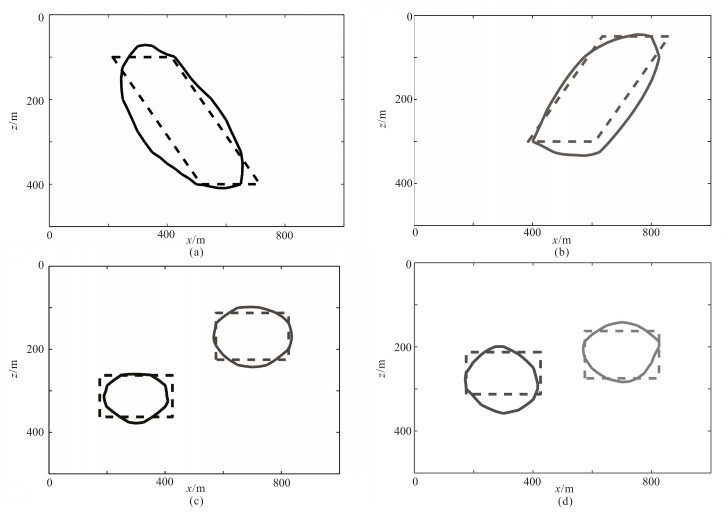
图 2 两个不同磁化率的倾斜棱镜体模型使用两个水平集的反演结果细节展示 (a)y=300m截面;(b)y=700m截面;(c)z=150m平面图;(d)z=250m平面图 虚线表示模型的真实边界,实线表示模型的恢复边界 |
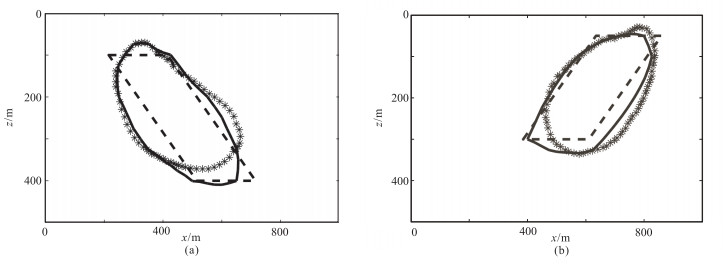
将本文反演结果与Li等[24]的反演结果做对比,见图 3。可以看出,本文采用基于任意四面体单元的磁法解析解算法[26]进行高精度正演,并引入HJ-WENO格式对水平集方程进行更新及重新初始化,反演得到的磁异常体边界与模型吻合更好。
|
图 3 本文反演结果与Li等[24]的反演结果对比 (a)y=300m截面(过磁性体①);(b)y=700m截面(过磁性体②) 虚线为模型的轮廓线,实线为本文反演磁性体边界,*线表示Li等反演的磁性体边界 |
实际地下地质情况是非常复杂的,需分析多个磁性体存在的情况下,本文方法是否有效。对于具有不同磁化率值的磁性体,需要引入更多的水平集函数,对其进行磁边界反演。
假设模型由三个具有不同磁化率的直立长方体组成(图 4a),且磁化率值已知。图 4b为加噪总磁异常图。根据图 4b,在反演算法中引入三个水平集函数ϕ1、ϕ2和ϕ3,初始猜测(图 4c)分别为

|
图 4 三个不同磁化率模型及三个水平集计算结果 (a)模型示意图;(b)加噪总磁异常图;(c)初始猜测模型;(d)三个水平集的反演模型;(e)图d正演磁异常图;(f)图e与图b的差值 图a中磁性体①、②、③的长方体中心坐标分别为(500m, 150m, 175m)、(500m, 475m, 350m)和(500m, 825m, 300m),大小分别为400m×200m×200m、200m×150m×200m和400m×150m×200m,磁化率分别为0.04、0.08、0.12SI |
| $ \begin{array}{l} {\phi _1} = 1 - \\ \ \ \ \ \ \ \ \ \sqrt {\frac{{{{(x - 500)}^2}}}{{{{400}^2}}} + \frac{{{{(y - 150)}^2}}}{{{{100}^2}}} + \frac{{{{(z - 250)}^2}}}{{{{150}^2}}}} \end{array} $ | (30) |
| $ \begin{array}{l} {\phi _2} = 1 - \\ \ \ \ \ \ \ \ \ \sqrt {\frac{{{{(x - 500)}^2}}}{{{{400}^2}}} + \frac{{{{(y - 850)}^2}}}{{{{100}^2}}} + \frac{{{{(z - 300)}^2}}}{{{{200}^2}}}} \end{array} $ | (31) |
| $ \begin{array}{l} {\phi _3} = 1 - \\ \ \ \ \ \ \ \ \ \sqrt {\frac{{{{(x - 500)}^2}}}{{{{400}^2}}} + \frac{{{{(y - 475)}^2}}}{{{{150}^2}}} + \frac{{{{(z - 350)}^2}}}{{{{100}^2}}}} \end{array} $ | (32) |
正则化参数$\alpha = {10^{ - 12}} \times {\left({\frac{1}{{4{\rm{ \mathsf{ π} }}}}{B_0}{\kappa _2}/\bar \sigma } \right)^2}$,数据拟合差Ed=0.5144。恢复得到的模型见图 4d。由图 4e可以看出,反演模型的正演磁异常与图 4b特征基本一致,可见反演结果与原始模型的大小和位置吻合较好。图 4f所示的误差分布直观地说明了反演结果的正确性。图 5是反演结果的一些细节展示,比较了不同方向上真实模型边界与反演模型边界,可见二者具有很高的一致性。

|
图 5 图 4d细节展示 (a)y=200m截面;(b)y=500m截面;(c)y=800m截面;(d)z=100m平面图 虚线为真实模型的轮廓线,实线为本文反演结果 |
前面两个模型中的磁异常体深度较小,说明了本反演算法对浅层磁性矿藏具有很好的圈定作用。为了进一步验证该方法对深部目标体边界的圈定效果,设计了图 6a所示的模型。
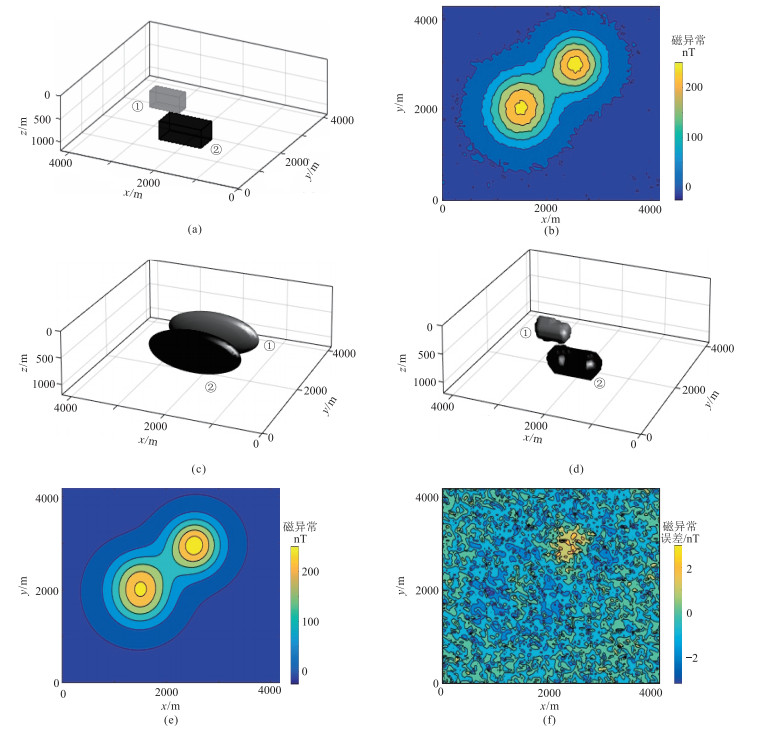
|
图 6 深部磁异常体模型及反演结果 (a)模型示意图;(b)加噪总磁异常图;(c)初始猜测模型;(d)基于两个水平集的反演结果;(e)图d正演磁异常图;(f)图e与图b的差值 |
模型包括两个磁性长方体,其中心坐标分别为(2000m, 1500m, 900m)、(2950m, 2550m, 825m),大小分别为1000m×500m×400m、700m×300m×350m, 极化率已知,分别为0.16、0.30SI。基于加噪总磁异常数据(图 6b),反演中引入两个水平集函数ϕ1和ϕ2,其初始猜测(图 6c)分别为
| $ \begin{array}{l} {\phi _1} = 1 - \\ \ \ \ \ \ \ \ \ \sqrt {\frac{{{{(x - 2000)}^2}}}{{{{1000}^2}}} + \frac{{{{(y - 1500)}^2}}}{{{{200}^2}}} + \frac{{{{(z - 600)}^2}}}{{{{400}^2}}}} \end{array} $ | (33) |
| $ \begin{array}{l} {\phi _2} = 1 - \\ \ \ \ \ \ \ \ \ \sqrt {\frac{{{{(x - 2000)}^2}}}{{{{1000}^2}}} + \frac{{{{(y - 2500)}^2}}}{{{{200}^2}}} + \frac{{{{(z - 600)}^2}}}{{{{400}^2}}}} \end{array} $ | (34) |
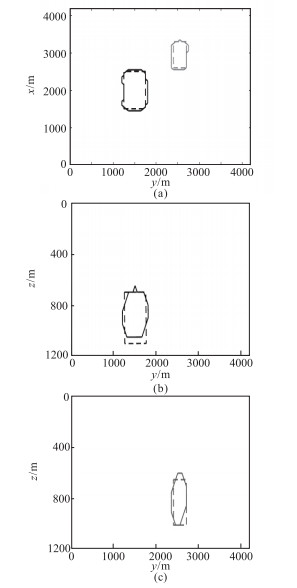
图 6d为反演结果,其数据拟合差Ed=0.5916。图 6e和图 6f分别为反演模型的正演磁异常图及误差。图 7是图 6d的细节展示。由图可见,反演结果在各个方向上对目标体的边界都吻合得很好,展现了真实磁性体的形状和空间位置。
|
图 7 图 6d细节展示 (a)z=800m平面图;(b)x=2000m截面;(c)x=3000m截面图。虚线表示原始模型轮廓线,实线表示反演模型边界 |
本算例验证了本文反演算法对深部矿产的圈定效果很好。
2.5 水平集数目对反演结果的影响基于多重水平集方法的磁界面反演算法的关键假设是地下异常体的磁化率已知。实际反演中,一般可以基于已有的地质知识或其他先验信息得到研究区磁性体确切的磁化率值,但无法确切知道某一区域具体对应哪个磁化率值。复杂的地质环境中,这个不可预知的因素可能会极大地限制多重水平集方法的应用。本节针对图 4a所示模型,假设仅知道一个磁化率值,分析水平集数目的选择对反演结果的影响。
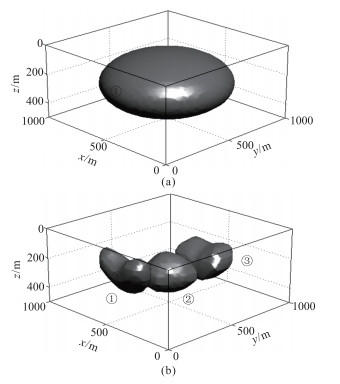
假设图 4a中仅知道②号异常体的磁化率(κ=0.08SI),并据此形成初始猜测(图 8a),并在反演中引入一个水平集函数
|
图 8 图 6a模型单水平集反演结果 (a)初始猜测;(b)反演模型 |
| $ \begin{array}{*{20}{l}} {\phi = 1 - }\\ \ \ \ \ \ \ \ \ {\sqrt {\frac{{{{(x - 500)}^2}}}{{{{400}^2}}} + \frac{{{{(y - 500)}^2}}}{{{{400}^2}}} + \frac{{{{(z - 250)}^2}}}{{{{200}^2}}}} } \end{array} $ | (35) |
图 8b为引入单水平集的反演结果。可见即使初始模型只假设了一个磁源体,反演结果也能准确地反映有三个独立的磁源体,说明水平集的个数对反演结果影响不大。
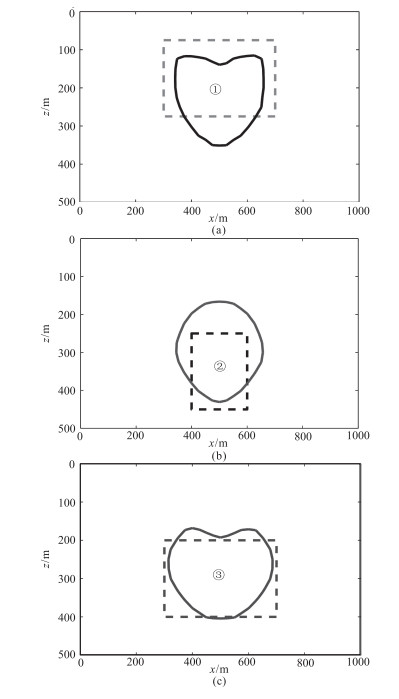
图 9是图 8b的细节展示。对比图 9a与图 6a可以清晰地看出,当κ=0.04SI的①号长方体被赋予大于其实际磁化率值(κ=0.08SI)时,反演得到的磁性边界范围更小、深度更大;对比图 9b与图 6a可以看出,当磁化率为κ=0.12SI的②号长方体被赋予低于其实际磁化率值(κ=0.08SI)时,反演得到的边界范围更大,且深度小于实际深度;图 9c中,反演的③号磁性体边界与模型(图 6a)几乎完全一致,这是因为反演时设定的磁化率值与实际情况完全一致。
|
图 9 图 8b细节展示 (a)y=200m截面(过①号磁性体);(b)y=500m截面 (过②号磁性体);(c)y=800m截面(过③号磁性体) 虚线表示原模型磁性体轮廓线,实线表示反演模型边界 |
该模型反演结果说明,基于水平集方法反演时模型的磁化率与真实值差别太大时,恢复的磁性体边界会出现较大偏差:如果反演模型的磁化率赋值低于实际值,反演结果中磁性源的体积会大于实际体积,且位置偏深;反之则会导致反演的磁源体积小于实际体积,且位置偏浅。
由本节反演结果可知,反演初始模型的各个子域磁化率值是否准确,对反演结果影响较大,而反演初始模型水平集的数目对反演结果的影响较小。因此,在实际应用中,需要利用先验信息尽量准确地估计各个区域的磁化率值,以各区域的平均磁化率作为各子域的磁化率进行多水平集反演,才可得到比较可靠的磁边界位置。
3 结论本文基于多重水平集的磁界面反演算法,实现了对磁化率已知的磁性目标体空间位置和几何形状的反演。
(1) 本文算法中,磁化率值由先验信息确定,采用任意四面体单元磁法解析解算法[24]进行高精度正演计算,并基于WENO格式对水平集函数进行更新及重新初始化。
(2) 具有两个水平集和三个水平集的反演算例验证了本算法的有效性与可靠性;深部异常体模型反演算例验证了本算法对深部矿产资源的圈定具有良好效果。
(3) 针对实际生产中,难以准确获取地下目标磁化率的情况,讨论了水平集数目的确定对反演结果的影响。即便水平集数目与实际不符,反演结果仍能准确划分磁性体区域,但各反演磁性体的深度和边界存在一定误差。若子域被赋予偏大的磁化率值时,反演得到的磁性体范围小于实际情况,且深度偏小;反之,若子域被赋予较小磁化率值时,则反演磁性体的范围大于实际情况,且深度偏大。
| [1] |
冯杰, 欧洋, 赵勇, 等. 三维井地磁测联合约束反演[J]. 地球物理学报, 2019, 62(10): 3686-3698. FENG Jie, OU Yang, ZHAO Yong, et al. 3D joint constrained inversion of borehole and ground magne-tic data[J]. Chinese Journal of Geophysics, 2019, 62(10): 3686-3698. DOI:10.6038/cjg2019M0428 |
| [2] |
邱耀东.联合CHAMP和Swarm卫星磁测数据反演中国大陆区域岩石圈磁场[D].湖北武汉: 武汉大学, 2017.
|
| [3] |
冯杰.井地磁测联合反演研究[D].北京: 中国地质大学(北京), 2010.
|
| [4] |
李志鹏, 高嵩, 王绪本. 特殊区域旋翼无人机航磁测量研究[J]. 地球物理学报, 2018, 61(9): 317-326. LI Zhipeng, GAO Song, WANG Xuben. New me-thod of aeromagnetic surveys with rotorcraft UAV in particular areas[J]. Chinese Journal of Geophysics, 2018, 61(9): 317-326. |
| [5] |
Cribb J. Application of the generalized linear inverse to the inversion of static potential data[J]. Geophy-sics, 1976, 41(6): 1365-1369. |
| [6] |
Li Y, Oldenburg D W. 3-D inversion of magnetic data[J]. Geophysics, 1996, 61(2): 394-408. DOI:10.1190/1.1443968 |
| [7] |
Pilkington M. 3-D magnetic imaging using conjugate gradients[J]. Geophysics, 1997, 62(4): 1132-1142. DOI:10.1190/1.1444214 |
| [8] |
Miguel B J. Joint inversion of gravity and magnetic data under lithologic constraints[J]. The Leading Edge, 2001, 20(8): 877-881. DOI:10.1190/1.1487299 |
| [9] |
Fregoso E, Gallardo L A. Cross-gradients joint 3D inversion with applications to gravity and magnetic data[J]. Geophysics, 2009, 74(4): L31-L42. DOI:10.1190/1.3119263 |
| [10] |
管志宁, 安玉林. 频率域磁性单界面反演方法[J]. 地球物理学报, 1984, 27(2): 190-204. GUAN Zhining, An Yulin. Inversion method of a single magnetic boundary in the frequency domain[J]. Chinese Journal of Geophysics, 1984, 27(2): 190-204. DOI:10.3321/j.issn:0001-5733.1984.02.008 |
| [11] |
Pilkington M, Crossley D J. Determination of crustal interface topography from potential fields[J]. Geophysics, 1986, 51(6): 1277-1284. DOI:10.1190/1.1442180 |
| [12] |
Wang X, Hansen R O. Inversion for magnetic ano-malies of arbitrary three-dimensional bodies[J]. Geophysics, 1990, 55(10): 1321-1326. DOI:10.1190/1.1442779 |
| [13] |
刘沈衡, 吴燕岗, 李永朴. 利用欧拉算法反演磁性界面[J]. 石油物探, 2000, 39(2): 101-106. LIU Shenheng, WU Yan'gang, LI Yongpu. Magne-tic interface inversion by Euler algorithm[J]. Geophysical Prospecting for Petroleum, 2000, 39(2): 101-106. DOI:10.3969/j.issn.1000-1441.2000.02.013 |
| [14] |
Fullagar P K, Pears G A, Mcmonnies B. Constrained inversion of geologic surfaces:Pushing the boundaries[J]. The Leading Edge, 2008, 27(1): 98-105. DOI:10.1190/1.2831686 |
| [15] |
赵文举, 刘云祥, 陶德强, 等. BP神经网络磁性体顶面埋深预测方法[J]. 石油地球物理勘探, 2020, 55(5): 1139-1148. ZHAO Wenju, LIU Yunxiang, TAO Deqiang, et al. Prediction of magnetic body top based on BP neural network[J]. Oil Geophysical Prospecting, 2020, 55(5): 1139-1148. |
| [16] |
郑强, 郭华, 张贵宾, 等. 基于磁力梯度全张量特征值的均衡边界识别方法[J]. 石油地球物理勘探, 2020, 55(2): 454-464. ZHENG Qiang, GUO Hua, ZHANG Guibin, et al. Balanced edge detection based on eigenvalues of full magnetic gradient tensor[J]. Oil Geophysical Prospecting, 2020, 55(2): 454-464. |
| [17] |
Chang C J, Hsieh, Jun W C, et al. Tracking multiple moving objects using a level-set method[J]. International Journal of Pattern Recognition and Artificial Intelligence, 2004, 18(2): 101-125. DOI:10.1142/S0218001404003071 |
| [18] |
Mansouri A R, Konrad J. Multiple motion segmentation with level sets[J]. IEEE Transactions on Image Processing, 2003, 12(2): 201-220. DOI:10.1109/TIP.2002.807582 |
| [19] |
Sussman M, Smereka P, Osher S. A level set ap-proach for computing solutions to incompressible two-phase flow[J]. Journal of Computational Phy-sics, 1994, 114: 146-159. DOI:10.1006/jcph.1994.1155 |
| [20] |
Tsai Y H R, Osher S. Total variation and level set methods in image science[J]. Acta Numerica, 2005, 14(2): 509-573. |
| [21] |
Zhao H K, Chan T, Merriman B, et al. A variational level set approach to multiphase motion[J]. Journal of Computational Physics, 1996, 127: 179-195. DOI:10.1006/jcph.1996.0167 |
| [22] |
Isakov V, Leung S, Qian J. A fast local level set method for inverse gravimetry[J]. Communications in Computational Physics, 2011, 10(4): 1044-1070. DOI:10.4208/cicp.100710.021210a |
| [23] |
Zheglova P, Farquharson C G, Hurich C. 2-D re-construction of boundaries with level set inversion of traveltimes[J]. Geophysical Journal International, 2013, 192(2): 688-698. DOI:10.1093/gji/ggs035 |
| [24] |
Li W B, Lu W T, Qian J L, et al. A multiple level set method for three dimensional inversion of magne-tic data[J]. Geophysics, 2017, 82(5): J61-J81. DOI:10.1190/geo2016-0530.1 |
| [25] |
Li W B, Qian J L, Li Y G. Joint inversion of surface and borehole magnetic data:A level-set approach[J]. Geophysics, 2020, 85(1): J15-J32. DOI:10.1190/geo2019-0139.1 |
| [26] |
Ren Z, Chen C, Tang J, et al. Closed-form formula of magnetic gradient tensor for a homogeneous polyhedral magnetic target:A tetrahedral grid example[J]. Geophysics, 2017, 82(6): V1-V34. |
| [27] |
Osher S, Fedkiw R. Level set methods and dynamic implicit surfaces[J]. Springer Science & Business Media, 2006, 153: 230-240. |
| [28] |
Lu W T, Leung S Y, Qian J L. An improved fast local level set method for three-dimensional inverse gravimetry[J]. Inverse Problems and Imaging, 2015, 9(1): 479-509. |
| [29] |
Jiang G S, Peng D. Weighted ENO schemes for Hamilton-Jacobi equations[J]. SIAM Journal on Scientific Computing, 2000, 21(6): 2126-2143. DOI:10.1137/S106482759732455X |
| [30] |
Guang S J, Chi W S. Efficient implementation of weighted ENO schemes[J]. Journal of Computational Physics, 1996, 126: 202-228. DOI:10.1006/jcph.1996.0130 |
| [31] |
Liu X D, Osher S, Chan T. Weighted essentially non-oscillatory schemes[J]. Journal of Computational Phy-sics, 1996, 115: 200-212. |
| [32] |
Shu C W, Osher S. Efficient implementation of essentially non-oscillatory shock-capturing schemes[J]. Journal of Computational Physics, 1988, 77: 439-471. DOI:10.1016/0021-9991(88)90177-5 |
| [33] |
Frederic G R F, Osher S. A review of level-set me-thods and some recent applications[J]. Journal of Computational Physics, 2018, 353: 82-109. DOI:10.1016/j.jcp.2017.10.006 |
| [34] |
Courant R, Friedrichs K, Lewy H. On the partial difference equations of mathematical physics[J]. IBM Journal of Research & Development, 1967, 11(2): 215-234. |
| [35] |
Li W, Leung S. A fast local level set adjoint state method for first arrival transmission traveltime tomography with discontinuous slowness[J]. Geophysical Journal International, 2013, 195: 582-596. DOI:10.1093/gji/ggt244 |
| [36] |
Li W, Leung S, Qian J L. A level-set adjoint-state method for crosswell transmission reflection traveltime tomography[J]. Geophysical Journal International, 2014, 199: 348-367. DOI:10.1093/gji/ggu262 |



 段雅婷, 湖南省长沙市岳麓区麓山南路932号中南大学校本部地学楼, 410083。Email:
段雅婷, 湖南省长沙市岳麓区麓山南路932号中南大学校本部地学楼, 410083。Email: