② 中南大学有色金属成矿预测与地质环境监测教育部重点实验室, 湖南长沙 410083;
③ 东方地球物理公司综合物化探处, 河北涿州 072751;
④ 青海省第三地质勘查院, 青海西宁 810029;
⑤ 南方科技大学前沿与交叉科学研究院, 广东深圳 518055;
⑥ 桂林理工大学地球科学学院, 广西桂林 541006
② Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring(Central South University), Ministry of Education, Changsha, Hunan 410083, China;
③ GME & Geochemical Surveys, BGP, CNPC, Zhuozhou, Hebei 072751, China;
④ Bureau of Geological Exploration & Deve-lopment of Qinghai Province, Xining, Qinghai 810029, China;
⑤ SUSTech Academy for Advanced Interdisciplinary Studies, Shenzheng, Guangdong 518055, China;
⑥ College of Earth Sciences, Guilin University of Technology, Guilin, Guangxi 541006, China
Goldstein[1]提出以人工场源代替天然场源的可控源音频大地电磁法(CSAMT),有效克服了大地电磁法(MT)和音频大地电磁法(AMT)天然场源的随机性和信号强度弱等缺陷。该方法采用接地导线和不接地回线为场源,在其一侧或者两侧60°张角的扇形区域内测量相互正交的电磁场切向分量,沿用MT中计算卡尼亚视电阻率的公式,且保留了AMT的数据解释方法。与MT相比,CSAMT采用人工场源,可弥补场源的随机性和信号微弱等不足。同时,该方法在工作效率及纵、横向分辨率等方面均有明显改进。因此,该方法经过40多年的长足发展,在金属矿产、水文、工程、环境等领域均得到广泛应用。但是,CSAMT也存在不足:①沿用MT法采用的卡尼亚视电阻率公式,只适用于“远区”数据,对于“非远区”数据,该公式便不再适用,这明显背离了采用人工源增强信号强度、提高观测精度的初衷,并且实际测量数据中很容易进入“过渡区”或“近区”数据;②CSAMT依然遵从卡尼亚公式计算视电阻率,该公式相对比较简单,人为地舍弃了代表“非远区”数据特点的高次项,引入了不必要的人为误差;③由于建场的局限性,探测深度受发射功率的限制。
对于CSAMT,何继善[2]利用人工场源克服了场源的随机性,利用磁偶源频率测深法(MELOS)“非远区”观测优势,提出了广域电磁法。该方法摒弃了CSAMT方法“远区”信号微弱的观测方式,拓展了观测范围;也摒弃了MELOS校正计算视电阻率的方法,保留了计算公式中的高次项。在理论上提出一种适用于全域的视电阻率计算公式,从根本上突破了CSAMT法“远区”理论的束缚,有效扩展了人工源电磁法的观测范围,提高了观测精度和野外工作效率[3]。
目前广域电磁法的资料处理与解释技术以一维和二维为主。但是,随着勘探难度的日益增加和方法技术应用的不断深入,人们对广域电磁法的勘探效果提出了更高的要求,因而以大范围观测为代表的三维精细勘探将逐渐发展成为广域电磁法的研究趋势和热点。其中,广域电磁法三维数值模拟作为反演成像与定量解释的基础,尤为重要。有关频率域电磁法三维正演方法的研究已经超过了30年[4-5],并且在各个方面均取得了很大的进展。从数值方法的角度而言,常用的电磁三维数值模拟方法主要有积分方程法[6-10]、有限差分法[11-13]、有限体积法[14-19]、有限单元法[20-24]等。尽管这些方法采用的数值算法有所不同,但总体研究目标都是提高算法的计算精度与计算效率。目前专门针对广域电磁法三维数值模拟研究主要包括:①李帝铨等[25]采用积分方程法实现了广域电磁法三维数值模拟,并分析了典型三维地电模型的电磁响应;②彭荣华等[19]采用交错网格有限体积法实现了基于二次耦合势的广域电磁法三维正演。
本文从麦克斯韦方程组出发,推导了基于库仑规范的矢量位和标量位控制方程。该方程具有非常完备的物理意义,可以将大地电磁法(MT)、直流电阻率法(DC)和可控源电磁法(CSEM)统一到一个耦合方程组。通过改变场源和频率,基于库仑规范的矢量位和标量位控制方程可以适用于MT、DC和CSEM三维数值模拟。广域电磁法属于频率域可控源电磁法(CSEM)中的一种方法,其基本理论完全相同。基于此,本文以库仑规范的矢量位和标量位控制方程为基础,对广域电磁法三维有限元数值模拟进行了研究。在模型算例中,设计棱柱体模型,对比了传统积分方程算法与本文算法的计算结果,验证了本文方法的正确性和计算精度。在此基础上,对比分析了广域电磁法与CSAMT对典型三维目标体的探测能力,结果表明在相同的条件下,广域电磁法能够更准确地反映地下目标体信息,具有更高的分辨能力。
1 理论与方法 1.1 基于库仑规范的矢量位和标量位控制方程假定时间谐变因子为e-iωt,频率域麦克斯韦方程组可以表示为
| $ {\nabla \times \mathit{\boldsymbol{E}} = {\rm{i}}\omega {\mu _0}\mathit{\boldsymbol{H}}} $ | (1) |
| $ {\nabla \times \mathit{\boldsymbol{H}} = {\mathit{\boldsymbol{J}}_{\rm{p}}} + (\sigma - {\rm{i}}\omega {\varepsilon _0})\mathit{\boldsymbol{E}}} $ | (2) |
式中:E为电场强度;H为磁场强度;ω是角频率;μ0是真空磁导率;σ为电导率;Jp为场源的电流密度;ε0为真空中的介电常数,对于广域电磁法频段而言,ε0可以忽略。
对式(1)两边取旋度,并将其带入式(2)可得关于电场强度E的二阶亥姆霍兹方程
| $ \nabla \times \nabla \times \mathit{\boldsymbol{E}} - {\rm{i}}\omega {\mu _0}\sigma \mathit{\boldsymbol{E}} = {\rm{i}}\omega {\mu _0}\sigma {\mathit{\boldsymbol{J}}_{\rm{p}}} $ | (3) |
采用数值方法,直接求解式(3)可得电场强度,既而得到磁场的分布。直接求解电磁场存在两个明显问题[26]:一是由于只利用了场矢量的旋度,对散度没有规范,存在“伪解现象”;二是电磁场分量在界面上不连续,与节点有限元在求解区域内连续这一基本假设相矛盾,这给求解带来很大的困难。一些学者利用矢量有限单元法[27-29]有效解决了以上问题,但同时也增加了方程组的复杂度。为了避免上述问题,先求取电磁场的势函数,进而通过差分格式间接求解电磁场[20, 30]。另外,这种间接求解方法还可以有效减小方程组系数矩阵的条件数,显著提高收敛速度[11]。
将磁矢量位和电标量位与电磁场的基本关系式[20]
| $ {\mathit{\boldsymbol{B}} = \nabla \times \mathit{\boldsymbol{A}}} $ | (4) |
| $ {\mathit{\boldsymbol{E}} = {\rm{i}}\omega \mathit{\boldsymbol{A}} - \nabla \varPhi } $ | (5) |
代入式(2),可得磁矢量位和电标量位的双旋度方程
| $ {\nabla \times (\nabla \times \mathit{\boldsymbol{A}}) = {\mu _0}{\mathit{\boldsymbol{J}}_{\rm{p}}} + {\mu _0}\sigma ({\rm{i}}\omega \mathit{\boldsymbol{A}} - \nabla \varPhi )} $ | (6) |
式中:A为矢量位;B为磁感应强度;Φ为标量位。
把矢量恒等式
| $ \nabla \times (\nabla \times \mathit{\boldsymbol{A}}) = \nabla (\nabla \cdot \mathit{\boldsymbol{A}}) - {\nabla ^2}\mathit{\boldsymbol{A}} $ |
代入式(6),得到
| $ \nabla (\nabla \cdot \mathit{\boldsymbol{A}}) - {\nabla ^2}\mathit{\boldsymbol{A}} = {\mu _0}{\mathit{\boldsymbol{J}}_{\rm{p}}} + {\mu _0}\sigma ({\rm{i}}\omega \mathit{\boldsymbol{A}} - \nabla \varPhi ) $ | (7) |
为了保证势函数的唯一性,把库仑规范
| $ \nabla \cdot \mathit{\boldsymbol{A}} = 0 $ | (8) |
代入式(7),得到
| $ {\nabla ^2}\mathit{\boldsymbol{A}} + {\rm{i}}\omega {\mu _0}\sigma \mathit{\boldsymbol{A}} - {\mu _0}\sigma \nabla \varPhi = - {\mu _0}{\mathit{\boldsymbol{J}}_{\rm{p}}} $ | (9) |
式中μ为相对磁导率。
由▽×H=J,可以得到
| $ \nabla \cdot (\nabla \times \mathit{\boldsymbol{H}}) = \nabla \cdot \mathit{\boldsymbol{J}} = 0 $ | (10) |
将$\boldsymbol{J}=\boldsymbol{J}_{\mathrm{s}}+\hat{y} \boldsymbol{E}$[47]代入式(10),有
| $ - \nabla \cdot {\mathit{\boldsymbol{J}}_{\rm{s}}} = \nabla \cdot \hat y\mathit{\boldsymbol{E}} $ | (11) |
式中:J为总电流密度;Js为激发场源外部的电流密度;
将式(5)代入式(11)可得
| $ \nabla \cdot (\hat y\nabla \varPhi ) - {\rm{i}}\omega \nabla \cdot (\hat y\mathit{\boldsymbol{A}}) = \nabla \cdot {\mathit{\boldsymbol{J}}_{\rm{p}}} $ | (12) |
根据微分算子▽恒等式
| $ \nabla \cdot (f\mathit{\boldsymbol{A}}) = f\nabla \cdot \mathit{\boldsymbol{A}} + \mathit{\boldsymbol{A}} \cdot \nabla f $ |
并将式(8)代入式(12),可得
| $ \sigma \nabla \cdot \nabla \varPhi + \nabla \varPhi \cdot \nabla \sigma - {\rm{i}}\omega \mathit{\boldsymbol{A}} \cdot \nabla \sigma = \nabla \cdot {\mathit{\boldsymbol{J}}_{\rm{p}}} $ | (13) |
式中f表示任意标量位。
综合式(9)和式(13)可得基于库仑规范的矢量位和标量位满足的耦合偏微分方程
| $ \left\{ \begin{array}{l} {\nabla ^2}\mathit{\boldsymbol{A}} + {\rm{i}}\omega \mu \sigma \mathit{\boldsymbol{A}} - {\mu _0}\sigma \nabla \varPhi = - {\mu _0}{\mathit{\boldsymbol{J}}_{\rm{p}}}\\ \sigma \nabla \cdot \nabla \varPhi + \nabla \varPhi \cdot \nabla \sigma - {\rm{i}}\omega \mathit{\boldsymbol{A}} \cdot \nabla \sigma = \nabla \cdot {\mathit{\boldsymbol{J}}_{\rm{p}}} \end{array} \right. $ | (14) |
将式(14)展开,写成分量形式
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\partial ^2}{A_x}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{A_x}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{A_x}}}{{\partial {z^2}}} + \sigma {A_x} - {\mu _0}\sigma \frac{{\partial \varPhi }}{{\partial x}} = - {\mu _0}J_{\rm{p}}^x}\\ {\frac{{{\partial ^2}{A_y}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{A_y}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{A_y}}}{{\partial {z^2}}} + \sigma {A_y} - {\mu _0}\sigma \frac{{\partial \varPhi }}{{\partial y}} = - {\mu _0}J_{\rm{p}}^y}\\ {\frac{{{\partial ^2}{A_z}}}{{\partial {x^2}}} + \frac{{{\partial ^2}{A_z}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{A_z}}}{{\partial {z^2}}} + \sigma {A_z} - {\mu _0}\sigma \frac{{\partial \varPhi }}{{\partial z}} = - {\mu _0}J_{\rm{p}}^z}\\ {\sigma \left( {\frac{{{\partial ^2}\varPhi }}{{\partial {x^2}}} + \frac{{{\partial ^2}\varPhi }}{{\partial {y^2}}} + \frac{{{\partial ^2}\varPhi }}{{\partial {z^2}}}} \right) + \frac{{\partial \varPhi }}{{\partial x}}\frac{{\partial \sigma }}{{\partial x}} + \frac{{\partial \varPhi }}{{\partial y}}\frac{{\partial \sigma }}{{\partial y}} + \frac{{\partial \varPhi }}{{\partial z}}\frac{{\partial \sigma }}{{\partial z}} - {\rm{i}}\omega \left( {{A_x}\frac{{\partial \sigma }}{{\partial x}} + {A_y}\frac{{\partial \sigma }}{{\partial y}} + {A_z}\frac{{\partial \sigma }}{{\partial z}}} \right) = \nabla \cdot {\mathit{\boldsymbol{J}}_{\rm{p}}}} \end{array}} \right. $ | (15) |
式中:Jpx、Jpy、Jpz分别表示外部激发场源电流密度的三个分量。
由式(15)可以看出:
(1) 该控制方程由4个方程表达式组成,矢量位A的三个分量形式Ax、Ay和Az之间本身并无直接联系,而是通过标量位Φ的一阶偏导耦合在一起的。
(2) 该控制方程相对比较完备,物理意义明确,可以通过改变场源和频率用于多种电磁勘探方法数值模拟:
① Jp≠0,即三个方向的场源分量Jpx、Jpy和Jpz不全为零时,为可控源电磁法(CSEM)的控制方程。当Jpx≠0、Jpy=Jpz=0时,场源为沿x方向布设的有限长线源;当Jpx=Jpz=0、Jpy≠0时,场源为沿y方向布设的有限长线源;当Jpx=Jpy=0、Jpz≠0时,场源为沿z方向布设的有限长线源(该方法也称为井中电磁法)。特别地,当有限长线源布设于地表时为地面可控源电磁法,布设于海洋时则为海洋可控源电磁法。
② Jp=0,即Jpx=Jpy=Jpz=0时,为大地电磁法(MT)控制方程。
③ Jp≠0,即Jpx、Jpy和Jpz均不为零,角频率ω=0时,为直流电阻率法控制方程,本质上是可控源电磁法的一种特殊情况。
1.2 边界条件目前可控源电磁法三维数值模拟中常用的边界条件主要包括Dirichlet边界条件(令边界处切向电场为零)[20]和Neumann边界条件(令边界处切向电场的空间一阶导数为零)[31-32]。这两种边界条件都是通过扩边来降低边界反射的影响。Streich[13]对上述两种边界条件进行过对比,认为Neumann边界条件会使线性方程组系统不对称。如果以截断边界上的近似场值作为边界条件,那么截断边界造成的边界反射就能得到相应的压制。在可控源电磁法中,总场为一次场和二次场的叠加,目标体产生的二次场由一次场激发,其数值远远小于一次场。当截断边界离计算区域较远时,可以忽略二次场对边界的影响,进而利用边界上一次场近似代替总场作为边界条件。
在均匀介质中,矢量位Ax、Ay和Az满足微分方程
| $ \left\{ \begin{array}{l} \frac{{{\partial ^2}{A_x}}}{{\partial {z^2}}} + {k^2}{A_x} = 0\\ \frac{{{\partial ^2}{A_y}}}{{\partial {z^2}}} + {k^2}{A_y} = 0\\ \frac{{{\partial ^2}{A_z}}}{{\partial {z^2}}} + {k^2}{A_z} = 0 \end{array} \right. $ | (16) |
式中
以式(16)中第一式为例,其基本解为
| $ {A_x} = A{{\rm{e}}^{ - kz}} + B{{\rm{e}}^{kz}} $ | (17) |
由于上界面只有上行波,从而可以得到上边界条件
| $ \frac{{{\rm{d}}{A_\xi }}}{{{\rm{d}}z}}{|_{{z_{{\rm{max}}}}}} = k{A_\xi }\quad (\xi = x,y,z) $ | (18) |
同理,可以得到下边界条件、左边界条件、右边界条件、前边界条件和后边界条件分别为
| $ \frac{{{\rm{d}}{A_\xi }}}{{{\rm{d}}z}}{|_{{z_{{\rm{min}}}}}} = - k{A_\xi } $ | (19) |
| $ \frac{{{\rm{d}}{A_\xi }}}{{{\rm{d}}x}}{|_{{x_{{\rm{min}}}}}} = - k{A_\xi } $ | (20) |
| $ \frac{{d{A_\xi }}}{{{\rm{d}}x}}{|_{{x_{{\rm{max}}}}}} = - k{A_\xi } $ | (21) |
| $ \frac{{{\rm{d}}{A_\xi }}}{{{\rm{d}}y}}{|_{{y_{{\rm{min}}}}}} = - k{A_\xi } $ | (22) |
| $ \frac{{{\rm{d}}{A_\xi }}}{{{\rm{d}}y}}{|_{{y_{{\rm{max}}}}}} = k{A_\xi } $ | (23) |
式中下标“min”和“max”分别表示极小值和极大值。
式(18)~式(23)构成了矢量位在截断边界的边界条件。可以看出,矢量位由长导线源产生的电磁感应场构成,在边界上可以当成平面波处理,与场源的大小和位置无关。
在截断边界上,标量位Φ的微分方程直接简化为直流电阻率法三维控制方程,故可以将直流电阻率法中的混合边界条件[33-34]作为标量位Φ在截断边界上的边界条件,具体形式如下
| $ \frac{{\partial \varPhi }}{{\partial \mathit{\boldsymbol{n}}}} + \frac{{\cos (\mathit{\boldsymbol{r}},\mathit{\boldsymbol{n}})}}{r}\varPhi = 0\quad {\rm{ }} \in {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_1}||{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{11}} $ | (24) |
| $ \frac{{\partial \varPhi }}{{\partial \mathit{\boldsymbol{n}}}} = - {k_0}\frac{{\partial \mathit{\boldsymbol{r}}}}{{\partial \mathit{\boldsymbol{n}}}}{\mu _0}{{\rm{e}}^{ - {k_0}r}} = - {k_0}\cos (\mathit{\boldsymbol{r}},\mathit{\boldsymbol{n}})\varPhi \quad \in {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_{02}} $ | (25) |
式中:
基于库仑规范的矢量位和标量位控制方程(式(15))及边界条件(式(18)~式(25))构成了广域电磁法三维数值模拟的边值问题。针对该边值问题,采用加权余量法将矢量位和标量位满足的边值问题转换为变分问题,并采用格林公式进行降阶处理,可得
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {\iiint_v {{N_i}} \hat y\frac{{{\partial ^2}\varPhi }}{{\partial {x^2}}}{\rm{d}}v = \oint_s {{N_i}} \hat y\frac{{\partial \varPhi }}{{\partial x}}{n_x}{\rm{d}}z{\rm{d}}y - \iiint_v {{N_i}} \frac{{\partial \hat y}}{{\partial x}}\frac{{\partial \varPhi }}{{\partial x}}{\rm{d}}v - \iiint_v {\hat y} \frac{{\partial {N_i}}}{{\partial x}}\frac{{\partial \varPhi }}{{\partial x}}{\rm{d}}v}\\ {\iiint_v {{N_i}} \hat y\frac{{{\partial ^2}\varPhi }}{{\partial {y^2}}}{\rm{d}}v = \oint_s {{N_i}} \hat y\frac{{\partial \varPhi }}{{\partial y}}{n_y}{\rm{d}}z{\rm{d}}x - \iiint_v {{N_i}} \frac{{\partial \hat y}}{{\partial y}}\frac{{\partial \varPhi }}{{\partial y}}{\rm{d}}v - \iiint_v {\hat y} \frac{{\partial {N_i}}}{{\partial y}}\frac{{\partial \varPhi }}{{\partial y}}{\rm{d}}v}\\ {\iiint_v {{N_i}} \hat y\frac{{{\partial ^2}\varPhi }}{{\partial {z^2}}}{\rm{d}}v = \oint_s {{N_i}} \hat y\frac{{\partial \varPhi }}{{\partial z}}{n_z}{\rm{d}}x{\rm{d}}y - \iiint_v {{N_i}} \frac{{\partial \hat y}}{{\partial z}}\frac{{\partial \varPhi }}{{\partial z}}{\rm{d}}v - \iiint_v {\hat y} \frac{{\partial {N_i}}}{{\partial z}}\frac{{\partial \varPhi }}{{\partial z}}{\rm{d}}v} \end{array}\\ \begin{array}{*{20}{l}} {\iiint_v {{N_i}} \frac{{{\partial ^2}{A_x}}}{{\partial {x^2}}}{\rm{d}}v = \oint_s {{N_i}} \frac{{\partial {A_x}}}{{\partial x}}{n_x}{\rm{d}}y{\rm{d}}z - \iiint_v {\frac{{\partial {A_x}}}{{\partial x}}\frac{{\partial {N_i}}}{{\partial x}}{\rm{d}}v} }\\ {\iiint_v {{N_i}} \frac{{{\partial ^2}{A_x}}}{{\partial {y^2}}}{\rm{d}}v = \oint_s {{N_i}} \frac{{{\partial }{A_x}}}{{\partial y}}{n_y}{\rm{d}}x{\rm{d}}z - \iiint_v {\frac{{{\partial }{A_x}}}{{\partial y}}\frac{{\partial {N_i}}}{{\partial y}}{\rm{d}}v} }\\ {\iiint_v {{N_i}} \frac{{{\partial ^2}{A_x}}}{{\partial {z^2}}}{\rm{d}}v = \oint_s {{N_i}} \frac{{{\partial }{A_x}}}{{\partial z}}{n_z}{\rm{d}}y{\rm{d}}x - \iiint_v {\frac{{{\partial }{A_x}}}{{\partial z}}\frac{{\partial {N_i}}}{{\partial z}}{\rm{d}}v} } \end{array} \end{array} \right. $ | (26) |
式中:Ni表示第i个节点的线性插值函数;nx、ny、nz表示边界上的方向法向分量;v和s分别表示体积分单元和面积分单元。
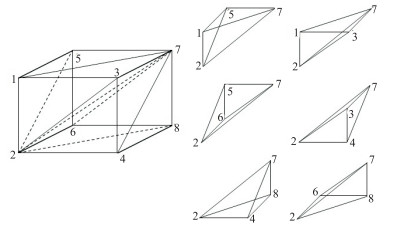
本文采用图 1所示的离散方案进行网格剖分。首先将三维模型进行六面体单元剖分,然后在六面体中进行四面体单元的剖分[35-36],每个六面体单元均被剖分成六个任意形状的四面体单元。该剖分方法具有很好的数值精度对称性[37]。在每个四面体单元内,采用线性插值,其计算表达式参见文献[34]。对变分问题式逐项进行单元分析,单元积分过程用到的积分表参见文献[34]。得到扩展矩阵或阵列
|
图 1 六面体单元及其四面体单元剖分示意图 |
| $ \mathit{\boldsymbol{As = b}} $ | (27) |
式中:A是大型稀疏复矩阵;s是解向量:b是源向量。
目前,求解大型稀疏线性方程组的方法主要有迭代法[38]和直接法[39]。
迭代解法的优点是算法相对简单,编程容易实现,耗费计算资源较少,当稀疏矩阵的条件数不大(良态)时收敛较快。缺点是当稀疏矩阵的条件数过大(病态)时收敛性很差或者发散,且在有限迭代次数内求解精度无法保证。采用最多的迭代解法是复线性方程组稳定双共轭梯度法[26, 31, 37, 40]。由于地—空和地下介质内部电阻率变化较大,以及网格的非均匀剖分,导致系数矩阵出现严重的病态或者条件数很大,从而使得迭代解法收敛很慢甚至发散。因此需要采用预处理技术对系数矩阵进行修正,降低其条件数。应用较多的预处理方法包括对角线系数、不完全Cholesky分解、SSOR及不完全LU分解法。预处理算法本身并不复杂,但是由于CSEM三维有限元数值模拟中系数矩阵是稀疏的,因此在存储的过程中通常只存入非零元素,通过编码的方式记录该非零元素对应的行和列位置。
直接解法的优点是求解精度较高,多源情形下可实现快速回代求解,当稀疏矩阵的条件数很大(病态或严重病态)时也可得到比较稳定的解。缺点是当稀疏矩阵维数很大时,需要占用大量的内存。近年来随着计算机技术的飞速发展和大型稀疏矩阵分解算法的不断优化[41-42],利用直接解法求解电磁法三维数值模拟中大型复线性稀疏方程组的案例逐渐增多[18, 24, 36, 43-44]。本文调用Pardiso_64位并行求解器进行求解,得到矢量位和标量位计算结果。
3 电磁场分量的计算根据电磁场与矢量位和标量位之间的关系式(式(4)和式(5))可以得到电磁场分量表达式
| $ \left\{ {\begin{array}{*{20}{l}} {{E_x} = {\rm{i}}\omega {A_x} - \frac{{\partial \varPhi }}{{\partial x}}}\\ {{E_y} = {\rm{i}}\omega {A_y} - \frac{{\partial \varPhi }}{{\partial y}}}\\ {{E_z} = {\rm{i}}\omega {A_z} - \frac{{\partial \varPhi }}{{\partial z}}} \end{array}} \right. $ | (28) |
式中的求导运算可采用五点差分法。
4 广域视电阻率的计算在可控源音频大地电磁法中,主要通过电场和磁场的正交分量计算卡尼亚视电阻率[1]
| $ \rho = \frac{1}{{\omega \mu }}{\left| {\frac{{{E_x}}}{{{H_y}}}} \right|^2} = \frac{1}{{\omega \mu }}{\left| {\frac{{{E_y}}}{{{H_x}}}} \right|^2} $ | (29) |
式中:Ex和Ey为地面电场水平分量;Hx和Hy为地面磁场水平分量。
卡尼亚视电阻率具有计算方便、简单的特点,式(29)在“远区”能比较客观地反应地电断面的变化,但在“过渡区”和“近区”计算的卡尼亚视电阻率会发生严重畸变。
为了突破卡尼亚视电阻率在“过渡区”和“近区”的局限性,何继善[2]根据电磁场表达式的特点,定义了广域视电阻率,将电磁测深的范围扩大到包括“远区”在内的广大区域。电偶极源激励的电场分量Ex对应的广域视电阻率为
| $ {\rho _{\rm{a}}} = {K_{E - {E_x}}}\frac{{\Delta {V_{MN}}}}{I}\frac{1}{{|{f_{E - {E_x}}}({\rm{i}}kr)|}} $ | (30) |
式中:KE-Ex=2πr3/(dL×MN)为装置系数,dL为偶极矩;ΔVMN=Ex×MN为测量电压,MN为测量电极之间的距离;I为电流强度;fE-Ex(ikr)=3×cos2ϕ-2+e-ikr(1+ikr),其中ϕ为x轴与径向矢量r的夹角,ρ为均匀半空间模型地下电阻率。一般采用迭代法或者逆插值法[45]对式(30)进行求解。
5 数值试验设计一个均匀半空间模型,验证本文算法的正确性及可靠性。在此基础上,设计长方体模型,利用本文正演算法对比分析广域电磁法与CSAMT对典型三维目标体的探测能力。算法代码采用Fortran 95语言编写,计算平台为Intel(R) Xeon(R) CPU3.1G,128GB RAM,16CPUs。
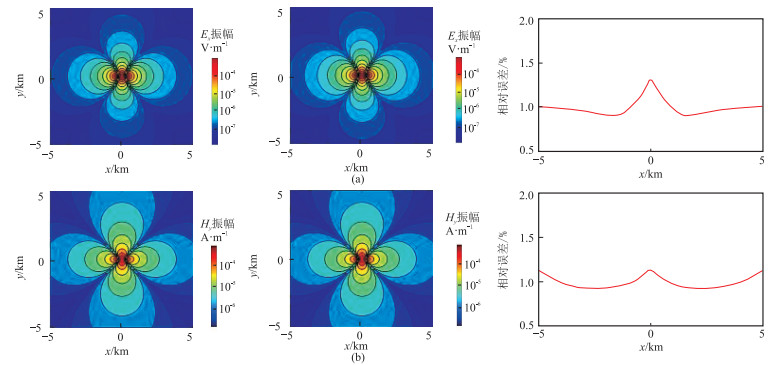
5.1 均匀半空间模型设定均匀半空间模型参数:电阻率为10000Ω·m,有限长线源沿x方向布设,起点为坐标原点,长度为500m,发射电流为1A,发射频率为1Hz。模拟计算区域大小为10km(x)×10km(y)×6km(z),x、y、z方向网格距均为100m,网格节点数为101×101×61,水平方向各取5个节点作扩边处理。图 2为解析解[46]、本文算法计算的数值解及相对误差。
|
图 2 均匀半空间模型Ex分量(a)和Hy分量(b)的解析解(左)、本文算法的数值解(中)及y=0时的相对误差(右) |
从图 2a~图 2c可以看出,电场分量Ex的数值解与解析解吻合度高,y=0时的最大相对误差为1.4%。从图 2d~图 2f可以看出,磁场分量Hy的数值解与解析解吻合度高,y=0时的最大相对误差为1.2%,这是因为场源具有奇异性,场源附近的相对误差相对较大,其他区域的数值精度较高,但都在误差允许的范围内,从而验证了本文算法的正确性及高精度。
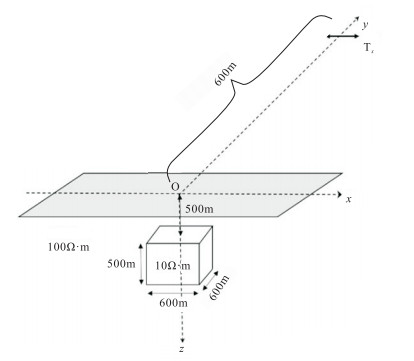
5.2 典型三维目标体模型设计图 3所示的三维低阻模型[19],分别进行可控源音频大地电磁法(CSAMT)和广域电磁法(WFEM)模拟计算,分析二者的分辨能力。
|
图 3 三维低阻模型示意图 |
以x方向的电偶极子作为发射源(Tx),发射频点数为12,频率在0.1~500Hz范围内呈对数等间隔分布。目标体剖分单元网格尺寸为100m×100m×50m,网格数为51×81×51,其中空气层深度方向网格剖分为11层。
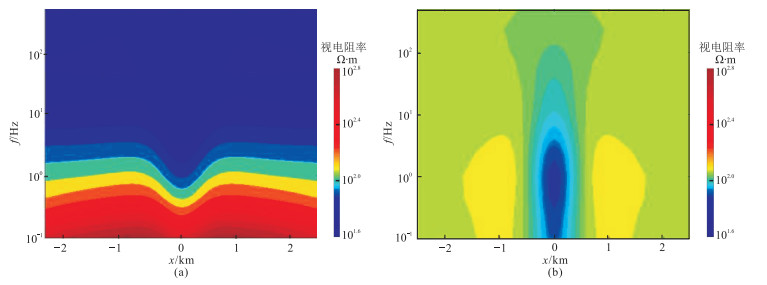
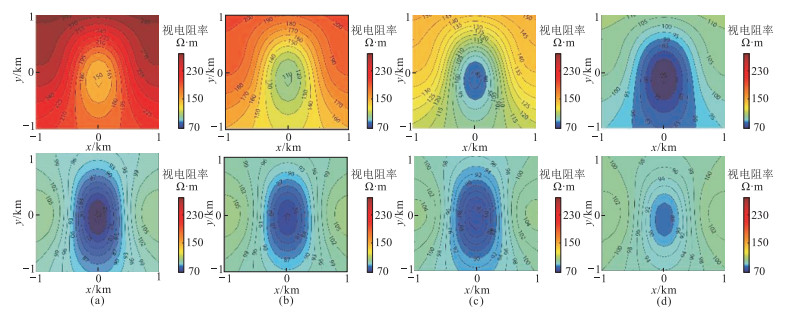
图 4为主测线y=0上卡尼亚视电阻率与广域视电阻率拟断面图。图 5是频率分别为1.02、2.21、4.80和10.40 Hz时卡尼亚视电阻率和广域视电阻率响应切片。可以看出:①卡尼亚视电阻率(图 4a和图 5上)不能较好地反映低阻异常体的空间位置。当发射频率较低时,测线上卡尼亚视电阻率已经远大于100Ω·m;随着频率的降低,卡尼亚视电阻率与真实电阻率偏离增大,这是由于频率越低,趋肤深度越大,y=0主测线位置已经不满足“远区”观测条件,即超出卡尼亚视电阻率公式的适用范围。②广域视电阻率(图 4b和图 5下)能清晰地反映低阻异常体的空间位置,不受“远区”测量条件的限制;频率的增大或降低都不影响广域视电阻率的异常幅值,即使在频率很低时也能很好地反映低阻异常体。所以,广域电磁法具有更大的有效观测范围,可以提高野外施工效率。
|
图 4 主测线y=0上卡尼亚视电阻率(a)与广域视电阻率(b)拟断面图 |
|
图 5 不同频率时卡尼亚视电阻率(上)与广域视电阻率(下)切片对比 (a)1.02Hz; (b)2.21Hz; (c)4.80Hz; (d)10.40Hz |
本文从频率域麦克斯韦方程出发,推导了库仑条件下的矢量位和标量位耦合方程,并结合边界条件给出了电磁场矢量位和标量位满足的边值问题。利用有限单元法对矢量位和标量位控制方程进行离散化,实现了广域电磁法的三维数值模拟,通过与均匀半空间模型的地面解析解对比,验证了本文三维数值模拟算法的正确性和高精度。在此基础上,设计了一个三维低阻模型,对比分析了广域电磁法与CSAMT对典型三维目标体的探测能力。
研究结果表明:广域电磁法提出了一种适用于全域的视电阻率计算公式,从根本上突破了CSAMT“远区”测量的束缚,在非“远区”依然能够有效反映地下三维目标体的电性特征和分布范围,有效地扩展了人工源电磁法的观测范围,提高了观测精度和野外工作效率。
| [1] |
Goldstein M A. Magnetotelluric Experiments Employing An Artificial Dipole Source[D]. University of Toronto, Ontario, 1971.
|
| [2] |
何继善. 广域电磁法和伪随机信号电法[M]. 北京: 高等教育出版社, 2010.
|
| [3] |
李帝铨, 胡艳芳. 强干扰矿区中广域电磁法与CSAMT探测效果对比[J]. 物探与化探, 2015, 39(5): 967-972. LI Diquan, HU Yanfang. A comparison of wide field electromagnetic with CSAMT method in strong interferential mining area[J]. Geophysical and Geochemical Exploration, 2015, 39(5): 967-972. |
| [4] |
Varentsov I M. Modern trends in the solution of forward and inverse 3D electromagnetic induction problems[J]. Geophysics Surveys, 1983, 6(1-2): 55-78. DOI:10.1007/BF01453995 |
| [5] |
Wannamaker P E. Advances in three-dimensional magnetotelluric modeling using integral equations[J]. Geophy-sics, 1984, 56(11): 1716-1728. |
| [6] |
Avdeev D B, Kuvshinov A V, Pankratov O V, et al. Three-dimensional induction logging problems, Part I:An integral equation solution and model comparisons[J]. Geophysics, 2002, 67(2): 413-426. DOI:10.1190/1.1468601 |
| [7] |
Hursán G, Zhanov M S. Contraction integeral equation method in three-dimensional electromagnetic modeling[J]. Radio Science, 2002, 37(6): 1-13. |
| [8] |
Zhdanov M S, Lee S K, Yoshioka K. Integral equation method for 3D modeling of electromagnetic fields in complex structures with inhomogeneous background conductivity[J]. Geophysics, 2006, 71(6): G333-G345. DOI:10.1190/1.2358403 |
| [9] |
Avdeev D, Knizhnik S. 3D integral equation modeling with a linear dependence on dimensions[J]. Geophy-sics, 2009, 74(5): F89-F94. |
| [10] |
王若, 底青云, 王妙月, 等. 用积分方程法研究源与勘探区之间的三维体对CSAMT观测线的影响[J]. 地球物理学报, 2009, 52(6): 1573-1582. WANG Rou, DI Qingyun, WANG Miaoyue, et al. Research on the effect of 3D body between transmitter and receivers on CSAMT response using integral equation method[J]. Chinese Journal of Geophysics, 2009, 52(6): 1573-1582. DOI:10.3969/j.issn.0001-5733.2009.06.019 |
| [11] |
Weiss C J, Newman G A. Electromagnetic induction in a fully 3-D anisotropic earth[J]. Geophysics, 2002, 67(4): 1104-1114. DOI:10.1190/1.1500371 |
| [12] |
沈金松. 用交错网格有限差分法计算三维频率域电磁响应[J]. 地球物理学报, 2003, 46(2): 280-288. SHEN Jinsong. Modeling of 3D electromagnetic responses in frequency domain by using staggered-grid finite difference method[J]. Chinese Journal of Geophysics, 2003, 46(2): 280-288. DOI:10.3321/j.issn:0001-5733.2003.02.032 |
| [13] |
Streich R. 3D finite-difference frequency-domain mode-ling of controlled source electromagnetic data:Direct solution and optimization for high accuracy[J]. Geophy-sics, 2009, 74(5): F95-F105. |
| [14] |
Weiss C J, Constable S. Mapping thin resistors and hydrocarbons with marine EM methods, Part Ⅱ:Modeling and analysis in 3D[J]. Geophysics, 2006, 71(6): G321-G332. DOI:10.1190/1.2356908 |
| [15] |
杨波, 徐义贤, 何展翔, 等. 考虑海底地形的三维频率域可控源电磁响应有限体积法模拟[J]. 地球物理学报, 2012, 55(4): 1390-1399. YANG Bo, XU Yixian, HE Zhanxiang, et al. 3D frequency-domain modeling of marine controlled source electromagnetic responses with topography using finite volume method[J]. Chinese Journal of Geophysics, 2012, 55(4): 1390-1399. DOI:10.6038/j.issn.0001-5733.2012.04.035 |
| [16] |
Jahandari H, Farquharson C G. A finite-volume solution to the geophysical electromagnetic forward problem using unstructured grids[J]. Geophysics, 2014, 79(6): E287-E302. DOI:10.1190/geo2013-0312.1 |
| [17] |
Jahandari H, Farquharson C G. Finite-volume modelling of geophysical electromagnetic data on unstructured grids using potentials[J]. Geophysical Journal International, 2015, 202(3): 1859-1876. DOI:10.1093/gji/ggv257 |
| [18] |
韩波, 胡祥云, Schultz A, 等. 复杂场源形态的海洋可控源电磁三维正演[J]. 地球物理学报, 2015, 58(3): 1059-1071. HAN Bo, HU Xiangyun, Schultz A, et al. Three-dimensional forward modeling of the marine controlled-source electromagnetic field with complex source geo-metries[J]. Chinese Journal of Geophysics, 2015, 58(3): 1059-1071. |
| [19] |
彭荣华, 胡祥云, 李建慧, 等. 基于二次耦合势的广域电磁法有限体积三维正演计算[J]. 地球物理学报, 2018, 61(10): 4160-4170. PENG Ronghua, HU Xiangyun, LI Jianhui, et al. 3-D finite-volume forward modeling of wide field EM using scattered potentials[J]. Chinese Journal of Geophysics, 2018, 61(10): 4160-4170. DOI:10.6038/cjg2018L0363 |
| [20] |
Badea E A, Everett M E, Newman G A, et al. Finite-element analysis of controlled-source electromagnetic induction using Coulomb gauged potentials[J]. Geophysics, 2001, 66(3): 786-799. DOI:10.1190/1.1444968 |
| [21] |
Ren Z, Kalscheuer T, Greenhalgh S, et al. A finite-element-based domain-decomposition approach for plane wave 3D electromagnetic modeling[J]. Geophysics, 2014, 79(6): E255-E268. DOI:10.1190/geo2013-0376.1 |
| [22] |
Ansari S, Farquharson C G. 3D finite element forward modeling of electromagnetic data using vector and scalar potentials and unstructured grids[J]. Geophysics, 2014, 79(4): E149-E165. DOI:10.1190/geo2013-0172.1 |
| [23] |
Grayver A V, Burg M. Robust and scalable 3D geo-electromagnetic modelling approach using the finite element method[J]. Geophysical Journal International, 2014, 198(1): 110-125. DOI:10.1093/gji/ggu119 |
| [24] |
杨军, 刘颖, 吴小平. 海洋可控源电磁三维非结构矢量有限元数值模拟[J]. 地球物理学报, 2015, 58(8): 2827-2838. YANG Jun, LIU Ying, WU Xiaoping. 3D simulation of marine CSEM using vector finite element method on unstructured grids[J]. Chinese Journal of Geophysics, 2015, 58(8): 2827-2838. |
| [25] |
李帝铨, 谢维, 程党性. E-Ex广域电磁法三维数值模拟[J]. 中国有色金属学报, 2013, 23(9): 2460-2470. LI Diquan, XIE Wei, CHENG Dangxing. Three-dimensional modeling for E-Ex wide field electromagnetic methods[J]. The Chinese Journal of Nonferrous Metals, 2013, 23(9): 2460-2470. |
| [26] |
汤井田, 任政勇, 化希瑞. Coulomb规范下地电磁场的自适应有限元模拟的理论分析[J]. 地球物理学报, 2007, 50(5): 1584-1594. TANG Jingtian, REN Zhengyong, HUA Xirui. Theoretical analysis of geo-electromagnetic modeling on Coulomb gauged potentials by adaptive finite element method[J]. Chinese Journal of Geophysics, 2007, 50(5): 1584-1594. DOI:10.3321/j.issn:0001-5733.2007.05.036 |
| [27] |
Mukherjee S, Everett M E. 3D controlled-source electromagnetic edge-based finite element modeling of conductive and permeable heterogeneities[J]. Geophysics, 2011, 76(4): F215-F226. DOI:10.1190/1.3571045 |
| [28] |
Jin J M. The Finite Element Method in Electromagnetics[M]. John Wiley and Sons, New York, 2014.
|
| [29] |
赵宁, 王绪本, 秦策, 等. 三维频率域可控源电磁反演研究[J]. 地球物理学报, 2016, 59(1): 330-341. ZHAO Ning, WANG Xuben, QIN Ce, et al. 3D frequency-domain CSEM inversion[J]. Chinese Journal of Geophysics, 2016, 59(1): 330-341. |
| [30] |
蔡红柱, 熊彬, Zhdanov M. 电导率各向异性的海洋电磁三维有限单元法正演[J]. 地球物理学报, 2015, 58(8): 2839-2850. CAI Hongzhu, XIONG Bin, Zhdanov M. Three-dimensional marine controlled-source electromagnetic modeling in anisotropic medium using finite element method[J]. Chinese Journal of Geophysics, 2015, 58(8): 2839-2850. |
| [31] |
刘云鹤.三维空源电磁法非线性共轭梯度反演研究[D].吉林长春: 吉林大学, 2011.
|
| [32] |
赵宁.三维海洋可控源电磁法矢量有限元与耦合势有限体积数值模拟[D].四川成都: 成都理工大学, 2014.
|
| [33] |
Dey A, Morrison H F. Resistivity modeling for arbitrarily shaped three-dimensional structures[J]. Geophysics, 1979, 44(1): 106-136. |
| [34] |
徐世浙. 地球物理中的有限单元法[M]. 北京: 科学出版社, 1994.
|
| [35] |
熊彬, 阮百尧, 罗延钟. 复杂地形条件下直流电阻率异常三维数值模拟研究[J]. 地质与勘探, 2003, 39(4): 60-64. XIONG Bin, RUAN Baiyao, LUO Yanzhong. 3D numerical simulation study of DC resistivity anomaly under complicated terrain[J]. Geology and Prospecting, 2003, 39(4): 60-64. DOI:10.3969/j.issn.0495-5331.2003.04.013 |
| [36] |
张钱江, 戴世坤, 陈龙伟, 等. 多源条件下直流电阻率法有限元三维数值模拟中一种近似边界条件[J]. 地球物理学报, 2016, 59(9): 3448-3458. ZHANG Qianjiang, DAI Shikun, CHEN Longwei, et al. An approximate boundary condition for FEM-based 3D numerical simulation with multi-source direct current resistivity method[J]. Chinese Journal of Geophysics, 2016, 59(9): 3448-3458. |
| [37] |
张钱江.可控源电磁法三维有限元数值模拟并行算法研究[D].北京: 中国石油大学(北京), 2011.
|
| [38] |
Saad Y. Iterative methods for sparse linear systems[J]. IEEE Computational Science & Engineering, 1996, 3(4): 88-89. |
| [39] |
Davis T A. Direct Methods for Sparse Linear Systems[M]. Society for Industrial and Applied Mathematics, 2006.
|
| [40] |
张继锋.基于电场双旋度方程的3D可控源电磁法有限单元法数值模拟[D].湖南长沙: 中南大学, 2008.
|
| [41] |
Liu J W H. The multifrontal method for sparse matrix solution:Theory and practice[J]. SIAM Review, 1992, 34(1): 82-109. DOI:10.1137/1034004 |
| [42] |
Schenk O, Gärtner K, Fichtner W, et al. PARDISO:a high-performance serial and parallel sparse linear solver in semiconductor device simulation[J]. Future Generation Computer Systems, 2000, 18(1): 69-78. |
| [43] |
Oldenburg D W, Haber E, Shekhtman R. Forward modelling and inversion of multi-source TEM data[C]. SEG Technical Program Expanded Abstracts, 2008, 27: 559-563.
|
| [44] |
Yang D, Oldenburg D W. Three-dimensional inversion of airborne time-domain electromagnetic data with applications to a porphyry deposit[J]. Geophysics, 2012, 77(2): B23-B34. DOI:10.1190/geo2011-0194.1 |
| [45] |
王顺国, 熊彬. 广域视电阻率的数值计算方法[J]. 物探化探计算技术, 2012, 34(4): 380-383. WANG Shunguo, XIONG Bin. A numerical method of apparent resistivity in wide area[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2012, 34(4): 380-383. DOI:10.3969/j.issn.1001-1749.2012.04.02 |
| [46] |
欧阳芳, 戴世坤, 张钱江, 等. 层状单轴各向异性介质中有限长线源电磁响应的快速计算[J]. 石油地球物理勘探, 2016, 51(5): 1012-1020. OUYANG Fang, DAI Shikun, ZHANG Qianjiang, et al. A fast calculation method for electromagnetic fields generated by finite-length wire sources in stratified uniaxial anisotropic medium[J]. Oil Geophysical Prospecting, 2016, 51(5): 1012-1020. |
| [47] |
纳比吉安, Misac N. 勘查地球物理电磁法[M]. 北京: 地质出版社, 1992.
|



 王金海, 青海省西宁市城西区羚羊路青海省第三地质勘查院, 810029。Email:
王金海, 青海省西宁市城西区羚羊路青海省第三地质勘查院, 810029。Email: