② 河海大学力学与材料学院, 江苏南京 211100
② College of Mechanics and Materials, Hohai University, Nanjing, Jiangsu 211100, China
最近十几年,基于Zoeppritz方程的叠前反演可以同时获得纵、横波阻抗及速度、纵横波速度比、密度、泊松阻抗、泊松比等储层参数,已经成为必不可少的特殊处理技术。尽管如此,叠后地震反演也不可替代,尤其是在一些早期勘探或叠前地震资料品质不高的探区,叠后地震反演可以作为一个必要的补充,需要结合叠前和叠后地震数据开展混合反演。王秀娟等[1]应用混合反演技术分析了中国南海北部水合物赋存情况;李磊等[2]分析了影响混合反演效果的层速度、角度道集等数据,提高了叠前反演的实用性,降低了叠后反演的多解性。
地震反演是一项复杂的系统工程[3],涉及正演物理数学模型、反演目标函数、适定性问题、搜索算法等。在正演物理数学模型方面,全波形反演依据的波动方程无疑具有巨大的理论优势[4-7],但是由于计算效率问题其商业化应用效果不高。因此,实际生产中使用的还是基于褶积模型的叠前反演和叠后反演。由于精确Zoeppritz方程的表达式较复杂,现有商业化软件多使用其近似式,如Aki-Richard近似式[8]、Shuey近似式[9]和Fatti近似式[10]等。但是这些近似式是建立在一定的假设条件之下,其应用受到不同程度的限制,因此人们尝试使用精确Zoeppritz方程开展叠前反演。纵横波速度比或泊松比对建立气水、油水识别模型至关重要,目前通过Shuey近似式或Gray近似式及基追踪理论反演泊松比[11],也可以依据叠前反演获得的纵、横波速度计算纵横波速度比,但不可避免地降低了参数反演精度。为此,需要尝试通过精确的Zoeppritz方程直接反演纵横波速度比或泊松比。
关于反演目标函数及适定性问题,叠后反演或叠前反演均使用褶积模型误差项的极小化或后验概率的极大化构建地震反演目标函数[12]。地震反演受不适定性所困扰,因此反演是一个病态问题,体现在正演模型的非线性、反演结果的非唯一性和数据误差引起的不稳定性等方面。目前,解决地震反演不适定性的主要方法是正则化方法,传统的正则化方法基于Tikhonov正则化思想[13-14],通过在目标函数中添加模型参数的零阶或高阶先验项稳定反演结果,但是反演结果可能过于平滑[15]。为此,人们提出了边界保护正则化的思想用于地震反演[16-18]。此外,在叠后或叠前地震多参数同步反演中,各参数之间数量级的巨大差异也会引起多参数同步反演结果的不稳定。为了控制不同数量级参数同步反演的稳定性,业界开展了一些有意义的研究,如在改进Fatti方程中引入密度与纵波速度、横波速度与纵波速度两个拟合式以及对应的密度偏差量、横波速度偏差量提高反演精度[19-20]。
地震反演算法的研究成果众多,如宽带约束反演、广义逆等线性反演算法[21-22]、最速下降法、共轭梯度法、拟牛顿法等局部非线性优化算法[23-24]以及粒子群算法、遗传算法、模拟退火算法等全局非线性优化算法[25-27]。现有的研究成果表明,全局非线性优化算法具有不依赖初始模拟、可以获得全局最优估计解等优点,但是其计算量远大于线性优化算法和局部非线性优化算法。目前,商业应用以线性反演算法和局部非线性优化算法为主。
本文重点关注叠前和叠后地震混合反演以及基于精确Zoeppritz方程直接反演纵横波速度比。首先,建立基于边界保护正则化的叠前或叠后地震反演目标函数,结合快速模拟退火算法进行非线性反演。利用叠后地震反演同步获得纵波速度和密度,基于精确Zoeppritz方程的叠前地震反演获得横波速度或纵横波速度比。最后,通过实际资料测试、验证方法的有效性。
1 叠前和叠后地震混合多参数反演 1.1 叠前和叠后地震响应数学模型通常使用褶积模型表征叠后地震响应的数学模型,即
| $ \mathit{\boldsymbol{Y}} = \mathit{\boldsymbol{R}} * \mathit{\boldsymbol{W}} + \mathit{\boldsymbol{N}} $ | (1) |
式中:Y为叠后地震记录;R为地震反射系数序列;W为叠后子波;N为随机噪声。一般情况下,假设N服从高斯分布,其数学期望为零,协方差为σ。垂直入射时R的离散形式为
| $ {R_i} = \frac{{{Z_{i + 1}} - {Z_i}}}{{{Z_{i + 1}} + {Z_i}}} = \frac{{{v_{{\rm{P}}i + 1}}{\rho _{{\rm{P}}i + 1}} - {v_{{\rm{P}}i}}{\rho _i}{\rm{ }}}}{{{v_{{\rm{P}}i + 1}}{\rho _{{\rm{P}}i + 1}} + {v_{{\rm{P}}i}}{\rho _i}{\rm{ }}}} $ | (2) |
式中:下标i为介质层号;Z为波阻抗;vP为纵波速度;ρ为密度。叠后地震反演通常反演波阻抗,如果同步反演纵波速度和密度,需要考虑反演的稳定性问题。
与叠后地震响应类似,叠前地震角度道集的数学模型可表示为
| $ \mathit{\boldsymbol{Y}}(\theta ) = \mathit{\boldsymbol{R}}(\theta ) * \mathit{\boldsymbol{W}}(\theta ) + \mathit{\boldsymbol{N}} $ | (3) |
式中:Y(θ)为叠前地震记录,θ为入射角;R(θ)为地震反射系数序列;W(θ)为叠前角度子波。R(θ)可以由Zoeppritz方程或其近似式模拟,理论基础是AVO理论,即描述平面波反射和透射系数相对入射角变化的Zoeppritz方程
| $ \mathit{\boldsymbol{M}}\left[ {\begin{array}{*{20}{c}} {{R_{{\rm{PP}}}}}\\ {{R_{{\rm{PS}}}}}\\ {{T_{{\rm{PP}}}}}\\ {{T_{{\rm{PS}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \sin {\theta _1}}\\ { - \cos {\theta _1}}\\ {\sin 2{\theta _1}}\\ { - \cos 2{\varphi _1}} \end{array}} \right] $ | (4) |
其中
| $ \mathit{\boldsymbol{M}} = \left[ {\begin{array}{*{20}{c}} {\sin {\theta _1}}&{\cos {\varphi _1}}&{ - \sin {\theta _2}}&{\cos {\varphi _2}}\\ { - \cos {\theta _1}}&{\sin {\varphi _1}}&{ - \cos {\theta _2}}&{ - \sin {\varphi _2}}\\ {\sin 2{\theta _1}}&{\frac{{{v_{{\rm{P}}1}}}}{{{v_{{\rm{S}}1}}}}\cos 2{\varphi _1}}&{\frac{{{\rho _2}}}{{{\rho _1}}}\frac{{{v_{{\rm{P}}1}}{\kern 1pt} v_{{\rm{S}}2}^2}}{{{v_{{\rm{P}}2}}{\kern 1pt} v_{{\rm{S}}1}^2}}\sin 2{\theta _2}}&{ - \frac{{{\rho _2}}}{{{\rho _1}}}\frac{{{v_{{\rm{P}}1}}{\kern 1pt} {v_{{\rm{S}}2}}}}{{{v_{{\rm{P}}2}}{\kern 1pt} {v_{{\rm{S}}1}}}}\cos 2{\varphi _2}}\\ {\cos 2{\varphi _1}}&{ - \frac{{{v_{{\rm{S}}1}}}}{{{v_{{\rm{P}}1}}}}\sin 2{\varphi _1}}&{ - \frac{{{\rho _2}}}{{{\rho _1}}}\frac{{{v_{{\rm{P}}2}}}}{{{v_{{\rm{P}}1}}}}\cos 2{\varphi _2}}&{ - \frac{{{\rho _2}}}{{{\rho _1}}}\frac{{{v_{{\rm{S}}2}}}}{{{v_{{\rm{P}}1}}}}\sin 2{\varphi _2}} \end{array}} \right] $ | (5) |
式中:T为透射系数;R为反射系数;v为速度;下标P和S分别对应纵波和转换横波(为方便表达和阅读,下文均用“横波”代替“转换横波”),下标两个字母中第一个字母表示入射波型,第二个字母表示反射或透射波型;θ为P波反射角或透射角,下标1和2分别指示反射界面上覆介质和下伏介质;φ为S波反射角或透射角。由式(5)可见:RPP不仅与介质的弹性参数有关,还与入射角θ1有关,即式(3)中的R(θ)=RPP;当垂直入射(θ1=0)时,RPP与式(2)的Ri相同。
考虑到式(5)较复杂,物理意义不明确,为此人们提出了一些简化的近似公式,如Aki近似式[8]、Shuey近似式[9]、Fatti近似式[10]等。这些近似公式物理意义明确,但是受假设条件(如相邻地层介质弹性参数变化较小、纵横波速度比为2.0以及小角度入射等)限制。为此,这里直接使用精确Zoeppritz方程求取反射系数,以便开展高精度非线性叠前反演。需要说明的是,针对不同的角道集,需要使用不同的角度子波。
1.2 基于边界保护正则化的反演目标函数针对式(1),将先验信息引入最小二乘问题,则叠后或叠前地震反演的目标函数为
| $ \begin{array}{l} J(X) = {J_1}(X) + \lambda \cdot {J_2}(X)\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{1}{{2{\sigma ^2}}}{\left\| {\mathit{\boldsymbol{Y}}(\theta ) - \mathit{\boldsymbol{W}}(\theta ) * \mathit{\boldsymbol{R}}(\theta )} \right\|_2} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \lambda \sum\limits_{{\mathit{\boldsymbol{C}}_k}} \varPhi \left[ {\frac{{{D_{{\mathit{\boldsymbol{C}}_k}}}(X)}}{\mathit{\boldsymbol{\delta }}}} \right] \end{array} $ | (6) |
式中:J1(X)为数据项,X为待反演的参数;J2(X)为先验项;D(X)为X的梯度值;Ck为Markov随机域(MRF)邻域系统的数据点集,k =1, 2, 3为平滑阶数;Φ为势函数;λ为权系数;δ为刻度参数,在被检测的不连续处调节梯度值。值得注意的是,多参数(纵、横波速度和密度)同步反演的J2(X)由三部分组成,即
| $ {J_2} = {J_{{\rm{2P}}}}({v_{\rm{P}}}) + {J_{{\rm{2S}}}}({v_{\rm{S}}}) + {J_{{\rm{2D}}}}(\rho ) $ | (7) |
式中J2P(vP)、J2S(vS)和J2D(ρ)分别为vP、vS和ρ的先验项。于是J2(X)可以重写为
| $ \begin{array}{l} {J_2}(X) = \sum\limits_{{\mathit{\boldsymbol{C}}_k}} \varPhi [{D_{{\mathit{\boldsymbol{C}}_k}}}({v_{\rm{P}}})/{\delta _{\rm{P}}}] + \sum\limits_{{\mathit{\boldsymbol{C}}_k}} \varPhi [{D_{{\mathit{\boldsymbol{C}}_k}}}({v_{\rm{S}}})/{\delta _{\rm{S}}}] + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{{\mathit{\boldsymbol{C}}_k}} \varPhi [{D_{{\mathit{\boldsymbol{C}}_k}}}(\rho )/{\delta _\rho }] \end{array} $ | (8) |
式中刻度参数δP、δS和δρ的取值不同。
需要说明的是,由于本文采用叠后与叠前混合反演,因此在叠后和叠前反演过程中J2(X)是不同的。在叠后反演中
| $ \begin{array}{l} {J_2}(X) = \sum\limits_{{\mathit{\boldsymbol{C}}_k}} \varPhi [{D_{{\mathit{\boldsymbol{C}}_k}}}({v_{\rm{P}}})/{\delta _{\rm{P}}}] + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\nolimits_{{\mathit{\boldsymbol{C}}_k}} \varPhi [{D_{{\mathit{\boldsymbol{C}}_k}}}(\rho )/{\delta _\rho }] \end{array} $ | (9) |
在叠前单参数(如横波速度)反演中
| $ {J_2}(X) = \sum\limits_{{\mathit{\boldsymbol{C}}_k}} \varPhi [{D_{{\mathit{\boldsymbol{C}}_k}}}({v_{\rm{S}}})/{\delta _{\rm{S}}}] $ | (10) |
如果反演纵横波速度比,则
| $ {J_2}(X) = \sum\limits_{{\mathit{\boldsymbol{C}}_k}} \varPhi [{D_{{\mathit{\boldsymbol{C}}_k}}}(\gamma )/{\delta _\gamma }] $ | (11) |
式中:γ=vP/vS为纵横波速度比;δγ是关于γ反演的刻度参数。
有关势函数,主要考虑其边界保护特性,详细内容见文献[28]。在实际资料反演中,仅使用具有边界保护特性的势函数ΦGM,势函数的具体形式见文献[14]。此外,为了加快反演收敛速度和改善反演结果,在反演迭代过程中不断调节正则参数,即要求λ逐渐减小,δP、δS、δρ和δγ逐渐增大。
1.3 基于模拟退火的反演搜索方法叠前或叠后地震多参数同步反演可以看作是使目标函数(式(6))极小化的优化问题。由于式(6)中模型参数与测量数据之间的非线性关系非常复杂,为了获得一个全局最优解,使用快速模拟退火算法(FSA)求解目标函数极小值。FSA需要解决3个问题:①下一个候选点的扰动值;②接受概率;③退火过程中冷却进度表,包括初始温度、终止温度和温度衰减系数。本文接受概率使用广义Gibbs分布函数,在数据测试中确定冷却进度表,尤其是温度衰减系数需要折中反演精度和计算效率。vP、ρ(叠后反演)、vS、γ(叠前单参数反演)的扰动值分别为
| $ \left\{ {\begin{array}{*{20}{l}} {v_{\rm{P}}^{(m + 1)} = v_{\rm{P}}^{(m)} + {T^{(m)}}{\mathop{\rm sign}\nolimits} \left( {{\zeta _1} - 0.5} \right) \times }\\ {\qquad \left\{ {{{\left[ {1 + \frac{1}{{{T^{(m)}}}}} \right]}^{\left| {2{\xi _1} - 1} \right|}} - 1} \right\}\left( {{v_{{\rm{Pmax}}}} - {v_{{\rm{Pmin}}}}} \right)}\\ {\begin{array}{*{20}{l}} {{\rho ^{(m + 1)}} = {\rho ^{(m)}} + {T^{(m)}}{\mathop{\rm sign}\nolimits} \left( {{\zeta _2} - 0.5} \right) \times }\\ {\qquad \left\{ {{{\left[ {1 + \frac{1}{{{T^{(m)}}}}} \right]}^{\left| {2{\xi _2} - 1} \right|}} - 1} \right\}\left( {{\rho _{\max }} - {\rho _{\min }}} \right)} \end{array}}\\ {\qquad m = 0,1, \cdots } \end{array}} \right. $ | (12) |
| $ \left\{ {\begin{array}{*{20}{l}} {v_{\rm{S}}^{(m + 1)} = v_{\rm{S}}^{(m)} + {T^{(m)}}{\rm{sign}}({\zeta _3} - 0.5) \times }\\ {\qquad \left\{ {{{[1 + 1/{T^{(m)}}]}^{\left| {2{\xi _3} - 1} \right|}} - 1} \right\}({v_{{\rm{S}}\max }} - {v_{{\rm{S}}\min }})}\\ {\qquad m = 0,1, \cdots } \end{array}} \right. $ | (13) |
| $ \begin{array}{l} {\gamma ^{(m + 1)}} = {\gamma ^{(m)}} + {T^{(m)}}{\rm{sign}}({\zeta _4} - 0.5) \times \\ \qquad \left\{ {{{[1 + 1/{T^{(m)}}]}^{\left| {2{\xi _4} - 1} \right|}} - 1} \right\}({\gamma _{\max }} - {\gamma _{\min }})\\ \qquad m = 0,1, \cdots \end{array} $ | (14) |
式中:vP(m)、vS(m)、ρ(m)和γ(m)表示当前值;vP(m+1)、vS(m+1)、ρ(m+1)和γ(m+1)为扰动后值;T(m)为当前温度值;[vPmin,vPmax]、[vSmin,vSmax]、[ρmin,ρmax]和[γmin,γmax]分别为4个反演参数的变化范围;ξ和ζ为0到1的随机数(下标1、2、3、4表示取不同的随机数);sign(·)为符号函数。
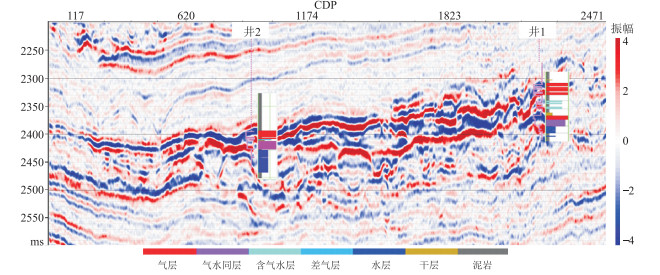
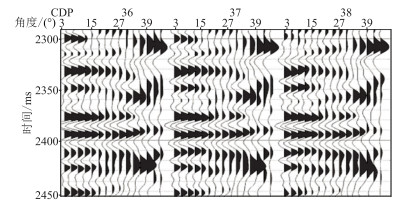
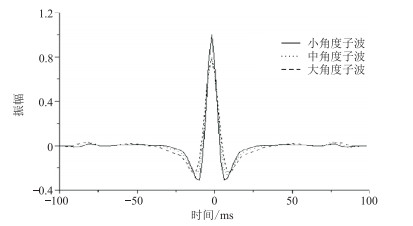
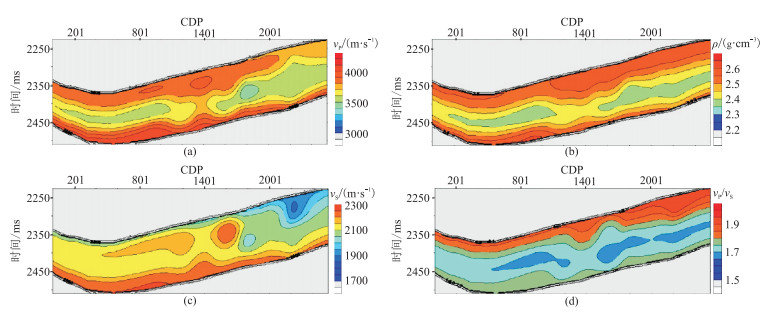
2 实测叠前和叠后地震数据混合反演图 1为研究区过井二维地震剖面A。由图可见,目的层横向变化很大,地震同相轴连续性较差。提取了叠前地震数据角度道集(图 2)的小、中、大角度子波(图 3)。使用3°~9°、18°~24°和33°~39°等3组角度道集数据进行叠前地震反演。图 4为vP、ρ、vS和vP/vS初始模型。本文的叠前和叠后混合反演步骤如下。
|
图 1 研究区过井二维地震剖面A 井1和井2分别位于CDP 2226和CDP 918。叠后地震数据包含2542个CDP,时间窗口为2200~2600ms,采样率为2ms |
|
图 2 叠前地震数据角度道集 每个CDP有15个角度道集,角度范围为3°~45°,角度间隔为3° |
|
图 3 小、中、大角度子波 |
|
图 4 vP(a)、ρ(b)、vS(c)和vP/vS(d)初始模型 |
(1) 叠后反演vP和ρ。使用vP(图 4a)、ρ(图 4b)初始模型反演vP和ρ,在搜索时利用式(12)进行扰动。
(2) 利用叠后反演获得的vP和ρ开展叠前反演。将vP和ρ作为已知值代入Zoeppritz方程,分别使用vS初始模型(图 4c)、vP/vS初始模型(图 4d)反演vS、vP/vS,在搜索时分别使用式(13)、式(14)进行扰动。
2.1 vP、vS和ρ的混合反演结果采用叠后和叠前多参数混合反演的理由为:①叠后地震资料的品质好于叠前地震资料;②由于各参数之间的数量级差异,叠前反演同步获得3参数的精度很难保证。为此,这里尝试使用叠后地震数据同时反演vP和ρ,在此基础上使用叠前角度道集地震数据进行单参数(vS、vP/vS、泊松比等)反演。
反演中为了提高稳定性,需要引入一些约束条件。通过在改进Fatti方程中引入ρ与vP、vS与vP两个拟合式以及对应的ρ偏差量、vS偏差量提高反演精度。叠后反演使用ρ与vP的拟合式
| $ \rho = 1.036 + 0.0003825{v_{\rm{P}}} $ | (14) |
式中ρ偏离拟合线的范围为(-0.125g/cm3,0.125g/cm3)。
叠前反演使用vS与vP的拟合式
| $ {v_{\rm{S}}} = 1775.2 + 0.08818{v_{\rm{P}}} $ | (15) |
式中vS偏离拟合线的范围为(-200m/s,200 m/s)。
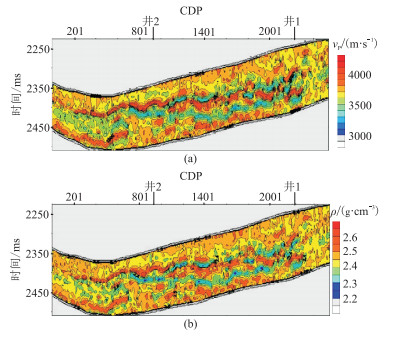
图 5为叠后地震反演的vP和ρ,其中叠后反演的反射系数为垂直入射反射系数。由图可见,横向连续性和纵向分层特点证明vP(图 5a)和ρ(图 5b)总体反演效果均较好,但在井1周围连续性很差,这与该处地层发育特点及地震资料品质有关。
|
图 5 叠后地震反演的vP(a)和ρ(b) vP的值域为(3200m/s,4100m/s),ρ的值域为(2.25g/cm3,2.60g/cm3)。模拟退火算法的初始温度为0.5,终止温度为0.00001,温度衰减系数为0.9。正则化势函数为ΦGM,正则参数λ=0.3,δ=(δP δS δρ δγ)=(150.0, 110.0, 0.15, 0.11)。利用两口井的测井参数约束反演 |
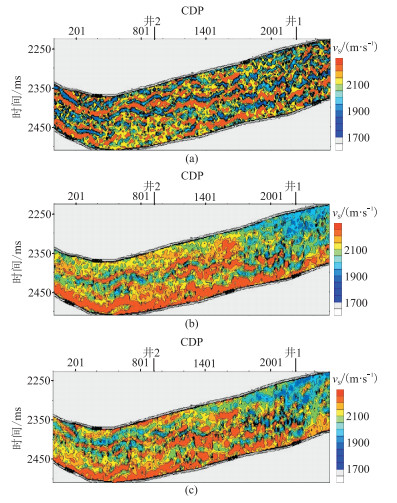
在叠后地震反演获得的vP和ρ基础上,进行叠前地震单参数(vS)反演(图 6),其中反射系数直接由Zoeppritz方程获得。可见,中(图 6b)、大(图 6c)角度道集的反演效果好于小角度道集(图 6a),这是由于小角度道集地震资料品质较差所致。图 7为18°~24°角度道集混合反演结果与井2、井1的测井数据对比。由图可见,叠后反演的ρ与井数据吻合很好,vP与井数据基本吻合。郭强等[29]认为,中角度道集叠前地震反演的vP、vS的参数敏感性总体优于大角度道集。因此后文重点分析中角度道集反演结果。
|
图 6 不同角度叠前地震反演vS (a)3°~9°;(b)18°~24°;(c)33°~39° vS的值域为(1600m/s,2300m/s),模拟退火算法的初始温度为0.5,终止温度为0.00001,温度衰减系数为0.9。正则化势函数为ΦGM,正则参数λ=0.3,δ=(δP δS δρ δγ)=(150.0, 110.0, 0.15, 0.11)。利用两口井的测井参数约束反演 |

|
图 7 18°~24°角度道集混合反演结果与井2(左)、井1(右)的测井数据对比 |
需要特别说明的是,由于研究区小角度道集地震数据品质不好,而中角度道集反演结果又略优于大角度道集。因此“中角度道集反演效果最好”的认识不具普适性。
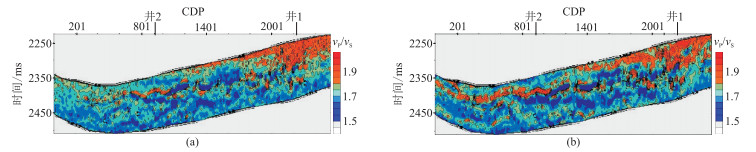
2.2 vP/vS直接反演结果利用vP/vS能够有效识别气层(或气水同层)与水层。取叠后反演vP(图 5a)与叠前反演vS(图 6)的比值,得到不同角度vP/vS(图 8)——间接反演结果。可见,在较深时间段vP/vS值明显降低,可能与含气有关。
|
图 8 不同角度vP/vS间接反演结果 (a)18°~24°;(b)33°~39° |
此外,通过叠前地震数据可直接反演vP/vS,再结合vP可以获得vS,然后由Zoeppritz方程计算反射系数。vP/vS初始模型(图 4d)由vP初始模型(图 4a)和vS初始模型(图 4c)获得。图 9为由不同角度叠前地震数据直接反演的vP/vS。对比图 9与图 8可见:前者(图 9)时窗上部的vP/vS值大于1.8,时窗下部的vP/vS值为1.7~1.8,都明显高于中部的值(1.6~1.7);后者(图 8)时窗上部的vP/vS值偏低,分布于1.65~1.8。

|
图 9 由不同角度叠前地震数据直接反演的vP/vS (a)18°~24°;(b)33°~39° |
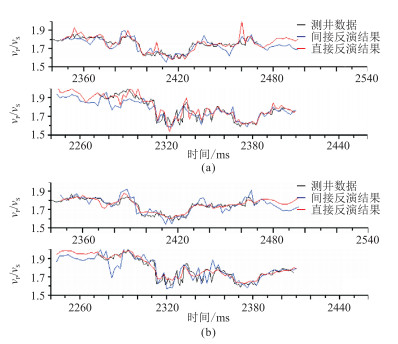
图 10为不同角度反演获得的vP/vS与井2、井1的测井数据对比。由图可见:vP/vS间接反演结果与井数据存在误差(与井2吻合较好,与井1吻合略差),这主要是因为单独反演vP、vS很难保证vP/vS的值稳定;vP/vS直接反演结果与井数据吻合很好,尤其是18°~24°角度道集的结果(图 10a)。
|
图 10 不同角度反演获得的vP/vS与井2(上)、井1(下)的测井数据对比 (a)18°~24°;(b)33°~39° |
(1) 直接使用Zoeppritz方程进行反演,可以避免Zoeppritz方程近似式反演引起的误差,对于大角度道集尤其重要。使用Zoeppritz方程直接反演几乎并不影响多参数反演的速度和效果。此外,由于多参数之间的量级差异以及多参数同步随机搜索增大了不确定性,在反演中引入两个附加约束条件,提高了多参数反演结果稳定性。
(2) 叠后和叠前混合多参数反演可以克服叠前地震多参数同步反演中不同参数数量级、参数敏感性、叠前地震资料品质差异引起的问题。由于研究区的实际叠前地震道集品质较差,而叠后地震数据品质较好,故可由叠后反演获得纵波速度和密度,由叠前反演获得横波速度、纵横波速度比、泊松比等。结果显示,叠后反演获得的纵波速度和密度精度较高,叠前反演获得的纵横波速度比的精度高于叠后反演,18°~24°角度道集的反演效果好于3°~9°和33°~39°角度道集。
| [1] |
王秀娟, 吴时国, 余鹏, 等. 混合地震反演技术及其在水合物勘探中的应用[J]. 石油物探, 2007, 46(3): 278-282. WANG Xiujuan, WU Shiguo, YU Peng, et al. Application of hybrid seismic inversion in hydrate exploration[J]. Geophysical Prospecting for Petroleum, 2007, 46(3): 278-282. DOI:10.3969/j.issn.1000-1441.2007.03.009 |
| [2] |
李磊, 王英民, 杨绍国, 等. 混合地震反演技术及其在东海南部陆架盆地中的应用[J]. 中国石油大学学报, 2007, 31(5): 28-34. LI Lei, WANG Yingmin, YANG Shaoguo, et al. Application of hybrid seismic inversion:a case study from the southern shelf basin of east China Sea[J]. Journal of China University of Petroleum, 2007, 31(5): 28-34. DOI:10.3321/j.issn:1000-5870.2007.05.006 |
| [3] |
杨文采. 地球物理反演的理论与方法[M]. 北京: 地质出版社, 1997.
|
| [4] |
Pratt R G, Shin C, Hicks G J. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion[J]. Geophysical Journal International, 1998, 133(2): 341-362. DOI:10.1046/j.1365-246X.1998.00498.x |
| [5] |
Virieux J, Operto S. An overview of full-waveform inversion in exploration geophysics[J]. Geophysics, 2009, 74(6): WCC1-WCC26. DOI:10.1190/1.3238367 |
| [6] |
张衡, 刘洪, 刘璐, 等. 基于平均导数方法的声波方程频率域高阶正演[J]. 地球物理学报, 2014, 57(5): 1599-1611. ZHANG Heng, LIU Hong, LIU Lu, et al. Frequency domain acoustic equation high-order modeling based on an average-derivative method[J]. Chinese Journal of Geophysics, 2014, 57(5): 1599-1611. |
| [7] |
陈生昌, 陈国新. 多主频波场的时间阻尼全波形反演[J]. 地球物理学报, 2017, 60(8): 3229-3237. CHEN Shengchang, CHEN Guoxin. Time-damping full waveform inversion of multi-dominant-frequency wavefields[J]. Chinese Journal of Geophysics, 2017, 60(8): 3229-3237. |
| [8] |
Aki K, Richards P G.Quantitative Seismology: Theory and Methods[M].W.H. Freeman and Co., 1980.
|
| [9] |
Shuey R T. A simplification of the Zoeppritz equations[J]. Geophysics, 1985, 50(4): 609-614. DOI:10.1190/1.1441936 |
| [10] |
Fatti J L, Smith G C, Vail P J. Detection of gas in sandstone reservoirs using AVO analysis:A 3-D seismic case history using the Geostack technique[J]. Geo-physics, 1994, 59(9): 1362-1376. |
| [11] |
刘畅, 李超, 朱振宇, 等. 杨氏模量和泊松比基追踪反演[J]. 石油地球物理勘探, 2019, 54(6): 1310-1315. LIU Chang, LI Chao, ZHU Zhenyu, et al. Basis pursuit inversion for Young's modulus and Poisson's ratio[J]. Oil Geophysical Prospecting, 2019, 54(6): 1310-1315. |
| [12] |
张宏兵, 尚作萍, 杨长春, 等. 波阻抗反演正则参数估计[J]. 地球物理学报, 2005, 48(1): 181-188. ZHANG Hongbing, SHANG Zuoping, YANG Changchun, et al. Estimation of regular parameters for the impedance inversion[J]. Chinese Journal of Geophy-sics, 2005, 48(1): 181-188. DOI:10.3321/j.issn:0001-5733.2005.01.024 |
| [13] |
吉洪诺夫, 阿尔先宁(著); 王秉忱(译).不适定问题的解法[M].北京: 地质出版社, 1979.
|
| [14] |
Sen M K, Roy I G. Computation of differential seismograms and iteration adaptive regularization in prestack waveform inversion[J]. Geophysics, 2003, 68(6): 2026-2039. DOI:10.1190/1.1635056 |
| [15] |
郭一豪, 陈晓, 杨海燕, 等. 大地电磁测深阶段式自适应正则化反演[J]. 石油地球物理勘探, 2020, 55(4): 906-914. GUO Yihao, CHEN Xiao, YANG Haiyan, et al. Staged adaptive regularized inversion of magnetotelluric data[J]. Oil Geophysical Prospecting, 2020, 55(4): 906-914. |
| [16] |
Luo Y, Marhoon M, Dossary S A, et al. Edge-preserving smoothing and applications[J]. The Leading Edge, 2006, 21(2): 136-158. |
| [17] |
Zhang H, Shang Z, Yang C. A non-linear regularized constrained impedance inversion[J]. Geophysical Prospecting, 2007, 55(6): 819-833. DOI:10.1111/j.1365-2478.2007.00637.x |
| [18] |
Zhang H, Guo Q, Liang L, et al. A nonlinear method for multiparameter inversion of pre-stack seismic data based on anisotropic Markov random field[J]. Geophysical Prospecting, 2018, 66(3): 461-477. DOI:10.1111/1365-2478.12555 |
| [19] |
Liang L F, Zhang H B, Dan Z W, et al. Prestack density inversion using the Fatti equation constrained by the P- and S-wave impedance and density[J]. Applied Geophysics, 2017, 14(1): 133-141. DOI:10.1007/s11770-017-0598-9 |
| [20] |
王保丽, 印兴耀, 张繁昌, 等. 基于Fatti近似的弹性阻抗方程及反演[J]. 地球物理学进展, 2008, 23(1): 192-197. WANG Baoli, YIN Xingyao, ZHANG Fanchang, et al. Elastic impedance equation based on Fatti approximation and inversion[J]. Progress in Geophysics, 2008, 23(1): 192-197. |
| [21] |
Tarantola A, Valette B. Generalized nonlinear inverse problems solved using the least squares criterion[J]. Review of Geophysics and Space Physics, 1982, 20(2): 219-232. DOI:10.1029/RG020i002p00219 |
| [22] |
张宏彬, 何礁登. 宽带约束反演[J]. 石油物探, 1995, 34(1): 1-10. ZHANG Hongbin, HE Qiaodeng. Broad-band constrained inversion[J]. Geophysical Prospecting for Petroleum, 1995, 34(1): 1-10. |
| [23] |
周竹生, 何继善, 赵荷晴. 利用广义共轭梯度算法求解地震道反演问题[J]. 石油地球物理勘探, 1998, 33(4): 439-447. ZHOU Zhusheng, HE Jishan, ZHAO Heqing. Solving a seismic trace inversion problem by using generalized conjugate gradient algorithm[J]. Oil Geophysical Prospecting, 1998, 33(4): 439-447. DOI:10.3321/j.issn:1000-7210.1998.04.002 |
| [24] |
刘璐, 刘洪, 张衡, 等. 基于修正拟牛顿公式的全波形反演[J]. 地球物理学报, 2013, 56(7): 2447-2451. LIU Lu, LIU Hong, ZHANG Heng, et al. Full waveform inversion based on modified quasi-Newton equation[J]. Chinese Journal of Geophysics, 2013, 56(7): 2447-2451. |
| [25] |
张霖斌, 姚振兴, 纪晨, 等. 快速模拟退火算法及应用[J]. 石油地球物理勘探, 1997, 32(5): 645-660. ZHANG Linbin, YAO Zhenxing, JI Chen, et al. Fast simulated annealing algorithm and its application[J]. Oil Geophysical Prospecting, 1997, 32(5): 654-660. DOI:10.3321/j.issn:1000-7210.1997.05.002 |
| [26] |
Guo Q, Zhang H B, Tian J B, et al. A nonlinear multiparameter prestack seismic inversion method based on hybrid optimization approach[J]. Arabian Journal of Geosciences, 2018, 11(3): 48-60. DOI:10.1007/s12517-018-3392-y |
| [27] |
方中于, 王丽萍, 杜家元, 等. 基于混合智能优化算法的非线性AVO反演[J]. 石油地球物理勘探, 2017, 52(4): 797-804. FANG Zhongyu, WANG Liping, DU Jiayuan, et al. Nonlinear AVO inversion based on hybrid intelligent optimization algorithm[J]. Oil Geophysical Prospecting, 2017, 52(4): 797-804. |
| [28] |
Charbonnier P, Blanc-Féraud L, Aubert G. Determi-nistic edge-preserving regularization in computed imaging[J]. IEEE Transactions on Image Processing, 1997, 6(2): 298-311. DOI:10.1109/83.551699 |
| [29] |
郭强, 张宏兵, 曹呈浩, 等. Zoeppritz方程叠前多参数反演及密度敏感性分析[J]. 石油地球物理勘探, 2017, 52(6): 1218-1225. GUO Qiang, ZHANG Hongbing, CAO Chenghao, et al. Density-sensitivity analysis about prestack multi-parameter inversion based on the exact Zoeppritz equation[J]. Oil Geophysical Prospecting, 2017, 52(6): 1218-1225. |



 张宏兵, 江苏省南京市江宁区佛城西路8号笃学楼河海大学地球科学与工程学院, 211100。Email:
张宏兵, 江苏省南京市江宁区佛城西路8号笃学楼河海大学地球科学与工程学院, 211100。Email: