砂岩储层内部的横向不连续结构通常是指沉积过程中砂体尖灭、同期砂体侧向接触、多期砂体纵向叠置等导致的岩性、物性变化以及由于构造运动导致的微小断层等[1]。这种不连续结构的存在是导致油田开发注采不受效、储量采出程度低和局部剩余油富集的重要原因[2-4]。
虽然在不连续结构位置存在一定程度的旅行时、地震振幅和波形等地震响应,但由于砂岩储层内部不连续结构的尺度通常小于地震资料的分辨率,因此难以通过常规地震反演、属性分析等储层预测手段精确地刻画不连续结构[5]。
目前,地震信号横向不连续性检测大多针对断层检测、识别和自动解释,相关研究包括边缘保持滤波技术[6-8]、相干体技术[9-13]、蚂蚁追踪技术[14-15]等,并已得到广泛应用。但对于小尺度不连续信息检测的研究较少。
本文对前人研究进行了技术集成和综合应用,以局部结构熵属性计算为核心,利用边缘保持滤波技术和基于蚁群算法的平面属性增强处理方法,形成了砂岩储层横向不连续性检测的技术组合,并在南海H油田目标砂体单元取得了良好的应用效果。
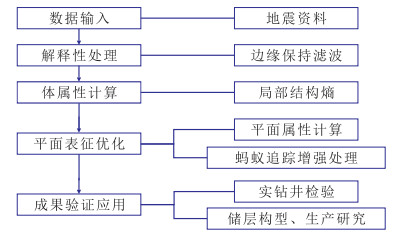
1 储层横向不连续性检测技术组合砂岩储层横向不连续性检测的技术流程主要包括(图 1):①地震资料解释性处理。利用边缘保持滤波处理方法,在滤除随机噪声、提高资料信噪比的同时,能够更好地保持反映储层横向边缘结构的不连续信息。②相干体属性计算。局部结构熵算法属于第三代相干算法,较前两代相干算法具有更好的抗噪性和更高的分辨率,对砂岩储层内部微小的不连续结构的检测精度更高。③平面表征及优化。在步骤②基础上进一步计算目标储层的平面属性,采用蚁群算法对平面属性增强处理,改善检测结果的平面显示效果,突出主要的不连续信息,得到较为连续的平面检测属性分布。④成果验证及应用。利用钻井信息验证检测结果的可靠程度,再利用检测结果研究储层构型及分析油田注采等。
|
图 1 砂岩储层横向不连续性检测技术流程 |
地震相干是相邻地震道之间地震信号相似性的度量,利用相干值的空间变化可以解释断层、裂缝、地质构造异常等储层横向非均质特征。相干体技术作为三维地震解释的重要技术之一,自1995年被提出以来[16],在地震勘探领域得到广泛应用和发展,形成了三代相干体算法(C1、C2、C3)。局部结构熵算法属于C3,较C1、C2具有更好的抗噪性和更高的分辨率,对于检测砂岩储层内部微小的不连续结构精度更高[17-18]。
局部结构熵属性将三维分析时窗分为4个块,把每个块中的分析数据点重新组成四个一维数组,利用这些新的数组对每个空间点构造一个4×4阶的协方差矩阵,最后由协方差矩阵计算结构熵。详细计算步骤如下。
(1) 对需要计算的三维地震数据体进行预处理。将每一地震道的数据修正为地震道数据减去地震道均值
| $ {\hat d_{xyt}} = {d_{xyt}} - {E_t}\left( {{d_{xyt}}} \right) = {d_{xyt}} - \frac{1}{{{N_t}}}\sum\limits_{k = 1}^{{N_t}} {{d_{xyk}}} $ | (1) |
式中:dxyt和
(2) 选取一个三维分析时窗,将分析时窗在
| $ \mathit{\boldsymbol{S}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{a}}_1^{\rm{T}}{\mathit{\boldsymbol{a}}_1}}& \cdots &{\mathit{\boldsymbol{a}}_1^{\rm{T}}{\mathit{\boldsymbol{a}}_4}}\\ \vdots & \ddots & \vdots \\ {\mathit{\boldsymbol{a}}_4^{\rm{T}}{\mathit{\boldsymbol{a}}_1}}& \cdots &{\mathit{\boldsymbol{a}}_4^{\rm{T}}{\mathit{\boldsymbol{a}}_4}} \end{array}} \right] $ | (2) |
由式(2)可见,S对角线上的元素由每个向量的自相关构成,而非对角线上的元素由不同向量的互相关构成。需要指出的是,S是一个对称矩阵。
(3) 计算S的局部结构熵
| $ \varepsilon (x,y,t) = \frac{{{\mathop{\rm tr}\nolimits} \mathit{\boldsymbol{S}}}}{{\left\| \mathit{\boldsymbol{S}} \right\|}} - 1 = \frac{{\sum\limits_{i = 1}^4 {\mathit{\boldsymbol{a}}_i^{\rm{T}}} {\mathit{\boldsymbol{a}}_i}}}{{\sqrt {\sum\limits_{i,j = 1}^4 {{{\left( {\mathit{\boldsymbol{a}}_i^{\rm{T}}{\mathit{\boldsymbol{a}}_j}} \right)}^2}} } }} - 1 $ | (3) |
式中||·||为Hilbert-Schmidt算子。由式(3)可见:若每个块中的向量都相关(不连续性较小),则S中的所有元素都相等,此时trS=||S||,ε(x,y,t)=0;若每个块中的向量都不相关(不连续性较大),则trS≤2||S||,ε(x,y,t) ≤1。利用ε(x,y,t)可以分析时窗内地震数据点的混乱程度(不确定性),是一种分析局部混沌效应和不连续信息的有利工具。
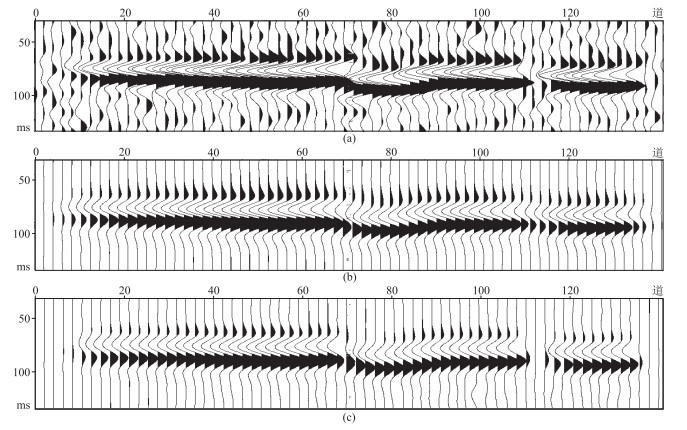
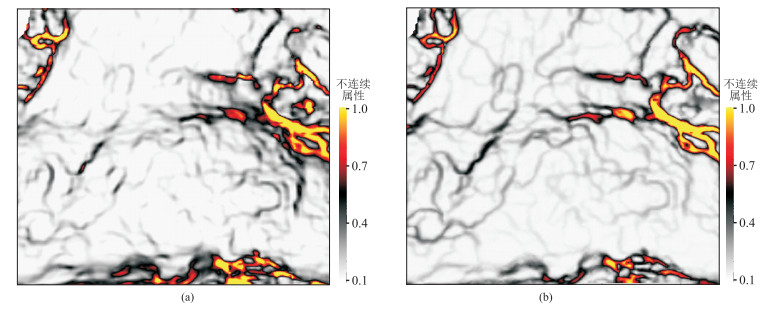
为验证局部结构熵属性对地震不连续信号的表征效果,设计了多期河道叠置的三维正演模型(图 2)模拟河流相储层的沉积特征,呈现了三维空间中单期河道在沉积过程中的高程变化、河道宽度和砂体厚度变化以及多期河道侧向迁移、叠置等特点,其中包含不同类型的储层横向边界特征。图 3为模型及属性剖面。由图可见,在储层内部的不同期次河道叠置部位(图 3a)的地震信号不连续(图 3b),局部结构熵属性(图 3d)的表征效果明显优于相干属性(图 3c)。图 4、图 5分别为正演模型、实际地震数据储层不连续性检测平面属性。由图可见,局部结构熵明显突出了储层内部地震反射信号的局部差异,明显反映了储层内部不同地质体的接触关系信息,异常值的对比度更强,对不连续位置的刻画精度更高(图 4c、图 5b)。

|
图 2 多期河道叠置的三维正演模型 |

|
图 3 模型及属性剖面 (a)A测线模型剖面;(b)地震剖面;(c)相干剖面;(d)局部结构熵剖面 |

|
图 4 正演模型储层不连续性检测平面属性 (a)正演模型俯视图;(b)相干属性;(c)局部结构熵 |

|
图 5 储层不连续性检测平面属性 (a)相干;(b)局部结构熵 |
利用地震属性研究砂体横向不连续性时,由于研究尺度较小,地震数据中的噪声更容易影响属性提取精度,导致检测结果中存在错误信息,无法清晰地识别边界信息。因此滤除随机干扰噪声是储层横向不连续性检测的必要环节。结构导向滤波技术是近年来成熟且应用较广泛的滤波技术,其核心是先分析计算点的倾角和方位角信息,然后沿着倾角和方位角的方向进行滤波,在消除随机噪声的同时,能够保持不连续的边缘信息。本文采用Luo等[19]提出的边缘保持滤波技术(Edge Preserving Smoothing, EPS),具体计算步骤为:①将以计算点为中心的滑动分析时窗内的地震数据分为9个子窗口,分别是8个绕中心点旋转的六边形或五边形,和1个以计算点为中心的规则正方形;②分别求取9个子窗口中数据的方差值;③将方差最小的子窗口的均值作为计算点的估计值。
为检验边缘保持滤波方法的效果,对图 3b加30%随机噪声,分别进行中值滤波和边缘保持滤波(图 6)。可见,与中值滤波(图 6b)相比,边缘保持滤波在滤除随机噪声的同时,更好地保持了地质体边缘的地震振幅和波形差异(图 6c)。
|
图 6 滤波结果 (a)对图 3b加30%噪声;(b)中值滤波;(c)边缘保持滤波 |
蚂蚁算法是模拟自然界中蚂蚁觅食行为提出的一种寻优算法,其基本原理是:在地震数据体中设定大量的“蚂蚁”,并让“蚂蚁”沿着可能的断层面向前移动,若“蚂蚁”往前能够追踪到断层面,则释放“信息素”并作出明显的标记;若前方不太可能是断层面,就不做标记或释放较弱的“信息素”。目前蚂蚁追踪算法已经被斯伦贝谢公司集成到软件中,作为一种识别低序级断层和裂缝的方法得到了广泛应用[20]。
地震资料解释性处理并不能完全滤除噪声干扰,表征地震数据空间不连续的地震属性在平面上往往出现不连续条带中断、边界模糊、次级信息干扰等。为改善检测结果的平面显示效果,采用基于蚁群算法的增强处理,以平面检测得到的不连续属性作为输入,通过蚂蚁平面追踪算法突出主要的不连续信息,得到较为连续的平面检测属性分布[21]。图 7为蚂蚁追踪增强处理前、后的不连续属性。
|
图 7 蚂蚁追踪增强处理前(a)、后(b)的不连续属性 |
H油田位于中国南海珠江口盆地惠州凹陷的一个低幅度披覆背斜构造,内部断层不发育。油田的主要含油层系分布在新近系珠江组,其中砂体L30up的储量占整个油田储量的85%,为油田的重点研究目标。L30up为辫状河三角洲前缘沉积,发育水下分流河道、河口坝、席状砂等沉积微相,储层埋深约为2600m,井点钻遇储层厚度为2~13m,平均厚度小于10m。
地震资料在L30up的频带宽度约为8~80Hz,主频约为40Hz。统计测井数据得到此段地层平均层速度约为3100~4300m/s,因此地震垂向分辨率约为20~27m。由于储层的平均厚度小于地震垂向分辨率,储层预测难度较大。
油田采用天然能量开采,在开发井生产过程中,地层能量下降快,生产井产量降低,目前考虑部署注水井提高地层能量。充分利用现有地震资料精确检测储层内部的不连续结构,对于指导L30up的注水方案,制定油田的开发调整方案具有非常重要的意义。
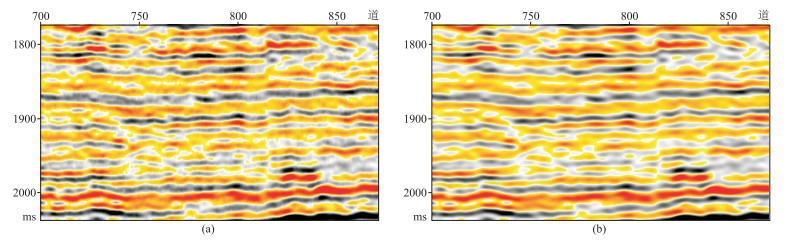
2.2 储层不连续性检测在对储层内部不连续性检测之前,应首先评估地震资料品质。当地震资料信噪比较低或地震分辨率不足时,采用适当的方法提高地震资料品质,但需注意保持地震数据中的不连续结构信息。图 8为H油田边缘保持滤波前、后地震剖面。由图可见:边缘保持滤波前地震剖面存在明显噪声,信噪比较低(图 8a);边缘保持滤波后有效滤除了噪声,同时保留了反映地质体边界的不连续信息(图 8b)。
|
图 8 H油田边缘保持滤波前(a)、后(b)地震剖面 |
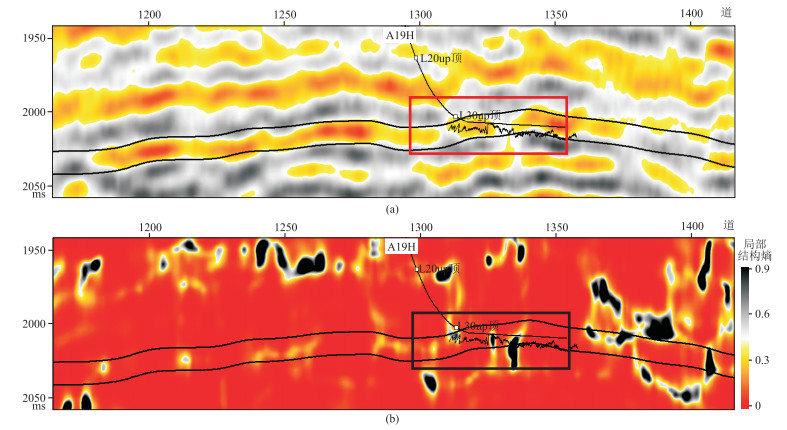
在边缘保持滤波后的地震数据体上计算局部结构熵属性体,用于检测砂岩储层内部不连续结构的分布。图 9为过水平井A19H地震剖面、局部结构熵剖面。由图可见,局部结构熵剖面(图 9b)在地震同相轴间断、扭动或振幅变化的位置(图 9a中A19H井钻遇泥岩段处)表现为异常高值,表明储层在上述位置存在横向不连续结构。
|
图 9 过水平井A19H地震剖面(a)、局部结构熵剖面(b) |
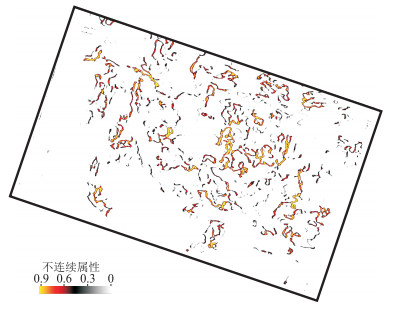
为进一步了解储层不连续结构的平面展布特征,根据目标储层的层位解释结果,利用局部结构熵数据体提取顶、底界面间的平面振幅属性,经过蚂蚁追踪平面增强处理,得到储层内部横向不连续结构的平面展布(图 10)。
|
图 10 储层内部横向不连续结构的平面展布 |
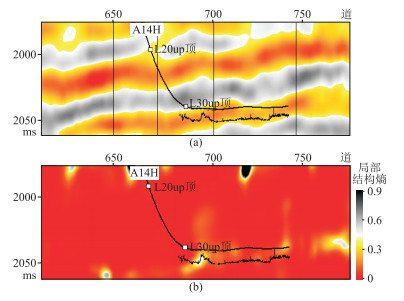
H油田L30up砂体目前有15口水平井,水平井的岩性、测井曲线变化等反映了储层横向岩性变化和砂体结构信息。因此开展水平井钻遇泥岩段与检测结果的标定分析,可以验证局部结构熵检测结果的可靠性和合理性。图 11为过A14H井地震剖面和局部结构熵剖面。由图可见,局部结构熵属性(图 11b)准确检测了水平井钻遇的储层不连续结构(泥岩段)。在实际标定、分析过程中发现,大部分井钻遇的泥岩段对应不连续结构,但存在一些特殊情况导致两者不对应。
|
图 11 过A14H井地震剖面(a)和局部结构熵剖面(b) A14H井水平段钻遇1个泥岩段,泥岩段宽度为25m |
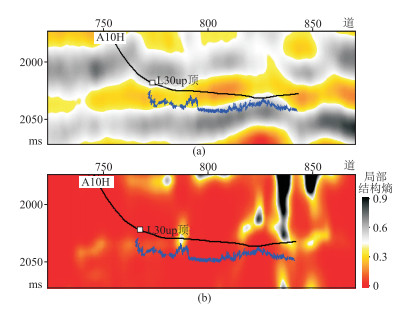
第一,水平井井轨迹纵向钻出储层这类非地质因素导致的泥岩段。图 12为过A10H井地震剖面和局部结构熵剖面。由图可见:局部结构熵属性准确反映了第1个泥岩段,但第2个泥岩段的局部结构熵属性没有异常响应(图 12b);从地震剖面上可以看到井轨迹钻出储层(图 12a),因此局部结构熵属性不能反映第2个泥岩段。
|
图 12 过A10H井地震剖面(a)和局部结构熵剖面(b) A10H井水平段钻遇了2个泥岩段,第1、第2个泥岩段宽度分别为32、98m |
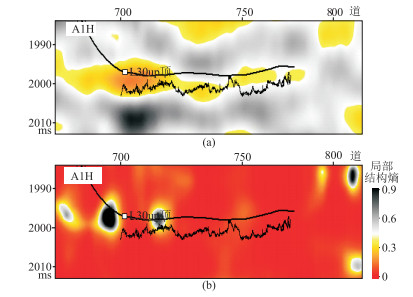
第二,储层厚度小导致地震响应较弱。虽然地震波形、振幅存在微弱变化,但提取的局部结构熵属性响应太弱,导致无法识别泥岩段。图 13为过A1H井地震剖面和局部结构熵剖面。由图可见:局部结构熵属性准确反映了A1H井水平段前半部分钻遇的泥岩段(图 13b);对于A1H井水平段后半部分钻遇的泥岩段,由于地震响应太弱(图 13a),局部结构熵响应也较弱,因此检测效果不理想。
|
图 13 过A1H井地震剖面(a)和局部结构熵剖面(b) A13H井位于沉积朵体边部,储层厚度约为3m |
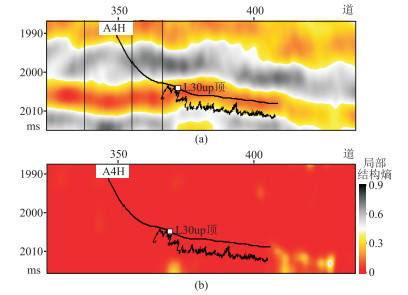
第三,地震资料横向分辨能力影响。图 14为过A4H井地震剖面和局部结构熵剖面。由图可见,无论是地震剖面(图 14a)还是局部结构熵剖面(图 14b),都不存在明显的储层不连续信息的响应。多个实际油田的资料证实,局部结构熵属性的横向检测宽度下限与地震采集面元尺寸相当。如H油田的采集面元为22.5m×22.5m,则局部结构熵属性可分辨的泥岩宽度下限约为20m。
|
图 14 过A4H井地震剖面(a)和局部结构熵剖面(b) A4H井水平段钻遇宽度为12m的泥岩段 |
根据标定结果,统计、分析15口水平井钻遇的泥岩段和检测结果的匹配关系,主要包括以下步骤:①整理目标储层所有水平井的泥岩段数量;②剔除水平井井轨迹纵向钻出储层这类非地质因素导致的泥岩段;③将过水平井轨迹的局部结构熵剖面与筛选后的水平井泥岩段进行标定,对于全水平井段未钻遇泥岩段的水平井,统计得到单井吻合率(如局部结构熵过井剖面无异常值,则吻合率为100%,否则吻合率为0);④统计所有水平井的总吻合率;⑤分析不吻合的原因。表 1为H油田储层横向不连续性检测结果水平井标定统计表。由表可见,H油田不连续性检测结果的最终吻合率达到76%,说明局部结构熵属性对于储层横向不连续结构的检测结果可靠、有效。
|
|
表 1 H油田储层横向不连续性检测结果水平井标定统计表 |
砂岩储层内部不连续结构的准确识别对油田开发意义重大,但基于常规储层预测方法的识别精度较低,且难度较大。局部结构熵算法属于第三代相干算法,本文以该方法为核心,与边缘保持滤波处理、蚂蚁追踪平面增强方法组合,形成适用于油田开发阶段储层内部不连续结构刻画的组合技术。利用储层横向不连续性检测技术组合得到的储层内部不连续结构评价结果可预测储层内部的连通性,在此基础上可进一步研究储层构型、预测剩余油等,并指导油田开发阶段的井位调整部署。
(1) 通过对地震数据计算局部结构熵数据体,可提取原始地震数据中的振幅、波形等微弱变化特征,用于检测储层内部横向不连续结构的分布,检测精度高于常规相干计算方法。
(2) 计算局部结构熵对地震资料的品质要求较高,利用边缘保持滤波可以提高地震资料品质,利用蚂蚁追踪平面增强可以改善平面属性检测效果。
(3) 储层横向不连续性检测效果可采用水平井钻遇泥岩段标定的方法进行验证。对于储层厚度远小于地震分辨率的位置、横向尺度小于地震采集面元尺度的不连续结构,局部结构熵方法的检测精度不高。
| [1] |
范廷恩.点坝砂体储层内部不连续界线类型及预测方法研究[D].四川成都: 西南石油大学, 2016. FAN Ting'en.The Discontinuous Boundary of Thin Fluvial Reservoir and Its Prediction[D].Southwest Petroleum University, Chengdu, Sichuan, 2016. |
| [2] |
赵伦, 王进财, 陈礼, 等. 砂体叠置结构及构型特征对水驱规律的影响:以哈萨克斯坦南图尔盖盆地Kumkol油田为例[J]. 石油勘探与开发, 2014, 41(1): 86-94. ZHAO Lun, WANG Jincai, CHEN Li, et al. Influences of sandstone superimposed structure and architecture on water-flooding mechanisms:a case study of Kumkol Oilfield in the South Turgay Basin, Kazakhstan[J]. Petroleum Exploration and Development, 2014, 41(1): 86-94. |
| [3] |
于兴河. 油田开发中后期储层面临的问题与基于沉积成因的地质表征方法[J]. 地学前缘, 2012, 19(2): 1-14. YU Xinghe. Existing problems and sedimentogenesis-based methods of reservoir characterization during the middle and later periods of oilfield development[J]. Earth Science Frontiers, 2012, 19(2): 1-14. |
| [4] |
范廷恩, 王海峰, 胡广义, 等. 海上油田复合砂体构型解剖方法及其应用[J]. 中国海上油气, 2018, 30(4): 102-112. FAN Ting'en, WANG Haifeng, HU Guangyi, et al. Anatomy method of composite sand body architecture in offshore oilfield and its application[J]. China Offshore Oil and Gas, 2018, 30(4): 102-112. |
| [5] |
彭达.河道砂体储层不连续性地震属性分析研究[D].四川成都: 西南石油大学, 2016. PENG Da.Study of Seismic Attributes for the Discontinuity of Channel Sandstone Reservoir[D].Southwest Petroleum University, Chengdu, Sichuan, 2016. |
| [6] |
刘洋, 王典, 刘财, 等. 基于非平稳相似性系数的构造导向滤波及断层检测方法[J]. 地球物理学报, 2014, 57(4): 1177-1187. LIU Yang, WANG Dian, LIU Cai, et al. Structure-oriented filtering and fault detection based on nonstationary similarity[J]. Chinese Journal of Geophysics, 2014, 57(4): 1177-1187. |
| [7] |
尹川, 杜向东, 赵汝敏, 等. 基于倾角控制的构造导向滤波及其应用[J]. 地球物理学进展, 2014, 29(6): 2818-2822. YIN Chuan, DU Xiangdong, ZHAO Rumin, et al. Dip steered structure oriented filter and its application[J]. Progress in Geophysics, 2014, 29(6): 2818-2822. |
| [8] |
赵凤全, 崔德育, 康婷婷, 等. 构造导向滤波技术在断裂识别中的应用[J]. 石油地球物理勘探, 2018, 53(增刊1): 214-218. ZHAO Fengquan, CUI Deyu, KANG Tingting, et al. Fault identification with structure-oriented filtering[J]. Oil Geophysical Prospecting, 2018, 53(S1): 214-218. |
| [9] |
刘传虎. 地震相干分析技术在裂缝油气藏预测中的应用[J]. 石油地球物理勘探, 2001, 36(2): 238-244. LIU Chuanhu. Application of seismic coherent analysis technology to prediction of fractured reservoir[J]. Oil Geophysical Prospecting, 2001, 36(2): 238-244. DOI:10.3321/j.issn:1000-7210.2001.02.015 |
| [10] |
苏朝光, 刘传虎, 王军, 等. 相干分析技术在泥岩裂缝油气藏预测中的应用[J]. 石油物探, 2002, 41(2): 197-201. SU Chaoguang, LIU Chuanhu, WANG Jun, et al. Application of coherence analysis technology in the prediction of fractured shale reservoirs and its effect analysis[J]. Geophysical Prospecting for Petroleum, 2002, 41(2): 197-201. DOI:10.3969/j.issn.1000-1441.2002.02.015 |
| [11] |
王怀洪, 王秀东, 田育鑫. 利用相干体技术探测煤矿微小构造方法研究[J]. 地球物理学进展, 2007, 22(5): 1642-1649. WANG Huaihong, WANG Xiudong, TIAN Yuxin. Study on the method to identify minor structure of coalmines with the coherence technology[J]. Progress in Geophysics, 2007, 22(5): 1642-1649. DOI:10.3969/j.issn.1004-2903.2007.05.047 |
| [12] |
王从镔, 龚洪林, 许多年, 等. 高分辨率相干体分析技术及其应用[J]. 地球物理学进展, 2008, 23(5): 1575-1578. WANG Congbin, GONG Honglin, XU Duonian, et al. High-resolution coherency analysis technique and its application[J]. Progress in Geophysics, 2008, 23(5): 1575-1578. |
| [13] |
胡滨. 复杂断裂精细解释技术组合及其应用[J]. 石油地球物理勘探, 2019, 54(3): 608-616. HU Bin. Multi-technique combination for the complex-fault elaborate interpretation[J]. Oil Geophysical Prospecting, 2019, 54(3): 608-616. |
| [14] |
龙旭, 武林芳. 蚂蚁追踪属性体提取参数对比试验及其在塔河四区裂缝建模中的应用[J]. 石油天然气学报, 2011, 33(5): 76-81. LONG Xu, WU Linfang. Parameter comparative experiments on ant-tracking attribute extraction and its application in fracture modeling in region 4 of Tahe Oilfield[J]. Journal of Oil and Gas Technology, 2011, 33(5): 76-81. |
| [15] |
姜晓宇, 张研, 甘利灯, 等. 花岗岩潜山裂缝地震预测技术[J]. 石油地球物理勘探, 2020, 55(3): 694-704. JIANG Xiaoyu, ZHANG Yan, GAN Lideng, et al. Seismic techniques for predicting fractures in granite buried hills[J]. Oil Geophysical Prospecting, 2020, 55(3): 694-704. |
| [16] |
Bahorich M, Farmer S. 3-D seismic discontinuity for faults and stratigraphic features; the coherence cube[J]. The Leading Edge, 1995, 14(10): 1053-1058. DOI:10.1190/1.1437077 |
| [17] |
Israel C, Ronald R C. Local discontinuity measures for 3-D seismic data[J]. Geophysics, 2002, 67(6): 1933-1945. DOI:10.1190/1.1527094 |
| [18] |
周艳辉, 高静怀, 陈文超. 检测地震不连续性结构的多分辨局部结构熵算法[J]. 西安交通大学学报, 2008, 42(2): 226-230. ZHOU Yanhui, GAO Jinghuai, CHEN Wenchao. On the method of multi-resolution local structural entropy for enhancing local discontinuities of seismic data[J]. Journal of Xi'an Jiaotong University, 2008, 42(2): 226-230. DOI:10.3321/j.issn:0253-987X.2008.02.022 |
| [19] |
Luo Y, Marhoon M. Edge-preserving smoothing and applications[J]. The Leading Edge, 2002, 21(2): 136-158. DOI:10.1190/1.1452603 |
| [20] |
李楠, 王龙颖, 黄胜兵, 等. 利用高清蚂蚁体精细解释复杂断裂带[J]. 石油地球物理勘探, 2019, 54(1): 182-190. LI Nan, WANG Longying, HUANG Shengbing, et al. 3D seismic fine structural interpretation in complex fault zones based on the high-definition ant-tracking attribute volume[J]. Oil Geophysical Prospecting, 2019, 54(1): 182-190. |
| [21] |
刘海燕.地震数据梯度一致性与不同数学算法结合的断层检测技术[D].吉林长春: 吉林大学, 2016. LIU Haiyan.Fault Detection Technology Using Seismic Data Gradient Coherence Combined with Different Mathematical Algorithms[D].Jinlin University, Changchun, Jinlin, 2016. |



 张晶玉, 北京市朝阳区太阳宫南街6号院中海油大厦A座1201室, 100028。Email:
张晶玉, 北京市朝阳区太阳宫南街6号院中海油大厦A座1201室, 100028。Email: