② 中国石化石油勘探开发研究院, 北京 100083
② Research Institute of Petroleum Exploration and Development, SINOPEC, Beijing 100083, China
富有机质页岩、泥岩是近年来油气勘探开发的热点目标,常规地震资料解释、AVO反演等仍是富有机质岩石“甜点”预测中应用最广泛的技术。作为井震结合、叠前反演、脆性因子计算及应力评价的重要基础数据之一,精确的横波速度对有效识别页岩“甜点”具有重要作用[1]。目前,针对砂岩、碳酸盐岩储层的岩石物理横波速度预测方法[2-5]较为成熟,而针对富有机质岩石的相关研究较少。富有机质岩石因含有一定的有机质(干酪根)成分而区别于砂岩、碳酸盐岩储层。此外,部分富有机质岩石表现为低孔隙度,如Bakken页岩[6];也有一些表现为中—高孔隙度,如Monterey页岩[6]。有机质的弹性特征与流体近似,与矿物差别较大,例如:盐水的体积模量为2.2GPa、剪切模量为0、密度为1.03g/cm3,黏土的体积模量是21GPa、剪切模量是9GPa、密度是2.55g/cm3,而干酪根的体积模量为2.9GPa、剪切模量为2.7GPa、密度为1.30g/cm3[7]。虽然干酪根与流体的体积模量、剪切模量和密度数值差别较小,但是两者有本质不同,即干酪根是具有剪切性的固体,而流体不具有剪切性[1]。因此,在构建富有机质岩石的物理模型过程中,需谨慎考虑干酪根的描述方式。
岩石中的孔隙形态十分复杂[8-9],对岩石速度影响极大:球形孔隙(如印模孔)使岩石速度变高;扁状孔隙(如裂缝)使岩石速度变低[2, 4]。据此认识,学者针对砂岩、碳酸盐岩构建了多个描述孔隙形态、孔隙度与速度之间关系的函数(岩石物理模型),并以此为基础进行横波速度预测[10-13]。在针对富有机质岩石的研究过程中,学者们参考砂岩、碳酸盐岩的岩石物理建模思路进行了诸多有益的探索[14-18]。对富有机质岩石的电子显微镜(BSE-SEM)扫描观察显示,干酪根以斑块状分布于岩石矿物颗粒间, 其形态多种多样[19-21],这种特征使岩石的弹性参数分散。Sayers[14]认为每个富有机质岩石样品中的干酪根形态不同,假设干酪根为硬币形状包含物,利用硬币的纵横比表征岩石中干酪根的形态变化,该方法能有效解释具有低—超低孔隙度、高干酪根含量特征的Bakken页岩的弹性参数分散现象。但由于只考虑干酪根及其形态的作用,忽略了孔隙及其形状对岩石速度的影响,因此上述方法在低—超低孔隙度岩石中应用效果较好,在孔隙度稍高的岩石中则无法应用。董宁等[15]利用SCA-DEM模型把孔隙加入岩石基质中,再利用固体替代理论将干酪根加入含孔隙岩石中,这种方法考虑了孔隙形状,但是没有考虑干酪根颗粒的形态,且计算过程中将干酪根与孔隙分步加入岩石中,因此忽略了干酪根与孔隙之间的相互作用。Guo等[16]将干酪根和孔隙看作包含物,基于SCA岩石物理模型将干酪根与矿物、孔隙结合构建富有机质岩石的物理模型,该方法将干酪根等效为一种固定形态的颗粒,将孔隙假设为多种形态,虽然考虑了孔隙形态的复杂性,却没有考虑不同干酪根颗粒之间形态差异。与Guo等[16]的方法类似,Liu等[18]将干酪根作为固定形态的包含物,利用DEM模型将干酪根与矿物、孔隙结合构建富有机质岩石的物理模型,通过试算、统计误差给定整个井段研究目标的固定干酪根颗粒形态参数。在富有机质岩石的物理模型构建及速度预测研究中,如何有效兼顾孔隙形状及干酪根形态因素的影响,关于这个问题学界研究较少。
本文基于Kuster-Toksöz(KT)模型构建了一种富有机质岩石的横波速度预测方法,该方法利用硬币形状包含物的纵横比表征干酪根形态和孔隙形状,在纵波速度约束下同时求算岩石中的等效干酪根颗粒和等效孔隙纵横比,在反演参数基础上预测横波速度。因针对每个样点求算得到干酪根颗粒形态和孔隙形状,提高了岩石物理模型对富有机质岩石的描述精度,从而降低了横波速度预测误差。需要说明的是,本文方法是预测垂直于页岩层理的速度,在直井中可与目前富有机质岩石“甜点”预测中广泛应用的地震资料解释、叠前叠后反演等各向同性方法匹配较好,在斜井中则需要先进行斜井的速度各向异性校正[22]。
1 基本原理 1.1 KT岩石物理模型等效介质岩石物理模型,如KT模型[8]、微分等效介质理论[23]、自洽模型[7]等,认为岩石的弹性模量不仅与岩石基质矿物、包含物的种类和含量有关,还与包含物的几何形态有关。其中,KT模型给出了实验室高频条件下,基质矿物中包含多种类型包含物时等效介质的体积模量和剪切模量的计算公式[7-8]
| $ ({K_{{\rm{KT}}}} - {K_{\rm{m}}})\frac{{3{K_{\rm{m}}} + 4{G_{\rm{m}}}}}{{3{K_{{\rm{KT}}}} + 4{G_{\rm{m}}}}} = \sum\limits_{i = 1}^N {{x_i}} ({K_i} - {K_{\rm{m}}}){P^{{\rm{m}}i}} $ | (1) |
| $ ({G_{{\rm{KT}}}} - {G_{\rm{m}}})\frac{{{G_{\rm{m}}} + {\zeta _{\rm{m}}}}}{{{G_{{\rm{KT}}}} + {\zeta _{\rm{m}}}}} = \sum\limits_{i = 1}^N {{x_i}} ({G_i} - {G_{\rm{m}}}){Q^{{\rm{m}}i}} $ | (2) |
式中:K和G是体积模量和剪切模量;
硬币形状包含物的形状因子为[24]
| $ {P^{{\rm{m}}i}} = \frac{{{K_{\rm{m}}} + \frac{4}{3}{G_i}}}{{{K_i} + \frac{4}{3}{G_i} + {\rm{ \mathsf{ π} }}{\alpha _i}{B_i}}} $ | (3) |
| $ \begin{array}{l} {Q^{{\rm{m}}i}} = \frac{1}{5}\left[ {1 + \frac{{8{G_{\rm{m}}}}}{{8{G_i} + {\rm{ \mathsf{ π} }}{\alpha_i}({G_{\rm{m}}} + 2{\beta _{\rm{m}}})}} + } \right.\\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2\frac{{{K_i} + \frac{2}{3}({G_i} + {G_{\rm{m}}})}}{{{K_i} + \frac{4}{3}{G_i} + {\rm{ \mathsf{ π} }}{\alpha _i}{\beta _{\rm{m}}}}}} \right] \end{array} $ | (4) |
式中:
在求算低频条件下饱和流体岩石的弹性模量时,一般使用KT模型求算干岩石的弹性模量,再用Gassmann方程[25]计算饱和流体岩石的弹性模量。
1.2 富有机质岩石的等效介质模型将富有机质岩石等效为由岩石基质、干酪根颗粒、孔隙(干孔隙或饱和流体孔隙)组成的混合物(图 1)。把干酪根和孔隙分别等效为随机分布的、具有单一纵横比的硬币形状固体颗粒和孔隙,其形态由硬币形状包含物的纵横比表征:当纵横比接近1时,颗粒形态接近球形;当纵横比接近0时,颗粒形态为裂缝形。设等效干酪根颗粒纵横比为αk、等效孔隙纵横比为αp,N=2,则式(1)、式(2)可写为
| $ \begin{array}{l} ({K_{{\rm{KT}}}} - {K_{\rm{m}}})\frac{{3{K_{\rm{m}}} + 4{G_{\rm{m}}}}}{{3{K_{{\rm{KT}}}} + 4{G_{\rm{m}}}}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {V_{\rm{k}}}({K_{\rm{k}}} - {K_{\rm{m}}}){P^{{\rm{mk}}}} + \varphi ({K_{\rm{f}}} - {K_{\rm{m}}}){P^{{\rm{mf}}}} \end{array} $ | (5) |
| $ \begin{array}{*{20}{l}} {({G_{{\rm{KT}}}} - {G_{\rm{m}}})\frac{{{G_{\rm{m}}} + {\zeta _{\rm{m}}}}}{{{G_{{\rm{KT}}}} + {\zeta _{\rm{m}}}}}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {V_{\rm{k}}}({G_{\rm{k}}} - {G_{\rm{m}}}){Q^{{\rm{mk}}}} + \varphi ( - {G_{\rm{m}}}){Q^{{\rm{mf}}}}} \end{array} $ | (6) |
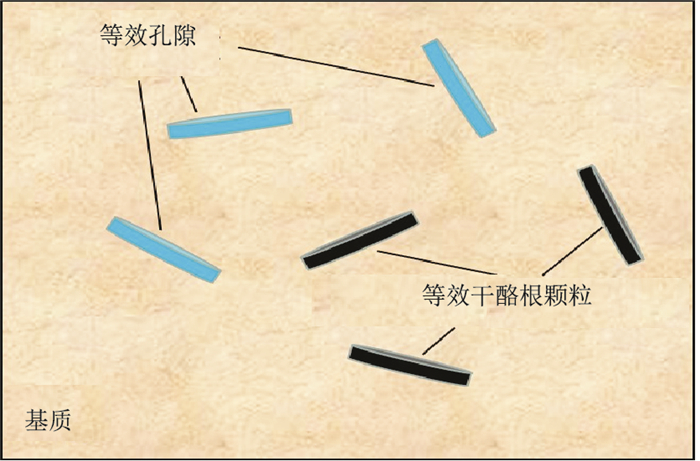
|
图 1 富有机质岩石的等效介质模型示意图 |
式中:Vk指干酪根的体积含量;φ指孔隙度;Kk、Gk指干酪根的体积模量和剪切模量;Kf指流体的体积模量;Pmk、Qmk指等效干酪根颗粒的形状因子,是关于αk的函数;Pmf、Qmf指等效孔隙的形状因子,是关于αp的函数。
得到弹性模量后,可求取岩石的纵、横波速度
| $ {v_{\rm{P}}} = \sqrt {\frac{{{K_{{\rm{KT}}}} + \frac{4}{3}{G_{{\rm{KT}}}}}}{\rho }} $ | (7) |
| $ {v_{\rm{S}}} = \sqrt {\frac{{{G_{{\rm{KT}}}}}}{\rho }} $ | (8) |
式中岩石密度ρ=ρkVk+ρfφ +ρm(1-Vk-φ),其中ρk、ρf、ρm分别是干酪根、流体、矿物基质的密度。
图 2是利用式(5)~式(8)得出的低频条件下饱和盐水岩石的纵、横波速度随αk、αp变化的规律。该算例参考Monterey页岩的孔隙度与干酪根含量。假设φ=0.08,Vk=0.08,背景基质为泥质,其体积模量、剪切模量分别取Km=39.54GPa、Gm=25.68GPa,密度取ρm=2.64g/cm3;干酪根颗粒的体积模量、剪切模量分别取Kk=2.9GPa、Gk=2.7GPa,密度取ρk=1.30g/cm3;假设孔隙中含盐水,其体积模量Kf=2.65GPa,密度ρf=0.99g/cm3,令αk和αp均在0.001~1.000之间变化。图 2显示等效干酪根颗粒纵横比和等效孔隙纵横比与岩石速度之间的关系是非线性的。抽取图 2中的部分数据并在图 3中显示。由图可见,在相同干酪根含量和孔隙度的情况下,等效干酪根颗粒和等效孔隙纵横比都会对速度造成较大影响,且纵横比越接近于1,速度越大;等效孔隙纵横比对速度的影响程度大于等效干酪根纵横比,原因在于干酪根的体积模量大于盐水,以及干酪根的剪切模量不为0。
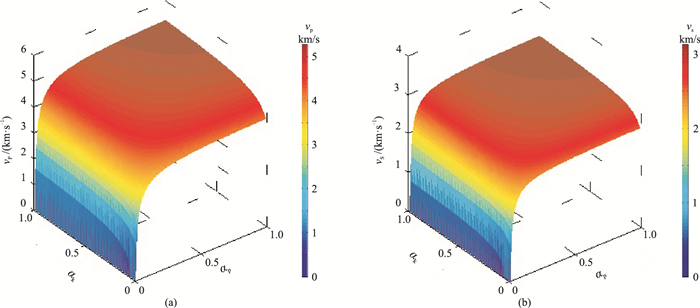
|
图 2 纵(a)、横(b)波速度随等效干酪根颗粒纵横比αk、等效孔隙纵横比αp变化曲面 |

|
图 3 纵(a)、横(b)波速度随等效干酪根颗粒纵横比αk、等效孔隙纵横比αp变化曲线 抽取图 2中几组数据 |
式(5)和式(6)表明,富有机质岩石的弹性模量不仅是矿物基质、干酪根、孔隙流体体积分数及其弹性模量的函数,还与岩石的等效干酪根颗粒纵横比αk以及等效孔隙纵横比αp密切相关。将式(5)、式(6)代入式(7)、式(8)中可以建立vP、vS与αk、αp的非线性关系式[vP, vS]=f(αk,αp),利用此式,既可根据岩石组分体积含量、弹性参数、αk、αp正演计算岩石的纵、横波速度,也可以根据岩石的纵波速度(或纵、横波速度联合)反演αk、αp。利用式(5)~式(8)反演求取αk、αp时的目标函数为
| $ \begin{array}{*{20}{l}} {{\rm{OF}} = {W_{\rm{p}}}|({v_{{\rm{Pt}}}} - {v_{{\rm{Pc}}}})|/{v_{{\rm{Pt}}}} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {W_{\rm{s}}}|({v_{{\rm{St}}}} - {v_{{\rm{Sc}}}})|/{v_{{\rm{St}}}}} \end{array} $ | (9) |
该式是关于αk、αp的二元非线性函数。式中:vPt、vSt为测量的纵、横波速度;vPc、vSc为预测的纵、横波速度;WP、WS为加权因子,且满足WP+WS=1.0。当只有纵波资料时,WP=1.0,WS=0;同时有纵、横波资料时,可取WP=WS=0.5。
使用Vernik等[6]的一个实测数据点为例说明求解目标函数OF的过程。该样点的实测孔隙度φ=0.043,Vk=0.182,纵、横波速度分别为vPt=3.70km/s、vSt=2.43km/s,密度为ρ=2.43g/cm3;背景基质和干酪根的参数与图 2一致,令αk和αp都在0.001~1.000之间变化。
图 4为WP=1.0和WP=0.5时的两种目标函数曲线,其中,vPc和vSc根据式(5)~式(8)求得。图 4显示在定义域内目标函数表现为二维曲面,极值点位于蓝色凹槽内。将图 4所示的数据在αk、αp两个方向上取极小值并在图 5显示,可见当WP=1.0和WP=0.5时,目标函数OF的形态基本一致;OF在0.001~1.000内的局部极值点[αk,αp]可取多个;OF的全局极值点大约为[αk,αp]=[0.035,0.070],说明利用纵波速度约束求解目标函数与利用纵、横波速度联合约束求解目标函数的结果接近,也从侧面说明利用纵波速度求算αk、αp,进而预测横波速度的方法是可行的。本文采用一种非线性全局寻优粒子群算法——混沌量子粒子群算法[26]求解式(9)。当缺乏横波测井资料时,可由纵波反演求取αk、αp,再将αk、αp代入式(5)~式(8)计算横波速度;反之,利用纵、横波联合反演求得的αk、αp计算纵、横波速度,并可以用来评估测量速度的质量。由于实际测量的纵、横波速度数据常存在噪声,特别是在井孔扩径层段,声波时差曲线出现周波跳跃,横波速度受扩径的影响更大,这种情况下实测数据不准确,需要进行必要的校正[27]。
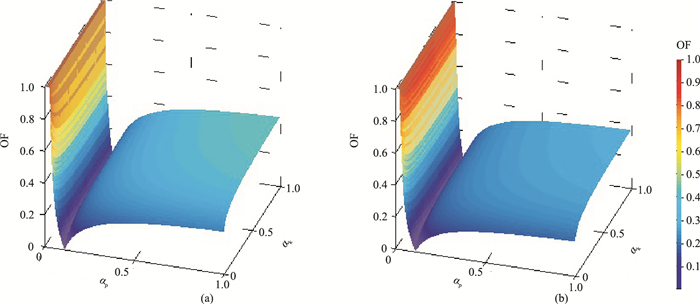
|
图 4 反演目标函数随αk、αp的变化曲面 (a)纵波速度约束反演(Wp=1.0, Ws=0)目标函数;(b)纵、横波速度联合约束反演(Wp=0.5, Ws=0.5)目标函数 |

|
图 5 纵波速度约束与纵、横波速度联合约束目标函数随αp(a)和αk(b)的变化曲线对比 |
使用Vernik等[6]在高频条件测量到的三组富有机质岩石数据(图 6)进行测试。这些数据在常温、有效压力70MPa条件下测得,样品为干岩石。由图 6可见,Bakken页岩的孔隙度为0.0104~0.0197,干酪根含量为0.122~0.423,属低孔、高干酪根含量页岩;Bazhenov页岩的孔隙度和干酪根含量分别为0.0199~0.0420、0.066~0.207,属低孔、高干酪根含量页岩,但其孔隙度高于Bakken页岩,干酪根含量低于Bakken页岩;Monterey页岩的孔隙度和干酪根含量分别为0.043~0.309、0.016~0.363,属高孔页岩,干酪根含量变化较大。
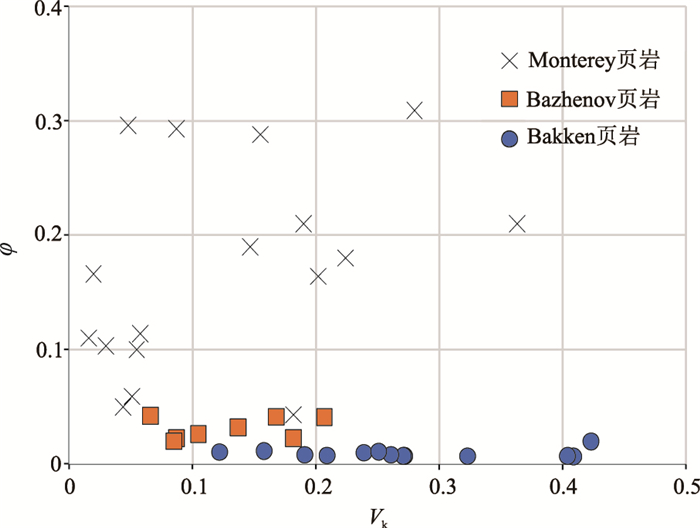
|
图 6 实测Bakken页岩、Bazhenov页岩、Monterey页岩的孔隙度与干酪根含量交会图 |
利用本文方法对上述三组样品进行试算。图 7为使用纵波速度约束和纵、横波速度联合约束下得到的预测与实测横波速度交会图。由图可见,数据均匀分布于对角线(图中红色线)附近,说明预测结果与实测结果吻合度较高。
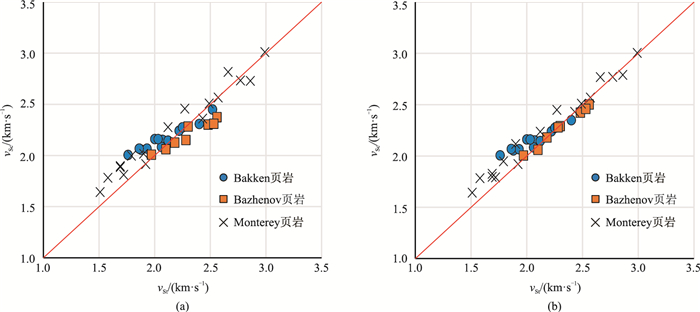
|
图 7 预测与实测横波速度交会图 (a)纵波速度约束;(b)纵、横波速度联合约束 |
使用预测与实测速度之间的相对误差平均值MAE、均方根误差RMSE、相关系数R2等三项指标定量评价预测结果的可靠性
| $ {\rm{MAE}} = \frac{1}{A}\sum\limits_{i = 1}^A {\left| {\frac{{{M_i} - {E_i}}}{{{M_i}}}} \right|} $ | (10) |
| $ {\rm{RMSE}} = \sqrt {\frac{1}{A}\sum\limits_{i = 1}^A {{{({M_i} - {E_i})}^2}} } $ | (11) |
| $ {R^2} = 1 - \frac{{\sum\limits_{i = 1}^A {{{({M_i} - {E_i})}^2}} }}{{\sum\limits_{i = 1}^A {{{({M_i} - {E_{\bar i}})}^2}} }} $ | (12) |
式中:A是样品数量;Mi是测量数据;Ei是预测数据;Ei是预测数据的平均值。
表 1给出了利用纵波速度约束和利用纵、横波速度联合约束所得横波速度的误差统计结果,可以看到:①针对三组岩样,利用纵波速度约束求算的结果与实测数据之间误差小,说明利用纵波资料反演αk和αp,进而预测横波速度的方法是可行的;②纵、横波速度联合约束反演所得结果的统计误差优于纵波单独约束,其原因在于横波速度的参与。
|
|
表 1 纵波速度约束与纵、横波速度联合约束所得横波速度与实测横波速度的误差统计 |
图 8a为根据纵波速度约束和纵、横波速度联合约束反演的αk与干酪根含量的交会图,图 8b为反演的αp与孔隙度的交会图。结果表明:利用纵波速度约束反演和利用纵、横波速度联合约束反演所得结果较为接近,说明单独利用纵波速度约束反演αp和αk是可行的。此外,对纵、横波速度联合约束反演的结果进行分析发现:①Bakken页岩的αk均小于0.2,而αp均大于0.4,说明Bakken页岩的等效干酪根颗粒以接近扁平的近裂缝形态为主,而其孔隙则接近球形;②Bazhenov岩样中,4个样品的αk在0.1以下,4个样品的αk为0.4~0.7,6个样品的αp小于0.1,2个样品的αp大于0.9,说明其等效干酪根颗粒和孔隙同时存在接近裂缝的形态和接近球形的形态;③Monterey岩样的αk为0~1.0,αp为0~0.8,说明其等效干酪根颗粒和孔隙也存在同时接近裂缝的形态和接近球形的形态;④对三个区块的页岩整体考虑,可以发现一个总趋势:干酪根含量高的页岩αk小;孔隙度大的页岩αp小。
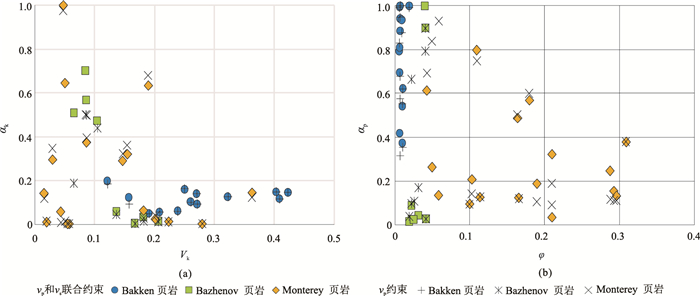
|
图 8 根据纵波速度约束和纵、横波速度联合约束反演的等效干酪根颗粒纵横比与干酪根含量的交会图(a)及等效孔隙纵横比与孔隙度的交会图(b) |
将本文方法与文献中的三种单一参数自适应方法进行对比,以说明同时反演αk、αp在横波速度预测中的作用。三种单一参数方法说明如下。
方法1将干酪根作为基质矿物的一种(不考虑干酪根颗粒的形态),将孔隙等效为硬币形状且令孔隙纵横比自适应变化。计算流程简述为:①通过Voigt-Reuss-Hill(VRH)平均公式[7]将基质矿物与干酪根混合;②利用KT模型将具有可变纵横比的孔隙加入岩石基质中,在纵波速度约束下求算孔隙纵横比;③将计算得到的孔隙纵横比代入KT模型,计算富有机质岩石的弹性模量,进而求算速度。
方法2与本文流程近似。将干酪根与孔隙等效为硬币状颗粒,令孔隙纵横比固定为常数(通过在有横波资料的井中做实验标定确定),令干酪根纵横比自适应。计算流程简述为:①利用KT模型将具常数纵横比的孔隙和具可变纵横比的干酪根颗粒加入岩石基质中,在纵波速度约束下求算等效干酪根纵横比;②将计算得到的等效干酪根纵横比和常数孔隙纵横比代入KT模型,计算富有机质岩石的弹性模量,进而求算速度。该方法赋予所有岩样以相同的干酪根颗粒纵横比,没有考虑不同样点间干酪根颗粒可能存在差别。
方法3与方法2流程近似,不同点在于令干酪根纵横比固定为常数,而令孔隙纵横比自适应。其计算流程为:①利用KT模型将具有常数纵横比的等效干酪根颗粒和具有可变纵横比的孔隙加入岩石基质中,在纵波速度约束下求算等效孔隙纵横比;②将计算得到的等效孔隙纵横比和常数等效干酪根纵横比代入KT模型,计算等效介质岩石弹性模量,进而求算速度。
这种方法赋予所有岩样以相同的孔隙纵横比,没有考虑不同样品之间孔隙可能存在差别。
利用图 6所示数据进行试算。在此例中,对于方法2和方法3,使每组岩样的固定参数在0~1之间以0.05的步长变化,在纵波速度的约束下求取最优可变参数。图 9为利用方法2、方法3预测的横波速度误差统计参数随αk或αp的变化,由图可见:对于方法2,当孔隙纵横比分别为0.05、0.35、0.10时,通过干酪根纵横比的自适应可使三组页岩的预测横波速度误差分别取得最优值;对于方法3,当干酪根纵横比分别为0.10、0.05、0.05时,通过孔隙纵横比的自适应可使得三组页岩的预测横波速度的误差分别取得最优值。说明要精准求取速度,不同页岩选取的参数是不同的,这也证明了同时反演两个参数进行横波速度预测的必要性。
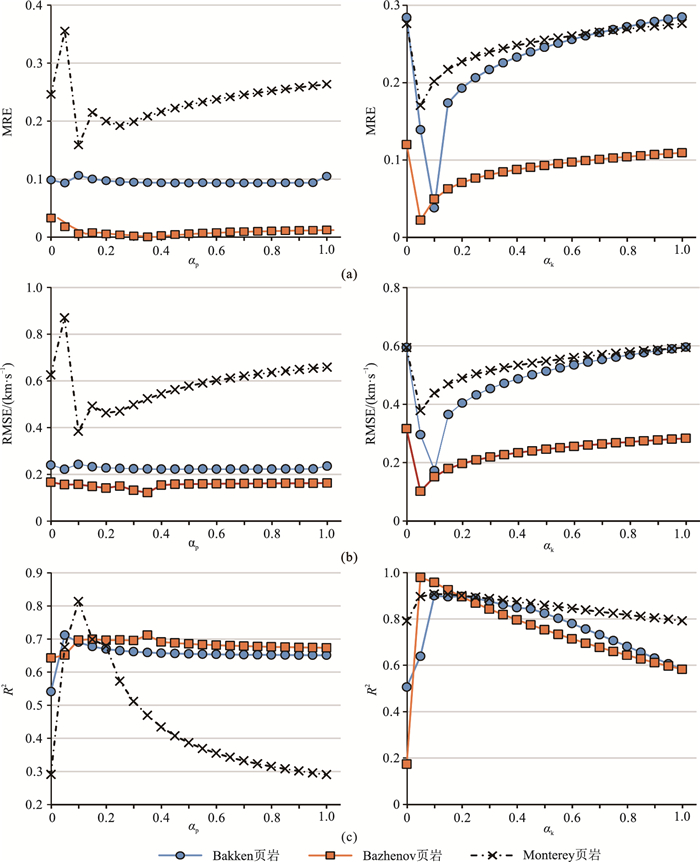
|
图 9 利用方法2(左)、方法3(右)预测的横波速度与实测速度的误差统计参数随αk或αp的变化 (a)MRE;(b)RMSE;(c)R2 |
表 2为三种单一参数自适应方法和本文方法预测横波速度的误差对比,其中方法2和方法3的αk或αp取图 9中的最优值。可以看出,相比三种单一参数自适应方法,本文方法的统计参数有明显改善。
|
|
表 2 四种方法预测横波速度与实测速度的误差统计 |
将本文方法应用到湖北省建南构造页岩气区块A井侏罗系东岳庙段。图 10展示了目的层段的岩性录井、储层位置、测井解释结果、速度预测结果及孔隙与干酪根纵横比计算结果。利用多矿物测井解释方法[28]估算孔隙度、矿物含量和含气饱和度,解释所得矿物主要为石英、长石、方解石、黏土。计算过程中使用的岩石组分的弹性参数和密度如表 3所示,利用CARBOLOG方法[29]求算干酪根的体积分数,利用VRH平均公式[7]计算岩石基质的体积模量和剪切模量,利用Wood方程[7]计算混合流体的体积模量。将矿物、干酪根的体积含量、孔隙度、流体饱和度数据引入岩石物理模型,在纵波速度的约束下反演αk和αp,进而预测横波速度。

|
图 10 建南构造页岩气区域A井侏罗系东岳庙段富有机质泥页岩速度预测值与实测值对比 |
由图 10可见,四种方法预测的结果与实测数据趋势基本一致,而新方法所得结果吻合度最高。表 4为四种方法在实际资料中应用所得结果误差统计,表明新方法预测结果优于其他三种对比方法。
|
|
表 4 四种方法应用于实际资料时的误差统计 |
本文提出一种根据纵波速度同时反演富有机质岩石中等效干酪根颗粒纵横比和等效孔隙纵横比,进而开展横波速度预测的方法。该方法利用KT模型建立矿物、干酪根、孔隙、流体、干酪根颗粒与孔隙纵横比之间的数学关系,使用非线性全局寻优算法反演等效干酪根颗粒纵横比和等效孔隙纵横比,将反演得到的两种纵横比代入岩石物理模型中计算横波速度。通过实验室与实际测井资料的应用,证明本文方法预测的结果与实测数据吻合度较高。将该方法预测结果与其他三种单一自适应参数方法进行对比,结果显示本文方法预测横波速度的统计参数具有明显优势,证明了该方法的可行性及可靠性。
| [1] |
刘致水, 孙赞东, 董宁, 等. 一种修正的Kuster-Toksöz岩石物理模型及应用[J]. 石油地球物理勘探, 2018, 53(1): 113-121. LIU Zhishui, SUN Zandong, DONG Ning, et al. A modified Kuster-Toksöz rock physics model and its application[J]. Oil Geophysical Prospecting, 2018, 53(1): 113-121. |
| [2] |
Xu S, White R E. A new velocity model for clay-sand mixtures[J]. Geophysical Prospecting, 1995, 43(1): 91-118. DOI:10.1111/j.1365-2478.1995.tb00126.x |
| [3] |
Liu Z S, Sun Z D. The differential Kuster-Toksöz rock physics model for predicting S-wave velocity[J]. Journal of Geophysics & Engineering, 2015, 12(5): 839-848. |
| [4] |
Xu S, Payne M. Modeling elastic properties in carbonate rocks[J]. The Leading Edge, 2009, 28(1): 66-74. DOI:10.1190/1.3064148 |
| [5] |
张广智, 李呈呈, 印兴耀, 等. 基于修正Xu-White模型的碳酸盐岩横波速度估算方法[J]. 石油地球物理勘探, 2012, 47(5): 717-722. ZHANG Guangzhi, LI Chengcheng, YIN Xingyao, et al. A shear velocity estimation method for carbonate rocks based on the improved Xu-White model[J]. Oil Geophysical Prospecting, 2012, 47(5): 717-722. |
| [6] |
Vernik L, Liu X Z. Velocity anisotropy in shales:a petrophysical study[J]. Geophysics, 1997, 62(2): 521-532. DOI:10.1190/1.1444162 |
| [7] |
Mavko G, Mukerji T, Dvorikin J. The Rock Physics Handbook: Tools for Seismic Analysis in Porous Media[M]. Cambridge University Press, Cambridge, 1998.
|
| [8] |
Kuster G T, Toksöz M N. Velocity and attenuation of seismic waves in two-phase media[J]. Geophysics, 1974, 39(5): 587-618. DOI:10.1190/1.1440450 |
| [9] |
李宏兵, 张佳佳. 多重孔岩石微分等效介质模型及其干燥情形下的解析近似式[J]. 地球物理学报, 2014, 57(10): 3422-3430. LI Hongbing, ZHANG Jiajia. A differential effective medium model of multiple porosity rock and its analytical approximations for dry rock[J]. Chinese Journal of Geophysics, 2014, 57(10): 3422-3430. DOI:10.6038/cjg20141028 |
| [10] |
张秉铭, 刘致水, 刘俊州, 等. 鄂尔多斯盆地北部复杂碳酸盐岩横波速度预测研究[J]. 石油物探, 2017, 56(3): 328-337. ZHANG Bingming, LIU Zhishui, LIU Junzhou, et al. An improved S-wave velocity prediction method for complex carbonate reservoir in North Ordos Basin, China[J]. Geophysical Prospecting for Petroleum, 2017, 56(3): 328-337. DOI:10.3969/j.issn.1000-1441.2017.03.003 |
| [11] |
刘雅杰, 李生杰, 王永刚, 等. 横波预测技术在苏里格气田储层预测中的应用[J]. 石油地球物理勘探, 2016, 51(1): 165-172. LIU Yajie, LI Shengjie, WANG Yonggang, et al. Re-servoir prediction based on shear wave in Sulige Gas Field[J]. Oil Geophysical Prospecting, 2016, 51(1): 165-172. |
| [12] |
蔡涵鹏, 贺振华, 唐湘蓉, 等. 碳酸盐岩孔隙结构影响分析和等效孔隙结构参数计算[J]. 石油物探, 2013, 52(6): 566-572. CAI Hanpeng, HE Zhenhua, TANG Xiangrong, et al. Impact analysis of pore structure and calculation of equivalent pore structure parameters for carbonate[J]. Geophysical Prospecting for Petroleum, 2013, 52(6): 566-572. |
| [13] |
郭栋, 印兴耀, 吴国忱, 等. 横波速度计算方法与应用[J]. 石油地球物理勘探, 2007, 42(5): 535-538. GUO Dong, YIN Xingyao, WU Guochen, et al. Computational approach of S-wave velocity and application[J]. Oil Geophysical Prospecting, 2007, 42(5): 535-538. DOI:10.3321/j.issn:1000-7210.2007.05.009 |
| [14] |
Sayers C M. The effect of kerogen on the elastic anisotropy of organic-rich shale[J]. Geophysics, 2013, 78(2): D65-D74. DOI:10.1190/geo2012-0309.1 |
| [15] |
董宁, 霍志周, 孙赞东, 等. 泥页岩岩石物理建模研究[J]. 地球物理学报, 2014, 57(6): 1990-1998. DONG Ning, HUO Zhizhou, SUN Zandong, et al. An investigation of rock physics model for shale[J]. Chinese Journal of Geophysics, 2014, 57(6): 1990-1998. |
| [16] |
Guo Z, Li X, Liu C, et al. A shale rock physics model for analysis of brittleness index, mineralogy and porosity in the Barnett shale[J]. Journal of Geophysics and Engineering, 2013, 10(2): 1742-2132. |
| [17] |
胡起, 陈小宏, 李景叶. 基于单孔隙纵横比模型的有机页岩横波速度预测方法[J]. 地球物理学进展, 2014, 29(5): 2388-2394. HU Qi, CHEN Xiaohong, LI Jingye. Shear velocity prediction for organic shales based on the single aspect ratio model[J]. Progress in Geophysics, 2014, 29(5): 2388-2394. |
| [18] |
Liu Z S, Sun S Z. New brittleness indexes and their application in shale/clay gas reservoir prediction[J]. Petroleum Exploration and Development, 2015, 42(1): 117-124. |
| [19] |
Leo A. Understanding organic matter structural changes with increasing thermal maturity from oil shale plays through SEM imaging[C]. Unconventional Resources Technology Conference (URTeC), San Antonio, Texas, USA, 2016.
|
| [20] |
Mark E, Goergen E, Jernigen J. Mapping of organic matter distribution on the centimeter scale with nanometer resolution[C]. Unconventional Resources Te-chnology Conference (URTeC), Denver, Colorado, USA, 2014.
|
| [21] |
Adam M, Waruntorn K, Tiziana V. A multiscale metho-dology for the analysis of velocity anisotropy in organic-rich shale[J]. Geophysics, 2015, 80(4): C73-C88. DOI:10.1190/geo2014-0192.1 |
| [22] |
Hornby B E, John M H, Donald W I. Anisotropy correction for deviated-well sonic logs:Application to seismic well tie[J]. Geophysics, 2003, 68(2): 464-471. DOI:10.1190/1.1567212 |
| [23] |
Norris A N. A differential scheme for the effective mo-duli of composites[J]. Mechanics of Materials, 1985, 4(6): 1-16. |
| [24] |
Berryman J G. Mixture Theories for Rock Properties//A Handbook of Physical Constants[M]. American Geophysical Union, Washington D C, 1995, 205-228.
|
| [25] |
Gassmann F. Elastic waves through a packing of spheres[J]. Geophysics, 1951, 16(4): 673-685. DOI:10.1190/1.1437718 |
| [26] |
刘立峰, 孙赞东, 韩剑发, 等. 量子粒子群模糊神经网络碳酸盐岩流体识别方法研究[J]. 地球物理学报, 2014, 57(3): 991-1000. LIU Lifeng, SUN Zandong, HAN Jianfa, et al. A carbonate fluid identification method based on quantum particle swarm fuzzy neural network[J]. Chinese Journal of Geophysics, 2014, 57(3): 991-1000. |
| [27] |
李宏兵, 张佳佳, 姚逢昌. 岩石的等效孔隙纵横比反演及其应用[J]. 地球物理学报, 2013, 56(2): 608-615. LI Hongbing, ZHANG Jiajia, YAO Fengchang. Inversion of effective pore aspect ratios for porous rocks and its applications[J]. Chinese Journal of Geophy-sics, 2013, 56(2): 608-615. |
| [28] |
雍世和, 张超谟. 测井数据处理与综合解释[M]. 山东东营: 中国石油大学出版社, 2002: 313-320. YONG Shihe, ZHANG Chaomo. Logging Data Processing and Comprehensive Interpretation[M]. Shandong, Dongying: China University of Petroleum Press, 2002: 313-320. |
| [29] |
刘俊民, 彭平安, 黄开权, 等. 改进评价生油岩有机质含量的CARBOLOG法及其初步应用[J]. 地球化学, 2008, 37(6): 581-586. LIU Junmin, PENG Anping, HUANG Kaiquan, et al. An improvement of CARBOLOG technique and its preliminary application to evaluating organic carbon content of source rocks[J]. Geochimica, 2008, 37(6): 581-586. DOI:10.3321/j.issn:0379-1726.2008.06.008 |



 刘致水, 陕西省西安市雁塔区雁塔北路南段126号长安大学地质工程与测绘学院地球物理系, 710061。Email:
刘致水, 陕西省西安市雁塔区雁塔北路南段126号长安大学地质工程与测绘学院地球物理系, 710061。Email: