② 东方地球物理公司西南物探分公司, 四川成都 610213
② Southwest Branch, BGP Inc., CNPC, Chengdu, Sichuan 610213, China
三维三分量(3D3C)VSP数据包含丰富的地震波场信息,实现了全方位观测,克服了2D-VSP成像区域有一定角度限制的不足。3D3C-VSP的采集数据比地面地震数据具有更高的信噪比和分辨率,且含有可靠的深度信息,因此,3D3C-VSP技术能够获得更为精确的地下地质体三维成像剖面、地下岩性信息、物性参数分布[1-3]。为了充分发挥3D3C-VSP技术的优势,除了获得高品质的3D3C-VSP原始数据外,目前急需发展适用于3D3C-VSP的PP波和PS波高精度成像方法。
对上行PP波、PS波的高精度成像是3D3C-VSP技术应用成功的关键。3D3C-VSP成像技术主要有VSP-CDP叠加法和偏移成像法:VSP-CDP叠加法[4-7]通过射线追踪求取反射点进行叠加,方法原理简单,但不适应于复杂地下结构。因此偏移成像法更常用,主要有Kirchhoff积分偏移法[8]、单程波波动方程成像方法、双程波波动方程成像方法[9-13]。Kirchhoff积分偏移法[14-15]由于焦散和多路径等问题,在复杂构造区难以获得满意的成像效果。近几年波动方程成像方法得到了业界普遍认可,特别是基于双程波波动方程的叠前逆时偏移技术[16-19],不受速度横向变化限制,能够对反射波、回折波、多次波等各类波进行成像,具有成像精度高的优点。但叠前逆时深度偏移方法受局限于速度模型的精度,且计算效率较低,未得到广泛应用。
速度模型对3D3C-VSP成像至关重要,有关3D3C-VSP速度分析研究却很少。传统VSP速度分析的方法利用下行直达波计算速度,包括直线法、折线法和走时反演法等[20-21],但只能获得井中检波器接收段的地层速度,且需假设初始速度后通过不断迭代速度模型,直到获得较好的成像结果[22]。基于共接收点或共炮点道集,苏媛媛等[23]研究了斜井三维VSP纵波动校正与建立速度场的方法,斯兴焱等[24]研究了斜井三维VSP多波速度分析方法。目前,应用于生产的速度模型多为一维速度场外推得到的二维速度场,速度横向无变化,精度较低,影响了3D3C-VSP地震数据成像质量;而三维速度场的建立需要不断迭代,计算复杂、耗时长。
针对上述问题,本文提出一种适用于3D3C-VSP观测系统的PP波与PS波成像方法,并给出了配套的速度分析方法。该方法根据VSP上行波的非对称旅行时方程,将接收道的振幅输出到反射面上干涉叠加,同时消除正常时差,并进一步将地震波t0旅行时校正至具有双曲特性的虚拟炮检距道集中;然后,对该道集进行反动校正处理、速度分析并叠加,从而获得高精度的偏移成像剖面。该方法对初始速度模型依赖小,速度分析无需反复迭代,处理效率高,易于实现和应用于生产。基于该方法建立的配套技术流程,对四川盆地A井3D3C-VSP地震数据进行了处理,最终获得了高精度PP波和PS波成像剖面。
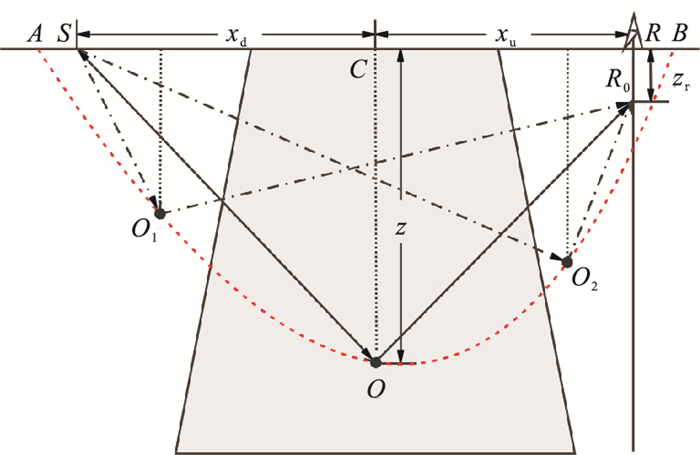
1 方法原理 1.1 基于散射时距关系的共成像点道集如图 1所示,炮点S激发地震波,地震波在在地下O点发生反射,被井下R0点的检波器接收。R0点在地表的投影为R,O点在地表的投影为C。地震波在SOR0之间传播的旅行时为
| $ t = \frac{{\sqrt {x_{\rm{d}}^2 + {z^2}} }}{{{v_{\rm{d}}}}} + \frac{{\sqrt {x_{\rm{u}}^2 + {{\left( {z - {z_{\rm{r}}}} \right)}^2}} }}{{{v_{\rm{u}}}}} $ | (1) |
|
图 1 输出道偏移成像示意图 |
式中:xd为炮点S与成像投影点C的水平距离;xu为检波器投影点R与成像投影点C的水平距离;z为反射点O的深度;zr为井中的检波点R0的深度(炮、检点不在同一深度);vd为下行波偏移速度;vu为上行波偏移速度。对于VSP-PP波,式(1)中的vd和vu均为P波速度;对于VSP-PS波,vd为P波速度,vu为S波速度。
假设地震波从S点传播至弧面AO1OO2B(反射面)上任意一点、再反射回井下检波器R0点的旅行时都为t,则该检波器的地震道上t时刻的振幅都可以“搬家”至该反射面上任意一点。这些地震波相互干涉叠加,真正的成像点叠加后的能量增强,振幅突出;假的成像点则被全部或部分消除。
由于弧面AO1OO2B上存在高角度绕射画弧,高角度部分在偏移过程中会形成较强的绕射噪声,所以需要设置偏移孔径,在该偏移孔径内实现地震波的归位,避免成像道集在远炮检距处出现偏移假象。由式(1)可得地层倾角为
| $ \theta = \frac{1}{2}\left| {{\rm{arctan}}\frac{z}{{{x_{\rm{d}}}}} - {\rm{arctan}}\frac{{z - {z_{\rm{r}}}}}{{{x_{\rm{u}}}}}} \right| $ | (2) |
则偏移孔径[25]为
| $ \begin{aligned} D=& \frac{v_{\mathrm{rms}} t\left(\tan ^{2} \theta-1\right)}{2 \tan \theta}+\\ & \frac{\sqrt{v_{\mathrm{rms}}^{2} t^{2} \sec ^{2} \theta+\left(x_{\mathrm{d}}+x_{\mathrm{u}}\right)^{2} \tan ^{2} \theta}}{2 \tan \theta} \end{aligned} $ | (3) |
式中vrms为均方根速度。地层倾角θ越大,偏移孔径则越大。
3D3C-VSP观测系统的特殊性会导致成像点覆盖次数不均,由近井到远井,覆盖次数递变减小。针对这种情况,在抽取共成像点道集时,计算每个共成像点上的覆盖次数,叠加后的振幅除以该点的覆盖次数,使纵、横向能量趋于一致,减小成像受覆盖次数不均的影响。
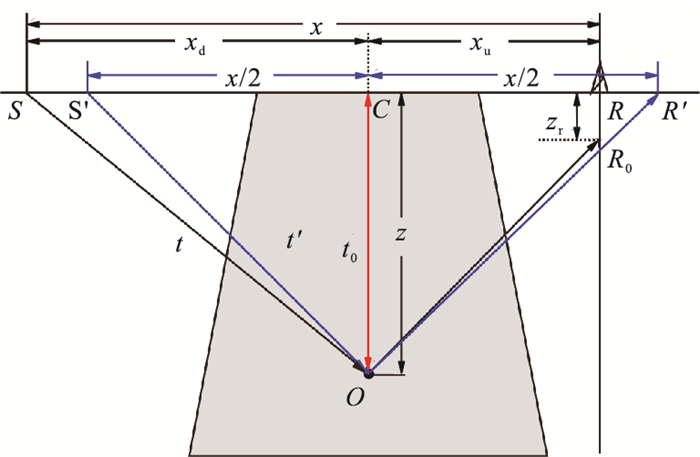
抽取共成像点道集时,将炮点与检波点位置在保持炮检距不变的情况下平移至虚拟的炮点S′与检波点R′ (图 2),并对地震波非对称双平方根旅行时反动校正至双曲时间。图 2中,黑色实线代表地震波在O点处发生反射的实际射线路径,红色实线为虚拟的自激自收射线路径。每个成像点都对应着自激自收时间t0,在抽取共成像点道集过程中,先将地震波旅行时t校正到
| $ {t_0} = \frac{z}{{{v_{\rm{d}}}}} + \frac{z}{{{v_{\rm{u}}}}} $ | (4) |
|
图 2 反动校正示意图 |
t0时间域的共成像点道集有助于判断初始速度模型是否准确。若该道集同相轴都被“拉平”,则认为速度模型足够准确,即可直接对道集进行叠加,获得成像剖面。若该道集不平,则需先进行反动校正。
1.2 反动校正与速度分析反动校正的目的是获得具有似双曲时距特性的虚拟共炮检距道集。设S、R点间距离(真实炮检距)为x,将S、R向检波器一侧平移至虚拟炮点S′与检波点R′。S′R′为虚拟炮检距,与真实炮检距相同。每个成像点都有相应的虚拟炮检距双平方根旅行时
| $ {t\prime = \frac{{\sqrt {{{\left( {\frac{x}{2}} \right)}^2} + {z^2}} }}{{{v_{\rm{d}}}}} + \frac{{\sqrt {{{\left( {\frac{x}{2}} \right)}^2} + {z^2}} }}{{{v_{\rm{u}}}}}} $ | (5) |
该旅行时补偿了井下检波器与地表之间的旅行时。
为了便于用常规速度分析软件进行速度分析,虚拟炮检距双平方根旅行时将进一步校正至双曲旅行时上。虚拟的炮点S′与检波点R′至成像点O的射线路径已相同,但是偏移速度依旧不一致。为了解决该问题,引入地面PS波处理中常用的等效PS波速度
| $ {{v_{\rm{C}}} = \frac{{2{v_{\rm{u}}}}}{{1 + \gamma }}} $ | (6) |
式中γ= vu/vd。将式(5)的双平方根旅行时方程改写为单平方根方程
| $ {t\prime = \frac{{\sqrt {{x^2} + 4{z^2}} }}{{{v_{\rm{C}}}}}} $ | (7) |
即
| $ {{{\left( {{t^\prime }} \right)}^2} = t_0^2 + \frac{{{x^2}}}{{v_{\rm{C}}^2}}} $ | (8) |
式(8)即为传统的双曲线时距曲线方程。将消除正常时差的VSP共成像点道集的t0时间进一步反动校正至虚拟炮检距道集的双曲旅行时t′上,消除了VSP观测系统下的射线路径不对称及上、下行波偏移速度的不一致。基于该成像道集的叠加速度可以用传统速度分析软件进行速度谱拾取。最后对重新速度分析后的成像道集进行精细的切除滤波处理,叠加后得到最终的VSP地震PP波、PS波偏移剖面。
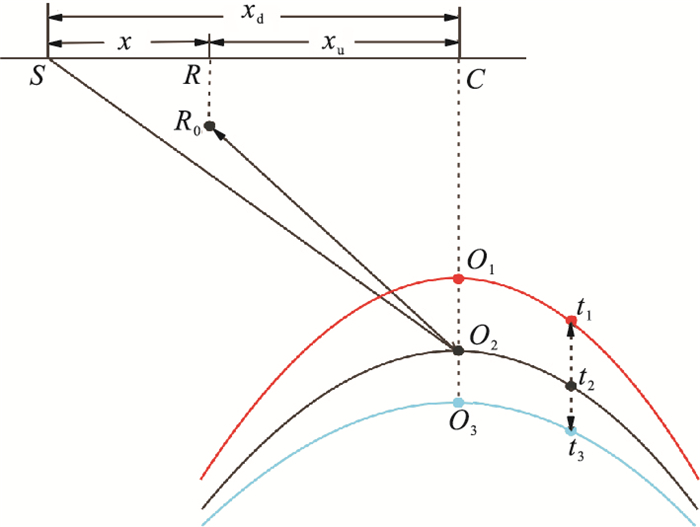
1.3 初始速度模型对成像道集的影响本文的VSP抽道集方法对速度模型不敏感。如图 3所示,地震道上的振幅值映射到共成像点道集上时,保留了其相应的炮检距和地震波时间,某一反射点偏移速度不准确不会导致成像点错位。
|
图 3 速度误差对成像道集的影响 |
假设在反射点O1、O2和O3处相应的偏移速度分别为v1、v2和v3,且v1 < v2 < v3。如果使用较大的偏移速度v3生成O2处的成像道集,则根据式(1)会得出错误的旅行时t1,该时间小于真实的旅行时t2。同理,使用较小的偏移速度v1生成O2处的成像道集,会得到错误的旅行时t3。因此,部分时窗的不准确偏移速度只会导致有效成像范围上移或下移,不会影响成像道集的生成,用于生成成像道集的初始速度模型也不需要反复迭代。
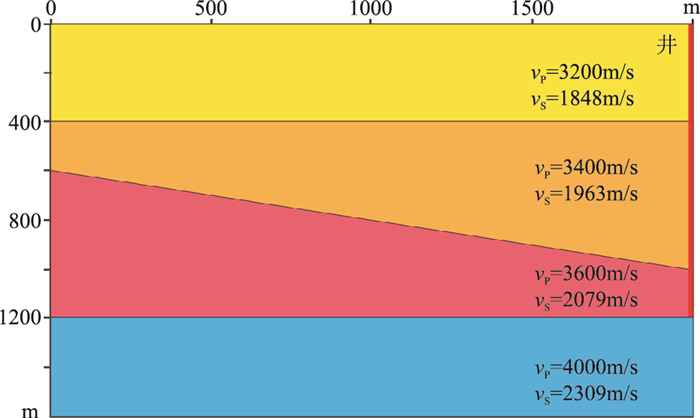
2 模型数据试验 2.1 模型正演用一个含倾斜地层的模型(图 4)测试本文提出的成像方法。模型尺寸为2000m×1600m,第二界面倾角约为10°。井位于最右端,最大深度为1200m,观测井段为10~1200m,检波点间距为10m。炮点位于地表,炮间距为20m。
|
图 4 VSP观测地震模型 |
用射线追踪法正演生成的VSP-PP、PS波上行波的共炮点集记录如图 5所示,未考虑地震反射的AVO效应。
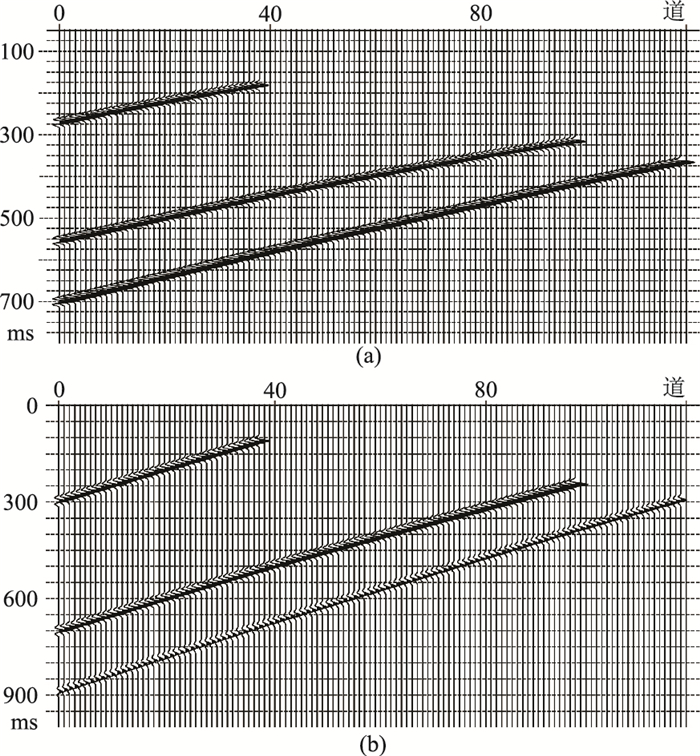
|
图 5 井源距为500m的上行波炮集记录 (a)PP波;(b)PS波 |
初始P波速度模型使用井位处的P波均方根速度扩展得到的二维速度场(图 6),纵横波速度比为固定值1.73,将所有界面看成水平面,以测试本文成像方法对速度模型的依赖性。然后,基于散射时距关系抽取PP波、PS波的共成像点道集(图 7),可以看出第一和第三界面同相轴平直,而第二界面的同相轴在近、远井源距处存在约10ms的移位,说明初始速度模型与真实速度模型在第二速度界面上略微存在偏差。为获得更精确的速度模型,需进行反动校正和速度分析。
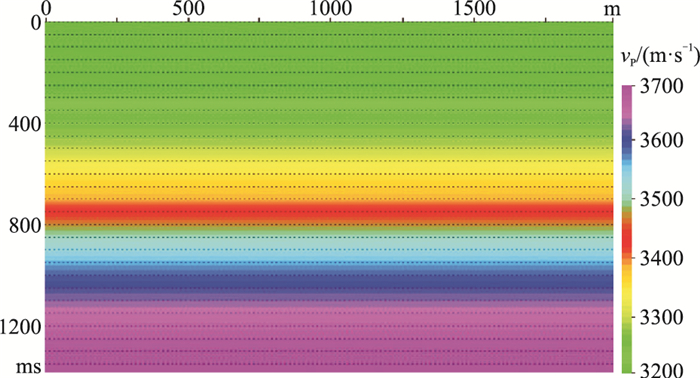
|
图 6 初始P波速度模型 |
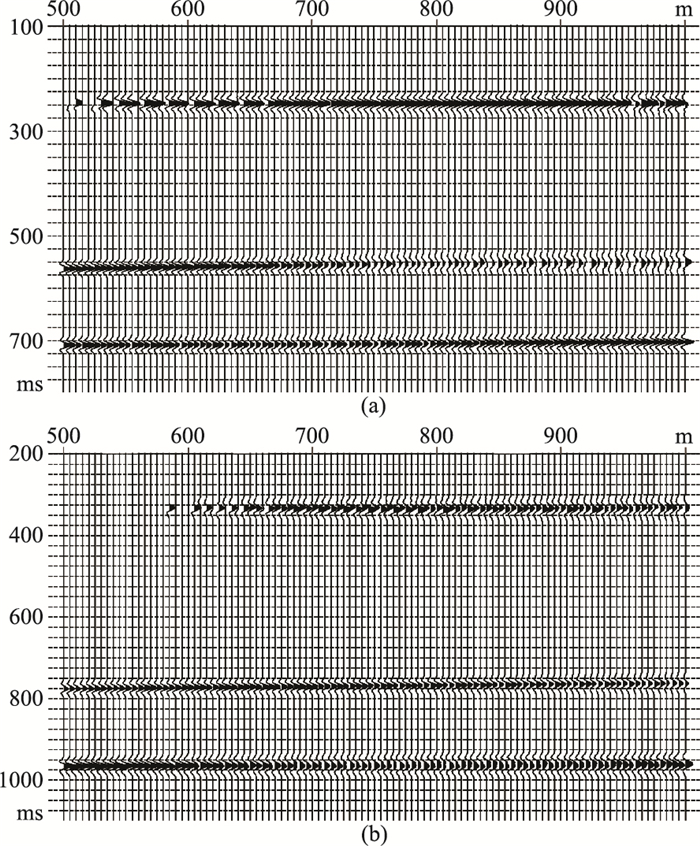
|
图 7 井源距为300m的共成像点道集 (a)PP波;(b)PS波 |
通过反动校正,将PP波、PS波上行波波场校正至具有拟双曲时距特征的虚拟炮检距道集(图 8);然后进行常规速度分析并叠加,获得PP波、PS波的成像剖面(图 9),第一与第三界面水平,第二界面倾斜,与地质模型完全吻合。同时,PP波与PS波成像剖面的波组关系完全一致。
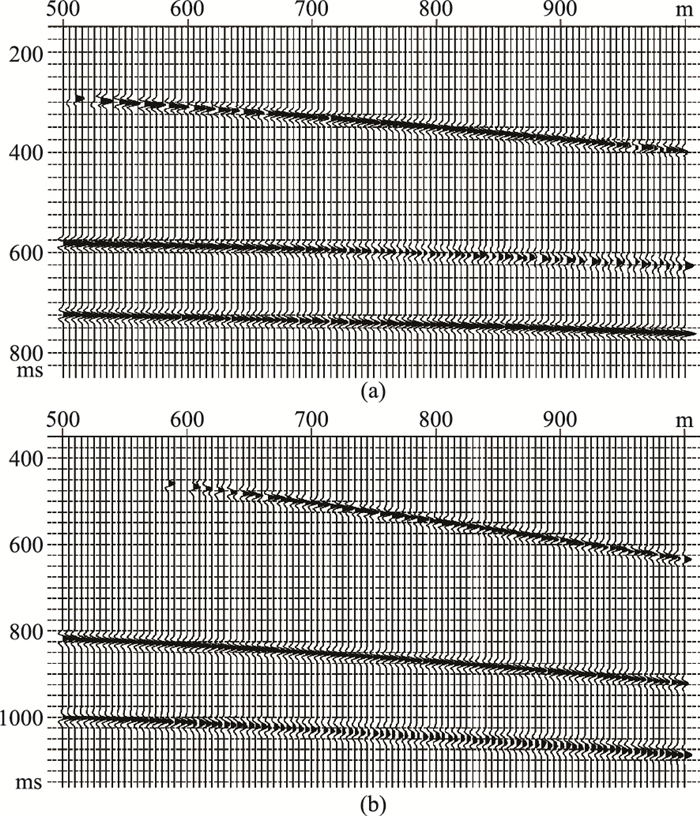
|
图 8 井源距为300m的虚拟炮检距道集 (a)PP波;(b)PS波 |
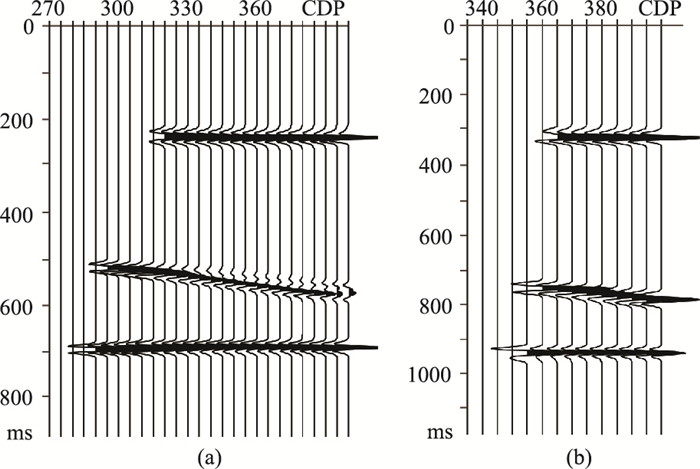
|
图 9 成像剖面 (a)PP波;(b)PS波 |
可见该方法适用于水平和倾斜地层,可以实现VSP-PP波和PS波的高精度成像。即使使用了不太精确的初始速度模型,经过后续的速度分析后,也能精确成像,速度模型无需反复迭代。
3 实际工区应用 3.1 观测系统如图 10a所示,四川盆地A井3D3C-VSP观测系统最大井源距为4850m,观测井段为1830~3090m,检波点距为15m,共9090炮,炮点覆盖面积为51.9km2。由于VSP观测系统特殊性,有效成像面积为14.3km2;根据有效成像面积,将VSP成像网格划分为20m×20m,Inline范围为1020~1180,Xline范围为270~470。A井位于Inline1097与Xline370交会处。
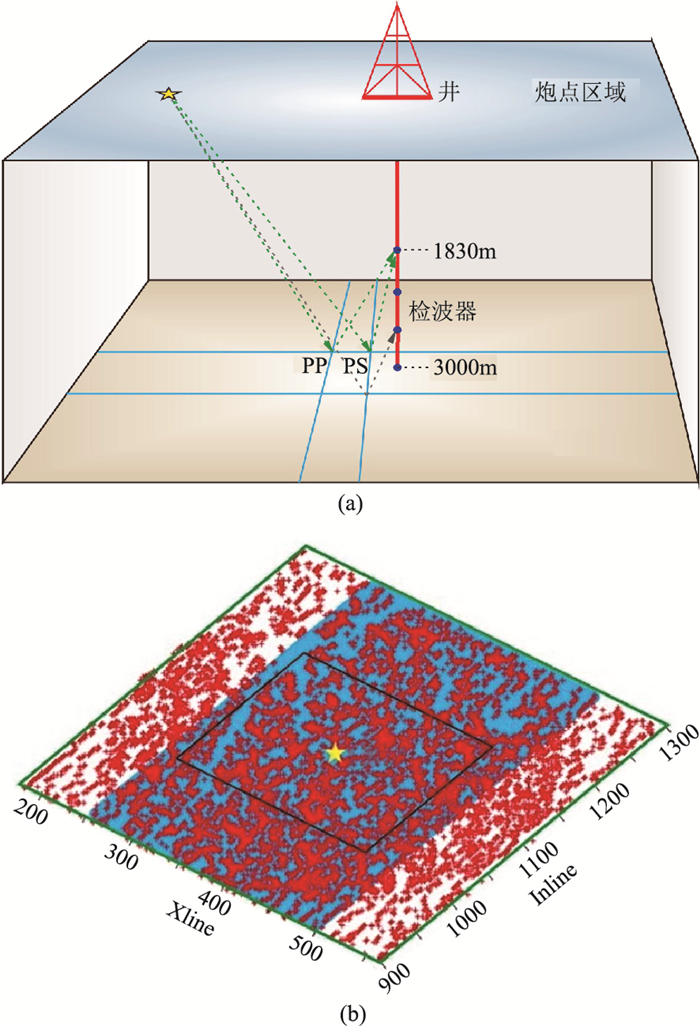
|
图 10 观测系统(a)和成像网格(b)示意图 黄星表示A井,红点表示炮点,黑框为有效成像范围;蓝色阴影区为井地联采的地面3D3C采集范围 |
速度建模直接关系到偏移成像质量,VSP速度建模,普遍采用的方法是从已有资料(零井源距VSP、声波测井等)获得初始一维速度模型,再根据偏移成像质量,反复迭代修改速度模型,直到获得高质量的偏移剖面。A井VSP资料是井地联采获得,故将该地区地面地震处理过程中建立的三维偏移速度体作为初始模型用于VSP资料的偏移成像。
如图 11a所示,P波偏移速度模型(PP波时间域)用于VSP的PP波偏移;接着,用固定纵横波速度比1.70将P波偏移速度拉伸至PS波时间域(图 11b),用于PS波偏移。
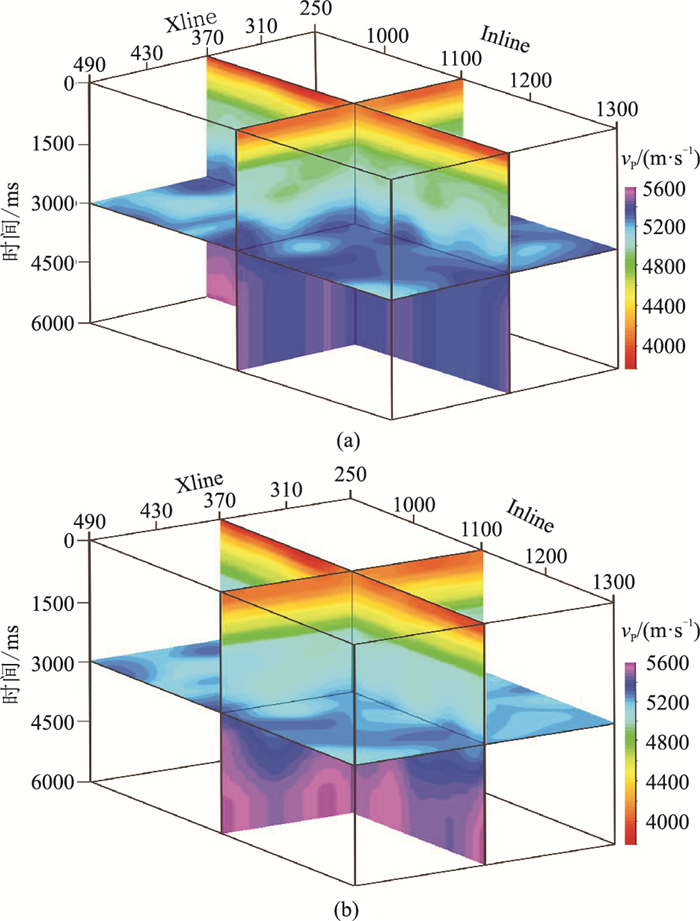
|
图 11 三维偏移速度模型 (a)PP时间域;(b)PS时间域 |
基于初始速度模型,抽取共成像点道集,如图 12和图 13所示。由图可以看出:靠近井的道集中近炮检距数据覆盖次数高,远炮检距数据在中深层有缺失;距井200m处的道集中近炮检距数据覆盖次数低,远炮检距数据满覆盖。因此后续进行偏移成像时,需要选择适当的炮检距,使覆盖次数相对均衡。
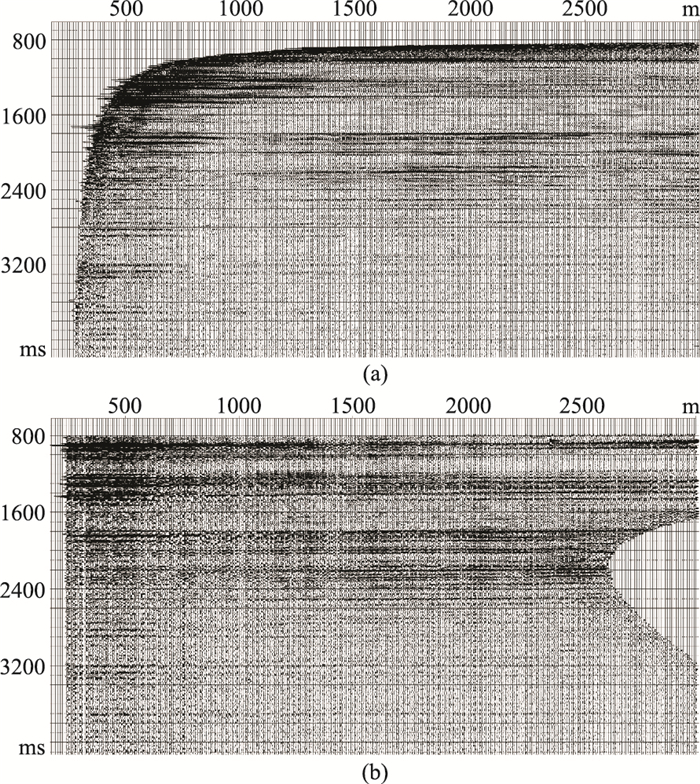
|
图 12 PP波成像道集 (a)距井位200m处;(b)井位处 |
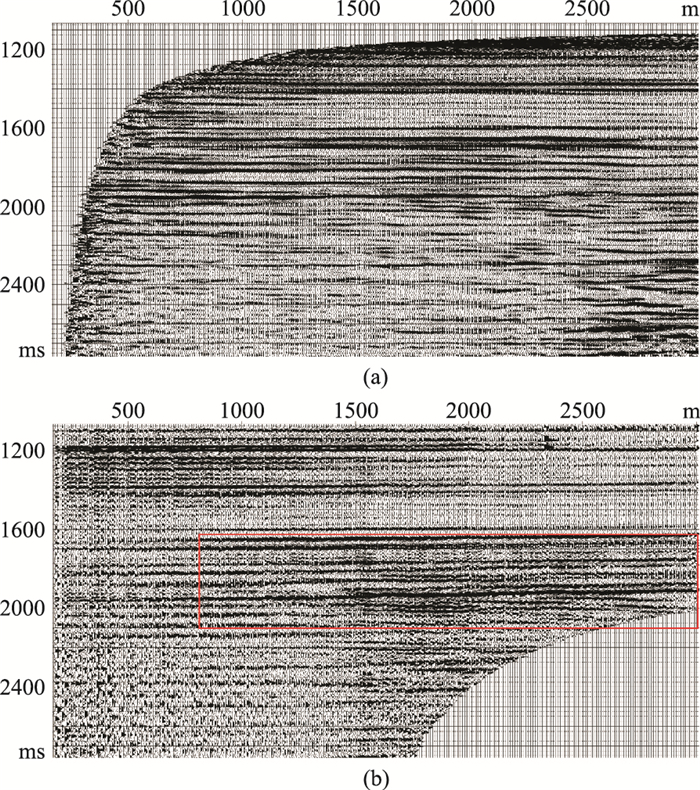
|
图 13 PS波成像道集 (a)距井位200m处;(b)井位处 |
在部分PP波、PS波共成像点道集中,同相轴在远炮检距处出现了“上翘”的现象,如图 13红框所示,这是初始速度模型不够精确所致,故需做进一步的速度分析。
3.4 虚拟炮检距道集基于初始速度模型生成的共成像点道集若直接进行偏移成像,会出现两端“上翘”、同相轴发散等问题。因此,为进一步提高剖面的整体成像质量,将共成像点道集进行反动校处理,再对反动校后的虚拟炮检距道集进行速度分析,实现三维速度模型的更新。反动校后的VSP-PP波和PS波虚拟炮检距道集如图 14和图 15所示。
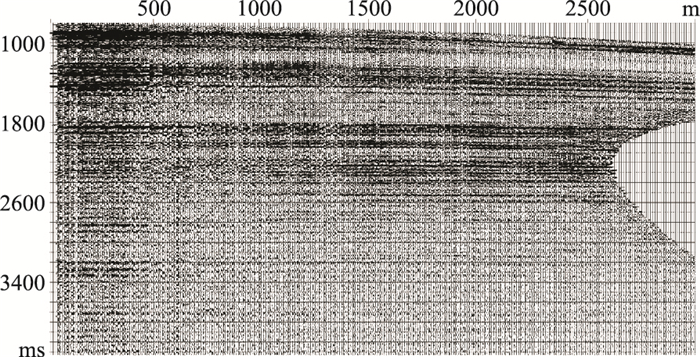
|
图 14 过井点PP波虚拟炮检距道集 |
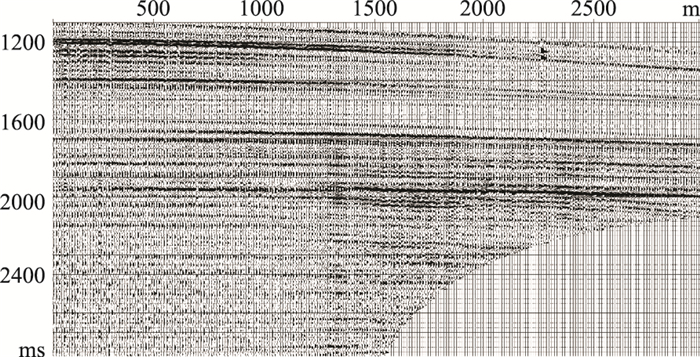
|
图 15 过井点PS波虚拟炮检距道集 |
对虚拟炮检距道集进行速度分析,实现三维速度场的更新,得到更精准的速度,以此减弱或消除VSP成像剖面中同相轴上翘或下弯等现象。以PS波为例,对比初始速度模型与更新速度模型生成的成像道集(图 16)可见,应用更新速度模型成功消除了成像道集远炮检距处同相轴“上翘”现象。
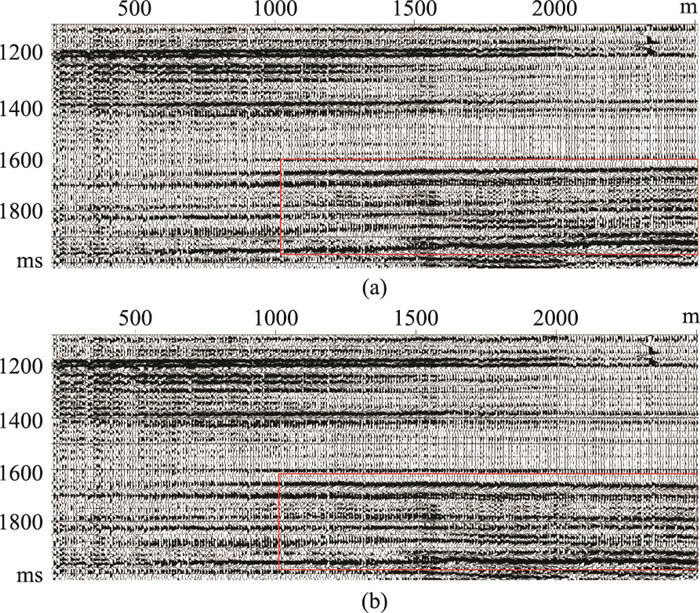
|
图 16 应用初始(a)与更新(b)速度模型PS波成像道集对比 |
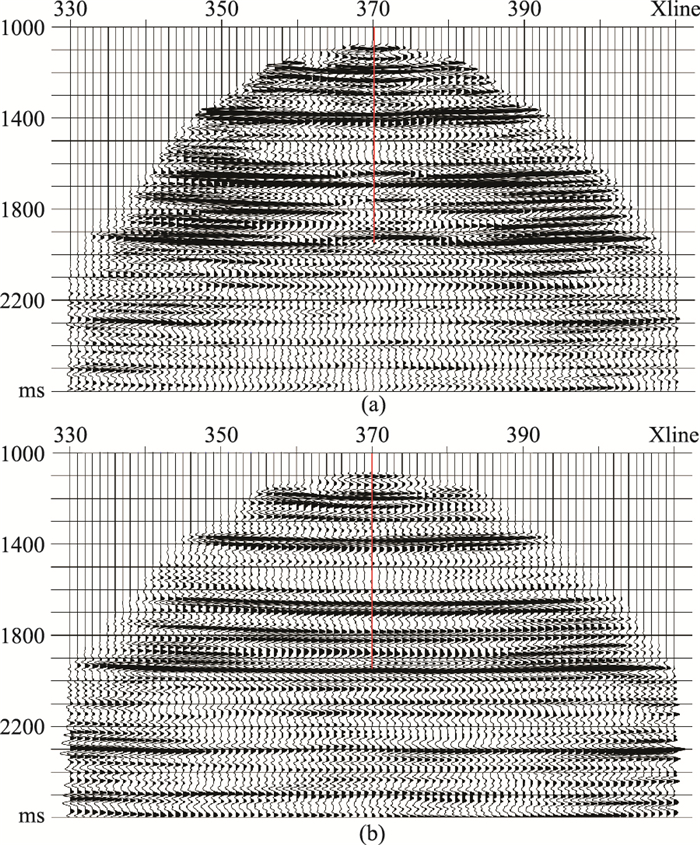
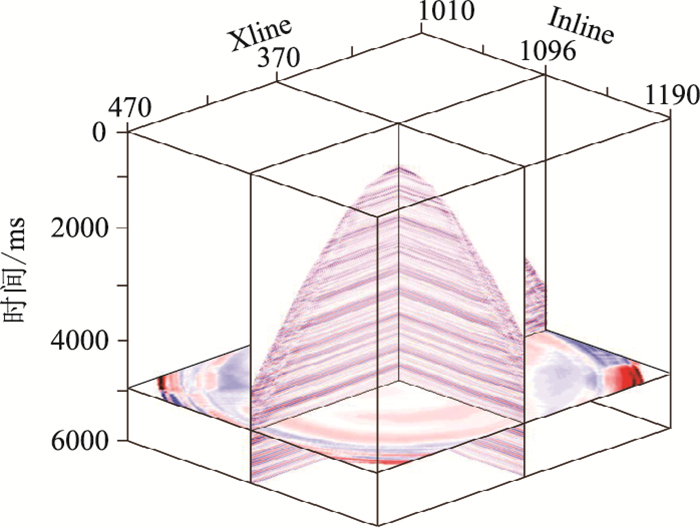
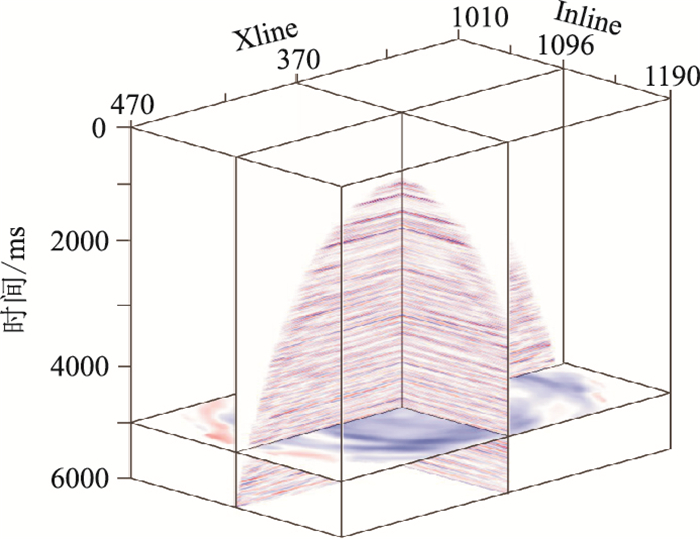
初始速度模型的PS波成像剖面(图 17a)同相轴井位处下凹、远处上翘现象明显,而精细速度分析后,成像剖面(图 17b)质量有明显改善。最后对PP波与PS波进行偏移成像,得到分辨率与信噪比较高的PP波和PS波的三维VSP成像数据体(图 18和图 19),为储层解释与预测提供高品质的多波成像资料。
|
图 17 初始(a)与更新(b)速度模型的PS波成像剖面对比 |
|
图 18 3D-VSP数据PP波偏移结果 |
|
图 19 3D-VSP数据PS波偏移结果 |
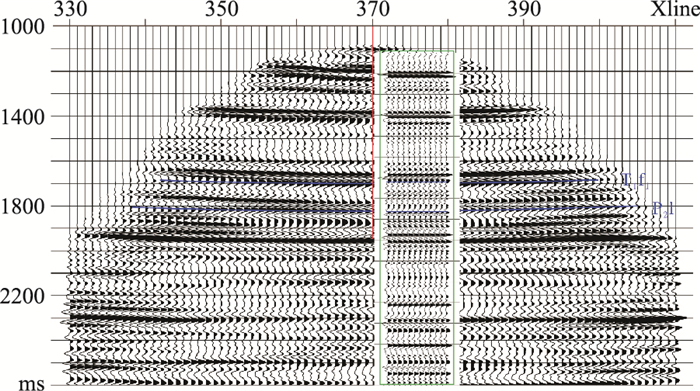
与走廊叠加结果对比(图 20和图 21),以验证本文方法的准确性与可靠性。整体上,VSP-PP和PS成像剖面的波组关系均与走廊叠加剖面(绿框内)一致,标志层下三叠统飞仙关组底(T1f1)和上二叠统的龙潭组底界(P2l)对应关系良好,表明本文方法成像剖面可以反映地层的真实情况。

|
图 20 VSP-PP偏移剖面与走廊叠加对比(Inline方向) |
|
图 21 VSP-PS偏移剖面与走廊叠加对比(Inline方向) |
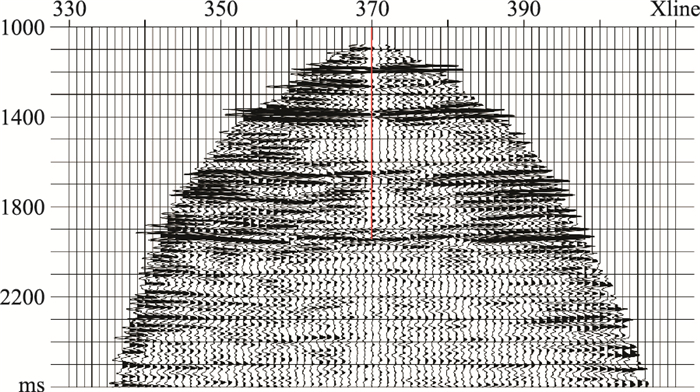
VSP-CDP叠加剖面(图 22)同相轴在横向上连续性差,井中覆盖次数低;本文方法的PS波成像结果(图 17b)横向较连续,覆盖次数较一致,成像范围远大于传统方法,提高了成像质量。
|
图 22 PS波VSP-CDP叠加剖面(Inline方向) |
本文基于四川盆地A井3D3C-VSP数据,研究了适用于3D3C-VSP地震数据的虚拟炮检距道集的生成、速度分析以及成像方法。本文方法将地震道上各时刻的振幅分别搬家至对应反射面上,通过共网格点干涉叠加获得共成像点道集,实现了地震波的归位,偏移后波的时间关系正确,提高了信噪比和分辨率。该方法通过基于双曲校正的速度分析法,将地震波双平方根旅行时反动校正至双曲时间上,有效消除了VSP观测系统下PP和PS波旅行时的非双曲影响,减少了速度分析过程中的迭代,改善了常规VSP成像剖面中远端明显上翘的现象,PP波与PS波VSP成像剖面具有横向连续性好、分辨率高等特点。与走廊叠加剖面对比,标志层匹配良好,波组关系准确,验证了本文成像方法的准确性与可靠性。实际应用结果表明本方法在3D3C-VSP实际生产中具有实施方便、效率和精度较高的优势。
| [1] |
Hokstad K, Sollie R, Petersen S. Horizontal resolution of 3-D VSP data[C]. SEG Technical Program Expanded Abstracts, 2001, 20: 2135-2140.
|
| [2] |
Landrø M. Repeatability issues of 3-D VSP data[J]. Geophysics, 1999, 64(6): 1673-1679. DOI:10.1190/1.1444671 |
| [3] |
朱光明. 垂直地震剖面方法[M]. 北京: 石油工业出版社, 1988.
|
| [4] |
庄东海. VSP旅行时反演应用于VSP-CDP转换[J]. 江汉石油学院学报, 1991, 13(2): 30-36. ZHUANG Donghai. VSP traveltime inversion applied in VSP-CDP conversion[J]. Journal of Jianghan Petroleum Institute, 1991, 13(2): 30-36. |
| [5] |
杨飞龙, 方金川, 郭文强, 等. 非零井源距VSP逆高斯束叠加成像[J]. 地球物理学进展, 2020, 35(3): 1077-1084. YANG Feilong, FANG Jinchuan, GUO Wenqiang, et al. The inverse Gaussian beam stack imaging of nonzero-offset VSP[J]. Progress in Geophysics, 2020, 35(3): 1077-1084. |
| [6] |
Chen G M, Peron J, Canales L, et al. Rapid VSP-CDP mapping of 3D VSP data[J]. Geophysics, 2000, 65(5): 1631-1640. DOI:10.1190/1.1444851 |
| [7] |
杨飞龙, 李辉峰, 孙辉, 等. 基于正态分布权函数的VSP-CDP叠加成像[J]. 石油地球物理勘探, 2020, 55(1): 101-110. YANG Feilong, LI Huifeng, SUN Hui, et al. VSP-CDP stack imaging based on the weight function of normal distribution[J]. Oil Geophysical Prospecting, 2020, 55(1): 101-110. |
| [8] |
李彦鹏, 易维启, 曾忠, 等. VSP处理新技术及应用[J]. 石油地球物理勘探, 2018, 53(增刊2): 42-49. LI Yanpeng, YI Weiqi, ZENG Zhong, et al. New processing approaches of VSP data[J]. Oil Geophysical Prospecting, 2018, 53(S2): 42-49. |
| [9] |
Zhang H H, Lu J, Chen B C, et al. Fluid prediction of a deep carbonate reservoir using walkaround 3D-3C vertical seismic profiling data[J]. Journal of Geophysics and Engineering, 2020, 17(1): 35-52. |
| [10] |
汪贵枫. 论F-K偏移[J]. 石油地球物理勘探, 1983, 18(1): 20-29. WANG Guifeng. On F-K migration[J]. Oil Geophysical Prospecting, 1983, 18(1): 20-29. |
| [11] |
李渊. VSP逆时偏移方法研究[D].湖南长沙: 中南大学, 2013. LI Yuan. The Research on VSP Reverse-time Migration Method[D]. Central South University, Changsha, Hunan, 2013. |
| [12] |
Alok K S, Xander S, Verschuur E. VSP imaging using all multiples: Full wavefield migration approach[C]. SEG Technical Program Expanded Abstracts, 2012, 31: 1-5.
|
| [13] |
陈生昌, 马在田, 陈林. 三维VSP数据的波动方程偏移成像[J]. 天然气工业, 2008, 28(3): 51-53. CHEN Shengchang, MA Zaitian, CHEN Lin. Wave equation migration for 3-D VSP data[J]. Natural Gas Industry, 2008, 28(3): 51-53. |
| [14] |
秦福浩, 郭亚曦, 王妙月. 弹性波克希霍夫积分偏移法[J]. 地球物理学报, 1988, 31(5): 577-587. QIN Fuhao, GUO Yaxi, WANG Miaoyue. The Kirchhoff elastic wave migration method[J]. Acta Geophysica Sinica, 1988, 31(5): 577-587. DOI:10.3321/j.issn:0001-5733.1988.05.010 |
| [15] |
Lou M, Cheng D J and Doherty F. Suppressing VSP migration artifacts and noise by selected-aperture migration and damped-least-square smoothing[C]. SEG Technical Program Expanded Abstracts, 2009, 28: 4144-4148.
|
| [16] |
王华忠, 徐蔚亚, 王建民, 等. VSP数据波动方程叠前深度偏移成像及立体地震成像[J]. 石油地球物理勘探, 2001, 36(5): 517-525. WANG Huazhong, XU Weiya, WANG Jianmin, et al. Prestack depth migration of VSP data and stereosco-pic seismic imaging[J]. Oil Geophysical Prospecting, 2001, 36(5): 517-525. DOI:10.3321/j.issn:1000-7210.2001.05.001 |
| [17] |
邹强, 黄建平, 雍鹏, 等. 平面波优化差分算子弹性波逆时偏移[J]. 石油地球物理勘探, 2020, 55(5): 1047-1059. ZOU Qiang, HUANG Jianping, YONG Peng, et al. An elastic-wave reverse-time migration method based on optimal finite-difference operators using a new plane wave solution[J]. Oil Geophysical Prospecting, 2020, 55(5): 1047-1059. |
| [18] |
陈可洋, 王建民, 关昕, 等. 逆时偏移技术在VSP数据成像中的应用[J]. 石油地球物理勘探, 2018, 53(增刊1): 89-93. CHEN Keyang, WANG Jianmin, GUAN Xin, et al. VSP data imaging with reverse time migration[J]. Oil Geophysical Prospecting, 2018, 53(S1): 89-93. |
| [19] |
Shi Y, Wang Y H. Reverse time migration of 3D vertical seismic profile data[J]. Geophysics, 2016, 81(1): S31-S38. DOI:10.1190/geo2015-0277.1 |
| [20] |
Dillon P B, Thomson R C. Offset source VSP surveys and their image construction[J]. Geophysical Prospecting, 1984, 32(5): 790-811. |
| [21] |
庄东海, 肖春燕. VSP资料求层速度的射线追踪折线法[J]. 江汉石油学院学报, 1994, 16(4): 50-53. ZHUANG Donghai, XIAO Chunyan. Ray-tracking method of computing interval velocities for VSP[J]. Journal of Jianghan Petroleum Institute, 1994, 16(4): 50-53. |
| [22] |
黄翼坚.多井源距VSP速度分析及逆时偏移[D].陕西西安: 长安大学, 2010. HUANG Yijian. Multi-offset Velocity Analysis and Reverse-time Migration[D]. Chang'an University, Xi'an, Shaanxi, 2010. |
| [23] |
苏媛媛, 李录明, 赵俊省, 等. 斜井三维VSP动校叠加处理方法[J]. 物探化探计算技术, 2010, 32(2): 132-137. SU Yuanyuan, LI Luming, ZHAO Junsheng, et al. The processing methods of NMO correction and sta-cking in deviated 3D-VSP[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2010, 32(2): 132-137. |
| [24] |
斯兴焱, 李录明, 胥良君, 等. 三维VSP多波速度分析方法及应用[J]. 石油物探, 2012, 51(1): 56-64. SI Xingyan, LI Luming, XU Liangjun, et al. 3D-VSP multiple velocity analysis method and its application[J]. Geophysical Prospecting for Petroleum, 2012, 51(1): 56-64. |
| [25] |
吴吉忠, 刘成权, 张建坤, 等. 倾角域自适应孔径叠前时间偏移[J]. 石油地球物理勘探, 2017, 52(3): 502-508. WU Jizhong, LIU Chengquan, ZHANG Jiankun, et al. Adaptive aperture prestack time migration in the dip angle domain[J]. Oil Geophysical Prospecting, 2017, 52(3): 502-508. |



 芦俊, 北京市海淀区学院路29号中国地质大学(北京)地球物理与信息技术学院, 100083。Email:
芦俊, 北京市海淀区学院路29号中国地质大学(北京)地球物理与信息技术学院, 100083。Email: