低幅度构造是指构造相对平缓、闭合幅度只有10~20m的地质体[1-2],又被称为小幅度构造、微幅度构造等。近年来,低幅度构造油气藏逐渐被重视,成为油气勘探的一个重要接替领域,因此得到了人们的广泛关注[3]。由于构造幅度较低,因此地震资料上表现为反射同相轴平直而变化幅度很小,不易被识别。低幅度构造的解释精度取决于地震数据的采集、处理和解释等各个环节,处理人员就低幅度构造圈闭地震资料处理中的关键点、横向速度变化对构造成像影响进行了大量研究[4-6],解释人员在低幅度构造解释技术、识别技术、储层横向预测等方面也取得了较大进展[7-8]。要研究低幅度构造,首先要探讨的就是地震资料是否有分辨低幅度构造的能力。
四川盆地西北部龙门山冲断带前缘地表岩性变化大,通过数值模拟和构造物理模拟证实该工区深层为低幅度潜伏构造。除地层岩性等一些固有因素外,长波长静校正是影响复杂地表区低幅度构造成像的关键因素之一[9],主要表现在:①由CMP叠加拾取的构造时间发生畸变而产生假构造;②当长波长静校正异常区的宽度约等于一个排列长度时,叠加速度会发生异常变化;③当叠后处理涉及到大的空间孔径时,长波长静校正异常影响地震资料处理方法的选择[10-11]。
偏移速度是影响低幅度构造成像的重要参数。如果速度分析不准确,那么真实存在的低幅度构造就会被抹掉或者导致假构造的出现[12]。地震速度场的横向变化会导致时间偏移的结果产生畸变,从而产生一些假构造,严重影响油气勘探中井位的部署。
在速度存在横向变化时,深度偏移结果相对准确,本文以地质层位为基础建立模型,然后在横向上沿地质层位网格进行参数更新,即基于模型的层析反演方法,具备层位约束和全局反演二者的优点,可以有效解决薄层速度建模问题和低幅度构造成像问题[13]。
1 深层低幅度构造数值、物理模拟 1.1 数值模拟工区位于四川盆地西北部龙门山冲断带前缘[14],地表起伏剧烈,纵、横向变化较大。工区内地表出露多套地层,岩性包括灰岩、砂泥岩、砾岩、河滩砾石等[15]。针对该工区的地震资料进行解释,浅部表现为低角度断层组合的叠瓦状构造,而深层则表现为低幅构造,存在明显的不协调变形,为验证解释方案,采用离散数值模拟技术[16]定量描述褶皱与断层的几何形态关系,能够根据浅层数据推断深部构造。
通过离散数值模拟实验揭示了滑脱层的数量、分布范围及其相对强度是影响盆山体系构造横向分带、纵向分层的关键因素。
由数值模拟结果(图 1b)可知,研究区发育深浅两种不同构造样式,浅层为低角度断层组合的叠瓦状构造,深层为低幅度潜伏构造,与地震解释结果一致。

|
图 1 过A井地震剖面(a)及构造数值模拟结果(b) |
物理模拟[17-18]是构造变形过程和形成机制研究的有效手段,在褶皱—冲断带研究中发挥了十分重要的作用。20世纪80年代以来,构造变形物理模拟方法在构造地质学研究领域取得了显著成效,对构造地质学的研究起到了重要作用。研究区地表、地下条件复杂,仅仅依靠数值模拟不能完全了解构造变形的特征和过程,因此数值模拟之后,又做了构造物理模拟实验。采用石英砂和硅胶模拟地层,通过两套滑脱层模型,研究中、浅层构造变形特征和过程。双层滑脱介质物理模拟结果(图 2)表明:变形剖面总体具有前展式的发育特征,由一组高角度叠瓦逆冲岩片和一组低角度叠瓦逆冲岩片组成。前者主要以垂直抬升为主,后者通过深部滑脱层和中部滑脱层的共同作用,形成3组叠置岩片体,在浅部形成高陡构造,深部形成低幅度构造。

|
图 2 构造变形物理模拟过程 |
通过数值模拟和构造物理模拟证实了该工区深层为低幅度潜伏构造,但四川盆地西北部龙门山冲断带前缘地表岩性变化大,激发、接收条件差,初至存在扭曲、错断现象,静校正问题较严重;有效反射能量弱,信噪比低,速度分析难度较大;近地表岩性变化快,表层速度模型建立困难;目的层下二叠统构造褶皱强烈,小断层发育,断块复杂,速度横向变化剧烈,速度场建立及深度域准确归位困难,鉴于以上地表、地质条件,若想获得准确的构造成像资料,就必须解决静校正和速度建模等问题。
2.1 微测井约束初至层析静校正层析静校正方法是目前常用且有效的方法,但该方法受初始速度的影响较大,因此在实际应用过程中,要采用多信息约束层析反演近地表速度模型。初始速度模型建立时,微测井资料具有在点上准确反映低速层信息的优势,但由于受探测深度的限制,刻画降速带的能力较低;另一方面,小折射资料则对降速层速度有较好的反映,但其刻画高速层顶界时受到小折射排列长度的限制,尤其是高速层顶界面起伏较大或者高速层速度横向变化较大时,对高速层顶界的形态刻画不准确,从而无法彻底解决长波长静校正问题。
为了解决影响低幅度构造成像的长波长静校正问题,本文采用分层约束的近地表建模方法[19-20]获得近地表速度模型,具体过程如下:
(1) 利用微测井信息建立低速层初始速度模型;
(2) 利用小折射和VSP资料建立降速层初始速度模型;
(3) 采用分层约束层析反演近地表速度模型,建立高精度的近地表速度模型;
(4) 通过VSP测井数据及实钻井深度约束高速层顶界;
(5) 计算静校正量,其中低频分量解决资料的长波长静校正问题,高频分量解决资料的成像问题。
2.1.1 约束层析反演近地表建模方法初至波旅行时层析速度建模[21-22]是一种非线性的模型反演技术,就是把地下介质离散成一个个相互毗连的小单元,利用射线追踪方法研究各个单元内的射线的路径与旅行时情况,进而反演每一个单元中的介质的速度,最后求取近地表的速度模型。在层析反演中,由M条射线和N个未知数建立的层析方程组为
| $ \mathit{\boldsymbol{A}}\Delta \mathit{\boldsymbol{s}} = \Delta \mathit{\boldsymbol{t}} $ | (1) |
式中A、Δs、Δt分别是Jacobi矩阵、慢度修正量和旅行时残差向量。L个约束条件建立的约束方程为
| $ \mathit{\boldsymbol{C}}\Delta \mathit{\boldsymbol{s}} = \mathit{\boldsymbol{F}} $ | (2) |
式中
| $ \mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} {{C_{11}}}&{{C_{12}}}& \cdots &{{C_{1N}}}\\ {{C_{21}}}&{{C_{22}}}& \cdots &{{C_{2N}}}\\ {}&{}& \vdots &{}\\ {{C_{L1}}}&{{C_{L2}}}& \cdots &{{C_{LN}}} \end{array}} \right] $ | (3) |
| $ \Delta \mathit{\boldsymbol{s}} = \left[ {\begin{array}{*{20}{c}} {\Delta {s_1}}\\ {\Delta {s_2}}\\ \vdots \\ {\Delta {s_N}} \end{array}} \right] $ | (4) |
| $ \mathit{\boldsymbol{F}} = \left[ {\begin{array}{*{20}{c}} {{f_1}}\\ {{f_2}}\\ \vdots \\ {{f_L}} \end{array}} \right] $ | (5) |
其中:N为速度模型单元数;si为第i个单元上一次迭代层析反演的慢度。
在初至波层析中,假设
| $ {f_i} = {{\tilde s}_i} - {s_i} $ | (6) |
| $ {C_{ij}} = \left\{ {\begin{array}{*{20}{l}} 1&{i = j}\\ 0&{i \ne j} \end{array}} \right. $ | (7) |
旅行时和约束方程构建的联合方程组可表示为
| $ \mathit{\boldsymbol{B}}\Delta \mathit{\boldsymbol{s}} = \mathit{\boldsymbol{H}} $ | (8) |
式中:
| $ \begin{array}{*{20}{l}} {e = {e_1} + \lambda {e_2} = {{(\mathit{\boldsymbol{A}}\Delta \mathit{\boldsymbol{s}} - \Delta \mathit{\boldsymbol{t}})}^{\rm{T}}}(\mathit{\boldsymbol{A}}\Delta \mathit{\boldsymbol{s}} - \Delta \mathit{\boldsymbol{t}}) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \lambda {{(\mathit{\boldsymbol{C}}\Delta \mathit{\boldsymbol{s}} - \mathit{\boldsymbol{F}})}^{\rm{T}}}(\mathit{\boldsymbol{C}}\Delta \mathit{\boldsymbol{s}} - \mathit{\boldsymbol{F}})} \end{array} $ | (9) |
式中:e1为观测数据目标函数;e2为已知约束条件的目标函数。
利用自适应算法求取正则化因子λ,即根据迭代层析反演中反演速度与初始模型速度自动确定。定义
| $ R = \frac{{{v_1}}}{{{v_{\rm{m}}}}} $ | (10) |
式中:v1为初始模型速度与层析迭代反演速度的较小者;vm是二者中的较大者。二者差别越小,R值越大,反之亦然。λ与R关系为
| $ \lambda = 1 - \frac{{{R_{{\rm{avg}}}} - {R_{{\rm{min}}}}}}{{{R_{\max }} - {R_{{\rm{min}}}}}} $ | (11) |
式中:Rmin和Rmax分别为R的最小值和最大值;Ravg为R的平均值。由上式可知:R越大,则λ越大,此时解比较稳定且收敛速度快,但如果数值过大将导致模型更新不足;R越小,λ越小,如果过小则解不稳定且收敛速度慢。只有取合理的值,则既能保证反演结果的稳定又能兼顾速度模型的有效更新。通过式(10)和式(11),可以根据迭代过程中的反演速度与初始模型速度的差自动确定正则化因子,实现正则化因子自适应计算。
2.1.2 高速层顶界确定方法在约束层析反演近地表速度模型后,高速层顶界误差较大。然后根据VSP测井及实钻井速度、深度信息,用协克里金方法优化获得降速带底界面的空间形态。
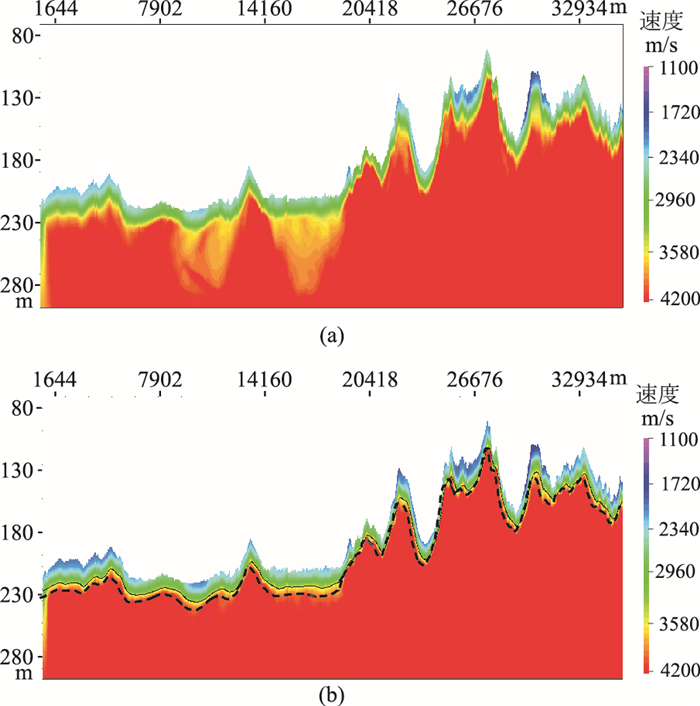
图 3a为无约束层析反演的近地表速度模型,图 3b为分层约束层析反演的近地表速度模型,后者反映的浅层结构信息更丰富。协克里金优化后的高速层顶界面与VSP资料更加吻合。图 4为约束层析静校正前、后叠加剖面,校正后陡倾地层(蓝色椭圆所示)成像明显改善,目的层(红色椭圆所示)成像信噪比得到提高,增强了连续性。
|
图 3 未约束(a)和分层约束(b)层析的近地表速度模型 图b中虚线为分层约束后得到的高速层顶界,实线为协克里金优化后得到的高速层顶界 |

|
图 4 约束层析静校正前(a)、后(b)叠加剖面 |
研究区地震数据的最大炮检距为7200m,常规NMO在出射角超过60°时则会引起动校过量。为了消除道集中存在的剩余时差,采用针对地下介质物性特征的速度分析方法即VTI各向异性动校正技术[23]消除剩余时差造成的道集不平、大炮检距动校不足或过量等现象。对于叠前时间偏移的CRP道集,关键问题是求取相对准确的速度各向异性参数。Alkhalifah等[24]提出的用各向异性参数和短排列动校正速度表示的非双曲线方程为
| $ {t^2} \approx t_0^2 + \frac{{{x^2}}}{{v_{{\rm{nmo}}}^2}} - \frac{{2\eta {x^4}}}{{v_{{\rm{nmo}}}^2[t_0^2v_{{\rm{nmo}}}^2 + (1 + 2\eta ){x^2}]}} $ | (12) |
式中:t为从炮点到接收点的反射波旅行时;t0为垂直反射旅行时;x是炮检距;vnmo为短排列动校正速度;η=(ε-δ)/(1+2δ),其中ε、δ为各向异性参数。这样,只需两个参数η和vnmo就可以进行时间域处理。处理过程中分两步进行参数扫描:第一步,利用近道进行双曲线速度分析,得到速度的估计值;第二步,将估计的速度函数带入方程,计算η谱。按时间拾取η之后,就可以对CRP道集按照式(12)进行四次时差校正。
Alkhalifah动校正公式是准确时距函数的泰勒近似,虽修正了炮检距的影响,但描述较大炮检距的时距关系时精度较低。为了提高精度,Vladimir等[25]引入经验校正系数c对大炮检距误差进行补偿
| $ {t^2} \approx t_0^2 + \frac{{{x^2}}}{{v_{{\rm{nmo}}}^2}} - \frac{{2\eta {x^4}}}{{v_{{\rm{nmo}}}^2[t_0^2v_{{\rm{nmo}}}^2 + c(1 + 2\eta ){x^2}]}} $ | (13) |
在弱各向异性情况下c≈1.2。
尤建军等[26]在分析VTI介质常规动校正方程的基础上,根据误差最小原理建立优化校正系数图版,实现对常规动校正公式大炮检距误差的修正,其最优化动校正方程为
| $ {t^2} \approx t_0^2 + \frac{{{x^2}}}{{v_{{\rm{nmo}}}^2}} - \frac{{2\eta {x^4}}}{{v_{{\rm{nmo}}}^2[t_0^2v_{{\rm{nmo}}}^2 + {c_{{\rm{opt}}}}(1 + 2\eta ){x^2}]}} $ | (14) |
式中copt为最优化校正系数。具体过程为:首先用式(13)反演得到vnmo和η的初始值;然后根据初始值范围在图板中查找最优化校正系数copt;最后应用式(14)实现对VTI介质大炮检距地震资料动校正。
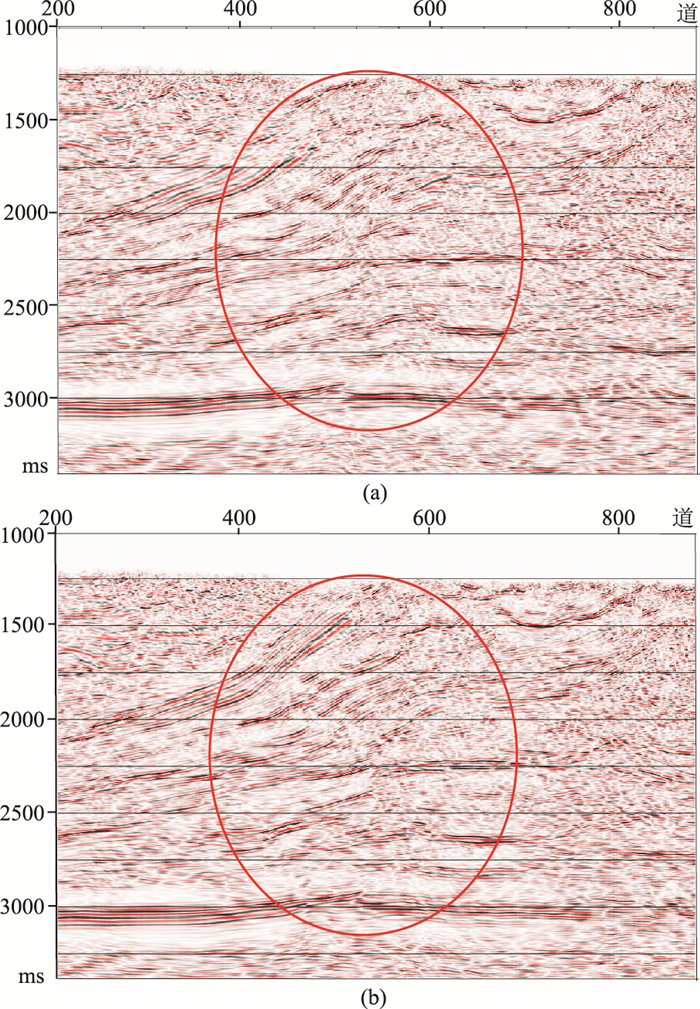
与常规动校正的叠前时间偏移剖面(图 5a)相比,应用VTI各向异性动校正技术后的叠前时间偏移剖面(图 5b)的成像质量,从浅层到目的层都有较大提高,尤其是浅层陡倾地层的成像(椭圆所示),达到了将大炮检距剩余动校正量最小化的目的。
|
图 5 各向异性动校正应用前(a)、后(b)的叠前时间偏移剖面 |
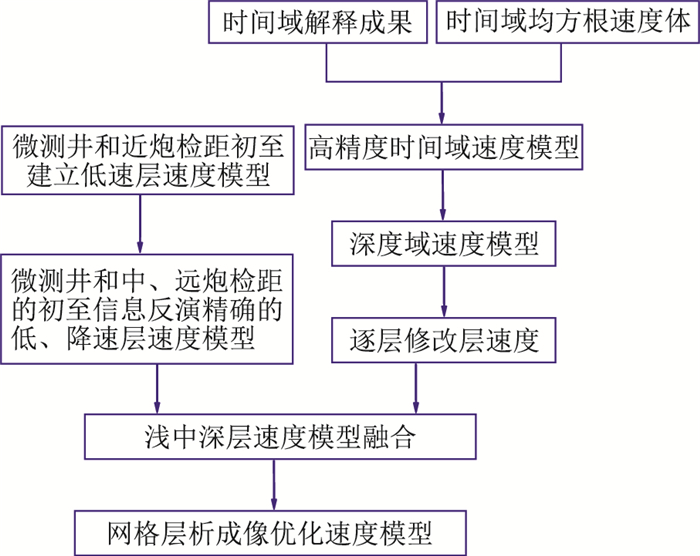
偏移速度场的精度直接影响叠前深度偏移成像的质量,四川盆地西北部龙门山冲断带前缘,在中、新生代之后主要经历了一系列的推覆、挤压运动,工区内地表出露志留系、泥盆系、石炭系、三叠系飞仙关组、雷口坡组、嘉陵江组、侏罗系白田坝组、千佛岩组、沙溪庙组、莲花口组和第四系共11套地层,岩性包括灰岩、砂泥岩、砾岩、河滩砾石等,并且近地表岩性变化快,表层速度模型建立困难。本文综合运用地面露头和井数据信息建立更合理的速度模型改善地下结构的成像效果,具体流程如图 6所示。
|
图 6 深度偏移速度建模流程 |
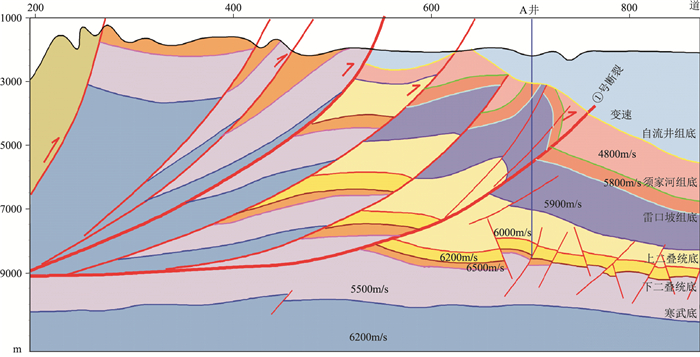
首先,采用分层约束层析静校正获得准确的近地表速度模型。然后参考井速度建立中深层初始速度模型,参考该区构造模式(图 7),最后将约束层析的近地表速度模型和初始中深层速度模型融合[27-28],得到完整的初始深度域速度模型,最后采用网格层析方法进一步优化速度模型。
|
图 7 过A井构造模式 |
网格层析[29-33]的主要步骤分为初始速度建模、网格层析偏移、剩余量拾取和反演迭代。首先,在叠前深度偏移共成像点道集(CIG)上进行剩余延迟谱分析。道集上每个角度对应的偏移深度可以表示为
| $ {z_\beta } = {z_0}\sqrt {{\gamma ^2} + ({\gamma ^2} - 1){{\tan }^2}\beta } $ | (15) |
式中:z0为零炮检距处的偏移深度;γ为z0与真实深度的比值;β为入射角。由下式可计算道集的剩余曲率为
| $ \Delta z = {z_0}[\sqrt {{\gamma ^2} + ({\gamma ^2} - 1){{\tan }^2}\beta } - 1] $ | (16) |
反演采用迭代算法,观测数据与参考模型的旅行时时差可通过慢度差沿射线l的线性积分获得,即
| $ \Delta t = \int_l \Delta s{\rm{d}}l $ | (17) |
通过矩形网格离散化后,可以得到反演公式
| $ \mathit{\boldsymbol{A}}\Delta \mathit{\boldsymbol{s}} = \Delta \mathit{\boldsymbol{t}} $ | (18) |
由于式(18)为病态层析反演方程组,为降低反演的多解性,加入正则化项,即
| $ \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{A}}\\ {\mu \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}} \end{array}} \right]\Delta \mathit{\boldsymbol{s}} = \left[ {\begin{array}{*{20}{c}} {\Delta \mathit{\boldsymbol{t}}}\\ 0 \end{array}} \right] $ | (19) |
式中Γ、μ分别为横向正则化矩阵和网格内的射线覆盖次数。求解该方程组就可得到慢度变化量,再通过一系列迭代,即可得到层析反演后的速度模型。
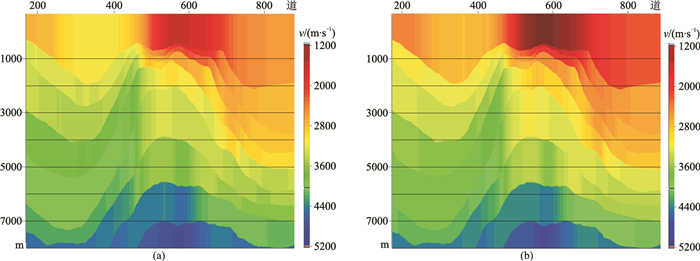
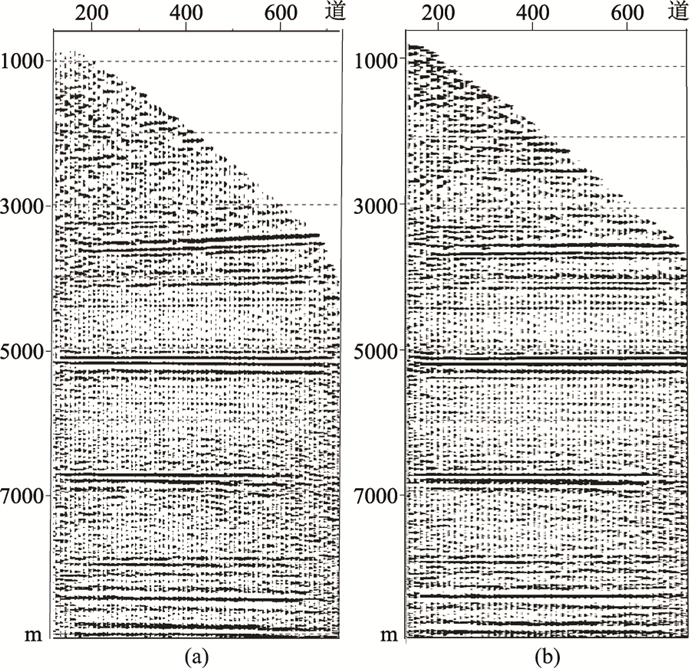
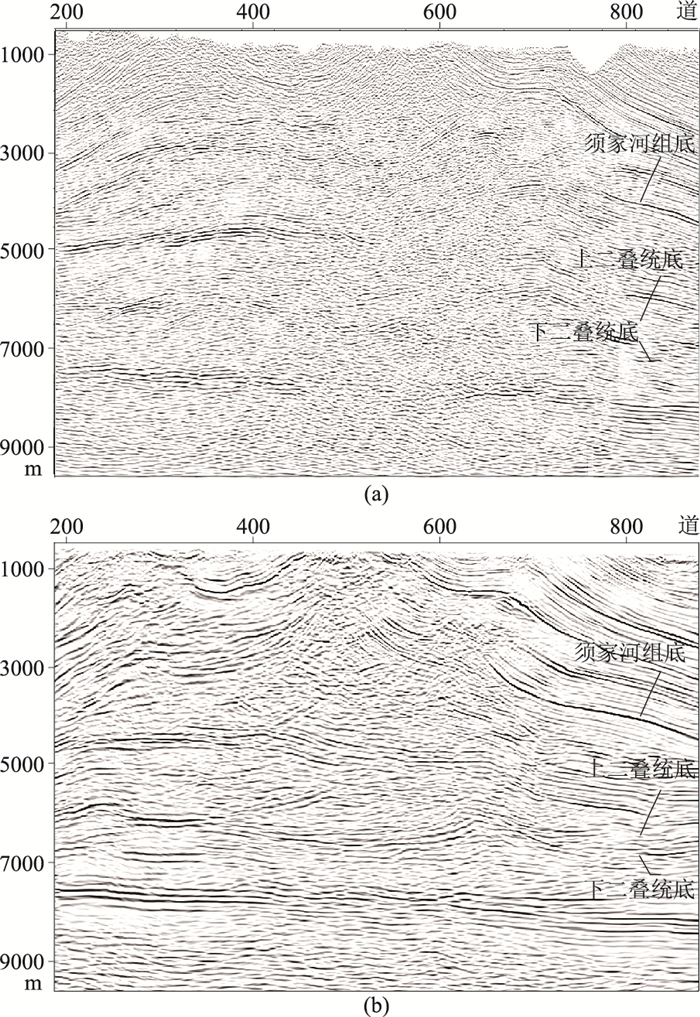
针对工区的特点,制定了以下相应的对策:对于浅层信噪比高、构造简单的情况,使用层约束的网格层析进行模型优化和质量控制;对于深层弱反射区及复杂反射区,在对道集进行信号加强的基础上做模型优化处理。通过多轮次的迭代,根据地质、测井信息优化速度模型,精确构建推覆构造带速度模型(图 8),不断提高①号断裂带下伏地层的成像精度。图 9为层约束网格层析前后共成像点道集对比,速度优化后,同相轴的拉平程度从浅到深都得到了较大改善,从而提高了叠前深度偏移的成像精度。层约束网格层析后的成像结果如图 10所示,层间信息更加丰富,构造形态更加合理,整体格局更加清楚。
|
图 8 速度优化前(a)、后(b)叠前偏移速度剖面对比 |
|
图 9 速度优化前(a)、后(b)叠前深度偏移道集对比 |
|
图 10 速度优化前(a)、后(b)叠前深度偏移剖面对比 |
(1) 用构造正演模拟的方法研究了低幅度构造的动力学成因,结果表明,模拟剖面与地震剖面的形态较为相似,证实了低幅度构造处理解释的可靠性;
(2) 分层约束的近地表建模方法可以获得高精度的近地表速度模型,计算得到的静校正能解决低幅度构造成像精度低的问题;
(3) VTI各向异性动校正技术避免了在大炮检距处产生的动校正过量问题,提高了浅层陡倾地层及深层低幅度构造的速度分析精度;
(4) 近地表与深层一体化建模技术能充分利用钻井数据等多信息指导初始速度模型的建立,从而获得较为可靠的叠前深度偏移资料。
| [1] |
梁国平. 低幅度构造识别技术研究综述[J]. 西部探矿工程, 2010, 22(3): 63-66. LIANG Guoping. A review of research on identification interpretation of low-amplitude structure[J]. West-China Exploration Engineering, 2010, 22(3): 63-66. DOI:10.3969/j.issn.1004-5716.2010.03.025 |
| [2] |
陈广军, 宋国奇. 低幅度构造地震解释探讨[J]. 石油物探, 2003, 42(3): 395-398. CHEN Guangjun, SONG Guoqi. Discussion on interpretation of low amplitude structures[J]. Geophysical Prospecting for Petroleum, 2003, 42(3): 395-398. DOI:10.3969/j.issn.1000-1441.2003.03.024 |
| [3] |
张涛, 王小卫, 田彦灿, 等. 火成岩速度-深度模型建立方法研究[J]. 石油地球物理勘探, 2015, 50(3): 431-435. ZHANG Tao, WANG Xiaowei, TIAN Yancan, et al. Igneous rock velocity depth model building[J]. Oil Geophysical Prospecting, 2015, 50(3): 431-435. |
| [4] |
张健, 黄芸. 二维地震资料落实低幅度圈闭方法探讨[J]. 中国石油勘探, 2002, 7(3): 54-59. ZHANG Jian, HUANG Yun. Method for using 2D seismic data for locating low-amplitude traps[J]. China Petroleum Exploration, 2002, 7(3): 54-59. DOI:10.3969/j.issn.1672-7703.2002.03.009 |
| [5] |
滕佃波, 汪鹏程, 王赟, 等. 利用叠前Kirchhoff积分偏移识别小断裂与低幅度构造[J]. 地球物理学进展, 2005, 20(4): 1035-1038. TENG Dianbo, WANG Pengcheng, WANG Yun, et al. The identification of small faults and low-amplitude structures by utilizing prestack Kirchhoff integral migration[J]. Progress in Geophysics, 2005, 20(4): 1035-1038. DOI:10.3969/j.issn.1004-2903.2005.04.025 |
| [6] |
邵雨, 李学义, 孔智勇, 等. 模型速度建场方法的应用研究[J]. 石油地球物理勘探, 2003, 38(6): 675-679. SHAO Yu, LI Xueyi, KONG Zhiyong, et al. Study on application of velocity-field model-building method[J]. Oil Geophysical Prospecting, 2003, 38(6): 675-679. DOI:10.3321/j.issn:1000-7210.2003.06.016 |
| [7] |
王时林, 石文武, 张博明, 等. 马头营凸起低幅度构造识别方法探讨[J]. 石油地质与工程, 2015, 29(5): 5-8. WANG Shilin, SHI Wenwu, ZHANG Boming, et al. Identification method of low amplitude structrue in Matouying bump salience[J]. Petroleum Geology and Engineering, 2015, 29(5): 5-8. DOI:10.3969/j.issn.1673-8217.2015.05.002 |
| [8] |
曹统仁, 周翼. 沙漠覆盖区的低幅度构造研究[J]. 新疆石油地质, 1999, 20(3): 218-220. CAO Tongren, ZHOU Yi. Study on low-extent structures in desert cover area[J]. Xinjiang Petroleum Geo-logy, 1999, 20(3): 218-220. DOI:10.3969/j.issn.1001-3873.1999.03.010 |
| [9] |
王孝, 刘文卿, 曾华会, 等. 复杂区分层约束近地表建模方法及应用[J]. 岩性油气藏, 2018, 30(5): 68-73. WANG Xiao, LIU Wenqing, ZENG Huahui, et al. Stratified constrained near-surface model building method and its application in complex surface area[J]. Lithologic Reservoirs, 2018, 30(5): 68-73. |
| [10] |
吴琳, 帕提幔, 薛慧. 静校正对低幅度构造资料处理的影响[J]. 石油地球物理勘探, 2008, 43(增刊1): 24-28. WU Lin, PA Timan, XUE Hui. Influence of static corrections on low amplitude structure[J]. Oil Geophysical Prospecting, 2008, 43(S1): 24-28. |
| [11] |
郑鸿明, 娄兵, 蒋在超. 复杂地貌区地震资料处理中的静校正方法[J]. 新疆石油地质, 2002, 23(3): 214-216. ZHENG Hongming, LOU Bing, JIANG Zaichao. Sta-tic correction methods for seismic data processing in complex geomorphic area[J]. Xingjiang Petroleum Geology, 2002, 23(3): 214-216. DOI:10.3969/j.issn.1001-3873.2002.03.011 |
| [12] |
宁松华, 漆立新. 低幅构造分析方法研究——以塔里木盆地三道桥构造为例[J]. 石油天然气学报, 2005, 27(3): 341-344. NING Songhua, QI Lixin. Method for analyzing a low amplitude structure[J]. Journal of Oil and Gas Technology, 2005, 27(3): 341-344. DOI:10.3969/j.issn.1000-9752.2005.03.021 |
| [13] |
管文胜, 段文胜, 查明, 等. 利用基于模型的层析速度反演进行低幅度构造成像[J]. 石油地球物理勘探, 2017, 52(1): 87-93. GUAN Wensheng, DUAN Wensheng, ZHA Ming, et al. Low-relief structural imaging with model-based tomographic velocity inversion[J]. Oil Geophysical Prospecting, 2017, 52(1): 87-93. |
| [14] |
韩嵩, 梁瀚, 关旭, 等. 川西北线束三维地震成像攻关及勘探意义[J]. 天然气勘探与开发, 2018, 41(3): 7-13. HAN Song, LIANG Han, GUAN Xu, et al. Application of swath 3D seismic imaging to northwestern Sichuan Basin:Implications for prospecting[J]. Natural Gas Exploration and Development, 2018, 41(3): 7-13. |
| [15] |
杨磊, 任旭虎, 綦耀光, 等. 多功能构造物理模拟装置的设计及应用[J]. 中国石油大学学报(自然科学版), 2010, 34(5): 152-157. YANG Lei, REN Xuhu, QI Yaoguang, et al. Design and application of multifunction tectophysics simulating apparatus[J]. Journal of China University of Petroleum(Edition of Natural Science), 2010, 34(5): 152-157. |
| [16] |
张宏方. 碳酸盐岩油藏缝洞单元离散数值模拟方法研究[J]. 石油钻探技术, 2015, 43(2): 71-77. ZHANG Hongfang. Research on discrete numerical simulation of fracture-cave unit in carbonate reservoir[J]. Petroleum Drilling Techniques, 2015, 43(2): 71-77. |
| [17] |
何文刚, 周建勋. 川东南马尾状褶皱带特征与形成机制的物理模拟[J]. 地球科学, 2018, 43(6): 2133-2148. HE Wengang, ZHOU Jianxun. Analogue modeling of feature and formation mechanism of horsetail-shaped fold belt in southeast Sichuan basin, south China[J]. Earth Science, 2018, 43(6): 2133-2148. |
| [18] |
吴奎, 何京, 张中巧, 等. 基于构造物理模拟实验的走滑量求取[J]. 石油地球物理勘探, 2019, 54(4): 891-900. WU Kui, HE Jing, ZHANG Zhongqiao, et al. Strike-slip fault displacement calculation based on structure physical simulation[J]. Oil Geophysical Prospecting, 2019, 54(4): 891-900. |
| [19] |
陈竹新, 李伟, 王丽宁, 等. 川西北地区构造地质结构与深层勘探层系分区[J]. 石油勘探与开发, 2019, 46(2): 397-408. CHEN Zhuxin, LI Wei, WANG Lining, et al. Structural geology and favorable exploration prospect belts in northwestern Sichuan Basin, SW China[J]. Petroleum Exploration and Development, 2019, 46(2): 397-408. |
| [20] |
王孝, 贺振华, 王述江, 等. 多信息约束层析反演静校正技术及其应用[J]. 天然气地球科学, 2010, 21(2): 316-320. WANG Xiao, HE Zhenhua, WANG Shujiang, et al. Technology of static correction for multi information constrained tomographic inversion and its application[J]. Natural Gas Geoscience, 2010, 21(2): 316-320. |
| [21] |
王志刚, 刘志伟, 王彦春, 等. 复杂近地表区综合长波长静校正方法[J]. 石油地球物理勘探, 2014, 49(3): 480-485. WANG Zhigang, LIU Zhiwei, WANG Yanchun, et al. An integrated long wavelength static correction me-thod for complex near-surface area[J]. Oil Geophysical Prospecting, 2014, 49(3): 480-485. |
| [22] |
李录明, 罗省贤. 复杂三维表层模型层析反演与静校正[J]. 石油地球物理勘探, 2003, 38(6): 636-641. LI Luming, LUO Shengxian. Tomographic inversion for 3-D complex near-surface model and static correction[J]. Oil Geophysical Prospecting, 2003, 38(6): 636-641. DOI:10.3321/j.issn:1000-7210.2003.06.010 |
| [23] |
张征, 狄帮让, 胡英, 等. CRP道集叠前精细处理技术应用[J]. 科技导报, 2012, 30(27): 35-40. ZHANG Zheng, DI Bangrang, HU Ying, et al. A-pplication of pre-stack detailed process technique on CRP traces gather[J]. Science Technology Review, 2012, 30(27): 35-40. DOI:10.3981/j.issn.1000-7857.2012.27.004 |
| [24] |
Alkhalifah T, Tsvankin I. Velocity analysis for transversely isotropic media[J]. Geophysics, 1995, 60(5): 1550-1566. DOI:10.1190/1.1443888 |
| [25] |
Vladimir G, Tsvankin I. Feasibility of nonhyperbolic moveout inversion in transversely isotropic media[J]. Geophysics, 1998, 63(3): 957-969. DOI:10.1190/1.1444407 |
| [26] |
尤建军, 常旭, 刘伊克. VTI介质长偏移距非双曲动校正公式优化[J]. 地球物理学报, 2006, 49(6): 1770-1778. YOU Jianjun, CHANG Xu, LIU Yike. Optimization of nonhyperbolic moveout correction equation of long offset seismic data in VTI media[J]. Chinese Journal of Geophysics, 2006, 49(6): 1770-1778. DOI:10.3321/j.issn:0001-5733.2006.06.025 |
| [27] |
赵玲芝, 谷跃民, 张建中. 多信息融合的近地表速度建模技术及应用[J]. 石油地球物理勘探, 2017, 52(1): 34-41. ZHAO Lingzhi, GU Yuemin, ZHANG Jianzhong. Near-surface model building with multi-discipline information fusion[J]. Oil Geophysical Prospecting, 2017, 52(1): 34-41. |
| [28] |
陈小静. 深度域浅中层速度融合建模技术应用[J]. 江汉石油科技, 2019, 29(2): 13-16. CHEN Xiaojing. Application of fusion modeling technology of shallow and middle velocity in depth domain[J]. Jianghan Petroleum Science and Technology, 2019, 29(2): 13-16. |
| [29] |
李慧, 成德安, 金婧. 网格层析成像速度建模方法应用[J]. 石油地球物理勘探, 2013, 48(增刊1): 12-17. LI Hui, CHENG Dean, JIN Jing. Velocity model building based on grid tomography[J]. Oil Geophysical Prospecting, 2013, 48(S1): 12-17. |
| [30] |
王华忠, 冯波, 王雄文, 等. 地震波反演成像方法与技术核心问题分析[J]. 石油物探, 2015, 54(2): 115-125. WANG Huazhong, FENG Bo, WANG Xiongwen, et al. Analysis of seismic inversion imaging and its technical core issues[J]. Geophysical Prospecting for Petroleum, 2015, 54(2): 115-125. DOI:10.3969/j.issn.1000-1441.2015.02.001 |
| [31] |
Berkhout A J. Combining full wavefield migration and full waveform inversion:a glance into the future of seismic imaging[J]. Geophysics, 2012, 77(2): S43-S50. DOI:10.1190/geo2011-0148.1 |
| [32] |
Lisle R J. Detection of zones of abnormal strains in structures using Gaussian curvature analysis[J]. AAPG Bulletin, 1994, 78(2): 1811-1819. |
| [33] |
王鹏, 王小卫, 雍运动, 等. 马头营地区低幅度构造速度建模方法[J]. 石油地球物理勘探, 2020, 55(4): 766-773. WANG Peng, WANG Xiaowei, YONG Yundong, et al. Velocity modeling of the low-relief structure in Matouying area of Jidong oilfield[J]. Oil Geophysical Prospecting, 2020, 55(4): 766-773. |



 王艳香, 甘肃省兰州市城关区雁儿湾路535号中国石油勘探开发研究院西北分院, 730020。Email:
王艳香, 甘肃省兰州市城关区雁儿湾路535号中国石油勘探开发研究院西北分院, 730020。Email: