② 中国石油勘探开发研究院西北分院, 甘肃兰州 730020;
③ 中国石油冀东油田公司勘探开发研究院, 河北唐山 063000
② Research Institute of Petroleum Exploration & Development-Northwest, PetroChina, Lanzhou, Gansu 730020, China;
③ Exploration and Development Research Institute, Jidong Oilfield Company, PetroChina, Tang-shan, Hebei 063000, China
低幅度构造是指构造平缓,闭合幅度相对较低的一类地质体,构造幅度在十几米到几十米。低幅度构造虽然规模不大,但是在有利的生储盖和油气运移条件下可能会形成“小而肥”的高产油气藏。马头营凸起发育基底披覆背斜构造。油藏主要分布于馆陶组,埋藏深度1300m左右,属层状岩性—构造油藏,低幅度构造对油藏起主控作用。大量水平井、斜井证实该区低幅度构造成像精度低,构造位置、高点解释精度低,与钻井结果存在较大误差。影响构造幅度、构造高点解释的主要因素为上覆地层速度建模的精度,上覆地层微弱的速度误差可以造成比低幅度构造本身都大的解释误差。中浅层断裂体系以及河道砂体导致的横向变速是影响低幅度构造成像精度的两个关键因素,这种速度误差一般为100~400m/s[1-2]。
本文利用二维数值模拟和三维物理模拟数据研究低幅度构造速度建模技术,定量检测速度建模技术的有效性。目前三维地震数字模拟代价十分昂贵,还不能实现全弹性波的三维数值模拟。地震物理模拟可以实现对三维地震勘探的全过程模拟[3]。物理模拟基于物理和几何相似原理,利用超声波在模型介质中的传播模拟地震波在地下介质中的传播过程,与野外地震有相同类型的弹性波场,遵循相同的物理定律。与数值模拟相比,不受各种波场传播理论的限制,模拟结果真实可靠,并且模拟结果不受各种假设条件的限制。数值模拟数据对速度模型精度更敏感,物理模拟的灵敏度略低。
本文主要采用沿层层析反演技术、高密度地质构造约束网格层析技术、完全数据驱动的高密度小网格层析技术对模型数据进行构造成像研究,定量测试技术的有效性。试验证明地质构造约束下的沿层层析和网格层析技术联合建模技术具有较强的抗干扰能力,可以较好地解决纵、横向变速问题,提高速度异常体的反演精度,为深度偏移提供精确的速度模型。
1 物理、数值模型建立基于模型的研究需要对实际地震资料进行简化,突出主要矛盾。物理模型建立主要包括模型设计、模具制作、模型制作、建立真实速度模型四部分[4]。物理模型与实际地层比例为1:10000。
1.1 模型设计马头营低幅度构造模型设计从浅到深考虑了四方面因素:地表及近地表、浅层上覆地层砂地比横向变化对下伏低幅度构造成像的影响、目的层内部河道砂体的识别及对下伏地层的影响、目的层低幅度圈闭模型。
模型的地层速度、密度参数主要参考工区测井数据。其中,中浅层Nm2为砂泥岩互层,地层内部随着砂岩地层厚度所占比例(砂地比)的增大,地层平均速度从2300m/s增大至2500m/s。砂地比的横向变化引起地层速度空间变化。Nm2的空间变速问题对下伏地层地震成像的影响是本文地震模拟实验研究的重点,能否准确描述速度空间变化规律是精确成像的关键。
简化模型共设计了九层(图 1),模型的第一层为近地表层,主要研究表层速度变化对下伏地层构造成像的影响。第二层Nm1为速度均匀的近似水平地层。第三层Nm2厚度较大,背景速度为2400m/s,在其内部设计三套厚度横向变化的速度异常体:速度为2000m/s的低速体、速度为2300m/s的中速体、速度为2600m/s的高速体。三套速度异常体纵向叠置,叠置的平均效应相当于模拟Nm2地层内部砂体含量变化导致的不规律空间速度变化,用于研究不同程度的横向变速对下伏地层构造成像的影响。第四层Nm3速度为2500m/s。第五到第七层为馆陶组三套地层,模拟低幅度构造,构造幅度为30~50m。三套地层速度差异小,分别为82、143m/s。其中Ng2顶界为低幅度圈闭的目标层。第八、第九层为高速基底层,速度差异较大。
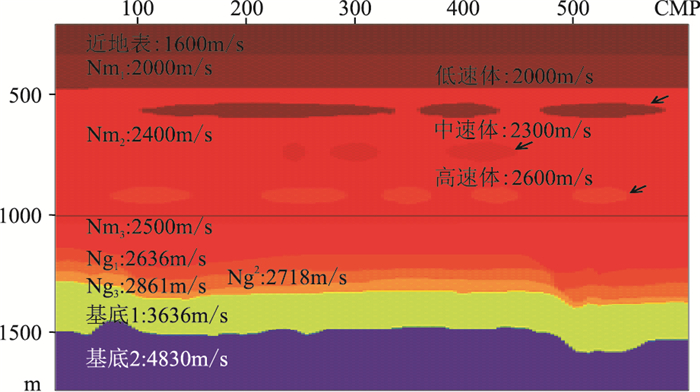
|
图 1 马头营低幅度构造简化剖面 |
物理模型的制作是一个非常复杂的过程。目前物理模型的主流制作工艺为浇注法。主要流程包括:根据地层结构设计图制作反向模具;根据各地层速度、密度等参数配制物理模型浇注材料;逐层模具搭建、加固、浇注和固化;逐层参数质控,浇注过程中用地层材料制作小尺寸样块,测试真实地层速度、密度参数;逐层层位形态质控。在模型制作过程中,地层材料的选取与配比十分关键,目前速度与密度精度非常高,同时材料本身的弹性参数也与实际地层具有较高的相似度。
与数值正演模拟一样,物理模型也可以建立真实速度场,真实速度模型建立需要两个关键参数:地层深度界面形态与层速度。模型制作过程中逐层表面扫描的结果就是物理模型的真实的层位界面,在模型制作过程中引入高精度激光形态扫描技术,每制作完成一个层位,精确测量该层的表面形态。通过层位形态质控可以确保实际地层形态与设计形态差异量化,并且扫描层位作为最终的地层界面,这些界面的深度、形态都可以当做先验信息。用已知层位和样块速度信息通过速度建模技术就可以得到模型真实的速度场(图 2)。真实模型与图 1所示的设计模型存在一定差异。首先,物理模型采集时需将模型完全浸入水中,所以模型顶部为水层。其次,模型制作过程中速度异常体是手工雕刻出来的,空间形态与设计存在一定差异。图 3为Nm2内部三套速度异常体的真实形态。
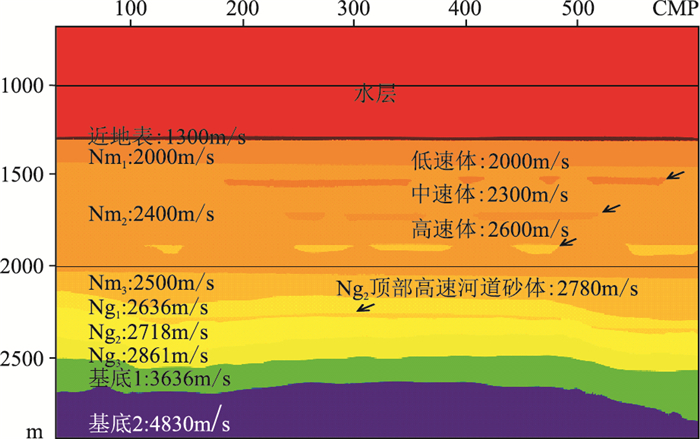
|
图 2 马头营低幅度构造物理模型剖面 |
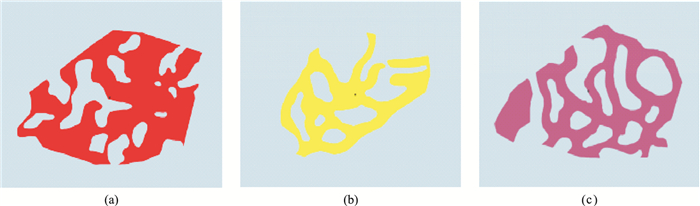
|
图 3 Nm2内部的三套速度异常体空间形态 (a)低速体(2000m/s);(b)中速体(2300m/s);(c)高速体(2600m/s) |
物理模型数据波场特征与三维地震物理模型数据采集系统有关,该系统由震源和接收器的定位系统、模型固定平台或水槽、震源和接收器及信号采集系统(发射、接收、模数转换)等设备组成[5-6]。
在物理模拟过程中,模拟起伏地表条件下的激发和接收才能达到真实模拟的目的,但这一直是物理模拟的难题。在地震物理模拟过程中要实现起伏地表采集需要解决两个问题:一是震源和接收器与模型的接触面尺寸;二是换能器与模型表面的耦合条件[7-10],目前这两个问题还是研究瓶颈。所以常规模型采集是将模型放入水槽中(图 4a),接近于海上采集。模型在水槽内完全浸没在水中,模型顶界面与水面一般有10~15cm的距离。采集时激发、接收探头贴近水面,与水介质完全耦合(图 4b),因此水层成为模型第一层介质。

|
图 4 水槽模型采集(a)及单道激发四道接收探头(b) |
物理模拟在水中采集,相对野外地震资料有两点不同:①无静校正问题,水槽采集形成水层—近地表低速夹层—地层结构模式,近地表折射波转换为反射波,无法开展静校正研究;②无低频噪声,主要干扰波为多次波。模型单炮记录(图 5a)上波场清晰且信噪比高,依次发育直达波、模型顶部反射波、地层反射波、模型底部反射波、模型顶部多次波。图 5b为物理模拟资料的叠前深度偏移成像剖面,所用速度为模型真实速度,图中红色箭头所指位置为Nm2内部的三套河道砂体及Ng2顶部河道砂。剖面上设计的地质体均能很好地成像,该模型能满足低幅度构造成像技术研究的需求。
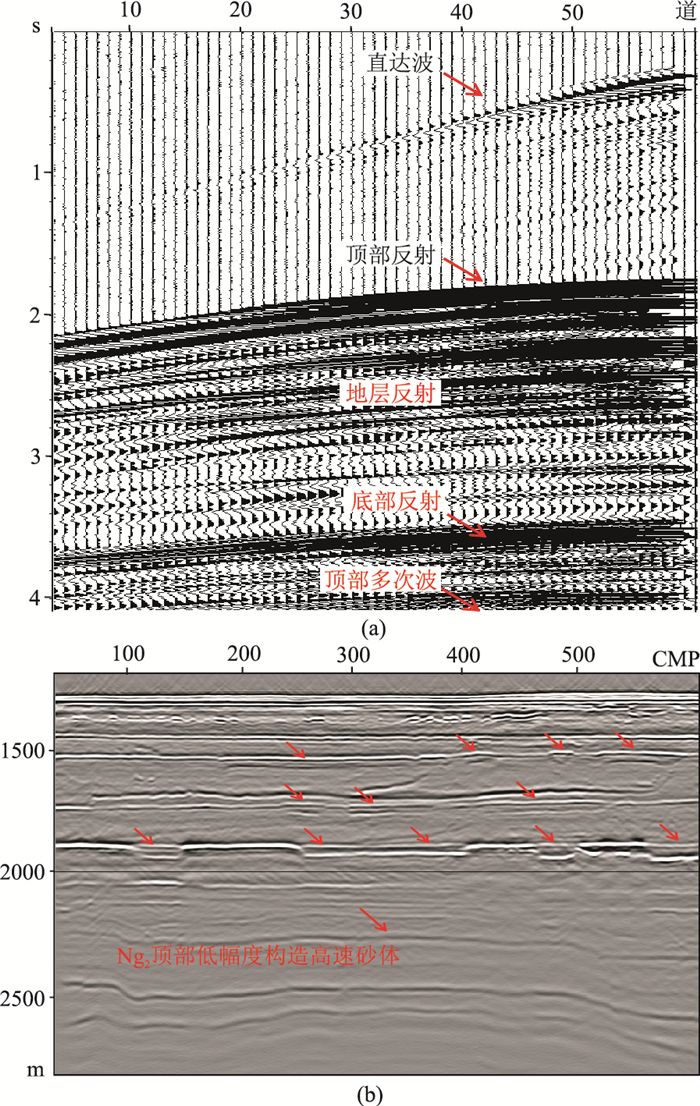
|
图 5 物理模拟单炮记录(a)和叠前深度偏移剖面(b) |
应用图 1所示模型进行弹性波动方程数值模拟,图 6为数值模拟的叠前深度偏移剖面,偏移速度为真实速度。数值模拟资料信噪比高,波场特征更清晰,在Nm2内部三套砂体的成像特征明显,Ng2低幅度构造成像准确。

|
图 6 数值模拟叠前深度偏移剖面 |
在模型相似的情况下,数值模拟资料与物理模拟资料存在较大差异。物理模型制作过程中,在Nm2内部采用水平浇筑方式,地层制作到规定厚度后进行河道的形态雕刻与充填,因而河道与地层融为一体,物理模拟资料与实际资料的河道沉积现象更相似。数值模拟资料信噪比高,河道砂体与围岩边界分明,更理想化。
3 基于数模—物模资料的低幅度构造速度建模本文的研究主要目的是建立一套适合低幅度构造成像的规范化流程。
目前,叠前深度偏移速度建模技术主要有两种:基于层位的沿层层析反演技术和基于网格的层析反演技术。沿层层析反演技术利用层位反演得到大套地层的平均速度,即速度场的低频分量,缺点是假设同一层纵向上是恒速的,不能精确反演出层间纵向存在的速度异常和横向微弱的速度变化。网格层析反演技术对小尺度速度异常比较敏感,可以反演出速度的高频分量,但是网格层析反演技术抗干扰能力差,尤其是短程多次波,严重影响网格层析结果的质量。如果用明确的构造层位信息去约束网格层析,那么反演更新的目标位置就会避开噪声发育区的影响,提高反演精度。本文联合两种建模技术进行低幅度构造速度建模,即采用沿层层析反演大套地层的速度场低频分量,采用地质构造约束网格层析反演小层速度场的横向变化,即速度场的高频分量,这样能够提高速度模型纵、横向的精度[11-13]。
3.1 沿层层析反演技术优化初始速度模型在实际资料处理过程中,初始速度模型有两种途径得到,第一种是由平滑的均方根速度根据Dix公式从时间域转换成深度域层速度,第二种由稀疏测井速度插值平滑获得。两种初始速度模型基本反映不出薄层速度异常体及构造趋势,与真实地层速度存在较大差异[14-15]。
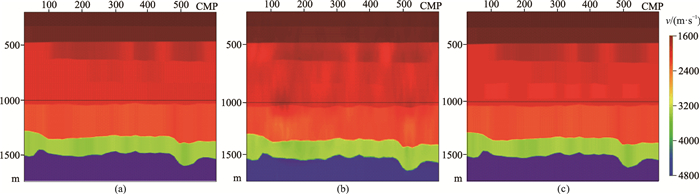
采用沿层层析反演技术优化初始速度模型,该方法具有较高的稳定性。在沿层层析速度反演过程中,在叠前深度偏移剖面上共拾取8个层位(图 7a剖面上彩色层位线),主要拾取大套地层速度界面,并在Nm2内部拾取两个层位控制砂体的变化趋势。受层位解释数目的限制,反演只能得到速度场的低频分量。从反演结果(图 8a)和成像结果(图 9a)看,速度模型只反映了大套地层特征,三套河道砂体速度异常变化略有反应,但精度不够;各个地质体均能成像;参考层及下伏低幅度构造地层均发生局部构造畸变,该模型有待进一步优化。
|
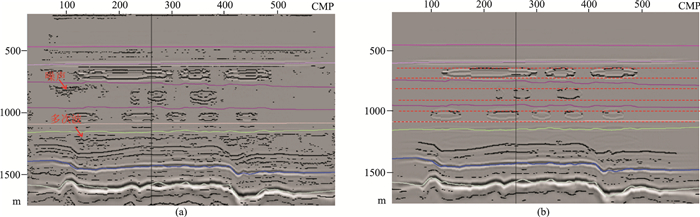
图 7 不同网格密度成像点拾取效果对比 (a)固定小网格成像点拾取;(b)加密构造约束成像点拾取 |
|
图 8 数值模拟数据不同方法的速度建模结果 (a)沿层层析模型;(b)高密度网格层析模型;(c)高密度构造约束网格层析模型 |
|
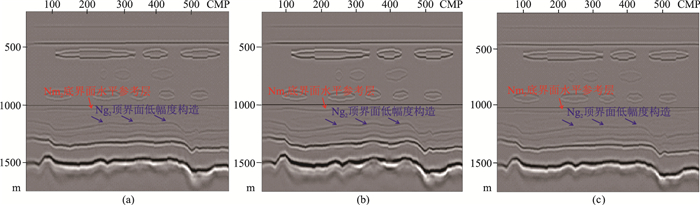
图 9 数值模拟数据不同速度模型叠前深度偏移剖面 (a)沿层层析模型;(b)高密度网格层析速度模型;(c)高密度构造约束网格层析速度模型 |
层析理论基础为Radon变换,将旅行时残差表示为慢度残差沿着射线路径的积分。通过沿着射线路径对旅行时残差进行反投影,求取速度场慢度的更新量。深度偏移常规层析目标函数为
| $ L(\mathit{\boldsymbol{s}}) = \left\| {\mathit{\boldsymbol{A}}\Delta \mathit{\boldsymbol{s}} - \Delta \mathit{\boldsymbol{t}}} \right\|_2^2 $ | (1) |
式中:A为灵敏度矩阵,其元素为射线在网格内的路径长度;Δt为慢度扰动前后的旅行时残差;Δs为慢度更新量。为了增强层析方程组的稳定性,减少多解性,应用正则化约束,则式(1)变为
| $ L(\mathit{\boldsymbol{s}}) = \left\| {\mathit{\boldsymbol{A}}\Delta \mathit{\boldsymbol{s}} - \Delta \mathit{\boldsymbol{t}}} \right\|_2^2 + \left\| {\mu \mathit{\boldsymbol{ \boldsymbol{\varGamma} }}\Delta \mathit{\boldsymbol{s}}} \right\|_2^2 $ | (2) |
式中:μ为射线在网格里的覆盖次数;Γ为一阶导数型正则化矩阵。加入约束条件后,速度反演结果更稳定[16-17]。
3.3 高密度构造约束网格层析反演技术网格层析成像利用旅行时优化速度误差,地层倾角信息可以提高速度模型的精度。在网格层析反演过程中,一般通过提高网格越密、减小网格尺寸来提高速度迭代精度。影响速度模型精度的因素除了速度反演算法,更重要的还有初始模型精度、参与计算的CRP道集的信噪比、覆盖次数、短程层间多次波等,如果忽略这些因素最终计算结果很难逼近真实速度。在低信噪比地区、工区边界、层间多次发育的区域采用固定小尺寸网格通常得不到理想的迭代效果,构造会发生畸变现象。
速度模型的构建与地质构造密切相关,在网格层析反演的基础上引入高密度地质层位做构造约束会大大提高迭代模型的精度[18-22]。用地质层位位置作为主要有效网格点,尤其是在地震信息不确定处,地质层位的选取可以明确有效信息,规避噪声。
3.4 试验对比分析图 7为数值模拟数据网格层析剩余曲率拾取对比。选取数值模拟数据进行两组试验:纯数据驱动高密度网格层析和高密度地质层位构造约束的网格层析。数模道集的信噪比要比物模和实际地震资料信噪比高,可以模拟具有较高信噪比的地震数据。另外道集上发育一些层间多次波,模拟实际资料多次波和有效波难以区分的情况。网格层析反演过程中剩余曲率拾取时,计算程序设置只要具有一定信噪比、双曲线能够连续分辨就可以作为网格点进行拾取。纯数据驱动高密度小尺度网格层析的最终拾取结果显示,有效波纵横向拾取精度都非常高,但存在一个致命的问题就是多次波和偏移噪声也参与进来(图 7a),导致速度场发生严重畸变(图 8b),构造假象增多。
高密度构造约束网格层析拾取结果如图 7b所示,不仅在主要地层界面定义地质层位(实线层位),在三套河道砂岩的顶、底界面也加密控制层位(红色虚线层位)。三套河道砂体模拟的是低信噪比状态,此时定义的加密层位的目的就是起到构造导向的作用。网格纵向尺度完全受控于层位拾取密度,成像点基本全部拾取在有效波同相轴上,成功规避了干扰波。图 8d为构造约束网格层析反演结果,三套砂体空间速度变化规律及形态均能反演出来,反演精度高于初始模型图 8a。
图 9为各速度模型的叠前深度偏移剖面,其中红色箭头所指地层为Nm2底界水平参考界面。虽然四个速度模型差异较大,但是模型设计的所有地质现象均得到很好地成像,只是构造幅度存在较大误差。①在速度准确情况下,水平参考层成像平直,其下低幅度构造完全准确(图 5b)。②沿层层析速度模型偏移结果在Nm2内部未反映出三套河道砂岩速度纵、横向变化规律,水平参考层发生明显畸变,其下伏低幅度构造均发生变形,在河道砂体正下方出现变形现象(图 9a蓝色箭头所示层位)。③以沿层层析速度为初始模型,在此基础上采用高密网格层析偏移结果,由于速度场发生畸变,水平参考层及目的层低幅度构造均存在较大误差(图 9b蓝色箭头所示层位)。④在沿层层析速度模型的基础上,采用高密度构造约束网格层析获得的模型虽然与真实模型存在一定误差,但是其深度偏移剖面成像结果却与真实模型成像结果非常接近,水平参考层无畸变,下伏低幅度构造幅度准确(图 9c蓝色箭头所示层位)。
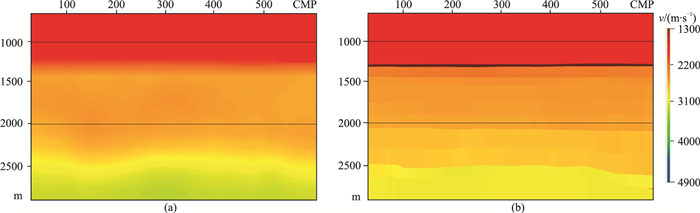
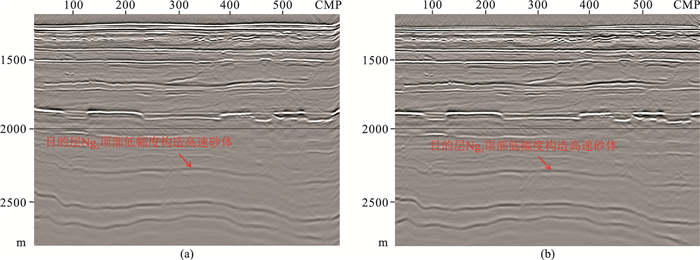
图 10为物理模型试验的两种速度场,图 11为对应的偏移剖面。物理模型的速度差异较大,尤其是Nm2地层内部,结果与数值模拟一样,所有地质现象均较好地得到成像,主要差别在于各地层的构造幅度。物理模型的第二个参考界面Nm2反射较弱,直接对比Ng2顶部河道砂低幅度构造区(红色箭头所指),纯数据驱动网格层析成像结果在模型边界构造变形比较严重,这与实际资料处理结论一致。图 12为用三种速度模型的叠前深度偏移结果所做的Ng2顶面构造图与真实形态的对比。表 1为三套叠前深度偏移数据的Ng2顶河道砂低幅度构造解释结果。可以看出:真实速度模型的偏移结果与真实模型(激光扫描结果)差异较小,主要由测量误差导致;高精度构造约束层析模型的偏移结果与真实模型吻合度高,高点的相对误差只有0.44%;数据驱动网格层析结果误差最大,绝对误差达到65m,比构造幅度都大,圈闭面积明显变小。
|
图 10 物理模拟数据的偏移速度模型 (a)高密度网格层析速度模型;(b)沿层层析+高密度层位约束网格层析速度模型 |
|
图 11 物理模拟数据不同速度模型的叠前深度偏移结果 (a)高密度网格层析速度模型;(b)沿层层析+高密度构造约束网格层析速度模型 |

|
图 12 物理模型数据不同速度模型偏移的Ng2顶面构造图与模型扫描结果的对比 (a)扫描结果;(b)真实速度模型;(c)高密度网格层析模型;(d)沿层层析+高密度构造约束网格层析速度模型 |
|
|
表 1 三套叠前深度偏移数据的Ng2顶河道砂低幅度构造解释结果 |
通过数值模拟、物理模拟联合的低幅度构造成像研究,可以得出以下几点结论:
(1) 速度模型误差对构造解释的影响程度大于对成像的影响,地质体能够成像不代表结果准确,应当进一步深入研究成像精度。
(2) 低幅度构造成像对速度模型精度要求较高,采取速度建模技术不当,会带来比构造本身都要大的误差。
(3) 完全数据驱动网格层析速度建模技术抗干扰能力差,必须借助对地质构造的认识才能得到满意的结果。
(4) 数值模拟是由不完全波场计算得到的结果,成像过程是个反算过程,因此只要模型正确,成像就正确。物理模拟波场复杂,即使模型正确,受成像算法限制,成像不一定完全正确。
| [1] |
管文胜, 段文胜, 查明, 等. 利用基于模型的层速度反演进行低幅度构造成像[J]. 石油地球物理勘探, 2017, 52(1): 87-93. GUAN Wensheng, DUAN Wensheng, ZHA Ming, et al. Low-relief structural imaging with model-based tomographic velocity inversion[J]. Oil Geophysical Prospecting, 2017, 52(1): 87-93. |
| [2] |
胡英, 张研, 陈立康, 等. 速度建模的影响因素与技术对策[J]. 石油物探, 2006, 45(5): 503-507. HU Ying, ZHANG Yan, CHEN Likang, et al. Influencing factors and technical strategies for velocity modeling[J]. Geophysical Prospecting for Petroleum, 2006, 45(5): 503-507. DOI:10.3969/j.issn.1000-1441.2006.05.013 |
| [3] |
魏建新, 牟永光, 狄帮让. 三维地震物理模型的研究[J]. 石油地球物理勘探, 2002, 37(6): 556-561. WEI Jianxin, MOU Yongguang, DI Bangrang. Study of 3-D seismic physical model[J]. Oil Geophysical Prospecting, 2002, 37(6): 556-561. DOI:10.3321/j.issn:1000-7210.2002.06.002 |
| [4] |
狄帮让, 魏建新, 夏永革. 三维地震物理模型技术的效果与精度研究[J]. 石油地球物理勘探, 2002, 37(6): 562-568. DI Bangrang, WEI Jianxin, XIA Yongge. Study on effects and precision of 3-D seismic physical model technique[J]. Oil Geophysical Prospecting, 2002, 37(6): 562-568. DOI:10.3321/j.issn:1000-7210.2002.06.003 |
| [5] |
李凡异, 魏建新, 狄帮让. 碳酸岩盐溶洞横向尺度变化的地震响应正演模拟[J]. 石油物探, 2009, 48(6): 557-562. LI Fanyi, WEI Jianxin, DI Bangrang. Forward simulation of seismic response in carbonate caverns with varied lateral scale[J]. Geophysical Prospecting for Petroleum, 2009, 48(6): 557-562. DOI:10.3969/j.issn.1000-1441.2009.06.004 |
| [6] |
张翊孟, 刘秋林, 张永科. 地震资料品质定量分析和采集参数优选[J]. 石油地球物理勘探, 2008, 43(增刊2): 1-5. ZHANG Yimeng, LIU Qiulin, ZHANG Yongke. Quantitative analysis of seismic data quality and optimization of acquisition on parameters[J]. Oil Geophysical Prospecting, 2008, 43(S2): 1-5. |
| [7] |
魏建新, 狄帮让. 起伏地表地震物理模型测试技术[J]. 石油地球物理勘探, 2006, 41(6): 619-624. WEI Jianxin, DI Bangrang. Test technique of seismic physical model for relief surface[J]. Oil Geophysical Prospecting, 2006, 41(6): 619-624. DOI:10.3321/j.issn:1000-7210.2006.06.003 |
| [8] |
裴正林. 任意起伏地表弹性波方程交错网格高阶有限差分法数值模拟[J]. 石油地球物理勘探, 2004, 39(6): 629-634. PEI Zhenglin. Numerical modeling using staggered-grid high-order finite-difference of elastic wave equation on arbitrary relief surface[J]. Oil Geophysical Prospecting, 2004, 39(6): 629-634. DOI:10.3321/j.issn:1000-7210.2004.06.002 |
| [9] |
董良国. 复杂地表条件下地震波传播数值模拟[J]. 勘探地球物理进展, 2005, 28(3): 187-194. DONG Liangguo. Numerical simulation of seismic wave propagation under complex near surface conditions[J]. Progress of Exploration Geophysics, 2005, 28(3): 187-194. |
| [10] |
牟永光, 裴正林. 三维复杂介质地震数值模拟[M]. 北京: 石油工业出版社, 2005.
|
| [11] |
彭海龙, 赫建伟, 任婷, 等. 基于地质构造约束的3D速度建模方法在琼东南盆地深水复杂断块区域成像中的应用[J]. 物探与化探, 2018, 42(3): 537-544. PENG Hailong, HE Jianwei, REN Ting, et al. The application of 3D velocity modeling based on geolo-gical constraint in Qiongdongnan basin deep water complex fault block area[J]. Geophysical and Geochemical Exploration, 2018, 42(3): 537-544. |
| [12] |
郝守玲, 赵群. 横向速度变化对构造成像影响的物理模拟研究[J]. 石油物探, 2008, 47(1): 49-54. HAO Shouling, ZHAO Qun. Physical modeling research for the effect of lateral velocity on structural imaging[J]. Geophysical Prospecting for Petroleum, 2008, 47(1): 49-54. DOI:10.3969/j.issn.1000-1441.2008.01.008 |
| [13] |
陈遵德, 徐广民, 贺振华, 等. 三维逐层层速度反演方法及误差分析[J]. 石油物探, 2000, 39(4): 12-18, 5. CHEN Zunde, XU Guangmin, HE Zhenhua, et al. The 3D inversion method of layer by layer interval velocity and error analysis[J]. Geophysical Prospecting for Petroleum, 2000, 39(4): 12-18, 5. DOI:10.3969/j.issn.1000-1441.2000.04.002 |
| [14] |
徐嘉亮, 周东红, 贺电波, 等. 高精度深度域层析速度反演方法[J]. 石油地球物理勘探, 2018, 53(4): 737-744. XU Jialiang, ZHOU Donghong, HE Dianbo, et al. High-precision velocity tomography inversion in the depth domain[J]. Oil Geophysical Prospecting, 2018, 53(4): 737-744. |
| [15] |
程玉坤, 刘建红, 周振晓, 等. 速度建模特色技术的实际应用[J]. 石油地球物理勘探, 2017, 52(增刊2): 110-115. CHENG Yukun, LIU Jianhong, ZHOU Zhenxiao, et al. Depth-domain velocity model building for prestack depth imaging[J]. Oil Geophysical Prospecting, 2017, 52(S2): 110-115. |
| [16] |
聂法健. 基于地震层位约束的速度建模技术在普光气田的应用[J]. 非常规油气, 2017, 4(2): 1-7. NIE Fajian. Application of velocity modeling techno-logy based on seismic horizon constraint in Puguang gasfield[J]. Unconventional Oil & Gas, 2017, 4(2): 1-7. DOI:10.3969/j.issn.2095-8471.2017.02.001 |
| [17] |
马彦彦, 李国发, 张星宇, 等. 叠前深度偏移速度建模方法分析[J]. 石油地球物理勘探, 2014, 49(4): 687-693. MA Yanyan, LI Guofa, ZHANG Xingyu, et al. Strategy of velocity model building in prestack depth migration[J]. Oil Geophysical Prospecting, 2014, 49(4): 687-693. |
| [18] |
谷延斌, 张旭东, 姚征, 等. 网格层析和高斯束偏移在深度域速度建模中的应用[J]. 石油地球物理勘探, 2018, 53(增刊1): 112-116. GU Yanbin, ZHANG Xudong, YAO Zheng, et al. Application of the grid tomography and Gauss beam migration in velocity modelling in the depth domain[J]. Oil Geophysical Prospecting, 2018, 53(S1): 112-116. |
| [19] |
王兆旗, 叶月明, 庄锡进, 等. 层控网格层析速度建模技术在陆上盐丘区的应用[J]. 天然气地球科学, 2016, 27(11): 2070-2076. WANG Zhaoqi, YE Yueming, ZHUANG Xijin, et al. Application of layer-constrained grid tomographic velocity modeling in onshore salt domes area[J]. Na-tural Gas Geoscience, 2016, 27(11): 2070-2076. DOI:10.11764/j.issn.1672-1926.2016.11.2070 |
| [20] |
肖艳玲, 范旭, 王晓涛, 等. 网格层析速度反演技术在齐古背斜叠前深度偏移中的应用[J]. 石油地球物理勘探, 2017, 52(增刊1): 98-103. XIAO Yanling, FAN Xu, WANG Xiaotao, et al. Mesh tomographic velocity inversion for the prestack depth migration of the Qigu anticline[J]. Oil Geophysical Prospecting, 2017, 52(S2): 98-103. |
| [21] |
张子良, 李振春, 张凯, 等. 地质模型约束的全波形速度建模反演及在复杂断块区的应用[J]. 石油地球物理勘探, 2020, 55(3): 599-606. ZHANG Ziliang, LI Zhenchun, ZHANG Kai, et al. Research of geological model-constrained FWI and application in complex fault-block zones[J]. Oil Geophysical Prospecting, 2020, 55(3): 599-606. |
| [22] |
张在金, 陈可洋, 范兴才, 等. 井控与构造约束条件下的网格层析速度建模技术及应用[J]. 石油物探, 2020, 59(2): 208-217. ZHANG Zaijin, CHEN Keyang, FAN Xingcai, et al. Seismic wave velocity modelling through grid tomography inversion constrained by well logging and structural modeling[J]. Geophysical Prospecting for Petroleum, 2020, 59(2): 208-217. |



 田彦灿, 甘肃省兰州市城关区雁儿湾路535号中国石油勘探开发研究院西北分院, 730020。Email:
田彦灿, 甘肃省兰州市城关区雁儿湾路535号中国石油勘探开发研究院西北分院, 730020。Email: