② 东方地球物理公司研究院地质研究中心, 河北涿州 072751;
③ 中国石油华北油田公司勘探开发研究院, 河北任丘 062550
② Geological Research Center, BGP, CNPC, Zhuozhou, Hebei 072751, China;
③ Exploration and Development Research Institute, Huabei Oilfield Company, PetroChina, Renqiu. Hebei 062552, China
在煤层气开采过程中,通过排水和气体抽采,可降低储层内压力,促进气体解吸。随着宏观孔隙中气体压力的降低,微观孔隙中的甲烷向宏观孔隙中扩散运动,导致微观孔隙中的气体与表面吸附气体之间形成浓度梯度,进而甲烷从表面解吸出来扩散到宏观孔隙中,形成达西流,流量取决于渗透率。因此,渗透率被认为是影响煤层气产量的重要参数之一。
目前煤层气渗透率预测方法主要有地质方法[1-3]、煤岩学方法[4-6]、直接测试推算法和实验室方法[7-8]等,这些方法均难以描述渗透率空间变化规律。前人研究[9-11]表明,地应力是影响煤储层渗透率的主要因素之一。Enever等[12]、何伟钢等[13]认为煤储层的渗透率随着地应力的增加呈指数降低的趋势。据此,可以通过地应力预测煤系地层的渗透率。获取地应力的方法主要包括测量法、测井计算、数值模拟及基于地震资料预测等。基于地震资料的地应力预测方法主要有反射系数反演[14]、岩石物理建模[15-18]和曲率属性预测[19-21]等。其中,基于曲率属性的地应力预测方法得到的地应力与地层变形程度相关,即地层变形程度越高,地应力越大。但是,煤系地层岩体强度低、性脆,地层变形程度高的地区易产生断裂,导致地应力释放而成为应力低值区,因此基于曲率的地应力预测结果不能准确表征煤系地层的渗透率分布规律。
为解决上述问题,首先利用地震资料的曲率属性预测地应力分布;其次利用基于特征值的相干算法预测断裂发育区;然后利用地应力与相干数据体融合,剔除不合理的地应力预测区(即断裂区);再根据地应力与渗透率的关系,最终定量预测煤系地层渗透率。
1 技术方法 1.1 基于曲率属性预测地应力曲率属性可以用于表示地层的弯曲程度。Murray[22]认为曲率越大,应变越大。Price等[23]推导了应力与曲率和弹性力学参数之间的定量关系, 从而奠定了利用曲率属性估算应力的理论基础。
虎克定律将应变与应力联系在一起, 而地层曲率与应变有着密切的关系。Hunt等[20]在广义虎克定律基础上建立了地层曲率与地应力之间的关系
| $ \sigma = Ee = E \cdot \frac{h}{2} \cdot {K_{\rm{c}}} $ | (1) |
式中: σ为应力;E为杨氏模量;e为应变;h为褶皱岩层的厚度;Kc为最大曲率属性。岩层厚度在区域内较稳定,因而可以忽略,则式(1)简化为
| $ \sigma = E \cdot {K_{\rm{c}}} $ | (2) |
由式(2)可知, 利用杨氏模量与曲率的乘积可近似表征地层的应力大小,地应力大小与曲率大小趋势一致。一般来说,在断裂发育区,曲率值大,预测地应力值相应也大,但实际上在地层断裂后,应力得到释放,地应力变得很小,与曲率趋势不一致。因此,根据曲率属性预测地应力时,需要区分断裂发育区与不发育区。
1.2 本征结构相干技术识别断裂相干体技术是用于描述断裂和地层特征的一种解释性处理技术[24],在油气田和煤田勘探中有着广泛的应用[25-29]。相干性是地震道之间相似性的度量,主要分析以目标点为中心的时窗内相邻地震道波形的相似性,可判断地层的连续性,即利用波形之间的相似性反映地层的连续性特征,以此指示断裂、地层岩性突变和特殊地质体的发育区。
地震资料相干体的算法主要经历了三次发展,第一代算法只限于计算相邻道间的相关性,适用于信噪比较高的地震资料,主要用于大断裂识别;第二代算法为相似性算法,沿倾角(方位角)计算多道间的相干性,抗噪能力较强,但横向分辨率较低;第三代算法在本征结构的分解基础上,利用特征结构计算相干,在保证抗噪能力的同时提高断裂的横向分辨能力。
研究区地层平缓,部分断裂在地震资料上仅表现为同向轴的小幅度错断,不易识别,故优选第三代相干算法识别断裂。
1.3 地应力与相干属性融合根据曲率属性预测的地应力在断裂发育处与实际情况不符,需要利用识别的断裂对预测的地应力加以约束。利用预测的地应力与相干属性融合,形成新的数据体,可以反映地应力真实的分布情况。
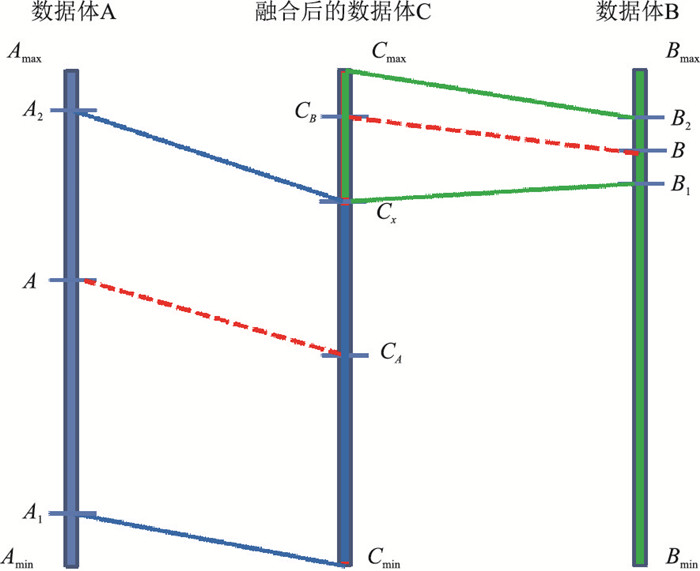
对于多幅图像中的对应象元逐个进行加、减、乘、除四则运算或矢量运算,求出复合图像的和、差、积、商等,可以达到图像增强的效果。图像相加可以减小噪声,增大对比度;图像相减有利于监测动态变化信息,或从模糊的背景中把有用的目标信息检测出来;图像相乘可使图像轮廓增强;图像相除可以求取比值图像,使得灰度值不大的图像在比值后反差增强。当然,也可以根据不同属性参数的特点设计出复杂的代数运算方程,达到再增强效果的目的。为了利用一维颜色表显示两种不同的地震属性,需要应用数学比例运算关系把两种属性数据融合在一起,即把地震属性数据体A和地震属性数据体B按比例关系融合生成新的地震属性数据体C,从而实现在一维颜色模式下同时显示两种属性的功能(图 1)[29],主要步骤如下。
|
图 1 属性数据融合示意图 |
(1) 确定数据A参与融合的数据范围。分析地震属性数据A的最大(Amax)、最小(Amin)值, 根据需求确定数据A中参与融合的部分数据(即A1与A2之间的数据), 且Amin≤A1 < A2≤Amax。
(2) 确定数据B参与融合的数据范围。分析地震属性数据B的最大(Bmax)、最小(Bmin)值, 根据需求确定数据B中参与融合的部分数据(即B1与B2之间的数据), 且Bmin ≤B1 < B2≤Bmax。
(3) 融合数据A和B,形成新的数据C。融合后的数据C的最大(Cmax)、最小(Cmin)值与属性数据A的最大、最小值比例化,使Cmax=Amax、Cmin=Amin。在数据C的最大、最小值之间选择一个合适的值作为分界点Cx, 且Cmin < Cx < Cmax(或Amin < Cx < Amax),将属性数据A和B按比例融合成数据C。将数据A中(A1, A2)范围的数据融合在数据C中的(Cmin, Cx)数据段, 数据B中(B1, B2)范围的数据融合在数据C中的(Cx, Cmax)数据段,即得到最终表征地应力的数据体。
本文将地应力作为数据A,相干属性作为数据B,两者按比例融合生成数据C,相干属性在数据C中占比小。
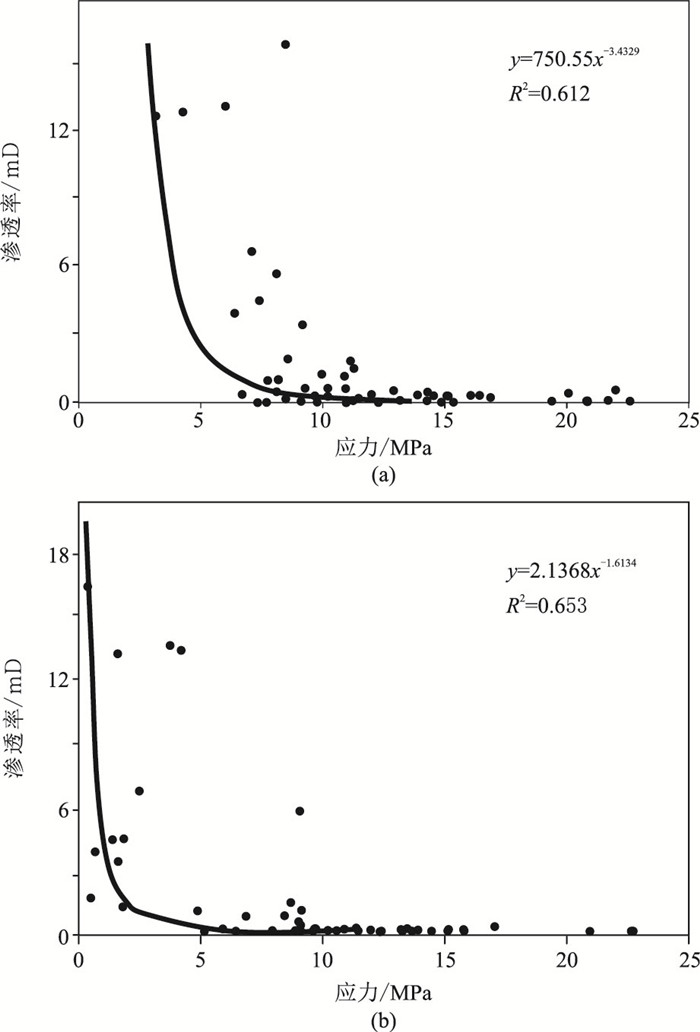
1.4 渗透率预测利用地应力与相干属性融合的数据C,可客观表示地层的有效应力大小。前人通过实验室测试与分析认为,最小主应力和有效应力均与渗透率呈幂指数关系(图 2)[13]。
|
图 2 地应力与渗透率关系示意图 (a)最小主应力;(b)有效应力。R为相关系数 |
由图 2可以看出,随着煤层孔隙内气体压力的降低,有效应力降低,煤层内孔隙趋于关闭,渗透率降低;随着气体压力的升高,煤层气储层中的孔隙呈张开趋势,渗透率也会升高。因此,当有效应力增大时,渗透率会降低;当有效应力减小时,渗透率会升高,据此可以通过地应力开展煤系地层的渗透率预测。
本文基于地应力预测渗透率可分为以下几个主要步骤:
(1) 利用式(1)预测地应力,并分析其合理性;
(2) 利用属性融合技术,剔除式(1)预测的不合理的地应力区域,也就是断层发育区;
(3) 收集钻井点的渗透率和地应力数据,利用交会图分析渗透率与地应力的关系;
(4) 根据交会分析结果,建立渗透率与地应力的数学关系式;
(5) 利用数学关系式将地应力转化为渗透率,实现渗透率的定量预测。
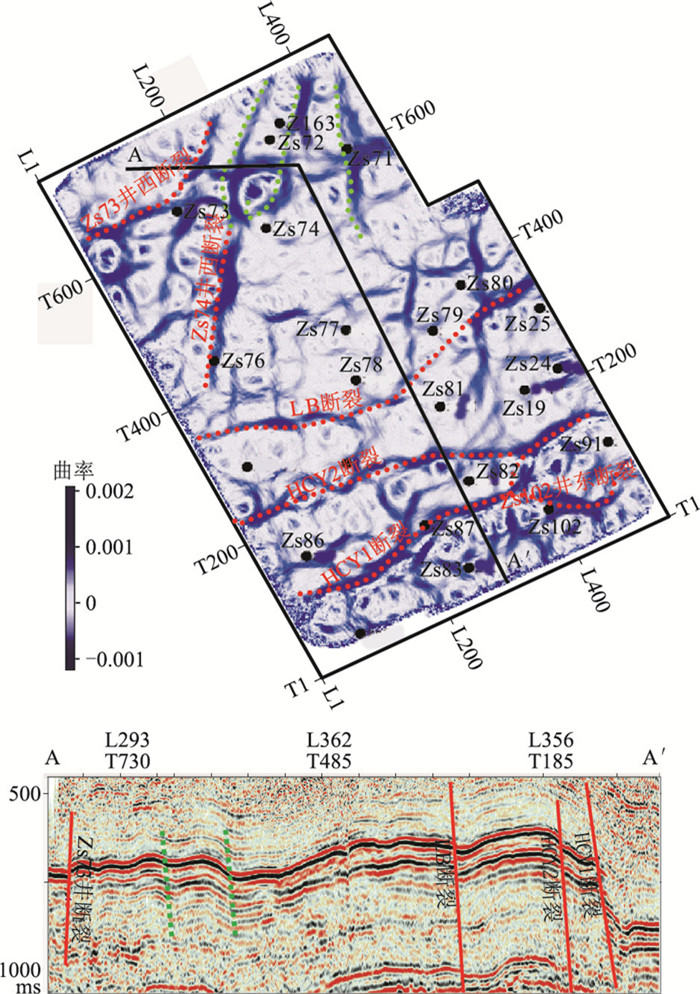
2 应用实例 2.1 工区概况沁水盆地LB区块发育以张扭应力体系为主的断裂(图 3),分别为NE向、NNE向和SN向。主断裂HCY1、HCY2和LB断裂控制构造格局;次级断裂(如Zs102井东、Zs74井西、Zs73井西断裂等)影响煤层裂缝的发育。

|
图 3 LB区块3#煤层顶面构造图 |
LB区块3#煤层非均质性强,导致钻井产气量差异大,中、低产井及干井约占71.5%。因此,准确刻画煤储层的渗透性空间分布特征,有助于开发井网的部署,提高单井产量及成功率。
2.2 地应力预测曲率属性反映地层变形程度,在断裂发育部位(红线处)和地层变形程度大部位(绿线处)曲率值大,如图 4所示。
|
图 4 3#煤层曲率属性(上)和AA′地震剖面(下) |
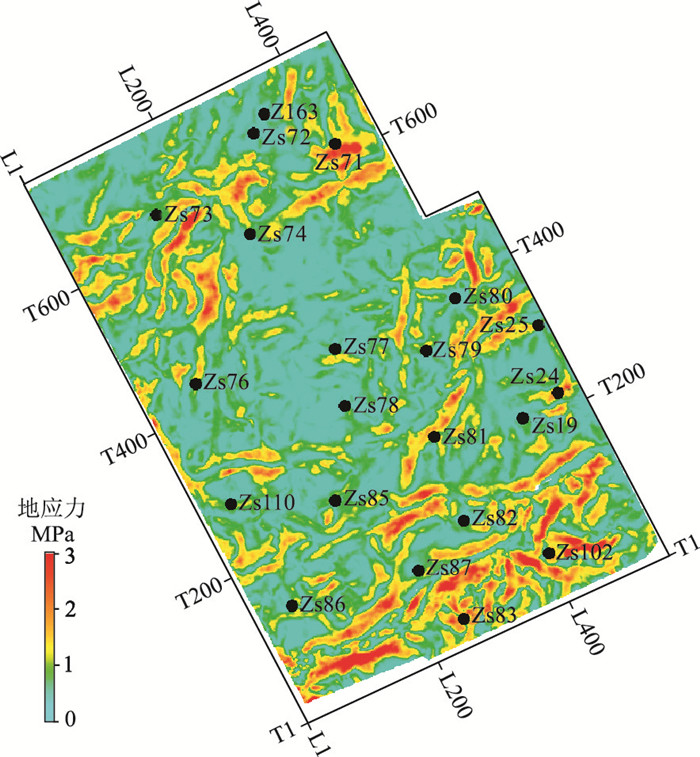
基于曲率属性预测的地应力(图 5)与曲率属性(图 3)趋势一致,断裂发育部位(红线处)地应力值相对较大。
|
图 5 基于曲率属性预测的3#煤层地应力 |
曲率属性表征的是构造运动后的地层变形程度,由其估算的地应力属于古构造应力,断裂发育区为古应力的高值区,但形成断裂后地应力释放,现今为地应力低值区。根据曲率属性预测的地应力结果与现今应力相矛盾。因此,通过数据体融合技术剔除(预测结果不准确的)断裂区,达到预测现今地应力的目的。
首先对地震数据进行构造导向滤波预处理,再优选本征构造相干的方法刻画断裂(图 6)。研究区的断裂整体上欠发育,仅在工区南部发育几条呈近东西向展布的大断裂(相干属性低值条带)。
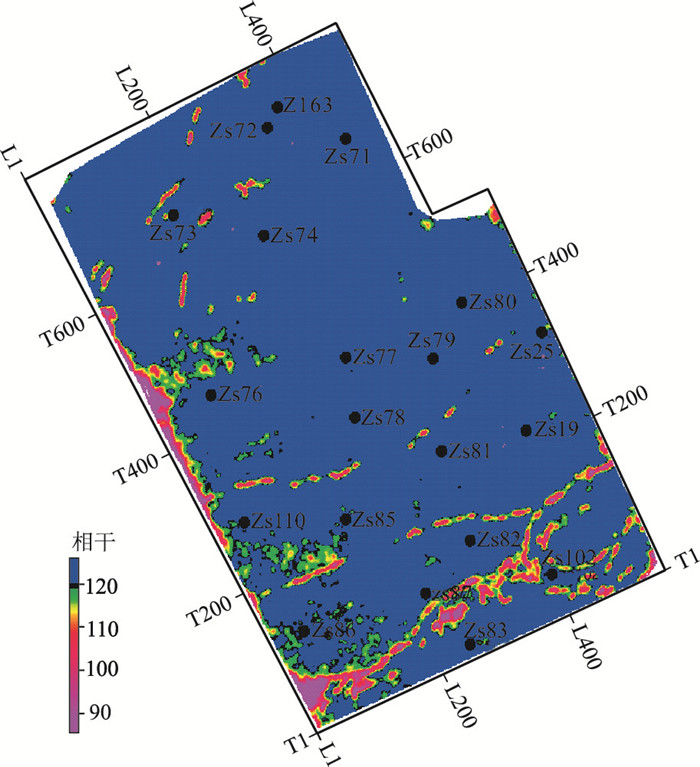
|
图 6 3#煤层相干属性 |
其次以基于曲率预测的地应力数据为背景, 选取全部值域数据(A1=0.1, A2=8.0)与相干属性数据中表征断裂部分的数据(B1=0, B2=120.0)融合。根据融合后的数据求取最终的地应力如图 7所示, 平缓的斜坡(蓝绿色区)为中等值域区;断裂区(深蓝色区)地应力最小;地应力高值区(红色区)与断裂分布位置不一致。
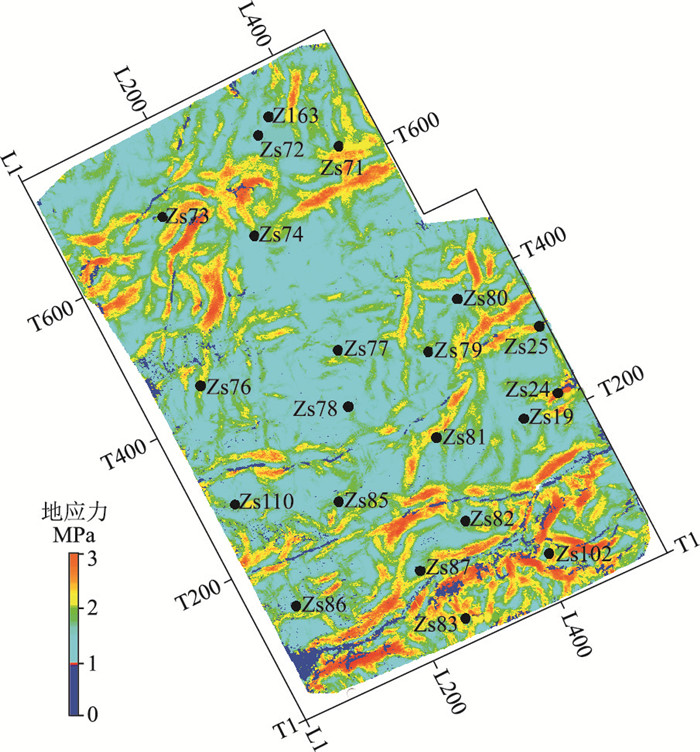
|
图 7 基于融合数据预测的3#煤层地应力 |
研究区内6口井有渗透率数据(表 1),渗透率随地应力增大呈幂指数降低(图 8),拟合幂函数为
| $ y = 0.0095{x^{ - 1.558}} $ | (3) |
|
|
表 1 渗透率与地应力对应表 |
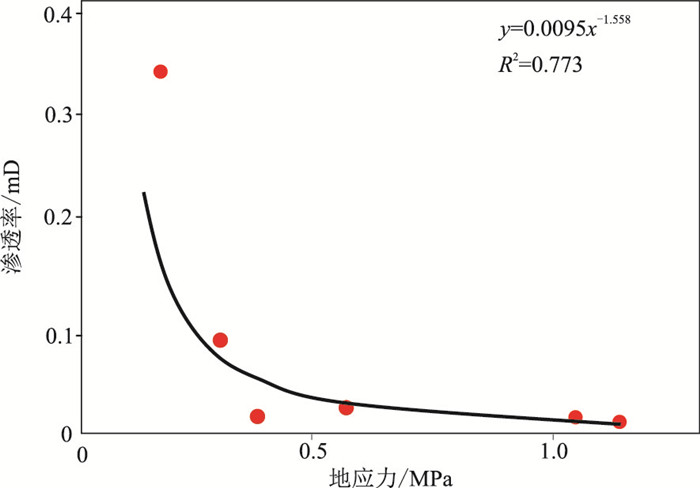
|
图 8 3#煤层地应力与渗透率交会图 |
据此可将地应力转换为渗透率(图 9)。
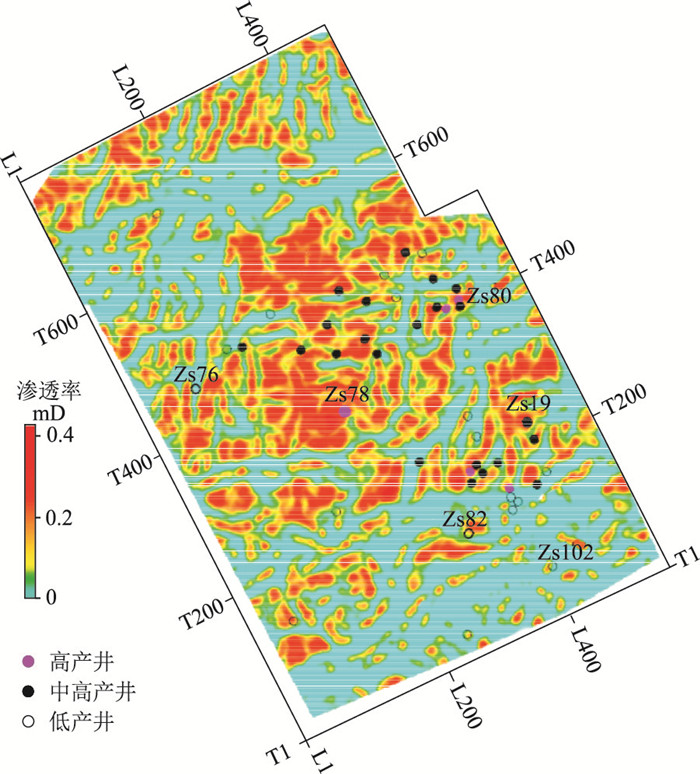
|
图 9 3#煤层预测渗透率 |
由图 9可以看出,斜坡区经过构造运动后,应力松弛,可以诱导煤层割理的产生, 并使其处于开启状态, 有利于提高煤层渗透率。已知评价井和开发井的实钻结果表明,高产井和中—高产井均位于渗透率高值区域,低产井位于渗透率低值区域。说明本文方法预测的煤层渗透率成果可以有效指导井位部署。
3 结论(1) 基于曲率属性预测的地应力在断裂处与实际不吻合;
(2) 根据地应力与渗透率的数学关系,能有效预测渗透率大小,可以为勘探开发提供参考依据;
(3) 本文方法预测渗透率精度还有待提高,首先,通过地震资料的相干属性识别断裂,尺度较大,预测结果会存在误差。另外,煤储层渗透率与地应力、地温及煤体内部孔隙结构均有关系,未来需要进一步研究。
| [1] |
赵庆波, 刘冰, 姚超. 世界煤层气工业发展现状[M]. 北京: 地质出版社, 1998.
|
| [2] |
员争荣. 构造应力场对煤储层渗透性的控制机制研究[J]. 煤田地质与勘探, 2004, 32(4): 44-46. YUN Zhengrong. Research on mechanism of tectonic stress field controlling coal permeability[J]. Coal Geology and Exploration, 2004, 32(4): 44-46. DOI:10.3969/j.issn.1001-1986.2004.04.014 |
| [3] |
张泓, 王绳祖, 郑玉柱, 等. 古构造应力场与低渗煤储层的相对高渗区预测[J]. 煤炭学报, 2004, 29(6): 708-711. ZHANG Hong, WANG Shengzu, ZHENG Yuzhu, et al. Palaeotectonic stress-fields and prediction of higher-permeability region for coalbed methane exploration in low-permeability coal reservoirs[J]. Journal of China Coal Society, 2004, 29(6): 708-711. DOI:10.3321/j.issn:0253-9993.2004.06.016 |
| [4] |
李小彦, 李静, 杨利军, 等. 铁法煤田煤储层渗透性预测[J]. 煤田地质与勘探, 1998, 26(2): 34-36. LI Xiaoyan, LI Jing, YANG Lijun, et al. The predic-tion of coal reservoir permeability in Tiefa coal field[J]. Coal Geology and Exploration, 1998, 26(2): 34-36. |
| [5] |
彭金宁, 傅雪海. 铁法矿区煤储层裂隙系统评价与渗透率预测研究[J]. 中国煤田地质, 2005, 17(5): 40-43. PENG Jinning, FU Xuehai. Coal reservoir fissure system assessment and permeability prediction in Tiefa mining area[J]. Coal Geology of China, 2005, 17(5): 40-43. DOI:10.3969/j.issn.1674-1803.2005.05.013 |
| [6] |
傅雪海, 秦勇. 多相介质煤层气储层渗透率预测理论与方法[M]. 江苏徐州: 中国矿业大学出版社, 2003. FU Xuehai, QIN Yong. Theories and Techniques of Permeability Prediction of Multi-phase Medium Coalbed Methane Reservoirs[M]. Xuzhou, Jiangsu: China University of Mining and Technology Press, 2003. |
| [7] |
孙培德, 鲜学福. 煤层瓦斯渗流力学的研究进展[J]. 焦作工学院学报, 2001, 20(3): 161-165. SUN Peide, XIAN Xuefu. Advances in study on coal gas seepage mechanics[J]. Journal of Jiaozuo Institute of Technology, 2001, 20(3): 161-165. DOI:10.3969/j.issn.1673-9787.2001.03.001 |
| [8] |
孙培德, 鲜学福. 煤层气越流的固气耦合理论及应用[J]. 煤炭学报, 1999, 24(1): 60-64. SUN Peide, XIAN Xuefu. Coupled models for coal seam deformation gas leakage and its applications[J]. Journal of China Coal Society, 1999, 24(1): 60-64. DOI:10.3321/j.issn:0253-9993.1999.01.014 |
| [9] |
Bustin R M, Cui X, Chikatamarla L. Impacts of volumetric strain on CO2 sequestration in coals and enhanced CH4 reeovery[J]. AAPG Bulletin, 2008, 92(1): 15-29. DOI:10.1306/08220706113 |
| [10] |
Harpalani S, Chen G. Gas slippage and matrix shrinkage effects on coal permeability[C]. 1993 International Coal-bed Methane Symposium, Tusealoosa, USA, 1993.
|
| [11] |
Chikatamarla L, Cui X, Bustin R M. Implications of volumetrie swelling/shrinkage of coal in sequestration of acid gases[C]. 2004 International Coalbed Methane Symposium, Tusealoosa, USA, 2004.
|
| [12] |
Enever J R, Henning A. The relationship between permeability and effective stress for Australian coal and its implications with respect to coalbed methane exploration and reservoir modeling[C]. 1997 Interna-tional Coalbed Methane Symposium, Tusealoosa, USA, 1997.
|
| [13] |
何伟钢, 唐书恒, 谢晓东. 地应力对煤层渗透性的影响[J]. 辽宁工程技术大学学报(自然科学版), 2000, 19(14): 353-355. HE Weigang, TANG Shuheng, XIE Xiaodong. Effect of in-situ stress on coalbed permeability[J]. Journal of Liaoning Technical University (Natural Science), 2000, 19(14): 353-355. |
| [14] |
宗兆云. 基于模型驱动的叠前地震反演方法研究[D]. 山东青岛: 中国石油大学(华东), 2013. ZONG Zhaoyun.Methodologies of Model Driven Inversion with Pre-stack Seismic Data[D]. China University of Petroleum(East China), Qingdao, Shandong, 2013. |
| [15] |
印兴耀, 马妮, 马正乾, 等. 地应力预测技术的研究现状与进展[J]. 石油物探, 2018, 57(4): 488-504. YIN Xingyao, MA Ni, MA Zhengqian, et al. Review of in-situ stress prediction technology[J]. Geophysical Prospecting for Petroleum, 2018, 57(4): 488-504. |
| [16] |
马妮, 印兴耀, 孙成禹, 等. 基于正交各向异性介质理论的地应力地震预测方法[J]. 地球物理学报, 2017, 60(12): 4766-4775. MA Ni, YIN Xingyao, SUN Chengyu, et al. The in-situ stress seismic prediction method based on the theory of orthotropic anisotropic media[J]. Chinese Journal of Geophysics, 2017, 60(12): 4766-4775. DOI:10.6038/cjg20171218 |
| [17] |
马妮, 印兴耀, 孙成禹, 等. 基于方位地震数据的地应力反演方法[J]. 地球物理学报, 2018, 61(2): 697-706. MA Ni, YIN Xingyao, SUN Chengyu, et al. Inversion for crustal stress based on azimuthal seismic data[J]. Chinese Journal of Geophysics, 2018, 61(2): 697-706. |
| [18] |
张广智, 陈娇娇, 陈怀震, 等. 基于页岩岩石物理等效模型的地应力预测方法研究[J]. 地球物理学报, 2015, 58(6): 2112-2122. ZHANG Guangzhi, CHEN Jiaojiao, CHEN Huaizhen, et al. Prediction for in-situ formation stress of shale based on rock physics equivalent model[J]. Chinese Journal of Geophysics, 2015, 58(6): 2112-2122. |
| [19] |
Starr J.Closure stress gradient estimation of the Marcellus shale from seismic data[C]. SEG Technical Program Expanded Abstracts, 2011, 30: 1789-1793.
|
| [20] |
Hunt L, Reynolds S, Hadley S, et al. Causal fracture prediction:curvature, stress, and geomechanics[J]. The Leading Edge, 2011, 30(11): 1274-1286. DOI:10.1190/1.3663400 |
| [21] |
何英. 高精度曲率分析方法及其在构造识别中的应用[D]. 四川成都: 成都理工大学, 2011. HE Ying.High Precision Curvature Analysis and Its Application of Structural Identification[D]. Chengdu University of Technology, Chengdu, Sichuan, 2011. |
| [22] |
Murray G H. Quantitative fracture study:Spanish Pool, McKenzie County, North Dakota[J]. AAPG Bulletin, 1968, 52(1): 57-65. |
| [23] |
Price N J, Cosgrove J W. Analysis of Geological Structures[M]. Cam-bridge, UK: Cambridge University Press, 1990.
|
| [24] |
Bahorich M S, Farmer S L. 3-D seismic discontinuity for faults and stratigraphic features:the coherence cube[J]. The Leading Edge, 1995, 14(10): 1053-1058. DOI:10.1190/1.1437077 |
| [25] |
李军, 张军华, 刘杨, 等. 图像熵各向异性扩散保边滤波方法及在断层识别中的应用[J]. 石油地球物理勘探, 2019, 54(2): 365-370. LI Jun, ZHANG Junhua, LIU Yang, et al. Anisotropic diffusion edge-preserved filter based on image entropy and application in fault identification[J]. Oil Geophy-sical Prospecting, 2019, 54(2): 365-370. |
| [26] |
霍丽娜, 张建军, 郑良合, 等. 多属性断层解释技术在煤层气储层解释中的应用[J]. 石油地球物理勘探, 2014, 49(增刊1): 221-227. HUO Li'na, ZHANG Jianjun, ZHENG Lianghe, et al. Fault interpretation with multiple attributes in coalbed methane interpretation[J]. Oil Geophysical Prospec-ting, 2014, 49(S1): 221-227. |
| [27] |
闫文华, 陈宗翠, 马喜梅, 等. 煤层气地震解释技术应用及效果——以沁水盆地郑庄区块三维为例[J]. 石油地球物理勘探, 2012, 47(增刊1): 66-71. YAN Wenhua, CHEN Zongcui, MA Ximei, et al. 3D seismic interpretation of coalbed methane in Zheng-zhuang Block, Qinshui Basin[J]. Oil Geophysical Pro-specting, 2012, 47(S1): 66-71. |
| [28] |
汪关妹, 周赏, 张宏伟, 等. "两宽一高"地震资料的断层解释技术[J]. 石油地球物理勘探, 2017, 52(增刊1): 77-83. WANG Guanmei, ZHOU Shang, ZHANG Hongwei, et al. Fault interpretation on broadband, wide-azimuth, and high-density(BWH) 3D seismic data[J]. Oil Geophysical Prospecting, 2017, 52(S1): 77-83. |
| [29] |
孟阳, 许颖玉, 李静叶, 等. OVT域地震资料属性分析技术在断裂精细识别中的应用[J]. 石油地球物理勘探, 2018, 53(增刊2): 289-294. MENG Yang, XU Yingyu, LI Jingye, et al. Fault identification with OVT-domain seismic attribute analysis[J]. Oil Geophysical Prospecting, 2018, 53(S2): 289-294. |



 汪关妹, 河北省涿州市华阳东路东方地球物理公司科技园区研究院地质研究中心, 072750。Email:
汪关妹, 河北省涿州市华阳东路东方地球物理公司科技园区研究院地质研究中心, 072750。Email: