随着勘探程度的加深、难度的加大,对地震数据处理的保真要求也越来越高。受野外采集条件限制,往往得不到空间规则采样的理想数据。数据在空间上不规则的缺失会造成成像能量不均匀甚至产生偏移假象,严重影响处理的保真性,无法满足后续精细解释和储层预测等地质需求。因此,数据规则化成为地震数据精细化处理必不可少的一步。
地震数据规则化是将不规则采样数据映射到规则网格,不同方法的映射空间不同。Chemingui等[1]组合DMO+逆DMO得到方位校正公式,插值得到规则的共方位角数据。Fomel[2]提出炮检距空间的映射类方法,是在已知速度模型基础上通过偏移算法将数据在不同炮检距之间建立映射,以这种映射关系得到规则的数据体。唐亚勋等[3]利用PSTM+逆PSTM方法进行地震数据的炮检距映射,是对Fomel方法的优化。该类方法依赖于速度模型的精度,在地下构造复杂、横向变化剧烈的情况下,往往会出现构造假象。另外,由于偏移孔径有限,在近炮检距往往效果不佳。
基于Fourier变换的规则化方法是另一种主流算法,该类方法的基本思想是估计最佳Fourier系数,进而通过估计的Fourier变换系数重构出规则空间位置的数据。当数据是规则稀疏的情况时,通过离散Fourier变换可以填补空缺地震道,然而,如果数据呈不规则稀疏,则Fourier的基函数不再正交,就会出现谱能量泄漏到其他频率(即谱泄漏现象),会严重影响插值效果。
近年来,比较流行的基于Fourier变换的方法主要有:MWNI(Minimum Weighted Norm Interpolation)方法[4]以最小加权范数为泛函,以频谱形态作为约束条件进行迭代求取最优频谱,具有计算效率高,易于推广到高维的优点,但抗假频性能差;COMFI(Compact Fourier Interpolation)方法[5]将插值道作为附近道的加权求和的结果输出,权函数用关于Fourier基函数的最小均方误差函数求得,该方法重构的地震道也是基于Fourier正交基组合求得,在原理上是符合插值方法的正交性这一基本条件,缺点是抗噪性差,炮检距域或向量炮检距域插值无法返回到炮域,无法作为波动方程偏移的叠前数据。
Xu等[6-7]提出的ALFT(Antileakage Fourier Transform)法在某种意义上与POCS(Projections Onto Convex Sets)法[8-9]类似,都是运用迭代Fourier变换实现插值,且都是用阈值方法而去掉弱的Fourier系数得到最大的Fourier系数。ALFT法应用NDFT(Nonuniform Discrete Fourier Transform)得到不规则数据的频谱,并假设造成频谱泄漏的是频谱中能量最大的成分。针对这个假设,从频谱中选出那个最大能量的频谱成分,将它通过反NDFT转换到时间空间域,再从原始的不规则数据中将这部分减掉以更新输入数据。但是,受迭代次数的影响,在假频严重的情况下,方法会失效。
目前,地震数据插值方法正在向高维拓展,高效、高精度、抗噪、抗假频等已成为插值重建方法研究的大趋势[10-12]。五维匹配追踪Fourier插值(Matching Pursuit Fourier Interpolation,MPFI)算法在ALFT的基础上,加入了抗假频的权重项,在反假频的同时又不影响到原始数据的相对振幅关系,虽然插值效果仍受迭代次数的影响,但在合理的范围内可以达到保幅抗噪的目的,这一点正顺应了当前对叠前数据的要求而逐渐得到推广[13-18]。
1 匹配追踪Fourier变换插值方法基于Fourier变换的数据规则化方法需要解决三个问题:反谱泄漏问题、Fourier系数的估计问题以及反假频问题。
Xu等[7]提出利用采样密度函数计算加权系数,实现高维空间Fourier变换系数的估计,是MPFI方法的核心所在。对此,本文不再赘述,就谱泄漏和反假频问题做详细阐述。
1.1 谱泄漏问题的解决方案非规则采样数据在频率域会出现能量泄漏,这是由于非规则采样破坏了Fourier基函数的正交性和归一性[19],造成部分能量泄漏到其他波数。反泄漏Fourier插值方法正是通过重新将能量集中到极大值位置重构正交性。
对于一维非规则采样信号f(x)的反泄漏Fourier变换为
| $ F(k)=\frac{1}{\mathit{\Delta} X} \sum\limits_{l \in N_{\mathrm{p}}} \mathit{\Delta} x_{l} f\left(x_{l}\right) \exp \left(-2 \pi k x_{l}\right) $ | (1) |
其反变换为
| $ f^{k}\left(x_{l}\right)=F(k) \exp \left(2 \pi k x_{l}\right) $ | (2) |
式中:xl为采样点;
反泄漏Fourier变换插值公式为
| $ \begin{array}{c} f^{u}\left(x_{l}\right)=f\left(x_{l}\right)-f^{k}\left(x_{l}\right) \end{array} $ | (3) |
| $ f^{k}\left(x_{l}\right)=F_{\max }(k) \exp \left(2 \pi k x_{l}\right) $ | (4) |
式中Fmax(k)为最大波数对应的能量。将该成分通过反Fourier变换到空间域,在原始数据中减去该成分,反复提取Fourier系数中能量最大的成分,迭代直到满足反泄漏的要求,对所有最大能量成分反Fourier变换后,得到规则化空间采样的地震数据。
可以看出,该方法的基本思路是通过减少能量在各波数间的泄漏实现的。具体做法是,反复迭代离散Fourier正、反变换,通过每一轮迭代过程循环提取出每个频率的能量极大值重构出没有泄漏的Fourier系数;然后,根据估计出的离散规则Fourier变换插值到期望输出位置。在重构正交基的过程中逐渐达到将谱泄漏最小化的目的[6]。
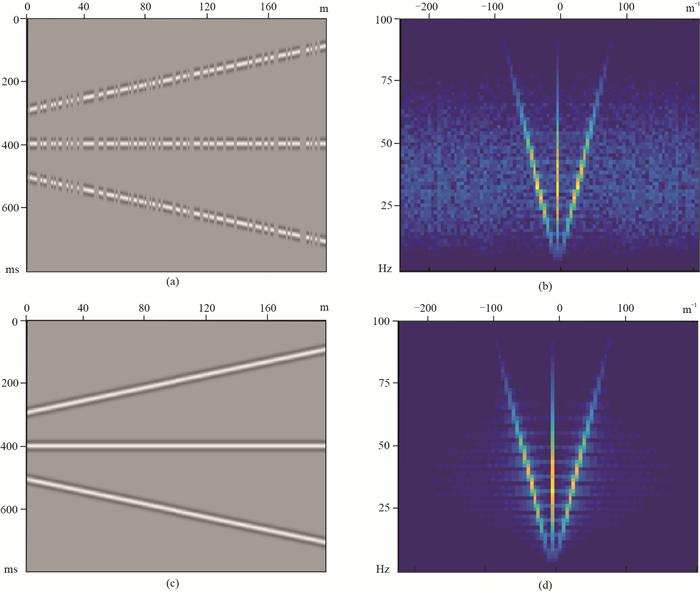
为了验证MPFI方法的插值效果,设计了简单的三个线性同相轴模型,图 1a是随机抽稀20%后的地震数据,从FK谱(图 1b)上可以看出能量泄漏到其他波数上,通过MPFI方法重构的地震道(图 1c),能够基本无泄漏地恢复缺失道,并且产生的噪声少,从FK谱上看,能量也重新集中在对应的三个分量上(图 1d)。
|
图 1 非规则采样的地震数据重构效果 (a)随机抽稀20%的原始数据;(b)图a数据的FK谱;(c)MPFI规则化后的数据;(d)图c数据的FK谱 |
改进的MPFI方法是在以上原始反泄漏Fourier插值算法的基础上,在选取最大能量的成分之前,对较高频率段的Fourier谱应用较小的权重,对真实信号应用较大的权值,实现反假频的目的,这也是改进MPFI区别于以往方法的优势所在。
改进的MPFI规则化方法具体实现步骤如下:
(1) 对数据进行离散Fourier变换;
(2) 对Fourier谱计算权重(先验值),并将权重应用在频谱的全频带上;
(3) 选取加权后最大能量的Fourier谱成分;
(4) 将该Fourier谱成分(未加权)加入“估算谱”上;
(5) 对该Fourier谱成分(未加权)进行反Fourier变换,并按照输入位置输出迭代结果;
(6) 从原始输入数据中减去该次迭代结果;
(7) 重复步骤(1)~步骤(6),直到达到设定迭代次数或者式(3)达到预设值;
(8) 对最终“估算谱”进行反Fourier变换,输出到期望位置。
值得注意的是,在步骤(4)中,将估计的Fourier谱成分返回到估算谱时,返回的是未加权的成分,这就保证在抗假频的同时,不影响到原始数据中数据的相对振幅关系,从而达到保真保幅的目的。
2 模型测试图 2a是Marmousi模型模拟数据随机缺失20%的道集,图 2b是对应的FK谱。由于地震数据缺失,频谱上表现为能量向其他波数分散、能量泄漏。通过改进的MPFI方法重构后的道集(图 2c)反射同相轴更连续,信噪比更高,频谱能量更集中,无频谱泄漏和假频的现象(图 2d),说明改进的MPFI是一种有效的保幅规则化方法。

|
图 2 Marmousi模型非规则采样数据的重构 (a)随机抽稀20%的原始数据;(b)图a数据的FK谱;(c)MPFI规则化后的数据;(d)图c数据的FK谱 |
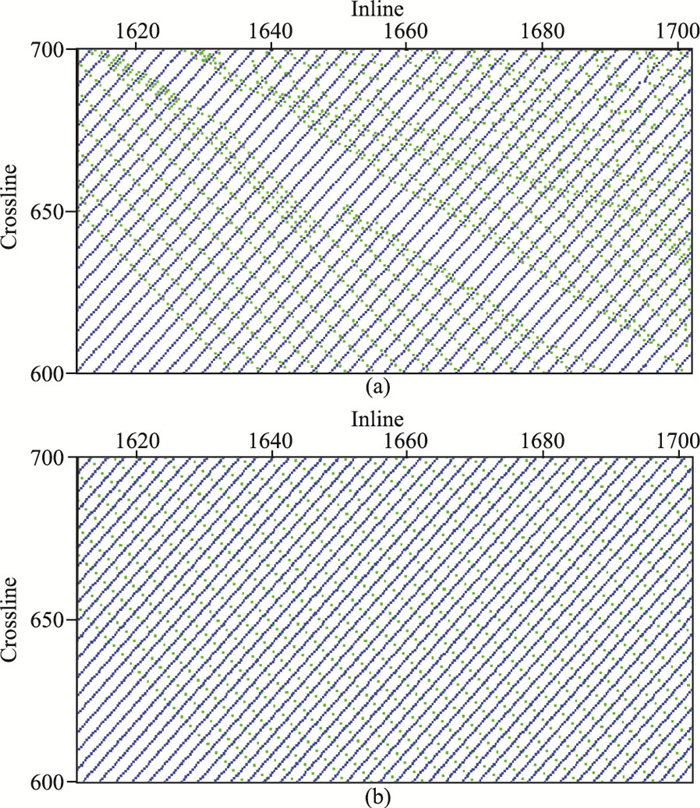
研究区位于柴达木盆地英雄岭南缘中部,处于柴达木盆地古近纪—新近纪沉积中心边缘,属于风险勘探领域。区内地形复杂,海拔2850~3640m,最大落差达800m,山大沟深、沟壑纵横、犬牙交错,多数断崖垂直落差达50~300m。中深层断裂发育,地层破碎,构造复杂,地震资料成像困难。区内有两块采集跨度为五年的三维数据。由于不同时期的采集方法不同,覆盖次数差异大,道集内能量不均衡,并且受研究区地表条件影响,出现沿着沟壑排布疏密不均的炮线现象(图 3a),不仅会造成面元有空洞,还会导致在沟壑附近数据信噪比极低,严重影响目的层的成像效果。为了落实油砂山构造带的构造特征,了解断裂发育及延伸规律,就必须通过规则化处理提高资料信噪比和成像精度。
|
图 3 规则化前(a)、后(b)的观测系统 绿色为炮线;蓝色为接收线 |
研究区内三维满覆盖面积为500km2,处理面元尺寸均为15m×30m。由图 3a可以看出,炮线极其不规则,导致目标区断裂成像模糊,影响构造落实和有关解释工作。本文的规则化处理是在炮检距域应用改进的MPFI实现五维插值。规则化处理后,重新定义了观测系统,输出为完全规则化的炮线和检波线(图 3b),面元更加均匀,空间采样也更加均匀。并且,由于数据利用了真实的坐标信息定义观测系统,数据可以反抽到炮域,不仅可在炮检距域,也可在炮域进行偏移,为后续处理提供了更加灵活的叠前数据。
3.2 应用效果分析图 4为研究区内典型低信噪比CMP道集规则化前、后的对比,在规则化前,道集信噪比极低,同相轴几乎只有在近炮检距附近隐约可见,有效信号难以辨别;通过改进的MPFI方法规则化处理后,信噪比明显得到提高,从近炮检距到远炮检距,振幅和相位特征都得到很好的恢复,同相轴连续性有明显改善,验证了该方法的抗噪性。

|
图 4 实际低信噪比数据规则化 前(a)、后(b)的CMP道集 |
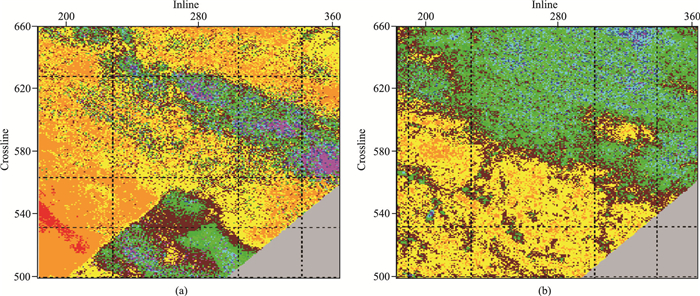
对规则化的道集进行叠加(图 5),提取T=2000ms的时间切片(图 6)、并提取T=1800~2200ms的振幅切片(图 7)等属性,规则化的优势不仅在于填补数据空缺、均匀覆盖次数,同时可以提高信噪比,这是由于MPFI方法有压制随机噪声的优势。规则化后,剖面振幅更均衡、一致性变好,构造形态及断裂刻画更清晰。证明该方法可以有效地解决由数据不规则缺失引起的振幅不均、道集能量差异大的问题。

|
图 5 规则化前(a)、后(b)的叠加剖面 |

|
图 6 规则化前(a)、后(b)T=2000ms的时间切片 |
|
图 7 规则化前(a)、后(b)T =1800~2200ms的均方根振幅属性切片 |
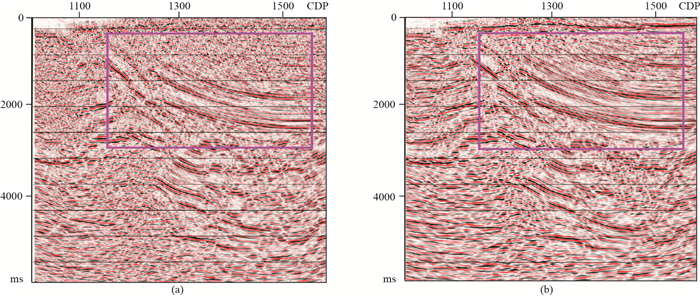
对比图 8的偏移成果可以看出,经过改进的MPFI方法进行规则化处理后,断裂构造主体,尤其是在红色方框内的中浅层构造区域,信噪比有很大提高,断裂破碎带突出,断点清晰,波组特征明显,中深层不同级次断裂、构造细节清楚,特别是小断裂的成像。因此提高了地震资料品质,构造主体形态得到了落实,有利于了解断裂展布规律,为后续储层预测和油藏评价奠定了基础。
|
图 8 规则化前(a)、后(b)偏移剖面 |
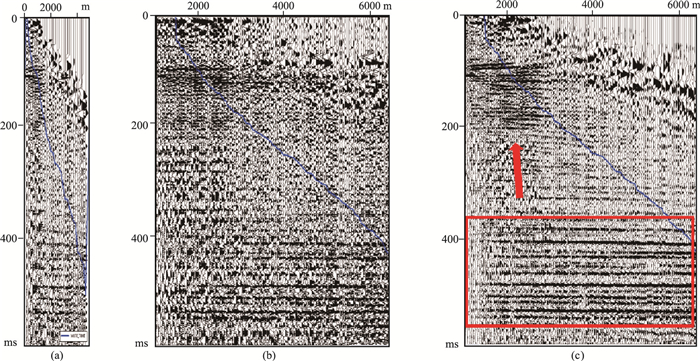
在研究区内选取严重缺失数据对比COMFI方法和MPFI方法的插值效果(图 9)。由图 9可以看出,经两种方法插值后,炮检距均得到了大幅展宽,但COMFI方法插值结果近炮检距噪声严重、远炮检距振幅不均匀,而MPFI方法在红色方框内及浅层区域,由于对随机噪声有压制的优点,可以明显提高地震数据的信噪比,使能量一致性更好,说明MPFI方法能更好地解决数据缺失严重和振幅不均匀性问题,并具有更强的抗噪能力。
|
图 9 COMFI与MPFI规则化后的道集 (a)插值前;(b)COMFI插值后;(c)MPFI插值后(蓝色曲线是切除线) |
通过对改进的MPFI方法的理论分析以及在柴达木盆地英雄岭低信噪比资料的实际应用,可以得出以下结论:
(1) 改进后的MPFI规则化方法在常规反泄漏Fourier插值方法的基础上,引入Fourier谱中低频部分作为权重,既有效防止了频谱泄漏,又有效消除了在高频端出现假频的现象,同时具有压制随机噪声的优点;
(2) 改进的MPFI规则化方法处理后的剖面能量一致性及信噪比都得到了大幅提高,为落实油砂山构造带的构造特征、了解断裂发育及延伸规律提供了资料基础。
| [1] |
Chemingui N, and Biondi B. Data regularization by inversion to common offset (ICO)[C]. SEG Technical Program Expanded Abstracts, 1999, 18: 1398-1401.
|
| [2] |
Fomel S. Seismic data interpolation with the offset continuation equation[R]. Stanford Exploration Pro-ject Report, 2000, 125-141.
|
| [3] |
唐亚勋, 王华忠, 王成礼. 最佳速度叠加与地震道插值[C]. 中国地球物理学会第十九届年会论文集, 2003, 458-458. TANG Yaxun, WANG Huazhong, WANG Chengli. Opti-mal velocity stack and seismic trace interpolation[C]. Proceedings of the 19th Annual Conference of the Chinese Geophysical Society, 2003, 458-458. |
| [4] |
Liu B, Sacchi M D. Minimum weighted norm interpolation of seismic records[J]. Geophysics, 2004, 69(6): 1560-1568. DOI:10.1190/1.1836829 |
| [5] |
Moor I, and Ferber R. Bandwidth optimization for compact Fourier interpolation[C]. Extended Abstra-cts of 70th EAGE Conference and Exhibition, 2008, G026.
|
| [6] |
Xu S, Zhang Y, Pham D, et al. Anti-leakage Fourier trans-form for seismic data regularization[J]. Geophysics, 2005, 70(4): V87-V95. DOI:10.1190/1.1993713 |
| [7] |
Xu S, Zhang Y, Lambaré G. Antileakage Fourier transform for seismic data regularization in higher dimensions[J]. Geophysics, 2010, 75(6): WB113-WB120. DOI:10.1190/1.3507248 |
| [8] |
Gao J J. Irregular seismic data reconstruction based on exponential threshold model of POCS method[J]. Applied Geophysics, 2010, 7(3): 229-238. DOI:10.1007/s11770-010-0246-5 |
| [9] |
陈小春, 陈辉, 喻勤, 等. 反假频POCS数据规则化及其在偏移成像中的应用[J]. 石油地球物理勘探, 2017, 52(1): 13-19. CHEN Xiaochun, CHEN Hui, YU Qin, et al. Seismic data interpolation with anti-aliasing POCS method and its application in seismic migration imaging[J]. Oil Geophysical Prospecting, 2017, 52(1): 13-19. |
| [10] |
Trad D. Five-dimensional interpolation: Recovering from acquisition constraints[J]. Geophysics, 2009, 74(6): V123-V132. DOI:10.1190/1.3245216 |
| [11] |
Poole G, Herrmann P. Multi-dimensional data regu-larization for modern acquisition geometries[C]. SEG Technical Program Expanded Abstracts, 2007, 26: 2585-2589.
|
| [12] |
王伟, 陈双廷, 王宝彬, 等. 五维规则化技术研究与应用[J]. 石油地球物理勘探, 2017, 52(增刊1): 28-33. WANG Wei, CHEN Shuangting, WANG Baobin, et al. Application of 5D regularization in seismic data pro-cessing[J]. Oil Geophysical Prospecting, 2017, 52(S1): 28-33. |
| [13] |
段文胜, 裴家定, 李飞, 等. OVT域内插炮检线压制采集脚印[J]. 石油地球物理勘探, 2016, 51(1): 40-48. DUAN Wensheng, PEI Jiading, LI Fei, et al. Acquisi-tion footprints supersession with source and receiver line interpolation in the OVT domain[J]. Oil Geo-physical Prospecting, 2016, 51(1): 40-48. |
| [14] |
段文胜, 王鹏, 党青宁, 等. 应用匹配追踪傅里叶插值技术实现OVT域连片处理[J]. 石油地球物理勘探, 2017, 52(4): 669-677. DUAN Wensheng, WANG Peng, DANG Qingning, et al. 5D data regularization based on matching pursuit Fourier interpolation for the OVT domain data merging processing[J]. Oil Geophysical Prospecting, 2017, 52(4): 669-677. |
| [15] |
Nguyen T, Winnett R. Seismic interpolation by opti-mally matched Fourier components[C]. SEG Tech-nical Program Expanded Abstracts, 2011, 30: 3085-3089.
|
| [16] |
徐兴荣, 苏勤, 王劲松, 等. 加权MPFI方法及其在三维连片处理中的应用[J]. 岩性油气藏, 2019, 31(1): 122-129. XU Xingrong, SU Qin, WANG Jinsong, et al. Weigh-ted MPFI method and its application in 3D joint processing[J]. Lithologic Reservoirs, 2019, 31(1): 122-129. |
| [17] |
王霞, 李丰, 张延庆, 等. 五维地震数据规则化及其在裂缝表征中的应用[J]. 石油地球物理勘探, 2019, 54(4): 844-852. WANG Xia, LI Feng, ZHANG Yanqing, et al. 5D seis-mic data regularization and application in fracture characterization[J]. Oil Geophysical Prospecting, 2019, 54(4): 844-852. |
| [18] |
吴丹, 龚仁彬, 王从镔, 等. 最小二乘叠前时间偏移在地震数据规则化中的应用[J]. 石油地球物理勘探, 2019, 54(1): 36-44. WU Dan, GONG Renbin, WANG Congbin, et al. Seismic data regularization via least-squares prestack time mi-gration[J]. Oil Geophysical Prospecting, 2019, 54(1): 36-44. |
| [19] |
Shannon C E. Communication in the presence of noise[J]. Proceedings of the IRE, 1949, 37(1): 10-21. |



 凌越, 甘肃省兰州市城关区雁儿湾路535号中国石油勘探开发研究院西北分院数据处理研究所, 730022。Email:
凌越, 甘肃省兰州市城关区雁儿湾路535号中国石油勘探开发研究院西北分院数据处理研究所, 730022。Email: